Statistical Arbitrage Through Mean Reversion in Pairs Trading: Beating the Market by Math
2 016
11
Introduction
“I can calculate the motions of heavenly bodies but not the madness of people.” (Sir Isaac Newton, in his nineties, after losing almost all his retirement savings by investing in stock markets.)
On May 10th, last year, the world lost Jim Simons, the most successful hedge fund manager of all time.
Jim Simons was a recognized mathematician, with several accolades and academic achievements in differential geometry and cryptography. However, his role in quantitative financial analysis made his name famous even among people not interested in math or finance.
He was the subject of several biographies, dozens of books about his life and career, hundreds of TV shows, and thousands of articles and blog posts around the world. The Man Who Solved the Market: How Jim Simons Launched the Quant Revolution is his most famous biography.
In the early eighties, Simons founded Renaissance Technologies (RenTech) and started gathering a team of highly skilled “mathematicians, physicists, signal processing experts, and statisticians”. Working together for decades, they proved that with enough data and computational power to find statistical patterns and anomalies in those patterns, the market could be “beaten by math”.
“In 1988, the firm established its most profitable portfolio, the Medallion Fund, which used an improved and expanded form of Leonard Baum's mathematical models, improved by algebraist James Ax, to explore correlations from which it could profit.” (Wikipedia)
The Medallion Fund returned 66% on average return per year between 1988 and 2018 making more than 104 billion dollars in trading profits in these three decades. The RenTech’s Medallion Fund is still active today making lots of money. As you may expect, many people would like to know how they operate, the details, the secret algorithm, the cheat code… you name it. But, as far as any mortal human knows, their secret sauce is preserved as a top-secret corporate agreement. When asked about the Medallion operational strategy by the author of his biography, Simons answered with the same laconic answer he would give several interviewers in the forthcoming years: portfolio-level statistical arbitrage. He also revealed that they have been using “a kind of machine learning” since the beginning to find the market anomalies.
Statistical arbitrage is, per se, a large research field. When we add machine learning to it, the average retail trader without a strong background in mathematics and statistics is left out. Let alone the novice trader. But, if it is true that it is really hard and a lot of resources are required to implement a fully-featured machine learning-powered portfolio-level statistical arbitrage without all that knowledge, it is also true that it is perfectly possible to understand what portfolio-level statistical arbitrage is, how it works, and more important: it is possible to start small with patience, hard work and time to grow up.
This article is by no means an attempt to reproduce, or worse, “to reveal the secret code” of RenTech/Jim Simons. As said above, that would be impossible for anyone not directly involved in their operations. It is an effort to share with you my understanding of the general principles that power their models. These principles can inform the trading system of even the most humble retail trader. The difference will be in the scale of the results, which will be proportional to the amount of resources invested in the system and operations.
So, what you will read below is the result of research in books, video documentaries, and specialized internet communities, merged with my personal experience of a few years in the finance segment (more on the business side than on the developer side). What RenTech runs is huge, but what we will see here is a miniature, let’s say, an action figure of a superhero, a scale model of a skyscraper.
The goal is to contribute with a low-cost, lightweight, and easy-to-develop method of analysis that can be tested and improved by the average retail trader using only the tools already available in the MetaTrader 5 platform running on a commodity consumer notebook, possibly a low-end notebook. The method should be useful to the algorithmic trader, and to the discretionary trader as well. We will start with the most straightforward setup, just enough to describe the process.
After understanding the general concepts behind the model, we will build a minimal portfolio for the most simple form of statistical arbitrage, trade it in automated mode with an Expert Advisor, take some notes about the results, and finally think about the required next steps. I hope that this experience can help you to get started with this powerful trading technique and to be able to expand this knowledge later, bringing other symbols to the portfolio and testing other algorithms beyond the one described here, to progressively build your own full-featured StatArb strategy adequate to your resources and objectives.
General concepts behind the model
Before creating RenTech, Jim Simons worked as a codebreaker for US Intelligence during the Cold War. When he started trading financial markets, he tried to predict stocks and commodities prices and failed. Then he changed his approach. He assumed that he would never be able to anticipate the future of the market. He understood that he had to accept that the market was an enigma. This is the first relevant concept behind the model.
The other concept is that the market is in a continuous state of change. That is, there is no such thing as a bullish or bearish market, candle/bar patterns, or “correlated stocks that play well together”. Everything is changing now and forever.
If you think for a second, you will see that both concepts are overlooked.
The market is an enigmaThe market is an enigma, but unlike that World War II Enigma machine whose code was broken by Alan Turing and his team, the market enigma doesn’t have a deterministic algorithm to be reverse-engineered and broken. Between the input and the output unexpected events may happen. While the rise of the interest rates by a central bank has the expected effect of making the currency of that country stronger, the eruption of a political conflict in another distant country may have the contrary effect, counter-balancing the interest rate rise by diminishing its impact, voiding it, or even making that currency weaker.
The market is an enigma because, between the input and the output, there is the irrationality of the economic agents, the unforeseeable nature of the politics, and the chaotic aspect of the interaction between the forces that drive it. Between the one-year-long bullish gold market and its next week one-month nosedive, there is human behavior. It was for no other reason that a psychologist, Daniel Kahneman, was awarded a Nobel Prize in Economic Sciences. Because he addresses this question precisely.Even though the market is an enigma ruled by irrational economic agents inside a chaotic environment, investment banks buy and sell stocks based on financial models, hedge funds use Black-Scholes to evaluate options and almost all the biggest market players spend millions of dollars in the development of quant trading strategies. Why? Because it works, of course. Why does it work if the market is unforeseeable, unpredictable, irrational, and chaotic?
Jim Simons, along with thousands of other successful quant, algo, and discretionary traders, has the most candid answer to this question. A lesson that any wannabe trader should recite as a mantra every morning before entering the market:
But with or without the use of financial models, any trading strategy may work pretty well for some time, an unknown amount of time. It may be profitable for a day, for a month, a year…, we don’t know. The only guarantee is that it worked in the past and was profitable on those symbols, period, and timeframe, with those parameter values used in the backtest. It may stop being profitable in the next minute, in the first run, or it may work forever. Again, we don’t know. We cannot know, because the market is an enigma. We cannot solve this enigma. There is no code to be broken. There is only a continuous state of change.
The market is in a continuous state of change
The market is changing all the time. The only constant in the market is change. The values of our parameters are chosen not because they are the best fit for a specific market state, but because they were the best fit for a specific market change. Between the moment when we placed a winning order and the moment that the order was closed, the market changed the way we were expecting. Conversely, between the moment when we placed a losing order and the moment that the order was closed, the market changed in a way we were not expecting. This is true even if we are not able to tell what change contributed the most to the final result.
To be clear: we will never be able to pinpoint the precise change that turned a profitable strategy into a money dragger or vice-versa. To improve a trading strategy, what we will be doing is to search for a pattern to increase the probabilities of repeating the right choices when we face similar changes in the market state in the future. Finding, learning, and understanding these patterns is what a seasoned trader does in months or years of trading the same asset or group of assets. It is for no other reason that we have trading diaries. It is to register what were our assumptions about the expected market changes and to be able to review them later to improve our assumptions.
Thanks to the large volume of data available nowadays and powerful computers to process this data, we can shorten these learning years of finding the patterns to hours or even minutes. We can automate the data gathering, the analysis, and the trade execution. We can automate the testing and reporting. We can even automate the choice of the symbol/asset to be traded and the strategy to be used by training a comprehensive machine learning model to learn those patterns. With an adequate amount of resources in money, qualified people, and time, yes, we can.
But, as said above, the focus of these notes is the average retail trader. With these two simple but overlooked principles in mind, let’s see how we can start understanding what StatArb is and how it works.
Building the portfolio
Because the market is an enigma in a continuous state of change, we will build our portfolio with no preconceptions, we will make no assumptions about what we suppose is true, and we will update it regularly. The updating interval will be determined by the trading strategy and limited by the computational power.
We must take into account that portfolio building, or portfolio management, is a large research field per se. According to a comprehensive academic literature review, ten years ago there were at least four main approaches to building a pairs trading statistical arbitrage portfolio: distance, cointegration, time series, and stochastic control. Besides these four main approaches, the author also identified other approaches which include machine learning, combined forecasts, copula, and Principal Component Analysis.
To preserve our focus on being simple and foundational, let’s start with a simple pairs trading portfolio. To some authors, pairs trading is a subset of statistical arbitrage, to others “pairs-trading is widely assumed to be the “ancestor” of statistical arbitrage” , the difference being the portfolio size and the statistical algorithms complexity. As its name implies, pairs trading is limited to two securities while statistical arbitrage may involve dozens, even hundreds of symbols to be tracked and eventually traded.
Pairs trading, as you probably already know, is nothing more than, giving two securities with correlated or cointegrated historical prices, simultaneously selling the trending-up security and buying the trending-down security when the historical spread between their prices widens beyond a chosen threshold. The underlying assumption is that the prices will “return to the mean”, converging around the historical price spread.
In a fully-featured statistical arbitrage, we are not limited to correlation or cointegration between prices. Since our primary goal in this article is to simplify the complexities of statistical arbitrage to the average retail trader, we will start collecting historical data to build a minimal pairs-trading portfolio for the forex market. Later you may expand to other markets and other statistical relationships beyond price correlation.
Choose a group of securities to start withAt the time of writing, my MetaTrader 5 terminal account reports more than ten thousand symbols available. We will be using the Python integration for Metatrader 5 in our analysis.
print("Total symbols =",mt5.symbols_total()) # display all symbols Total symbols = 10563So, for practical reasons, first, we need to choose a subset of all available symbols. Let’s start with XAU pairs.
# get symbols containing XAU in their names xau_symbols=mt5.symbols_get("*XAU*") print('len(*XAU*): ', len(xau_symbols)) for s in xau_symbols: print(s.name) len(*XAU*): 6 XAUUSD XAUEUR XAUAUD * XAUG XAUCHF XAUGBP
* XAUG is an ETF, so we can exclude it for now and focus on the other five pairs. Let’s see how they each correlate with the XAUUSD.
Now we need to calculate their historical price correlation. In a real scenario we might want to explore all possible permutations among the chosen symbols, possibly hundreds of stock symbols, because we are assuming no knowledge about them. But here we’ll filter them out to see only the price correlation between the quotation of gold in US dollars (XAUUSD) and the quotation of gold in Euros, Australian Dollars, Swiss Francs, and British Sterling Pounds.We want data for one-year daily closing prices from the current day, which is approximately 250 trading days for forex markets.
# get 250 D1 bars from the current day xauusd_rates = mt5.copy_rates_from_pos("XAUUSD", mt5.TIMEFRAME_D1, 0, 250) xaueur_rates = mt5.copy_rates_from_pos("XAUEUR", mt5.TIMEFRAME_D1, 0, 250) xauaud_rates = mt5.copy_rates_from_pos("XAUAUD", mt5.TIMEFRAME_D1, 0, 250) xauchf_rates = mt5.copy_rates_from_pos("XAUCHF", mt5.TIMEFRAME_D1, 0, 250) xaugbp_rates = mt5.copy_rates_from_pos("XAUGBP", mt5.TIMEFRAME_D1, 0, 250) (...) # calculate correlation coefficients import numpy as np usd_eur_corr = np.corrcoef(xauusd_close['close'], xaueur_close['close']) usd_aud_corr = np.corrcoef(xauusd_close['close'], xauaud_close['close']) usd_chf_corr = np.corrcoef(xauusd_close['close'], xauchf_close['close']) usd_gbp_corr = np.corrcoef(xauusd_close['close'], xaugbp_close['close'])
This will give us the following results:
| XAUUSD correlation (Pearson) | |
|---|---|
| XAUEUR | 0.9692368 |
| XAUAUD | 0.96677962 |
| XAUCHF | 0.8418827 |
| XAUGBP | 0.90490282 |
Table 1 - daily closing price correlation of gold in US dollars (XAUUSD) and gold in Euros, Australian Dollars, Swiss Francs, and the British Sterling Pounds between 2024-04-09 and 2025-03-26.
We can assert visually what a near 0.97 price correlation looks like in the graph below.
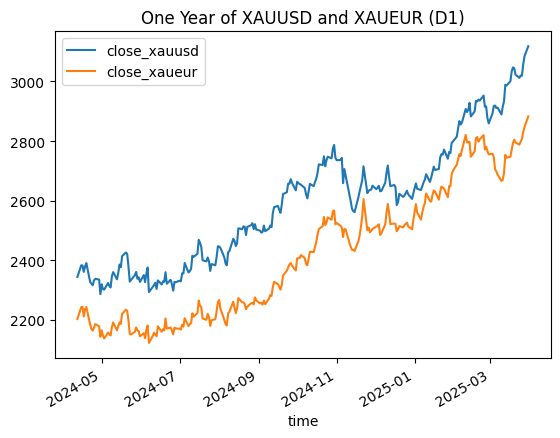
Fig 1 - One year of daily closing prices of gold quoted in US Dollars and Euros
Note that the graph above may be misleading. We may be tempted to “trade the spread” between the pairs, but it is not the real spread, if any. Let’s convert the XAUEUR to US dollars according to the exchange rate of the day.adjusted_for_dollars = pd.concat([xauusd_close, xaueur_close['close'], eurusd_close['close']], join='inner', axis=1) adjusted_for_dollars.columns = ['time', 'xauusd', 'xaueur', 'eurusd'] adjusted_for_dollars['xaueur_dollars'] = adjusted_for_dollars['xaueur'] * adjusted_for_dollars['eurusd'] adjusted_for_dollars['diff'] = abs(adjusted_for_dollars['xauusd'] - adjusted_for_dollars['xaueur_dollars']) print(adjusted_for_dollars) time xauusd xaueur eurusd xaueur_dollars diff 0 2024-04-12 2344.22 2202.92 1.06237 2340.316120 3.903880 1 2024-04-15 2383.10 2242.90 1.06181 2381.533649 1.566351 2 2024-04-16 2382.85 2243.81 1.06720 2394.594032 11.744032 3 2024-04-17 2361.16 2212.14 1.06425 2354.269995 6.890005 4 2024-04-18 2378.86 2234.79 1.06557 2381.325180 2.465180 .. ... ... ... ... ... ... 245 2025-03-25 3019.81 2797.81 1.07918 3019.340596 0.469404 246 2025-03-26 3018.85 2807.50 1.07370 3014.412750 4.437250 247 2025-03-27 3056.42 2829.26 1.07975 3054.893485 1.526515 248 2025-03-28 3084.20 2847.12 1.08276 3082.747651 1.452349 249 2025-03-31 3118.19 2882.78 1.08152 3117.784226 0.405774 [250 rows x 6 columns]
adjusted_for_dollars.plot(title = 'One Year of XAUUSD and XAUEUR in US Dollars (D1)', x='time', y=['xauusd', 'xaueur_dollars']) plt.show()
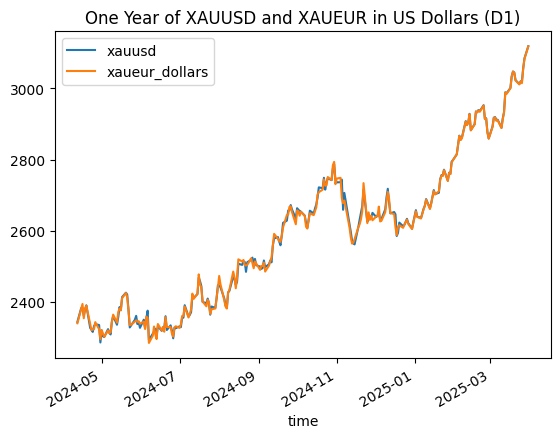
Fig 2 - One year of daily closing prices of gold quoted in US Dollars and Euros adjusted for US Dollars
By looking at the difference between the gold quotation in USD and the gold quotation in Euros…
print("median: ", adjusted_for_dollars['diff'].median()) adjusted_for_dollars['diff'].describe() median: 4.052404150000029 count 250.000000 mean 5.894673 std 6.238511 min 0.050646 25% 1.279615 50% 4.052404 75% 8.587763 max 51.483719 median: 4.052404150000029
… we’ll note that the real mean spread in this one-year period was ~5.9 dollars with a standard deviation of ~6.2 dollars. If we oversimplify and assume that the difference (spread) between both quotations after the conversion by the current exchange rate should be near zero, we may consider any spread above the mean as a tradable anomaly in the market.
Choose the statistical relationship to look for
Then we choose to start building our statistical arbitrage portfolio based on the high correlation we found between XAUUSD and XAUEUR in the last trading year (~250 days). But, is price correlation the right, or even the better statistical relationship to look for when building a stat arb portfolio?
When we talk about correlation in historical prices we are subject to be misguided by some differences between the popular use of the term and its proper statistical meaning. This fact is yet more evident in the forex community. A simple search for “forex correlated pairs” will point us to many resources listing the most/least correlated pairs along with tips on how to trade them. It is not our goal here to say that this or that resource, listing, or trading tip is right or wrong. What we must keep in mind is that we are setting up the foundations for a portfolio-level statistical arbitrage that is meant to not be limited to forex pairs. Instead, our system must generalize to any asset class, in any market, and timeframe, subject only to the requirements of being market-neutral and testable.
According to statisticians, the Pearson correlation coefficient function is expected to be used on stationary series and a price time series is not stationary. By calculating the correlation in a non-stationary time series we may get what they call “spurious correlations”.
“Non-stationary data, as a rule, are unpredictable and cannot be modeled or forecasted. The results obtained by using non-stationary time series may be spurious in that they may indicate a relationship between two variables where one does not exist. To receive consistent, reliable results, the non-stationary data needs to be transformed into stationary data.” (Nason, G. P. (2006). Stationary and non-stationary time series. Investopedia)
Then, as the trader looking to build a statistical arbitrage portfolio, we have to make a decision: is that “spurious correlation” enough, or do we need a proper correlation in the statistical sense? For now, we are accepting the first, not perfect measure as enough for our simplified model. But we must not forget that correlated pairs may go on widening the spread for long periods while rising or falling together, that is, they may not return to the mean for long periods, and yet the statistical correlation still applies. This condition is exceptional when dealing with currencies, but very common when dealing with commodities, futures or stock price time series. So, stop-loss levels and position timing is mandatory when dealing with “expected return to the mean” strategies.
Choose the statistical measure to be the trading triggerWhy choose mean or median as a measure of our historical spread? According to statisticians, we should use the mean when our data has few outliers and the median when the dataset has extreme peaks because the median is less affected by these peaks. For example, if you want to filter out the large spread caused by high-impact news, you may choose the median. Conversely, if you want to take into account these high-impact news effects on the spread, you might want to choose the mean.
So, there is no “recipe”. You must decide by yourself based on your data and good judgment. You might even choose not to use either the mean or the median. Instead, you may investigate and decide that another relationship is better for your use case.
I’ll go with the mean and set a parameter for our trading strategy based on the widening of the mean spread. Let’s say when the spread between XAUUSD and XAUEUR widens by more than 50% of the mean, we trigger the trade, buying the symbol that is losing the race and simultaneously selling the symbol that is rising faster.
How can we determine which symbol is rising and which symbol is falling? For our specific case here, since we are assuming that both gold quotes should be the same after conversion, we can simply get the symbol with the bigger price as the rising pair and the other as the falling pair. If we were dealing with the spread of stock prices returning to the mean, we could use an exponential moving average with a very short period and assume that the symbol that is trading above the EMA is rising and vice-versa.
bool IsRising(const int symbol) { switch(symbol) { case BASE_PAIR: //Print("Base pair is rising? ", quotes_base[0] > ema_base[0]); return quotes_base[0] > ema_base[0]; case CORR_PAIR: //Print("Corr pair is rising? ", quotes_corr[0] > ema_corr[0]); return quotes_corr[0] > ema_corr[0]; default: return false; } } bool IsFalling(const int symbol) { switch(symbol) { case BASE_PAIR: //Print("Base pair is falling? ", quotes_base[0] < ema_base[0]); return quotes_base[0] < ema_base[0]; case CORR_PAIR: //Print("Corr pair is falling? ", quotes_corr[0] < ema_corr[0]); return quotes_corr[0] < ema_corr[0]; default: return false; } }Or we can use the slope.
void CalculateSlopes(double & slope_b[], double & slope_c[]) { slope_b[0] = MathAbs((quotes_base[0] - quotes_base[SlopePeriod]) / SlopePeriod); slope_c[0] = MathAbs((quotes_corr[0] - quotes_corr[SlopePeriod]) / SlopePeriod); }In our case, we are simply using the symbol with the highest price.
if(quotes_base[0] > quotes_corr[0])
Trading the portfolio
We’ve built a simple EA to test our hypothesis in a backtest.
We get the initial quotes at OnInit() and update them in OnTimer(). That’s because we cannot rely on the OnTick event handler to update the quotes of the pair which is not that of the current working chart, since OnTick() is called only for the current symbol/chart. See multi-currency or multi-symbol Expert Advisors.
int OnInit() { ArrayResize(quotes_base, CountQuotes); ArrayResize(quotes_corr, CountQuotes); ArrayResize(quotes_conv, CountQuotes); //--- Get start quotes for both pairs GetQuotes(); //--- EMA indicators EMA_Handle_Base = iMA(BasePair, _Period, EMAPeriod, 0, MODE_EMA, PRICE_CLOSE); EMA_Handle_Corr = iMA(CorrPair, _Period, EMAPeriod, 0, MODE_EMA, PRICE_CLOSE); if(EMA_Handle_Base == INVALID_HANDLE || EMA_Handle_Corr == INVALID_HANDLE) { printf(__FUNCTION__ + ": EMA initialization failed"); return(INIT_FAILED); } //--- create timer EventSetTimer(5); // seconds //--- return(INIT_SUCCEEDED); } bool GetQuotes() { if(CopyClose(BasePair, _Period, 0, CountQuotes, quotes_base) != CountQuotes) { Print(__FUNCTION__ + ": CopyClose failed. No data"); //printf("Size quotes base pair %i ", ArraySize(quotes_base)); return false; } if(CopyClose(CorrPair, _Period, 0, CountQuotes, quotes_corr) != CountQuotes) { Print(__FUNCTION__ + ": CopyClose failed. No data"); //printf("Size quotes corr pair %i ", ArraySize(quotes_corr)); return false; } if(CheckMode == PRICE) { if(CopyClose(ConvPair, _Period, 0, CountQuotes, quotes_conv) != CountQuotes) { Print(__FUNCTION__ + ": CopyClose failed. No data"); //printf("Size quotes conv pair %i ", ArraySize(quotes_conv)); return false; } //--- for(int i = 0; i < CountQuotes; i++) { quotes_corr[i] *= quotes_conv[i]; } } return true; } void OnTimer() { UpdateQuotes(); CalculateMeanSpread(); if(CheckMode == EMA) { GetEMAs(); } } void UpdateQuotes() { ArrayRemove(quotes_base, ArraySize(quotes_base) - 1); double new_quote_base[1]; CopyClose(BasePair, _Period, 0, 1, new_quote_base); ArrayInsert(quotes_base, new_quote_base, 0, 0); //--- ArrayRemove(quotes_corr, ArraySize(quotes_corr) - 1); double new_quote_corr[1]; CopyClose(CorrPair, _Period, 0, 1, new_quote_corr); ArrayInsert(quotes_corr, new_quote_corr, 0, 0); //--- if(CheckMode == PRICE) { ArrayRemove(quotes_conv, ArraySize(quotes_conv) - 1); double new_quote_conv[1]; CopyClose(ConvPair, _Period, 0, 1, new_quote_conv); ArrayInsert(quotes_conv, new_quote_conv, 0, 0); quotes_corr[0] *= quotes_conv[0]; } }
Calculate the mean spread
bool CalculateMeanSpread() { int sz_base_p = ArraySize(quotes_base); int sz_corr_p = ArraySize(quotes_corr); int sz_conv_p = ArraySize(quotes_conv); if(sz_base_p != sz_corr_p || sz_corr_p != sz_conv_p) { Print(__FUNCTION__ + " Failed: Arrays must be of same size"); return false; } //--- ArrayResize(pairs_spread, CountQuotes); for(int i = 0; i < sz_base_p; i++) { pairs_spread[i] = MathAbs(quotes_base[i] - quotes_corr[i]); } double max_spread = pairs_spread[ArrayMaximum(pairs_spread)]; double min_spread = pairs_spread[ArrayMinimum(pairs_spread)]; mean_spread = MathMean(pairs_spread); //--- //printf("Last quote XAUUSD %f ", quotes_base[0]); //printf("Last quote XAUEUR %f ", quotes_corr[0]); //printf("Last spread %f ", pairs_spread[0]); //printf("Max spread %f ", max_spread); //printf("Min spread %f ", min_spread); //printf("Mean spread %f ", mean_spread); return true; }
We check for trading signals on OnTick.
void OnTick() { //--- CheckForClose(); CheckForOpen(); }
when the spread is greater than the mean by at least the percentage we have set
bool HasSpreadTrigger() { double trigger_spread = mean_spread + (mean_spread * (PercentTrigger / 100.0)); //printf(" trigger spread %f ", trigger_spread); double current_spread = pairs_spread[0]; //printf(" current spread %f ", current_spread); return current_spread >= trigger_spread; }
We buy the symbol that is priced low and sell the symbol that is priced high. In our example this switch is performed on the CheckMode enumeration (enum).
void CheckForOpen()
{
if(PositionsTotal() == 0 && HasSpreadTrigger())
{
switch(CheckMode)
{
case EMA:
if(IsRising(BASE_PAIR) && IsFalling(CORR_PAIR))
{
OpenShort(BasePair);
OpenLong(CorrPair);
}
if(IsFalling(BASE_PAIR) && IsRising(CORR_PAIR))
{
OpenLong(BasePair);
OpenShort(CorrPair);
}
break;
case SLOPE:
CalculateSlopes(slope_base, slope_corr);
if(slope_base[0] > slope_corr[0])
{
OpenShort(BasePair);
OpenLong(CorrPair);
}
else
{
OpenLong(BasePair);
OpenShort(CorrPair);
}
break;
case PRICE:
if(quotes_base[0] > quotes_corr[0])
{
OpenShort(BasePair);
OpenLong(CorrPair);
}
else
{
OpenLong(BasePair);
OpenShort(CorrPair);
}
}
}
}
Positions will be closed by stop-loss/take-profit or by mean reversion on CheckForClose().
void CheckForClose() { int total = PositionsTotal(); ulong ticket = 0; if(total > 0) { if(PositionSelect(BasePair) || PositionSelect(CorrPair)) { for(int i = 0; i < total; i++) { ticket = PositionGetTicket(i); if(ticket == 0) continue; if(pairs_spread[0] <= mean_spread) { ExtTrade.PositionClose(ticket); } } } } }
The backtest confirms that the mean reversion strategy is viable for pairs trading.
Fig 3. Backtest equity graph
Although the backtest validates our hypothesis, you can see that this specific algorithm requires improvements to smooth the capital curve. Maybe a dynamic order size (the trading volume here is fixed in the minimum 0.01 - micro lot) and optimizations for the stop-loss/take-profit ratio. But profitability is not our main concern here in this article. That said, let’s take a look at some interesting results that - according to some authors - seem to be common in statistical arbitrage operations.
Fig 4. Backtest results
There are a great number of trades, the ratio between wins and losses is small (~55/~45), and the maximum balance drawdown is relatively low.
Fig 5. Backtest trading times
The concentration around specific periods (hours, days of week etc.). In our case, the concentration is around the opening of the USA session, with a peak in April 2024.
Fig 6. Backtest position holding time X profit
The great number of very short operations indicates that our system has been exploring moments of market instability by re-entering after winning trades.
What could be better?
Now, I would like to draw your attention to the point that the seller of a trading strategy or setup will try to show you the best possible past results to foster your interest in its product. Eventually, they will cherry-pick the most performing parameters after careful optimization to emphasize the potential gains, diminishing the risk of losses.
But, except for the idea that you can understand the principles and start small with statistical arbitrage, I’m not “selling” you anything here. On the contrary, I would say I’m happy that the backtest shows that we are dealing with an algorithm that requires improvements. Because this is the cornerstone of every statistical arbitrage system.
That is, until now for this simplistic automation, we have been limited to arbitrarily chosen parameters to manage the risk. Instead, what we need is:
- To control the number of positions to be opened according to the assessed risk at each point
- To have a float trigger spread percentage that takes into account the volatility
- To develop a dynamic stop-loss/take-profit strategy that derives the probability of gain from the trigger spread value and possibly other variables
These are some possible ways for future improvement of this EA.
Summary of the scale model
1. Start with a hypothesis
The spread between correlated pairs tends to revert to the mean. This is our hypothesis here.
From the trader’s perspective, the concept of mean reversion is simple and intuitive: when the current price is below the average price one can expect the price to rise and when the current price is above the average price one can expect the price to fall. As the saying goes, the price is always “searching for the mean”.
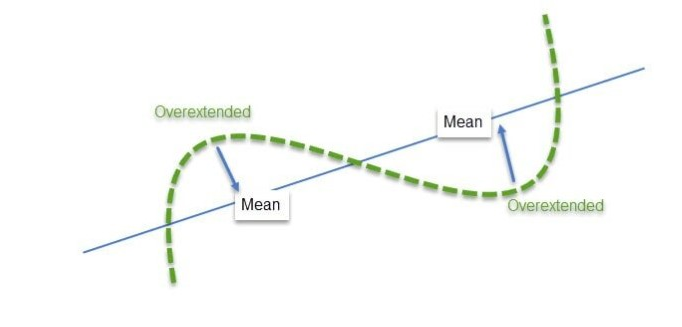
Fig 7. Overbought or oversold securities tend to revert to the mean price (Source: ResearchGate CC BY 4.0)
In trending markets the mean turns into a dynamic support for bullish trends and into a dynamic resistance for bearish trends. In consolidating markets the mean tends to run in the channel, the middle point between the highest highs and lowest lows.
This feature is more observable in short timeframes for currency exchange rates because while any other asset price can, at least in theory, rise or fall indefinitely, currency exchange rates are “capped” by the rules of trade between nations.
For example: “Apple went public on December 12, 1980 at $22.00 per share. The stock has split five times since the IPO, so on a split-adjusted basis the IPO share price was $.10.”
At the time of writing Apple is quoted at US$192.00 (~ 875%). And it is still rising. There is no theoretical limit.
On the other hand, you cannot expect even a 50% appreciation or depreciation in the exchange rates between two currencies without at the same time thinking about extreme factors like hyperinflation or even a large-scale war. In normal conditions, the exchange rate that defines the “price” of the pair in Forex trading should return to the mean much earlier.
2. Search for patterns in the data to test the hypothesis
The Pearson correlation of 0.97 between XAUUSD and XAUEUR denotes our pattern: the prices of these two securities tend to rise or fall simultaneously.
3. Monitor for anomalies in the patterns
The mean spread between XAUUSD and XAUEUR going far away from the mean is our anomaly. Finding anomalies in market patterns is the bread and butter of the portfolio level statistical arbitrage as it was used by Simons’ team operations.
4. Develop an automation to trade the anomalies
The simplistic EA represents our automation, but as said above, the algorithm requires many improvements, it is just a tool to help us to better understand the principles. Besides that, the EA itself requires all the usual error checking.
Conclusion
Portfolio-level statistical arbitrage as it is done by the big players is practically impossible to the average retail trader. Because we would need to operate in High-Frequency Trading (HFT), with a high-skilled team, high-quality big data, and big money. To turn our scale model into something similar or even near a Jim Simons’ hedge fund operation, I would say, with a tong-in-cheek, that all that we need is to be able to
- Make market analysis in subsecond granularity for hundreds of asset symbols in each portfolio in real time. (At some point, Simmons’ team was dealing with more than eight thousand different stocks, in a dozen markets and territories.)
- Send a million dollars orders, and have them filled in a millionth seconds
- Update the model regularly
Well, I suppose that we can start updating the model regularly. 🙂
But seriously, what Isaac Newton's quote above teaches us is that math alone is not enough to thrive in financial markets. Many mathematicians failed where Simons succeeded. But Simons did not go to the battlefield with math only. He started his career in finance by doing trades as any other trader, searching for trends, relying on technical analysis and intuition, and making and losing money. He tried several methods, he learned the rules of engagement, talked, partnered, and worked with professional traders while he was trying to find a sustainable way of trading.
Nevertheless, his conceptual framework is accessible to anyone willing to make the required effort to select the right portfolio, choose the right features to be studied, search for patterns and anomalies, prototype with free data, and buy high-quality data when the prototype is promising enough to reach the most balanced model for a specific portfolio. Probably many retail traders around the world are paying for this effort with serious work on a day-to-day basis. Most of them are not becoming billionaires, but certainly, many of them have turned their trading activity into a sustainable business.
We can even follow the machine learning path to discover these patterns and anomalies. It is accessible to the mortals and it seems to be the future already present, right here, right now. There are, literally, hundreds of high-quality articles about the use of machine learning in the MetaTrader 5 environment. Today we are NOT required to know the low-level math to use machine learning in our trading system. We can use MQL5 or Python, both with batteries included, meaning with high-level machine learning libraries.
In summary, this article proposes to retail traders with limited resources one schematic way to understand the fundamentals behind portfolio-level statistical arbitrage.
As the saying goes, past results are not a guarantee of future results. But we can make more informed decisions if we analyze those past results with the right tools and objective data.
| Attached file | Description |
|---|---|
| pairs-trading.mq5 | This file contains the sample Expert Advisor code to reproduce the experiment. It requires (#<include>) the file PairsTradingFunctions.mqh. |
| PairsTradingFunctions.mqh | This file is the include required by the previous file in this list and at the moment contains only one enumeration (enum) of the check mode used by the EA to identify the rising/falling symbol in the pairs. |
| pairs-trading.ipynb | This file is a Jupyter notebook file containing Python code to run the statistical analysis. |
| stat_arb_pairs_trading_GOLD_XAUEUR.ini | This file is a Metratrader 5 Tester configuration settings to reproduce the experiment. |
Developing a Trading System Based on the Order Book (Part I): Indicator
From Basic to Intermediate: The Include Directive
Introduction to MQL5 (Part 15): A Beginner's Guide to Building Custom Indicators (IV)
Atmosphere Clouds Model Optimization (ACMO): Theory
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Hello. Very interesting article. I was trying to replicate the results but nothing happen. What am I missing? I uploaded the pairs-trading.mq5 and PairsTradingFunctions.mqh files.
Thanks
XXXUSD = XXXEUR * EURUSD.
XXX = XAU, AUD, ....
The 5 sec intervals are arbitrary at this point. It could be 1 sec or 10 sec. The idea is to have an initial window to calculate the mean spread and, eventually, other stats for the period covered by the CountQuotes. Then keep updating a moving window at X sec intervals no matter the timeframe.
You are right about the bars: I'm not interested in them or in keeping them synchronized because it seems to me that they are irrelevant in this specific case. Almost all trades last for a couple of seconds, opening and closing intrabar.
That said, what do you think about this approach? Is it more clear now? Do you see any critical flaw that can lead to wrong calculations, affect the performance, or anything?
Then the whole mode with iMA is incorrect, because it's bound to bars. You need to calculate the MA by 5-second samples manually.
Then the whole mode with iMA is incorrect, because it's bound to bars. You need to calculate the MA by 5-second samples manually.
How
Read the tick history (implement yourself using CopyTicks/CopyTickRange functions or find a ready-made indicator/script in the codebase) and calculate 5-second virtual bars as an array, then apply smoothing algorithms from the standard library (mqh-files provided along with MT5).