Market / MetaTrader 5 / Indikatoren /

SV Harmozup Pattern

149 USD

Demo heruntergeladen: 48

Veröffentlicht: 26 Dezember 2022

Aktuelle Version: 1.2

Weitere Produkte dieses Autors

Keinen passenden Roboter gefunden?
Geben Sie Ihren Eigenen in Auftrag
auf Freelance!

Gehen Sie zu Freelance

Wie man einen Roboter oder Indikator kaufen kann

Starte Deinen EA im
Virtual Hosting

Teste einen Indikator/Roboter vor dem Kauf

Möchtest Du Geld im Market verdienen?

Wie man Produkte richtig präsentiert

Übersicht
Bewertungen
Diskussion (3)
Neue Funktionen

SV Harmozup Pattern

Indikatoren
Minh Truong Pham
Minh Truong Pham
Freelancer in Home

Vietnam

18290
4.4 (44)
Hello, my name is Pham and I am a programmer and trader! At here, I create amazing forex indicators and expert advisors for Metatrader.
I will try:
+ Provide best tools base on my 5 years experience as a trader and 10 years as a programmer.

174 Produkte 13 Themen 36 Kommentare
Version: 1.2
Aktualisiert: 22 Februar 2023
Aktivierungen: 5

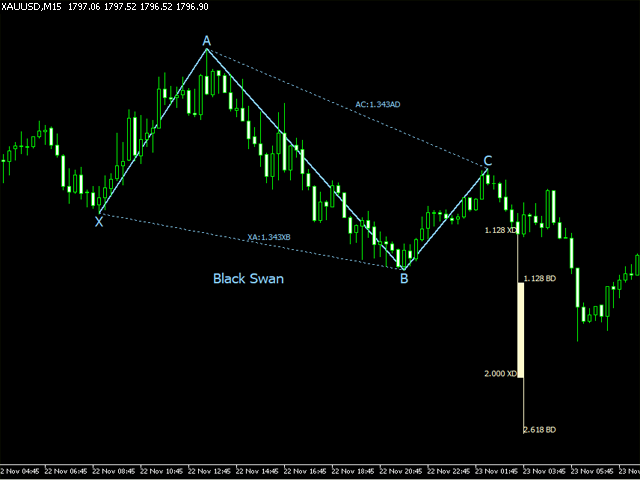
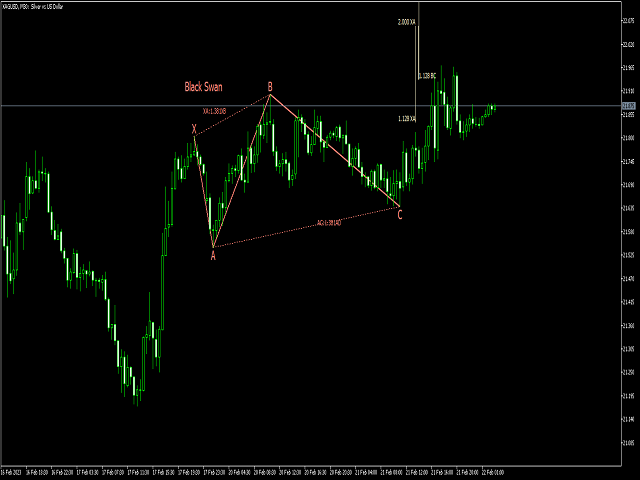
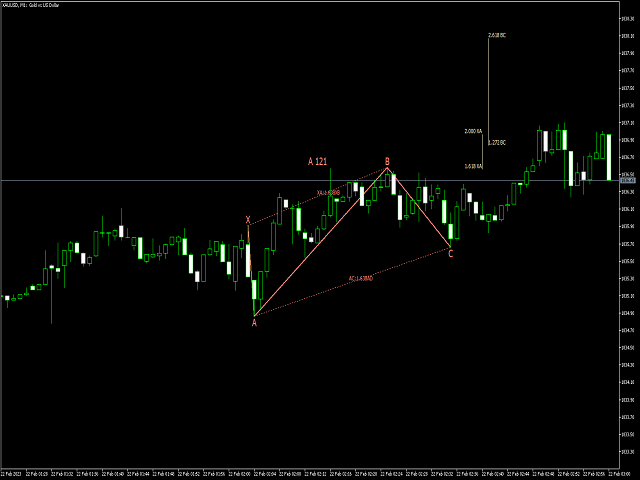
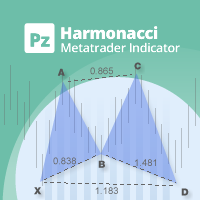
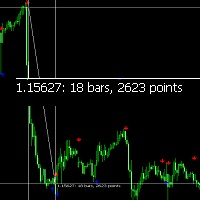
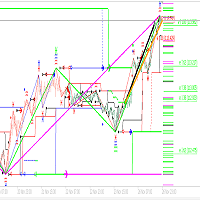
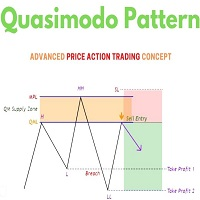
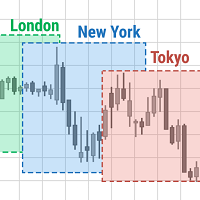
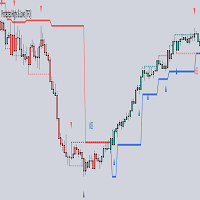
Das Konzept der Harmonic Patterns wurde 1932 von H.M. Gartley entwickelt. Gartley schrieb über ein 5-Punkte-Muster (XABCD) (bekannt als Gartley) in seinem Buch Profits in the Stock Market. Dieser Indikator scannt und warnt, wenn der 4. Punkt (C) abgeschlossen ist und sagt voraus, wo D sein sollte.

Zu den traditionellen Gartley-Mustern gehören das BAT-Muster, das Gartley-Muster, das Schmetterlingsmuster, das Krabbenmuster, das tiefe Krabbenmuster und das Hai-Muster. Jedes Muster hat seinen eigenen Satz von Fibonacci. In diesem Indikator fügen wir ein weiteres erweitertes Muster namens ZUP-Muster hinzu. Wir haben also insgesamt 37 Muster wie folgt:

		MinXB	MaxXB	MinAC	MaxAC	MinBD	MaxBD	MinXD	MaxXD
1	Gartley	0.618	0.618	0.382	0.886	1.272	1.618	0.786	0.786
2	Fledermaus	0.382	0.5	0.382	0.886	1.618	2.618	0.886	0.886
3	A alt Hai	0.446	0.618	0.618	0.886	1.618	2.618	0.886	0.886
4	A Nen Stern	0.5	0.886	0.467	0.707	1.618	2.618	0.786	0.786
5	Schmetterling 113	0.786	1	0.618	1	1.128	1.618	1.128	1.128
6	Schmetterling	0.786	0.786	0.382	0.886	1.618	2.618	1.272	1.618
7	Krabbe	0.382	0.618	0.382	0.886	2.24	3.618	1.618	1.618
8	A Hai	0.446	0.618	0.618	0.886	1.618	2.618	1.128	1.128
9	Eine neue Chiffre	0.5	0.886	0.476	0.707	1.618	2.618	1.272	1.272
10	Leonardo	0.5	0.5	0.382	0.886	1.128	2.618	0.786	0.786
11	A Schmetterling	0.382	0.618	1.128	2.618	1.272	1.272	0.618	0.786
12	A Krabbe	0.276	0.446	1.128	2.618	1.618	2.618	0.618	0.618
13	Hai	0.382	0.618	1.128	1.618	1.618	2.236	0.886	0.886
14	Neue Ziffernkombination	0.382	0.618	1.414	2.14	1.128	2	0.786	0.786
15	Seepony	0.128	3.618	0.382	0.5	1.618	2.618	0.618	3.618
16	A Gartley	0.618	0.786	1.128	2.618	1.618	1.618	1.272	1.272
17	A Fledermaus	0.382	0.618	1.128	2.618	2	2.618	1.128	1.128
18	Alt Hai	0.382	0.618	1.128	1.618	1.618	2.236	1.128	1.128
19	Nen Star	0.382	0.618	1.414	2.14	1.128	2	1.272	1.272
20	Partizan	0.128	3.618	0.382	0.382	1.618	1.618	0.618	3.618
21	Alt Fledermaus	0.382	0.382	0.382	0.886	2	3.618	1.128	1.128
22	Tiefe Krabbe	0.886	0.886	0.382	0.886	2.618	3.618	1.618	1.618
23	Schwarzer Schwan	1.382	2.618	0.236	0.5	1.128	2	1.128	2.618
24	121	0.5	0.618	1.272	2	0.447	0.618	0.382	0.786
25	Max Fledermaus	0.382	0.618	0.382	0.886	1.272	2.618	0.886	0.886
26	Max Gartley	0.382	0.618	0.382	0.886	1.128	2.236	0.618	0.786
27	Max Schmetterling	0.618	0.886	0.382	0.886	1.272	2.618	1.272	1.618
28	A 121	1.618	0.786	0.447	0.786	1.618	2	1.272	2.618
29	Weißer Schwan	0.382	0.724	2	4.237	0.5	0.886	0.382	0.886
30	Navarro 200	0.382	0.786	0.886	1.128	0.886	3.618	0.886	1.128
31	3 Laufwerke	1.272	1.618	0.618	0.786	1.272	1.618	1.618	2.618
32	A 3 Laufwerke	0.618	0.786	1.272	1.618	0.618	0.786	0.31	0.886
33	Gesamt 1	0.382	0.786	0.382	0.886	1.271	2.618	0.786	0.886
34	Gesamt 2	0.382	0.786	0.382	0.886	1.618	3.618	1.128	1.618
35	Insgesamt 3	0.276	0.618	1.128	2.618	1.272	2.618	0.618	0.886
36	Insgesamt 4	0.382	0.786	1.128	2.618	1.618	2.618	1.128	1.272
37	Insgesamt	0.276	0.786	0.382	2.618	1.272	3.618	0.618	1.618

Dieser Indikator hat zwei Modi, jeder Modus hat zwei Optionen:

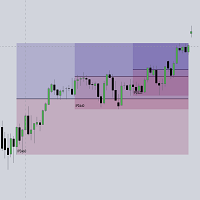
1) Suchmuster im Bereich: 4 Punkte (X,A,B,C) liegen zwischen (min-tolence) und (max+tolence) der Fibonacci-Ebene. In diesem Fall sollten Sie einen Toleranzwert reduzieren.

a. Die Option No need to confirm peak (Is fast=true) sucht ab dem ersten (nicht bestätigten) Extrempunkt. Mit dieser Option wird das Muster so schnell wie möglich gefunden, aber der Punkt C bewegt sich, weil sich der erste Extrempunkt bewegt.

b. Bei der Option "Have to confirm peak" (Is fast=fast) wird ab dem zweiten (stabilen) Extrempunkt gesucht. Diese Option hat eine längere Latenzzeit, ist aber stabiler.

2) Suche Muster in genau: 4 Punkt ist genaul fibonancy Ebene nebeneinander. Wenn also der Fib-Level bei xbmin liegt (plus oder minus tolence), muss bd auch bei min liegen. Verwenden Sie diese Option, sollten Sie tolence erhöhen.

a. Option No need to confirm peak (Is fast=true) ist im ersten Modus gleich, aber C bewegt sich nicht viel.

b. Option Muss bestätigen, dass der Peak (Is fast=fast) im ersten Modus der gleiche ist

Wenn ein Muster gefunden wurde, zeichnet dieser Indikator 2 vertikale Linien (XDmin,XDmax) und (BDmin,BDmax). Der Schnittpunkt der 2 Linien ist D potetial. Bei der genauen Mustersuche im Modus gibt es in manchen Fällen keinen Schnittpunkt der 2 Linien (besonders wenn die Tolenz niedrig ist). Das bedeutet, dass das Harmozup-Muster in diesem Fall nicht vollständig sein kann.

mehr...

Übersicht Harmonic Patterns MT5 ist ein Indikator für die technische Analyse, der für die Plattform MetaTrader 5 entwickelt wurde. Er identifiziert und zeigt harmonische Preismuster, wie Butterfly, Cypher, Crab, Bat, Shark und Gartley, sowohl in Aufwärts- als auch in Abwärtsrichtung an. Der Indikator berechnet wichtige Kursniveaus, einschließlich Einstiegs-, Stop-Loss- und drei Take-Profit-Niveaus, um Händler bei der Analyse von Marktbewegungen zu unterstützen. Visuelle Elemente und anpassbare W

40 USD

Dies ist wahrscheinlich der vollständigste Indikator für die automatische Erkennung der harmonischen Preisbildung, den Sie für die MetaTrader-Plattform finden können. Es erkennt 19 verschiedene Muster, nimmt Fibonacci-Projektionen genauso ernst wie Sie, zeigt die potenzielle Umkehrzone (PRZ) an und findet geeignete Stop-Loss- und Take-Profit-Werte. [ Installationsanleitung | Update-Anleitung | Fehlerbehebung | FAQ | Alle Produkte ] Es erkennt 19 verschiedene harmonische Preisbildungen Darges

149 USD

Harmonische Muster-Struktur Harmonic Pattern Structure ist ein professioneller MetaTrader 5-Indikator, der automatisch klassische harmonische Muster unter Verwendung strenger Fibonacci-Ratio-Validierung und XABCD-Preisstruktur erkennt. Der Indikator wurde für Händler entwickelt, die Wert auf Präzision, saubere Grafiken und strukturierte Analysen legen. Er hebt potenzielle Umkehrzonen auf der Grundlage der Preisgeometrie hervor und unterstützt so eine konsistente und objektive Entscheidungsfind

39 USD

Triangle Pattern Gann v3.1 - Complete Feature Documentation Core Functionality OverviewTriangle Pattern Gann v3.1 ist ein hochentwickelter MetaTrader 5-Indikator, der die geometrischen Handelsprinzipien von W.D. Gann mit fortschrittlicher Dreiecksmustererkennung kombiniert, um umsetzbare Handelssignale zu liefern. Primary Features1. Dreiecksmuster-ErkennungssystemAufsteigendes Dreieck Erkennung Funktion: Identifiziert automatisch bullische Fortsetzungsmuster Erkennungs-Kriterien: Flache h

90 USD

Der Indikator identifiziert die harmonischen Muster (XABCD) gemäß den Entwicklungen von H.M. Gartley („Profits in the Stock Market“, 1935г). Der D-Punkt wird als Punkt in der perspektivischen Projektion projiziert (geben Sie in den Einstellungen ProjectionD_Mode = true an). Wird nicht neu gezeichnet. Wenn ein Balken des Arbeitszeitraums schließt und sich der identifizierte Musterpunkt während der Balken von Patterns_Fractal_Bars nicht bewegt hat, erscheint ein Pfeil auf dem Diagramm (in Richt

270 USD

Monster Harmonics Indicator ist ein Indikator für harmonische Muster. Er erkennt Gartley-, Fledermaus-, Krebs-, Butterfly-, Cypher-, White Swan-, Black Swan-, Shark- und AB=CD-Muster. Auch projizierte Muster, die noch nicht abgeschlossen sind, werden erkannt. Monster zeigt sogar die PRZ (Potential Reversal Zone) an. Benutzer können Monster ihre eigenen benutzerdefinierten Muster hinzufügen. Neben dem aktuellen Muster zeigt Monster auch alle Muster in der Symbolhistorie an. Monster gibt Warnunge

99 USD

Beschreibung des Indikators: Der Advanced Force Index kombiniert Volumen und Preis, um die Stärke des Trends zu des Trends zu bestimmen. Er wurde entwickelt, um eine genaue Messung der Er wurde entwickelt, um eine genaue Messung der Verkäufer- und Käufermacht auf dem Markt zu ermöglichen, mit mehreren Glättungs- und Anzeigeoptionen. Hauptmerkmale: Zwei Anzeigemodi: Farbiges Histogramm (zweifarbig) oder durchgezogene Linie 4 gleitende Durchschnittsmethoden: SMA, EMA, SMMA, LWMA 7 Pre

Der Indikator erstellt aktuelle Notierungen, die mit historischen verglichen werden können, und auf dieser Grundlage eine Preisbewegungsprognose erstellen. Der Indikator verfügt über ein Textfeld zur schnellen Navigation zum gewünschten Datum. Optionen: Symbol - Auswahl des Symbols, das der Indikator anzeigen soll; SymbolPeriod - Auswahl des Zeitraums, aus dem der Indikator Daten aufnimmt; IndicatorColor - Indikatorfarbe; HorisontalShift - Verschiebung der vom Indikator gezeichneten Kurse u

30 USD

## NUR GOLD ## NUR GOLD **Mercaria Professional Trading Zones - Vollständiger Leitfaden** ## **Mercaria Professionelle Handelszonen - Vollständiger Leitfaden** ### **Wie Mercaria-Zonen funktionieren** **Englisch:** Mercaria Zones ist ein fortschrittlicher Handelsindikator, der mithilfe von ZigZag-Extremen in Kombination mit mathematischen Zonenberechnungen hochwahrscheinliche Unterstützungs- und Widerstandsbereiche identifiziert. Der Indikator arbeitet auf mehreren Zeitrahmen gleichzeitig un

693.69 USD

SophieSMC One ist ein Premium-Indikator von Smart Money Concepts, der speziell für XAUUSD (Gold)-Händler entwickelt wurde, die einen klareren, strukturierteren und institutionellen Ansatz für den Markt wünschen. SophieSMC One basiert auf realen Marktstrukturkonzepten und kombiniert mehrere Smart Money Concepts-Tools in einem leistungsstarken und visuell sauberen Handelssystem für MetaTrader 5. FEATURES: - BOS & CHoCH Marktstrukturerkennung - Fair Value Gap (FVG) Identifikation - Liquidity Swee

249 USD

Der Weis Wave Chart Forex für MT5 ist ein Preis- und Volumenindikator. Die Lesart von Preis und Volumen wurde durch Richard Demille Wyckoff auf der Grundlage der drei von ihm geschaffenen Gesetze verbreitet: Angebot und Nachfrage, Ursache und Wirkung und Aufwand vs. Ergebnis. Bereits 1900 verwendete R.Wyckoff das Wellendiagramm in seinen Analysen. Viele Jahre später, um 1990, automatisierte David Weis das Wellendiagramm von R. Wyckoff, und heute bringen wir Ihnen die Entwicklung des Wellendiagra

100 USD

Der Indikator erkennt und zeigt М. Gartley's Butterfly-Muster. Das Muster wird durch die Extremwerte des ZigZag-Indikators gezeichnet (in den Ressourcen enthalten, muss nicht installiert werden). Nach der Erkennung des Musters benachrichtigt der Indikator über ein Pop-up-Fenster, eine mobile Benachrichtigung und eine E-Mail. Das Muster und die Wellenparameter werden auf den Screenshots angezeigt. Die Standardparameter werden nur zu Demonstrationszwecken verwendet, um die Anzahl der erkannten Mus

30 USD

CurvedSmoothChannel_Enhanced - Erweiterter Preiskanal-Indikator **CurvedSmoothChannel_Enhanced** ist ein leistungsstarker und visuell ansprechender Preiskanal-Indikator für MetaTrader 5, der Ihnen hilft, Trends, potenzielle Umkehrungen und wichtige Kursniveaus präzise zu erkennen. Diese verbesserte Version kombiniert die Leistung des Hull Moving Average (HMA) und des Super Smooth Filters von John Ehlers und schafft so einen dynamischen, adaptiven Kanal, der sich über mehrere Zeitrahmen hinweg

60 USD

Der Durchschnittliche Richtungsindex(ADX) Multicurrency Scanner MT5 ist ein fortschrittlicher Handelsindikator, der entwickelt wurde, um mehrere Währungspaare gleichzeitig zu analysieren. Er bietet Händlern, die ihren Entscheidungsprozess verbessern möchten, Echtzeitsignale basierend auf dem Durchschnittlichen Richtungsindex, was eine effiziente Markttrend-Analyse ermöglicht. Dieses Tool optimiert das Handelserlebnis, indem es die Identifizierung der Trendstärke und der Richtungsbewegung vereinf

30 USD

Überblick Der Market Perspective Structure Indicator ist ein umfassender MetaTrader-Indikator, der Händlern eine detaillierte Analyse der Marktstruktur über mehrere Zeitrahmen hinweg bietet. Er identifiziert und visualisiert wichtige Preisaktions-Elemente, einschließlich Swing-Hochs und -Tiefs, Break of Structure (BOS), Change of Character (CHOCH), interne Strukturen, gleiche Hochs/Tiefs, Premium/Discount-Levels, frühere Levels aus höheren Zeitrahmen und Handelssitzungszonen. Dank umfangreicher

60 USD

Indikator zur grafischen Analyse. Markiert die wichtigsten japanischen Candlestick-Muster auf dem Chart. Derzeit stehen dem Händler die folgenden Muster zur Verfügung: - Bearish/Bullish Abandoned Baby; - Bearish Advance Block; - Bearish Deliberation; - Bearish/Bullish Belt Hold; - Bearish/Bullish Engulfing; - Bearish Shooting Star; - Bearish Evening Star; - Bearish Evening Doji Star; - Bearish/Bullish Doji Star; - Bearish/Bullish Tri-Star; - Bearish Hanging Man; - Bearish/Bullish

99 USD

Volumenstrom-Indikator für MetaTrader 5 Prüfen Sie alle unsere Produkte über den untenstehenden Link Unser beliebtester Indikator Was sind die Spezifikationen dieses Indikators? Plattform: MetaTrader 5 (MT5) Art der Anwendung: Benutzerdefinierter Handelsindikator Stufe: Fortgeschritten Zeitrahmen: Alle Timeframes (Multi-Timeframe Unterstützung) Handelsstile: Scalping, Day Trading, Swing Trading, Positionshandel Handelsmärkte: Forex, Aktien, Rohstoffe, Indizes und Kryptowährungen Was macht di

30 USD

FiveStarFX Gold Reversal Edge Professionelle automatisierte Handelslösung für die strukturierte Ausführung und das kontrollierte Risikomanagement im Goldmarkt. Entwickelt für Händler, die Disziplin, Präzision und Beständigkeit schätzen. Hauptmerkmale Vollautomatischer Handel Immer nur ein Trade (kontrolliertes Engagement) Fester Stop Loss und Take Profit Intelligenter Break-Even-Schutz Gewinnsperre mit Puffer Stufenbasiertes Trailing-Management Spread-Schutzsystem Funktioniert be

Cumulative Volume Delta MA-X MTF (mit Gradient Momentum) Dieser Indikator führt eine Multi-Timeframe-Analyse der kumulativen Volumendelta (CVD) für MetaTrader 5 durch. Er berechnet die Nettodifferenz zwischen Kauf- und Verkaufsdruck durch die Analyse von Tick- oder Realvolumendaten und bietet so eine visuelle Darstellung des Orderflow-Sentiments. Logik und Funktionen des Indikators Der Indikator nutzt einen mathematischen Ansatz zur Volumenanalyse: Datenquellen: Unterstützt sowohl Real Volume (

124 USD

Kumulativer Delta-Indikator Wie die meisten Händler glauben, bewegt sich der Kurs unter dem Druck von Marktkäufen oder -verkäufen. Wenn jemand ein in der Tasse stehendes Angebot einlöst, handelt es sich um einen "Kauf". Wenn jemand in das in der Tasse stehende Angebot einsteigt, geht das Geschäft in Richtung "Verkauf". Das Delta ist die Differenz zwischen Käufen und Verkäufen. Ein kumulatives Delta - die Differenz zwischen der kumulativen Summe der Käufe und Verkäufe für einen bestimmten Zeitrau

50 USD

Gartley Butterfly Pattern EA Beschreibung Der Expert Advisor (EA) handelt automatisch basierend auf harmonischen Mustern — beliebten Figuren der technischen Analyse, die erstmals von Harold McKinley Gartley vorgestellt und später von Scott Carney, dem Autor der Muster Bat, Crab, Shark, Deep Crab und Alternate Bat, systematisiert und erweitert wurden. Der Roboter erkennt und arbeitet mit den folgenden Mustern: Gartley, Butterfly, Bat, Crab, Shark, Cypher, Deep Crab, Alternate Bat, AB=CD, Three

50 USD

Zonenstruktur-Scanner-Panel für MT5 Finden Sie schneller bessere Setups - ohne stundenlang Charts scannen zu müssen. Das Zonenstruktur-Scanner-Panel für MT5 hilft Ihnen, automatisch mehrere Symbole zu scannen, wichtige wöchentliche und tägliche Unterstützungs-/Widerstandszonen zu erkennen, die Marktstruktur zu lesen, Zusammenflüsse hervorzuheben und Setups zu markieren, die durch eine H4-Ablehnung bestätigt wurden - alles in einem einzigen leistungsstarken Panel. Anstatt von Chart zu Chart zu

1 000 USD

Orderbuch, auch bekannt als Marktbuch, Markttiefe, Level 2, - ist eine dynamisch aktualisierte Tabelle mit den aktuellen Volumina der Kauf- und Verkaufsaufträge für ein bestimmtes Finanzinstrument zu Preisen nahe Bid und Ask. MetaTrader 5 bietet die Möglichkeit, das Marktbuch von Ihrem Broker zu erhalten, allerdings nur in Echtzeit und ohne Zugriff auf die Historie. Der Indikator OrderBook Cumulative Indicator akkumuliert die Marktbuchdaten online und stellt sie auf dem Chart dar. Darüber hinaus

49 USD

Equinox Gold ist ein Hightech-Expert Advisor (EA), der speziell für den Goldmarkt ( XAUUSD ) entwickelt wurde. Das System basiert auf einem einzigartigen Market Equilibrium-Algorithmus , der Bereiche des Ungleichgewichts zwischen Angebot und Nachfrage bei extremer Volatilität identifiziert. Im Gegensatz zu den meisten Robotern, die gefährliche Abwarten-Methoden verwenden, stützt sich Equinox Gold auf eine mathematische Momentum-Bestätigung und eine strenge Risikokontrolle für jeden Handel. HAUP

865 USD

Der SMC Venom Model BPR Indikator ist ein professionelles Tool für Trader, die mit dem Smart Money (SMC)-Konzept arbeiten. Er identifiziert automatisch zwei wichtige Muster im Kurschart: FVG (Fair Value Gap) ist eine Kombination aus drei Kerzen, wobei zwischen der ersten und dritten Kerze eine Lücke besteht. Diese bildet eine Zone zwischen den Niveaus, in der es keine Volumenunterstützung gibt, was häufig zu einer Kurskorrektur führt. BPR (Balanced Price Range) ist eine Kombination aus zwe

45 USD

MonsterDash Harmonics Indicator ist ein Dashboard für harmonische Muster. Es erkennt alle wichtigen Muster. MonsterDash ist ein Dashboard, das alle erkannten Muster für alle Symbole und (fast) alle Zeitrahmen in einem sortierbaren und scrollbaren Format anzeigt. Benutzer können ihre eigenen benutzerdefinierten Muster hinzufügen. MonsterDash kann Charts mit den gefundenen Mustern öffnen und aktualisieren . Einstellungen Die Standardeinstellungen von MonsterDash sind in den meisten Fällen gut gen

169 USD

Noize Absorption Index - ist das manuelle Handelssystem, das den Druckunterschied zwischen den Kräften der Bären und der Bullen misst. Die grüne Linie - ist ein noizefreier Index, der die aktuelle Situation anzeigt. Werte über dem Nullniveau zeigen an, wie stark die bullische Welle ist und Werte unter dem Nullniveau messen die bärischen Kräfte. Das System verfügt über mehrere Handelsmodi, die Sie während des Handels direkt auf dem Chart ändern können. Hauptmerkmale des Indikators Die Signale we

199 USD

War: $249 Jetzt: $99 Market Profile definiert eine Reihe von Tagestypen, die dem Händler helfen können, das Marktverhalten zu bestimmen. Ein Schlüsselmerkmal ist der Value-Bereich, der den Bereich der Kursbewegung darstellt, in dem 70 % des Handels stattfand. Das Verständnis des Value-Bereichs kann Händlern einen wertvollen Einblick in die Marktrichtung geben und den Handel mit höheren Gewinnchancen festlegen. Es ist eine hervorragende Ergänzung zu jedem System, das Sie verwenden. Inspiriert von

99 USD

Das 123-Muster ist eines der beliebtesten, leistungsstärksten und flexibelsten Diagrammmuster. Das Muster besteht aus drei Preispunkten: einem Boden, einem Gipfel oder Tal und einem Fibonacci-Retracement zwischen 38,2% und 71,8%. Ein Muster gilt als gültig, wenn der Preis jenseits des letzten Gipfels oder Tals abbricht, in dem der Indikator einen Pfeil zeichnet, einen Alarm auslöst und der Handel platziert werden kann. [ Installationsanleitung | Update-Anleitung | Fehlerbehebung | FAQ | Alle Pr

75 USD

Signal Strike ist ein professioneller Handelsindikator für MetaTrader 5, der klare Einstiegssignale mit hohem Vertrauen direkt auf Ihrem Chart liefert. Mit einer fortschrittlichen Logik, die Trend, Momentum, Volatilität und Volumenbestätigung kombiniert, hilft dieses Tool Händlern, präzise KAUF- und VERKAUFSgelegenheiten mit Zuversicht zu identifizieren. Im Gegensatz zu generischen Indikatoren ist Signal Strike so konzipiert, dass er unentschlossene Kerzen und schwache Setups herausfiltert. We

30 USD

Neuro Poseidon ist ein neuer Indikator von Daria Rezueva. Er kombiniert präzise Handelssignale mit adaptiven TP/SL-Levels - das Ergebnis sind bestmögliche Trades! Senden Sie mir eine Nachricht und erhalten Sie Neuro Poseidon Assistant als Geschenk, um Ihren Handelsprozess zu automatisieren! Was macht ihn so besonders? 1. Nachgewiesene Rentabilität für alle Vermögenswerte und Zeitrahmen 2. Nur bestätigte KAUF- und VERKAUFSSIGNALE auf dem Chart 3. Adaptive TP & SL Levels , die von der Software

189 USD

PrimeScalping ist ein leistungsstarker Handelsbegleiter, der hochwahrscheinliche Einstiegssignale mit dynamischen TP/SL/DP-Levels auf Basis der Volatilität generiert. Das integrierte Performance-Tracking zeigt Gewinn/Verlust-Statistiken, PP1/PP2-Treffer und Erfolgsquoten - alles live aktualisiert. Hauptmerkmale: Kauf-/Verkaufssignale mit adaptiven Volatilitätsbändern Echtzeit TP/SL/DP-Levels basierend auf ATR Eingebauter MA-Filter mit optionaler ATR/StdDev-Volatilität Performance-Statistik-Pane

3 500 USD

SmartScalping ist ein leistungsstarker Handelsbegleiter, der hochwahrscheinliche Einstiegssignale mit dynamischen TP/SL/DP-Levels auf Basis der Volatilität generiert. Das integrierte Performance-Tracking zeigt Gewinn/Verlust-Statistiken, PP1/PP2-Treffer und Erfolgsquoten - alles live aktualisiert. Hauptmerkmale: Kauf-/Verkaufssignale mit adaptiven Volatilitätsbändern TP/SL/DP-Levels in Echtzeit auf Basis von ATR Eingebauter MA-Filter mit optionaler ATR/StdDev-Volatilität Performance-Statistik-P

3 500 USD

ScalpPoint ist ein leistungsstarker Handelsbegleiter, der hochwahrscheinliche Einstiegssignale mit dynamischen TP/SL/DP-Levels auf Basis der Volatilität generiert. Das integrierte Performance-Tracking zeigt Gewinn/Verlust-Statistiken, PP1/PP2-Treffer und Erfolgsquoten - alles live aktualisiert. Hauptmerkmale: Kauf-/Verkaufssignale mit adaptiven Volatilitätsbändern TP/SL/DP-Levels in Echtzeit auf Basis von ATR Eingebauter MA-Filter mit optionaler ATR/StdDev-Volatilität Performance-Statistik-Pane

3 500 USD

SignalTech MT5 ist ein einzigartiges, vollständig regelbasiertes Handelssystem für EURUSD, USDCHF, USDJPY, AUDUSD, NZDUSD, EURJPY, AUDJPY, NZDJPY, CADJPY. Alle erfolgreichen Trades mit Chart-Setups werden auf der Kommentar-Seite veröffentlicht. 2026-05 4107 Pips (bis 29.05. NY geschlossen) 2026-04 2243 Punkte 2026-03 2165 Kerne 2026-02 2937 Kerne 2026-01 2624 Kerne 2025-12 1174 Kerne Es kann Signale mit Kauf-/Verkaufspfeilen und Pop-Up-/Ton-Warnungen erzeugen. Jedes Signal hat klare Einstiegs- u

396 USD

MasterTrend-Indikator für MT5 Ein leistungsstarkes Trendfolge- und Signalauswertungstool MasterTrend ist ein benutzerdefinierter MT5-Indikator, der gleitende Durchschnitte und ATR-basierte Risiko-/Ertragslogik kombiniert, um klare Kauf-/Verkaufssignale zu generieren. Er visualisiert dynamische SL/TP-Levels, wertet vergangene Handelsergebnisse aus und zeigt Gewinn/Verlust-Statistiken in einem übersichtlichen Chart-Panel an. Die wichtigsten Funktionen sind: Kauf-/Verkaufssignale auf Basis von MA-

3 500 USD

Azimuth Pro V2: Synthetische fraktale Strukturanalyse und bestätigte Einstiege für MT5 Überblick Azimuth Pro ist ein Multi-Level-Swing-Struktur-Indikator von Merkava Labs . Vier verschachtelte Swing-Ebenen, Swing-verankerter VWAP, ABC-Mustererkennung, Drei-Zeitrahmen-Strukturfilterung und bestätigte Einstiege auf Schlusskursbasis — ein Chart, ein Workflow von Mikro-Swings bis zu Makro-Zyklen. Dies ist kein blindes Signalprodukt. Es ist ein struktur-orientierter Workflow für Trader, die Wert auf

399 USD

Dieses Produkt wurde für den Markt 2026 aktualisiert und für die neuesten MT5-Builds optimiert. PREISUPDATE-HINWEIS: Smart Price Action Concepts ist derzeit für $200 erhältlich. Der Preis wird nach den nächsten 30 Käufen auf $299 steigen. SONDERANGEBOT: Nach dem Kauf senden Sie mir eine private Nachricht, um einen kostenlosen Bonus + ein Geschenk zu erhalten. Zunächst ist es wichtig zu betonen, dass dieses Trading-Tool ein Indikator ohne Repainting, ohne Redrawing und ohne Verzögerung ist, was

200 USD

RelicusRoad Pro: Quantitatives Markt-Betriebssystem 70% RABATT AUF LEBENSLANGEN ZUGANG (BEGRENZTE ZEIT) - ÜBER 2.000 TRADER Warum scheitern die meisten Trader trotz "perfekter" Indikatoren? Weil sie einzelne Konzepte isoliert handeln. Ein Signal ohne Kontext ist ein Glücksspiel. Für konstante Gewinne benötigen Sie KONFLUENZ . RelicusRoad Pro ist kein einfacher Pfeil-Indikator. Es ist ein vollständiges quantitatives Markt-Ökosystem . Es bildet die „Fair Value Road“ ab und unterscheidet zwischen R

247 USD

ARIPoint ist ein leistungsstarker Handelsbegleiter, der hochwahrscheinliche Einstiegssignale mit dynamischen TP/SL/DP-Levels auf Basis der Volatilität generiert. Das integrierte Performance-Tracking zeigt Gewinn/Verlust-Statistiken, PP1/PP2-Treffer und Erfolgsraten, die alle live aktualisiert werden. Hauptmerkmale: Kauf-/Verkaufssignale mit adaptiven Volatilitätsbändern TP/SL/DP-Levels in Echtzeit auf Basis von ATR Eingebauter MA-Filter mit optionaler ATR/StdDev-Volatilität Performance-Statisti

3 500 USD

MetaForecast prognostiziert und visualisiert die Zukunft eines beliebigen Marktes basierend auf den Harmonien in den Preisdaten. Obwohl der Markt nicht immer vorhersehbar ist, kann MetaForecast, wenn es ein Muster im Preis gibt, die Zukunft so genau wie möglich voraussagen. Im Vergleich zu ähnlichen Produkten kann MetaForecast durch die Analyse von Markttrends genauere Ergebnisse erzeugen. Eingabeparameter Past size (Vergangene Größe) Gibt an, wie viele Balken MetaForecast verwendet, um ein Mod

199 USD

Tool der Market Maker. Meravith wird: Alle Zeitrahmen analysieren und den aktuell gültigen Trend anzeigen. Liquiditätszonen (Volumen-Gleichgewicht) hervorheben, in denen bullisches und bearisches Volumen gleich sind. Alle Liquiditätsniveaus aus verschiedenen Zeitrahmen direkt im Chart anzeigen. Eine textbasierte Marktanalyse generieren und zur Orientierung bereitstellen. Ziele, Unterstützungsniveaus und Stop-Loss-Punkte basierend auf dem aktuellen Trend berechnen. Das Risiko-/Chance-Verhältnis I

150 USD

Die meisten Pfeil-Indikatoren geben Ihnen ein Signal und überlassen Ihnen den Rest. KT Alpha Hunter Arrows liefert Ihnen einen vollständigen Trading-Plan. Jeder Signalpfeil erscheint mit einem bereits eingezeichneten kompletten Plan: Einstiegslinie, Stop-Loss, vier Take-Profit-Level und ein Live-Edge-Urteil, das Ihnen zeigt, ob dieses Symbol und dieser Timeframe im aktuellen Moment überhaupt handelnswert sind. Der enthaltene Trade Manager EA übernimmt die Ausführung, nachdem Sie manuell eingesti

247 USD

Der UZFX {SSS} Scalping Smart Signals MT5 ist ein leistungsstarker Trading-Indikator ohne Repainting, der speziell für Scalper, Daytrader und Swingtrader entwickelt wurde, die präzise Echtzeit-Signale in schnelllebigen Märkten benötigen. Dieser von (UZFX-LABS) entwickelte Indikator kombiniert Kursaktionsanalyse, Trendbestätigung und intelligente Filterung, um Kauf- und Verkaufssignale mit hoher Wahrscheinlichkeit für alle Währungspaare und Zeitrahmen zu generieren. EMPFOHLENE* BESTE ZEITRAHMEN:

198.98 USD

ARICoin ist ein leistungsstarker Handelsbegleiter, der hochwahrscheinliche Einstiegssignale mit dynamischen TP/SL/DP-Levels auf Basis der Volatilität generiert. Das integrierte Performance-Tracking zeigt Gewinn/Verlust-Statistiken, PP1/PP2-Treffer und Erfolgsraten, die alle live aktualisiert werden. Hauptmerkmale: Kauf-/Verkaufssignale mit adaptiven Volatilitätsbändern TP/SL/DP-Levels in Echtzeit auf Basis von ATR Eingebauter MA-Filter mit optionaler ATR/StdDev-Volatilität Performance-Statistik-

3 500 USD

Chronos Fractal Engine ist ein innovativer Preisprognose-Indikator für MetaTrader 5, der Ihre technische Analyse durch intelligente Identifizierung und Projektion historischer Preismuster verändert. Basierend auf einem fortschrittlichen Korrelationsalgorithmus und den fraktalen Prinzipien des Marktes visualisiert dieses leistungsstarke Tool potenzielle zukünftige Kursbewegungen und verschafft Ihnen einen einzigartigen Vorteil bei Ihren Handelsentscheidungen. Was ist die Chronos Fractal Engine?

490 USD

ZIVA LSE System Ein professionelles Liquiditäts- und Strukturausführungssystem Exekutive Übersicht Das ZIVA LSE System ist ein professionell entwickeltes Analysesystem, das entwickelt wurde, um das Marktverhalten durch strukturelle Logik und Liquiditätsdynamik zu interpretieren. Es ist nicht als konventioneller Indikator positioniert. Vielmehr fungiert es als strukturierte Ausführungsumgebung , die das Preisgeschehen in einem klaren, disziplinierten Entscheidungsmodell organisiert. Das System is

179 USD

AriX Indicator für MT5 Ein leistungsstarkes Trendfolge- und Signalauswertungstool AriX ist ein benutzerdefinierter MT5-Indikator, der gleitende Durchschnitte und ATR-basierte Risiko/Ertrags-Logik kombiniert, um klare Kauf-/Verkaufssignale zu generieren. Er visualisiert dynamische SL/TP-Levels, wertet vergangene Handelsergebnisse aus und zeigt Gewinn/Verlust-Statistiken in einem übersichtlichen On-Chart-Panel an. Die wichtigsten Funktionen sind: Kauf-/Verkaufssignale auf Basis von MA-Crossovers

3 500 USD

GEM Signal Pro GEM Signal Pro ist ein Trendfolge-Indikator für MetaTrader 5 und wurde für Trader entwickelt, die klarere Signale, strukturiertere Setups und ein praktisches Risikomanagement direkt im Chart wünschen. Anstatt nur einen einfachen Pfeil anzuzeigen, hilft GEM Signal Pro dabei, die komplette Handelsidee klarer und übersichtlicher darzustellen. Wenn die Bedingungen bestätigt sind, kann der Indikator Einstiegskurs, Stop Loss und Take-Profit-Ziele direkt im Chart anzeigen, damit der Trad

259 USD

Einzigartiger Gann-Indikator für XAUUSD IQ Gold Gann Levels ist ein Präzisionsinstrument, das ausschließlich für den Intraday-Handel mit XAUUSD/Gold entwickelt wurde und nicht nachgemalt wird. Es verwendet die Quadratwurzelmethode von W.D. Gann, um Unterstützungs- und Widerstandsniveaus in Echtzeit darzustellen, und hilft Händlern, hochwahrscheinliche Einstiegsmöglichkeiten mit Vertrauen und Klarheit zu erkennen. William Delbert Gann (W.D. Gann) war ein außergewöhnlicher Marktanalyst, dessen Han

189 USD

Spezialisiert auf (Alle Broker werden unterstützt): Professionelle Trading Tools Wollen Sie die gleichen Tools, die von professionellen Tradern verwendet werden? Holen Sie sie sich jetzt und beginnen Sie, die Märkte zu dominieren! Treten Sie kostenlos unseren Premium-Communities bei: Spezialisiert auf (Alle Broker werden unterstützt): Gold (XAUUSD) - Unerreichte Genauigkeit Forex-Paare - Umfassende globale Marktabdeckung Binäre Optionen - Hochpräzise Signale ️ Synthetische

599 USD

Analytik auf institutionellem Niveau für MT5 Die CGE Trading Suite bietet den analytischen Vorsprung, der normalerweise professionellen Trading Desks vorbehalten ist. Die Plattform integriert eine ganze Reihe von Analysetools in einen nahtlosen Workflow: dynamisches Grid Mapping, Liquiditätsverhaltensanalyse, ECM, Trendlinien, MIDAS, Handelszyklen und direktionale Kanalprojektionen. Zusammen bieten sie eine einheitliche Sicht auf die Marktstruktur und -dynamik. Der Kapitalflussindex, der die St

2 499 USD

Euro Escalper — Professioneller institutioneller Scalping-Indikator Euro Escalper ist ein leistungsstarker Trading-Indikator fuer Trader, die institutionelle Praezision bei jedem Einstieg fordern. Er funktioniert mit Synthetischen Indizes (Deriv), Forex und jedem Vermoegenswert auf MetaTrader 5. Er kombiniert Fibonacci-basierte Liquiditaetszonen, eine integrierte SuperTrend-Engine und ein professionelles Echtzeit-Dashboard. Hauptvorteile Kein Neuzeichnen: Signalpfeile erscheinen nur beim Kerzens

3 500 USD

Die Propfolio Master Suite ist die ultimative analytische All-in-One-Workstation für professionelle Trader. Die Suite kombiniert die Leistungsfähigkeit der Beat The Market Maker (BTMM)-Methode, der Smart Money Concepts (SND/Liquidität) und des Advanced Volume Profile und ersetzt mehrere verschiedene Indikatoren durch eine optimierte Engine. Überwachen Sie bis zu 14 Paare gleichzeitig von einem einzigen Diagramm aus, erkennen Sie sofort Marktzyklen und bilden Sie mit einem Mausklick nahtlos insti

175 USD

Der Berma Bands (BBs)-Indikator ist ein wertvolles Werkzeug für Händler, die Markttrends erkennen und daraus Kapital schlagen möchten. Durch die Analyse der Beziehung zwischen dem Preis und den BBs können Händler erkennen, ob sich ein Markt in einer Trend- oder Schwankungsphase befindet. Besuchen Sie den [ Berma Home Blog ], um mehr zu erfahren. Berma-Bänder bestehen aus drei unterschiedlichen Linien: dem oberen Berma-Band, dem mittleren Berma-Band und dem unteren Berma-Band. Diese Linien werden

150 USD

MightyPips Sentiment Pro ist ein Marktstimmungsindikator für MetaTrader 5, der Händlern hilft, den Kauf- und Verkaufsdruck auf dem Markt zu analysieren. Der Indikator wertet das Marktverhalten aus, um eine klarere Sicht auf die Trendrichtung, die Stärke des Momentums und die allgemeinen Stimmungsbedingungen zu erhalten. Er hilft Händlern zu verstehen, ob Käufer oder Verkäufer derzeit den Markt dominieren. Merkmale Käufer-Verkäufer-Analyse Zeigt das Gleichgewicht zwischen Kauf- und Verkaufsdruck

180 USD

Der AX Forex Indicator MT5 ist ein hochentwickeltes Handelsinstrument, das Händlern eine umfassende Analyse mehrerer Währungspaare bietet. Dieser leistungsstarke Indikator vereinfacht die komplexe Natur des Forex-Marktes und macht ihn sowohl für Anfänger als auch für erfahrene Trader zugänglich. AX Forex Indicator verwendet fortschrittliche Algorithmen zur Erkennung von Trends und Mustern und ist ein unverzichtbares Werkzeug für Händler, die ihre Leistung im Devisenhandel verbessern möchten. Mi

159 USD

[Special Limited Price] Release Commemoration Sale! Zur Zeit zu einem Sonderpreis erhältlich, um seine Veröffentlichung zu feiern. Der Preis wird nach einer bestimmten Zeit oder einem bestimmten Umsatzvolumen ohne Vorankündigung auf den Normalpreis zurückgesetzt. Verpassen Sie nicht die Chance, eine professionelle Handelsumgebung zum niedrigsten Preis zu erhalten! Quasar Edge & Dual Dashboard ~ Verwandeln Sie das "Chaos" von 28 Paaren in "sichere Gewinne" mit dem ultimativen MT5-Marktstruk

200 USD

Bill Williams Advanced ist für die automatische Chartanalyse nach dem System "Profitunity" von Bill Williams konzipiert. Der Indikator analysiert vier Zeitrahmen auf einmal. Manual (Be sure to read before purchasing) Vorteile 1. Analysiert den Chart nach dem "Profitunity"-System von Bill Williams. Die Signale werden in einer Tabelle in der Ecke des Bildschirms und auf dem Kurschart angezeigt. 2. Findet alle bekannten AO- und AC-Signale, sowie Zonensignale. Ausgestattet mit einem Trendfilter auf

150 USD

Dieser Indikator zeigt an, wann die vom Benutzer eingestellten Sitzungen aktiv sind, und liefert verschiedene Tools + Metriken, wobei der Schlusskurs innerhalb der aktiven Sitzungen als Eingabe verwendet wird. Benutzer haben die Möglichkeit, bis zu 4 Sitzungszeiten zu ändern. Der Indikator wird zunehmend ungenauer, wenn der Zeitrahmen des Charts größer als 1 Stunde ist. Einstellungen Sitzungen Sitzung aktivieren: Ermöglicht das Aktivieren oder Deaktivieren aller mit einer bestimmten benu

49 USD

Dies ist ein Forex Scalping Trading System, das auf den Bollinger Bändern basiert. Paare:Major Zeitrahmen: 1M oder höher. Spread max:0,0001. Indikatoren (nur ein Vorschlag) Bollinger Bänder (20, 2); ADX (14 Periode); RSI (7 Perioden). Sie sollten dieses System nur zwischen 2 Uhr morgens und 5 Uhr nachts EST, 8 Uhr morgens und 12 Uhr nachts EST und 19.30 Uhr bis 22 Uhr EST handeln. Handeln Sie nicht 30 Minuten vor einer orangefarbenen oder roten Meldung und nicht eine Stunde danach. Setup: Der K

Dies ist eine Ergänzung des effektiven SV Squeeze-Momentums , das das Bolliger-Band und den Keltner-Kanal zum Chartfenster hinzufügt. Der Squeeze-Indikator für MT5, der von John Carter eingeführt wurde, ist ein volatilitätsbasiertes Tool. Unabhängig davon können wir den Squeeze-Indikator auch als Momentum-Indikator betrachten, da viele Trader ihn nutzen, um die Richtung und Stärke von Kursbewegungen zu identifizieren. Tatsächlich zeigt der Tradingview Squeeze-Indikator an, wann ein Finanzinstrum

Der ICT Concepts-Indikator fasst die wichtigsten Konzepte des Traders und Ausbilders "The Inner Circle Trader" (ICT) in einem All-in-One-Toolkit zusammen. Zu den Funktionen gehören Marktstruktur (MSS & BOS), Orderblöcke, Ungleichgewichte, Liquidität auf der Kauf-/Verkaufsseite, Verschiebungen, ICT-Killzones und neue Wochen-/Tageseröffnungslücken. Das ist eine Art von Smart Money-Konzepten. ANWENDUNG: Bitte lesen Sie dieses Dokument ! DETAILS Struktur des Marktes Marktstruktur-Etiketten wer

55 USD

Der Indikator "Breaker Blocks with Signals" zielt darauf ab, eine vollständige Methodik auf der Grundlage von Breaker-Blöcken aufzuzeigen. Ausbruchssignale zwischen dem Preis und den Breaker-Blöcken werden hervorgehoben und Premium-/Discount-Swing-Levels sind enthalten, um potenzielle Take-Profit-/Stop-Loss-Levels bereitzustellen. Dieses Skript enthält auch Alarme für jedes hervorgehobene Signal. EINSTELLUNGEN Breaker-Blöcke Länge: Empfindlichkeit der erkannten Ausschläge, die zur

69 USD

Mehrere Dochte, die sich bei überverkauften und überkauften Niveaus bilden, erzeugen Kauf- und Verkaufsdruck. Dieser Indikator versucht, das Wesen des Kauf- und Verkaufsdrucks zu erfassen, der durch diese Dochte entsteht. Dochtdruck zeigt an, dass der Trend erschöpft ist. Der Orderblock sollte angezeigt werden, wenn der Docht Kauf- oder Verkaufsdruck erzeugt. Wenn der Preis innerhalb des Kaufauftragsblocks und bis außerhalb des Auftragsblocks geht, sollte der Händler einen Kaufauftrag in Betrach

50 USD

Der Inversion Fair Value Gaps (IFVG)-Indikator basiert auf dem Inversions-FVG-Konzept von ICT und liefert Unterstützungs- und Widerstandszonen, die auf abgeschwächten Fair Value Gaps (FVGs) basieren. Abbildung 1 ANWENDUNG Sobald die Abschwächung eines FVG erfolgt ist, erkennen wir die Zone als "Inverted FVG". Diese Zone wird nun als potenzielle Unterstützung oder Widerstand betrachtet. Eine Abschwächung tritt ein, wenn der Kurs über oder unter dem FVG-Bereich in der entgegengesetzten Rich

39 USD

Einführung Eines der Muster in "RTM" ist das "QM"-Muster, auch bekannt als "Quasimodo". Sein Name leitet sich von der Gestalt des "Glöckners von Notre-Dame" aus Victor Hugos Roman ab. Es ist eine Art "Kopf-Schulter-Muster". Entstehungsmethode Aufwärtstrend In einem Aufwärtstrend bildet sich die linke Schulter, und der Kurs bildet einen neuen Höchststand, der höher ist als der Höchststand der linken Schulter. Nach einem Rückgang gelingt es dem Kurs, das vorherige Tief zu durchbrech

49 USD

Alles über Smart Money Concepts Strategie: Markt-Struture: Interner oder Swing BOS, CHoCH; Orderblock; Liquity gleich; Fair Value Gap mit folgendem Eingriff, Ausgeglichene Preisspanne; Level mit Vormonats-, Wochen-, Tageslevel oder im Tageslevel (PMH, PWH, PDH, HOD); BuySell Stops Liquidität (BSL, SSL); Liquiditätsleere Long Wicks; Premium und Discount; Kerzenmuster ... "Smart Money Concepts" (SMC) ist ein relativ neuer, aber dennoch weit verbreiteter Begriff unter Price Action Traders, die vers

50 USD

Der Indikator liefert Pivotpunkt-basierte Trendlinien mit hervorgehobenen Ausbrüchen . Die Trendlinie wird durch den Pivot-Punkt berechnet und andere Anhaltspunkte sind ATR, Stdev. Der Indikator beinhaltet auch integrierte Alarme für Trendlinienausbrüche und die Weiterleitung von Nachrichten an Telegram-Kanäle oder Gruppen, wenn Sie dies wünschen. Einstellungen - Rückblick Bar: Standardmäßig 200 ist die Anzahl der Balken, die beim Start des Indikators kalkuliert werden. - Länge: Zeitraum der Piv

50 USD

Dieser All-in-One-Indikator zeigt die Marktstruktur in Echtzeit an (interne & Swing BOS / CHoCH), Orderblöcke, Premium- & Discount-Zonen, gleiche Hochs & Tiefs und vieles mehr... und ermöglicht Händlern, ihre Charts automatisch mit weit verbreiteten Preisaktionsmethoden zu markieren. Nach der Veröffentlichung unseres Fair Value Gap-Skripts erhielten wir zahlreiche Anfragen aus unserer Community, weitere Funktionen in derselben Kategorie zu veröffentlichen. //------------------------------------

50 USD

69 USD

55 USD

Der FollowLine-Indikator ist ein Trendfolgeindikator. Die blauen/roten Linien werden aktiviert, wenn der Kurs oberhalb des oberen Bollinger Bandes oder unterhalb des unteren Bandes schließt. Sobald der Trigger der Trendrichtung erfolgt ist, wird die FollowLine auf dem Hoch oder Tief platziert (je nach Trend). Ein ATR-Filter kann ausgewählt werden, um die Linie auf einem weiter entfernten Niveau zu platzieren als der normale Modus, der sich an den Hochs/Tiefs der Kerzen festsetzt. Einige Fu

39 USD

Der ICT Silver Bullet-Indikator ist von den Vorträgen des "The Inner Circle Trader" (ICT) inspiriert und hebt das Silver Bullet-Fenster (SB) hervor, ein spezifisches 1-Stunden-Intervall, in dem sich ein Fair Value Gap (FVG) Muster bilden kann. Ein ausführliches Dokument über ICT Silver Bullet finden Sie hier . Es gibt 3 verschiedene Silver Bullet-Fenster (New Yorker Ortszeit): Das London Open Silver Bullet (3 AM - 4 AM ~ 03:00 - 04:00) Die AM Session Silver Bullet (10 AM - 11 AM ~ 10:00 - 11:00

55 USD

49 USD

Der Liquiditätsschwankungsindikator hebt Schwankungsbereiche mit bestehender Handelsaktivität hervor. Die Anzahl der Kursrückgänge in einem Swing-Bereich wird durch eine Zone hervorgehoben, die die Swing-Bereiche begrenzt. Zusätzlich wird das kumulierte Volumen innerhalb der Swing-Bereiche durch Beschriftungen im Diagramm hervorgehoben. Eine Option zum Herausfiltern von Swing-Bereichen mit Volumen/Zahlen, die einen vom Benutzer festgelegten Schwellenwert nicht erreichen, ist ebenfalls enthalten.

46 USD

Der SuperTrend AI-Indikator ist ein neuartiger Ansatz, um die Lücke zwischen der maschinellen Lernmethode K-Means-Clustering und technischen Indikatoren zu schließen. In diesem Fall wenden wir K-Means-Clustering auf den berühmten SuperTrend-Indikator an. ANWENDUNG Benutzer können den SuperTrend AI Trailing Stop ähnlich wie den regulären SuperTrend-Indikator interpretieren. Die Verwendung höherer Minimum/Maximum-Faktoren führt zu längerfristigen Signalen. (Abbildung 1) Die für jedes Signal ang

99 USD

" ÜBERBLICK Ein Lorentzian Distance Classifier (LDC) ist ein Klassifikationsalgorithmus des maschinellen Lernens, der historische Daten aus einem mehrdimensionalen Merkmalsraum kategorisieren kann. Dieser Indikator zeigt, wie die Lorentzsche Klassifizierung auch zur Vorhersage der Richtung zukünftiger Kursbewegungen verwendet werden kann, wenn sie als Abstandsmetrik für eine neuartige Implementierung eines ANN-Algorithmus (Approximate Nearest Neighbors) eingesetzt wird. Dieser Indikator liefer

99 USD

Dieses Skript berechnet und aktualisiert automatisch die täglichen IPDA-Rückblick-Zeitintervalle und die entsprechenden Abschläge/Gleichgewichte/Aufschläge, damit Sie das nicht tun müssen :) IPDA steht für Interbank Price Delivery Algorithm. Dieser Algorithmus bezieht sich auf die Intervalle der letzten 20, 40 und 60 Tage als Bezugspunkte für die Definition von Spannen und zugehörigen PD-Bereichen. Intraday-Händler können den größten Wert in der 20-Tage-Look-Back-Box finden, indem sie Ungleichge

39 USD

Ein Implied Fair Value Gap (IFVG) ist eine von ICT konzipierte Ungleichgewichtsformation aus drei Kerzen, die auf der Erkennung eines größeren Kerzenkörpers und der anschließenden Messung des Durchschnitts zwischen den beiden benachbarten Kerzenschatten basiert. Dieser Indikator erkennt diese Ungleichgewichtsformation automatisch auf Ihren Charts und kann um eine vom Benutzer festgelegte Anzahl von Balken erweitert werden. Der IFVG-Durchschnitt kann auch verlängert werden, bis ein neues IFVG

30 USD

Von Konsolidierung spricht man, wenn sich der Kurs innerhalb einer klaren Handelsspanne bewegt. Wenn die Kurse konsolidiert sind, zeigt dies, dass der Market Maker Aufträge auf beiden Seiten des Marktes platziert. Dies ist vor allem darauf zurückzuführen, das uninformierte Geld zu manipulieren. Dieser Indikator identifiziert automatisch Konsolidierungszonen und zeichnet sie auf dem Chart ein. Die Methode zur Bestimmung der Konsolidierungszonen basiert auf Pivot-Punkten und ATR, was eine präzise

39 USD

Dieser Indikator stellt einen alternativen Ansatz zur Ermittlung der Marktstruktur dar. Die verwendete Logik ist von Lernmaterial abgeleitet, das von DaveTeaches (auf X) erstellt wurde Upgrade v1.10: Option hinzufügen, um geschützte Hoch-/Tiefwerte in den Puffer zu legen (Abbildung 11, 12) Bei der Quantifizierung der Marktstruktur ist es üblich, fraktale Hochs und Tiefs zu verwenden, um "signifikante" Swing-Pivots zu identifizieren. Wenn der Kurs durch diese Pivots schließt, können wir einen M

45 USD

Dieser Indikator bietet die Möglichkeit, das SMC-Muster zu erkennen, im Wesentlichen eine verkürzte Version des Wyckoff-Modells. Sobald das Muster von RTO bestätigt wird, stellt es eine bedeutende Investitionsmöglichkeit dar. Es gibt zahlreiche Indikatoren, die sich auf SMC über den Markt hinaus beziehen, aber dies ist der erste Indikator, der Muster nutzt, um spezifische Aktionen von BigBoy zu identifizieren, um den Markt zu steuern. Aktualisierung 2024-03-08: Hinzufügen der Funktion TP by RR.

79 USD

Erstellt von imjesstwoone und mickey1984, versucht dieses Handelsmodell, die Expansion von 10:00-14:00 EST 4h Kerze mit nur 3 einfachen Schritten zu erfassen. Alle in dieser Beschreibung dargestellten Informationen wurden von den Machern des Modells zusammengestellt, ich habe sie lediglich auf MQL4 übertragen. Alle Grundeinstellungen des Handelsmodells können bearbeitet werden, so dass die Benutzer mehrere Varianten testen können. Diese Beschreibung wird jedoch das standardmäßige, beabsichtigte

59 USD

Der Buyside & Sellside Liquidity Indikator zielt darauf ab, das erste und wohl wichtigste Konzept innerhalb der IKT-Handelsmethodik, die Liquiditätsniveaus , zu erkennen und hervorzuheben . EINSTELLUNGEN Liquiditätsniveaus Erkennungslänge: Lookback-Periode Spanne: Legt die Marge/Empfindlichkeit für eine Liquiditätsstufenerkennung fest Liquiditätszonen Liquiditätszonen auf der Käuferseite: Aktiviert die Anzeige der Liquiditätszonen auf der Käuferseite. Spanne: Legt die Marge/Empfi

50 USD

Der experimentelle Indikator Liquidation Estimates (Real-Time) versucht, Long- und Short-Liquidationen auf allen Zeitskalen in Echtzeit aufzuzeigen. Mit Liquidationen ist hier der Prozess gemeint, bei dem die Position eines Händlers im Markt zwangsweise geschlossen wird. Durch die Analyse von Liquidationsdaten können Händler die Marktstimmung einschätzen, potenzielle Unterstützungs- und Widerstandsniveaus identifizieren, mögliche Trendumkehrungen erkennen und fundierte Entscheidungen über Ein-

39 USD

Der ICT Unicorn Model Indikator hebt das Vorhandensein von "Einhorn"-Mustern auf dem Chart des Benutzers hervor, die aus den Lehren von "The Inner Circle Trader" (ICT) abgeleitet sind. Auf die erkannten Muster folgen Ziele mit einem vom Benutzer kontrollierten Abstand. ANWENDUNG (Bild 2) Das ICT Unicorn Model basiert im Kern auf zwei populären Konzepten: Fair Value Gaps und Breaker Blocks. Diese Kombination hebt einen zukünftigen Unterstützungs-/Widerstandsbereich hervor. Ein Bullish Un

69 USD

" Übersicht Der Volume SuperTrend AI ist ein fortschrittlicher technischer Indikator zur Vorhersage von Preistrends durch eine Kombination aus traditioneller SuperTrend-Berechnung und KI-Techniken, insbesondere dem k-nearest neighbors (KNN)-Algorithmus. Der Volume SuperTrend AI wurde entwickelt, um Händlern Einblicke in potenzielle Markttrends zu geben, indem er sowohl volumengewichtete gleitende Durchschnitte (VWMA) als auch den k-nearest neighbors (KNN)-Algorithmus verwendet. Durch die Komb

49 USD

" ÜBERBLICK K-means ist ein Clustering-Algorithmus, der häufig beim maschinellen Lernen verwendet wird, um Datenpunkte auf der Grundlage ihrer Ähnlichkeiten in verschiedene Cluster einzuteilen. K-means wird zwar in der Regel nicht direkt zur Identifizierung von Unterstützungs- und Widerstandsniveaus auf den Finanzmärkten verwendet, kann aber als Werkzeug in einem umfassenderen Analyseansatz dienen. Unterstützungs- und Widerstandsniveaus sind Kursniveaus auf den Finanzmärkten, auf denen der

49 USD

Auswahl:

Keine Bewertungen

SV Harmozup Pattern

Minh Truong Pham