Einführung in die empirische Bandzerlegung (EMD)
2 193
0
Einleitung
Alle Vorgänge, mit denen wir es in der Praxis tatsächlich zu tun haben, sind komplex und bestehen in der Regel aus einer Vielzahl unterschiedlicher Elemente. Nehmen wir beispielsweise das Wetter. Bei der Analyse eines Niederschlagsdiagramms müssen wir uns vergegenwärtigen, dass wir ein Diagramm vor uns haben, das Wechselwirkungen einer Reihe ganz unterschiedlicher Abläufe wiedergibt, wie Jahreszeitenwechsel, die globale Erwärmung/Abkühlung, Änderungen der Meeresströmungen, die Entwicklungsdynamik von Hoch- und Tiefdruckgebieten, die Menge der Kohlendioxidemissionen in die Atmosphäre, Sonnenaktivitätszyklen usw. Diese Aufstellung ließe sich endlos fortsetzen.
Deshalb ist es recht schwierig, ein derartiges Diagramm unmittelbar zu analysieren, da seine einander wechselseitig beeinflussenden Bestandteile die Gesetzmäßigkeiten, die wir herausarbeiten möchten, verschleiern und verzerren. In diesem Fall entsteht der legitime Wunsch, den zu beobachtenden Vorgang in seine Einzelglieder zu zerlegen und diese jeweils einzeln zu untersuchen. Die Analyse der einzelnen Elemente und die Untersuchung des Beitrages eines jeden von ihnen zu dem betreffenden Vorgang verbessern das Verständnis der Abläufe und erhöhen die Zuverlässigkeit von Vorhersagen.
Keine Ausnahme bilden auch die unterschiedlichen Börseninformationen, die wir erhalten, darunter auch diejenigen bezüglich der Notierungen von Währungspaaren, die ebenfalls unter Wechselwirkung einer großen Anzahl unterschiedlicher Faktoren gebildet werden. Es ist deshalb absolut angemessen zu erwarten, dass ihre vorherige Zerlegung in einzelne Bestandteile ihre weitere Analyse erheblich erleichtern kann.
Der Begriff „Dekomposition“ bedeutet förmlich die Zerlegung eines zusammengesetzten Vorgangs oder Werkstoffs in seine jeweiligen Einzelteile. Bereits seit geraumer Zeit wird dieser Begriff im Zusammenhang mit der Analyse verschiedenster Vorgänge, der Signalanalyse, der Untersuchung von Folgen unterschiedlichster Art usw. in einem wesentlich umfassenderen Sinn verwendet, der häufig genug nicht die Zerlegung in die tatsächlich vorhandenen ursprünglichen Bestandteile bezeichnet, sondern die in irgendwelche Funktionen, die bei der Zusammenstellung der ursprünglichen Daten in der Realität gar nicht vorhanden waren. Diese Funktionen werden im Verlauf der Zerlegung der Ausgangsdaten zwar gleichsam künstlich angelegt, ermöglichen aber trotz dieses „unnatürlichen“ Ursprungs die Durchführung einer tiefer gehenden Analyse besagter Daten, indem sie zur Enthüllung verborgener Gesetzmäßigkeiten beitragen.
Die überwältigende Mehrzahl der bei der Marktanalyse eingesetzten Methoden gehört direkt oder indirekt zu den Verfahren zur Aussonderung einzelner Elemente aus dem jeweils zu untersuchenden Vorgang, das heißt zu den Verfahren zu dessen Zerlegung. Wir wollen uns einige davon kurz ansehen.
1. Zerlegung (Dekomposition)
Es gibt eine große Zahl vielfältigster in der Praxis verwendeter Verfahren zur Zerlegung einer zu untersuchenden Folge. Diese Verfahren können auf unterschiedlichen mathematischen oder empirischen Ansätzen beruhen und ein unterschiedliches Maß an Komplexität sowie verschiedene Anwendungsbereiche aufweisen.
So kann beispielsweise selbst die fundamentale Marktanalyse, wenn auch etwas bemüht, zu den Zerlegungsverfahren gezählt werden. Bei dieser Art der Analyse wird der Versuch der Untersuchung unternommen, die unmittelbaren Auswirkungen einer Auswahl von Ausgangsereignissen auf das Marktgeschehen zu untersuchen. Das heißt, es erfolgt eine nicht ausdrückliche Zerlegung des zu untersuchenden Marktgeschehens in eine Reihe von Ereignissen, aus denen es sich zusammensetzt.
Weiter werden wir uns mit Fragen bezüglich der grundlegenden Analyse nicht befassen. Wir gehen davon aus, dass wir über keinerlei weitere Informationen über den zu untersuchenden Vorgang verfügen, sondern uns lediglich auf eine Folge stützen können, die diesen Vorgang abbildet.
Das einfachste Beispiel für eine Zerlegung ist die Untergliederung einer Folge in mehrere Einzelteile mithilfe der üblichen allgemein bekannten Verfahren. Etwa wenn wir in dem Diagramm eines beliebigen Währungspaares (Kürzels) den gleitenden Durchschnittswert (MA) bilden. Den resultierenden Graphen ziehen wir anschließend von der ursprünglichen Folge ab. Daraufhin erhalten wir zwei Bestandteile der Ausgangsfolge, den Graphen der gleitenden Durchschnittswertes (MA) und das Residuum, den Rest. Wenn wir auf das resultierende Residuum dasselbe Verfahren anwenden allerdings mit einem MA für einen längeren Zeitraum, erhalten wir bereits drei Elemente: zwei MA-Graphen sowie das Residuum, den Rest, der Umwandlung. Unübersehbar ist der Zerlegungsvorgang auch mit den vorhandenen Mitteln leicht zu organisieren. Der entscheidende Punkt sind die Eigenschaften der Ergebnisse dieses Vorgangs.
Unter den bekannten Zerlegungs- und Spektralanalyseverfahren ist vor allem die Umwandlung nach Fourier hervorzuheben. Die Fourier-Transformation gehört zur Klasse der orthogonalen Umwandlungen, in denen eine feste Basis harmonischer Funktionen zum Einsatz kommt. Das Ergebnis der Fourier-Transformation können wir uns als Zerlegung des ursprünglichen Vorgangs in harmonische Funktionen mit fester Frequenz und Amplitude vorstellen. Wir halten zwei für uns wichtige Aspekte fest.
Zunächst einmal wird die Umwandlung stets in einer festen, vorher festgelegten Basis orthogonaler Funktionen ausgeführt. Das heißt, die Transformationsbasis hängt nicht von der Eigenschaft der umzuwandelnden Folge ab.
Zweitens weisen die resultierenden harmonischen Elemente stets konstante Amplituden- und Frequenzwerte auf. Das heißt, ihre Parameter sind über die gesamte Länge der Ausgangsfolge unveränderlich sind. Was wiederum bedeutet, dass bei einer Änderung der Eigenschaften der Ausgangsfolge während des betrachteten Zeitraums diese Änderungen in den Umwandlungsergebnissen nicht widergespiegelt werden. Die in einem solchen Fall erhaltenen Ergebnisse geben nur einen bestimmten gemittelten Zustand des Vorgangs wieder, da diese Umwandlung unter der Annahme der Stationarität der Ausgangsdaten angelegt wurde.
Um die mit der Nichtstationarität der Ausgangsfolge verbundenen Beschränkungen zu umgehen, können wir von der Fourier- zur Wavelet-Transformation übergehen. Wie Erstere führt auch die Wavelet-Transformation die Zerlegung in einer festen Basis von Funktionen aus. Anders als bei der Fourier-Transformation muss diese Basis voreingestellt sein, das heißt, die bei der Umwandlung zu verwendende Wavelet-Funktion muss bereits ausgewählt worden sein.
Ebenfalls im Gegensatz zur Fourier-Transformation weist jedes aus einer Wavelet-Transformation resultierende Element Parameter auf, durch die sein Maßstab und sein Niveau zeitlich bestimmt werden. Damit wäre das Problem der möglichen Nichtstationarität des zu analysierenden Vorgangs gelöst.
Sowohl die Fourier- als auch die Wavelet-Transformation verdanken ihre weite Verbreitung den in ihnen verwendeten bewährten mathematischen Verfahren und der Verfügbarkeit effektiver Algorithmen zu ihrer Umsetzung. Außerdem sind beide Umwandlungen, wie die Praxis zeigt, recht vielseitig und können erfolgreich in den unterschiedlichsten Bereichen eingesetzt werden.
Aber für den praktischen Einsatz bräuchte man eine Umwandlung, die nicht nur die Arbeit mit nichtstationären Vorgängen ermöglicht, sondern bei der Umwandlung auch eine anpassungsfähige, durch die jeweiligen Ausgangsdaten bestimmte Basis verwendet. Eine solche Umwandlung gibt es, wir sehen sie uns kurz an, bevor wir zum eigentlichen Thema dieses Beitrags kommen.
2. Die empirische Bandzerlegung (Empirical Mode Decomposition)
Die empirische Bandzerlegung (EMD) wurde als elementarer Bestandteil der Hilbert-Huang-Transformation (HHT) vorgeschlagen. Die Hilbert-Huang-Transformation erfolgt gleichsam in zwei Etappen. Zunächst ermitteln wir mithilfe des EMD-Algorithmus die empirischen Bänder oder inneren Schwingungen (Intrinsic Mode Functions, kurz IMF).
Anschließend wird auf deren Grundlage in der zweiten Etappe mithilfe der Hilbert-Transformation das momentane Frequenzspektrum der Ausgangsfolge ermittelt. Die Hilbert-Huang-Transformation ermöglicht die Ermittlung des momentanen Frequenzspektrum nichtlinearer nichtstationärer Folgen. Entsprechend ist auch die empirische Bandzerlegung für die Arbeit mit derartigen Folgen gedacht.
In diesem Beitrag werden wir die Abbildung des momentanen Frequenzspektrums mithilfe der Hilbert-Transformation nicht weiter betrachten. Wir halten uns einzig an den Algorithmus der empirischen Bandzerlegung (EMD).
Im Gegensatz zu den bereits vorgestellten Fourier- und Wavelet-Transformationen erfolgt im Verlauf der empirischen Bandzerlegung die Zerlegung in empirische Bänder (innere Schwingungen, IMF), die nicht analytisch festgelegt wurden und lediglich durch die zu untersuchende Folge selbst bestimmt werden. Dabei werden die Basisfunktionen der Umwandlung variabel, unmittelbar aus den Eingangsdaten gebildet. Die bei der Verwendung des EMD-Verfahrens ausgesonderten inneren Schwingungen (IMF) müssen folgende Vorgaben erfüllen:
- Die Anzahl der Extremwerte der IMF (die Summe der Höchst- und Tiefstwerte) sowie die Anzahl der Schnittpunkte der Nulllinie dürfen nicht um mehr als „1“ voneinander abweichen;
- An einem beliebigen Punkt einer inneren Schwingung muss der Durchschnittswert der durch die lokalen Höchst- und Tiefstwerte bestimmten Umhüllenden (Envelopes) gleich Null sein.
Im Verlauf der Zerlegung erhalten wir eine Familie der Frequenz nach geordneter Funktionen der inneren Schwingungen (IMF). Die jeweils nächste IMF weist eine geringere Frequenz auf als die vorhergehende. Die Verwendung des Begriffs „Frequenz“ ist in Bezug auf IMF nicht ganz korrekt, obwohl er vermutlich am besten zur Bestimmung von deren Eigenschaften geeignet ist. Es geht darum, dass, auch wenn die IMF Schwingungseigenschaften aufweist, gerade diese Schwingung zeitlich sowohl der Frequenz als auch der Amplitude nach modelliert werden kann.
Das Ergebnis der Arbeit des EMD-Algorithmus verbal darzustellen ist recht schwierig, weshalb wir uns seiner Umsetzung in Programmform zuwenden, was uns die Möglichkeit eröffnet, die Besonderheiten der Funktionsweise des besagten Algorithmus kennenzulernen.
3. Der EMD-Algorithmus
Die Grundlage des von Huang vorgeschlagenen Algorithmus bildet die Erstellung geglätteter Umhüllender (Envelopes) anhand der Höchst- und Tiefstwerte der Folge sowie die anschließende Subtraktion des Durchschnittswertes dieser Umhüllenden von der Ausgangsfolge. Dazu werden die Höchst- und Tiefstwerte ermittelt und die durch diese Punkte verlaufenden Spline-Kurven angelegt, die als obere und untere Umhüllende dienen.
Der Vorgang der Erstellung der Umhüllenden (Envelopes) wird in der Abbildung 1 wiedergegeben:
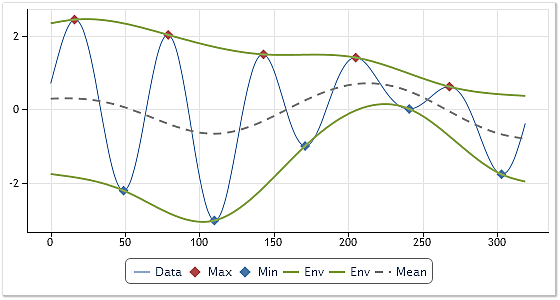
Abb. 1. Anlegen der Umhüllenden und ihrer Mittellinie
Die zu analysierende Folge wird in der Abbildung 1 als schmale blaue Linie wiedergegeben. Die Höchst- und Tiefstwerte dieser Folge sind in roter bzw. blauer Farbe gekennzeichnet. Die Umhüllenden werden grün dargestellt.
Aus den beiden Umhüllenden wird der in der Abbildung 1 als gestrichelte Linie dargestellte Durchschnittswert errechnet. Der so ermittelte Durchschnittswert wird dann von der Ausgangsfolge subtrahiert.
Im Ergebnis der aufgeführten Schritte findet sich die gesuchte empirische Funktion bei der ersten Annäherung. Um die IMF vollständig abzugrenzen, müssen die Höchst- und Tiefstwerte bei dieser Berechnung der IMF erneut ermittelt und dann die oben aufgeführten Schritte werden. Dieser wiederholte Vorgang wird als Sieben (Sifting) bezeichnet. Der Siebevorgang wird solange fortgesetzt, bis das vorgegebene Haltekriterium erreicht ist. Die Auswahl der Haltekriterien für den Siebevorgang ist eines der Schlüsselmomente mit Auswirkungen auf das Ergebnis der Zerlegung insgesamt. Auf diese Frage kommen wir etwas später noch zurück.
Nach erfolgreichem Abschluss des Siebevorgangs erhalten wir als Ergebnis die erste gefundene empirische Funktion (IMF). Weiterhin müssen wir zur Ermittlung der nächsten IMF die bereits gefundene von dem Ausgangssignal abziehen und anschließend das vorgestellte Verfahren wiederholen und immer so weiter, bis alle IMF ermittelt sind. Die Suche nach der jeweils nächsten IMF endet für gewöhnlich dann, wenn das Residuum beispielsweise nicht mehr als zwei Extrempunkte aufweist.
Wie zu sehen beruht das beschriebene Verfahren der empirischen Bandzerlegung nicht auf strengen mathematischen Berechnungen, sondern ist, quasi als wollte es seinen Namen rechtfertigen, wirklich vollkommen empirisch. Ungeachtet seiner Einfachheit und Transparenz weist der oben beschriebene, von Huang vorgeschlagene Algorithmus eine Reihe von Gesichtspunkten auf, die man ihm als Nachteile anlasten kann.
In verschiedenen Veröffentlichungen zu diesem Thema findet sich auch eine ausführliche Betrachtung der Schwächen des von Huang vorgeschlagenen Algorithmus sowie Wege zu seiner Überarbeitung. In dem vorliegenden Beitrag werden wir unsere Aufmerksamkeit nicht auf die möglichen Varianten der Überarbeitung dieses Verfahrens zuspitzen, sondern lediglich versuchen, ihn in Programmform umzusetzen. Die Besonderheiten dieser Umsetzung wollen wir hier kurz ins Visier nehmen.
4. Die Klasse CEMDecomp
Auf der Grundlage der im Internet gefundenen Literatur zur Hilbert-Huang-Transformation und zur empirischen Bandzerlegung wurde die Klasse CEMDecomp angelegt, in der der EMD-Algorithmus umgesetzt wird. Der umgesetzte Algorithmus ähnelt im Grunde sehr dem ursprünglich von Huang vorgeschlagenen Algorithmus und weist keine weitreichenden Überarbeitungen auf.
Es folgt ein Ausschnitt aus dem in der Datei CEMDecomp.mqh am Ende dieses Beitrages enthaltenen Quellcode.
//------------------------------------------------------------------------------------ // The Empirical Mode Decomposition (EMD). //------------------------------------------------------------------------------------ class CEMDecomp:public CObject { public: int N; // Input and output data size double Mean; // Mean of input data int nIMF; // IMF counter int MaxIMF; // Maximum number of IMF int MaxIter; // Maximum number of iterations int FixedIter; // 0-variable number of sifting iterations; // 1-always ten sifting iterations. double IMFResult[]; // Result private: double X[]; double Imf[]; double XMax[]; // x of local maxima double YMax[]; // y of local maxima double XMin[]; // x of local minima double YMin[]; // y of local minima double EnvUpp[]; // Upper envelope double EnvLow[]; // Lower envelope double Eps; // Accuracy comparison of floating-point numbers double Tol; // Accuracy of calculation IMF public: void CEMDecomp(void); int Decomp(double &y[]); // Decomposition void GetIMF(double &x[], int nn); // Get IMF number nn private: int arrayprepare(void); void extrema(double &y[],int &nmax,double &xmax[],double &ymax[], int &nmin,double &xmin[],double &ymin[]); int SplineInterp(double &x[],double &y[],int n,double &x2[], double &y2[],int btype=0); };
Wir betrachten die in der Klasse CEMDecomp deklarierten öffentlich zugänglichen (public) Variablen und Methoden.
N steht für die Anzahl der Elemente in der Folge. Der Wert der Variablen N wird nach dem Aufruf der Methode Decomp() gebildet und ist gleich der Länge der Eingangsfolge. Die gefundene IMF muss dieselbe Größe aufweisen.
Mean ist der Durchschnittswert der Eingangsfolge. Der Wert wird nach dem Aufruf der Methode Decomp() gebildet.
nIMF ist der IMF-Zähler. Nach dem Aufruf der Methode Decomp() enthält er die Anzahl der ermittelten IMF plus zwei. Somit gibt diese Größe an, wie viele Elemente mithilfe der Methode GetIMF() ausgelesen werden können. Dabei enthält das Element mit der Kennziffer „0“ stets die ursprüngliche Folge, von der der Durchschnittswert subtrahiert wurde, während das Element mit der Kennziffer nIMF den Rest der Zerlegung, das Residuum, enthält.
MaxIMF ist die zulässige Höchstzahl an IMF. Die Zerlegung der Eingangsfolge in einzelne IMF endet, wenn deren Zahl den Wert MaxIMF erreicht. Der Wert dieser Variablen kann vor dem Aufruf der Methode Decomp() eingegeben werden. Er ist auf 16 voreingestellt.
MaxIter ist die zulässige Höchstzahl der Iterationen beim Sieben (Sifting). Wenn die Anzahl der Iterationen beim Sieben diesen Wert erreicht, wird der Siebevorgang unabhängig davon abgeschlossen, ob die vorgegebene Genauigkeit erreicht worden ist oder nicht. Der Wert dieser Variablen kann vor dem Aufruf der Methode Decomp() eingegeben werden. Die Voreinstellung lautet 2.000.
FixedIter ist die Markierung (Fahne), mit deren Hilfe ein Haltekriterium für den Siebevorgang festgelegt werden kann. Wenn der Wert für FixedIter gleich Null ist, wird der Siebevorgang für jede IMF bei Erreichen der vorgegebenen Genauigkeit beendet. Zum Erreichen der vorgegebenen Genauigkeit bei der Ermittlung unterschiedlicher IMF ist möglicherweise eine wechselnde Anzahl von Iterationen erforderlich. Wird der Wert für FixedIter auf „1“ eingestellt, so erfolgt die Ermittlung einer beliebigen IMF stets in 10 Iterationen. Der Wert dieser Variablen kann vor dem Aufruf der Methode Decomp() eingegeben werden. Er ist werksseitig auf „0“ voreingestellt.
Decomp(double &y[]) bildet die die Zerlegung umsetzende Hauptmethode der Klasse. Als Eingangsparameter erhält sie eine Verknüpfung zu dem Datenfeld mit den Eingangsdaten. Nach erfolgreicher Ausführung entspricht die Variablen N der Länge des Eingangsdatenfeldes. Dasselbe Maß müssen auch die gefundenen IMF aufweisen. Die Variable Mean entspricht dem Durchschnittswert der Eingangsfolge, und die Variable nIMF der Anzahl der Elemente, die mithilfe der Methode GetIMF() ausgelesen werden können.
GetIMF(double &x[], int nn) dient der Gewährleistung des Zugriffs auf die mithilfe der Methode Decomp() ermittelten Ergebnisse. Als Eingangsparameter erhält sie die Adresse des Datenfeldes, in das das Element mit einer durch den Parameter nn festgelegten Kennziffer kopiert wurde. Dabei enthält das Element mit der Kennziffer „0“ stets die ursprüngliche Folge, von der der Durchschnittswert subtrahiert wurde, während das Element mit der Kennziffer nIMF den Rest der Zerlegung, das Residuum, enthält. Erweist sich die Länge des als Parameter weitergegebenen Datenfeldes als kürzer als die Länge des resultierenden Elements, so wird das Datenfeld nur in dem Umfang gefüllt, den seine Länge zulässt.
Die Anwendung der Klasse CEMDecomp wird im folgenden Beispiel veranschaulicht:
#include "CEMDecomp.mqh" //------------------------------------------------------------------------------------ // Script program start function //------------------------------------------------------------------------------------ void OnStart() { int n,ret; double yy[],imf2[]; n=400; // Input sequence length ArrayResize(yy,n); // Array of input data ArrayResize(imf2,n); // Array for reading the results CopyOpen(_Symbol,PERIOD_CURRENT,0,n,yy); // Generation of input data CEMDecomp *emd=new CEMDecomp(); // Creation of the CEMDecomp class instance ret=emd.Decomp(yy); // Decomposition of the input sequence if((ret==0)&&(emd.nIMF>3)) // If there is no error and the sufficient // number of components was extracted, emd.GetIMF(imf2,2); // copy component number 2 into // array imf2[]. delete(emd); // Deletion of the CEMDecomp class instance // One of the extracted components in array imf2[]. } //------------------------------------------------------------------------------------
Am Ende dieses Beitrages findet sich in der gepackten Datei CEMDecomposition.zip ein vollständiges Beispiel für eine Zerlegung einschließlich der Wiedergabe der gefundenen IMF mithilfe eines Webbrowsers. Um dieses Beispiel aufzurufen, muss die genannte gepackte Datei entpackt und das Verzeichnis \CEMDecomposition einschließlich seines gesamten Inhalts in dem Verzeichnis \Indicators oder \Scripts des Ausgabegerätes (Terminals) abgelegt werden. Danach kann das Skript EMDecomp_Test.mq5 zusammengestellt und ausgeführt werden. Es sei daran erinnert, dass dazu auf dem Ausgabegerät die Verwendung externer Bibliotheken zugelassen sein muss.
In der Abbildung 2 wird ein weiteres Beispiel für eine Zerlegung aufgeführt, in dem die Zerlegung der Kursnotierungen für das Kürzel USDJPY, Daily, mit einer Länge von 100 Elementen wiedergegeben wird. Wie zu sehen wurden infolge der Zerlegung dieser Folge vier IMF mit einem Residuum gefunden.
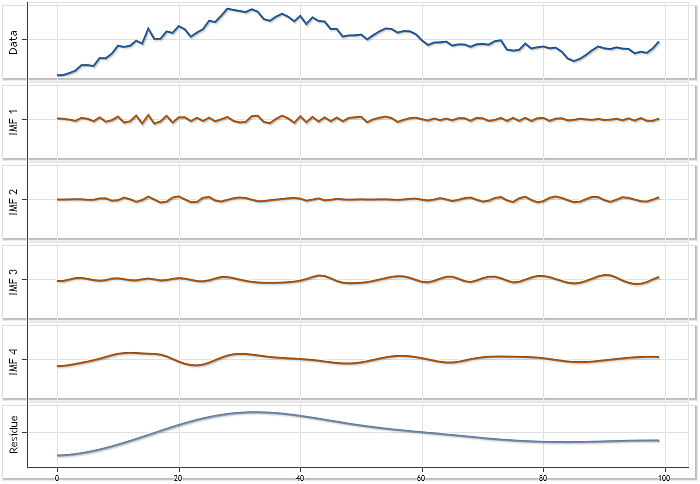
Abb. 2. Zerlegung der Folge der USDJPY-Tagesnotierungen mit N=100
In der Abbildung 2 werden alle Diagramme in einem einheitlichen Maßstab wiedergegeben, was die Beurteilung des Beitrags jeder der ermittelten IMF ermöglicht. Bei einer solchen Anlage der Diagramme treten die Besonderheiten jeder einzelnen dieser IMF jedoch nicht ausreichend deutlich zutage. In der Abbildung 3 sind dieselben Ergebnisse dargestellt, aber diesmal kommt bei jedem der Diagramme das Verfahren der automatischen Maßstabeinstellung zur Anwendung.
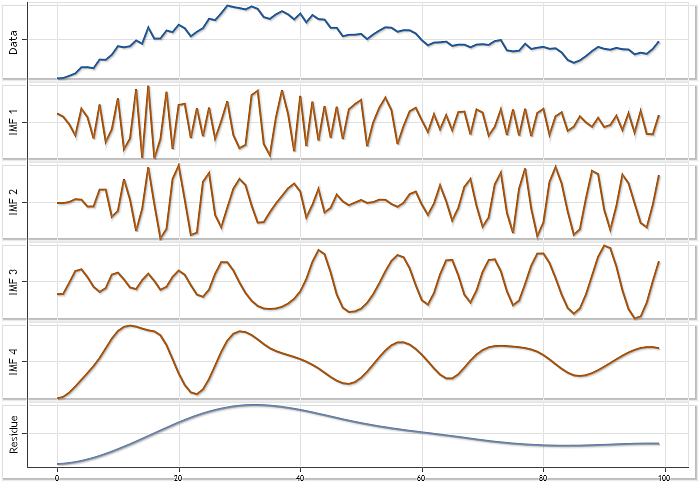
Abb. 3. Zerlegung der Folge der USDJPY-Tagesnotierungen mit N=100. Automatische Maßstabeinstellung.
Obwohl die Abbildung nicht das tatsächliche Verhältnis der Amplituden der einzelnen Bestandteile wiedergibt, vermittelt die verwendete automatische Einstellung des Maßstabs eine ausführlichere Vorstellung von jedem von ihnen.
5. Erläuterungen zu der vorliegenden Umsetzung des EMD-Algorithmus
Das Erste, worauf zu achten ist, ist das Verfahren zur Bestimmung der Höchst- und Tiefstwerte der Ausgangsfolge. In unserem Fall geht es um zwei mögliche Varianten.
In der Abbildung 4 wird das Ergebnis der Ausführung des Algorithmus zur Bestimmung der Extremwerte vorgestellt
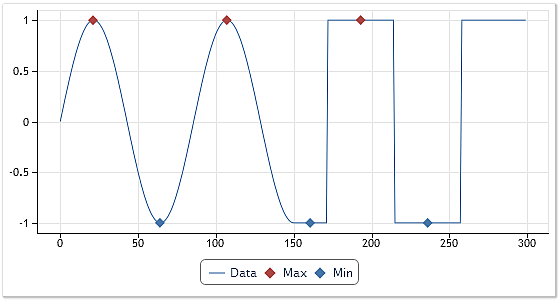
Abb. 4. Ermittlung der Extremwerte. Variante 1.
Wenn es um die Suche nach den Höchst- und Tiefstwerten der Funktion geht, wird meistens die Verwendung des folgenden Algorithmus vorgeschlagen:
- Der Wert des aktuellen Elementes der Folge wird mit denen des vorhergehenden und des nachfolgenden verglichen;
- Ist der aktuelle Wert sowohl größer als der vorhergehende als auch als der nachfolgende, so wird er als Höchstwert (Maximum) der Funktion festgelegt;
- Ist er dagegen kleiner als der vorhergehende und auch kleiner als der nachfolgende, bildet er den Tiefstwert (das Minimum) der Funktion;
Bei Folgen mit deutlich ausgeprägten Extremwerten stellt die Ermittlung der Höchst- und Tiefstwerte keine nennenswerte Schwierigkeit dar. Der vorgestellte Algorithmus funktioniert bestens. Dieser Fall wird in der ersten Hälfte des in der Abbildung 4 dargestellten Diagramms veranschaulicht. Dieser Algorithmus spricht allerdings nicht auf flache Verläufe an, bei denen die benachbarten Werte einer Folge einander gleichen.
Bei Verwendung des vorgestellten Algorithmus hätten wir den letzten Höchst- und die beiden letzten Tiefstwerte in der Abbildung 4 nicht erhalten. Einerseits wäre diese ein zu erwartendes und korrektes Ergebnis gewesen, andererseits wären jedoch in Analogie zu den Schwingungsvorgängen bei Vorliegen von Überschneidungen mit der Nulllinie ganz eindeutig einige Extremwerte verpasst worden. Es ist allerdings nicht ganz klar, ob nicht die flachen Verläufe einer Folge von rechteckiger Form oder Abschnitte mit identischen Werten als Extremwerte betrachtet werden können.
Nichtsdestotrotz wurde bei der Umsetzung der Klasse EMDecomp zur Ermittlung der Extremwerte ein gegenüber dem vorgestellten leicht überarbeiteter Algorithmus verwendet. Die Ergebnisse der Ausführung eben dieses überarbeiteten Algorithmus zeigt die Abbildung 4. Dieser Algorithmus akzeptiert als Extremwerte auch Intervalle mit gleichen Werten und platziert die Extremstellen in der Mitte dieser Intervalle.
Der Suchalgorithmus für die Höchst- und Tiefstwerte, dessen Arbeitsergebnis die Abbildung 4 zeigt, wird in der Klasse CEMDecomp zur Ermittlung der Anzahl der Extremwerte bei der Bestimmung des Zeitpunktes der Beendigung des Zerlegungsvorgangs verwendet. Wenn zum Beispiel eine IMF erhalten wird, die keinen Extremwert aufweist, wird der Zerlegungsvorgang abgebrochen, und die betreffende IMF wird aussortiert.
Wenn zur Suche nach den Extremwerten derselbe Algorithmus verwendet wird wie beim Anlegen der Umhüllenden (Envelopes), werden in Fällen, in denen die Eingangsfolge beispielsweise eine Form wie in der Abbildung 4 aufweist, Umhüllende in der Form von zwei parallel verlaufenden Linien erhalten. Des Weiteren vermag der Siebevorgang in keinster Weise, die Eingangsfolge umzuwandeln, was dazu führt, dass diese Folge nicht in ihre Bestandteile zerlegt werden kann.
Als Ausweg aus dieser Situation kann die Verwendung eines etwas anderen Algorithmus für die Suche nach den zum Anlegen der Umhüllenden benötigten Extremwerten dienen.
In der Abbildung 5 wird das Ergebnis der Arbeit eines anderen Algorithmus zur Ermittlung der Extremwerte vorgestellt.
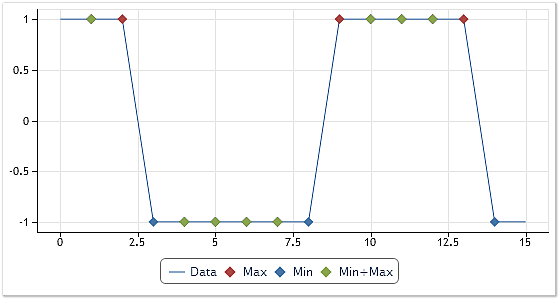
Abb. 5. Ermittlung der Extremwerte. Variante 2.
Werfen wir einen genaueren Blick auf die Abbildung 5. Anders als in der Abbildung 4 sind hier in grüner Farbe die Punkte gekennzeichnet, die gleichzeitig Höchst- und Tiefstwert, also Maximum und Minimum, sind. Wenn Umhüllende anhand derartiger Extremwerte angelegt werden, sind es bereits keine parallellaufenden Linien mehr, und im weiteren Verlauf des Siebevorgangs können überdies verborgene Bestandteile der Folge in rechteckiger Form zutage gefördert werden. Eine gute Veranschaulichung dafür ist das Muster in der gepackten Datei CEMDecomposition.zip am Ende dieses Beitrages.
Leider löst dieser Ansatz nicht alle mit der Auffindung der verborgenen Bestandteile verbundenen Probleme. Beispielsweise können die verborgenen Bestandteile einer Folge in Dreiecksform auf diese Weise nicht zutage gefördert werden. Diesen Umstand müssen wir den Nachteilen der Umsetzung dieses EMD-Algorithmus zurechnen. Möglicherweise besteht ein Ausweg aus dieser misslichen Lage darin, sich bei der Zerlegung des erweiterten Algorithmus des in dem hier vorliegenden Beitrag jedoch nicht näher betrachteten CEEMD-Verfahrens (Complementary Ensemble Empirical Mode Decomposition) zu bedienen.
Außer auf die mit der Umsetzung der Algorithmen für die Suche nach den Extremwerten verbundenen Besonderheiten ist auch das für Algorithmen dieser Art typische Problem der Randeffekte zu beachten. Zur Erläuterung des Gesagten wenden wir uns der Abbildung 1 zu. In der Abbildung 1 ist deutlich zu erkennen, dass die obere Umhüllende mithilfe einer interpolierenden Spline-Funktion mit den höchsten Punkten (den Maxima) verbunden ist.
Dabei muss die Umhüllende sowohl für die links von dem ersten als auch rechts von dem letzten höchsten Punkt liegenden Abschnitte ermittelt werden. Davon, auf welche Weise die Verlängerung der Umhüllenden erfolgt, hängt höchstwahrscheinlich der Charakter der in der Nähe ihrer Ränder ermittelten IMF ab. Ohne hinsichtlich der Umsetzung der Randeffektkorrektur in einem Programm ins Detail zu gehen, möchten wir unsere Leser lediglich auf diesen Umstand hinweisen.
Außerdem möchten wir anmerken, dass das beim Anlegen der IMF gewählte Verfahren für den Abbruch des Siebevorgangs den Charakter und die Anzahl der ermittelten IMF ebenfalls beeinflussen kann und wird. In der Klasse CEMDecomp kommt als wesentliches Verfahren zum Abbrechen des Siebevorgangs die Berechnung des Verhältnisses zum Einsatz, das angibt, wie groß die in Bezug auf den letzten Siebedurchgang ermittelte Veränderung der aktuellen IMF ist.
Hat das Sieben de facto gar keine Auswirkungen mehr auf die gesuchte IMF, so wird der Siebevorgang beendet, und die IMF gilt als fertiggestellt. Im Konstruktor der Klasse wird ein Schwellenwert als Voreinstellung für die Genauigkeit der IMF-Bildung festgelegt. Je nach Voreinstellung dieses Schwellenwertes kann die Anzahl der Siebeiterationen manchmal bis zu 200 oder gar 300 betragen. In Veröffentlichungen zu diesem Thema warnen zahlreiche Autoren vor der Verwendung einer derart hohen Zahl von Siebeiterationen. Nichtsdestoweniger ist bei dieser Umsetzung des EMD-Algorithmus die Wahl auf eben diesen voreingestellten Schwellenwert gefallen.
Diese Umsetzung des EMD-Algorithmus ermöglicht auch die Verwendung eines anderen Haltekriteriums zum Abbruch der Siebevorgänge. Dazu muss der Variablen FixedIter vor dem Aufruf der Methode Decomp() der Wert „1“ zugewiesen werden. In diesem Fall werden beim Sieben für alle IMF stets 10 Iterationen verwendet. Wir können uns leicht davon überzeugen, dass dabei diesem Vorgehen bei der Zerlegung im Vergleich zu dem voreingestellten Verfahren etwas andere Ergebnisse zutage gefördert werden.
6. Die Anwendung des EMD-Algorithmus
Da der EMD-Algorithmus ursprünglich Bestandteil der Hilbert-Huang-Transformation war, besteht ein Anwendungsbeispiel für diesen Algorithmus selbstredend in der Berechnung des Augenblicksfrequenzspektrums einer Folge. Dazu muss auf die mithilfe der EMD ermittelten Bänder die Hilbert-Transformation angewendet werden. Dieser Vorgang wird allerdings hier nicht dargestellt.
Außer zur Berechnung des Spektrums kann der EMD-Algorithmus auch zum Glätten von Folgen verwendet werden.
Die Abbildung 6 veranschaulicht diese Glättung anhand eines Beispiels:
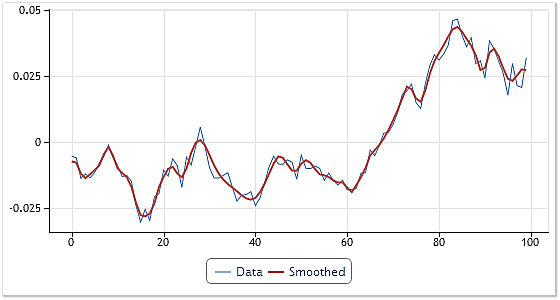
Abb. 6. Glättung einer Eingangsfolge
Für die Glättung wurde ein willkürlicher, aus 100 „offenen“ (open) Kurswerten bestehender Ausschnitt aus dem Notierungsverlauf für das Kürzel USDCHF, Daily gewählt. Während der Zerlegung ergaben sich 4 IMF und ein Rest (Residuum). Weiterhin wurde die Summe aus allen IMF mit Ausnahme der ersten und dem Residuum gebildet.
Auf diese Weise wurde aus der Eingangsfolge der ermittelte Bestandteil mit der höchsten Frequenz ausgeschlossen. Hätten wir bei der Summenbildung die ersten beiden Bestandteile ausgelassen, wäre die resultierende Kurve noch glatter.
Als weiteres Beispiel für die Verwendung der EMD kann die Erstellung einer Vorhersage auf der Grundlage der aus der Eingangsfolge ermittelten IMF dienen. Zur Erstellung der Vorhersage kann jeder Einflusswert verwendet werden, mit dessen Hilfe für jede IMF und das Residuum eine gesonderte Vorhersage abgegeben werden kann.
Anschließend wird die Summe der einzelnen Vorhersagen und damit das gesuchte Vorhersageergebnis für die ursprüngliche Folge gebildet. Unter Berücksichtigung des Schwingungscharakters der einzelnen IMF lässt sich vermuten, dass es zweckmäßig wäre, für die Vorhersage solche Einflusswerte zu wählen, die die Periodizität der vorherzusagenden Folgen mit einbeziehen.
In dem hier vorliegenden Fall betrachten wir als Beispiel das Ergebnis der Arbeit eines recht einfachen Einflusswertes, bei dem die Vorhersage für jede der IMF mittels linearer Extrapolation um 10 Schritte erstellt wird. Das Ergebnis einer solchen Vorhersage zeigt die Abbildung 7:
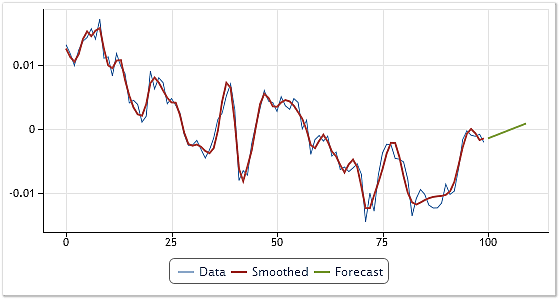
Abb. 7. Vorhersage für die Notierungen des Kürzels USDCHF, H4
Es sei darauf hingewiesen, dass bei der Erstellung der Vorhersage einer oder mehrere der Bestandteile mit den höchsten Frequenzen weggelassen werden können. Auf diese Weise können wir den Einfluss des Hochfrequenzrauschens auf die Vorhersagen abmildern. In der Abbildung 7 wird das Ergebnis der Vorhersage ohne Berücksichtigung der allerersten IMF wiedergegeben. Die Vorhersagefähigkeit dieses Verfahrens wurde in diesem Fall nicht bewertet. Eine umfassende Analyse der auf der empirischen Bandzerlegung beruhenden Vorhersageverfahren erfolgt hier nicht, da dieses Thema den Rahmen des hier vorliegenden Artikels sprengen würde.
Die Verfahren zur Entfernung des Trends sollten nicht unerwähnt bleiben. Nach der Ermittlung der einzelnen Bestandteile der Folge mithilfe des EMD-Verfahrens lässt sich jetzt ein recht anpassungsfähiger Algorithmus zur Entfernung des Trends anlegen. Als Trend kommen das Residuum der Zerlegung oder die Summe aus dem Residuum und der oder mehrerer der letzten IMF infrage. Die Anzahl der zusammen mit dem Residuum bei der Bildung der Trendlinie beteiligten IMF kann in Abhängigkeit davon variieren, wie viele Bestandteile mit niedriger Frequenz nach der Entfernung des Trends in der Folge erhalten bleiben müssen.
Somit reicht es zur Entfernung des Trends aus, die Summe aus allen bei der Zerlegung gefundenen IMF mit Ausnahme der oder einiger der letzten zu bilden. Dieses Vorgehen lässt sich sehr leicht mit der Glättung des gewonnenen Ergebnisses kombinieren, wenn auch die IMF mit der höchsten Frequenz aus dem Summenbildungsvorgang ausgeschlossen wird. In der Abbildung 8 sehen wir ein Beispiel für die Entfernung des Trends unter Verwendung des dargestellten Verfahrens:
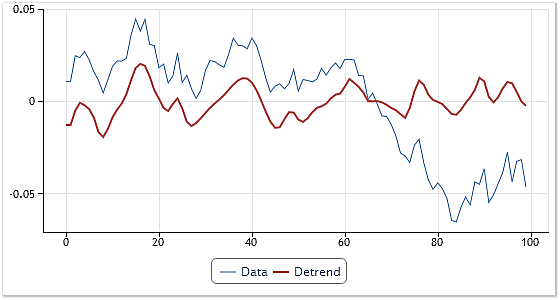
Abb. 8. Trendentfernung und Glättung
Als Eingangsdaten diente eine Folge von Kursnotierungen des Kürzels EURUSD, Daily. Nach der Zerlegung wurde die Summe aus allen ermittelten Bestandteilen mit Ausnahme des Residuums der Zerlegung sowie der letzten und der allerersten IMF gebildet. Dabei wurde nicht nur der Trend entfernt, sondern es kam auch zu einer gewissen Glättung des resultierenden Graphen.
Die Anwendung des Verfahrens der empirischen Bandzerlegung ist natürlich nicht auf die hier vorgestellten einfachen Beispiele beschränkt. Da der hier vorliegende Beitrag eher den Fragen der Umsetzung des EMD-Verfahrens gewidmet ist als seiner Anwendung, belassen wir es bei den hier vorgestellten Beispielen.
Als weitere Veranschaulichung der Funktionstüchtigkeit dieser Umsetzung des EMD-Verfahrens kann die Abbildung 9 dienen, in der das mithilfe der in der Datei CEMDecomp.mqh voreingestellten Parameter gewonnene Ergebnis der Zerlegung wiedergegeben. Für dieses Beispiel wurden Notierungen des Kürzels XAUUSD, H4, verwendet. Die Länge der Folge betrug 150 Elemente.
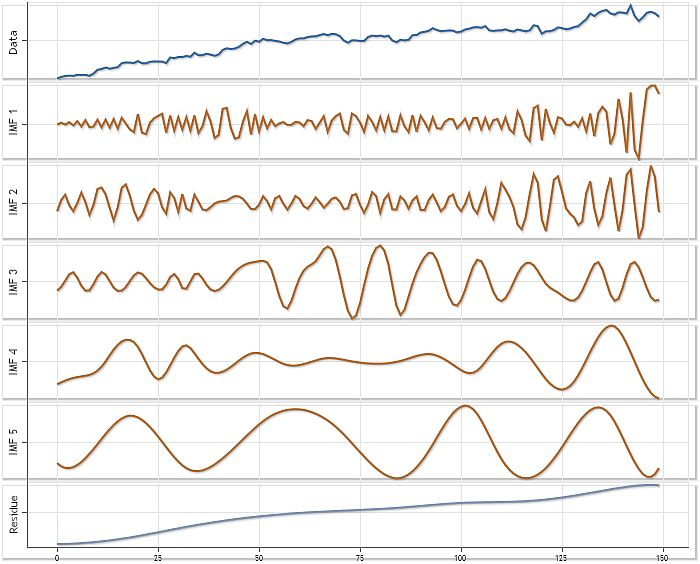
Abb. 9. Zerlegungsmuster anhand: XAUUSD, H4.
In der Abbildung 9 wurde bei jedem Element die automatische Maßstabanpassung verwendet.
Fazit
Es sei daran erinnert, dass sowohl das Verfahren der empirischen Bandzerlegung als auch die Hilbert-Huang-Transformation zur Analyse nichtlinearer nichtstationärer Vorgänge gedacht sind. Das bedeutet nicht, dass diese Herangehensweise nicht auch in Bezug auf lineare und stationäre Folgen verwendet werden kann.
Am Anfang dieses Beitrags wurden einige der in Zerlegungsalgorithmen verwendeten Ansätze kurz vorgestellt. Und es wurde gesagt, dass die Mehrzahl dieser Algorithmen eine Folge in einzelne Bestandteile zerlegt, die in Wirklichkeit nicht zu den Vorgängen gehören, aus denen die jeweils untersuchte Folge tatsächlich besteht.
Es handelt sich um gleichsam synthetische Bestandteile, deren Extraktion schlicht dazu beiträgt, den Aufbau der Eingangsfolge besser zu verstehen, und es in vielen Fällen ermöglicht, deren Analyse zu erleichtern. Das EMD-Verfahren stellt da keine Ausnahme dar. Keinesfalls sollte man annehmen, dass die mithilfe dieses Verfahrens gewonnenen Bestandteile die realen physikalischen Vorgänge abbilden, aus denen die zu analysierenden Ausgangsdaten ursprünglich hervorgegangen sind.
Was die in diesem Beitrag vorgestellte Umsetzung selbst betrifft, so erfordert diese eine weitere Überprüfung und Überarbeitung. Da sie als alles andere als ideal zu betrachten ist.
Hauptanliegen dieses Beitrages war es, den Leser mit dem EMD-Verfahren sowie mit einigen mit seiner Umsetzung verbundenen Besonderheiten vertraut zu machen.
Wir kommen zu folgendem Schluss:
- In dem Beitrag wurden in aller Kürze einige allgemeine mit Zerlegungen verbundene Fragen angesprochen.
- Das Wesen des Verfahrens der empirischen Bandzerlegung (EMD) wurde kurz umrissen.
- Vorgestellt wurden die Auflistung sowie eine Kurzbeschreibung der Schnittstellenkomponente der Klasse CEMDecomp, in der das EMD-Verfahren umgesetzt wird.
- Ein Beispiel zur Veranschaulichung der Interaktion mit der Klasse CEMDecomp und für den Aufruf ihrer Methoden wurde aufgeführt.
- Auf einige Besonderheiten dieser Umsetzung des EMD-Verfahrens wurde hingewiesen.
- Einige einfache Anwendungsbeispiele für das EMD-Verfahren bei der Datenanalyse wurden beigebracht.
- Am Ende des Beitrages befinden sich die Datei CEMDecomp.mqh, in der das EMD-Verfahren umgesetzt wird, sowie die gepackte Datei EMDecomposition.zip mit einem vollständigen Anwendungsbeispiel für die Klasse CEMDecomp.
Literaturhinweise:
- Die Hilbert-Huang-Transformation.
- Die Hilbert-Huang-Transformation.
- Die empirische Bandzerlegung (Empirical Mode Decomposition).
Ergänzung
Der ursprüngliche Beitrag wurde am 28. Juni 2012 veröffentlicht. Dieser Anhang ist am 5. Juli 2012 dazugekommen.
Eine alternative Umsetzung des EMD-Verfahrens wird als Anlage zu dem Artikel angeboten. Sie befindet sich als die Klasse CEMD in der unten angehängten Datei CEMD_2.mqh.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/439
Markttheorie
Anwendung des Verfahrens der eigenen Koordinaten auf die Analyse des Aufbaus einfacher statistischer Verteilungen
Der Indikator für "Spindles" Charting
Verdienen Sie 200 USD für Ihren Artikel über algorithmischen Handel!
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.