
経験的モード分解メソッドのイントロダクション
はじめに
実際に扱う手順はいくつものコンポーネントからなり、複雑なものです。例えば、降水量チャートを分析する際、それは季節による変化、地球温暖化・寒冷化、海流変化、低気圧・高気圧の動き、待機中の二酸化炭素量、太陽活動周期など様々なプロセスの相互作用から成り立っています。そのリストは永遠かのように続きます。
お互いに作用し合う際、そのコンポーネントは特定したい規則性を歪めるので、このタイプのチャートはかなり分析しずらいものです。これは、個別のコンポーネントを考慮に入れ、そのプロセスを分割し、個別に分析したいという考えにつながります。個別に分析し、全体への影響を考えるということは、予測の信頼性をあげ、進行中のプロセスのより良い理解を促進します。
そして、様々な要因に基づき形成される通貨価格を含め、トレーディングにおける様々な情報においても例外ではありません。そのため、個別にコンポーネントを分割すると、さらなる分析を促進できると期待できます。
その「分解」という用語は、複合物などを個別の要素に分けることを意味します。しかし、異なるプロセスの分析に関連する多くの分野にて、シグナル分析、シーケンス分析など、この単語は初期のコンポーネントではなく、初期にデータが形成された時にはなかった特定の機能に分割することを意味する幅広い意味にて使用されてきました。これらの機能は、人工的にデータ分解プロセスにおいて形成されましたが、「人工的」なものであるにも関わらず、隠れたパターンを認識する手助けとなる深いデータ分析を可能とします。
市場分析にて使用されるメソッドの大半は、分解メソッドなど分析プロセスから特定のコンポーネントを抜粋するメソッドに起因されます。いくつかを簡単に見てみましょう。
1. 分解
特定のシーケンスに実際に適用できる様々な分解メソッドがあります。これらのメソッドは、様々な根底の数学的、経験的アプローチや、様々な複雑さの度合い、適用分野を持ちます。
例えば、基礎的な市場分析は、分解メソッドの一つと考えられています。この分析は、市場に直接影響する初期のイベントによって生まれる効果を扱います。つまり、分析された市場プロセスは、いくつかのイベントに分解されるのです。
ファンダメンタル分析に関連する問題は、後ほど触れられます。そのプロセスのさらなる情報は、取得できないと想定しましょう。特定のプロセスを示すシーケンスしか持ちません。
最もシンプルな分解例は、よく知られたメソッドを用いたシーケンスのいくつかのコンポーネントへの分解により示されます。例えば、通貨ペアのチャートに関するMAを描画します。そして、初期のシーケンスからその曲線を引きます。結果として、初期のシーケンス二つ、MA曲線とその残りを得ることができます。より長い期間のMAを用いた同じ手続きは、取得された残りのものに適用された場合、3つのコンポーネントを生み出しますー2つのMA曲線ち、その変換の残りです。ご覧の通り、分解のプロセスは、平均値を用いて調整されます。重要な点は、そのプロセスの結果の特性にあります。
よく知られた分解とスペクトル分析メソッドにおいて、Fourier変換は、言及される価値があります。Fourier変換は、固定の調和的な基礎関数を使用した直交の変換クラスに所属します。Fourier変換の結果は、初期のプロセスの固定の頻度と大きさでの調和的な関数への分解として示されます。二つの重要な点があります。
まず、その変換は常に、固定にセットされた直交関数の基礎です。つまり、変換の基礎は変換されるシーケンスに依存しません。
次に、結果として生じる調和的なコンポーネントの大きさと頻度の値は一定です。これは、その値が初期のシーケンスにいおいて一定であるということです。つまり、もし特定の初期シーケンスの性質が特定のインターバルにおいて変化する場合、そのような変化は変換結果に反映されないということです。ここで取得された結果は、この変換は初期データの定常性を想定しているので特定の平均化されたプロセスの状態のみ反映します。
初期シーケンスの非定常性に関連した制限を避けるために、Fourier変換からウェーブレット変換に切り替えることができます。ウェーブレット変換は、Fourier変換のように、固定の機能における分解を実行します。Fourier変換とは異なり、この基礎はあらかじめ調節されており、変換に使用されるウェーブレットが選択されます。
さらに、Fourier変換と比べて、ウェーブレット変換から生じるすべてのコンポーネントは、分析プロセスにおける非定常性に関連した問題を解決するレベルや規模を決定するパラメーターを持ちます。
Fourier変換やウェーブレット変換は、よくできた数学的な技術や、効果的な実装アルゴリズムにより幅広い認知を得ています。さらに、両方の変換は多才で、様々な分野に適用されます。
しかし、実際の目的のため、非定常的なプロセスだけではなく、初期データによって決定される順応的な変換の基礎を使用する変換を持つことが良いでしょう。この変換の種類は存在し、以下にて紹介され、この記事の主題となっています。
2. 経験的モード分解
経験的モード分解 (EMD) Hilbert–Huang変換 (HHT)の基礎部分として提唱されました。Hilbert Huang変換はいわゆるステージ2にて実行されます。まず、EMDアルゴリズムを用いて固有モード関数(IMF)を取得します。
そして、ステージ2にて、初期シーケンスの即座の頻度スペクトラムは、Hilbert変換を上記のステップの結果に適用し取得できます。HHTは、非線形的・非定常的なシーケンスの頻度スペクトラムを取得できます。これらのシーケンスは、結果的に経験的モード分解によって処理されます。
しかし、この記事はHilbert変換を用いた頻度スペクトラムの描画を扱いません。EMDアルゴリズムのみに焦点を当てます。
以前言及されたFourier変換やウェーブレット変換と対して、EMDはいかなるデータも分析的にセットされず、分析されたシーケンスによって決定される固有モード関数(IMF)に分解します。その基礎的な関数は、この場合入力データから由来しています。EMDから生じるIMFは以下の要件のみ満たします。
- IMF局地の数(最大値と最小値の合計)やゼロ交差数は等しく、多くても1の違いである必要があります。
- IMFのどのポイントにおいても、ローカルの最大値によって定義されるエンベロープの中間値とローカルの最小値によって定義されたエンベロープは等しく0です。
分解結果は、頻度IMFコンポーネントに帰結します。それぞれの連続したIMFはより低い頻度のオシレーターを含みます。そして、「頻度」という単語はIMFに関連してその特性を定義するために使用された際、あまり正しくはありません。オシレーターの特性のであるが、異なる大きさや頻度をその時間軸にて持つことができます。
その記述に基づいてEMDアルゴリズムの結果をビジュアル化するのは難しいので、そのアルゴリズムの特性を知る機会を提供するソフトウェアの実装に進みましょう。
3. EMDアルゴリズム
Huangに提案された通り、そのあるリズムは初期シーケンスのエンベロープの中間値の連続的な引き算とシーケンスの最小・最大値によって定義された平滑なエンベロープを生み出すことに基づいています。これは、上部と下部のエンベロープを生み出すため、立体のスプライン線によって繋がれたすべてのローカル値の特定を必要とします。
エンベロープの描画手順は、図1に示されています。
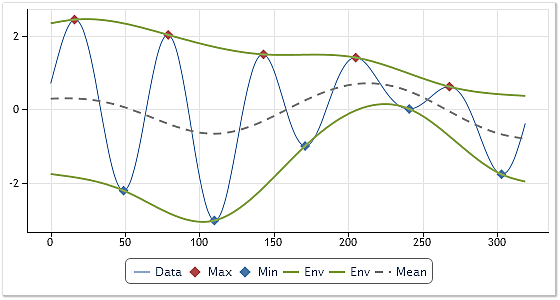
図1. エンベロープとその中間値の描画
図1 は太い青線で分析されたシーケンスを提供しています。シーケンスの最大・最小値は、赤と青でそれぞれ示されています。そのエンベロープは、緑で示されています。
その中間値は、二つのエンベロープに基づき計算され、図1にダッシュ線で示されています。そのように計算された中間値は、さらに初期シーケンスから引かれます。
上記のステップは、必要な経験的関数の摘出につながります。最終的なIMFを取得するためには、新しい最大。最小値が再び特定され、上記のステップすべてが繰り返される必要があります。その繰り返しのプロセスはふるいにかける、と言います。そのプロセスは、特定の停止義順が満たされるまで繰り返されます。停止基準の選択は、分解結果に影響する重要なポイントの一つです。この問題については後ほど紹介します。
もしそのプロセスが終了すれば、最初のIMFを取得します。次のIMFは元のシグナルから引き抜かれた以前のIMFを引き、上記の手続きをもう一度行うことで取得されます。これは、すべてのIMFが摘出されるまで続きます。そのプロセスは例えば、残りが二つ以下の極値うぃ持っている場合終了します。
ご覧の通り、経験的モード分解の手続きは、厳格な数学的計算ではなく、名前を正当化する経験的なものに基づきます。上記のアルゴリズムのシンプルさや明確さにも関わらず、欠点がいくつか存在します。
様々な発酵物がこのテーマについて欠点について紹介しており、また、Huanのアルゴリズムの現代化についても記しています。この記事は、このメソッドの可能な現代化について焦点を当てず、シンプルにソフトウェアの実装を作成方法を紹介します。その実装の特徴は、以下に示されています。
4. CEMDecompクラス
EMDアルゴリズムを実装するCEMDecompクラスは、Hilbert-Huang変換や経験モード分解について紹介するインターネットの記事に基づいて作成されました。その実装済みアルゴリズムは、とてもHuangにより提示されたアルゴリズムに類似しており、大きな修正も含みません。
以下は、この記事の最後のCEMDecomo.mqhファイルにて見られるソースコードの一部です。
//------------------------------------------------------------------------------------ // The Empirical Mode Decomposition (EMD). //------------------------------------------------------------------------------------ class CEMDecomp:public CObject { public: int N; // Input and output data size double Mean; // Mean of input data int nIMF; // IMF counter int MaxIMF; // Maximum number of IMF int MaxIter; // Maximum number of iterations int FixedIter; // 0-variable number of sifting iterations; // 1-always ten sifting iterations. double IMFResult[]; // Result private: double X[]; double Imf[]; double XMax[]; // x of local maxima double YMax[]; // y of local maxima double XMin[]; // x of local minima double YMin[]; // y of local minima double EnvUpp[]; // Upper envelope double EnvLow[]; // Lower envelope double Eps; // Accuracy comparison of floating-point numbers double Tol; // Accuracy of calculation IMF public: void CEMDecomp(void); int Decomp(double &y[]); // Decomposition void GetIMF(double &x[], int nn); // Get IMF number nn private: int arrayprepare(void); void extrema(double &y[],int &nmax,double &xmax[],double &ymax[], int &nmin,double &xmin[],double &ymin[]); int SplineInterp(double &x[],double &y[],int n,double &x2[], double &y2[],int btype=0); };
CEMDecompクラスに宣言されているパブリック変数やメソッドを見てみましょう。
Nは、シーケンスの要素数です。変数Nの値は、Decomp()メソッドを呼び出した後生成され、入力シーケンスの長さに等しいです。抽出されたIMFは、同じサイズを持っています。
Meanは、入力シーケンスの平均値です。その値はDecompメソッドの後生成されます。
nIMFはIMFカウンターです。Decomp()を呼び出した後、引き抜かれたIMF+2の数を含みます。そして、この値は、GetIMFメソッドを用いて何回コンポーネントが読み込まれたかを示します。つまり、0インデックスのコンポーネントは、常に初期のシーケンスを含み、その中間値はそこから引き抜かれ、一方インデックスnIMFのコンポーネントは、分解の残りを含みます。
MaxIMFは、IMFの最大許容数です。IMFの数がMaxIMFの値に達した際、入力シーケンスの個別IMFの分解は止まります。この変数の値は、Decomp()メソッドを呼び出す前に設定されます。その標準値は、16です。
MaxIterは、ふるいにかけるプロセスにて認められる繰り返しの最大数です。もし繰り返しの数がこの変数に達するなら、そのプロセスは必要な正確さが達成されたかに関わらず、終了します。この変数の値は、Decomp()メソッドを呼び出す前に設定されます。標準値は2000です。
FixedIterは、ふるいの停止基準を設定するフラッグです。FixedIter値が0であれば、各IMFにおいて、そのふるいのプロセスは特定の正確さが達せられれば、停止します。異なるIMFの抽出における特定の正確さを達成するために必要な繰り返し数は、異なります。FixedIterもし1にセットされれば、IMFは常に10回の繰り返し摘出されます。この変数の値は、Decomp()メソッドを呼び出す前に設定されます。標準の値は0です。
Decomp(double &y[]) は、分解を実行するメインのクラスメソッドです。入力パラメーターとして、入力データを含む配列への関連を受け取ります。うまく完成すれば、その変数Nは、入力配列の大きさと等しくなります。抽出されたIMFは、同じサイズを持っています。その変数Meanは、入力シーケンスの中間値に等しく、変数nIMFはGetIMFメソッドを用いて読まれるコンポーネント数に等しくなります。
GetIMF(double &x[], int nn)は、Decomp()メソッドを用いて取得された結果へのアクセスを確保します. nnに設定された数字を持つコンポーネントがコピーされるその配列のアドレスは入力パラメータとして渡されます。つまり、0インデックスのコンポーネントは、常に初期のシーケンスを含み、その中間値はそこから引き抜かれ、一方インデックスnIMFのコンポーネントは、分解の残りを含みます。もしパラメーターとして渡されたその配列の大きさが結果のコンポーネントの大きさよりも小さければ、その配列はその長さが許容する限り格納されます。
CEMDecompクラスの使用は以下の例にて示されています。
#include "CEMDecomp.mqh" //------------------------------------------------------------------------------------ // Script program start function //------------------------------------------------------------------------------------ void OnStart() { int n,ret; double yy[],imf2[]; n=400; // Input sequence length ArrayResize(yy,n); // Array of input data ArrayResize(imf2,n); // Array for reading the results CopyOpen(_Symbol,PERIOD_CURRENT,0,n,yy); // Generation of input data CEMDecomp *emd=new CEMDecomp(); // Creation of the CEMDecomp class instance ret=emd.Decomp(yy); // Decomposition of the input sequence if((ret==0)&&(emd.nIMF>3)) // If there is no error and the sufficient // number of components was extracted, emd.GetIMF(imf2,2); // copy component number 2 into // array imf2[]. delete(emd); // Deletion of the CEMDecomp class instance // One of the extracted components in array imf2[]. } //------------------------------------------------------------------------------------
Webインターフェースを通して摘出されたIMFを表示する分解の例は、記事の最後のCEMDecomposition.zipアーカイブにてご覧になれます。この例を稼働するために、特定のアーカイブを展開し、\CEMDecompositionディレクトリに置き、そのコンテンツはターミナルの\Indicatorsか\Scriptsに格納します。その後、EMDecomp_Test.mq5スクリプトをコンパイル、稼働できます。ターミナルでの外部ライブラリの使用は認められる必要があります。
図2は、100の要素を持つシーケンスのUSDJPYの価格の分解についての他の例を示しています。このシーケンスの分解は、4つのIMFと残りの摘出につながります。
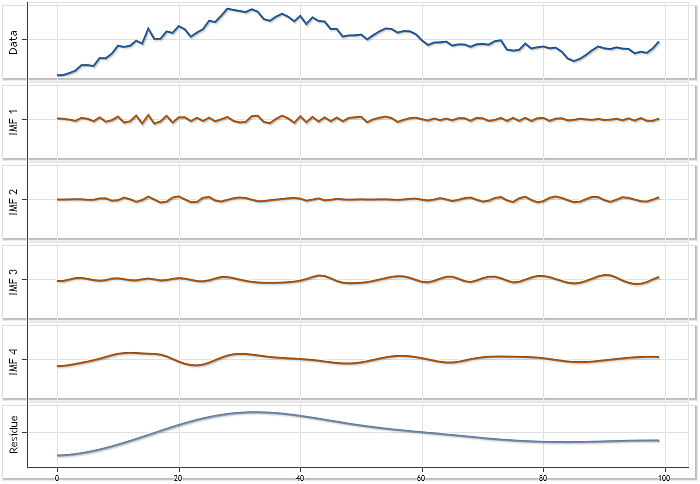
図 2. USDJPY Daily価格、N=100のシーケンスの分解
図2の全チャートは、それぞれの引き抜かれたIMFによる貢献を評価する同じ規模にて表示されています。しかし、この描画方法はそれぞれのIMFの特徴を見るための明確な図を提供できません。図3は、自動スケーリングモードを使用した同じ結果です。
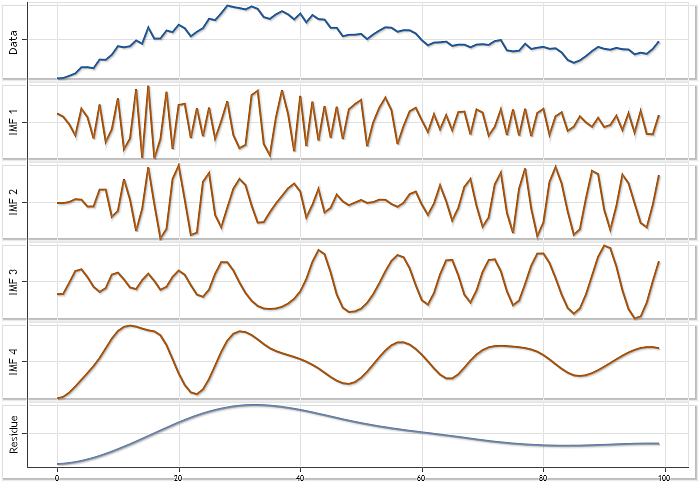
図3. USDJPY Daily価格、N=100のシーケンスの分解自動スケーリングモード
図3は、個別のコンポーネントの大きさの相関関係を示していませんが、自動スケーリングモードは、より詳しい一つ一つのビジュアル化を行います。
5. EMDアルゴリズムの提案された実装について
注意を向けてほしい一つ目の点として、初期シーケンスの最大・最小値の特定におけるメソッドがあります。この場合、二つの選択肢があります。
図4は、極値の特定におけるアルゴリズムの結果を示します。
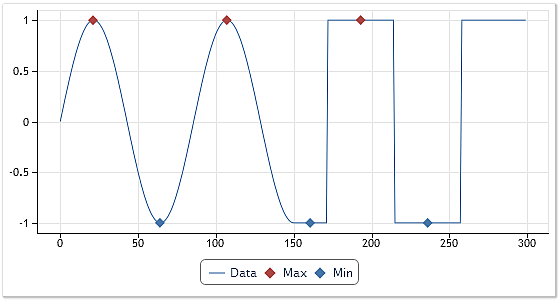
図4. 極値の特定最初のオプション
関数の最大・最小値の認識になると、共通して使用されるアルゴリズムは以下のようになります;
- そのシーケンスの現在の要素の値は、先行する値と比較されます。
- もし現在の値が先行する値より大きければ、関数として認識されます。
- もし現在の値が小さければ、関数として認識されます。
明確に定義された極値のシーケンスにおいて、最大・最小値の特定は難しくありません。そのアルゴリズムはうまく稼働します。この場合は図4にて示されたチャートの最初半分にて示されます。しかし、このアルゴリズムはシーケンスの近似値と等しい上面には対応しません。
そのアルゴリズムが使用されると、最後の最大値と二番目の最小値は特定されません。一方、この結果は予想され、正しいものでした。しかし、他方でオシレーターのプロセスへの類似物を描く際、もし0交差が起こると、これらの極値は見過ごされます。長方形の上面か、等しいシーケンス値のセクションは極値と考えられるかどうかは明確ではありません。
にも関わらず、極値の特定に使用されるアルゴリズムはEMDecompクラス実装時、上記のアルゴリズムの改善版です。そのパフォーマンス結果は図4にて見られます。そのアルゴリズムは等しいシーケンスの値のインターバルを極値として認識し、これらのインターバルの中間地点に極値点を置きます。
図4に示されるパフォーマンス結果を生み出す最大・最小値の特定におけるアルゴリズムは、分解サイクルが終了すべき点を判断する際に、CEMDecomクラスにて最大値の計算のために使用されます。例えば、もしIMFの抽出値がいかなる極値も持たない場合、その分解は終了し、そのIMFは除去されます。
この特定アルゴリズムがエンベロープの描画の際に使用されると、例えば、入力シーケンスが図4のような形式をとる場合、結果のエンベロープは二つの平行線によって表現されます。そのふるいにかけるプロセスは、入力シーケンスの変換に失敗し、このシーケンスは次はコンポーネントの分解において適さなくなります。
この状況の突破口はエンベロープを描画する極値の特定における異なるアルゴリズムの使用にて見つけられます。
図5は、極値の特定における代替的なアルゴリズムの使用にて取得される結果を紹介します。
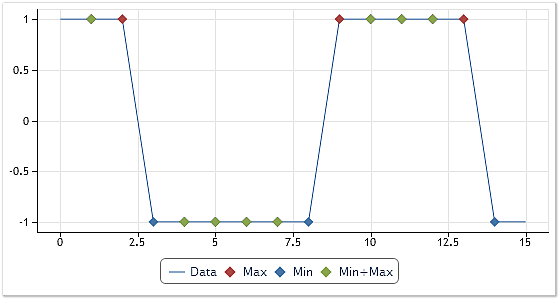
図5. 極値の特定二番目のオプション
図5をよく見てみましょう。図4とは異なり、最大・最小値に同時に存在するポイントを示します。もしエンベロープがこれらの極値に基づいて描画されていれば、それらはもはや直線の平行線ではなく、長方形のシーケンスの隠された部分は、そのプロセスでのさらなる抽出において使用されます。上記の良い例は、記事の最後にあるCEMDecomposition.zipアーカイブにあるテストケースになります。
不幸にも、このアプローチは隠されたコンポーネントの抽出に関連するすべての問題を解決しません。例えば、隠されたコンポーネントは三角形のシーケンスにおけるこの方法にて抽出できません。この事実はEMDアルゴリズムの実装の欠点の一つです。この困難な状況はこの記事にて扱われていない分解のためのCEEMD(Complementary Ensemble Empirical Mode Decomposition Method))アルゴリズムへの移行により解決できるかもしれません。
極値の特定におけるアルゴリズムの実装に関連する特徴とは別に、この種類のアルゴリズムに典型的な効果の問題に注意を向ける必要があります。上記を考察するため、図1を見てみましょう。図1は、最大値が上方のエンベロープとしての挿入スプライン関数により接続されていることを示します。
つまり、そのエンベロープは最初の最大値の左側と最後の最大値の右側の両方にあるセクションにて定義されています。そのようなエンベロープが延長される方法は、抽出されるIMFの特徴を決定します。効果の相関関係のソフトウェアの実装の詳細は扱わず、この事実はシンプルに読者の注目にさらしておきます。
摘出されるIMの数や性質はふるいにかけるサイクルを停止するために選択されたメソッドに依存しています。CEMDecompクラスは、そのプロセスを停止させる収容なメソッドと同じように最後のサイクルにて判断される現在のIMFにおける違いの範囲を示す比率の計算を使用します。
もしそのプロセスがIMFに何も影響を与えないのであれば、そのプロセスは停止し、IMFは生成されたと考えられます。IMF摘出の正確性を決定する制限値はクラスコンストラクターに設定されます。標準の制限値を設定することで、ふるいにかける繰り返し数は200や300にまで達します。この主題における発酵物の中で、多くの筆者がそのような多くの反復を使用することを警告しています。にもかかわらず、EMDアルゴリズムの実装においてこの標準の制限値を使用することにしました。
EMDアルゴリズムの実装は別の停止基準の使用を認めます。このために、変数FixedlterはDecomp()メソッドを呼び出す前に1にセットされなければなりません。この場合、すべてのIMFは10の繰り返し数にて摘出されます。この停止基準を用いて取得された分解結果は標準のメソッドのものよりも異なっていることがわかります。
6. EMDアルゴリズムの適用
EMDアルゴリズムがHilbert-Huang変換の一部であったので、シーケンスの頻度スペクトラムの計算がこのアルゴリズムの適用方法を紹介する例となります。これは、EMDを用いて抽出されたIMFコンポーネントにおけるHilbert変換のパフォーマンスと関連します。この手続きはこの記事では考慮されていません。
スペクトラムの計算とは別に、EMDアルゴリズムはシーケンスを平滑化するために使用されます。
図6は、そのような平滑化の例を示します。
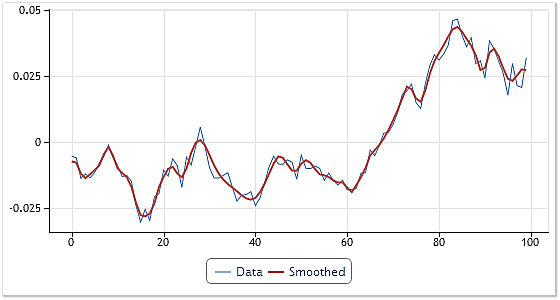
図6. 入力シーケンスの平滑化
100の「オープン」価格値からなるUSDCHF価格の一部が平滑化のため選択されます。分解のプロセスにおいて、4つのIMFと、その残りが取得されました。最初のものを覗いて全てのIMFは、その残りに追加されます。
そして、最も高い頻度のコンポーネントが入力シーケンスから除去されました。合計時に最初の二つのコンポーネントを無視すると、結果の曲線はよりなだらかになります。
EMDの適用の別の例は入力シーケンスから抽出されたIMFの予想の生成です。予測を生成するために、それぞれのIMFや残りに個別に生成される外挿を使用します。
この方法で作成された予想は、入力シーケンスにおける必要な予想結果を生成するために追加されます。個別のIMFのオシレーターの性質を考慮し、予想を生成するために、予想シーケンスの周期行動を考慮に入れる外挿を使用することが妥当です。
この場合、それぞれのIMFのための予想が10ステップ先の線形外挿入を用いて生成されるシンプルな外挿処理の例を見ます。図7にて示される予想結果
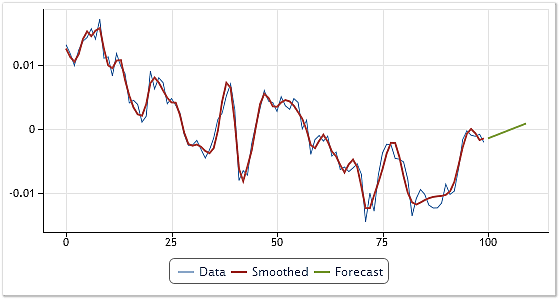
図7. USDCHF,、H4価格における予想の生成
予想を生成する際、一つか、それ以上の高い頻度を持つコンポーネントが無視されます。従って、この予想における高い頻度の音の効果は緩和されます。最初のIMFを除く予想の結果は図7にて示されています。このメソッドの予想可能性は査定されません。経験モード分解に基づいた予想メソッドの詳細な分析は、この主題がこの記事の範囲を超えたところにあるため提供されません。
トレンド除去を言及せずにはいられません。個別のシーケンスコンポーネントがEMDを用いて取得されたのち、かなり柔軟なアルゴリズムがトレンド除去のために開発されます。分解の残りか、最後のIMFに追加された残りはトレンドとして取得されます。その残りによるトレンド線作成に関するIMFの数は、トレンド除去ののちのシーケンスに残る必要とされる低頻度のコンポーネントの数に依存します。
従って、トレンド除去のために最後のコンポーネントなどを覗いた分解の結果として摘出されるIMFを合計するので十分です。もし高頻度のコンポーネントがコンポーネントの合計のプロセスから除去されると、この手続きは、取得された結果の平滑化に組み合わせられます。図8は、上記の技術を用いるトレンド除去の例を示します。
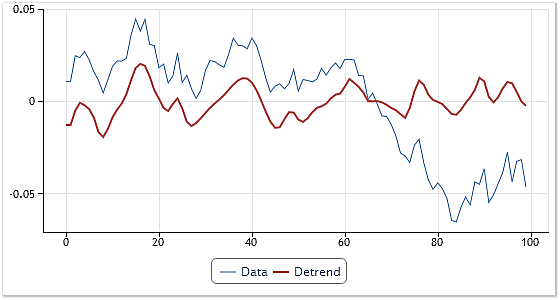
図8. 平滑化と組み合わさったトレンド除去
EURUSD価格のシーケンスは初期データとして取得されます。分解ののちに、全ての摘出されたコンポーネントが合計され、最後と最初のIMF、分解の残りを省きます。トレンド除去に終止するだけではなく、結果の曲線の平滑化にもつながりました。
経験モード分解メソッドの適用範囲は、記事で紹介されているシンプルなものだけではありません。しかし、この記事がEMDメソッドの実装の問題について焦点を当てているので、以下で紹介されている例を見てみましょう。
CEMDecomp.mqhに標準で設定されたパラメーターを用いて取得された分解結果を示す図9は、EMDメソッドの実装によって提供される機能性の追加の例示として機能します。この例は、XAUUSD H4価格の使用に基づきます。そのシーケンスのサイズは、150要素です。
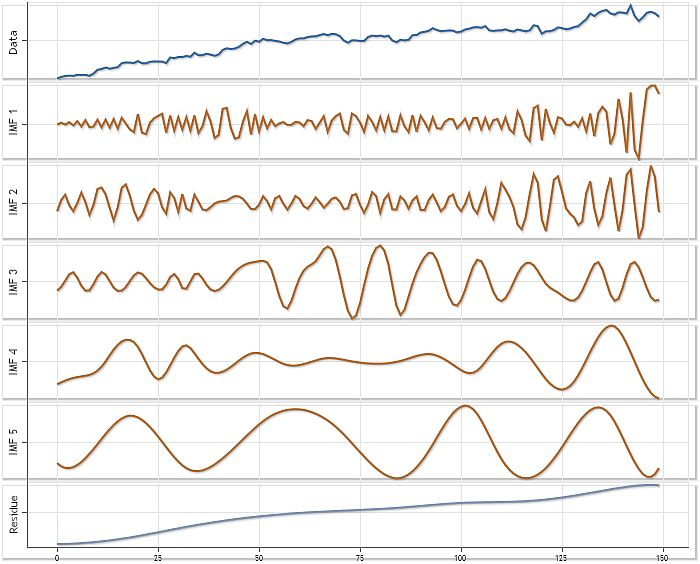
図9. XAUUSD H4価格を用いた分解例
自動スケーリングは、図9にて各コンポーネントに適用されました。
結論
Hilbert-Huang変換と同様、経験モード分解メソッドは非定常、非線形プロセスからのデータの分析に使用されます。このアプローチは、線形・定常シーケンスに適用されないというわけではありません。
分解アルゴリズムにて使用されたいくつかのアプローチは、簡潔に記事の最初に触れられています。そして、これらのアルゴリズムの大半は、シーケンスをシーケンスを作成する初期のプロセスを示さないコンポーネントに分解するということが述べられました。
これらのコンポーネントは、その部品が入力シーケンスの構造を理解するのに手助けとなり、分析を可能にするという意味で、統合的なものです。EMDも例外ではありません。このメソッドを用いて取得されたコンポーネントが実際の物理プロセスを反映し、それは初期の分析データがもともと形成されたプロセスです。
この記事で紹介された実装は、理想的ではなく、さらなるテストや改善が必要です。
この記事の主な目的は、EMDメソッドやその特徴に関連した特異点に読者が親しんでもらうことでした。
まとめ
- この記事は、簡単に分解に関連した問題を扱っています。
- それは、経験モード分解メソッドのエッセンスを明らかにします。
- そのリストと、EMDメソッドが実装されるCEMDecompクラスインターフェースの詳細が紹介されています。
- CEMDecompクラスとの連携の例は、そのメソッドがどのように呼ばれているのかを示します。
- そのEMDメソッドの実装の特徴はまとめられています。
- EMDメソッドのデータ分析における適用を示すいくつかの例が提供されています。
- この記事の最後に、EMDメソッドの実装を行うCEMDecomp.mqhファイルや、CEMDecompクラスの使用に関するテストケースを含んだEMDecomposition.zip アーカイブをご覧ください。
参照
添付書類
7/28, 2012年に記事は掲載されました。7/5, 2012年にこの添付書類は提供されました。
別のEMDメソッドの実装は、記事の追加として提供されます。その実装は、CEMDクラスとして紹介され、CEMD_2.mqhファイルに保存されています。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/439
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 MQL5.community 人名鑑
MQL5.community 人名鑑
 自動売買システム作成にたいする新手法としてのオートマタ準拠プログラミング
自動売買システム作成にたいする新手法としてのオートマタ準拠プログラミング
 UML ツールを用いたExpert Advisorの開発方法
UML ツールを用いたExpert Advisorの開発方法
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
まず第一に、記事を書いてくれた著者に心から感謝する!この記事は興味深く、明快で簡潔だ。入門講義のようなものだ。その上、著者は最初のテストのためのベースを与えてくれた。これには心から感謝したい。
さて、私は、指一本動かす必要がないように、すべてを一度に、同時に必要とする人々に対処する。皆さん、頭のスイッチを入れて、怠け心と戦ってください。単純に読んでいて不快な記事もある。著者は一生懸命やっているのに、あなたはそれを評価しない。
新しい記事「 経験的モード分解入門」を掲載しました:
著者:ビクター・ライクス
実際、これは良い記事ではない。EMDは因果関係のある手法ではない。つまり、過去の値がリアルタイムで変化するため、トレーディングにはまったくもって役に立たない。特異スペクトル分析、ホドリック・プレスコット・フィルター、あらゆる種類のスプラインと同じカテゴリーだ。静的なチャート上ではとても良く見えますが、リアルタイムではLWMAと変わりません。EMDラインの結果にSMA(1)を置くだけで、それがどれだけでこぼこになるかわかるだろう...研究/科学的な観点からは良いが、取引では役に立たない。
皆さん、こんにちは、
私はEMD技術をSVM-回帰とともに実装するための論理的な道筋を立てるのに苦労しています。私が読んだ(E)EMD-SVMに関するほとんどの論文(例えば "Short-term prediction of stock index based on EMD and SVMs")は、SVM学習経路を実装する前に、まず完全な時系列を分解します。
しかし、時系列に1つのデータセット(t+1)を追加すると、EMDアルゴリズムはほとんど全てのIMFの値を変更することに気づきました(IMFの数さえも(過去の同じ日付について)変更することができます)。
したがって、データセットを学習期間(例えば2002-2010)に分割し、サンプル外予測(例えば2011)を行いたい場合、EMD分解されたIMFは、2011年を予測するために2002-2010のデータのみを含む必要がありますよね?EMDデータセット(2002-2011)で計算されたIMF時系列で2011年を予測すると、「未来」からの情報を取り込むことになり、私のバックテスト 結果は有効ではなくなりますよね?
だから、1ステップ進むごとに、EMDを追加データポイントで計算しなければならない・・・そうすれば、SVM-回帰を実行して、そのようなモデルをバックテストできるよね?この再帰的な方法は、MisterHが前述したように "BUMPY "である可能性があり、バックテストやトレーディング戦略には役に立たないのでは?
2つ目に同封されている「EMDの実装が若干異なる」ことについて、一言もらえないだろうか。 長所 短所 短所 違い
記事に大きなプラス