Introducción al método de descomposición de modo empírico

Introducción

Todos los procesos reales con los que hemos trabajado en la práctica son complejos, por lo general, comprendiendo un gran número de componentes. Por ejemplo, el clima. Al analizar los gráficos de precipitaciones, debemos tener en cuenta que representan la interacción entre un gran número de procesos muy diversos como cambios estacionales, procesos de calentamiento/enfriamiento globales, cambios en las corrientes oceánicas, dinámica de ciclones y anticiclones, cantidad de dióxido de carbono emitida a la atmósfera, ciclos de actividad solar, etc. La lista podría ampliarse indefinidamente.

Un gráfico de este tipo resulta muy difícil de analizar ya que sus componentes, al interactuar unos con otros, enmascaran y distorsionan las regularidades que nos guarían identificar. Esto da lugar al deseo legítimo de descomponer el proceso a considerar en sus elementos individuales y analizar cada uno de ellos por separado. El análisis de los componentes individuales y la consideración de la contribución que estos hacen al proceso, nos ayuda a comprender mejor este último, así como, por ejemplo, a incrementar la fiabilidad de la predicción.

Y no hay una excepción cuando se trata de varios tipos de información sobre trading, incluyendo las cotizaciones de moneda que también se forman en base a un gran número de factores diversos. Esta es la razón por la que es muy natural esperar que un desglose previo en sus componentes individuales puede facilitar en gran medida su análisis posterior.

El término "descomposición" significa, formalmente, el desglose de un proceso compuesto o un material compuesto en sus elementos constituyentes. Pero en muchas áreas relacionadas con el análisis de distintos procesos, análisis de señal, análisis de varios tipos de series, etc., este término ha sido utilizado durante mucho tiempo con un significado más amplio, significando muy a menudo no un desglose en sus componentes iniciales reales, sino, más bien, un desglose en ciertas funciones que no estaban realmente presentes cuando los datos iniciales se formaron. Estas funciones son de un tipo formado artificialmente en el proceso descomposición de datos, pero a pesar de su origen "artificial", permite un análisis más profundo de los datos, ayudando a identificar los patrones ocultos.

La gran mayoría de métodos utilizados en el análisis de mercado pueden atribuirse explícitamente o implícitamente a métodos que destacan determinados componentes del proceso analizado, es decir, métodos de descomposición. Vamos a revisar brevemente algunos de ellos.

1. Descomposición

Existen muchos métodos de descomposición distintos que pueden aplicarse en la práctica a una determinada serie. Estos métodos pueden tener enfoques matemáticos o empíricos subyacentes distintos, diferente grado de complejidad y distintas áreas de aplicación.

Por ejemplo, incluso un análisis de mercado fundamental puede considerarse, hasta cierto punto, uno tipo de método de descomposición. Este análisis trata sobre el efecto producido por un conjunto de eventos iniciales que influyen directamente sobre las condiciones del mercado. En otras palabras, un proceso de mercado analizado es implícitamente descompuesto en una serie de eventos que lo constituyen.

No se hará referencia más tarde a las cuestiones relativas al análisis fundamental. Asumiremos que cualquier información posterior sobre el proceso considerado no está disponible y que lo que tenemos es solo una serie que representa el comportamiento de un proceso determinado.

El ejemplo de descomposición más simple puede ilustrarse mediante una descomposición de una serie en varios componentes usando métodos bien conocidos. Por ejemplo, trazamos una media móvil (MA) en un gráfico para cualquier par de divisas. A continuación restamos la curva resultante a la serie inicial. Como resultado obtendremos dos componentes de la serie inicial, la curva de la media móvil y el residuo. El mismo procedimiento, usando solo un periodo de la media móvil más largo al aplicarse al residuo obtenido, dará como resultado tres componentes, dos curvas de la media móvil y un residuo de la transformada. Como puede ver, el proceso de descomposición puede realizarse fácilmente utilizando cualquier media disponible. Todo depende de las propiedades de los resultados de dicho proceso.

Entre los métodos conocidos de análisis de descomposición y espectrales, la transformada de Fourier merece ser mencionada aquí. La transformada de Fourier pertenece al tipo de transformaciones ortogonales que utilizan funciones armónicas básicas. El resultado de la transformada de Fourier puede verse como una descomposición del proceso inicial en funciones armónicas con frecuencias y amplitudes fijas. Deben destacarse aquí dos puntos de particular importancia para nosotros.

El primero es que la trasformada se realiza siempre según una configuración fija y previa de funciones ortogonales. Es decir, el principio de una transformada no depende de la naturaleza de la serie transformada.

En segundo lugar, los valores de la amplitud y la frecuencia de los componentes armónicos resultantes son constantes. Es decir, sus valores son constantes sobre toda la serie inicial. Esto significa que si la naturaleza de una serie inicial determinada ha cambiado en el intervalo considerado, dichos cambios no se verán reflejados en los resultados de la transformada. Los resultados obtenidos en este caso solo reflejarán un cierto estado promediado del proceso, ya que esta transformada se basa en la suposición de estacionariedad de los datos iniciales.

Para evitar las limitaciones asociadas con la no estacionariedad de la serie inicial, podemos pasar de la transformada de Fourier a una transformada de ondícula. Una transformada de ondícula, como la de Fourier, realiza una descomposición sobre una base fija de funciones. A diferencia de la transformada de Fourier, esta base debe establecerse de antemano, es decir, debe elegirse una ondícula en la transformada.

Además, al contrario que la transformada de Fourier, cada componente resultante de una transformada de ondícula posee parámetros que determinan su escala y nivel en el tiempo que solucionan el problema asociado con una posible falta de estacionariedad en el proceso analizado.

Las transformadas de Fourier y de ondículas han recibido ambas un amplio reconocimiento debido a las técnicas matemáticas consolidadas que utilizan y a los algoritmos de implementación disponibles. Además, ambas transformadas parecen ser bastante versátiles y pueden aplicarse con éxito en áreas distintas.

Pero por razones prácticas, estaría bien tener una transformada que no solo permitiera trabajar con procesos no estacionarios, sino que también usara una transformada adaptativa determinada por los datos iniciales. No existe este tipo de transformada y la veremos a continuación brevemente al tratar el tema principal de este artículo.

2. Descomposición de modo empírico

La descomposición de modo empírico (EMD) fue propuesta como parte fundamental de la transformada de Hilbert-Huang (HHT). La transformada de Hilbert Huang se realiza, digámoslo así, en 2 etapas. En la primera, usando el algoritmo EMD obtenemos funciones de modo intrínseco (IMF).

Posteriormente, en una segunda etapa, se obtiene el espectro de frecuencia instantáneo de la serie inicial aplicando la transformada de Hilbert a los resultados del paso anterior. La transformada de Hilbert Huang permite obtener el espectro de frecuencia instantáneo de las series no estacionarias no lineales. También puede trabajarse con estas series usando la descomposición de modo empírico.

Sin embargo, este artículo no va a cubrir el trazado del espectro de frecuencia instantáneo usando la transformada de Hilbert. Nos centraremos en el algoritmo EMD.

Al contrario de la transformada de Fourier antes citada y la transformada de ondículas, el algoritmo EMD descompone cualquier conjunto de datos en funciones de modo intrínseco (IMF) que no se establecen analíticamente y, en lugar de esto, se determinan mediante una sola serie analizada. Las funciones básicas son en este caso obtenidas de forma adaptativa directamente a partir de los datos de entrada. Una IMF obtenida a partir de la EMD debe satisfacer solo los siguientes requisitos:

1. El número de IMF extrema (la suma del máximo y el mínimo) y el número de cruces cero deben ser iguales o distintos en al menos uno;
2. En cualquier punto de una IMF, el valor medio de la envolvente definida por el máximo local y la definida por el mínimo local deben ser cero.

La descomposición da como resultado una familia de componentes IMF ordenados según la frecuencia. Cada IMF contiene oscilaciones con una frecuencia inferior a la precedente. Y aunque el término "frecuencia" nos es muy correcto cuando se usa para hacer referencia a las IMF, es probablemente más adecuado para definir su naturaleza. El caso es que aunque una IMF sea de naturaleza oscilatoria, esta puede tener una amplitud y frecuencia variable a lo largo del eje de tiempo.

Es difícil visualizar los resultados del funcionamiento del algoritmo EMD solo en base a la descripción, por lo que vamos a realizar la implementación del software que nos dará la oportunidad de conocer las peculiaridades del algoritmo.

3. Algoritmo de EMD

Este algoritmo, propuesto por Huang, se basa en generar envolventes de ajuste definidas por máximos y mínimos de una serie y la consiguiente sustracción de la media de estas envolventes a la serie inicial. Esto requiere la identificación de todos los extremos locales que están conectados por líneas de esplines cúbicos para producir las envolventes superiores e inferiores.

El procedimiento para trazar las envolventes se muestra en la Figura 1.

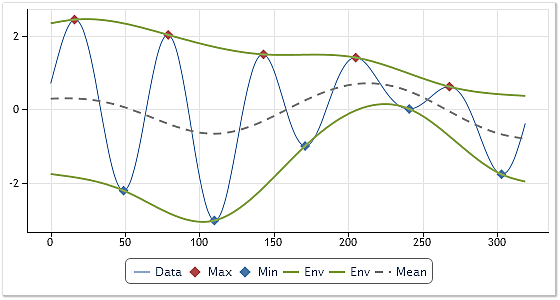
Fig. 1. Trazado de las envolventes y sus medias.

La Figura 1 muestra la serie analizada en línea fina azul. El máximo y el mínimo de la serie se muestra en rojo y azul, respectivamente. Las envolventes se muestran en verde.

La media se calcula en base a las dos envolventes y se muestra en la Figura 1 con línea a trazos. El valor medio así calculado es posteriormente restado a la serie inicial.

Los pasos anteriores dan como resultado la extracción de la función empírica necesaria en la primera aproximación. Para obtener la IMF final, deben identificarse de nuevo los máximos y mínimos y han de repetirse todos los pasos anteriores. Este proceso reiterativo se denomina cribado. El proceso de cribado se repite hasta cumplir un cierto criterio. La elección de dicho criterio es uno de los puntos clave del resultado global de la descomposición. Volveremos a esta cuestión un poco más tarde.

Si se completa con éxito el proceso de cribado obtendremos la primera IMF. La siguiente IMF puede obtenerse restando a la señal original la IMF extraída previamente y repitiendo el procedimiento anterior una vez más. Esto sigue hasta que se extraen todas las IMF. El proceso de cribado suele terminar cuando el residuo, por ejemplo, contiene no más de dos extremos.

Como puede comprobarse, el procedimiento de descomposición de modo empírico no se basa en cálculos matemáticos estrictos sino que es realmente empírico, con lo que su nombre queda justificado. A pesar de la simplicidad y claridad del algoritmo anterior propuesto por Huang, hay pocos puntos que puedan ser considerados inconvenientes.

Hay varios trabajos sobre esta materia que proporcionan un análisis detallado de sus puntos débiles y las formas de modernizar dicho algoritmo. Este artículo no se va a centrar en las posibles actualizaciones de este método sino que simplemente intentará crear la implementación de su software. Las peculiaridades de esta implementación se describen brevemente a continuación.

4. Clase CEMDecomp

La clase CEMDcomp que implementa el algoritmo EMD se creó basándose en las publicaciones de internet dedicadas a la transformada de Hilbert-Huang y a la descomposición del modo empírico. El algoritmo implementado es sustancialmente muy similar al inicialmente propuesto por Huang y no contiene mayores modificaciones.

A continuación se muestra un fragmento de código fuente que puede encontrarse en el archivo CEMDecomp.mqh al final del artículo.

//------------------------------------------------------------------------------------
// The Empirical Mode Decomposition (EMD).
//------------------------------------------------------------------------------------
class CEMDecomp:public CObject
  {
public:
  int     N;                 // Input and output data size
  double  Mean;              // Mean of input data
  int     nIMF;              // IMF counter
  int     MaxIMF;            // Maximum number of IMF
  int     MaxIter;           // Maximum number of iterations
  int     FixedIter;         // 0-variable number of sifting iterations;
                             // 1-always ten sifting iterations.
  double  IMFResult[];       // Result
private:
  double  X[];
  double  Imf[];
  double  XMax[];            // x of local maxima
  double  YMax[];            // y of local maxima
  double  XMin[];            // x of local minima
  double  YMin[];            // y of local minima
  double  EnvUpp[];          // Upper envelope
  double  EnvLow[];          // Lower envelope
  double  Eps;               // Accuracy comparison of floating-point numbers
  double  Tol;               // Accuracy of calculation IMF
public:  
  void    CEMDecomp(void);
  int     Decomp(double &y[]);          // Decomposition
  void    GetIMF(double &x[], int nn);  // Get IMF number nn
private:
  int     arrayprepare(void);
  void    extrema(double &y[],int &nmax,double &xmax[],double &ymax[], int &nmin,double &xmin[],double &ymin[]);
  int     SplineInterp(double &x[],double &y[],int n,double &x2[], double &y2[],int btype=0);
  };

Vamos a echar un vistazo a las variables públicas y métodos declarados en la clase CEMDecomp.

N es el número de elementos en la serie. El valor de la variable N se genera después de llamar al método Decomp() y es igual a la longitud de la serie de entrada. Las IMF extraídas tendrán el mismo tamaño.

Mean es el valor medio de la serie de entrada. El valor es generado después de llamar al método Decomp().

nIMF es el contador de IMF. Después de llamar a Decomp(), este contiene el número de IMF extraídas más dos. De esta forma, este valor indica cuántos componentes pueden leerse usando el método GetIMF(). Dicho esto, un componente con índice 0 siempre contendrá la serie inicial a partir de la cual se resta su valor medio, mientras que un componente con índice nIMF contendrá el residuo de la descomposición.

MaxIMF es el número máximo permisible de IMF. La descomposición de la serie de entrada en IMF independientes cesará cuando el número de IMF alcance el valor MaxIMF. El valor de esta variable puede establecerse antes de llamar al método Decomp(). El valor por defecto es 16.

Maxlter es el número máximo de iteraciones permitidas en el proceso de cribado. Si el número de iteraciones en el proceso de cribado alcanza este valor, dicho proceso finalizará con independencia de si se ha alcanzado o no la precisión necesaria. El valor de esta variable puede establecerse antes de llamar al método Decomp(). El valor por defecto es 2000.

Fixedlter es el flag que establece un criterio de parada en el cribado. Si el valor de Fixedlter es cero, el proceso de cribado para cada IMF finalizará una vez que se alcance la precisión dada. El número de iteraciones necesarias para alcanzar la precisión dada para la extracción de las diferentes IMF puede variar. Si Fixedlter se establece en cero, siempre se extraerá una IMF por cada 10 iteraciones. El valor de esta variable puede establecerse antes de llamar al método Decomp(). El valor por defecto es 0.

Decomp(double &y[]) es el método de la clase principal que realiza la descomposición. Recibe una referencia a una matriz que contiene los datos de entrada como parámetros de entrada. Una vez finalizado con éxito, la variable N será igual a la longitud de la matriz de entrada. Las IMF extraídas tendrán el mismo tamaño. La variable Mean será igual al valor medio de la serie de entrada, mientras que la variable nIMF será igual al número de componentes que pueden ser leídos utilizando el método GetIMF().

GetIMF(double &x[], int nn) permite garantizar el acceso a los resultados obtenidos usando el método Decomp(). La dirección de la matriz donde se copiará el componente con el número establecido por nn se pasa como parámetro de entrada. Dicho esto, un componente con índice 0 siempre contendrá la serie inicial a partir de la cual se resta su valor medio, mientras que un componente con índice nIMF contendrá el residuo de la descomposición. Si la longitud de la matriz pasada como parámetro resulta ser inferior a la de los componentes obtenidos, la matriz será completada en la medida que lo permitida su longitud.

El uso de la clase CEMDecomp puede mostrarse mediante el siguiente ejemplo:

#include "CEMDecomp.mqh"
//------------------------------------------------------------------------------------
// Script program start function
//------------------------------------------------------------------------------------
void OnStart()
  {
  int n,ret;
  double yy[],imf2[];
  
  n=400;                                    // Input sequence length
  ArrayResize(yy,n);                         // Array of input data
  ArrayResize(imf2,n);                       // Array for reading the results
  
  CopyOpen(_Symbol,PERIOD_CURRENT,0,n,yy);      // Generation of input data
  
  CEMDecomp *emd=new CEMDecomp();           // Creation of the CEMDecomp class instance
  ret=emd.Decomp(yy);                       // Decomposition of the input sequence
  
  if((ret==0)&&(emd.nIMF>3))                // If there is no error and the sufficient
                                            // number of components was extracted,
    emd.GetIMF(imf2,2);                     // copy component number 2 into
                                            // array imf2[].
  delete(emd);                              // Deletion of the CEMDecomp class instance
  
  // One of the extracted components in array imf2[].
  }
//------------------------------------------------------------------------------------

En el archivo CEMDecomposition.zip, disponible al final del artículo, se encuentra disponible un ejemplo completo de la descomposición que muestra las IMF extraídas a través de la interfaz de la web. Para ejecutar este ejemplo debemos desempaquetar el archivo indicado y colocar todo el directorio \CEMDecomposition junto con su contenido en el directorio del terminal \Indicators o \Scripts. Después de todo, podemos compilar y ejecutar el script EMDecomp_Test.mq5. Tenga en cuenta que para que esto puede realizarse debe estar permitido el uso de las librerías externas en el terminal.

La Figura 2 muestra otro ejemplo de la descomposición de las cotizaciones diarias USDJPY una longitud de la serie de 100 elementos. Puede comprobarse que la descomposición de esta serie da como resultado la extracción de cuatro IMF y el residuo.

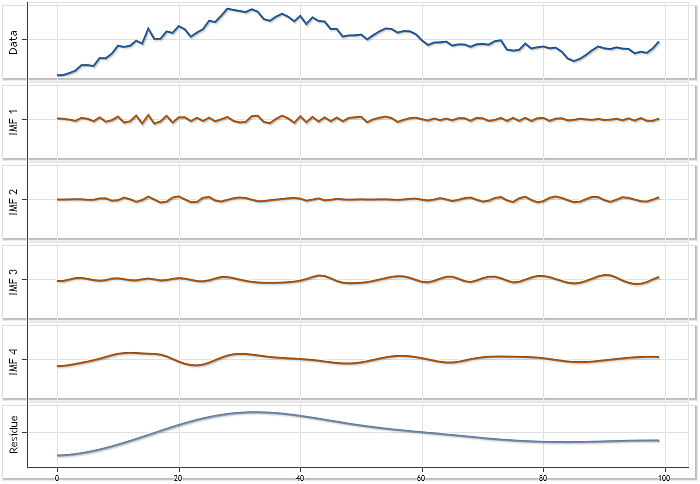
Fig. 2. Descomposición de la serie de cotizaciones diarias USDJPY donde N=100.

Todos los gráficos de la Figura 2 se muestran en la misma escala permitiendo evaluar la contribución realizada por cada una de las IMF extraídas. Sin embargo, esta forma de trazar no proporciona una perspectiva lo suficientemente clara para ver las peculiaridades de cada IMF. La Figura 3 muestra los mismos resultados usando solo el modo de autoescalado para cada uno de los gráficos.

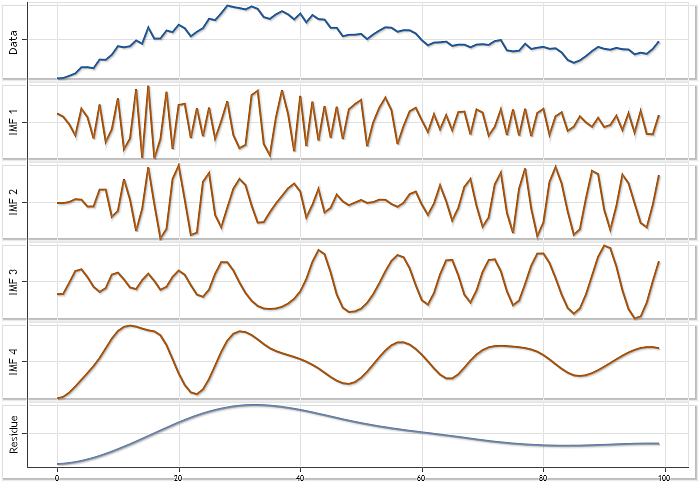
Fig. 3. Descomposición de la serie de cotizaciones diarias USDJPY donde N=100. Modo de autoescalado.

Aunque la Figura 3 no muestra la correlación actual de las amplitudes de los componentes individuales, el uso del modo de autoescalado permite conseguir una visualización más detallada de cada uno de ellos.

5. Notas a la implementación propuesta del algoritmo de EMD

Lo primero que me gustaría destacar es el método de identificación del máximo y el mínimo de la serie inicial. En este caso, hay dos opciones disponibles.

La Figura 4 muestra los resultados del comportamiento en la identificación de los extremos.

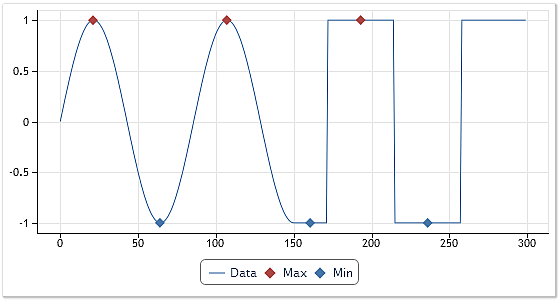
Fig. 4. Identificación de extremos La primera opción.

Cuando se trata de identificar el máximo o el mínimo de una función, el algoritmo más utilizado es el siguiente:

1. El valor del elemento actual de la serie se compara con los valores anteriores y posteriores;
2. Si el valor actual es mayor que el anterior y el posterior, se considera un máximo de la función;
3. Si el valor actual es menor que el anterior y el posterior, se considera un mínimo de la función;

Para series con extremos claramente definidos la identificación de los máximos y mínimos no implica ninguna dificultad. El algoritmo proporcionado funciona bien. Este caso se describe en la primera mitad del gráfico mostrado en la Figura 4. No obstante, este algoritmo no responderá a las zonas superiores planas en las que los valores próximos de la serie sean iguales.

Si hubiéramos usado el algoritmo proporcionado, el último máximo y los dos últimos mínimos mostrados en la Figura 4 nunca habrían sido identificados. Por un lado, este resultado habría sido de esperar y correcto. Pero por otro, haciendo una analogía con los procesos oscilatorios, si se produjeran los cruces cero, estos extremos habrían pasado desapercibidos. No está muy claro si las zonas superiores planas de una serie rectangular de secciones con valores de la serie iguales pueden considerarse extremos.

No obstante, el algoritmo utilizado para la identificación de los extremos al implementar la clase EMDecomp es una versión mejorada del algoritmo anterior. Sus resultados pueden apreciarse en la Figura 4. Este algoritmo identifica los intervalos con valores de la serie iguales como extremos y sitúa los puntos de los extremos en mitad de estos intervalos.

El algoritmo para la identificación de los máximos y mínimos cuyos resultados se muestran en la Figura 4 se usa en la clase CEMDecomp para el cálculo del número de extremos al determinar el punto en el que debe finalizar el ciclo de descomposición. Por ejemplo, si una IMF extraída no tiene ningún extremo, la descomposición se para y dicha IMF es expulsada.

Si este algoritmo de identificación se utiliza al trazar envolventes, en los casos en que la serie de entrada, por ejemplo, adopte la forma mostrada en la Figura 4, las envolventes resultantes estarán representadas por dos líneas rectas paralelas. El proceso de cribado fallará luego a la hora de transformar la serie de entrada y esta serie, a su vez, no será adecuada para la descomposición en componentes.

Una forma de salir de esta situación consiste en usar algún algoritmo distinto para la identificación de los extremos para trazar las envolventes.

La Figura 5 muestra los resultados obtenidos usando este algoritmo alternativo para la identificación de los extremos.

Fig. 5. Identificación de extremos La segunda opción.

Veamos con mayor detenimiento la Figura 5. A diferencia de la Figura 4, muestra puntos verdes con máximos y mínimos al mismo tiempo. Si las envolventes se trazan en base a estos extremos, ya no serán más líneas rectas paralelas y los componentes ocultos de la serie rectangular estarán disponibles para una extracción posterior en el proceso de cribado. Un buen ejemplo de lo anterior puede ser una prueba ubicada en el archivo CEMDecomposition.zip al final del artículo.

Por desgracia, este enfoque no soluciona todos los problemas relativos a la extracción de los componentes ocultos. Por ejemplo, los componentes ocultos no pueden extraerse de esta forma para una serie triangular. Esto puede ser una de los inconvenientes de esta implementación del algoritmo EMD. Esta difícil situación puede abordarse probablemente cambiando el algoritmo del método descomposición de modo empírico de conjunto complementario (CEEMD, Complementary Ensemble Empirical Mode Decomposition Method) para la descomposición cuya revisión no se tratará en este artículo.

Aparte de las peculiaridades asociadas con la implementación de los algoritmos para la identificación de los extremos, debe prestarse atención al problema de los efectos finales típicos de este tipo de algoritmos. Para analizar en detalle lo anterior, vamos a volver a la Figura 1. Dicha figura muestra claramente que los máximos están conectados por una función spline de interpolación cúbica como la envolvente superior.

Dicho esto, la envolvente debe ser definida para las secciones situadas tanto a la izquierda del primer máximo como a la derecha del último. La forma en que se alarga dicha envolvente es probable que condicione la naturaleza de las IMF extraídas junto a sus extremos. Sin entrar mucho en los detalles de la implementación del software de la correlación del efecto final, simplemente se llama la atención aquí al lector sobre este hecho.

Debemos tener en cuenta además que la naturaleza y el número de IMF extraídas dependerá del método elegido para finalizar el cicle de cribado. La clase CEMDecomp usa el cálculo del ratio indicando la magnitud de la diferencia en la IMF actual, según fue determinada por el último ciclo de cribado, como el método principal que sirve para finalizar el proceso de cribado.

Si el cribado no tiene apenas efecto sobre una IMF desconocida, el proceso de cribado se para y se considera generada la IMF. En la clase del constructor se establece un valor límite por defecto que determina la precisión en la extracción de la IMF. Una vez establecido el valor máximo, el número de iteraciones de cribado puede a veces alcanzar el valor de 200 e incluso 300. En publicaciones sobre esta materia, muchos autores advierte de los peligros del uso de un número tan grande de iteraciones de cribado. No obstante se decidió usar este valor límite por defecto en la implementación del algoritmo EMD.

Esta implementación del algoritmo EMD permite usar otro criterio de parada. Para este propósito de establecerse la variable Fixedlter a 1 antes de llamar al método Decomp(). En este caso, todas las IMF se extraerán siempre en 10 iteraciones de cribado. Y es fácil ver que los resultados de la descomposición obtenidos usando este criterio de parada serán de algún modo distintos respecto a los del método por defecto.

6. Aplicación del algoritmo EMD

Como el algoritmo EMD fue inicialmente parte de la transformada de Hilbert-Huang, el cálculo del espectro de frecuencia instantáneo para una serie puede servir como ejemplo que muestre la aplicación de este algoritmo. Esto implica realizar la transformada de Hilbert sobre los componentes de la IMF extraídos usando el algoritmo EMD. No obstante, este procedimiento no será tratado en este artículo.

Aparte de calcular el espectro, el algoritmo EMD puede usarse para ajustar las series.

La Figura 6 muestra un ejemplo de dicho ajuste.

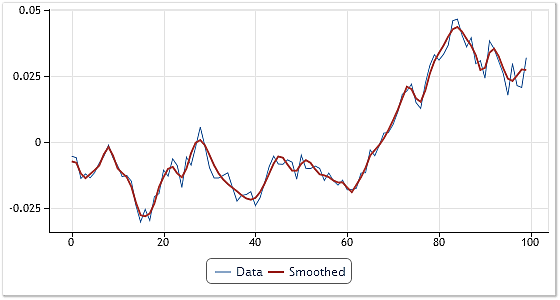
Fig. 6. Ajuste de la serie de entrada.

Se ha elegido un fragmento arbitrario de las cotizaciones diarias de USDCHF con 100 valores de precio "abiertos" para el ajuste. En el proceso de descomposición se han obtenido cuatro IMF y el residuo. Todas las IMF, excepto la primera, fueron añadidas al residuo.

De esta forma, el componente de mayor frecuencia se excluyó de la serie de entrada. Si hubiésemos obviado los dos primeros componentes al añadirlos, la curva resultante habría quedado aún más ajustada.

Otro ejemplo de la aplicación del algoritmo EMD puede ser la generación de una predicción en base a las IMF extraídas de la serie de entrada. Para realizar una predicción podemos usar cualquier extrapolador por el que se genere una de aquellas para cada IMF y el residuo por separado.

Las predicciones generadas de esta forma se añaden luego para obtener los resultados de la predicción requeridas para la serie de entrada. Al considerar la naturaleza oscilatoria de las IMF individuales, podemos suponer que para generar una predicción sería razonable usar extrapolaciones teniendo en cuenta el comportamiento periódico de las series de predicción.

En nuestro caso revisaremos un ejemplo de funcionamiento de un extrapolador simple en el que se generará una predicción para cada IMF usando una extrapolación lineal con 10 pasos por delante. El resultado de esta predicción se muestra en la Figura 7.

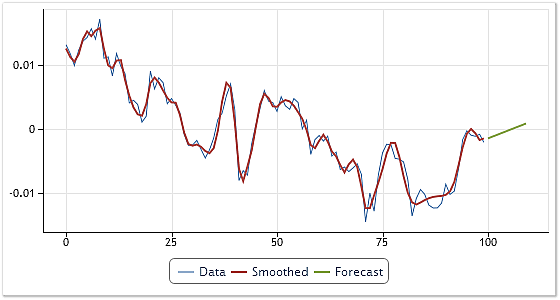
Fig. 7. Generación de una predicción para cotizaciones USDCHF H4.

Debe señalarse que al generar una predicción, pueden descartarse uno o más componentes de alta frecuencia. De esta forma puede mitigarse el efecto del ruido de alta frecuencia sobre la predicción. El resultado de la predicción que excluye la primera IMF se muestra en la Figura 7. La capacidad de predicción de este método no ha sido evaluada en este caso. No se proporciona aquí un análisis detallado de los métodos de predicción basados en la descomposición de modo empírico ya que esta materia cae fuera del ámbito de este artículo.

Tampoco podemos tratar la eliminación de la tendencia tampoco. Después de obtener los componentes individuales de la serie usando el algoritmo EMD, puede desarrollarse un algoritmo muy flexible para la eliminación de la tendencia. El residuo de la descomposición o el residuo añadido a una o más IMF extraídas en último lugar puede considerarse una tendencia. El número de IMF implicadas en la creación de una línea de tendencia junto con el residuo puede variar en función del número de componentes de baja frecuencia que es necesario que permanezcan en la serie después de la eliminación de la tendencia.

De esta forma, para eliminar la tendencia es suficiente añadir todas las IMF extraídas como resultado de la descomposición, excepto el último componente o varios de los obtenidos en último lugar. Este procedimiento puede combinarse fácilmente con el ajuste del resultado obtenido si el componente de frecuencia más alta también se excluye del proceso de adición de componentes. La Figura 8 muestra un ejemplo de eliminación de tendencia usando la técnica anterior.

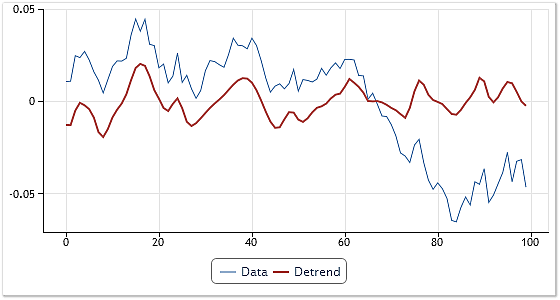
Fig. 8. Eliminación de tendencia combinada con ajuste.

Se ha tomado como datos iniciales una serie de cotizaciones diarias de EURUSD. Después de la descomposición se añadieron todos los componentes extraídos a excepción del residuo, el último y las primeras IMF. Esto dio como resultado, no solo en una eliminación de la tendencia sino también un cierto ajuste de la curva obtenida.

El área de aplicación del método de descomposición de modo empírico no está limitada a los ejemplos simples dados en el artículo. Aunque dado que este artículo se centra más en las cuestiones de implementación del método del algoritmo EMD como tal, más que en su aplicación, vamos a considerar los ejemplos que se muestran a continuación.

La Figura 9 que muestra el resultado de la descomposición obtenido al usar los parámetros establecidos por defecto en el archivo CEMDecomp.mqh puede servir como ilustración adicional de la funcionalidad ofrecida por la implementación del método del algoritmo EMD. Este ejemplo está basado en el uso de las cotizaciones de XAUUSD H4. La longitud de la serie es de 150 elementos.

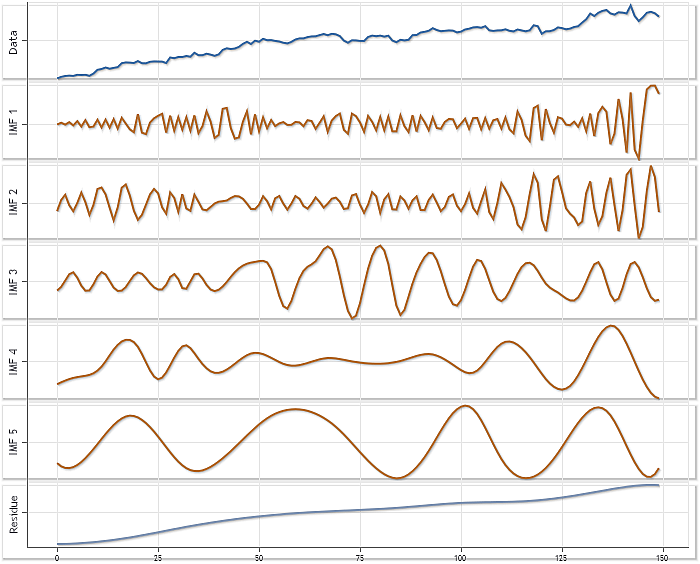
Fig. 9. Ejemplo de descomposición usando las cotizaciones XAUUSD H4.

Se ha aplicado un autoescalado a cada uno de los componentes de la Figura 9.

Conclusión

Recuerde que el método de descomposición de modo empírico así como la transformada de Hilbert-Huang tiene por objeto analizar los datos de los procesos no estacionarios y no lineales. Esto no significa que este enfoque no puede ser aplicado a las serie lineales y estacionarias.

Al inicio de este artículo se han visto brevemente algunos enfoques usados en los algoritmos de descomposición. Y se ha mencionado que la mayoría de ellos descomponen una serie en componentes que, de hecho, no representan los procesos iniciales que realmente dan lugar a la serie considerada.

Estos componentes son, de algún modo, sintéticos ya que su extracción solo ayuda a comprender mejor la estructura de una serie de entrada y, en muchos casos, facilita su análisis. El método del algoritmo EMD no es una excepción. No debe nunca pensar que los componentes obtenidos con este método reflejan los procesos físicos reales a partir de los cuales se formaron los datos iniciales analizados.

La implementación propuesta en este artículo puede probablemente requerir más pruebas y mejoras ya que difícilmente puede considerarse ideal.

El principal objetivo de este artículo ha sido familiarizar al lector con el método del algoritmo EMD y con algunas peculiaridades de su implementación.

Resumiendo todo.

1. El artículo trata brevemente algunas cuestiones generales relativas a la descomposición.
2. En pocas palabras, establece la esencia del método de descomposición de modo empírico.
3. Se introduce el listado y la descripción breve de la interfaz de la clase CEMDecomp en la que se implementa el método del algoritmo EMD.
4. Se muestra el ejemplo de la interacción con la clase CEMDecomp demostrando también cómo son llamados sus métodos.
5. Se esbozan algunas peculiaridades de la implementación propuesta del método del algoritmo EMD.
6. Se proporcionan algunos ejemplos simples que muestran la aplicación del método del algoritmo EMD sobre los datos del análisis.
7. Al final del artículo encontrará el archivo CEMDecomp.mqh que implementa el método del algoritmo EMD así como el archivo EMDecomposition.zip que contiene todo el caso de prueba con el uso de la clase CEMDecomp.

Bibliografía

1. Hilbert-Huang transform.
2. Hilbert-Huang transform.
3. Empirical Mode Decomposition.

Anexo

El artículo original fue publicado el 28 de junio de 2012. Este anuncio está disponible desde el 5 de julio de 2012.

Además del artículo, se ofrece una implementación alternativa del método del algoritmo EMD. Dicha implementación se encuentra en la clase CEMD ubicada en el archivo CEMD_2.mqh más abajo.