MetaTrader 5 / Statistik und Analyse
English Русский 中文 Español 日本語 Português 한국어 Français Italiano Türkçe
Die Box-Cox-Transformation

Die Box-Cox-Transformation

MetaTrader 5 — Statistik und Analyse | 13 Mai 2016, 09:40
2 290 0
Victor
Victor


Einleitung

Dank steigender Rechnerleistung eröffnen sich Devisenhändlern und -analysten immer neue Möglichkeiten zur Nutzung hoch entwickelter komplexer mathematischer Algorithmen, die beträchtliche Rechenkapazitäten erfordern. Aber ausreichende Rechnerleistung allein beantwortet noch nicht alle für Devisenhändler brennenden Fragen. Es bedarf effizienter Algorithmen zur Analyse der vom Markt gelieferten Kursnotierungen.

Bis heute wurden auf Gebieten wie der mathematischen Statistik, der Wirtschaftswissenschaften und der Ökonometrie zahlreiche Verfahren, Modelle sowie geprüfte und effiziente Algorithmen entwickelt, derer sich selbstredend vor allem Devisenhändler bei der Analyse des Marktes bedienen. In den meisten Fällen handelt es sich dabei um herkömmlicher parametergestützte Verfahren auf der Grundlage der Annahme der Stationarität und Normalverteilung der untersuchten Folgen.

Es ist jedoch kein Geheimnis, dass es sich bei Devisenkursnotierungen um Folgen handelt, für die weder Stationarität noch eine Normalverteilung bezeichnend ist. Deshalb sind wir bei der Analyse von Kursnotierungen formell nicht berechtigt, die „klassischen“ parametergestützten Verfahren der mathematischen Statistik, Ökonometrie usw. zu nutzen.

In seinem Artikel Mathcad in der Hand des Wirtschaftwissenschaftlers: Die Box-Cox-Transformation und die Illusion der „Normalverteilung makroökonomischer Reihen [1] schreibt A.N. Porunov unter anderem: 

„Häufig haben Analysten mit statistischen Daten zu tun, die die Normalitätsprüfung aus irgendeinem Grund nicht bestehen. Aus dieser Situation gibt es zwei Auswege: entweder bedient man sich nicht parametergestützter Verfahren, was für Wirtschaftswissenschaftler nie ganz einfach ist, da dazu gründliche mathematische Kenntnisse erforderlich sind, oder besondere Methoden anzuwenden, die es ermöglichen, eine „nicht normal verteilte Statistik“ in eine „normale“ umzuwandeln, was ebenfalls nicht ganz ohne ist.“

Ungeachtet der Nennung von Analysten in dem angeführten Zitat von A.N. Porunov gilt das Gesagte in vollem Umfang auch für Versuche zur Analyse „nicht normal verteilter“ Devisenkursnotierungen mithilfe parametergestützter Verfahren der mathematischen Statistik und Ökonometrie. Die überwiegende Mehrzahl dieser Verfahren wurde zur Analyse von normal verteilten Folgen entwickelt und konzipiert. Aber häufig wird bei ihrer Anwendung der Umstand, dass die Ausgangsdaten „nicht normal verteilt“ sind, ausgeblendet. Außerdem setzen die genannten Verfahren häufig nicht nur eine Normalverteilung sondern auch die Stationarität der Ausgangsfolgen voraus.

Zu diesen „klassischen“, eine Normalverteilung der Ausgangsdaten voraussetzenden Verfahren zählen u. a. die Regressions- und die Varianzanalyse (ANOVA). Es ist nicht möglich, alle parametergestützten Verfahren, die Beschränkungen hinsichtlich der Normalität der Verteilung aufweisen, aufzuzählen, da sie den gesamten Bereich, etwa der Ökonometrie, mit Ausnahme ihrer nicht parametergestützten Verfahren umfassen.

Um der Gerechtigkeit Genüge zu tun, ist zu erwähnen, dass unterschiedliche „klassische“ parametergestützte Verfahren eine unterschiedliche Empfindlichkeit gegenüber Abweichungen der Verteilungsgesetzmäßigkeit der Eingangsdaten von der Normalverteilung aufweisen. Deshalb führt eine Abweichung von der „Normalität“ bei der Anwendung dieser Methoden nicht immer zwangsläufig zu katastrophalen Folgen, erhöht jedoch auch nicht gerade die Genauigkeit und Zuverlässigkeit der erhaltenen Ergebnisse.

Das Gesagte zwingt dazu, ernsthaft über den Wechsel zu nicht parametergestützten Verfahren zur Analyse und Vorhersage von Kursnotierungen nachzudenken. Nichtsdestotrotz bleiben die parametergestützten Verfahren allemal anziehend. Das erklärt sich durch ihre große Verbreitung und folglich die ausreichende Anzahl an Informationen, einsatzfertigen Algorithmen und Anwendungsbeispielen. Zur sachgemäßen Anwendung dieser Verfahren gilt es, mindestens zwei mit den Ausgangsfolgen verbundene Probleme zu überwinden: ihre „Nichtstationarität“ und ihre „Nichtnormalität“.

Wenn wir schon die Stationarität der Eingangsfolgen nicht beeinflussen können, so können wir dennoch versuchen, ihre Verteilungsgesetzmäßigkeit der Normalität anzunähern. Zur Lösung dieses Problems gibt es eine Reihe von Transformationen. Eine Übersicht über die bekanntesten von ihnen bietet The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses [2]. In diesem Beitrag befassen wir uns nur mit der Box-Cox-Transformation [1], [2] und [3].

Es sei gleich darauf hingewiesen, dass die Verteilungsgesetzmäßigkeit der Ausgangsfolge sowohl bei Verwendung der Box-Cox-Transformationen als auch bei jeder anderen nur bis zu einem gewissen Grad an die Normalverteilung angenähert werden kann. Das bedeutet, dass die Verwendung der jeweiligen Transformation allein nicht garantiert, dass wir als Ergebnis eine normal verteilte Folge erhalten.


1. Die Box-Cox-Transformation

Für die Ausgangsfolge X mit der Länge N

Die Box-Cox-Transformation mit einem Parameter wird wie folgt ermittelt:


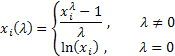
mit .

Wie wir sehen, besitzt diese Transformation nur einen Parameter - Lambda. Ist Lambda gleich „0“, erfolgt die logarithmische Umwandelung der Eingangsfolge, bei jedem anderen Wert als Null erfolgt diese schrittweise. Ist der Parameter Lambda gleich „1“, so bleibt die Verteilungsgesetzmäßigkeit der Ausgangsfolge unverändert, obwohl die Folge eine Verschiebung erfährt, da von jedem ihrer Werte jeweils eine Einheit subtrahiert wird.

Je nach Lambda-Wert schließt die Box-Cox-Transformation folgende Sonderfälle ein:


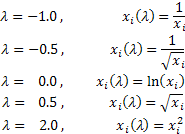
Bei Verwendung der Box-Cox-Transformation müssen alle Werte der Eingangsfolge größer als und verschieden von „0“ sein. Erfüllt die Eingangsfolge diese Voraussetzungen nicht, kann sie um die Größe in den positiven Bereich verschoben werden, durch die die „Positivität“ all ihrer Werte gewährleistet ist.

Bleiben wir ein wenig bei der Box-Cox-Transformation mit nur einem Parameter und bereiten wir die Eingangsdaten für sie entsprechend auf. Zur Vermeidung des Auftretens negativer oder von Werten gleich „0“ unter den Eingangsdaten suchen wir stets den niedrigsten Wert der Eingangsfolge und subtrahieren ihn von jedem ihrer Elemente, wodurch wir eine zusätzliche Verschiebung um die geringfügige Größe von 1e-5 vollziehen. Diese zusätzliche Verschiebung ist erforderlich, um die Verschiebung der Folge in den positiven Wertebereich zu gewährleisten, falls deren kleinster Wert gleich „0“ ist.

Für Folgen mit ausschließlich positiven Werten wäre eine solche Verschiebung verzichtbar, aber um bei der Transformation die Wahrscheinlichkeit des Auftretens übermäßig großer Werte im Fall einer Potenzierung zu verringern, verwenden wir denselben Verschiebungsalgorithmus auch bei „positiven“ Folgen. Somit wird jede Eingangsfolge nach der Verschiebung im positiven Wertebereich liegen und ihren niedrigsten Wert jeweils nahe Null haben.

In der Abbildung 1 sehen wir die Graphen der Box-Cox-Transformation mit unterschiedlichen Werten für den Parameter Lambda. Die Abbildung 1 wurde dem Artikel Box-Cox Transformations [3] entnommen. Die waagerechte Stricheinteilung des Diagramms entspricht dem Maßstab des Logarithmus.

Abb. 1. Die Box-Cox-Transformation mit unterschiedlichen Werten für den Parameter Lambda

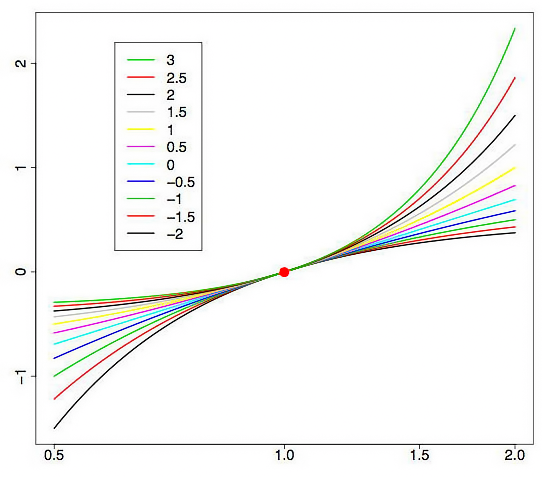
Abb. 1. Die Box-Cox-Transformation mit unterschiedlichen Werten für den Parameter Lambda

Unübersehbar können die „Schwänze“ bei einer Änderung des Parameters Lambda entweder „ausgestreckt“ oder „eingezogen“ werden. Der obere Graph in Abbildung 1 entspricht dem Wert Lambda = 3, der untere hingegen Lambda = -2.

Damit die Verteilung der resultierenden Folge im Ergebnis der Box-Cox-Transformation der Normalverteilung möglichst nahekommt, muss für den Parameter Lambda unbedingt der optimale Wert gewählt werden.

Eine Möglichkeit, ihn zu ermitteln, besteht in der Maximierung des Logarithmus der Wahrscheinlichkeitsfunktion.

mit

Das bedeutet, dass für den Parameter Lambda der Wer ausgewählt werden muss, bei dem die gegebene Funktion ihren höchsten Wert erreicht.

In dem Beitrag Box-Cox-Transformationen [3] wird ein anderes Verfahren zur Bestimmung des optimalen Wertes für diesen Parameter skizziert. Es beruht auf der Suche nach dem höchsten Wert für den Koeffizienten der Korrelation zwischen den Quantilen der Funktion der Normalverteilung und der ausgesonderten umgewandelten Folge. Höchstwahrscheinlich ließen sich noch weitere Verfahren zur Optimierung des Parameters Lambda finden, aber für den Anfang bleiben wir bei der Suche nach dem Höhepunkt des Logarithmus der bereits erwähnten Wahrscheinlichkeitsfunktion.

Dieser Höhepunkt kann auf verschiedenen Wegen ermittelt werden. Zum Beispiel durch einfaches Durchprobieren. Dazu muss der Wert der Wahrscheinlichkeitsfunktion bei einer kleinschrittigen Änderung des Wertes für den Parameter Lambda innerhalb des gewählten Wertebereichs berechnet werden. Und als optimaler Wert für Lambda sollte derjenige gewählt werden, bei dem der höchste Wert der Wahrscheinlichkeitsfunktion erwartet wird.

Dabei bestimmt die Größe des Schritts die Genauigkeit der Berechnung des optimalen Wertes für den Parameter Lambda. Je kleiner der Schritt desto größer die Genauigkeit, aber proportional zu der Schrittverkleinerung nimmt auch die Anzahl der erforderlichen Berechnungen zu. Zur Steigerung der Effektivität der Berechnungen können unterschiedliche Algorithmen für die Suche nach dem Maximum/Minimum der Funktion verwendet werden, darunter bspw. genetische Algorithmen.


2. Umwandlung (Transformation) in eine Normalverteilung

Eine der Aufgaben der Box-Cox-Transformation, vielleicht ihre wichtigste, ist die Annäherung der Verteilungsgesetzmäßigkeit der Eingangsfolge an die „Normalform“. Wir versuchen herauszufinden, wie gut diese Aufgabe mithilfe dieser Umwandlung erfüllt werden kann.

Um nicht allzu weit von dem Thema dieses Beitrages abzuschweifen und erneut irgendeinen Algorithmus für die Suche nach dem Maximum/Minimum der Funktion zu betrachten, werden wir zur Bestimmung des optimalen Wertes für den Parameter Lambda im Weiteren den in den Artikeln Zeitreihenvorhersage mittels exponentieller Glättung und Zeitreihenvorhersage mittels exponentieller Glättung (Fortsetzung) behandelten Algorithmus für die Suche nach dem Minimum der Funktion mithilfe der Methode von Powell verwenden.

Für die Suche nach dem optimalen Wert für den Transformationsparameter legen wir die Klasse CBoxCox an, in der als Zielfunktion die oben genannte Wahrscheinlichkeitsfunktion umgesetzt wird. Als Basisklasse kommt dabei die Klasse PowellsMethod ([4] und [5]) zum Einsatz. Sie führt den Suchalgorithmus unmittelbar aus.

//+------------------------------------------------------------------+
//|                                                      CBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| CBoxCox class                                                    |
//+------------------------------------------------------------------+
class CBoxCox:public PowellsMethod
  {
protected:
   double            Dat[];          // Input data
   double            BCDat[];        // Box-Cox data
   int               Dlen;          // Data size
   double            Par[1];         // Parameters
   double            LnX;            // ln(x) sum
public:
   void   CBoxCox(void) { }
   void              CalcPar(double &dat[]);
   double GetPar(int n) { return(Par[n]); }
private:
   virtual double    func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CBoxCox::CalcPar(double &dat[])
  {
   int i;
   double a;
   //--- Lambda initial value
   Par[0]=1.0;                
   Dlen=ArraySize(dat);
   ArrayResize(Dat,Dlen);
   ArrayResize(BCDat,Dlen);
   LnX=0;
   for(i=0;i<Dlen;i++)
     {
    //--- input data
      a=dat[i]; Dat[i]=a;
     //--- ln(x) sum
     LnX+=MathLog(a);             }
    //--- Powell optimization
    Optimize(Par);            
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CBoxCox::func(const double &p[])
  {
   int i;
   double a,lamb,var,mean,k,ret;

   lamb=p[0]; var=0; mean=0; k=0;
   if(lamb>5.0){k=(lamb-5.0)*400; lamb=5.0;}         // Lambda >  5.0
   else if(lamb<-5.0){k=-(lamb+5.0)*400; lamb=-5.0;} // Lambda < -5.0

   //--- Lambda != 0.0
   if(lamb!=0)                                     
     {
      for(i=0;i<Dlen;i++)
        {
          //--- Box-Cox transformation
         BCDat[i]=(MathPow(Dat[i],lamb)-1.0)/lamb;            //--- average value calculation
         mean+=BCDat[i]/Dlen;
        }
     }
    //--- Lambda == 0.0
    else                                                 {
      for(i=0;i<Dlen;i++)
        {
          //--- Box-Cox transformation
         BCDat[i]=MathLog(Dat[i]);
          //--- average value calculation
         mean+=BCDat[i]/Dlen;        }
     }
   for(i=0;i<Dlen;i++)
     {
      a=BCDat[i]-mean;
       //--- variance
      var+=a*a/Dlen;
     }
   //--- log-likelihood
   ret=Dlen*MathLog(var)/2.0-(lamb-1)*LnX;         
   return(k+ret);
  }
//------------------------------------------------------------------------------------

Jetzt reicht es zur Ermittlung des optimalen Wertes für den Parameter Lambda aus, sich der Methode CalcPar der genannten Klasse zu bedienen und eine Verknüpfung zu dem Datenfeld mit den Eingangsdaten als Parameter an sie weiterzugeben. Beziehen können wir den ermittelten optimalen Parameterwert durch Aufruf der Methode GetPar. Wie bereits erwähnt müssen die Eingangsdaten dabei positiv sein.

Die Klasse PowellsMethod setzt den Algorithmus für die Suche nach dem Minimum einer Funktion mit mehreren Variablen um, in unserem Fall wird jedoch nur ein einziger Parameter optimiert. Das führt dazu, dass die Dimension des Datenfeldes Par[] gleich „1“ ist. Es enthält also lediglich einen Wert. Theoretisch könnte in einem solchen Fall statt des Parameterdatenfeldes auch eine gewöhnliche Variable verwendet werden, aber dann müsste der Programmcode der Basisklasse PowellsMethod überarbeitet werden. Es ist anzunehmen, dass es bei der Übersetzung des ursprünglichen MQL5-Codes unter Verwendung von Datenfeldern, die nicht mehr als ein Element enthalten, keine Probleme gibt.

Es ist zu beachten, dass in der Funktion CBoxCox::func() eine Begrenzung des zulässigen Wertebereichs für den Parameter Lambda angelegt ist. In unserem Fall ist der Wertebereich auf -5 bis 5 beschränkt. Das geschieht, um zu vermeiden, dass es bei der Potenzierung der Eingangsdaten mit Lambda zu übermäßig großen oder kleinen Werten kommt.

Außerdem kann es, wenn bei der Optimierung zu große oder zu kleine Werte für Lambda auftreten, sein, dass die Folge für die gewählte Art der Transformation ungeeignet ist, weshalb es sich in keinem Fall lohnt, bei der Bestimmung des Wertes für Lambda über einen realistischen Wertebereich hinauszugehen.


3. Zufallsfolgen

Wir legen ein Versuchsskript an, das mithilfe der Klasse CBoxCox die Box-Cox-Transformation einer von uns erstellten pseudozufälligen Folge ausführt.

Es folgt der Quellcode eines solchen Skripts:

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest1.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- data size
   n=1600;
//--- input array preparation
   ArrayResize(dat,n);
//--- transformed data array
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- random sequence generation
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Exp();

//--- input data shift
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- optimization by lambda  
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- input data
//--- bcdat[] <-- transformed data
  }
//-----------------------------------------------------------------------------------

Das abgebildete Beispielskript verwendet als umzuwandelnde Eingangsdaten die Daten einer exponentiell verteilten pseudozufälligen Folge. Die Länge der Folge wird in der Variablen n festgelegt und beträgt in unserem Fall 1.600 Werte.

Zur Erzeugung einer pseudozufälligen Folge bedienen wir uns der Klasse RNDXor128 (George Marsaglia, Xorshift RNG). Eine Darstellung dieser Klasse bietet der Artikel Analyse der wesentlichen Merkmale von Zeitreihen [6]. Alle zur Übersetzung des Skriptes BoxCoxTest1.mq5 benötigten Dateien befinden sich in der gepackten Datei Box-Cox-Transformation_MQL5.zip. Für eine erfolgreiche Übersetzung müssen sie alle in ein und demselben Ordner abgelegt werden.

Bei der Ausführung des aufgeführten Skripts wird eine zunächst Eingangsfolge angelegt und in den positiven Wertebereich verschoben, bevor nach dem optimalen Wert für den Parameter Lambda gesucht wird. Anschließend wird eine Meldung mit dem für Lambda ermittelten Wert und der Anzahl der Durchläufe des Suchalgorithmus ausgegeben. Die umgewandelte Folge wird in dem Ausgabedatenfeld bcdat[] ausgegeben.

In der hier abgebildeten Form ermöglicht dieses Skript lediglich die Aufbereitung der umgewandelten Folge zu deren weiterer Verwendung, nimmt jedoch keine Manipulationen an ihr vor. Beim Schreiben dieses Beitrages wurde zur Berechnung der Umwandlungsergebnisse das in dem Artikel Analyse der wesentlichen Merkmale von Zeitreihen [6] beschriebene Analyseverfahren verwendet. Die verwendeten Skripte werden in diesem Beitrag aus Platzgründen nicht aufgeführt. Es werden im Folgenden nur die fertigen grafischen Ergebnisse der Analyse abgebildet.

In der Abbildung 2 sehen wir das Histogramm und das Diagramm der Normalverteilung für die in dem Skript BoxCoxTest1.mq5 verwendete exponentiell verteilte pseudozufällige Folge. Ergebnis des Jarque-Bera-Tests JB=3.241,73, p = 0,000. Wie wir sehen, ist die Eingangsfolge alles andere als „normal“, und ihre Verteilung ist wie zu erwarten war eher einer exponentiellen vergleichbar.

Abb. 2

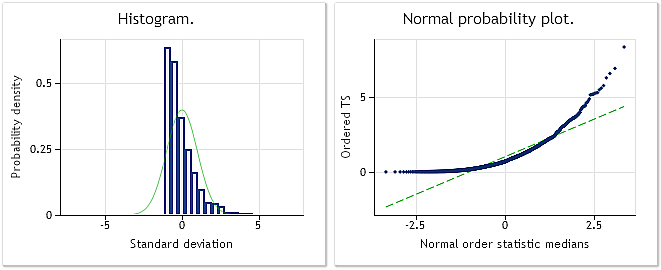
Abb. 2. Exponentiell verteilte pseudozufällige Folge. Ergebnis des Jarque-Bera-Tests JB=3.241,73, p = 0,000.

 Abb. 3

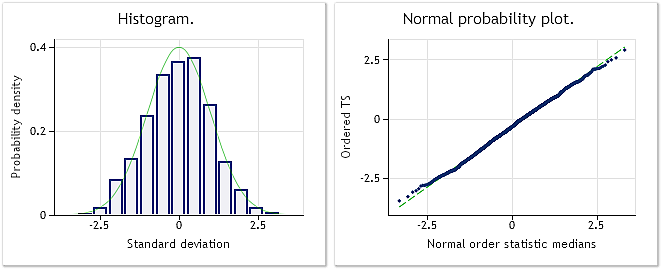
Abb. 3. Die umgewandelte Folge. Lambda = 0,2779; Ergebnis des Jarque-Bera-Tests JB=4,73, p = 0,094

In der Abbildung 3 wird das Ergebnis der Analyse der umgewandelten Folge dargestellt (mit dem Skript BoxCoxTest1.mq5 und dem Datenfeld bcdat[]). Die Gesetzmäßigkeit der Verteilung der umgewandelten Folge kommt der Normalverteilung wesentlich näher, was auch durch die Ergebnisse des Jarque-Bera-Tests, JB=4,73, p = 0,094, bestätigt wird. Der ermittelte Wert für den Parameter Lambda beträgt 0,2779.

In dem angeführten Beispiel hat sich die Box-Cox-Transformation als hinreichend geeignet erwiesen. Allem Anschein nach hat sich die resultierende Folge der „Normalverteilung“ beträchtlich angenähert, während das Ergebnis des Jarque-Bera-Tests von JB=3.241,73 auf JB=4,73 zurückgegangen ist. Aber das überrascht nicht, da die von uns gewählte Eingangsfolge für diese Art Umwandlung offenkundig recht gut geeignet ist.

Wir sehen uns ein weiteres Beispiel für die Box-Cox-Transformation einer pseudozufälligen Folge an. Bedenkt man, dass die Box-Cox-Transformation schrittweise erfolgt, legen wir eine für sie „geeignete“ Eingangsfolge an. Dazu erzeugen wir eine pseudozufällige Folge (mit einer bereits an die Normalverteilung angenäherten Verteilungsgesetzmäßigkeit) und verzerren sie, indem wir ihre gesamten Werte mit 0,35 potenzieren. Es ist zu erwarten, dass die Box-Cox-Transformation der Eingangsfolge mit großer Genauigkeit ihre ursprüngliche Normalverteilung zurückgeben wird.

Unten folgt der Code des Testskripts BoxCoxTest2.mq5.

Dieses Skript unterscheidet sich von dem vorhin betrachteten lediglich dadurch, dass in ihm eine andere Eingangsfolge erzeugt wird.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest2.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- data size
   n=1600;
//--- input data array
   ArrayResize(dat,n);
//--- transformed data array
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- random sequence generation
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Norm();

//--- input data shift
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;
   for(i=0;i<n;i++)dat[i]=MathPow(dat[i],0.35);

//--- optimization by lambda
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);

   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0) { for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;   }
   else          { for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);  }     // Lambda == 0.0

//-- dat[]   <-- input data
//-- bcdat[] <-- transformed data
  }
//-----------------------------------------------------------------------------------

In diesem Skript wird eine normal verteilte pseudozufällige Eingangsfolge erzeugt, in den positiven Wertebereich verschoben, und anschließend werden ihre Werte mit 0,35 potenziert. Nach Abschluss der Ausführung des Skripts enthält das Datenfeld dat[] die Eingangsfolge, das Datenfeld bcdat[] dagegen die umgewandelte.

Abbildung 4 zeigt die Merkmale der Eingangsfolge nach dem Verlust ihrer ursprünglichen Normalverteilung infolge der Potenzierung mit 0,35. Dabei ergibt der Jarque-Bera-Test JB=3609,29, p = 0,000.

Abb. 4

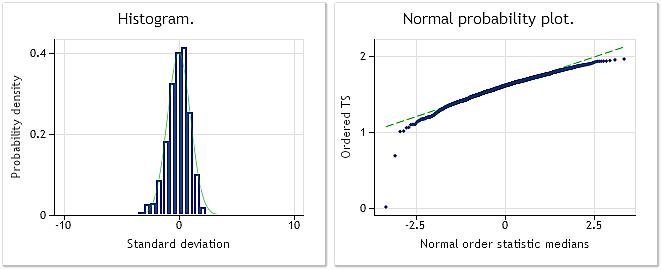
Abb. 4. Pseudozufällige Eingangsfolge. Ergebnis des Jarque-Bera-Tests JB=3609,29, p = 0,000.

Abb. 5

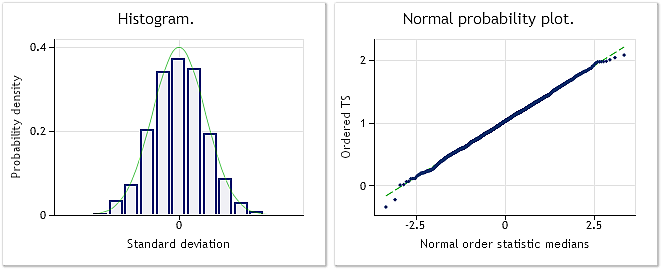
Abb. 5. Die umgewandelte Folge. Lambda = 2,9067; Ergebnis des Jarque-Bera-Tests JB=0,30, p = 0,859

Wie in Abbildung 5 dargestellt, kommt die Gesetzmäßigkeit der Verteilung der umgewandelten Folge der Normalverteilung ausreichend nahe, was auch durch den Wert des Jarque-Bera-Tests, JB=0,30, p = 0,859, bestätigt wird.

Die vorgestellten Anwendungsbeispiele für die Box-Cox-Transformation haben sehr gute Ergebnisse geliefert. Dabei sollte jedoch nicht vergessen werden, dass in beiden Fällen als Eingangsfolgen solche gewählt worden sind, bei denen diese Umwandlung offenkundig recht unproblematisch war. Deshalb können die gewonnenen Ergebnisse schlicht als Bestätigung der Verwendbarkeit des von uns aufgestellten Algorithmus betrachtet werden.


4. Kursnotierungen

Nachdem wir uns von der Verwendbarkeit des Algorithmus zur Umsetzung der Box-Cox-Transformation vergewissert haben, versuchen uns an seiner Anwendung auf echte Devisenhandelsnotierungen, da wir genau diese in eine Normalverteilung überführen wollen.

Als Versuchsnotierungen verwenden wir die bereits in dem Artikel Zeitreihenvorhersage mittels exponentieller Glättung (Fortsetzung) [5] beschriebenen Folgen. Sie sind in dem Ordner \Dataset2 der gepackten Datei Box-Cox-Transformation_MQL5.zip abgelegt. Es handelt sich um echte Kursnotierungen, von denen 1.200 Werte in die entsprechenden Dateien gespeichert wurden. Um den Zugriff auf diese Dateien zu gewährleisten, muss der der gepackten Datei entnommene Ordner \Dataset2 in den Ordner \MQL5\Files der Ausgabeinstanz (Terminal) kopiert werden.

Darüber hinaus setzen wir voraus, dass es sich bei diesen Notierungen nicht um stationäre Folgen handelt. Deshalb dehnen wir die Ergebnisse der Analyse auf die so genannte Grundgesamtheit aus, sondern betrachten sie lediglich als Merkmale der konkreten gegebenen Folge mit endlicher Länge.

Außerdem müssen wir im Auge behalten, dass es bei nicht vorliegender Stationarität in unterschiedlichen Ausschnitten des Kursverlaufs ein und desselben Währungspaares zu vollkommen verschiedenen Verteilungsgesetzmäßigkeiten kommen kann.

Wir legen ein Skript zum Auslesen der Werte einer Folge aus der Datei und zu ihrer Umwandlung mittels Box-Cox-Transformation an. Von den weiter oben eingeführten Versuchsskripten unterscheidet es sich lediglich durch die Art und Weise der Bildung der Eingangsfolge. Unten sehen Sie den Quellcode dieses Skriptes. Das Skript BoxCoxTest3.mq5 selbst befindet sich in der beigefügten gepackten Datei.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest3.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
CBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
   string fname;
//--- input data file
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- data reading
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- data size
   n=ArraySize(dat);
//--- transformed data array
   ArrayResize(bcdat,n);

//--- input data array
   min=dat[ArrayMinimum(dat)]-1e-5;
   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- lambda parameter optimization
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- input data
//--- bcdat[] <-- transformed data
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//-----------------------------------------------------------------------------------

In diesem Skript werden aus der Datei mit den Kursnotierungen, deren Name in der Variablen fname angegeben wird, alle Werte (in unserem Fall 1.200) in das Datenfeld dat[] ausgelesen. Zudem erfolgen, wie bereits beschrieben, die Verschiebung der Eingangsfolge, die Suche nach dem optimalen Parameterwert und die Box-Cox-Transformation. Nach Abschluss der Ausführung des Skripts wird das Ergebnis der Umwandlung in dem Datenfeld bcdat[] abgelegt.

Wie der abgebildete Quellcode zeigt, wurde in dem Skript für die Umwandlung eine Folge von Kursnotierungen für EURUSD M1 gewählt. Das Ergebnis der Analyse der ursprünglichen bzw. der umgewandelten Folge zeigen die Abbildungen 6 und 7.

Abb. 6

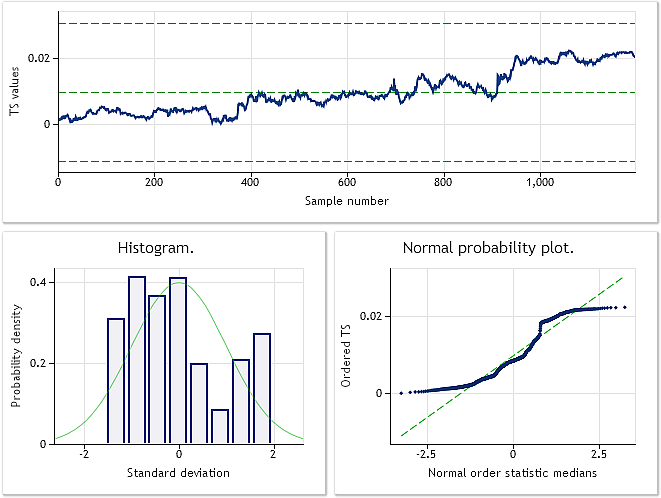
Abb. 6. Die Eingangsfolge EURUSD M1. Ergebnis des Jarque-Bera-Tests JB=100,94, p = 0,000.

Abb. 7

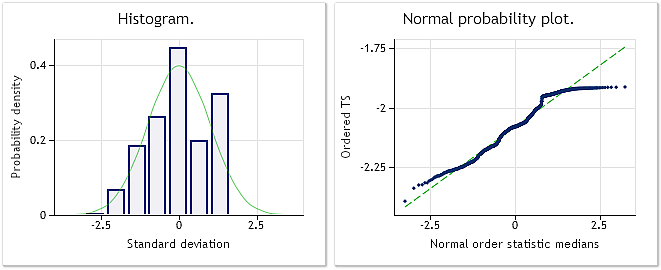
Abb. 7. Die umgewandelte Folge. Lambda = 0,4146; Ergebnis des Jarque-Bera-Tests JB=39,30, p = 0,000

Aus den in der Abbildung 7 ausgewiesenen Merkmalen geht hervor, dass das Ergebnis der Umwandlung der Notierungen für EURUSD M1 nicht so eindrucksvoll ausfällt wie die weiter oben präsentierten Ergebnisse der Umwandlung pseudozufälliger Folgen. Obwohl die Box-Cox-Transformation als hinreichend universell betrachtet werden kann, ist sie nicht allen Arten von Eingangsfolgen gewachsen. Von einer schrittweisen Transformation ist beispielweise die Umwandlung einer Verteilung mit zwei Höhepunkten in eine Normalverteilung nur schwerlich zu erwarten.

Aber obwohl die in der Abbildung 7 dargestellte Verteilungsgesetzmäßigkeit kaum als normal gelten kann, sehen wir nichtsdestoweniger wie in den vorhergehenden Beispielen auch eine deutliche Absenkung des Wertes für den Jarque-Bera-Test. Bei der Eingangsfolge lag dieser noch bei 100,94, nach der Umwandlung dagegen bei 39,30. Das spricht dafür, dass die Verteilung, auch wenn sie nach der Umwandlung noch nicht normal ist, sich der Normalität in gewisser Hinsicht angenähert hat.

In etwa dieselben Ergebnisse haben wir auch bei der Umwandlung unterschiedlicher Fragmente anderer Kursnotierungen erhalten. Jedes Mal hat die Box-Cox-Transformation die Verteilungsgesetzmäßigkeit in mehr oder weniger großem Umfang an die Normalverteilung angenähert. Auch wenn sie nie ganz normal wurde.

Eine Reihe von Experimenten mit der Umwandlung unterschiedlicher Kursnotierungen führt zu einer recht erwartbaren Schlussfolgerung, die da lautet: Die Box-Cox-Transformation ermöglicht in der überwältigenden Mehrzahl der Fälle die Annäherung der Verteilungsgesetzmäßigkeit der Devisenkursnotierungen an die Normalverteilung, auch wenn sie dabei das Erreichen einer echten Normalverteilung der umgewandelten Daten nicht garantieren kann.

Inwiefern ist es überhaupt zweckdienlich, eine Transformation vorzunehmen, durch die die ursprüngliche Folge ohnehin nicht in eine normal verteilte Folge umgewandelt wird? Diese Frage lässt sich nicht eindeutig beantworten. Über die Notwendigkeit der Verwendung der Box-Cox-Transformation muss von Fall zu Fall entschieden werden. Vieles wird dann davon abhängen, mithilfe welcher parametergestützten Verfahren die Analyse der Kursnotierungen durchgeführt werden soll, und wie empfindlich diese Verfahren gegenüber der Abweichung der Ausgangsdaten von der Normalverteilung sind.


5. Entfernung des Trends

Im oberen Teil der Abbildung 6 sehen wir das Diagramm für die in dem Skript BCTransform.mq5 verwendete Ausgangsfolge EURUSD M1. Es ist unschwer zu erkennen, dass die Werte dieser Folge über ihren ganzen Verlauf fast gleichmäßig ansteigen. Auf den ersten Blick könnte man fast vom Vorliegen eines linearen Trends in der Folge sprechen. Das Vorhandensein einer dergestalt augenfälligen „Trendigkeit“ legt den Gedanken nahe, zunächst zu versuchen, den Trend auszuschließen und erst danach mit der Durchführung der unterschiedlichen Umwandlungen und der Analyse der resultierenden Folge zu beginnen.

Die Entfernung des Trends aus den zu analysierenden Eingangsfolgen ist wahrscheinlich nicht das für absolut alle Fälle zu empfehlende Mittel. Aber nehmen wir einmal an, wir hätten vor, die in der Abbildung 6 dargestellte Folge im Blick auf das Vorhandensein periodischer (oder zyklischer) Bestandteile in ihr zu analysieren. In diesem Fall können wir, nach der Entdeckung auf einen linearen Trend hinweisender Parameter, diesen Trend selbstredend aus der Eingangsfolge entfernen.

Die Entfernung des linearen Trends sollte nicht nur keinen Einfluss auf die Ermittlung der periodischen Bestandteile haben, sondern sich je nach Analyseverfahren zudem noch als nützlich erweisen und die Analyseergebnisse in gewissem Umfang genauer und zuverlässiger machen.

Wenn wir zu dem Schluss gekommen sind, dass die Entfernung des Trends in bestimmten Fällen hilfreich sein kann, dürfte es sinnvoll sein, zu prüfen, wie die Box-Cox-Transformation mit einer Folge zurechtkommt, nachdem der Trend aus dieser entfernt wurde.

In jeder Situation stellt sich bei der Entfernung des Trends zwangsläufig die Frage danach, welcher Graph zur Annäherung des Trends verwendet werden sollte. Es kann sich um eine Gerade handeln, Kurven höherer Ordnung, gleitende Durchschnittswerte und so fort. In unserem Fall beschränken wir unsere Auswahl, wenn man so sagen kann, auf die Extremvariante, um nicht in eine Untersuchung zur Ermittlung des optimalen Grafen abzugleiten. Wir werden anstelle der Ausgangsfolge deren Inkremente verwenden, das heißt, die Differenz zwischen ihren aktuellen und ihren vorherigen Werten.

Wenn schon vom Übergang zur Analyse der Inkremente die Rede ist, kommt man keinesfalls darum herum, einige damit verbundene Aspekte zu kommentieren.

In unterschiedlichen Veröffentlichungen und Foren wird die Notwendigkeit des Übergangs zur Analyse der Inkremente bisweilen so unglücklich begründet, dass ein falscher Eindruck von den Eigenschaften dieses Übergangs entstehen kann. Der Übergang zur Analyse der Inkremente wird häufig als eine Transformation dargestellt, die in der Lage ist, die ursprüngliche Folge in eine stationäre zu verwandeln oder ihre Verteilungsgesetzmäßigkeit zu „normalisieren“. Doch ist dem so? Gehen wir der Sache auf den Grund.

Wir fangen damit an, dass dem Übergang zur Analyse der Inkremente eine banale Vorstellung zugrunde liegt, deren Wesen in der Aufspaltung der Ausgangsfolge in zwei Bestandteile besteht. Das kann an folgendem Beispiel veranschaulicht werden.

Angenommen wir haben als Eingangsfolge:

Aus irgendeinem Grund haben wir uns entschieden, diese Folge in einen Trend und einen aus der Subtraktion der Trendwerte von den Elementen der Ausgangsfolge resultierenden Rest, das Residuum, zu teilen, Nehmen wir einmal an, wir haben uns entschieden, zur Annäherung des Trends einen einfachen gleitenden Durchschnittswert mit einem Glättungszeitraum von zwei Elementen der Folge zu verwenden.

Ein solcher gleitender Durchschnittswert wird als die durch zwei dividierte Summe zweier benachbarter Elemente der Folge ermittelt. Anschließend erscheint das Residuum aus der Subtraktion dieses Durchschnittswertes von der Ausgangsfolge als die durch zwei dividierte Differenz zwischen denselben zwei benachbarten Elementen.

Wir bezeichnen den oben angesprochenen Durchschnittswert als „S“ und das Residuum als „D“. Wenn der stetige Faktor 2 der Anschaulichkeit halber auf die linke Seite der Gleichung übertragen wird, erhalten wir:


Im Ergebnis dieser unkomplizierten Umwandlungen haben wir unsere Ausgangsfolge in zwei Bestandteile aufgegliedert, von denen der eine die Summe der benachbarten Werte der Folge ist, während der zweite aus Differenzen besteht. Diese Differenzen haben wir als Inkremente bezeichnet, die Summe dagegen als Trend.

In diesem Zusammenhang wäre es logischer, die Inkremente lediglich als einen gewissen Teil der Ausgangsfolge zu betrachten. Deshalb sollte nicht vergessen werden, dass beim Übergang zur Analyse der Inkremente der andere, durch die Summen bestimmte Teil der Folge häufig einfach ausgeblendet wird, es sei denn, wir untersuchen ihn gesondert.

Um sich eine Vorstellung davon machen zu können, welchen Nutzen diese Aufgliederung der Folge bringen kann, ist es am einfachsten, sich der spektralen Methode anzunehmen.

Unmittelbar aus den aufgeführten Ausdrücken folgt, dass der Bestandteil „S“ das Ergebnis der Filterung der Ausgangsfolge mithilfe eines Niederfrequenzfilters mit einer Impulskennlinie von h = 1,1 ist. Dementsprechend ist der „D“-Bestandteil das Ergebnis der Filterung mit einem Hochfrequenzfilter mit einer Impulskennlinie von h = -1,1. In der Abbildung 8 ist das bedingte Frequenzverhalten dieser Filter dargestellt.

Abb. 8

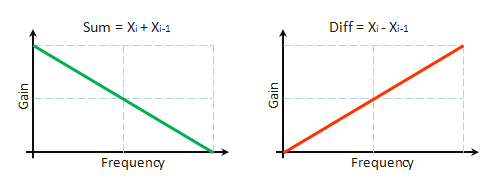
Abb. 8. Amplitudenfrequenzgänge

Angenommen, wir sind von der Analyse der Folge selbst zur Analyse ihrer Differenzen übergegangen. Was können wir uns davon versprechen? Es gibt unterschiedliche Möglichkeiten, von denen wir hier nur einige kurz betrachten werden:

  1. Wenn die Hauptenergie des betrachteten Vorgangs im Niederfrequenzbereich der Ausgangsfolge gebündelt ist, wird sie durch den Übergang zur Differenzanalyse (DA) entweder einfach unterdrückt, was ihre weitere Untersuchung erschwert, wenn nicht gänzlich unmöglich macht.
  2. Ist die Hauptenergie des betrachteten Vorgangs dagegen im Hochfrequenzbereich der Ausgangsfolge gebündelt ist, so ist beim Übergang zur DA aufgrund der Herausfilterung der störenden niederfrequenten Bestandteile zwar eine positive Wirkung zu erwarten, aber lediglich in dem Fall, wenn die Eigenschaften des untersuchten Vorgangs durch die Filterung in ihrer Substanz nicht beeinträchtigt werden.
  3. Zudem sei die Variante erwähnt, bei der die Energie des betrachteten Vorgangs gleichmäßig über den gesamten Frequenzbereich der Folge verteilt ist. In diesem Fall verzerren wir nach dem Übergang zur DA wahrscheinlich unumkehrbar den Charakter dieses Vorgangs, indem wir seinen niederfrequenten Bestandteil unterdrücken.

Ein vergleichbares Vorgehen lässt auch Schlussfolgerungen bezüglich der Ergebnisse des Übergangs zur DA bei anderen Trendkombinationen, einem kurzzeitigen Trend, Rauschen usw. zu. In keinem Fall jedoch führt der Übergang zur DA zu einem stationären Aussehen des uns interessierenden Vorgangs oder dazu, dass seine Verteilung „normaler“ wird.

Aus diesen Ausführungen können wir schließen, dass es beim Übergang zur DA nicht zu einer „automatischen“ Verbesserung der Folge kommt. Es ist anzunehmen, dass es in einigen Fällen sinnvoll ist, sowohl unmittelbar die Eingangsfolge selbst als auch die Differenzen und Summen ihrer jeweils benachbarten Werte zu untersuchen, um sich ein etwas vollständigeres Bild von dieser Folge machen zu können und ihre Eigenschaften anhand der gemeinsamen Betrachtung aller gewonnenen Ergebnisse abschließend zu beurteilen.

Kommen wir zurück zum eigentlichen Gegenstand unseres Beitrags und sehen wir nach, wie sich die Box-Cox-Transformation beim Übergang zur Analyse der Inkremente der in Abbildung 6 vorgestellten Folge EURUSD M1 verhält. Dazu verwenden wir das bereits eingeführt Skript BoxCoxTest3.mq5, in welchem wir nach dem Auslesen der Werte der Folge aus der Datei diese Werte selbst durch die Differenzen (Inkremente) ersetzen. Da an dem ursprünglichen Code des Skripts keine weiteren Änderungen vorgenommen wurden, wird er hier nicht noch einmal aufgeführt. Stattdessen zeigen wir hier die Ergebnisse einer erfolgreichen Analyse mit seiner Hilfe.

Inkremente für EURUSD M1. Ergebnis des Jarque-Bera-Tests JB=32.494,8; p = 0,000.

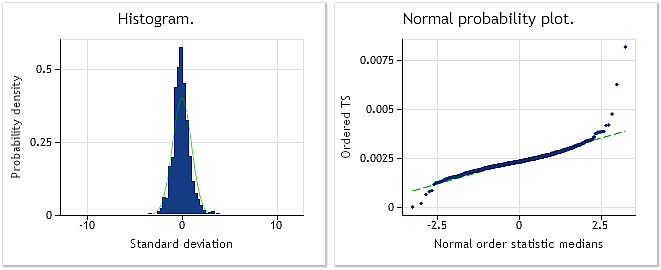
Abb. 9. Inkremente für EURUSD M1. Ergebnis des Jarque-Bera-Tests JB=32.494,8; p = 0,000.

Abb. 10. Die umgewandelte Folge. Lambda = 0,6662; Ergebnis des Jarque-Bera-Tests JB=10302,5, p = 0,000

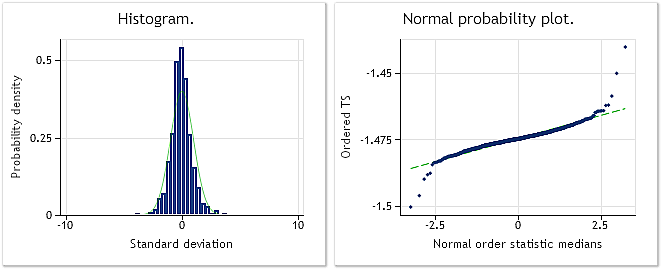
Abb. 10. Die umgewandelte Folge. Lambda = 0,6662; Ergebnis des Jarque-Bera-Tests JB=10302,5, p = 0,000

In der Abbildung 9 sind die Merkmale der aus den Inkrementen (Differenzen) für EURUSD M1 bestehenden Folge dargestellt, die Abbildung 10 dagegen zeigt die Merkmale, die sie nach der Box-Cox-Transformation aufweist. Ungeachtet dessen, dass das Ergebnis des Jarque-Bera-Tests nach der Umwandlung von JB = 32.494,8 auf JB = 10.302,5 um mehr als das Dreifache gesunken ist, liegt die Verteilungsgesetzmäßigkeit der umgewandelten Folge noch immer fernab der Normalverteilung.

Nichtsdestoweniger ist vor voreiligen Schlussfolgerungen zu warnen, die dahin gehen, dass die Box-Cox-Transformation zur Umwandlung der Inkremente generell nicht gut geeignet sei. Wir haben schließlich lediglich einen besonderen Einzelfall betrachtet. Bei anderen Eingangsfolgen werden möglicherweise vollkommen andere Ergebnisse gezeitigt.


6. Die vorgeführten Beispiele

Alle oben eingeführten Beispiele für die Box-Cox-Transformation beziehen sich auf den Fall, in dem die Verteilungsgesetzmäßigkeit einer Ausgangsfolge an die Normalverteilung bzw. an eine dieser möglichst nahekommende Verteilung herangeführt werden soll. Wie bereits zu Beginn dieser Ausführungen erwähnt wurde, kann eine solche Umwandlung bei Verwendung parametergestützter Analyseverfahren unerlässlich sein, das Letztere ziemlich empfindlich gegenüber Abweichungen der Gesetzmäßigkeit der Verteilung der zu untersuchenden Folge von der Normalverteilung sein können.

Die vorgestellten Beispiele haben gezeigt, dass wir gemessen an den Ergebnissen des Jarque-Bera-Tests nach der Umwandlung in allen Fällen tatsächlich Folgen erhalten haben, deren Verteilungsgesetzmäßigkeit verglichen mit derjenigen der Ausgangsfolge näher bei der Normalverteilung lagen. Das spricht für den Erfolg der Box-Cox-Transformation und belegt ihre Universalität und Nützlichkeit.

Allerdings sollten die Möglichkeiten der Box-Cox-Transformation auch nicht überschätzt und angenommen werden, dass jede beliebige Eingangsfolge unbedingt in eine streng normal verteilte Folge umgewandelt wird. Unsere Beispiele haben gezeigt, dass es sich bei weitem nicht so verhält. Bei echten Kursnotierungen können weder die ursprüngliche noch die umgewandelte Folge als normal verteilt betrachtet werden.

Bislang haben wir die Box-Cox-Transformation nur in ihrer anschaulichsten Form mit lediglich einem Parameter untersucht, um den Einstieg zu vereinfachen und das Verständnis zu erleichtern. Ein solches Herangehen ist zur Vorstellung ihrer Möglichkeiten vollkommen gerechtfertigt, für den praktischen Einsatz dürfte es jedoch wesentlich zielführender sein, eine umfassendere Ausgestaltung einzuführen.


7. Die allgemeine Form der Box-Cox-Transformation

Wie wir uns erinnern, kann die Box-Cox-Transformation nur auf Folgen angewendet werden, die nur Elemente beinhalten, die größer als „0“ sind. In der Praxis kann diese Bedingung durch eine einfache Verschiebung der Folge in den positiven Wertebereich erfüllt werden, wobei die Größe der Verschiebung innerhalb des positiven Wertebereichs allerdings unmittelbare Auswirkungen auf das Ergebnis der Umwandlung haben kann.

Aus diesem Grund ist die Verschiebungsgröße als zusätzlicher Parameter bei der Umwandlung zu betrachten und muss zusammen mit dem Parameter Lambda optimiert werden, wobei natürlich zu verhindern ist, dass die Werte der Folge in den negativen Wertebereich entweichen.

Für eine Ausgangsfolge X mit der Länge N:

sehen die Ausdrücke, die die verbreitetere Form der Box-Cox-Transformation mit zwei Parametern folgendermaßen aus:

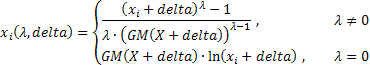
mit:

;

GM() = geometrisches Mittel.

Das GM einer Folge kann wie folgt berechnet werden:

Wie wir sehen, kommen in den vorgestellten Ausdrücken bereits zwei Parameter zum Einsatz: Lambda und Delta. Beide müssen jetzt im Verlauf der Umwandlung gleichzeitig optimiert werden. Obwohl der Algorithmus dadurch etwas komplizierter wird, kann die Einführung eines zusätzlichen Parameters zweifelsohne zu einer Steigerung der Effektivität der Umwandlung beitragen. Außerdem sind gegenüber der zuvor verwendeten Umwandlung in den Ausdrücken weitere normalisierende Faktoren aufgetreten, dank derer das Ergebnis der Umwandlung bei einer Änderung des Parameters Lambda seine Dimension behalten wird.

Weitere Informationen zur Box-Cox-Transformation bieten [7] und [8]. In der aufgeführten Literatur [8] finden sich zudem kurze Darstellungen einer Reihe vergleichbarer Transformationsverfahren.

Hier folgt jetzt eine Aufzählung der wesentlichen Besonderheiten dieser umfangreicheren Form der Transformation:

  1. Die Umwandlung selbst setzt nach wie vor voraus, dass die eingehende Folge lediglich positive Werte umfasst. Allerdings ermöglicht die Aufnahme des zusätzlichen Parameters Delta unter bestimmten Voraussetzungen die automatische Ausführung der erforderlichen Verschiebung der Folge:
  2. Bei der Auswahl des optimalen Wertes für den Parameter Delta muss dessen Größe die „Positivität“ aller Werte der Folge gewährleisten.
  3. Die Transformation ist bei einer Änderung des Parameters Lambda, einschließlich einer solchen unweit seines Nullwertes, kontinuierlich.
  4. Das Ergebnis der Umwandlung behält bei einer Änderung der Größe des Parameters Lambda seine Dimension.

In allen oben aufgeführten Beispielen wurde bei der Suche nach dem optimalen Wert für den Parameter Lambda das Kriterium zur Maximierung des Logarithmus der Wahrscheinlichkeitsfunktion verwendet. Das ist natürlich nicht die einzige Möglichkeit zur Berechnung des optimalen Wertes der Umwandlungsparameter.

Beispielhaft kann ein Verfahren zur Parameteroptimierung vorgeführt werden, bei dem das Maximum des Koeffizienten der Korrelation zwischen einer in aufsteigender Ordnung sortierten umgewandelten Folge und einer Folge von Quantilen der Normalverteilungsfunktion gesucht wird. Diese Variante wurde in diesem Beitrag bereits erwähnt. Die Werte der Quantile der Normalverteilungsfunktion können mithilfe der von James J. Filliben [9] vorgeschlagenen Ausdrücke berechnet werden.

Die Ausdrücke, die die allgemeine Form der Transformation mit zwei Parametern bestimmen, sind zweifelsfrei etwas sperriger als die weiter oben betrachteten. Das rührt möglicherweise daher, dass Transformationen dieser Art in Paketen mit mathematischen oder statistischen Programmen eher selten anzutreffen sind. Um die Box-Cox-Transformation in ihrer allgemeinen Form gegebenenfalls verwenden zu können, wurden alle hier vorgestellten Ausdrücke und Formeln in MQL5 umgesetzt.

Die Datei CFullBoxCox.mqh enthält den Quellcode der Klasse CFullBoxCox, die die Suche nach dem optimalen Wert der Umwandlungsparameter ausführt. Wie bereits gesagt fußt der Optimierungsvorgang dabei auf der Berechnung des Korrelationskoeffizienten.

//+------------------------------------------------------------------+
//|                                                  CFullBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+

#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| CFullBoxCox class                                                |
//+------------------------------------------------------------------+
class CFullBoxCox:public PowellsMethod
  {
protected:
  int    Dlen;                     // data size
  double Dat[];                    // input data array
  double Shift[];                  // input data array with the shift
  double BCDat[];                  // transformed data (Box-Cox)
  double Mean;                     // transformed data average value
  double Cdf[];                    // Quantile of the distribution cumulative function
  double Scdf;                     // Square root of summ of Quantile^2
  double R;                        // correlation coefficient
  double DeltaMin;                 // Delta minimum value
  double DeltaMax;                 // Delta maximum value
  double Par[2];                   // parameters array
public:
  void   CFullBoxCox(void)       { }
  void   CalcPar(double &dat[]);
  double GetPar(int n)           { return(Par[n]); }
private:
  double ndtri(double y0);         // the function opposite to the normal distribution function
  virtual double func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CFullBoxCox::CalcPar(double &dat[])
  {
  int i;
  double a,max,min;
  
  Dlen=ArraySize(dat);
  ArrayResize(Dat,Dlen);
  ArrayResize(Shift,Dlen);
  ArrayResize(BCDat,Dlen);
  ArrayResize(Cdf,Dlen);
//--- copy the input data array
  ArrayCopy(Dat,dat);  
  Scdf=0;
  a=MathPow(0.5,1.0/Dlen);
  Cdf[Dlen-1]=ndtri(a); Scdf+=Cdf[Dlen-1]*Cdf[Dlen-1];
  Cdf[0]=ndtri(1.0-a); Scdf+=Cdf[0]*Cdf[0];
  a=Dlen+0.365;
  for(i=1;i<(Dlen-1);i++)
    {
    //--- calculation of the distribution cumulative function Quantile
    Cdf[i]=ndtri((i+0.6825)/a);
    //--- calculation of the sum of Quantile^2
    Scdf+=Cdf[i]*Cdf[i];    }

//--- square root of the sum of Quantile^2
  Scdf=MathSqrt(Scdf);             
  
  min=dat[0]; max=min;
  for(i=0;i<Dlen;i++)
    {
//--- copy the input data
    a=dat[i]; Dat[i]=a;
    if(min>a)min=a;
    if(max<a)max=a;
    }
  
//--- Delta minimum value
  DeltaMin=1e-5-min;
//--- Delta maximum value
  DeltaMax=(max-min)*200-min;//--- Lambda initial value
  Par[0]=1.0;
//--- Delta initial value  Par[1]=(max-min)/2-min;//--- optimization using Powell method
  Optimize(Par);             
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CFullBoxCox::func(const double &p[])
  {
  int i;
  double a,b,c,lam,del,k1,k2,gm,gmpow,mean,ret;
  
  lam=p[0]; del=p[1]; k1=0; k2=0;
  if (lam>5.0){k1=(lam-5.0)*400; lam=5.0;}                    // Lambda >  5.0
  else if(lam<-5.0){k1=-(lam+5.0)*400; lam=-5.0;}             // Lambda < -5.0
  if (del>DeltaMax){k2=(del-DeltaMax)*400; del=DeltaMax;}    // Delta > DeltaMax
  else if(del<DeltaMin){k2=(DeltaMin-del)*400; del=DeltaMin; // Delta < DeltaMin
  
  gm=0;
  for(i=0;i<Dlen;i++)
    {
    Shift[i]=Dat[i]+del;
    gm+=MathLog(Shift[i]);
    }

//--- geometric mean
  gm=MathExp(gm/Dlen);
  gmpow=lam*MathPow(gm,lam-1);
  mean=0;
//--- Lambda != 0.0
   if(lam!=0)                                  
    {
    for(i=0;i<Dlen;i++)
      {
      a=(MathPow(Shift[i],lam)-1.0)/gmpow;
       //--- transformed data (Box-Cox)
      BCDat[i]=a;
       //--- average value
      mean+=a;
      }
    }
  //--- Lambda == 0.0
  else                                        
     {
    for(i=0;i<Dlen;i++)
      {
      a=gm*MathLog(Shift[i]);
       //--- transformed data (Box-Cox)
      BCDat[i]=a;
      //--- average value
      mean+=a;
      }
    }
  mean=mean/Dlen;
  //--- sorting of the transformed data array
  ArraySort(BCDat);
  a=0; b=0;
  for(i=0;i<Dlen;i++)
    {
    c=(BCDat[i]-mean);
    a+=Cdf[i]*c;
    b+=c*c;
    }
  //--- correlation coefficient
  ret=a/(Scdf*MathSqrt(b)); 
  return(k1+k2-ret);
  }
//+------------------------------------------------------------------+
//| The function opposite to the normal distribution function        |
//| Prototype:                                                       |
//| Cephes Math Library Release 2.8: June, 2000                      |
//| Copyright 1984, 1987, 1989, 2000 by Stephen L. Moshier           |
//+------------------------------------------------------------------+
double CFullBoxCox::ndtri(double y0)
  {
  static double s2pi =2.50662827463100050242E0; // sqrt(2pi)
  static double P0[5]={-5.99633501014107895267E1,  9.80010754185999661536E1,
                       -5.66762857469070293439E1,  1.39312609387279679503E1,
                       -1.23916583867381258016E0};
  static double Q0[8]={ 1.95448858338141759834E0,  4.67627912898881538453E0,
                        8.63602421390890590575E1, -2.25462687854119370527E2,
                        2.00260212380060660359E2, -8.20372256168333339912E1,
                        1.59056225126211695515E1, -1.18331621121330003142E0};
  static double P1[9]={ 4.05544892305962419923E0,  3.15251094599893866154E1,
                        5.71628192246421288162E1,  4.40805073893200834700E1,
                        1.46849561928858024014E1,  2.18663306850790267539E0,
                       -1.40256079171354495875E-1,-3.50424626827848203418E-2,
                       -8.57456785154685413611E-4};
  static double Q1[8]={ 1.57799883256466749731E1,  4.53907635128879210584E1,
                        4.13172038254672030440E1,  1.50425385692907503408E1,
                        2.50464946208309415979E0, -1.42182922854787788574E-1,
                       -3.80806407691578277194E-2,-9.33259480895457427372E-4};
  static double P2[9]={ 3.23774891776946035970E0,  6.91522889068984211695E0,
                        3.93881025292474443415E0,  1.33303460815807542389E0,
                        2.01485389549179081538E-1, 1.23716634817820021358E-2,
                        3.01581553508235416007E-4, 2.65806974686737550832E-6,
                        6.23974539184983293730E-9};
  static double Q2[8]={ 6.02427039364742014255E0,  3.67983563856160859403E0,
                        1.37702099489081330271E0,  2.16236993594496635890E-1,
                        1.34204006088543189037E-2, 3.28014464682127739104E-4,
                        2.89247864745380683936E-6, 6.79019408009981274425E-9};
  double x,y,z,y2,x0,x1,a,b;
  int i,code;
  if(y0<=0.0){Print("Function ndtri() error!"); return(-DBL_MAX);}
  if(y0>=1.0){Print("Function ndtri() error!"); return(DBL_MAX);}
  code=1; y=y0;
  if(y>(1.0-0.13533528323661269189)){y=1.0-y; code=0;}  // 0.135... = exp(-2)
  if(y>0.13533528323661269189)                         // 0.135... = exp(-2)
    {
    y=y-0.5; 
    y2=y*y;
    a=P0[0]; for(i=1;i<5;i++)a=a*y2+P0[i];
    b=y2+Q0[0]; for(i=1;i<8;i++)b=b*y2+Q0[i];
    x=y+y*(y2*a/b);
    x=x*s2pi; 
    return(x);
    }
  x=MathSqrt(-2.0*MathLog(y));
  x0=x-MathLog(x)/x;
  z=1.0/x;
//--- y > exp(-32) = 1.2664165549e-14
  if(x<8.0)
    {
    a=P1[0]; for(i=1;i<9;i++)a=a*z+P1[i];
    b=z+Q1[0]; for(i=1;i<8;i++)b=b*z+Q1[i];
    x1=z*a/b;
    }
  else
    {
    a=P2[0]; for(i=1;i<9;i++)a=a*z+P2[i];
    b=z+Q2[0]; for(i=1;i<8;i++)b=b*z+Q2[i];
    x1=z*a/b;
    }
  x=x0-x1;
  if(code!=0)x=-x;
  return(x);
  }
//------------------------------------------------------------------------------------

Bei der Optimierung unterliegt Änderungsbereich der Umwandlungsparameter einigen Beschränkungen. Der Wertebereich für den Parameter Lambda wird durch 5,0 und -5,0 begrenzt. Die Grenzen für den Parameter Delta werden in Abhängigkeit von dem kleinsten Wert (dem Minimum) der Eingangsfolge festgelegt. Dieser Parameter wird durch die Werte DeltaMin=(0,00001-min) und DeltaMax=(max-min)*200-min begrenzt, mit min für das Minimum und max für das Maximum der Elemente der Eingangsfolge.

Das Skript FullBoxCoxTest.mq5 veranschaulicht den Einsatz der Klasse CFullBoxCox. Der Quellcode für dieses Skript folgt:

//+------------------------------------------------------------------+
//|                                               FullBoxCoxTest.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include  "CFullBoxCox.mqh"
CFullBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],shift[],bcdat[],lambda,delta,gm,gmpow;
   string fname;

//--- input file name
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- reading the data
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- data size
   n=ArraySize(dat);
//--- shifted input data array
   ArrayResize(shift,n);
//--- transformed data array
   ArrayResize(bcdat,n);

//--- lambda and delta parameters optimization
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   delta=Bc.GetPar(1);

   PrintFormat("Iterations= %i,   lambda= %.4f,   delta= %.4f",
               Bc.GetIter(),lambda,delta);
   gm=0;
   for(i=0;i<n;i++)
     {
      shift[i]=dat[i]+delta;
      gm+=MathLog(shift[i]);
     }
//--- geometric mean
   gm=MathExp(gm/n);
   gmpow=lambda*MathPow(gm,lambda-1);
   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(shift[i],lambda)-1.0)/gmpow;}
   else         {for(i=0;i<n;i++)bcdat[i]=gm*MathLog(shift[i]);}
//--- dat[]   <-- input data
//--- shift[] <-- input data with the shift
//--- bcdat[] <-- transformed data
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//------------------------------------------------------------------------------------

Am Anfang des Skripts wird die Eingangsfolge aus der Datei in das Datenfeld dat[] geladen, anschließend erfolgt die Suche nach den optimalen Werten für die Umwandlungsparameter. Weiter wird unter Verwendung der ermittelten Werte die eigentliche Umwandlung ausgeführt. Danach enthält das Datenfeld dat[] die ursprüngliche Folge, das Datenfeld shift[] dieselbe Folge allerdings um den Wert Delta verschoben und das Datenfeld bcdat[] das Ergebnis der Box-Cox-Transformation.

Alle zur Übersetzung des Skriptes FullBoxCoxTest.mq5 benötigten Dateien befinden sich in der gepackten Datei Box-Cox-Transformation_MQL5.zip.

Mithilfe des Skripts FullBoxCoxTest.mq5 wurde die Umwandlung der von uns verwendeten Versuchsfolgen durchgeführt. Aus der Analyse der gewonnenen Daten geht hervor, dass diese Form der Umwandlung mit zwei Parametern gegenüber der mit nur einem Parameter erwartungsgemäß etwas bessere Ergebnisse liefert. Für die Folge EURUSD M1 weisen die in der Abbildung 6 dargestellten Analyseergebnisse beispielsweise für den Jarque-Bera-Test den Wert JB=100,94 aus. Nach der Umwandlung mit nur einem Parameter betrug dieser Wert JB=39,30 (siehe Abbildung 7), nach derjenigen mit zwei Parametern (s. das Skript FullBoxCoxTest.mq5) ist er auf JB=37,49 zurückgegangen.


Fazit

In diesem Beitrag wurden Beispiele vorgestellt, in denen die Parameter der Box-Cox-Transformation so optimiert wurden, dass die Verteilungsgesetzmäßigkeit der resultierenden Folge der Normalverteilung möglichst nahekam. In der Praxis kann man auf Situationen treffen, in denen es zweckmäßiger sein könnte, die Box-Cox-Transformation in leicht veränderter Weise zu verwenden. So könnte beispielsweise bei der Zeitreihenvorhersage nach folgendem Algorithmus vorgegangen werden:

  1. Auswahl der vorläufigen Werte für die Parameter der Box-Cox-Transformation;
  2. Box-Cox-Transformation der Eingangsdaten;
  3. Vorhersage anhand der aktuellen Parameterwerte;
  4. Umgekehrte Box-Cox-Transformation der Vorhersageergebnisse;
  5. Berechnung des Vorhersagefehlers für die nicht umgewandelte Eingangsfolge;
  6. Änderung der Parameterwerte dergestalt, dass der Vorhersagefehler minimiert wird, anschließend Rückkehr zu Punkt 2 des Algorithmus.

In dem vorgestellten Algorithmus wird vorgeschlagen, die Umwandlungsparameter wie die eines Vorhersagemodells anhand des Kriteriums des kleinsten Vorhersagefehlers zu minimieren. In diesem Fall besteht die Aufgabe der Box-Cox-Transformation nicht mehr in der Umwandlung der Eingangsfolge in eine normal verteilte Folge.

Jetzt geht es darum, die Eingangsfolge so umzuwandeln, dass am Ende eine Verteilungsgesetzmäßigkeit herauskommt, die den minimalen Vorhersagefehler gewährleistet. Je nach Vorhersageverfahren muss diese Verteilungsgesetzmäßigkeit nicht zwangsläufig „normal“ sein.

Die hier behandelte Box-Cox-Transformation selbst kann unmittelbar nur auf Folgen angewendet werden, deren Werte ausnahmslos größer als „0“ sind. In allen übrigen Fällen muss die Eingangsfolge verschoben werden. Diese Besonderheit des besprochenen Umwandlungsverfahrens kann man als eine seiner Schwachstellen bezeichnen. Dennoch ist die Box-Cox-Transformation dessen ungeachtet das universellste und effizienteste aller vergleichbaren Umwandlungsverfahren.


Literaturnachweise

  1. А.N. Porunov. Mathcad in Hands of the Economist: Box-Сox Transformation and the Illusion of «Normality» of Macroeconomic Series. Business Informatics, Fachzeitschrift, Nr. 2(12)-2010, S. 3 - 10.
  2. http://jetems.scholarlinkresearch.org/articles/The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses.pdf Journal of Emerging Trends in Economics and Management Sciences (JETEMS) 2(1):32-39.
  3. Box-Cox-Transformationen
  4. Zeitreihenvorhersage mittels exponentieller Glättung
  5. Zeitreihenvorhersage mittels exponentieller Glättung (Fortsetzung)
  6. Analyse der wesentlichen Merkmale von Zeitreihen.
  7. Power transform.
  8. N. R. Draper und H. Smith, Applied Regression Analysis, 3. Aufl., 1998, John Wiley & Sons, New York.
  9. Q-Q plot.

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/363

Beigefügte Dateien |
ZIP herunterladen
box-cox-transformation_mql5.zip (91.48 KB)
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum
Den Ballast selbstgemachter "dynamischer Programmbibliotheken" loswerden Den Ballast selbstgemachter "dynamischer Programmbibliotheken" loswerden
Wenn der Funktionsumfang der Programmiersprache MQL5 zur Erfüllung bestimmter Aufgaben nicht ausreicht, muss sich ein MQL5-Programmierer weiterer Hilfsmittel bedienen. Ein Weg besteht im Wechsel zu einer anderen Programmiersprache und dem Anlegen einer zwischengelagerten dynamischen Programmbibliothek (DLL). MQL5 bietet die Möglichkeit, unterschiedliche Datenarten abzubilden und sie an eine Programmierschnittstelle (API) weiterzugeben, leider ist MQL5 jedoch nicht in der Lage, das Problem des Auszugs von Daten aus einer zugelassenen Speicheradresse zu lösen. In diesem Beitrag wollen wir auf jedes „i“ einen Punkt setzen und einige einfache Mechanismen für den Austausch und die Arbeit mit komplexen Datenarten vorstellen.
Tipps für unerfahrene Auftraggeber Tipps für unerfahrene Auftraggeber
Eine Volksweisheit, die häufig den unterschiedlichsten Berühmtheiten zugeschrieben wird, lautet: „Nur wer nichts tut, macht keine Fehler.“ Wenn man nicht das Nichtstun selbst für einen Fehler hält, lässt sich diese Behauptung kaum bestreiten. Dagegen ist es absolut möglich, einmal begangene Fehler (eigene ebenso wie die anderer) zu analysieren, um die Anzahl zukünftiger Fehler zu minimieren. Hier wird der Versuch unternommen, mögliche Situationen auszuwerten, die bei der Arbeit mit dem Dienst „Freie Mitarbeit“ entstehen können.
Wer ist wer in der MQL5.community? Wer ist wer in der MQL5.community?
Die Webseite MQL5.com vergisst nichts und niemanden! Wie viele Abschlüsse legendär geworden sind, welcher Beliebtheit sich die einzelnen Artikel erfreuen, und wie oft die in der Codedatenbank gespeicherten Programme heruntergeladen wurden, all das ist nur ein kleiner Teil dessen, was MQL5.com nicht vergisst. In den Profilen werden die Errungenschaften jedes Einzelnen aufbewahrt, aber wie sieht das Gesamtbild aus? Dieser Beitrag soll eine Gesamtübersicht über die Leistungen aller Mitglieder der MQL5.community zeigen.
Multiple Regressionsanalyse. Anlegen und Prüfen von Strategien aus einer Hand Multiple Regressionsanalyse. Anlegen und Prüfen von Strategien aus einer Hand
Dieser Beitrag schildert die Anwendung der multiplen Regressionsanalyse bei der Entwicklung automatischer Handelssysteme (im Weiteren Expert-Systeme). Es werden Beispiele für ihren Einsatz bei der Automatisierung der Suche nach der richtigen Strategie sowie für eine ohne nennenswerte Vorkenntnisse in Sachen Programmierung angelegte und in ein Expert-System integrierte Regressionsgleichung.