Zeitreihenvorhersage mittels exponentieller Glättung
2 498
0
Einleitung
Zurzeit kennt man eine große Anzahl unterschiedlicher Vorhersagemethoden, die sich einzig auf die Analyse zurückliegender Werte zeitlicher Folgen oder Verläufe stützen, das heißt: Methoden, die Grundsätze verwenden, wie sie in der technischen Analyse üblich sind. Wesentliches Werkzeug dieser Methoden ist ein Extrapolationsmodell, bei dem die in dem beobachteten Zeitabschnitt entdeckten Eigenschaften eines Verlaufs über die Grenzen des Beobachtungszeitraums hinaus ausgedehnt werden.
Dabei wird davon ausgegangen, dass die Eigenschaften des Verlaufs in der Zukunft dieselben bleiben werden wie in Vergangenheit und Gegenwart. Seltener zum Einsatz kommt bei der Vorhersage ein komplizierteres Extrapolationsmodell, das die Untersuchung der Dynamik der Veränderung der Eigenschaften einer Folge sowie die Berücksichtigung dieser Dynamik in dem Vorhersageintervall voraussetzt.
Die wahrscheinlich bekanntesten auf der Extrapolation beruhenden Vorhersageverfahren sind Methoden, die das Modell der Autoregression und des integrierten gleitenden Durchschnitts (ARIMA) nutzen. Ihre Beliebtheit verdanken diese Methoden in erster Linie den Arbeiten von Box und Jenkins, die das verallgemeinerte ARIMA-Modell vorgeschlagen und entwickelt haben. Über die von Box und Jenkins vorgestellten Modelle hinaus gibt es jedoch noch zahlreiche weitere Vorhersagemodelle und -verfahren.
Dieser Artikel behandelt in aller Kürze einfachere Modelle, nämlich die von Holt und Brown noch vor dem Erscheinen der Arbeiten von Box und Jenkins vorgeschlagenen Modelle zur exponentiellen Glättung.
Ungeachtet des wesentlich einfacheren und zugänglicheren mathematischen Rüstzeugs liefert die Vorhersage mittels exponentieller Glättungsmodelle häufig ein Ergebnis, das dem mithilfe eines ARIMA-Modells gewonnenen entspricht. Das ist nicht weiter erstaunlich, da es sich bei den exponentiellen Glättungsmodellen um einen Sonderfall der ARIMA-Modelle handelt. Mit anderen Worten liegt für jedes in diesem Beitrag vorgestellte Modell der exponentiellen Glättung jeweils ein gleichwertiges ARIMA-Modell vor. Diese gleichwertigen Modelle werden hier nicht behandelt, sondern lediglich zu Informationszwecken genannt.
Bekanntermaßen erfordert eine Vorhersage in jedem konkreten Fall ein individuelles Herangehen und umfasst in der Regel eine ganze Reihe von Vorgängen.
Zum Beispiel:
- Die Untersuchung der zeitlichen Folge auf fehlende Werte und Ausreißer. Die Korrektur dieser Werte.
- Die Ermittlung des Vorliegen eines Trends und ggf. dessen Art. Die Ermittlung des Vorliegens einer Periodizität in dem Verlauf.
- Die Überprüfung des Verlaufs auf Stationarität.
- Die Untersuchung der Folge hinsichtlich der Notwendigkeit einer vorhergehenden Aufbereitung (Logarithmenbildung, Differenzbildung u. dgl.).
- Die Auswahl des Modells.
- Die Festlegung der Modellparameter. Vorhersage anhand des gewählten Modells.
- Die Berechnung der Vorhersagegenauigkeit des Modells.
- Die Untersuchung der Art der Fehler des gewählten Modells.
- Die Bestimmung der Angemessenheit des gewählten Modells sowie ggf. sein Austausch und die Rückkehr zu den vorausgehenden Punkten.
Das sind noch längst nicht alle für eine effektive Vorhersage benötigten Vorgänge.
Es sei betont, dass die Festlegung der Modellparameter und der unmittelbare Erhalt einer Vorhersage lediglich einen kleinen Teil des gesamten Prognosevorgangs darstellen. Aber die Erörterung des gesamten Komplexes der wie auch immer mit der Vorhersage verbundenen Fragen in einem Beitrag ist so gut wie unmöglich.
Deshalb beschränken wir uns in dem hier vorliegenden Artikel auf die Behandlung der Modelle zur exponentiellen Glättung selbst und verwenden als Testsequenzen Devisenkursnotierungen ohne jegliche vorherige Aufbereitung. Natürlich kann es nicht gelingen, in diesem Beitrag alle begleitenden Fragen auszuklammern, diese werden jedoch nur in dem zur Erläuterung der eigentlichen Modelle erforderlichen Umfang erörtert.
1. Stationarität
Der Begriff „Extrapolation“ selbst legt nahe, dass sich der beobachtete Vorgang in der Zukunft genauso weiterentwickelt, wie er es in der Vergangenheit getan hat und gegenwärtig tut. Anders ausgedrückt, die Rede ist von der Stationarität des Vorgangs. Die Stationarität ist eines Vorgangs ist aus Sicht der Erstellung von Vorhersagen äußerst anziehend, kommt jedoch bedauerlicherweise in der Natur dieser Vorgänge nicht vor, da jeder reale Vorgang je nach Entwicklungsstand Veränderungen unterworfen ist.
Bei realen Vorgängen können sich im Lauf der Zeit merkliche Veränderungen hinsichtlich der mathematischen Erwartung, der Streuung und der Verteilungsgesetzmäßigkeit einstellen, während Vorgänge, bei denen sich diese Merkmale nur sehr langsam verändern, mit einer gewissen Wahrscheinlichkeit den stationären Vorgängen zuzurechnen sind. In diesem Fall bedeutet der Begriff „sehr langsam“, dass sich die Veränderung der Merkmale des Vorgangs in dem begrenzten Beobachtungsintervall als derart unerheblich erweist, dass sie vernachlässigt werden kann.
Es liegt auf der Hand, dass die Wahrscheinlichkeit einer falschen Annahme bezüglich der Stationarität des Vorgangs insgesamt umso höher wird, je kürzer das verfügbare Beobachtungsintervall (eine kleine Stichprobe) ist. Andererseits kann die Verkleinerung des Umfangs der Stichprobe, wenn wir in höherem Maße an dem Zustand des Vorgangs zu späteren Zeitpunkten interessiert sind und wir uns anschicken, die Vorhersage für ein sehr kurzes Intervall vorzunehmen, zu einer Steigerung der Genauigkeit dieser Vorhersage führen.
Wenn der Vorgang Veränderungen unterliegt, ändern sich die in dem Beobachtungsintervall ermittelten Verlaufsparameter jenseits der Intervallgrenzen. Auf diese Weise vergrößert sich der Einfluss der Veränderlichkeit der Verlaufsmerkmale auf die Fehlerhaftigkeit der Vorhersage mit zunehmender Länge des Vorhersageintervalls. Dieser Umstand zwingt uns dazu, uns auf eine lediglich kurzfristige Vorhersage zu beschränken, da eine erhebliche Verkürzung des Vorhersageintervalls erwarten lässt, dass die sich langsam ändernden Verlaufsmerkmale der Genauigkeit der Vorhersage nicht sonderlich abträglich sein werden.
Darüber hinaus führt die Veränderlichkeit der Verlaufsparameter dazu, dass sich bei der Berechnung anhand des Beobachtungsintervalls einige Durchschnittswerte ergeben, da die Parameter nicht über das gesamte Intervall konstant geblieben sind. Deshalb beziehen sich die erhaltenen Parameterwerte nicht auf das auf den letzten Zeitpunkt besagten Intervalls, sondern geben vielmehr irgendeinen Durchschnittswert wieder. Die vollständige Beseitigung dieser unerfreulichen Erscheinung ist leider nicht möglich, aber sie kann abgeschwächt werden, indem wir die Dauer des Beobachtungsintervalls, innerhalb dessen die Berechnung der Modellparameter erfolgt (das untersuchte Intervall), möglichst kurz halten.
Bis ins Unendliche darf dieses Intervall indes ebenfalls nicht verkürzt werden, da bei einer übermäßigen Verkürzung des untersuchten Intervalls sicher auch die Genauigkeit der Berechnung der Verlaufsparameter abnehmen wird. Es muss ein Kompromiss zwischen der Auswirkung der mit der Veränderlichkeit der Verlaufsmerkmale verbundenen Fehler und der zunehmenden Verzerrung durch die übertriebene Verkürzung des untersuchten Intervalls gefunden werden.
All das Gesagte bezieht sich in vollem Umfang auf die Vorhersage mithilfe von Modellen der exponentiellen Glättung, da diese Modelle ausgehend von der Annahme der Stationarität der Vorgänge angelegt wurden wie übrigens auch die ARIMA-Modelle. Nichtsdestoweniger gehen wir der Einfachheit halber im Weiteren davon aus, dass sich die Parameter aller von uns betrachteten Verläufe in dem Beobachtungsintervall ändern, jedoch nur so langsam, dass diese Veränderungen vernachlässigt werden können.
Somit behandelt dieser Artikel mit der kurzfristigen Vorhersage von Verläufen mit sich langsam ändernden Merkmalen verbundene Fragen auf der Grundlage exponentieller Glättungsmodelle. In diesem Fall steht der Begriff „kurzfristige Vorhersage“ für eine Prognose für ein, zwei oder mehrere zukünftige Intervalle und nicht für einen Vorhersagezeitraum von weniger als einem Jahr, wie es in der Wirtschaft häufig vorkommt.
2. Kursverläufe für die Überprüfung
Beim Schreiben dieses Beitrages wurden die zuvor gespeicherten Kursnotierungen der Kürzel EURRUR, EURUSD, USDJPY bzw. XAUUSD für die Zeiträume M1, M5, M30 und H1 verwendet. Jede der gespeicherten Dateien enthält 1.100 Eröffnungswerte „open“. Der „älteste“ von diesen befindet sich am Anfang der jeweiligen Datei und der „jüngste“ entsprechend an deren Ende. Der zuletzt in die Datei eingetragene Wert entspricht dem Zeitpunkt der Erstellung der Datei. Die Dateien mit den Kursverläufen für die Überprüfung wurden mithilfe des Skripts HistoryToCSV.mq5 angelegt. Die Dateien mit den Daten sowie das Skript, mit dessen Hilfe sie angelegt wurden, befinden sich in der gepackten Datei Files.zip am Ende dieses Artikels.
Wie bereits erwähnt werden die gespeicherten Kursverläufe in diesem Beitrag ohne jegliche vorherige Aufbereitung verwendet und das ungeachtet der offenkundigen Probleme, die ich Ihrer Aufmerksamkeit nicht vorenthalten möchte. So beinhalten beispielsweise die Notierungen des Kürzels EURRUR_H1 innerhalb von 24 Stunden mal 12, mal 13 Balken, und die XAUUSD-Notierungen an Freitagen jeweils einen Balken weniger als an den übrigen Tagen der Woche. Diese Beispiele zeigen, dass die Kursverläufe mit ungleichmäßigen Quantelungsstufen wiedergegeben werden, was für auf die Arbeit mit korrekten zeitlichen Folgen, die gleichartige Quantelungsstufen voraussetzen, ausgelegte Algorithmen unannehmbar ist.
Selbst wenn mithilfe der Interpolation die fehlenden Kursverlaufswerte wiederhergestellt werden, bleibt die Frage nach dem Fehlen von Kursnotierungen an den handelsfreien Tagen unbeantwortet. Es ist anzunehmen, dass Ereignisse, die sich an handelsfreien Tagen in der Welt zutragen, keinen geringeren Einfluss auf die Weltwirtschaft haben, als Vorkommnisse an Handelstagen. Umstürze, Naturkatastrophen, Skandale, Regierungswechsel und andere mehr oder weniger bedeutsame Ereignisse vergleichbarer Art können sich jederzeit einstellen. Geschieht etwas Derartiges an einem Sonnabend dürften dies Auswirkungen auf die Weltmärkte kaum geringer sein, als wäre es an einem Werktag dazu gekommen.
Möglicherweise führen gerade solche Ereignisse dazu, dass wir Brüche in den Kursverläufen nicht selten an den Rändern der Handelswoche beobachten. Aller Wahrscheinlichkeit nach dreht sich die Welt einfach wie gewohnt weiter, auch wenn die Devisenbörse ruht. Bislang ist vollkommen unklar, ob in für die technische Analyse gedachten Kursverläufen die Wiederherstellung den handelsfreien Tagen entsprechender Werte erforderlich ist, und welchen Nutzen sie bringen würde.
Diese Fragen sprengen sichtlich den Rahmen des hier vorliegenden Beitrages, dennoch ist ein lückenloser Verlauf zumindest unter dem Gesichtspunkt der Ermittlung zyklischer (saisonbedingter) Komponenten für die Analyse auf den ersten Blick attraktiver.
Die Bedeutung der vorhergehenden Aufbereitung der Daten für die anschließende Analyse lässt sich nur schwer ermessen, in unserem Fall handelt es sich dabei um ein gesondertes großes Thema, da die Kursnotierungen in der Art, in der sie auf dem Ausgabegerät erscheinen, für die technische Analyse generell eher ungeeignet sind. Zu den bereits erwähnten Schwierigkeiten mit den Datenlücken kommt noch eine ganze Reihe weiterer hinzu.
Zum Beispiel werden bei der Zusammenstellung der Kursnotierungen einem festgelegten Zeitpunkt die diesem nicht zugehörigen Werte „open“ und „close“ zugeordnet. Diese Werte richten sich nach dem Zeitpunkt des Auftretens einer Kursschwankung (Tick) und nicht nach dem festgelegten Zeitpunkt des gewählten Diagrammzeitraums, wobei Kursschwankungen bekanntermaßen bisweilen recht selten auftreten.
Ein weiteres Beispiel besteht in der vollständigen Außerachtlassung des Kostel‘nikov-Theorems, da niemand die Gewähr bietet, dass die Quantelungsfrequenz besagtem Theorem zumindest im Minutenintervall genügt (ganz zu schweigen von anderen, älteren Intervallen). Neben alledem sei auch das Vorhandensein einer veränderlichen Spannbreite nicht vergessen, denen die Kursnotierungen in einigen Fällen ausgeliefert sein können.
Aber lassen wir all diese Fragen im Rahmen dieses Beitrages außen vor und kommen wir zurück zu unserem eigentlichen Thema!
3. Exponentielle Glättung
Sehen wir uns zunächst das Elementarmodell an:
mit:
- X(t) für den untersuchten (modellierten) Vorgang
- L(t) für den veränderlichen Grad des Vorgangs und
- r(t) für eine Zufallsgröße mit dem Zentralwert Null.
Wie zu sehen beinhaltet das Modell die Summe zweier Bestandteile, von denen uns der Grad des Vorgangs L(t) interessiert, und genau diesen versuchen wir hier herauszuarbeiten.
Bekanntermaßen kann man bei der Mittelung einer Zufallssequenz versuchen, ihre Streuung einzudämmen, das heißt, das Ausmaß ihrer Abweichung vom Durchschnittswert zu verringern. Deshalb ist davon auszugehen, dass wir, wenn der mithilfe unseres elementaren Modells beschriebene Vorgang gemittelt (geglättet) wird, die Zufallskomponente r(t), wenn wir ihr schon nicht ganz entgehen können, merklich abschwächen und dadurch den für uns interessanten Grad L(t) aussondern können.
Dazu greifen wir zur einfachen exponentiellen Glättung (Simple Exponential Smoothing, kurz: SES).
In diesem weithin bekannten Ausdruck wird der Glättungsgrad durch den Koeffizienten „Alpha“ angegeben, der in dem Intervall von 0 bis 1 festgelegt werden kann. Wird Alpha auf den Wert Null gesetzt, haben neu eingehende Größen der Eingangssequenz X keinerlei Einfluss auf das Ergebnis der Glättung. Das Ergebnis der Glättung wird zu jedem Zeitpunkt eine konstante Größe sein.
Somit unterdrücken wir in diesem Extremfall die störende Zufallskomponente vollständig, wobei der uns interessierende Grad des Vorgangs auf das Niveau einer waagerechten Geraden geglättet wird. Wird der Wert des Koeffizienten Alpha auf Eins gesetzt, so hat der Glättungsvorgang keinerlei Einfluss auf die Eingangssequenz. Dabei unterliegt der uns interessierende Grad L(t) keiner Verzerrung, aber auch die Zufallskomponente wird nicht unterdrückt.
Es wird intuitiv klar, dass bei der Festlegung des Wertes für Alpha einander widersprechende Bedingungen gleichzeitig erfüllt sein müssen. Einerseits muss Alpha nahe Null sein, um die Zufallskomponente r(t) erfolgreich zu unterdrücken. Auf der anderen Seite ist es ratsam, für Alpha einen Wert nahe Eins zu wählen, damit der uns interessierende Bestandteil L(t) nicht verzerrt wird. Zur Ermittlung des optimalen Wertes für Alpha müssen wir ein Kriterium festlegen, anhand dessen dieser Wert optimiert werden kann.
Bei der Bestimmung dieses Kriteriums sollten wir bedenken, dass es in diesem Beitrag um die Vorhersage und nicht bloß um die Glättung von Verläufen geht.
In diesem Fall gilt für das einfache Modell der exponentiellen Glättung als Vorhersage um eine beliebige Anzahl von Schritten voraus üblicherweise der für den betreffenden Zeitpunkt ermittelte Wert 
.
mit 
als Vorhersage zum Zeitpunkt t um m Schritte voraus.
Das bedeutet, dass es sich bei der Vorhersage für den Verlaufswertes zum Zeitpunkt t um die im vorhergehenden Schritt getätigte Vorhersage um einen Schritt voraus handelt:
In diesem Fall kann der Fehler bei der Vorhersage um einen Schritt voraus als Kriterium für die Optimierung des Wertes des Koeffizienten Alpha verwendet werden.
Der optimale Wert des Koeffizienten Alpha für eine gegebene Folge kann somit bestimmt werden, indem die Summe der Quadrate dieser Fehler für die gesamte Stichprobe minimiert wird. Natürlich wird der beste Wert für Alpha der sein, bei dem die Größe der Summe der Fehlerquadrate minimal ist.
Die Abbildung 1 zeigt das Diagramm der Abhängigkeit der Summe der Fehlerquadrate bei der Vorhersage um einen Schritt voraus von der Größe des Koeffizienten Alpha für den Ausschnitt aus dem untersuchten Kursverlauf für USDJPY M1.
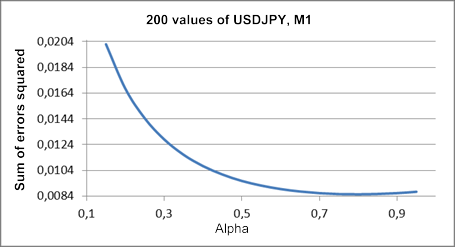
Abbildung 1. Einfache exponentielle Glättung (SES)
In dem resultierenden Diagramm ist der Tiefstwert etwa im Bereich des Wertes von Alpha schwach zu erkennen, Letzterer ist gleich 0,8. Aber ein solches Bild ist bei einer einfachen exponentiellen Glättung bei weitem nicht immer zu beobachten. Bei dem Versuch, den optimalen Wert von Alpha für die Teilbereiche der in dem Beitrag zur Überprüfung verwendeten Verläufe zu bestimmen, werden wir in den meisten Fällen ein stetig gegen eins abnehmendes Diagramm erhalten.
Diese recht hohen optimalen Werte des Glättungskoeffizienten lassen vermuten, dass dieses elementare Modell für die Abbildung der von uns untersuchten Folgen (Kursverläufe) nur schlecht geeignet ist. Entweder ändert sich der Grad des Vorgangs L(t) zu schnell oder innerhalb des Vorgangs liegt ein Trend vor.
Wir machen unser Modell etwas komplexer, indem wir einen weiteren Bestandteil hinzufügen:
,
mit:
- X(t) für den untersuchten (modellierten) Vorgang;
- L(t) für den veränderlichen Grad des Vorgangs;
- T(t) für den linearen Trend; und
- r(t) für eine Zufallsgröße mit dem Zentralwert Null.
Bekanntermaßen können die Koeffizienten einer linearen Regression bestimmen, indem man den Verlauf einer zweifachen Glättung unterzieht:
Für die so gewonnenen Koeffizienten a1 und a2 ist die zum Zeitpunkt t erhaltene Vorhersage für m Schritte im Voraus gleich:
Es ist zu beachten, dass in den vorgestellten Ausdrücken bei der ersten und der wiederholten Glättung jeweils derselbe Koeffizient Alpha eingesetzt wird. Ein solches Modell wird als additives einparametriges lineares Wachstumsmodell bezeichnet.
Wir veranschaulichen den Unterschied zwischen dem einfachen Modell und dem linearen Wachstumsmodell.
Wir setzen voraus, dass sich der untersuchte Vorgang auf lange Frist als konstanter Bestandteil erweist, das heißt, dass er in dem Diagramm wie eine waagerechte Gerade aussieht, und zu irgendeinem Zeitpunkt ein linearer Trend beginnt. Eine Vorhersage dieses mithilfe der genannte Modelle ausgeführten Vorgangs zeigt Abbildung 2.
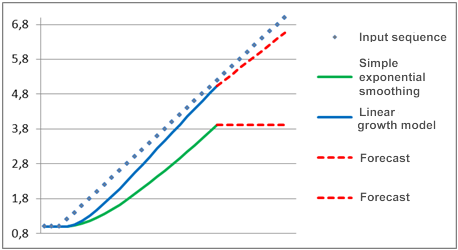
Abbildung 2. Vergleich der Modelle
Offensichtlich bleibt das Modell der einfachen exponentiellen Glättung merklich hinter der sich linear ändernden Eingangssequenz zurück, weswegen die mithilfe dieses Modells angestellte Vorhersage noch stärker davon abweicht. Bei Verwendung des linearen Wachstumsmodells ergibt sich ein anderes Bild. Wenn ein Trend entsteht, strebt dieses Modell nachgerade danach, die sich linear verändernde Folge einzuholen, und deine Vorhersage stimmt eher mit der Veränderungsrichtung der eingehenden Werte überein.
Wäre in dem angeführten Beispiel ein höherer Glättungskoeffizient gewählt worden, so wäre es dem linearen Wachstumsmodell gelungen, in dem angegebenen Zeitabschnitt das Eingangssignal vollständig „einzuholen“, wobei seine Vorhersage de facto mit der Eingangssequenz zusammenfallen würde.
Ungeachtet des Umstandes, dass das lineare Wachstumsmodell bei Vorliegen eines linearen Trends ein gutes Ergebnis liefert, ist schwerlich zu verkennen, dass es eine gewisse Zeit benötigt, um den Trend „einzuholen“. Deshalb wird bei einem häufigen Wechsel der Trendrichtung zwischen dem Modell und der Eingangssequenz stets eine gewisse Abweichung zu beobachten sein. Außerdem wird das lineare Wachstumsmodell außerstande sein, den Trend „einzuholen“, wenn dieser nicht linear ansteigt, sondern dem Quadratgesetz folgt. Trotz dieser Schwächen verfügt das Modell bei einem linearen Trendverlauf jedoch über deutliche Vorteile gegenüber dem Modell der einfachen exponentiellen Glättung.
Wie bereits erwähnt haben wir ein lineares Wachstumsmodell mit nur einem Parameter verwendet. Zur Ermittlung des optimalen Wertes für den Parameter Alpha in dem Teilbereich des überprüften Kursverlaufs für USDJPY M1 legen wir ein Diagramm für die Abhängigkeit der Summe der Quadrate der Fehler bei der Vorhersage für den nächsten Schritt von der Größe besagten Parameters an.
Dieses Abhängigkeitsdiagramm wird in der Abbildung 3 vorgestellt, bei deren Erstellung derselbe Teilbereich des Kursverlaufs verwendet wurde wie beim Anlegen des in der Abbildung 1 wiedergegebenen Diagramms.
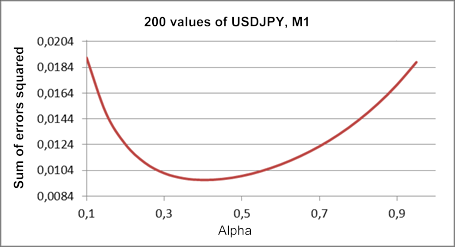
Abbildung 3. Lineares Wachstumsmodell
Verglichen mit dem in der Abbildung 1 angezeigten Ergebnis hat sich die Größe des optimalen Wertes für den Koeffizienten Alpha in diesem Fall auf einen Wert von etwa 0,4 verringert. In diesem Modell wird für die erste und die zweite Glättung derselbe Koeffizient gewählt, obwohl beide theoretisch auch unterschiedliche Werte haben könnten. Zu dem linearen Wachstumsmodell mit zwei unterschiedlichen Glättungskoeffizienten kommen wir noch.
Die beiden betrachteten exponentiellen Glättungsmodelle besitzen ihre jeweiligen Entsprechungen in Form von Indikatoren im Lieferumfang der MetaTrader 5-Anwendung. Dabei handelt es sich um die weithin bekannten EMA und DEMA, die jedoch nicht zur Gewinnung von Vorhersagen gedacht sind, sondern für die Glättung der Werte einer gegebenen Folge.
Es ist zu berücksichtigen, dass bei der Verwendung des Indikators DEMA auf dem Bildschirm der dem Koeffizienten a1 entsprechende Wert ausgegeben wird, und nicht der Wert der Vorhersage für den nächsten Schritt. Der Koeffizient a2 (s. die oben aufgeführten Ausdrücke für das lineare Wachstumsmodell) wird dabei weder verwendet noch berechnet. Darüber hinaus wird der Wert des Glättungskoeffizienten anhand der Größe des äquivalenten Zeitraums n ermittelt:
In unserem Beispiel entspricht dem 0,8 entsprechenden Wert von Alpha die etwa 2 betragende Größe n, und bei einem Alpha von 0,4 hat n den Wert 4.
4. Anfangswerte
Wie bereits erwähnt wurde, muss bei der Anwendung der exponentiellen Glättung die Größe des Glättungskoeffizienten auf die eine oder andere Weise ausgewählt werden. Damit allein ist es allerdings noch nicht getan. Da der aktuelle Wert bei der exponentiellen Glättung auf der Grundlage des vorhergehenden berechnet wird, ergibt sich zum Zeitpunkt Null eine Situation, in der noch kein vorhergehender Wert vorhanden ist. Das bedeutet, dass für den Zeitpunkt Null der Anfangswert für S oder im Fall eines linearen Wachstumsmodells für S1 und S2 irgendwie bestimmt werden muss.
Das Problem der Auswahl der Anfangswerte ist nicht immer leicht zu lösen. Wenn (wie im Fall der Verwendung von Kursnotierungen in MetaTrader 5) uns ein sehr langer Kursverlauf zur Verfügung steht, gelingt es der exponentiellen Glättungskurve selbst bei nicht genau bestimmten Anfangswerten, sich bis zum aktuellen Zeitpunkt zu stabilisieren und dabei unseren anfänglichen Fehler zu korrigieren. Dazu können je nach Größe des Glättungskoeffizienten etwa 10 bis 200 (und manchmal sogar mehr) Zeiträume erforderlich sein.
In einer solchen Situation reicht es aus, die Anfangswerte grob zu schätzen und den exponentiellen Glättungsvorgang 200 - 300 Zeiträume vor dem uns interessierenden Zeitabschnitt auszulösen. Das wird erheblich schwieriger, wenn wir lediglich eine Auswahl mit, sagen wir, insgesamt 100 Werten zur Hand haben.
In der Literatur begegnen uns zahlreiche Empfehlungen bezüglich der Auswahl der Anfangswerte. Zum Beispiel kann der Anfangswert für eine einfache exponentielle Glättung mit dem ersten Element der Folge gleichgesetzt oder in der Hoffnung auf eine Glättung der zufälligen Ausreißer als Durchschnittswert von drei bis vier Anfangswerten der Sequenz ermittelt werden. Bei einem linearen Wachstumsmodell können die Anfangswerte S1 und S2 ausgehend von der Annahme bestimmt werden, dass die Anfangsebene der Vorhersagekurve gleich dem ersten Element der Folge ist und das Gefälle des linearen Trends gleich Null.
In unterschiedlichen Quellen ist noch eine ganze Reihe weiterer Empfehlungen zur Auswahl der Anfangswerte zu finden, aber keine von ihnen kann das Nichtvorliegen äußerst empfindlicher Fehler bei den ersten Schritten des Glättungsalgorithmus gewährleisten. Das macht sich beim Einsatz von Glättungskoeffizienten mit niedrigen Werten besonders bemerkbar, bei denen zum Erreichen eines stabilen Zustands eine große Anzahl von Zeiträumen benötigt wird.
Deshalb wird zur Minimierung der Auswirkungen der mit der Auswahl der Anfangswerte verbundenen Probleme (insbesondere bei kurzen Verläufen) mitunter auf eine Methode zurückgegriffen, die die Suche nach solchen Werten voraussetzt, bei denen der Vorhersagefehler minimal ist. Es ist die Rede von der Berechnung des Vorhersagefehlers für die sich in kleinen Schritten ändernden Größen der Anfangswerte über die gesamte Folge.
Die erfolgreichste Variante kann nach der Berechnung der Größe des Fehlers aus dem Raster aller möglichen Kombinationen von Anfangswerten ausgewählt werden. Aber das ist ein äußerst arbeitsaufwändiges Verfahren, es erfordert eine große Anzahl von Berechnungen und wird in reiner Form praktisch nie verwendet.
Bei der beschriebenen Aufgabe handelt es sich um nichts weniger als die Optimierung oder Ermittlung des Tiefstwertes einer Funktion mit mehreren Variablen. Zur Lösung derartiger Aufgaben wurden unterschiedliche Algorithmen entwickelt, mit deren Hilfe der Umfang der erforderlichen Berechnungen erheblich verringert werden kann. Auf die Fragen der Optimierung der Glättungsparameter und der Anfangswerte bei der Vorhersage kommen wir noch zurück.
5. Berechnung der Vorhersagegenauigkeit
Während der Vorhersage und der Auswahl der Anfangswerte oder -parameter des Modells ergibt sich die Aufgabe der Berechnung der Genauigkeit der Vorhersage. Die Berechnung der Genauigkeit ist auch beim Vergleich zweier unterschiedlicher Modelle oder bei der Bestimmung der Schlüssigkeit der erhaltenen Vorhersage von Bedeutung. Es gibt eine große Zahl wohl bekannter Berechnungsverfahren zur Bestimmung der Vorhersagegenauigkeit, aber zur Berechnung jeder einzelnen von ihnen muss der Vorhersagefehler bei jedem Schritt bekannt sein.
Wie bereits erwähnt ist der Fehler bei Vorhersagen für den jeweils nächsten Schritt zum Zeitpunkt t gleich:
mit:
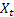für den Eingangssequenzwert zum Zeitpunkt t; und
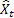für den im vorherigen Schritt ermittelten Vorhersagewert für den Zeitpunkt t.
Das wahrscheinlich verbreitetste Verfahren zur Berechnung der Vorhersagegenauigkeit ist der Durchschnittswert des Quadrates der Fehler (Mean Squared Error, kurz: MSE):
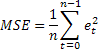
mit n für die Anzahl der Elemente in der Folge (Sequenz).
Manchmal erweist sich die übermäßige Empfindlichkeit gegenüber seltenen einmaligen Fehlern mit hohen Werten als Nachteil der Berechnung mittels MSE. Das lässt sich damit erklären, dass der Wert des Fehlers bei der Berechnung mit dem MSE quadriert wird. Alternativ empfiehlt sich in diesem Fall die Verwendung des Wertes des mittleren absoluten Fehlers (Mean Absolute Error, kurz: MAE).
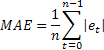
Hier wurde der Vorgang der Quadrierung des Wertes des Fehlers durch die Verwendung seines absoluten Wertes ersetzt. Es wird angenommen, dass sich mithilfe des MAE belastbarere Berechnungen gewinnen lassen.
Beide Berechnungsverfahren eignen sich zum Beispiel gut zur Bestimmung der Vorhersagegenauigkeit für ein und dieselbe Folge mit unterschiedlichen Modellparametern oder bei Verwendung unterschiedlicher Modelle, erweisen sich jedoch als wenig brauchbar für den Vergleich anhand unterschiedlicher Folgen gewonnener Vorhersageergebnisse.
Zudem lässt sich vom Wert dieser Berechnungen nicht unmittelbar darauf schließen, wie gut das Vorhersageergebnis ist. Wenn wir beispielsweise einen MAE-Wert von 0,03 oder einen anderen erhalten haben, können wir nicht sagen, ob das gut oder schlecht ist.
Um uns die Möglichkeit zum Vergleich der Vorhersagegenauigkeit bezüglich unterschiedlicher Folgen zu verschaffen, können wir die relativen Berechnungsverfahren RelMSE bzw. RelMAE verwenden:
Dabei werden die ermittelten Werte der Vorhersagegenauigkeit durch die entsprechenden mithilfe des Verfahrens zur Prüfung der Vorhersage gewonnenen Werte dividiert. Als derartiges Prüfverfahren kann der Bequemlichkeit halber die so genannte „naive Prognose“ verwendet werden, bei der angenommen wird, dass der Wert des Vorgangs in der Zukunft derselbe sein wird wie zum aktuellen Zeitpunkt.
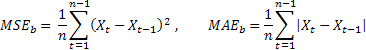
Wenn der Durchschnittswert der Vorhersagefehler gleich der Größe der mithilfe der naiven Prognose ermittelten Fehler ist, wird der Wert der relativen Berechnungen gleich „1“ sein. Ist der Wert der relativen Berechnungen kleiner als „1“, so bedeutet das, dass der Wert der Vorhersagefehler im Durchschnitt kleiner ist als bei der naiven Prognose. Das heißt, die Genauigkeit der Vorhersageergebnisse ist größer als bei der naiven Prognose. Und umgekehrt, wenn der Wert der relativen Berechnungen größer als „1“ ist, ist die Genauigkeit der Vorhersageergebnisse im Durchschnitt geringer als bei der Methode der naiven Prognose.
Diese Berechnungen eignen sich auch zur Bestimmung der Genauigkeit der Vorhersage für zwei oder mehr zukünftige Schritte. Dazu muss bei ihrer Berechnung lediglich statt des Fehlers bei der Vorhersage für den nächsten Schritt der Wert der Vorhersagefehler für die entsprechende Anzahl künftiger Schritte verwendet werden.
Als Beispiel werden in der Tabelle die Fehler einer Vorhersage für den nächsten Schritt in Form des relativen mittleren absoluten Fehlers (RelMAE) mithilfe eines einparametrigen linearen Wachstumsmodells wiedergegeben. Die Berechnung der Fehler erfolgte anhand der 200 letzten Werte der jeweils überprüften Folge.
|
Tabelle 1. Fehler der RelMAE-Vorhersage für den nächsten Schritt
Die Berechnung gemäß RelMAE ermöglicht den Vergleich der Effektivität des gewählten Verfahrens bei der Vorhersage bezüglich unterschiedlicher Folgen. Wie aus den in der Tabelle 1 abgebildeten Ergebnissen ersichtlich wird, ist es uns nicht ein einziges Mal gelungen, eine genauere Vorhersage zu liefern als mit der naiven Prognose, bei der alle RelMAE-Werte größer als „1“ sind.
6. Additive Modelle
Weiter oben wurde bereits ein Modell vorgestellt, das die Summe aus dem Grad des Vorgangs, dem linearen Trend und einer Zufallsgröße beinhaltet. Wir erweitern die Aufstellung der in diesem Artikel behandelten Modelle um ein weiteres, das als Ergänzung zu den aufgeführten Bestandteilen eine zyklische saisonbedingte Komponente in Form einer Summe enthält.
Die exponentiellen Glättungsmodelle, in die alle Bestandteile in Form einer Summe eingehen, werden als additive Modelle bezeichnet. Neben diesen gibt es multiplikative Modelle, in die eine, einige oder alle Komponenten als Produkt eingehen. Wenden wir uns nun der Gruppe der additiven Modelle zu.
In den vorausgehenden Abschnitten wurde der Fehler bei Vorhersagen für den nächsten Schritt bereits mehrmals erwähnt. In nahezu jeder mit Vorhersagen auf der Grundlage der exponentiellen Glättung verbundenen Anwendung muss der Wert für diesen Fehler berechnet werden. In Kenntnis der Größe des Vorhersagefehlers können die Ausdrücke für die oben bereits eingeführten exponentiellen Glättungsmodelle in leicht veränderter Form (nämlich mit korrigiertem Fehler) aufgezeichnet werden.
In diesem Fall verwenden wir eine Form der Modellpräsentation, in deren Ausdrücken (Formeln) der Fehler ganz oder teilweise zu den zuvor ermittelten Werten addiert wird. Eine solche Präsentationsform wird als Modell mit additivem Fehler bezeichnet. Die exponentiellen Glättungsmodelle können darüber hinaus auch in einer Form mit multiplikativem Fehler wiedergegeben werden, aber in dem hier vorliegenden Beitrag findet diese Form der Modellpräsentation keine Anwendung.
Schauen wir uns einige additive exponentielle Glättungsmodelle genauer an.
Die einfache exponentielle Glättung (SES):
Das entsprechende Modell heißt ARIMA(0,1,1):
Das additive lineare Wachstumsmodell:
Im Unterschied zu dem weiter oben vorgestellten linearen Wachstumsmodell mit nur einem Parameter kommen in dem hier vorliegenden Fall zwei unterschiedliche Glättungsparameter zum Einsatz.
Das entsprechende Modell heißt ARIMA(0,2,2): 
Das gedämpfte lineare Wachstumsmodell:
Der Sinn dieser Dämpfung besteht darin, dass sich die Steilheit des Trends je nach Höhe des Wertes des Dämpfungskoeffizienten in jedem nachfolgenden Vorhersageschritt verringern wird Diesen Effekt gibt die Abbildung 4 wieder.
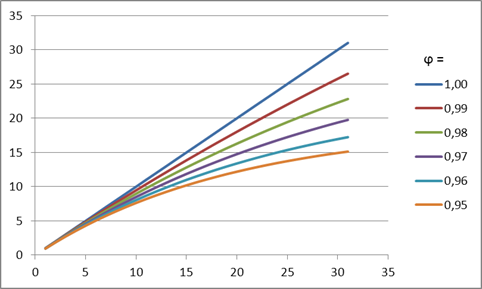
Abbildung 4. Der Einfluss des Dämpfungskoeffizienten
Wie aus dieser Abbildung folgt, verliert der Trend bei einer mit einer verringerten Größe des Dämpfungskoeffizienten vorgenommenen Vorhersage immer schneller an Kraft, sodass das lineare Wachstum noch stärker gedämpft wird.
Das entsprechende Modell heißt ARIMA(1,1,2): 
Zu jedem dieser drei Modelle kann eine saisonbedingte Komponente in Form einer Summe hinzugefügt werden, wodurch wir drei weitere Modelle erhalten.
Einfaches Modell mit additiver Saisonbedingtheit:
Lineares Wachstumsmodell mit additiver Saisonbedingtheit:
Lineares Wachstumsmodell mit Dämpfung und additiver Saisonbedingtheit:
Auch für die Modelle mit Saisonbedingtheit gibt es entsprechende ARIMA-Modelle, die hier allerdings nicht vorgestellt werden, da sie kaum von praktischer Bedeutung sein dürften.
In den hier aufgeführten Ausdrücken und Formeln werden folgende Bezeichnungen verwendet:
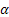für den Glättungsparameter für den Grad der Folge, [0:1];
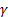für den Glättungsparameter für den Trend, [0:1];
für den Glättungsparameter für die saisonbedingten Kennziffern, [0:1];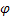
für den Dämpfungsparameter, [0:1];
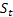für den zum Zeitpunkt t nach Auftreten des Wertes 
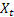berechneten geglätteten Grad der Folge;
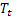für den zum Zeitpunkt t berechneten geglätteten additiven Trend;
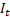für den zum Zeitpunkt t berechneten geglätteten saisonbedingten Trend;
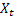für den Wert der Folge zum Zeitpunkt t;- m für die Anzahl der Schritte, für die die Vorhersage erfolgt;
- p für die Anzahl der Zeiträume in dem saisonbedingten Zyklus;
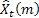für die zum Zeitpunkt t vorgenommene Vorhersage für die m nächsten Schritte;
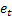für den Fehler bei der Vorhersage für den nächsten Schritt zum Zeitpunkt t, 
.
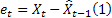Es ist unschwer zu erkennen, dass die Ausdrücke für das letzte der vorgestellten Modelle alle sechs betrachteten Varianten beinhalten.
Wenn in den Ausdrücken für die linearen Wachstumsmodelle mit Dämpfung und additiver Saisonbedingtheit
,
gelten, wird die Saisonbedingtheit bei der Berechnung der Vorhersage nicht berücksichtigt. Weiterhin ergibt sich bei 
ein lineares Wachstumsmodell, während wir bei 
ein lineares Wachstumsmodell mit Dämpfung erhalten.
Der Wert 
entspricht dem Modelle der einfachen exponentiellen Glättung.
Bei der Anwendung der Modelle, die die Saisonbedingtheit berücksichtigen, müssen zunächst auf irgendeine verfügbare Weise das Vorliegen einer Zyklizität sowie der Zeitraum des entsprechenden Zyklus ermittelt werden, um diese Daten anschließend zur Bereitstellung der Werte der saisonbedingten Kennziffern verwenden zu können.
In unserem Fall, in dem die Vorhersage für kurze Zeitintervalle erfolgt, ist es nicht gelungen, in den Ausschnitten der überprüften Folge eine hinreichend stabile Zyklizität festzustellen. Deshalb werden in diesem Beitrag weder Beispiele angeführt noch die mit der Berücksichtigung der Saisonbedingtheit verbundenen Besonderheiten behandelt.
Zur Bestimmung der wahrscheinlichen Grenzen der Vorhersage (prediction intervals) hinsichtlich der betrachteten Modelle werden die in der Literatur [3] vorgestellten analytischen Schlussfolgerungen verwendet. Als Wert für die Streuung der Fehler bei der Vorhersage für den jeweils nächsten Schritt wird der über die gesamte Stichprobe mit dem Umfang „n“ berechnete Durchschnittswert der Summe ihrer Quadrate herangezogen.
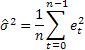
Folglich ist für die betrachteten Modelle zur Bestimmung der Streuungsgröße bei Vorhersagen für 2 oder mehr weitere Schritte folgender Ausdruck gerechtfertigt:
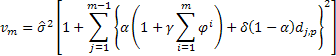
mit 
gleich „1“, wenn „j“ Modulo p = 0, andernfalls ist 
gleich „0“.
Jetzt, da wir den Streuungswert der Vorhersage für jeden Schritt m berechnet haben, können wir die Grenzen des Intervalls für die 95-prozentige Zuverlässigkeit der Vorhersage bestimmen.
Wir vereinbaren, diese Wahrscheinlichkeitsspanne im weiteren Verlauf als Zuverlässigkeitsintervall der Vorhersage zu bezeichnen.
Nachdem wir die Ausdrücke für die exponentiellen Glättungsmodelle eingeführt haben, kommen wir jetzt zu ihrer Umsetzung in Form einer in MQL5 programmierten Klasse.
7. Umsetzung der Klasse AdditiveES in Programmform
Bei der Umsetzung als Klasse wurden die Ausdrücke für das lineare Wachstumsmodell mit Dämpfung und additiver Saisonbedingtheit verwendet.
Wie bereits erwähnt können die übrigen Modelle durch Auswahl der entsprechenden Parameter abgeleitet werden.
//----------------------------------------------------------------------------------- // AdditiveES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //----------------------------------------------------------------------------------- // Forecasting. Exponential smoothing. Additive models. // References: // 1. Everette S. Gardner Jr. Exponential smoothing: The state of the art – Part II. // June 3, 2005. // 2. Rob J Hyndman. Forecasting based on state space models for exponential // smoothing. 29 August 2002. // 3. Rob J Hyndman et al. Prediction intervals for exponential smoothing // using two new classes of state space models. 30 January 2003. //----------------------------------------------------------------------------------- class AdditiveES:public CObject { protected: double Alpha; // Smoothed parameter for the level of the series double Gamma; // Smoothed parameter for the trend double Phi; // Autoregressive or damping parameter double Delta; // Smoothed parameter for seasonal indices int nSes; // Number of periods in the seasonal cycle double S; // Smoothed level of the series, computed after last Y is observed double T; // Smoothed additive trend double Ises[]; // Smoothed seasonal indices int p_Ises; // Pointer for Ises[] shift register double F; // Forecast for 1 period ahead from origin t public: AdditiveES(); double Init(double s,double t,double alpha=1,double gamma=0, double phi=1,double delta=0,int nses=1); double GetS() { return(S); } double GetT() { return(T); } double GetF() { return(F); } double GetIs(int m); void IniIs(int m,double is); // Initialization of smoothed seasonal indices double NewY(double y); // Next calculating step double Fcast(int m); // m-step ahead forecast double VarCoefficient(int m); // Coefficient for calculating prediction intervals }; //----------------------------------------------------------------------------------- // Constructor //----------------------------------------------------------------------------------- void AdditiveES::AdditiveES() { Alpha=0.5; Gamma=0; Delta=0; Phi=1; nSes=1; ArrayResize(Ises,nSes); ArrayInitialize(Ises,0); p_Ises=0; S=0; T=0; } //----------------------------------------------------------------------------------- // Initialization //----------------------------------------------------------------------------------- double AdditiveES::Init(double s,double t,double alpha=1,double gamma=0, double phi=1,double delta=0,int nses=1) { S=s; T=t; Alpha=alpha; if(Alpha<0)Alpha=0; if(Alpha>1)Alpha=1; Gamma=gamma; if(Gamma<0)Gamma=0; if(Gamma>1)Gamma=1; Phi=phi; if(Phi<0)Phi=0; if(Phi>1)Phi=1; Delta=delta; if(Delta<0)Delta=0; if(Delta>1)Delta=1; nSes=nses; if(nSes<1)nSes=1; ArrayResize(Ises,nSes); ArrayInitialize(Ises,0); p_Ises=0; F=S+Phi*T; return(F); } //----------------------------------------------------------------------------------- // Calculations for the new Y //----------------------------------------------------------------------------------- double AdditiveES::NewY(double y) { double e; e=y-F; S=S+Phi*T+Alpha*e; T=Phi*T+Alpha*Gamma*e; Ises[p_Ises]=Ises[p_Ises]+Delta*(1-Alpha)*e; p_Ises++; if(p_Ises>=nSes)p_Ises=0; F=S+Phi*T+GetIs(0); return(F); } //----------------------------------------------------------------------------------- // Return smoothed seasonal index //----------------------------------------------------------------------------------- double AdditiveES::GetIs(int m) { if(m<0)m=0; int i=(int)MathMod(m+p_Ises,nSes); return(Ises[i]); } //----------------------------------------------------------------------------------- // Initialization of smoothed seasonal indices //----------------------------------------------------------------------------------- void AdditiveES::IniIs(int m,double is) { if(m<0)m=0; if(m<nSes) { int i=(int)MathMod(m+p_Ises,nSes); Ises[i]=is; } } //----------------------------------------------------------------------------------- // m-step-ahead forecast //----------------------------------------------------------------------------------- double AdditiveES::Fcast(int m) { int i,h; double v,v1; if(m<1)h=1; else h=m; v1=1; v=0; for(i=0;i<h;i++){v1=v1*Phi; v+=v1;} return(S+v*T+GetIs(h)); } //----------------------------------------------------------------------------------- // Coefficient for calculating prediction intervals //----------------------------------------------------------------------------------- double AdditiveES::VarCoefficient(int m) { int i,h; double v,v1,a,sum,k; if(m<1)h=1; else h=m; if(h==1)return(1); v=0; v1=1; sum=0; for(i=1;i<h;i++) { v1=v1*Phi; v+=v1; if((int)MathMod(i,nSes)==0)k=1; else k=0; a=Alpha*(1+v*Gamma)+k*Delta*(1-Alpha); sum+=a*a; } return(1+sum); } //-----------------------------------------------------------------------------------
Sehen wir uns kurz die Methoden der Klasse AdditiveES an.
Die Methode Init
Eingangsparameter:
- double s ist der einstellbare Anfangswert des geglätteten Grades;
- double t ist der einstellbare Anfangswert des geglätteten Trends;
- double Alpha=1, ist der einstellbare Glättungsparameter für den Grad der Folge;
- double gamma=0, ist der einstellbare Glättungsparameter für den Trend;
- double phi=1 ist der einstellbare Dämpfungsparameter;
- double delta=0, ist der einstellbare Glättungsparameter für die saisonbedingten Kennziffern;
- int nses=1 ist die einstellbare Anzahl der Zeiträume innerhalb eines Saisonzyklus.
Ausgegebener Wert:
- Ausgegeben wird eine Vorhersage für den nächsten Schritt auf der Grundlage der eingestellten Anfangswerte.
Die Methode Init muss stets als erste aufgerufen werden. Das ist zur Einstellung der Glättungsparameter und Anfangswerte unerlässlich. Es sei darauf hingewiesen, dass die Methode Init keine Möglichkeit zur Bereitstellung saisonbedingter Kennziffern mit beliebigen Werten vorsieht; wird sie aufgerufen, werden alle saisonbedingten Werte auf null gesetzt.
Die Methode IniIs
Eingangsparameter:
- Int m ist die Nummer der saisonbedingten Kennziffer;
- double is ist der einstellbare Wert der saisonbedingten Kennziffer mit der Nummer m.
Ausgegebener Wert:
- keiner
Der Aufruf der Methode IniIs(...) erfolgt dann, wenn den saisonbedingten Kennziffern andere Anfangswerte als Null zugeordnet werden müssen. Die Bereitstellung der saisonbedingten Kennziffern muss unmittelbar im Anschluss an den Aufruf der Methode Init(...) erfolgen.
Die Methode NewY
Eingangsparameter:
- double y ist der neue Wert in der Eingangsfolge
Ausgegebener Wert:
- Ausgegeben wird eine Vorhersage für den nächsten Schritt auf der Grundlage der eingestellten Anfangswerte.
Die Methode ist zur Berechnung einer Vorhersage für den nächsten Schritt bei Auftreten des jeweils nächsten Wertes der Eingangssequenz gedacht. Der Aufruf der Methode sollte erst nach der Bereitstellung der Klasse mithilfe der Methoden Init und ggf. IniIs erfolgen.
Die Methode Fcast
Eingangsparameter:
- int m ist der Vorhersagehorizont für 1,2,3,… Zeiträume;
Ausgegebener Wert:
- Ausgegeben wird der Vorhersagewert für m Schritte in die Zukunft.
Diese Methode berechnet lediglich den Vorhersagewert und hat keinerlei Auswirkungen auf den Zustand des Glättungsvorgangs. Für gewöhnlich muss sie nach der Methode NewY aufgerufen werden.
Die Methode VarCoefficient
Eingangsparameter:
- int m ist der Vorhersagehorizont für 1,2,3,… Zeiträume;
Ausgegebener Wert:
- Ausgegeben wird der Wert des Koeffizienten zur Berechnung der Streuung der Vorhersage.
Es wird der Wert des Koeffizienten berechnet, der angibt, um wie viel die Größe der Streuung bei einer Vorhersage um m Schritte im Vergleich zu der Streuung der Vorhersage für den unmittelbar nächsten Schritt zunimmt.
Die Methoden GetS, GetT, GetF und GetIs
Diese Methoden gewährleisten den Zugriff auf die geschützten Variablen der Klasse. GetS, GetT und GetF geben jeweils die geglätteten Grenz-, Trend- und Vorhersagewerte für einen Schritt aus. Die Methode GetIs gewährt den Zugriff auf die saisonbedingten Kennziffern und fordert als Eingangsparameter die Angabe des Wertes der Kennziffer m.
Das komplexeste der hier betrachteten Modelle ist das lineare Wachstumsmodell mit Dämpfung und additiver Saisonbedingtheit, auf dessen Grundlage auch die Klasse AdditiveES beruht. Absolut folgerichtig stellt sich die Frage, wozu wir dann noch die übrigen, einfacheren Modelle benötigen.
Obwohl die komplexesten Modelle auf den ersten Blick gegenüber den einfacheren einen deutlichen Vorteil zu haben scheinen, ist dem bei weitem nicht immer so. Einfachere Modelle mit einer geringeren Zahl an Parametern gewährleisten in der überwältigenden Mehrzahl der Fälle eine geringere Streuungsrate bei den Vorhersagefehlern, was bedeutet, dass sie stabiler arbeiten. Dieser Umstand wird bei der Aufstellung der auf der gleichzeitigen parallelen Arbeit aller verfügbaren Modelle, von den elementarsten bis zu den komplexesten, beruhenden Vorhersagealgorithmen genutzt.
Nach der vollständigen Verarbeitung der Folge wird das Modell ausgewählt, das unter Berücksichtigung der Anzahl seiner Parameter (m.a.W. seiner Komplexität) die geringste Fehlerzahl an den Tag gelegt hat. Für diese Auswahl wurde eine Reihe von Kriterien entwickelt wie z. B. das Informationskriterium nach Akaike (Akaike’s Information Criterion, kurz: AIC). Im Endeffekt wird das Modell ausgewählt, das die Gewinnung der belastbarsten Vorhersage erwarten lässt.
Zur Veranschaulichung der Verwendung der Klasse AdditiveES wurde ein einfacher Indikator angelegt, in dem alle Glättungsparameter von Hand eingegeben werden.
Es folgt der Programmcode für den Indikator AdditiveES_Test.mq5:
//----------------------------------------------------------------------------------- // AdditiveES_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" // Forecast #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "PInterval+" // Prediction interval #property indicator_type3 DRAW_LINE #property indicator_color3 clrCadetBlue #property indicator_style3 STYLE_SOLID #property indicator_width3 1 #property indicator_label4 "PInterval-" // Prediction interval #property indicator_type4 DRAW_LINE #property indicator_color4 clrCadetBlue #property indicator_style4 STYLE_SOLID #property indicator_width4 1 double HIST[]; double FORE[]; double PINT1[]; double PINT2[]; input double Alpha=0.2; // Smoothed parameter for the level input double Gamma=0.2; // Smoothed parameter for the trend input double Phi=0.8; // Damping parameter input double Delta=0; // Smoothed parameter for seasonal indices input int nSes=1; // Number of periods in the seasonal cycle input int nHist=250; // History bars, nHist>=100 input int nTest=150; // Test interval, 50<=nTest<nHist input int nFore=12; // Forecasting horizon, nFore>=2 #include "AdditiveES.mqh" AdditiveES fc; int NHist; // history bars int NFore; // forecasting horizon int NTest; // test interval double ALPH; // alpha double GAMM; // gamma double PHI; // phi double DELT; // delta int nSES; // Number of periods in the seasonal cycle //----------------------------------------------------------------------------------- // Custom indicator initialization function //----------------------------------------------------------------------------------- int OnInit() { NHist=nHist; if(NHist<100)NHist=100; NFore=nFore; if(NFore<2)NFore=2; NTest=nTest; if(NTest>NHist)NTest=NHist; if(NTest<50)NTest=50; ALPH=Alpha; if(ALPH<0)ALPH=0; if(ALPH>1)ALPH=1; GAMM=Gamma; if(GAMM<0)GAMM=0; if(GAMM>1)GAMM=1; PHI=Phi; if(PHI<0)PHI=0; if(PHI>1)PHI=1; DELT=Delta; if(DELT<0)DELT=0; if(DELT>1)DELT=1; nSES=nSes; if(nSES<1)nSES=1; MqlRates rates[]; CopyRates(NULL,0,0,NHist,rates); // Load missing data SetIndexBuffer(0,HIST,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,FORE,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFore); SetIndexBuffer(2,PINT1,INDICATOR_DATA); PlotIndexSetString(2,PLOT_LABEL,"Conf+"); PlotIndexSetInteger(2,PLOT_SHIFT,NFore); SetIndexBuffer(3,PINT2,INDICATOR_DATA); PlotIndexSetString(3,PLOT_LABEL,"Conf-"); PlotIndexSetInteger(3,PLOT_SHIFT,NFore); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } //----------------------------------------------------------------------------------- // Custom indicator iteration function //----------------------------------------------------------------------------------- int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,j,init,start; double v1,v2; if(rates_total<NHist){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated>rates_total||prev_calculated<=0||(rates_total-prev_calculated)>1) {init=1; start=rates_total-NHist;} else {init=0; start=prev_calculated;} if(start==rates_total)return(rates_total); // New tick but not new bar //----------------------- if(init==1) // Initialization { i=start; v2=(open[i+2]-open[i])/2; v1=(open[i]+open[i+1]+open[i+2])/3.0-v2; fc.Init(v1,v2,ALPH,GAMM,PHI,DELT,nSES); ArrayInitialize(HIST,EMPTY_VALUE); } PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFore); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFore); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFore); for(i=start;i<rates_total;i++) // History { HIST[i]=fc.NewY(open[i]); } v1=0; for(i=0;i<NTest;i++) // Variance { j=rates_total-NTest+i; v2=close[j]-HIST[j-1]; v1+=v2*v2; } v1/=NTest; // v1=var j=1; for(i=rates_total-NFore;i<rates_total;i++) { v2=1.96*MathSqrt(v1*fc.VarCoefficient(j)); // Prediction intervals FORE[i]=fc.Fcast(j++); // Forecasting PINT1[i]=FORE[i]+v2; PINT2[i]=FORE[i]-v2; } return(rates_total); } //-----------------------------------------------------------------------------------
Bei Aufruf oder der erneuten Bereitstellung des Indikators werden die Anfangswerte der exponentiellen Glättung eingestellt.
Für die saisonbedingten Kennziffern werden in diesem Indikator keine Anfangseinstellungen vorgenommen, weshalb deren Anfangswerte stets gleich „0“ sind. Bei einer solchen Bereitstellung wird der Einfluss der Saisonbedingtheit auf das Vorhersageergebnis bei Auftreten neuer Werte schrittweise bis zu einer vorgegebenen Größe über Null hinauswachsen.
Die Anzahl der zur Erreichung einer vorgegebenen Arbeitsgüte erforderlichen Durchgänge hängt von der Größe des Koeffizienten zur Glättung der saisonbedingten Kennziffern ab: je niedriger der Wert des Glättungskoeffizienten desto größer der Zeitbedarf.
Die Abbildung 5 zeigt das Ergebnis der Arbeit des Indikators AdditiveES_Test.mq5 mit Standardeinstellungen.
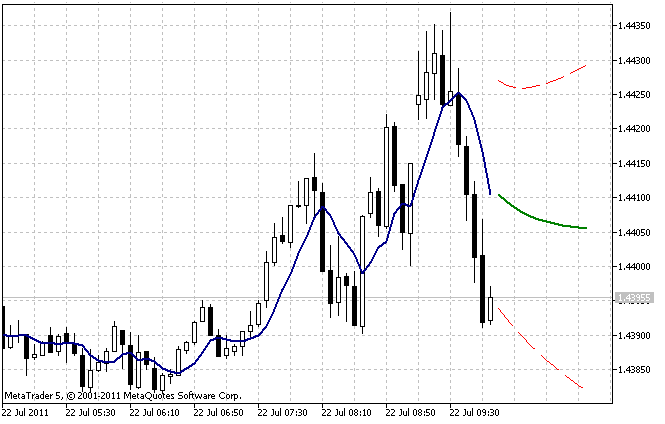
Abbildung 5. Der Indikator AdditiveES_Test.mq5
Neben der reinen Vorhersage gibt der Indikator zusätzlich eine Linie aus, die der Vorhersage für den nächsten Schritt für die vorausgegangen Werte der Folge entspricht, sowie die Grenzen des 95%-Zuverlässigkeitsintervalls der Vorhersage.
Das Zuverlässigkeitsintervall wird auf der Grundlage der Berechnung der Fehlerstreuung der Vorhersage für den nächsten Schritt angelegt. Zur Verringerung des Einflusses der bei der Auswahl der Anfangswerte zulässigen Ungenauigkeit erfolgt diese Berechnung nicht über die gesamte Länge nHist, sondern lediglich auf den letzten Balken, deren Anzahl in dem Eingangsparameter nTest angegeben wird.
Am Ende dieses Beitrages finden Sie die gepackte Datei Files.zip mit den Dateien AdditiveES.mqh und AdditiveES_Test.mq5. Bei der Zusammenstellung des Indikators muss sich die enthaltene Datei AdditiveES.mqh in demselben Verzeichnis befinden wie AdditiveES_Test.mq5.
Auch wenn das Problem der Auswahl der Anfangswerte bei der Erstellung des Indikators AdditiveES_Test.mq5 irgendwie gelöst wurde, so ist das Problem der Auswahl der optimalen Werte nach wie vor offen.
8. Auswahl der optimalen Parameterwerte
Das einfache Modell der exponentiellen Glättung verfügt über lediglich einen Glättungsparameter, dessen optimaler Wert mithilfe einfachen Ausprobierens ermittelt werden kann. Nach der Berechnung der Größe des Vorhersagefehlers für die gesamte Folge wird der Parameterwert kleinschrittig geändert, anschließend erfolgt eine erneute vollständige Berechnung. Dieser Vorgang wird solange wiederholt, bis alle möglichen Parameterwerte durchprobiert wurden. Des Weiteren müssen wir nur noch den Parameterwert herauspicken, der den geringsten Fehler geliefert hat.
Auf der Suche nach dem optimalen Wert für den Glättungskoeffizienten in dem Bereich von 0,1 bis 0,9 mit Iterationen von 0,05 müssen siebzehn vollständige Berechnungsvorgänge für die Größe des Vorhersagefehlers ausgeführt werden. Das sind offenkundig gar nicht so viele Berechnungen. Bei dem linearen Wachstumsmodell mit Dämpfung sind dagegen bereits drei Glättungsparameter zu optimieren, und um alle möglichen Kombinationen dieser drei in demselben Raster mit Iterationen von 0,05 durchzuprobieren, sind 4.913 Berechnungsdurchgänge erforderlich.
Die Anzahl der zum Durchprobieren aller möglichen Parameterwerte erforderlichen vollständigen Durchgänge wächst mit zunehmender Parameterzahl, verringerter Iteration und vergrößertem Suchbereich sehr schnell an. Sollte sich im weiteren Verlauf die Notwendigkeit ergeben, außer den Glättungsparametern auch die Anfangswerte des Modells optimieren zu müssen, so dürfte dies mithilfe einfachen Ausprobierens recht schwierig werden.
Die mit der Suche nach dem Tiefstwert von Funktionen mit zahlreichen Variablen verbundenen Schwierigkeiten sind gut erforscht, und es gibt zahlreiche Algorithmen der entsprechenden Art. Darstellungen und Vergleiche unterschiedlicher Verfahren zur Suche nach dem Minimum einer Funktion finden Sie in der Literatur [7]. Ziel all dieser Verfahren ist in erster Linie die Verringerung der Anzahl der Aufrufe der betreffenden Funktion, das heißt: die Senkung des Rechenaufwandes bei der Minimumsuche.
In der Literatur finden nicht selten die so genannten Quasi-Newton-Verfahren zur Optimierung Erwähnung. Aller Wahrscheinlichkeit nach ist das mit deren hoher Effektivität verbunden, zur Veranschaulichung des Ansatzes zur Optimierung des Vorhersagevorgangs reicht es jedoch aus, eine einfachere Methode in die Tat umzusetzen. Wir entscheiden uns für die Methode von Powell. Sie erfordert keine Berechnung der Ableitungen der betreffenden Funktion und gehört zu den Suchverfahren.
Diese Methode kann im Übrigen wie jede andere programmiertechnisch auf unterschiedliche Weise umgesetzt werden. Der Abschluss der Suche kann bei Erreichen einer bestimmten Genauigkeit des Wertes der Zielfunktion oder des Arguments erfolgen. Außerdem kann die jeweilige Umsetzung die Möglichkeit des Einsatzes von Beschränkungen für den zulässigen Änderungsbereich der Funktionsparameter.
In unserem Fall wird der Algorithmus für die bedingungslose Suche nach dem Minimum mithilfe der Methode Powell in der Klasse PowellsMethod umgesetzt. Der Algorithmus stellt die Suche bei Erreichen einer vorgegebenen Genauigkeit des Wertes der Zielfunktion ein. Als Prototyp wurde bei der Umsetzung dieser Methode ein in der Literatur [8] angeführter Algorithmus verwendet.
Im Anschluss sehen wir den Programmcode der Klasse PowellsMethod.
//----------------------------------------------------------------------------------- // PowellsMethod.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #define GOLD 1.618034 #define CGOLD 0.3819660 #define GLIMIT 100.0 #define SHFT(a,b,c,d) (a)=(b);(b)=(c);(c)=(d); #define SIGN(a,b) ((b) >= 0.0 ? fabs(a) : -fabs(a)) #define FMAX(a,b) (a>b?a:b) //----------------------------------------------------------------------------------- // Minimization of Functions. // Unconstrained Powell’s Method. // References: // 1. Numerical Recipes in C. The Art of Scientific Computing. //----------------------------------------------------------------------------------- class PowellsMethod:public CObject { protected: double P[],Xi[]; double Pcom[],Xicom[],Xt[]; double Pt[],Ptt[],Xit[]; int N; double Fret; int Iter; int ItMaxPowell; double FtolPowell; int ItMaxBrent; double FtolBrent; int MaxIterFlag; public: void PowellsMethod(void); void SetItMaxPowell(int n) { ItMaxPowell=n; } void SetFtolPowell(double er) { FtolPowell=er; } void SetItMaxBrent(int n) { ItMaxBrent=n; } void SetFtolBrent(double er) { FtolBrent=er; } int Optimize(double &p[],int n=0); double GetFret(void) { return(Fret); } int GetIter(void) { return(Iter); } private: void powell(void); void linmin(void); void mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc); double brent(double ax,double bx,double cx,double &xmin); double f1dim(double x); virtual double func(const double &p[]) { return(0); } }; //----------------------------------------------------------------------------------- // Constructor //----------------------------------------------------------------------------------- void PowellsMethod::PowellsMethod(void) { ItMaxPowell= 200; FtolPowell = 1e-6; ItMaxBrent = 200; FtolBrent = 1e-4; } //----------------------------------------------------------------------------------- void PowellsMethod::powell(void) { int i,j,m,n,ibig; double del,fp,fptt,t; n=N; Fret=func(P); for(j=0;j<n;j++)Pt[j]=P[j]; for(Iter=1;;Iter++) { fp=Fret; ibig=0; del=0.0; for(i=0;i<n;i++) { for(j=0;j<n;j++)Xit[j]=Xi[j+n*i]; fptt=Fret; linmin(); if(fabs(fptt-Fret)>del){del=fabs(fptt-Fret); ibig=i;} } if(2.0*fabs(fp-Fret)<=FtolPowell*(fabs(fp)+fabs(Fret)+1e-25))return; if(Iter>=ItMaxPowell) { Print("powell exceeding maximum iterations!"); MaxIterFlag=1; return; } for(j=0;j<n;j++){Ptt[j]=2.0*P[j]-Pt[j]; Xit[j]=P[j]-Pt[j]; Pt[j]=P[j];} fptt=func(Ptt); if(fptt<fp) { t=2.0*(fp-2.0*(Fret)+fptt)*(fp-Fret-del)*(fp-Fret-del)-del*(fp-fptt)*(fp-fptt); if(t<0.0) { linmin(); for(j=0;j<n;j++){m=j+n*(n-1); Xi[j+n*ibig]=Xi[m]; Xi[m]=Xit[j];} } } } } //----------------------------------------------------------------------------------- void PowellsMethod::linmin(void) { int j,n; double xx,xmin,fx,fb,fa,bx,ax; n=N; for(j=0;j<n;j++){Pcom[j]=P[j]; Xicom[j]=Xit[j];} ax=0.0; xx=1.0; mnbrak(ax,xx,bx,fa,fx,fb); Fret=brent(ax,xx,bx,xmin); for(j=0;j<n;j++){Xit[j]*=xmin; P[j]+=Xit[j];} } //----------------------------------------------------------------------------------- void PowellsMethod::mnbrak(double &ax,double &bx,double &cx, double &fa,double &fb,double &fc) { double ulim,u,r,q,fu,dum; fa=f1dim(ax); fb=f1dim(bx); if(fb>fa) { SHFT(dum,ax,bx,dum) SHFT(dum,fb,fa,dum) } cx=bx+GOLD*(bx-ax); fc=f1dim(cx); while(fb>fc) { r=(bx-ax)*(fb-fc); q=(bx-cx)*(fb-fa); u=bx-((bx-cx)*q-(bx-ax)*r)/(2.0*SIGN(FMAX(fabs(q-r),1e-20),q-r)); ulim=bx+GLIMIT*(cx-bx); if((bx-u)*(u-cx)>0.0) { fu=f1dim(u); if(fu<fc){ax=bx; bx=u; fa=fb; fb=fu; return;} else if(fu>fb){cx=u; fc=fu; return;} u=cx+GOLD*(cx-bx); fu=f1dim(u); } else if((cx-u)*(u-ulim)>0.0) { fu=f1dim(u); if(fu<fc) { SHFT(bx,cx,u,cx+GOLD*(cx-bx)) SHFT(fb,fc,fu,f1dim(u)) } } else if((u-ulim)*(ulim-cx)>=0.0){u=ulim; fu=f1dim(u);} else {u=cx+GOLD*(cx-bx); fu=f1dim(u);} SHFT(ax,bx,cx,u) SHFT(fa,fb,fc,fu) } } //----------------------------------------------------------------------------------- double PowellsMethod::brent(double ax,double bx,double cx,double &xmin) { int iter; double a,b,d,e,etemp,fu,fv,fw,fx,p,q,r,tol1,tol2,u,v,w,x,xm; a=(ax<cx?ax:cx); b=(ax>cx?ax:cx); d=0.0; e=0.0; x=w=v=bx; fw=fv=fx=f1dim(x); for(iter=1;iter<=ItMaxBrent;iter++) { xm=0.5*(a+b); tol2=2.0*(tol1=FtolBrent*fabs(x)+2e-19); if(fabs(x-xm)<=(tol2-0.5*(b-a))){xmin=x; return(fx);} if(fabs(e)>tol1) { r=(x-w)*(fx-fv); q=(x-v)*(fx-fw); p=(x-v)*q-(x-w)*r; q=2.0*(q-r); if(q>0.0)p=-p; q=fabs(q); etemp=e; e=d; if(fabs(p)>=fabs(0.5*q*etemp)||p<=q*(a-x)||p>=q*(b-x)) d=CGOLD*(e=(x>=xm?a-x:b-x)); else {d=p/q; u=x+d; if(u-a<tol2||b-u<tol2)d=SIGN(tol1,xm-x);} } else d=CGOLD*(e=(x>=xm?a-x:b-x)); u=(fabs(d)>=tol1?x+d:x+SIGN(tol1,d)); fu=f1dim(u); if(fu<=fx) { if(u>=x)a=x; else b=x; SHFT(v,w,x,u) SHFT(fv,fw,fx,fu) } else { if(u<x)a=u; else b=u; if(fu<=fw||w==x){v=w; w=u; fv=fw; fw=fu;} else if(fu<=fv||v==x||v==w){v=u; fv=fu;} } } Print("Too many iterations in brent"); MaxIterFlag=1; xmin=x; return(fx); } //----------------------------------------------------------------------------------- double PowellsMethod::f1dim(double x) { int j; double f; for(j=0;j<N;j++) Xt[j]=Pcom[j]+x*Xicom[j]; f=func(Xt); return(f); } //----------------------------------------------------------------------------------- int PowellsMethod::Optimize(double &p[],int n=0) { int i,j,k,ret; k=ArraySize(p); if(n==0)N=k; else N=n; if(N<1||N>k)return(0); ArrayResize(P,N); ArrayResize(Xi,N*N); ArrayResize(Pcom,N); ArrayResize(Xicom,N); ArrayResize(Xt,N); ArrayResize(Pt,N); ArrayResize(Ptt,N); ArrayResize(Xit,N); for(i=0;i<N;i++)for(j=0;j<N;j++)Xi[i+N*j]=(i==j?1.0:0.0); for(i=0;i<N;i++)P[i]=p[i]; MaxIterFlag=0; powell(); for(i=0;i<N;i++)p[i]=P[i]; if(MaxIterFlag==1)ret=-1; else ret=Iter; return(ret); } //-----------------------------------------------------------------------------------
Die wesentliche Methode der Klasse ist die Methode Optimize.
Die Methode Optimize
Eingangsparameter:
- double &p[] für ein Datenfeld, das beim Eingang die Anfangsgrößen der Parameter enthält, deren optimaler Wert gefunden werden müssen, beim Ausgang enthält das Datenfeld die ermittelten optimalen Werte dieser Parameter.
- int n=0 für die Anzahl der Argumente in dem Datenfeld p[]. Bei n=0 gilt die Anzahl der Parameter als gleich dem Umfang des Datenfeldes p[].
Ausgegebener Wert:
- Ausgegeben wird die Anzahl der für die Funktionsfähigkeit des Algorithmus erforderlichen Iterationen, oder „-1“, wenn deren zulässige Höchstzahl erreicht ist.
Bei der Suche nach den optimalen Parameterwerten erfolgt eine iterative Annäherung an das Minimum der Zielfunktion. Die Methode Optimize gibt die Anzahl der zur Erreichung des Minimums der Funktion mit der vorgegebenen Genauigkeit erforderlichen Iterationen aus. Bei jeder Iteration erfolgen mehrere Aufrufe der Zielfunktion, das heißt, die Anzahl der Aufrufe der Zielfunktion kann die von der Methode Optimize ausgegebene Anzahl der Iterationen erheblich (um das Zehn- bis Hundertfache) übersteigen.
Weitere Methoden der Klasse.
Die Methode SetItMaxPowell
Eingangsparameter:
- Int n ist die Höchstzahl der zulässigen Iterationen für die Powell-Methode. Die Standardeinstellung ist 200.
Ausgegebener Wert:
- Keiner.
Es erfolgt die Festlegung der zulässigen Höchstzahl an Iterationen, bei deren Erreichen die Suche eingestellt wird und zwar unabhängig davon, ob das Minimum der Zielfunktion mit der vorgegebenen Genauigkeit gefunden werden konnte oder nicht. In dem Protokoll erscheint eine entsprechende Meldung.
Die Methode SetFtolPowell
Eingangsparameter:
- double er ist die Genauigkeit. Die Größe der Abweichung von dem Minimum der Zielfunktion, bei deren Erreichen die Methode Powell die Suche einstellt. Die Standardeinstellung ist 1e-6.
Ausgegebener Wert:
- Keiner.
Die Methode SetItMaxBrent
Eingangsparameter:
- Int n ist die Höchstzahl der zulässigen Iterationen für die Hilfsmethode nach Brent. Die Standardeinstellung ist 200.
Ausgegebener Wert:
- Keiner.
Es wird die zulässige Höchstzahl an Iterationen festgelegt. Sobald sie erreicht wird, stellt die Hilfsmethode nach Brent die Suche ein, und in dem Protokoll erscheint eine entsprechende Meldung.
Die Methode SetFtolBrent
Eingangsparameter:
- double er ist die Genauigkeit, der Wert, der die Suchgenauigkeit nach dem Minimum für die Hilfsmethode nach Brent festlegt. Die Standardeinstellung ist 1e-4.
Ausgegebener Wert:
- Keiner.
Die Methode GetFret
Eingangsparameter:
- Keine.
Ausgegebener Wert:
- Ausgegeben wird der ermittelte Wert des Minimums der Zielfunktion.
Die Methode GetIter
Eingangsparameter:
- Keine.
Ausgegebener Wert:
- Ausgegeben wird die Anzahl der für die Funktionsfähigkeit des Algorithmus benötigten Iterationen.
Die virtuelle Funktion func(const double &p[])
Eingangsparameter:
- const double &p[] ist die Adresse des Datenfeldes mit den optimierten Parametern. Die Größe des Datenfeldes entspricht der Anzahl der Parameter der Funktion.
Ausgegebener Wert:
- Ausgegeben wird der den an sie weitergegebenen Parametern entsprechende Wert der Funktion.
Die virtuelle Funktion func() muss in jedem Einzelfall in der jeweiligen Ableitung der Klasse PowellsMethod neu festgelegt werden. Bei der Funktion func() handelt es sich um die Zielfunktion, für die bei Aufruf des Suchalgorithmus diejenigen ihrer Argumente gefunden werden, die dem kleinsten von der Funktion ausgegebenen Wert entsprechen.
Diese Umsetzung der Methode von Powell zur Bestimmung der Suchrichtung zu jedem einzelnen Parameter nutzt die eindimensionale Methode der parabolischen Interpolation von Brent. Die Genauigkeit und die zulässige Höchstzahl der Iterationen für diese Methoden können durch Aufruf der Methoden SetItMaxPowell, SetFtolPowell, SetItMaxBrent und SetFtolBrent gesondert festgelegt werden.
Auf diese Weise können die voreingestellten Parameter des Algorithmus geändert werden. Das kann in dem Fall erforderlich sein, wenn sich beispielsweise die für eine konkrete Zielfunktion voreingestellte Genauigkeit als überhöht erwiesen hat, und der Algorithmus bei der Suche eine zu große Menge Iterationen erfordert. Durch eine Änderung des Wertes der erforderlichen Genauigkeit kann der Suchvorgang für unterschiedliche Kategorien der Zielfunktion optimiert werden.
Ungeachtet der scheinbaren Vielschichtigkeit des Algorithmus, der die Methode Powell umsetzt, ist dessen Anwendung recht einfach.
Wir liefern ein Beispiel. Nehmen wir an, wir haben die Funktion
und wir müssen die Werte für die Parameter 
und 
finden, bei denen die Funktion den geringsten Wert einnehmen wird.
Wir erstellen ein Skript, das eine Lösung für diese Aufgabe vorführt.
//----------------------------------------------------------------------------------- // PM_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- class PM_Test:public PowellsMethod { public: void PM_Test(void) {} private: virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- double PM_Test::func(const double &p[]) { double f,r1,r2; r1=p[0]-0.5; r2=p[1]-6.0; f=r1*r1*4.0+r2*r2; return(f); } //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { int it; double p[2]; p[0]=8; p[1]=9; // Initial point PM_Test *pm = new PM_Test; it=pm.Optimize(p); Print("Iter= ",it," Fret= ",pm.GetFret()); Print("p[0]= ",p[0]," p[1]= ",p[1]); delete pm; } //-----------------------------------------------------------------------------------
Beim Schreiben des Skripts wurde zunächst die Funktion func() zur Berechnung des Wertes der vorgegebenen Testfunktion anhand der an sie weitergegebenen Werte der Parameter p[0] und p[1] als Element der Klasse PM_Test angelegt. Des Weiteren werden den gesuchten Parametern im Hauptteil der Funktion OnStart() Anfangswerte zugeordnet. Bei diesen Werten beginnt die Suche.
Anschließend wird eine Instanz der Klasse PM_Test angelegt, und durch Aufruf der Methode Optimize wird der Suchvorgang nach den gesuchten Größen p[0] und p[1] gestartet; wobei die Methoden der Ausgangs- oder Elternklasse PowellsMethod die von uns neu definierte Funktion func() aufrufen. Nach Abschluss des Suchvorgangs wird die Anzahl der durchgeführten Iterationen, der Wert der Funktion an der Stelle des gefundenen Minimums sowie die gefundenen Werte der Parameter p[0]=0,5 und p[1]=6 im Protokoll wiedergegeben.
Die Datei PowellsMethod.mqh und das Testbeispiel PM_Test.mq5 befinden sich am Ende des Artikels in der gepackten Datei Files.zip. Zur Kompilierung der Datei PM_Test.mq5 muss diese sich in demselben Verzeichnis befinden wie die Datei PowellsMethod.mqh.
9. Optimierung der Werte der Modellparameter
In dem vorhergehenden Abschnitt wurden die Umsetzung der Methode zur Suche nach dem Minimum einer Funktion sowie ein einfaches Beispiel für ihre Anwendung vorgestellt. Jetzt kommen wir zur Betrachtung der mit der Optimierung der Parameter eben dieses exponentiellen Glättungsmodells verbundenen Fragen.
Wir beginnen mit der Vereinfachung der bereits eingeführten Klasse AdditiveES, indem wir aus ihr alle mit der Berücksichtigung des saisonbedingten Bestandteils verbundenen Elemente entfernen, da die Betrachtung von Modellen, die die Saisonbedingtheit berücksichtigen, im weiteren Verlauf dieses Beitrags ohnehin nicht vorgesehen ist. Das ermöglicht es, den Programmcode der Klasse verständlicher zu gestalten und die Anzahl der Berechnungen zu verringern. Darüber hinaus schließen wir zur Erleichterung der Darstellung des Optimierungsansatzes für das verwendete lineare Wachstumsmodell mit Dämpfung alle mit der Vorhersage und Berechnung der Zuverlässigkeitsintervalle der Vorhersage verbundenen Rechenoperationen aus.
//----------------------------------------------------------------------------------- // OptimizeES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- // Class OptimizeES //----------------------------------------------------------------------------------- class OptimizeES:public PowellsMethod { protected: double Dat[]; // Input data int Dlen; // Data lenght double Par[5]; // Parameters int NCalc; // Number of last elements for calculation public: void OptimizeES(void) {} int Calc(string fname); private: int readCSV(string fnam,double &dat[]); virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- // Calc //----------------------------------------------------------------------------------- int OptimizeES::Calc(string fname) { int i,it; double relmae,naiv,s,t,alp,gam,phi,e,ae,pt; if(readCSV(fname,Dat)<0){Print("Error."); return(-1);} Dlen=ArraySize(Dat); NCalc=200; // number of last elements for calculation if(NCalc<0||NCalc>Dlen-1){Print("Error."); return(-1);} Par[0]=Dat[Dlen-NCalc]; // initial S Par[1]=0; // initial T Par[2]=0.5; // initial Alpha Par[3]=0.5; // initial Gamma Par[4]=0.5; // initial Phi it=Optimize(Par); // Powell's optimization s=Par[0]; t=Par[1]; alp=Par[2]; gam=Par[3]; phi=Par[4]; relmae=0; naiv=0; for(i=Dlen-NCalc;i<Dlen;i++) { e=Dat[i]-(s+phi*t); relmae+=MathAbs(e); naiv+=MathAbs(Dat[i]-Dat[i-1]); ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } relmae/=naiv; PrintFormat("%s: N=%i, RelMAE=%.3f",fname,NCalc,relmae); PrintFormat("Iter= %i, Fmin= %e",it,GetFret()); PrintFormat("p[0]= %.5f, p[1]= %.5f, p[2]= %.2f, p[3]= %.2f, p[4]= %.2f", Par[0],Par[1],Par[2],Par[3],Par[4]); return(0); } //----------------------------------------------------------------------------------- // readCSV //----------------------------------------------------------------------------------- int OptimizeES::readCSV(string fnam,double &dat[]) { int n,asize,fhand; fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI); if(fhand==INVALID_HANDLE) { Print("FileOpen Error!"); return(-1); } asize=512; ArrayResize(dat,asize); n=0; while(FileIsEnding(fhand)!=true) { dat[n++]=FileReadNumber(fhand); if(n+128>asize) { asize+=128; ArrayResize(dat,asize); } } FileClose(fhand); ArrayResize(dat,n-1); return(0); } //------------------------------------------------------------------------------------ // func //------------------------------------------------------------------------------------ double OptimizeES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 sse=0; for(i=Dlen-NCalc;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(NCalc*MathLog(k1*k2*k3*sse)); } //------------------------------------------------------------------------------------
Die Klasse OptimizeES wurde als Ableitung (Kindklasse) der Klasse PowellsMethod angelegt und beinhaltet eine Neudefinition der virtuellen Funktion func(). Wie bereits erwähnt müssen am Eingang dieser Funktion die Parameter an sie weitergegeben werden, deren im Verlauf der Optimierung zu minimierender Wert zu berechnen ist.
Gemäß der Methode der maximalen Wahrscheinlichkeit wird in der Funktion func() der Logarithmus der Summe der des Quadrates der Fehler bei der Vorhersage für den jeweils nächsten Schritt berechnet. Die Berechnung der Fehler erfolgt in einem Durchlauf für die NCalc letzten Werte der Folge.
Zur Aufrechterhaltung der Stabilität des Modells müssen wir den Änderungsbereich seiner Parameter begrenzen. Wir legen diesen Bereich für die Parameter Alpha und Gamma auf 0,05 bis 0,95 sowie für Phi auf 0,05 bis 1,0 fest. In unserem Fall kommt zur Optimierung jedoch die Methode der bedingungslosen Suche nach dem Minimum zur Anwendung, in der der Einsatz von Begrenzungen für die Werte der Argumente der Zielfunktion nicht vorgesehen ist.
Um die den Parametern auferlegten Begrenzungen zu berücksichtigen, ohne dabei den Suchalgorithmus zu verändern, versuchen wir die Aufgabe der Suche nach dem Minimum einer Funktion mit mehreren Variablen und Beschränkungen in eine Aufgabe der bedingungslosen Suche nach dem Minimum umzuwandeln. Dazu bedienen wir uns der Methode der so genannten Straffunktionen. Diese Methode ist an einem eindimensionalen Beispiel leicht darzustellen.
Angenommen wir haben eine Funktion mit nur einem Argument (dessen Definitionsbereich zwischen 2,0 und 3,0 liegt) sowie einem Algorithmus, der dem Parameter dieser Funktion im Verlauf des Suchvorgangs beliebige Werte zuordnen kann. In diesem Fall können wir folgendermaßen vorgehen: Wenn der Suchalgorithmus ein Argument liefert, das den zulässigen Höchstwert übersteigt, sagen wir 3,5, dann kann die Funktion so berechnet werden, als wäre das Argument gleich 3,0, worauf das ermittelte Ergebnis mit dem der Größe der Überschreitung des zulässigen Höchstwertes proportionalen Koeffizienten multipliziert wird, zum Beispiel: k=1+(3,5-3)*200=300.
Wenn wir die unterhalb der zulässigen Untergrenze liegenden Werte des Argumentes in gleicher Weise behandeln, ist sicher, dass die resultierende Zielfunktion über die Grenzen des zulässigen Änderungsbereiches ihres Argumentes hinauswachsen wird. Diese künstliche Erweiterung des Ausgabewertes der Zielfunktion ermöglicht es, dem die Suche ausführenden Algorithmus den Umstand zu verheimlichen, dass das an die Funktion weitergegebene Argument irgendwie begrenzt wurde, und gewährleistet, dass das Minimum der resultierenden Funktion innerhalb der vorgegebenen Grenzen für das Argument liegen wird. Diese Vorgehensweise lässt sich problemlos auch auf Fälle mit mehreren Variablen übertragen.
Die Hauptmethode der Klasse OptimizeES ist die Methode Calc. Beim Aufruf dieser Methode erfolgen die Auslesung der Daten aus der Datei, die Suche nach den optimalen Werten für die Modellparameter sowie die Berechnung der Genauigkeit der Vorhersage RelMAE für die ermittelten Parameterwerte. Dabei wird die Anzahl der zu verarbeitenden, aus der Datei der Folge auszulesenden Werte in der Variablen NCalc festgelegt.
Es folgt das Beispiel des Skriptes Optimization_Test.mq5, das die Klasse OptimizeES verwendet.
//----------------------------------------------------------------------------------- // Optimization_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "OptimizeES.mqh" OptimizeES es; //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { es.Calc("Dataset\\USDJPY_M1_1100.TXT"); } //-----------------------------------------------------------------------------------
Als Ergebnis der Ausführung dieses Skripts sollten wir folgendes Ergebnis erhalten:
Abbildung 6. Ergebnis der Ausführung des Skripts Optimization_Test.mq5
Obwohl wir jetzt die Möglichkeit haben, die optimalen Parameterwerte und Anfangswerte des Modells zu ermitteln, bleibt dennoch ein Parameter übrig, der mit einfachen Mitteln nicht optimiert werden kann: die Anzahl der Werte der Folge, anhand derer die Optimierung erfolgt. Bei der Durchführung der Optimierung an einer Folge mit großer Länge erhalten wir optimale Parameterwerte, die im Durchschnitt über die gesamte Länge der Folge einen minimalen Fehler sicherstellen.
Aber wenn sich der Charakter der Folge im Verlauf dieses Intervalls ändert, sind die für einzelne ihrer Abschnitte ermittelten Werte schon nicht mehr optimal. Wenn die Länge der Folge dagegen erheblich verkürzt wird, erhalten wir zwar die optimalen Parameterwerte für diesen kurzen Teilbereich, haben aber keinerlei Garantie dafür, dass sie auch für einen längeren Zeitraum optimal sein werden.
Die Dateien OptimizeES.mqh und Optimization_Test.mq5 befinden sich am Ende des Artikels in der gepackten Datei Files.zip. Bei der Zusammenstellung müssen sich die Dateien OptimizeES.mqh und PowellsMethod.mqh in demselben Verzeichnis befinden wie die bereits kompilierte Datei Optimization_Test.mq5. In dem vorgestellten Beispiel wird die Datei USDJPY_M1_1100.TXT mit der zu prüfenden Folge verwendet, sie befindet sich in dem Verzeichnis \MQL5\Files\Dataset\.
In der Tabelle 2 sind die mithilfe dieses Skripts ermittelten Werte für die Genauigkeit der Vorhersage mittels RelMAE aufgeführt. Die Vorhersage wurde für die acht zu prüfenden Folgen durchgeführt, von denen am Anfang dieses Beitrages die Rede war. Verwendet wurden zur Erstellung der Vorhersage jeweils die letzten 100, 200 und 400 Werte jeder dieser Folgen.
|
Tabelle 2. Vorhersagefehler mit RelMAE
Unübersehbar haben sich die Berechnungen der Vorhersagefehler unweit eins eingependelt, in der Mehrzahl der Fälle liegt die Vorhersagegenauigkeit des verwendeten Modells für die gegebenen Folgen jedoch über der der naiven Prognose.
10. Der Indikator IndicatorES.mq5
Weiter oben wurde bei der Vorstellung der Klasse AdditiveES.mqh auch der auf dieser beruhende Indikator AdditiveES_Test.mq5 angesprochen. In diesen Indikator wurden alle Glättungsparameter manuell eingegeben.
Jetzt, nachdem wir eine Methode kennen, die die Durchführung der Optimierung der Modellparameter ermöglicht, können wir denselben Indikator anlegen, dessen optimale Parameter- und Anfangswerte automatisch eingestellt werden, von Hand muss nur noch die Länge der zu verarbeitenden Stichprobe festgelegt werden. Dabei bleiben die mit der Berücksichtigung der Saisonbedingtheit verbundenen Berechnungen ausdrücklich außen vor.
Es folgt der beim Programmieren des Indikators verwendete Quellcode der Klasse CIndiсatorES:
//----------------------------------------------------------------------------------- // CIndicatorES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- // Class CIndicatorES //----------------------------------------------------------------------------------- class CIndicatorES:public PowellsMethod { protected: double Dat[]; // Input data int Dlen; // Data lenght double Par[5]; // Parameters public: void CIndicatorES(void) { } void CalcPar(double &dat[]); double GetPar(int n) { if(n>=0||n<5)return(Par[n]); else return(0); } private: virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- // CalcPar //----------------------------------------------------------------------------------- void CIndicatorES::CalcPar(double &dat[]) { Dlen=ArraySize(dat); ArrayResize(Dat,Dlen); ArrayCopy(Dat,dat); Par[0]=Dat[0]; // initial S Par[1]=0; // initial T Par[2]=0.5; // initial Alpha Par[3]=0.5; // initial Gamma Par[4]=0.5; // initial Phi Optimize(Par); // Powell's optimization } //------------------------------------------------------------------------------------ // func //------------------------------------------------------------------------------------ double CIndicatorES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 sse=0; for(i=0;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(Dlen*MathLog(k1*k2*k3*sse)); } //------------------------------------------------------------------------------------
Die genannte Klasse enthält die Methoden CalcPar und GetPar, deren erste zur Berechnung der optimalen Werte für die Modellparameter gedacht ist und die zweite für den Zugriff auf diese Werte. Außerdem beinhaltet die Klasse CIndicatorES die Neudefinition der virtuellen Funktion func().
Der Programmcode des Indikators IndicatorES.mq5:
//----------------------------------------------------------------------------------- // IndicatorES.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" // Forecast #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "ConfUp" // Confidence interval #property indicator_type3 DRAW_LINE #property indicator_color3 clrCrimson #property indicator_style3 STYLE_DOT #property indicator_width3 1 #property indicator_label4 "ConfDn" // Confidence interval #property indicator_type4 DRAW_LINE #property indicator_color4 clrCrimson #property indicator_style4 STYLE_DOT #property indicator_width4 1 input int nHist=80; // History bars, nHist>=24 #include "CIndicatorES.mqh" #define NFORE 12 double Hist[],Fore[],Conf1[],Conf2[]; double Data[]; int NDat; CIndicatorES Es; //----------------------------------------------------------------------------------- // Custom indicator initialization function //----------------------------------------------------------------------------------- int OnInit() { NDat=nHist; if(NDat<24)NDat=24; MqlRates rates[]; CopyRates(NULL,0,0,NDat,rates); // Load missing data ArrayResize(Data,NDat); SetIndexBuffer(0,Hist,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,Fore,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFORE); SetIndexBuffer(2,Conf1,INDICATOR_DATA); // Confidence interval PlotIndexSetString(2,PLOT_LABEL,"ConfUp"); PlotIndexSetInteger(2,PLOT_SHIFT,NFORE); SetIndexBuffer(3,Conf2,INDICATOR_DATA); // Confidence interval PlotIndexSetString(3,PLOT_LABEL,"ConfDN"); PlotIndexSetInteger(3,PLOT_SHIFT,NFORE); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } //----------------------------------------------------------------------------------- // Custom indicator iteration function //----------------------------------------------------------------------------------- int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,start; double s,t,alp,gam,phi,e,f,a,a1,a2,a3,var,ci; if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar start=rates_total-NDat; //----------------------- PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat); PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE); for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data Es.CalcPar(Data); // Optimization of parameters s=Es.GetPar(0); t=Es.GetPar(1); alp=Es.GetPar(2); gam=Es.GetPar(3); phi=Es.GetPar(4); f=(s+phi*t); var=0; for(i=0;i<NDat;i++) // History { e=Data[i]-f; var+=e*e; a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1; f=(s+phi*t); Hist[start+i]=f; } var/=(NDat-1); a1=1; a2=0; a3=1; for(i=rates_total-NFORE;i<rates_total;i++) { a1=a1*phi; a2+=a1; Fore[i]=s+a2*t; // Forecast ci=1.96*MathSqrt(var*a3); // Confidence intervals a=alp*(1+a2*gam); a3+=a*a; Conf1[i]=Fore[i]+ci; Conf2[i]=Fore[i]-ci; } return(rates_total); } //-----------------------------------------------------------------------------------
In dem Indikator wird bei Auftreten eines jeden neuen Balkens nach den optimalen Werten für die Modellparameter gesucht, das Modell wird für die jeweilige Anzahl NHist-Balken berechnet und eine Vorhersage sowie deren Zuverlässigkeitsgrenzen erstellt.
Der einzige Parameter des Indikators ist die Länge der verarbeiteten Folge, deren Mindestwert auf 24 Balken begrenzt ist. Alle Berechnungen in dem Indikator erfolgen auf der Grundlage der Werte open[] für die Eröffnungskurse. Der Vorhersagehorizont umfasst 12 Balken. Der Programmcode des Indikators IndicatorES.mq5 sowie die Datei CIndicatorES.mqh befinden sich in der gepackten Datei Files.zip am Ende dieses Beitrags.
Abbildung 7. Ergebnis der Tätigkeit des Indikators IndicatorES.mq5
Abbildung 7 zeigt ein Beispiel für die Tätigkeit des Indikators IndicatorES.mq5. Bei der Arbeit des Indikators nimmt das 95%-Zuverlässigkeitsintervall der Vorhersage Werte an, die den ermittelten optimalen Werten der Modellparameter entsprechen. Je größer die Glättungsparameterwerte, desto schneller die Erweiterung des Zuverlässigkeitsintervalls bei einer Vergrößerung des Vorhersagehorizonts.
Nach unkomplizierten Nachbesserungen kann der Indikator IndicatorES.mq5 nicht mehr nur zur Vorhersage der unmittelbaren Wechselkursnotierungen verwendet werden sondern auch zur Erstellung von Vorhersagen für die Werte unterschiedlicher Indikatoren oder bereits aufbereiteter Daten.
Fazit
Ein wesentliches Ziel dieses Beitrages bestand darin, den Leser mit den für die Vorhersage verwendeten additiven exponentiellen Glättungsmodellen vertraut zu machen. Bei der Vorführung ihrer praktischen Anwendung wurden auch einige begleitende Fragen berührt. Allerdings ist das in dem Beitrag vorgestellte Material lediglich als erste Annäherung an die riesige Schicht der mit Vorhersagen verbundenen Probleme und Lösungen zu betrachten.
Ich möchte Ihre Aufmerksamkeit darauf lenken, dass die hier dargestellten Klassen, Funktionen, Skripte und Indikatoren beim Schreiben des Artikels angelegt worden sind und in erster Linie zur Verwendung als Veranschaulichungsmaterial für die Ausführungen dieses Beitrages gedacht waren. Deshalb wurden sie nicht wirklich auf Fehlerlosigkeit überprüft. Darüber hinaus sind die in dem Artikel eingeführten Indikatoren lediglich als Beispiele für die Umsetzung der betrachteten Methoden in Programmform gedacht.
Aller Wahrscheinlichkeit nach kann die Vorhersagegenauigkeit des hier vorgestellten Indikators IndicatorES.mq5 etwas gesteigert werden, wenn man sich der Modifikationen des angewandten Modells bedient, die die Besonderheiten der betrachteten Kursverläufe besser berücksichtigen. Außerdem kann der Indikator mithilfe der anderen Modelle erweitert werden. Aber diese Fragen würden den Rahmen dieses Beitrages sprengen.
Zum Abschluss sei darauf hingewiesen, dass die exponentiellen Glättungsmodelle in bestimmten Fällen in der Lage sind, Vorhersagen zu liefern, die denen mithilfe komplexerer Modelle gewonnenen in Sachen Genauigkeit nicht nachstehen, wobei zum wiederholten Male erwähnt sei, dass das komplexeste Modell bei weitem nicht immer auch das Beste ist.
Verweise/Weblinks:
- Everette S. Gardner Jr. Exponential Smoothing: The State of the Art – Part II. 3. Juni 2005.
- Rob J Hyndman. Forecasting Based on State Space Models for Exponential Smoothing. 29. August 2002.
- Rob J Hyndman et al. Prediction Intervals for Exponential Smoothing Using Two New Classes of State Space Models. 30. Januar 2003.
- Rob J Hyndman and Muhammad Akram. Some Nonlinear Exponential Smoothing Models Are Unstable. 17. Januar 2006.
- Rob J Hyndman and Anne B Koehler. Another Look at Measures of Forecast Accuracy. 2. November 2005.
- Ju. P. Lukaschin. Adaptive Methoden zur kurzfristigen Vorhersage von Zeitreihen: Fachbuch. - Мoskau: Finanzen und Statistik, 2003. 416 ff.
- D. Himmelblau. Angewandte nichtlineare Programmierung. - Мoskau: Mir, 1975.
- Numerical Recipes in C. The Art of Scientific Computing. Zweite Ausgabe. Cambridge University Press.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/318
Analyse der statistischen Eigenschaften von Indikatoren
Analyse der wesentlichen Merkmale von Zeitreihen
Erstellung von Handelssystemen mittels Diskriminanzanalyse
Leistungsfähige adaptive Indikatoren - Theorie und Umsetzung in MQL5
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.