
Selbstoptimierende Expert Advisors in MQL5 (Teil 14): Betrachtung von Datentransformationen als Tuning-Parameter unseres Feedback-Controllers
Die Vorverarbeitung ist ein leistungsstarker und dennoch oft übersehener Tuning-Parameter in jedem Framework oder jeder Pipeline für maschinelles Lernen.
Er ist ein wichtiger Regler in der Pipeline, der oft im Schatten seiner größeren Brüder versteckt ist. In der Regel stehen Optimierer oder glänzende Modellarchitekturen im Mittelpunkt der Forschungsarbeit, und es werden große Mengen an akademischen Mitteln in diese Richtungen fließen. Es wird jedoch wenig Zeit darauf verwendet, die Auswirkungen der Vorverarbeitungstechniken zu untersuchen.
Die Vorverarbeitung, die wir auf die vorliegenden Daten anwenden, wirkt sich unbemerkt auf die Leistung des Modells aus, und zwar in einem Ausmaß, das überraschend sein kann. Selbst kleine prozentuale Verbesserungen bei der Vorverarbeitung können sich im Laufe der Zeit summieren und die Rentabilität und das Risiko unserer Handelsanwendungen erheblich beeinflussen.
Allzu oft eilen wir durch die Vorverarbeitung, ohne uns viele Gedanken zu machen oder uns viel Zeit zu nehmen, um zu überprüfen, ob wir wirklich die bestmögliche Transformation für die Eingabedaten gefunden haben.
Die fortschrittlichen Optimierer und Architekturen des maschinellen Lernens, auf die wir uns in unserem modernen Zeitalter verlassen, werden durch die Transformationen, die wir auf die vorliegenden Daten anwenden, stillschweigend behindert – oder gestärkt. Leider gibt es zum Zeitpunkt der Erstellung dieses Berichts keinen etablierten Rahmen, um zu beweisen, dass eine bestimmte Transformation optimal ist. Darüber hinaus sind wir nicht sicher, dass es keine bessere Alternative gibt. Tatsächlich gibt es nur wenige Forschungsarbeiten, die sich mit der Kombination verschiedener Umwandlungen zu hybriden Lösungen befassen – und genau hier könnte die ungenutzte Leistung möglicherweise erschlossen werden.
Unser Ziel ist es daher, die Effizienz eines Rückkopplungsreglers zu verbessern, den wir gemeinsam in einer früheren Diskussion sorgfältig entwickelt haben (siehe hier).
Über die normale Rentabilität hinaus wollen wir eine Verringerung des Risikos und ein robusteres – und in gewissem Maße auch ausgereifteres – Handelsverhalten unserer Handelsanwendung beobachten. Im Wesentlichen wird bei dieser Übung die Vorverarbeitung selbst als eigenständiger Tuning-Parameter behandelt – ein Parameter, der bei richtiger Handhabung die Ergebnisse von Handelsanwendungen wesentlich verändern kann.
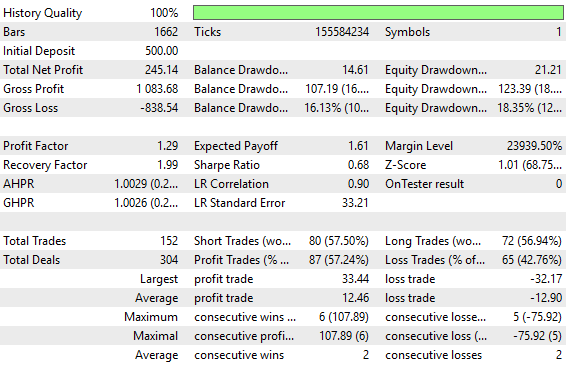
Abbildung 1: Die alten Backtest-Statistiken, die mit der alten Version unserer Rückkopplungssteuerung erstellt wurden
Die Leistung unseres alten Rückkopplungsreglers war sicherlich nach allen Maßstäben akzeptabel, aber wir werden natürlich zeigen, dass die Zeit, die Sie für das Testen der richtigen Transformationen aufwenden, potenziell Alpha in Ihrer Strategie freisetzen kann, das schlummerte, weil das Signal nicht effektiv ausgesetzt war.
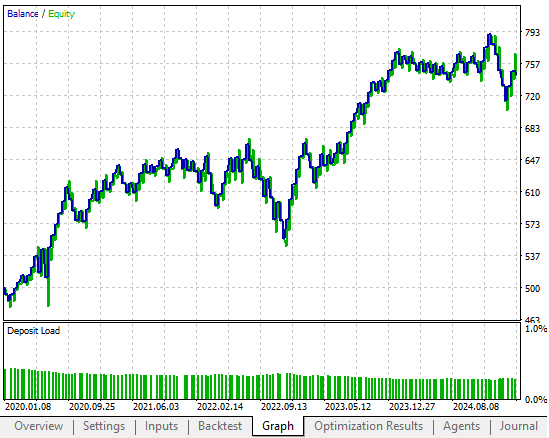
Abbildung 2: Die alte Kapitalkurve, die wir übertreffen wollen, indem wir eine geeignete Transformation für unsere Eingabedaten finden
Wenn Sie die reichhaltigen Muster in Ihrem Datensatz nicht aufdecken, schwindet das Kapital der Anleger mit der Zeit. Wir haben drei verschiedene Transformationen der Eingabedaten getestet, die wir an unseren Feedback-Controller weitergegeben haben. Zur Kontrolle haben wir einen Benchmark mit den unbearbeiteten und untransformierten Eingaben aus der vorherigen Diskussion durchgeführt. Anschließend wurde jede von uns bewertete Transformation anhand identischer historischer Daten getestet, wobei alle anderen Variablen konstant gehalten wurden. Die Performance wurde anhand der Rentabilität, der Sharpe-Ratio, der Anzahl der platzierten Handelsgeschäfte, des gesamten Bruttoverlustes und des Gesamtanteils der profitablen Handelsgeschäfte gemessen. Auf diese Weise konnten wir die Auswirkungen der Vorverarbeitung isolieren und gleichzeitig einen fairen Vergleich über alle drei Tests hinweg aufrechterhalten.
Die erste Transformation, die wir getestet haben, war der statistische Standard-Z-Score. Der z-Score wird berechnet, indem der Mittelwert jeder Spalte subtrahiert und jede Spalte durch ihre Standardabweichung geteilt wird. Wir haben festgestellt, dass diese Umstellung unsere Rentabilität um 30 Prozent gegenüber dem Ausgangswert reduziert hat. Dies ist in keiner Weise attraktiv. Darüber hinaus sank unsere Sharpe Ratio gegenüber dem Ausgangsniveau um erstaunliche 10 Prozent.
Daher war die z-Score-Transformation für uns nicht ideal. Danach haben wir eine Transformation aus dem Bereich der linearen Algebra angewendet. Diese Transformation wird als Einheitsskalierung bezeichnet und erfolgt durch Division einer Matrix durch ihre Norm. In diesem speziellen Fall haben wir die L1-Norm der Matrix als Divisor gewählt. Nach der Skalierung mit der L1-Norm haben wir festgestellt, dass sich die Rentabilität unserer Anwendung um 12 Prozent gegenüber der Basis verbessert hat, was sehr attraktiv ist. Darüber hinaus verbesserte sich die Sharpe Ratio um 30 Prozent gegenüber der Einheitsskalierung.
Ein weiteres großartiges Zeichen für Handelsgeschick ist es, wenn unsere Anwendung höhere Rentabilitätsniveaus mit insgesamt weniger Trades erreichen kann. Dies war auch hier der Fall: Nach der Einheitsskalierung sank die Gesamtzahl der erforderlichen Abschlüsse um 8 Prozent, und auch der Gesamtverlust ging um 15 Prozent zurück. Schließlich stieg der Gesamtanteil der Handelsgeschäfte mit Gewinn um 5 Prozent. Dies gab uns die Gewissheit, dass die Skalierung der Einheiten die Leistung unseres Rückkopplungsreglers positiv beeinflusst hat.
Schließlich haben wir eine Mischung aus z-Score und Einheitsskalierung getestet. Leider wurden dadurch alle Verbesserungen zunichte gemacht, die wir allein durch die Skalierung der Einheiten erreicht hatten. Unsere Rentabilität sank um 58 Prozent unter den Ausgangswert, und unsere Sharpe Ratio ging um 19 Prozent zurück. Daher war die Kombination dieser beiden Transformationen zu einem Hybrid trotz unserer starken Intuition destruktiv für die Leistung und brachte keine zusätzliche Struktur zutage, aus der wir lernen konnten.
Aus all dem können wir leicht erkennen, dass die Vorverarbeitung nicht nur ein weiteres Mittel zum Zweck bei der Erstellung von maschinellen Lernmodellen für den Handel ist. Vielmehr ist die Vorverarbeitung an sich schon eine eigene Strategie. Die Wahl der Transformation beeinflusst stillschweigend die Leistung unserer maschinellen Lernmodelle – sie beeinflusst Gewinne, verzerrt Verluste und verändert unbeabsichtigt unsere Risikoexposition in einer Weise, die wir nicht direkt verstehen.
Das klassische statistische Lernen bietet, wenn überhaupt, nur wenig Anhaltspunkte in dieser Richtung. Es gibt keine allgemeingültigen, vereinbarten Standards, die über die Brute-Force-Exploration durch Kreuzvalidierung für Partitionen hinausgehen. Das bedeutet, dass wir Zeit in das Benchmarking von Pre-Processing-Pipelines investieren und sie als das behandeln, was sie sind: hochwirksame Tuning-Parameter in unserer Pipeline für maschinelles Lernen.
Dies sollte auch andere Forscher und Artikelschreiber dazu anregen, mehr und mehr Transformationen zu erforschen, die in unserem Bereich angewendet werden könnten. Denn in Bereichen wie der Bild- und Spracherkennung setzen Praktiker des maschinellen Lernens oft robuste und umfangreiche Pipelines von Transformationen ein, bevor überhaupt eine Vorhersage versucht wird. Doch in Bereichen wie unserem, dem maschinellen Lernen im Finanzbereich, verbringen wir oft sehr wenig Zeit mit dem Aufbau robuster Pipelines für die Vorverarbeitung von Transformationen.
Unter den derzeitigen Bedingungen sind Brute-Force-Tests eine gute Strategie. Je mehr wir erforschen, desto besser verstehen wir die Merkmale jeder Transformation, die wir auf diesen speziellen Markt anwenden. Auf diese Weise können wir herausfinden, welche der beobachteten Transformationen die beste sein könnte.
Überprüfung der aktuellen Ausgangssituation
Bevor wir beginnen, ist es wichtig, dass wir uns zunächst die Kontrolleinrichtung ansehen, die wir übertreffen wollen. Jede Optimierungsmaßnahme ist schwer zu interpretieren, wenn es keinen Benchmark oder ein Basisleistungsniveau gibt, mit dem man sich vergleichen kann. Daher werden wir zunächst kurz den ursprünglichen Rückkopplungsregler, den wir implementiert haben, überprüfen. Den Lesern, die schon einmal hier waren, wird der folgende Code bereits bekannt sein. Für die Leser, die zum ersten Mal dabei sind, möchte ich die wichtigsten Erkenntnisse aus der von uns erstellten Anwendung und unserer vorherigen Diskussion hervorheben.
Die Anwendung stützt sich auf eine kleine Anzahl von Systemdefinitionen, die wir während ihrer gesamten Lebensdauer konstant halten. Zum Beispiel die Periode der verwendeten technischen Indikatoren, die Anzahl der beobachteten Handelstage, bevor der Feedback-Controller Input geben darf, und die Gesamtzahl der Merkmale, die der Controller als Input nimmt. In diesem Fall benötigt der Rückkopplungsregler 12 Eingangsmerkmale. Wichtig ist, dass wir im vorigen Beispiel auf keine der 12 Eingaben Transformationen, Standardisierungen oder Skalierungstechniken angewendet haben.
Die Anwendung hängt auch von einigen globalen Variablen und Bibliotheken ab, wie z. B. der Handelsanwendung für das Eröffnen und Schließen von Handelsgeschäften, der Zeitbibliothek für die Verfolgung der Kerzenbildung und der Handelsinfobibliothek für Details wie die Mindestlosgröße und die aktuellen Geld- und Briefkurse.
Bei der erstmaligen Initialisierung erstellt die Anwendung neue Instanzen der nutzerdefinierten Bibliotheken, richtet technische Indikatoren ein und initialisiert die meisten globalen Variablen mit Standardwerten. Wenn die Anwendung nicht mehr verwendet wird, werden die dynamischen Objekte und technischen Indikatoren freigegeben.
Wird die On-Tick-Funktion aufgerufen, prüft das System zunächst, ob sich eine vollständige Kerze gebildet hat. Ist dies der Fall, werden die Puffer für den gleitenden Durchschnitt mit dem letzten Schlusskurs aktualisiert. Wenn keine Positionen offen sind, wird die Handelslogik angewandt: ein gleitender Durchschnittskanal, der aus einem hohen und einem niedrigen gleitenden Durchschnitt mit einer gemeinsamen Periode gebildet wird. Jedes Mal, wenn die Kurse über den Kanal ausbrechen, kaufen wir. Im Gegenteil, sobald wir unter die Marke fallen, verkaufen wir. Andernfalls werden wir warten.
In den ersten 90 Tagen ist es dem System erlaubt, fast sofort zu kaufen und zu verkaufen. Nach diesem Zeitraum benötigen die Handelsgeschäfte jedoch eine Prognose vom Rückkopplungsregler. Ist der Kontrolleur zuversichtlich, dass der Handel gewinnbringend sein wird, wird die Genehmigung erteilt; andernfalls hält er das System zurück.
Das ist das Wesen des rückgekoppelten Controllers: Er wartet die ersten 90 Tage ab, bevor er dem System Input gibt. Von dort aus definieren wir eine Methode namens take_snapshots, um in regelmäßigen Abständen Beobachtungen der Systemleistung zu sammeln, und eine weitere Methode namens fit_snapshots, um lineare Lösungen für diese Beobachtungen zu finden. Sobald die Lösungen gefunden sind, kann das System Vorhersagen treffen.
Dies ist die Basisversion unserer Handelsstrategie.
//+------------------------------------------------------------------+ //| Closed Loop Feedback.mq5 | //| Gamuchirai Ndawana | //| https://www.mql5.com/en/users/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" /** Closed Loop Feedback Control allows us to learn how to control our system's dynamics. It is challenging to perform in action, but worth every effort made towards it. Certain tasks, such as deciding when to increase your lot size, are not always easy to plan explicitly. We can rather observe our average loss size after say, 20 trades at minimum lot. From there, we can calculate how much on average, we expect to lose on any trade. And then set meaningful profit targets to accumulate, before increasing out lot size. We do not always know these numbers ahead of time. Additionally, we can train predictive models, that attempt to learn when our system is loosing and keep us out of loosing trades. The models we desire are not directly predicting the market per say. Rather, they are observing the relationship between a fixed strategy and a dynamic market. After allowing a certain number of observations, the predictive model may be permitted to give inputs that override the original strategy only if the model expects the strategy to lose, yet again. These family of algorithms may one day make it possible for us to truly design strategies that require no tuning parameters at all! I am excited to present this to you, but there is a long road ahead. Let us begin. **/ //+------------------------------------------------------------------+ //| System definitions | //+------------------------------------------------------------------+ #define MA_PERIOD 10 #define OBSERVATIONS 90 #define FEATURES 12 #define ACCOUNT_STATES 3 //+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ int ma_h_handler,ma_l_handler,atr_handler,scenes,b_matrix_scenes; double ma_h[],ma_l[],atr[]; matrix snapshots,OB_SIGMA,OB_VT,OB_U,b_vector,b_matrix; vector S,prediction; vector account_state; bool predict,permission; //+------------------------------------------------------------------+ //| Dependencies | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> #include <VolatilityDoctor\Time\Time.mqh> #include <VolatilityDoctor\Trade\TradeInfo.mqh> CTrade Trade; Time *DailyTimeHandler; TradeInfo *TradeInfoHandler; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- DailyTimeHandler = new Time(Symbol(),PERIOD_D1); TradeInfoHandler = new TradeInfo(Symbol(),PERIOD_D1); ma_h_handler = iMA(Symbol(),PERIOD_D1,MA_PERIOD,0,MODE_EMA,PRICE_HIGH); ma_l_handler = iMA(Symbol(),PERIOD_D1,MA_PERIOD,0,MODE_EMA,PRICE_LOW); atr_handler = iATR(Symbol(),PERIOD_D1,14); snapshots = matrix::Ones(FEATURES,OBSERVATIONS); scenes = 0; b_matrix_scenes = 0; account_state = vector::Zeros(3); b_matrix = matrix::Zeros(1,1); prediction = vector::Zeros(2); predict = false; permission = true; //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete DailyTimeHandler; delete TradeInfoHandler; IndicatorRelease(ma_h_handler); IndicatorRelease(ma_l_handler); IndicatorRelease(atr_handler); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- if(DailyTimeHandler.NewCandle()) { CopyBuffer(ma_h_handler,0,0,1,ma_h); CopyBuffer(ma_l_handler,0,0,1,ma_l); CopyBuffer(atr_handler,0,0,1,atr); double c = iClose(Symbol(),PERIOD_D1,0); if(PositionsTotal() == 0) { account_state = vector::Zeros(ACCOUNT_STATES); if(c > ma_h[0]) { if(!predict) { if(permission) Trade.Buy(TradeInfoHandler.MinVolume(),Symbol(),TradeInfoHandler.GetAsk(),(TradeInfoHandler.GetBid()-(atr[0]*2)),(TradeInfoHandler.GetBid()+(atr[0]*2)),""); } account_state[0] = 1; } else if(c < ma_l[0]) { if(!predict) { if(permission) Trade.Sell(TradeInfoHandler.MinVolume(),Symbol(),TradeInfoHandler.GetBid(),(TradeInfoHandler.GetAsk()+(atr[0]*2)),(TradeInfoHandler.GetAsk()-(atr[0]*2)),""); } account_state[1] = 1; } else { account_state[2] = 1; } } if(scenes < OBSERVATIONS) { take_snapshots(); } else { matrix temp; temp.Assign(snapshots); snapshots = matrix::Ones(FEATURES,scenes+1); //--- The first row is the intercept and must be full of ones for(int i=0;i<FEATURES;i++) snapshots.Row(temp.Row(i),i); take_snapshots(); fit_snapshots(); predict = true; permission = false; } scenes++; } } //+------------------------------------------------------------------+ //| Record the current state of our system | //+------------------------------------------------------------------+ void take_snapshots(void) { snapshots[1,scenes] = iOpen(Symbol(),PERIOD_D1,1); snapshots[2,scenes] = iHigh(Symbol(),PERIOD_D1,1); snapshots[3,scenes] = iLow(Symbol(),PERIOD_D1,1); snapshots[4,scenes] = iClose(Symbol(),PERIOD_D1,1); snapshots[5,scenes] = AccountInfoDouble(ACCOUNT_BALANCE); snapshots[6,scenes] = AccountInfoDouble(ACCOUNT_EQUITY); snapshots[7,scenes] = ma_h[0]; snapshots[8,scenes] = ma_l[0]; snapshots[9,scenes] = account_state[0]; snapshots[10,scenes] = account_state[1]; snapshots[11,scenes] = account_state[2]; } //+------------------------------------------------------------------+ //+------------------------------------------------------------------+ //| Fit our linear model to our collected snapshots | //+------------------------------------------------------------------+ void fit_snapshots(void) { matrix X,y; X.Reshape(FEATURES,scenes); y.Reshape(FEATURES-1,scenes); for(int i=0;i<scenes;i++) { X[0,i] = snapshots[0,i]; X[1,i] = snapshots[1,i]; X[2,i] = snapshots[2,i]; X[3,i] = snapshots[3,i]; X[4,i] = snapshots[4,i]; X[5,i] = snapshots[5,i]; X[6,i] = snapshots[6,i]; X[7,i] = snapshots[7,i]; X[8,i] = snapshots[8,i]; X[9,i] = snapshots[9,i]; X[10,i] = snapshots[10,i]; X[11,i] = snapshots[11,i]; y[0,i] = snapshots[1,i+1]; y[1,i] = snapshots[2,i+1]; y[2,i] = snapshots[3,i+1]; y[3,i] = snapshots[4,i+1]; y[4,i] = snapshots[5,i+1]; y[5,i] = snapshots[6,i+1]; y[6,i] = snapshots[7,i+1]; y[7,i] = snapshots[8,i+1]; y[8,i] = snapshots[9,i+1]; y[9,i] = snapshots[10,i+1]; y[10,i] = snapshots[11,i+1]; } //--- Find optimal solutions b_vector = y.MatMul(X.PInv()); Print("Day Number: ",scenes+1); Print("Snapshot"); Print(snapshots); Print("Input"); Print(X); Print("Target"); Print(y); Print("Coefficients"); Print(b_vector); Print("Prediciton"); Print(y.Col(scenes-1)); prediction = b_vector.MatMul(snapshots.Col(scenes-1)); if(prediction[4] > AccountInfoDouble(ACCOUNT_BALANCE)) permission = true; else if((account_state[0] == 1) && (prediction[6] > ma_h[0])) permission = true; else if((account_state[1] == 1) && (prediction[7] < ma_l[0])) permission = true; else permission = false; if(permission) { if(PositionsTotal() == 0) { if(account_state[0] == 1) Trade.Buy(TradeInfoHandler.MinVolume(),Symbol(),TradeInfoHandler.GetAsk(),(TradeInfoHandler.GetBid()-(atr[0]*2)),(TradeInfoHandler.GetBid()+(atr[0]*2)),""); else if(account_state[1] == 1) Trade.Sell(TradeInfoHandler.MinVolume(),Symbol(),TradeInfoHandler.GetBid(),(TradeInfoHandler.GetAsk()+(atr[0]*2)),(TradeInfoHandler.GetAsk()-(atr[0]*2)),""); } } Print("Current Balabnce: ",AccountInfoDouble(ACCOUNT_BALANCE)," Predicted Balance: ",prediction[4]," Permission: ",permission); } //+------------------------------------------------------------------+
Die Testdaten unserer Anwendung sind ein weiterer wichtiger Parameter, der bei allen Tests, die wir durchführen, gleich bleiben muss. In der vorangegangenen Diskussion haben wir unsere Anwendung vom 1. Januar 2020 bis zum Jahr 2025 einem Backtest unterzogen. Daher werden wir diese Daten für alle Prüfungen beibehalten.

Abbildung 3: Die Testdaten, die wir in der einleitenden Diskussion über Rückkopplungsregler verwendet haben
Nachfolgend finden Sie einen Screenshot der bisherigen Leistungsstufen, die vom Feedback-Controller ermittelt wurden. In unserer Eröffnungsdiskussion haben wir dem Leser diesen Screenshot zur Verfügung gestellt, um ihn mit dem Leistungsniveau zu vergleichen, das wir heute erreichen wollen.
In der Einleitung des Artikels haben wir bereits eine umfassende Zusammenfassung der wichtigsten Unterschiede zwischen den früher erreichten Leistungsniveaus und den jetzt angestrebten Leistungsniveaus gegeben. Der Screenshot ist beigefügt, damit der Leser auch die Freiheit hat, seine eigenen Abfragen zu machen.

Abbildung 4: Eine detaillierte Analyse der Leistungsniveaus, die unsere Benchmark während ihres 5-Jahres-Backtests erzielt hat
Die unten dargestellte Kapitalkurve hat in unserer Eröffnungsdiskussion ein vielversprechendes Potenzial aufgezeigt. Wie der Leser jedoch sehen wird, beschleunigte eines der heute vorgestellten Beispiele das Wachstum in einem wesentlich rentableren Tempo als in der Vergangenheit.

Abbildung 5: Die Kapitalkurve, die wir mit der ersten Version des Rückkopplungsreglers erzeugten, war für unsere Anforderungen bereits akzeptabel
Z-Score (statistische Standardtransformation)
Die z-Score-Transformation ist ein statistisches Standardverfahren, das im Allgemeinen als ein guter erster Schritt für jeden Datensatz angesehen wird. Das Ziel dieser Umwandlung ist es, die verschiedenen Maßstäbe und Dimensionen, die jede Spalte annehmen kann, sowie die Verhältnisse zwischen ihnen zu erhalten. Dadurch wird sichergestellt, dass Ihr Modell aussagekräftige und kohärente Wachstumsvergleiche anstellen kann. Ohne Berücksichtigung der Größenordnung könnte das Modell unverhältnismäßige Urteile über das Wachstum in jeder Säule und seine Auswirkungen auf das Ziel abgeben. Die z-Score-Transformation löst dieses Problem, indem sie den Mittelwert (den Durchschnittswert jeder Spalte) subtrahiert und dann durch die Standardabweichung dividiert. Infolgedessen endet jede Spalte mit einem Durchschnittswert von Null und einer Standardabweichung von Eins.
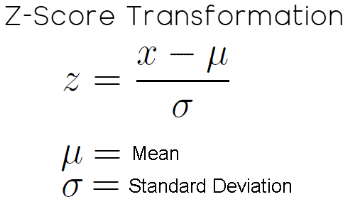
Abbildung 6: Die mathematische Formel für die statistische Z-Score-Transformation, die wir auf die Eingangsdaten unseres Rückkopplungsreglers angewendet haben, lautet
if(PositionsTotal() == 0) { //--- Find optimal solutions //--- Z-Score X = ((X - X.Mean())/X.Std()); b_vector = y.MatMul(X.PInv()); Print("Day Number: ",scenes+1); Print("Snapshot"); Print(snapshots); Print("Input"); Print(X); Print("Target"); Print(y); Print("Coefficients"); Print(b_vector); Print("Prediciton"); prediction = b_vector.MatMul(snapshots.Col(scenes-1)); Print("Expected Balance at next candle: ",prediction[4],". Expected Balance after 10 candles: ",prediction[8]);
Wie in der Einleitung unseres Artikels erwähnt, werden die von uns verwendeten Testdaten für alle Tests gleich bleiben. Wie in Abbildung 3 dargestellt, wird der Zeitraum vom 1. Januar 2020 bis zum Mai 2025 betrachtet.
Abbildung 7: Die oben angegebenen Backtest-Tage werden für alle Tests gleich gehalten
Wie bereits erwähnt, hat die Z-Score-Transformation nicht dazu beigetragen, unser Leistungsniveau über den 5-Jahres-Test zu verbessern. Tatsächlich wirkte sich dies auf unsere wichtigsten Leistungskennzahlen in allen Bereichen negativ aus.
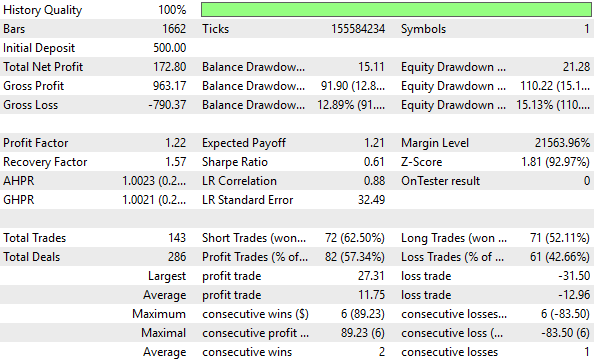
Abbildung 8: Eine detaillierte Analyse der durch die z-Score-Transformation ermittelten Leistungskennzahlen zeigt keine signifikanten Verbesserungen
Unser Kontrollsystem aus der vorangegangenen Diskussion ist profitabler als die unten dargestellte Kapitalkurve durch die von uns vorgenommene Transformation. Daraus lässt sich schließen, dass diese Umwandlung das in den Rohdaten vorhandene Signal zerstört hat.
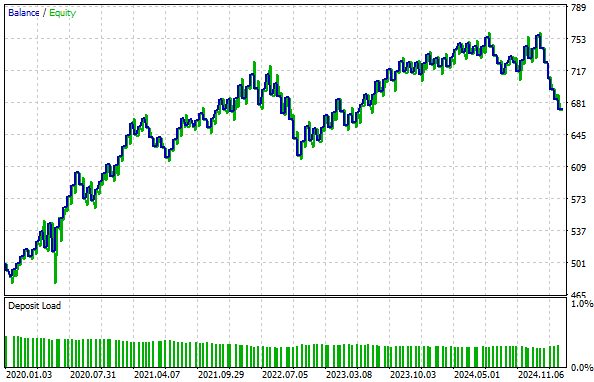
Abbildung 9: Die durch die z-Score-Transformation erzeugte Kapitalkurve konnte nicht höher ausfallen als die Kapitalkurve, die wir im Kontroll-Setup erzeugt hatten
Einheitsskalierung (Standardtransformation der linearen Algebra)
Die Idee der Einheitsskalierung stammt aus dem Bereich der linearen Algebra. Um dieses Konzept vollständig zu verstehen, ist ein wenig Kontext erforderlich, da wir es in unserer Diskussion nicht auf die übliche Weise anwenden. Daher ist es notwendig, eine kurze Einführung für Leser zu geben, die zum ersten Mal mit dieser Idee in Berührung kommen.
Wann immer wir eine Liste von Zahlen haben – denken Sie an ein einfaches Array in MQL5 mit, sagen wir, 10 Zahlen – gibt es viele Möglichkeiten, die Größe dieses Arrays zu messen. In der linearen Algebra wird diese Größe als die Norm eines Objekts bezeichnet. Dieses Objekt könnte ein Vektor oder eine Matrix sein, aber in diesem einfachen Beispiel werden wir nur ein Zahlenfeld betrachten. Von nun an werde ich die Begriffe „Array“ und „Vektor“ synonym verwenden, da sie sich beide auf dieselbe Idee beziehen.
Es gibt viele Möglichkeiten, die Größe eines Arrays zu definieren:
- Wir könnten sie daran messen, wie viele Elemente sie derzeit hat.
- Außerdem können wir sie daran messen, wie viele Elemente sie bei maximaler Kapazität aufnehmen kann.
- Um das Ganze zu verdeutlichen, könnte man auch erwägen, sie durch Summierung aller Werte ihrer aktuellen Elemente zu messen.
Um dies zu vermeiden, können wir vor der Summierung Transformationen durchführen. Wir könnten zum Beispiel den absoluten Wert jeder Zahl nehmen oder sie vor der Addition quadrieren. Diese verschiedenen Ansätze bilden eine Familie von Normen, die als Lp-Normen bekannt sind.
Eine wichtige Norm aus dieser Familie ist die L1-Norm, die einfach die Summe der absoluten Werte aller Elemente in der Matrix ist. Mathematisch wird dies in Abbildung 10 unten dargestellt.
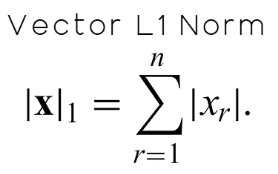
Abbildung 10: Definition der L1-Norm eines Vektors als die absolute Summe aller seiner Elemente.
Nachdem wir die L1-Norm berechnet haben, können wir jeden Wert in der Matrix durch diese Norm teilen. Dies wird in der linearen Algebra als Einheitsskalierung bezeichnet und ergibt einen normierten Vektor, dessen neue Norm gleich 1 ist. Das heißt, wenn man die Norm des Vektors noch einmal nimmt, ist das Ergebnis genau eins.
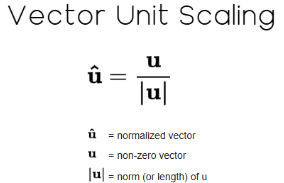
Abbildung 11: Die Einheitsskalierung eines Vektors ist eine Standardtransformation in der linearen Algebra.
Bei Vektoren ist das ganz einfach. Unser Fall ist jedoch etwas anders, da wir mit einer Matrix und nicht nur mit einem Vektor arbeiten. Erinnern Sie sich an den Anfang unserer Diskussion, dass unsere Datenmatrix, X, 12 Merkmale hat. In diesem Fall müssen wir die L1-Norm einer Matrix verwenden, die nicht dasselbe ist wie die L1-Norm eines Vektors, obwohl die beiden miteinander verwandt sind.
Nach der aktuellen MQL5-Dokumentation ist die L1-Norm der Matrix zum Zeitpunkt der Erstellung dieses Artikels wie folgt definiert: „MATRIX_NORM_P1 ist die maximale p1-Norm des Vektors unter den horizontalen Matrixvektoren.“
Auch wenn diese Definition präzise ist, mag sie sich zunächst nicht sehr intuitiv anfühlen, insbesondere für Leser, die sich zum ersten Mal mit diesem Thema beschäftigen. Daher kann ich die Dokumentation für den Leser in praktischere Anweisungen umschreiben, die damit beginnen, dass zunächst die L1-Norm für jede Zeile der Matrix berechnet wird. Anschließend ist die Zeile mit der größten L1-Norm zu ermitteln. Dieser größte Wert ist dann die L1-Norm der Matrix. Dies ist die Idee, die in der MQL5-Dokumentation definiert ist, und sie wird mathematisch durch die in Abbildung 12 unten dargestellte Notation definiert:
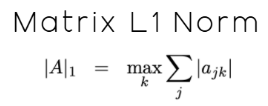
Abbildung 12: Die L1-Norm einer Matrix ist nicht dasselbe wie die L1-Norm eines Vektors, obwohl die beiden miteinander verwandt sind
Nach der Berechnung der L1-Norm wird schließlich jede Spalte des Datensatzes durch diesen Wert geteilt, wodurch eine Variante der Einheitsskalierung auf die Daten angewendet wird.
if(PositionsTotal() == 0) { //--- Find optimal solutions //--- We Must Take The Additional Steps Needed To Standardize & Scale Our Inputs X = X/X.Norm(MATRIX_NORM_P1); b_vector = y.MatMul(X.PInv()); Print("Day Number: ",scenes+1); Print("Snapshot"); Print(snapshots); Print("Input"); Print(X); Print("Target"); Print(y); Print("Coefficients"); Print(b_vector); Print("Prediciton"); prediction = b_vector.MatMul(snapshots.Col(scenes-1)); Print("Expected Balance at next candle: ",prediction[4],". Expected Balance after 10 candles: ",prediction[8]);
Wie wir bereits erwähnt haben, werden wir alle Backtest-Tage in allen Tests gleich halten, um faire Vergleiche zu gewährleisten.
Abbildung 13: Die Backtest-Tage, die wir für unsere Tests verwendet haben, sind für alle Beispiele gleich geblieben
Wie der Leser bereits weiß, hat die Skalierung der Einheiten unsere Leistung im Vergleich zum Benchmark erheblich verbessert und zu neuen Höhen geführt, die wir zuvor nicht erreicht hatten. Diese Umwandlung hat eindeutig mehr Signale in den Daten aufgedeckt und unserem Modell geholfen, aussagekräftigere Muster zu erkennen. Nicht jede Umstellung funktioniert auf diese Weise, aber wenn sie funktioniert, führt sie zu messbaren Verbesserungen – und messbare Verbesserungen sind die einzigen Verbesserungen, die wirklich zählen.
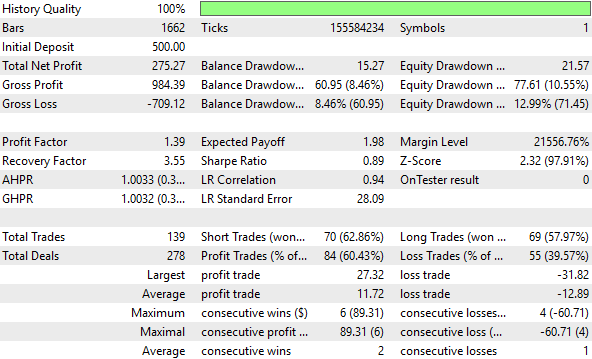
Abbildung 14: Eine detaillierte Analyse der von unserem verbesserten Rückkopplungsregler erreichten Leistungswerte
Wenn wir uns die erstellte Equity-Kurve ansehen, sehen wir, dass unsere Rentabilität jetzt Höchstwerte von 800 erreicht, die wir in unserem vorherigen Setup nicht erreichen konnten. Außerdem hat sich, wie in der Einleitung erwähnt, die Zeit, die unser Konto brauchte, um von 500 auf 700 zu wachsen, um fast ein Drittel verkürzt – eine bemerkenswerte Steigerung der Wachstumsgeschwindigkeit.
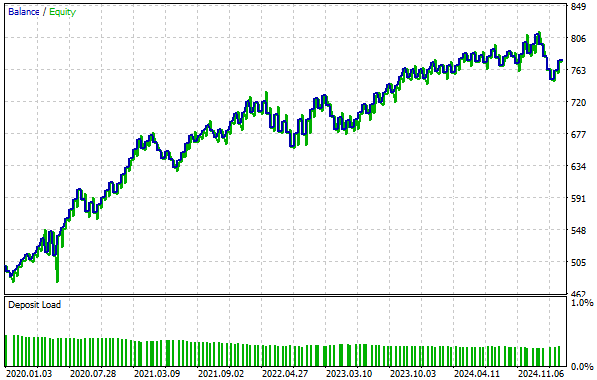
Abbildung 15: Die neue Kapitalkurve, die wir erstellt haben, steigt sogar noch schneller an als der alte Rückkopplungsregler, mit dem wir begonnen haben
Hybrider Ansatz (Einheitsskalierung & Z-Score)
An dieser Stelle des Artikels gibt es, wie wir in der Einleitung festgestellt haben, keine formalisierten Regeln für Transformationen. In diesem Bereich sind Brute-Force-Tests einigermaßen vertretbar, denn wir können kaum etwas anderes tun, als Ideen auszuprobieren und ihre Leistung zu beobachten. Mit dieser Intuition im Hinterkopf haben wir versucht, zwei Transformationen zu kombinieren, in der Hoffnung, ein noch wirkungsvolleres Ergebnis zu erzielen.
if(PositionsTotal() == 0) { //--- Find optimal solutions //--- We Must Take The Additional Steps Needed To Standardize & Scale Our Inputs X = X/X.Norm(MATRIX_NORM_P1); X = ((X-X.Mean())/X.Std()); b_vector = y.MatMul(X.PInv()); Print("Day Number: ",scenes+1); Print("Snapshot"); Print(snapshots); Print("Input"); Print(X); Print("Target"); Print(y); Print("Coefficients"); Print(b_vector); Print("Prediciton"); prediction = b_vector.MatMul(snapshots.Col(scenes-1)); Print("Expected Balance at next candle: ",prediction[4],". Expected Balance after 10 candles: ",prediction[8]);
Leider erwies sich dieser hybride Ansatz als weitgehend unrentabel. Obwohl es zunächst vielversprechend schien, wirkten sich die kombinierten Umstellungen negativ auf alle unsere wichtigsten Leistungskennzahlen aus.
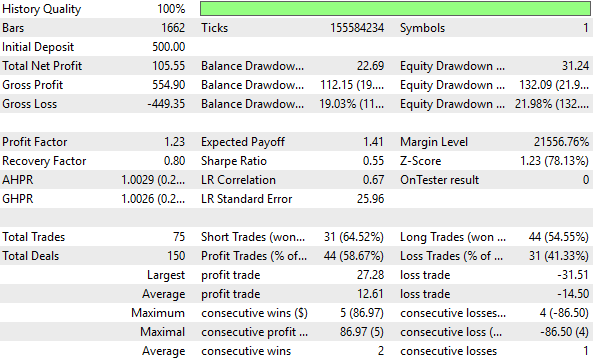
Abbildung 16: Unser hybrider Ansatz führte zu den schlechtesten Leistungswerten, die wir in diesem Test beobachtet haben
Der Gesamtanteil profitabler Handelsgeschäfte stieg zwar leicht an – von 57,24 % auf 58,67 % im hybriden Setup – dies ist jedoch keine signifikante Verbesserung. Darüber hinaus bleibt die von der Hybridstrategie erzeugte Kapitalkurve zwischen 500 und 600 stecken, sodass das Konto im Laufe der Zeit nicht wachsen kann. Daraus können wir schließen, dass diese Umwandlung das Signal in unseren Eingabedaten zerstört hat und keine wertvollen Beziehungen mehr zu unserem Modell herstellt.
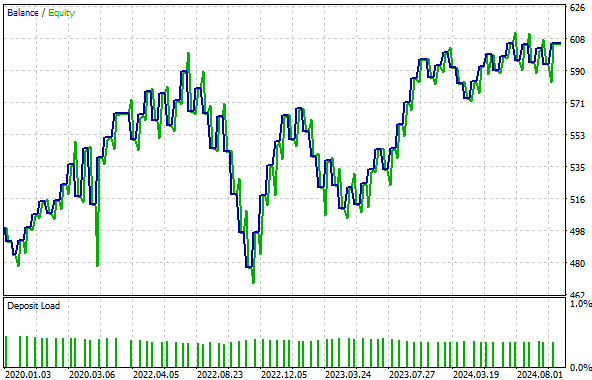
Abbildung 17: Die von uns ermittelte Kapitalkurve wächst nicht mehr, sondern scheint in einem unrentablen Modus zu verharren
Schlussfolgerung
Nach dieser Diskussion sollte der Leser mit einem neuen Verständnis für die Vorverarbeitung der Daten, mit denen wir unsere maschinellen Lernmodelle füttern, ausgestattet sein. Ich hoffe, dass der Leser diesen Schritt der Pipeline für maschinelles Lernen nun als einen hochwirksamen Tuning-Parameter ansieht – einen Parameter, der mit Sorgfalt und Ausdauer eingesetzt werden sollte, um wirklich Vorteile zu erzielen.
Es gibt viele Transformationen, die wir auf einen bestimmten Datensatz anwenden können, und leider wissen wir oft nicht, welche Transformation die beste ist, und wir können auch nicht immer feststellen, ob eine bestimmte Transformation hilfreich ist. Durch die Verwendung eines kontrollierten Rahmens – wie in diesem Artikel demonstriert – können wir jedoch, ausgehend von einem Benchmark-Leistungsniveau und dem konsequenten Testen von Ideen im Vergleich dazu, Strukturen und Muster aufdecken, die möglicherweise in den ursprünglichen Daten verborgen waren.
Daher ist es für den Leser auch wichtig, sich ständig so vielen Transformationen wie möglich auszusetzen, um verschiedene Ansätze zu testen und herauszufinden, was die Leistung wirklich verbessert.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/19382
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung des Price Action Analysis Toolkit (Teil 38): Tick Buffer VWAP und Short-Window Imbalance Engine
Entwicklung des Price Action Analysis Toolkit (Teil 38): Tick Buffer VWAP und Short-Window Imbalance Engine
 Aufbau eines Handelssystems (Teil 3): Bestimmung des Mindestrisikoniveaus für realistische Gewinnziele
Aufbau eines Handelssystems (Teil 3): Bestimmung des Mindestrisikoniveaus für realistische Gewinnziele
 Dynamic Mode Decomposition angewandt auf univariate Zeitreihen in MQL5
Dynamic Mode Decomposition angewandt auf univariate Zeitreihen in MQL5
 Vereinfachung von Datenbanken in MQL5 (Teil 1): Einführung in Datenbanken und SQL
Vereinfachung von Datenbanken in MQL5 (Teil 1): Einführung in Datenbanken und SQL
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.