Aufbau eines Handelssystems (Teil 2): Die Wissenschaft der Positionsbestimmung

Einführung

Die Positionsgröße ist eine der wichtigsten, aber häufig missverstandenen Komponenten des erfolgreichen Handels. Sie ist der Eckpfeiler des Risikomanagements und spielt eine entscheidende Rolle für die langfristige Tragfähigkeit eines jeden Handelssystems – insbesondere eines, das auf einer positiven Erwartungshaltung beruht.

In Teil 1 dieses Artikels haben wir erörtert, wie man ein Handelssystem mit positiver Erwartung aufbaut, indem man sich auf die Gewinnrate und das Rendite-zu-Risiko-Verhältnis (RRR) konzentriert. Außerdem haben wir anhand von Simulationen gezeigt, wie sich das Risiko von 1 % des Kontosaldos pro Handel unter verschiedenen Bedingungen verhält.

In diesem zweiten Teil gehen wir noch einen Schritt weiter und untersuchen, wie die Variation des prozentualen Risikos pro Handel die Leistung des Systems, das Drawdown-Profil und die emotionale Belastung des Händlers erheblich beeinflussen kann. Wir werden verschiedene Risikomodelle mit Hilfe der Monte-Carlo-Simulation untersuchen, um die Auswirkungen der Positionsgröße unter realistischen Marktszenarien zu veranschaulichen.

Professionelle Händler plädieren oft dafür, nur 1 bis 2 % des Kontosaldos pro Handel zu riskieren. Einige vertreten eine noch konservativere Haltung und empfehlen weniger als 1 %, insbesondere in Zeiten der Marktvolatilität oder Unsicherheit. Diese Richtlinien sind nicht willkürlich, sondern dienen dem Kapitalerhalt und dem Schutz der Händler vor den emotionalen und finanziellen Schäden, die durch Pechsträhnen entstehen können.

Es bleibt jedoch eine wichtige Frage offen: Handelt es sich bei diesen Empfehlungen um allgemeingültige Regeln, oder können Händler die Positionsgröße an ihre spezifische Kontogröße, ihre Ziele und ihre Risikobereitschaft anpassen? 

In diesem Artikel gehen wir dieser Frage auf den Grund, indem wir die Theorie mit quantitativen Daten kombinieren. Mithilfe von Monte-Carlo-Simulationen werden wir die Ergebnisse verschiedener Risikoniveaus analysieren, die Wahrscheinlichkeit von Kontoblows untersuchen und beurteilen, ob eine aggressivere Risikobereitschaft überhaupt sinnvoll ist. 

Am Ende dieses Artikels werden Sie besser gerüstet sein, um zu entscheiden, ob Sie die Regel von 1 % – 2 % befolgen oder auf intelligente Weise von ihr abweichen wollen.

Die Realität des Risikos bei verschiedenen Kontogrößen

Um die Dinge ins rechte Licht zu rücken, denken Sie an einen Händler, der ein Konto von 1 Million Dollar verwaltet. Ein Risiko von 1 % pro Handel würde bedeuten, dass Sie 10.000 $ auf eine einzige Position setzen. Vergleichen Sie das mit einem Händler mit einem 1.000-Dollar-Konto – 1 % entspricht nur 10 Dollar. Der Unterschied ist eindeutig.

Für einen Händler mit einem kleinen Konto ist es verlockender, einen größeren Prozentsatz – oder sogar das gesamte Konto – auf ein scheinbar hochwahrscheinliches (A-plus) Setup zu setzen. Die Logik lautet oft: „Wenn das funktioniert, könnte ich mein Konto schnell verdoppeln oder verdreifachen.“ Während die Vorteile verlockend erscheinen, können die Nachteile leider verheerend sein. Ein fehlgeschlagener Handel kann das Konto vollständig auslöschen, was nicht nur zu finanziellen Verlusten, sondern auch zu erheblichem emotionalen Leid führt.

Ist 1 % – 2 % eine universelle Regel?

Die Regel 1 % – 2 % dient eher als Leitlinie denn als feste Regel. Ihr Ziel ist es, die Kohärenz und den Kapitalerhalt zu fördern. Sie ist jedoch möglicherweise nicht für die Strategie, die Psychologie oder die finanzielle Situation eines jeden Händlers geeignet.

Aggressive Händler mit kleinen Konten könnten sich durch diese Regel eingeschränkt fühlen, vor allem, wenn ihr Ziel ein schnelles Wachstum ist. Aber ohne ein klares Verständnis der Wahrscheinlichkeiten, die hinter Verlusten und den damit verbundenen Drawdowns stehen, führt das Eingehen höherer Risiken oft eher zum Ruin als zur Belohnung.

Monte-Carlo-Simulation: Quantifizierung des Risikos

In diesem Artikel werden wir eine Monte-Carlo-Simulation entwickeln, um tiefer in das Thema Positionsgröße einzutauchen und Händlern zu helfen, ihre gewünschten Ergebnisse zu erzielen. Diese Simulation ermöglicht es uns, Hunderte oder Tausende von möglichen Handelsergebnissen zu modellieren, die auf der Gewinnrate, dem Risiko-Ertrags-Verhältnis und der Positionsgröße eines Systems basieren. 

Unser Ziel ist es, mit Hilfe von Wahrscheinlichkeitsrechnungen zu verstehen, ob ein Händler besser dran ist, wenn er sich an die Regel von einem Risiko zwischen 1 % – 2 % hält, oder ob er eine individuelle Risikostrategie entwickelt – ohne in ein emotionales oder psychologisches Burnout zu verfallen oder einen Totalverlust des Kontos zu erleben.

Bevor wir jedoch mit der eigentlichen Simulation beginnen, werden wir zunächst das Konzept der aufeinanderfolgenden Verluste bei unterschiedlichen Gewinnraten untersuchen und wie diese Streifen mit der Positionsgröße interagieren, um verschiedene Ebenen des Drawdowns zu erzeugen. Die Monte-Carlo-Simulation wird diese Szenarien zum Leben erwecken und einen datengestützten Einblick geben, wie selbst eine mathematisch fundierte Strategie bei schlechtem Risikomanagement scheitern kann.

Gewinnrate und die damit verbundenen aufeinanderfolgenden Niederlagen

Um die Auswirkungen der Positionsgröße auf verschiedene Handelsprofile zu demonstrieren, haben wir eine Reihe synthetischer Handelssysteme mit realistischen Kombinationen von Gewinnraten und Rendite-zu-Risiko-Verhältnis (RRR) erstellt, die die tatsächlichen Handelsbedingungen widerspiegeln. Jedes System wurde so konstruiert, dass es einen positiven Erwartungswert aufweist, d. h. die RRR übersteigt die Mindestschwelle, die für die Rentabilität bei der jeweiligen Gewinnrate erforderlich ist.

Eine detaillierte Aufschlüsselung der Berechnung der Mindest-RRR-Schwellenwerte für bestimmte Gewinnraten finden Sie in Teil 1 dieser Serie.

Nachfolgend finden Sie eine Zusammenfassung der in unserer Simulation verwendeten Handelssysteme:

Tabelle 1:

System	Gewinnrate %	RRR
1	30%	2.6
2	50%	1.7
3	65%	0.9
4	76%	0.6
5	83%	0.3

Zur visuellen Überprüfung der positiven Erwartungshaltung stellen wir für jedes Handelssystem Diagramme zur Verfügung, die zeigen, wie die jeweiligen Gewinnraten und Rendite-zu-Risiko-Verhältnisse im Laufe der Zeit einen statistisch profitablen Vorteil generieren. Diese Visualisierungen helfen dabei, die mathematische Solidität jedes Setups zu bestätigen, bevor wir in den Monte-Carlo-Simulationen Variationen der Positionsgrößen anwenden.

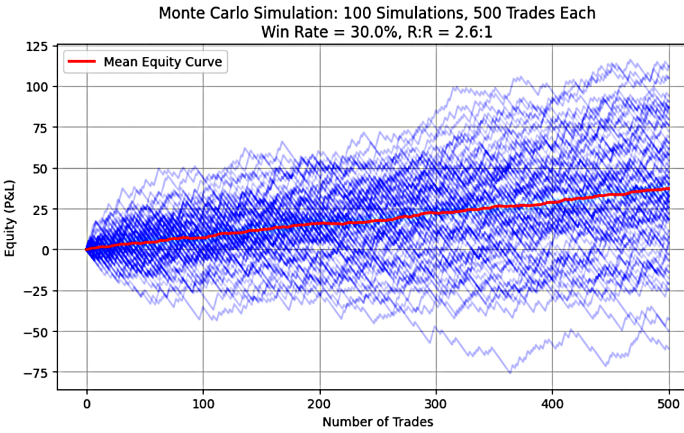
Abbildung 1: System 1(30%, 2.6)

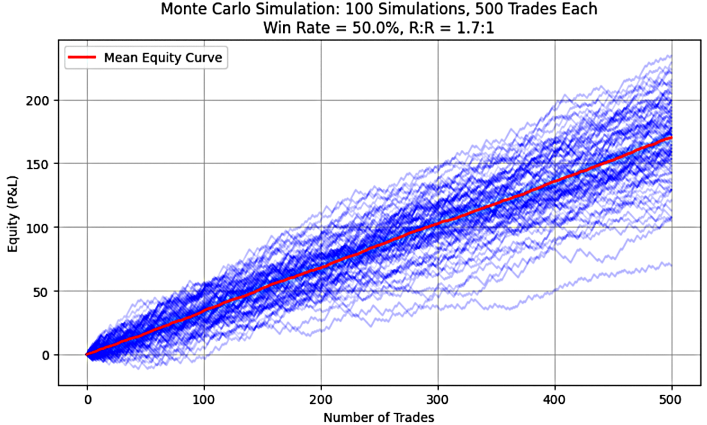
Abbildung 2: System 2(50%, 1.5)

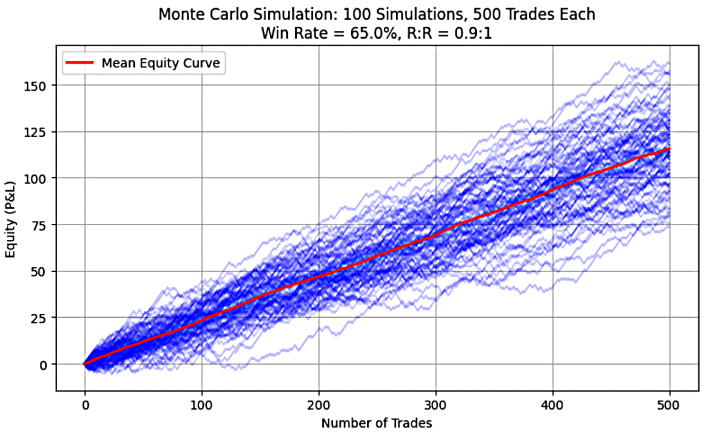
Abbildung 3: System 3(65%, 0,9)

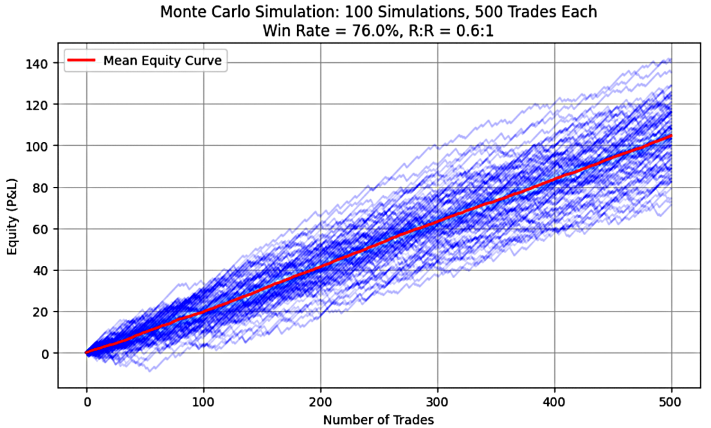
Abbildung 4: System 4(76%, 0,6)

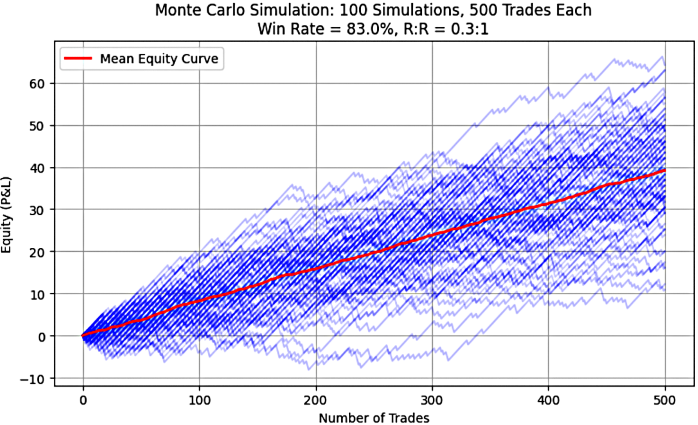
Abbildung 5: System 5(83%, 0.3)

Wie in den Abbildungen 1 bis 5 zu sehen ist, zeigt jedes Diagramm eine steigende oder nach oben geneigte Kurve des mittleren Aktienwerts, was das Vorhandensein einer positiven Erwartung in allen simulierten Handelssystemen visuell bestätigt. Der Python-Code, der zur Erstellung dieser Diagramme verwendet wird, ist in Teil 1 dieser Serie zu finden.

Das Unvermeidliche annehmen: Pechsträhnen in Handelssystemen

Obwohl alle Systeme eine positive Erwartungshaltung aufweisen, sind sie dennoch anfällig für aufeinanderfolgende Verlustphasen. Dies ist oft die emotional schwierigste Phase für Händler. In solchen Phasen beginnen viele an der Rentabilität des Systems zu zweifeln und geben es möglicherweise vorzeitig auf.

Wenn ein Händler jedoch das Potenzial für Verlustphasen auf der Grundlage der Gewinnrate des Systems versteht und vorhersieht, ist er besser in der Lage, diszipliniert zu bleiben, destruktive emotionale Entscheidungen zu vermeiden und das Risiko effektiv zu steuern. Mit der Zeit lernt ein Händler, der diese Realität akzeptiert, sich psychologisch mit den natürlichen Schwankungen des Systems zu arrangieren und erkennt, dass kein System immer gewinnt. So wie Pechsträhnen unvermeidlich sind, so gibt es auch Gewinnsträhnen.

Um diesen Aspekt zu quantifizieren, verwenden wir Monte-Carlo-Simulationen, um die Bandbreite möglicher aufeinanderfolgender Pechsträhnen für jede Gewinnrate zu schätzen. Dies hilft den Händlern, realistische Erwartungen zu setzen und emotionale Belastbarkeit aufzubauen. 

Abbildung 6 zeigt ein Boxplot, das die Verteilung der aufeinanderfolgenden Pechsträhnen über die verschiedenen Gewinnsatzsysteme nach 100 Simulationen mit jeweils 500 Handelsgeschäfte darstellt.

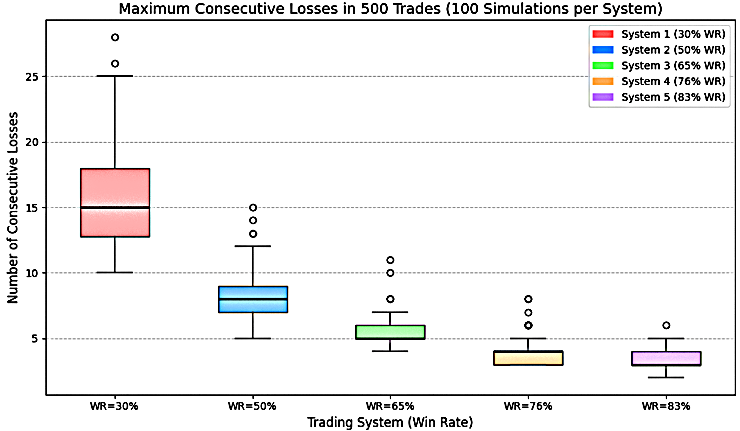
Abbildung 6: Gewinnrate vs. aufeinanderfolgenden Verluste

 Tabelle 2 zeigt das Minimum, den Median und das Maximum an aufeinanderfolgenden Verlusten für jede Gewinnrate, wie in Abbildung 6 dargestellt.

Die Gewinnrate des Systems	Minimum	Median	maximum
30%	10	15	28
50%	5	8	15
65%	4	5	11
76%	3	4	8
83%	2	3	6

Verstehen von Pechsträhnen: Leitfaden zur emotionalen Widerstandsfähigkeit eines Händlers

Das Verständnis der Wahrscheinlichkeit und des Ausmaßes aufeinanderfolgender Pechsträhnen ist für den Aufbau emotionaler Disziplin und eines effektiven Risikomanagements beim Handel unerlässlich. Selbst bei rentablen Systemen mit positiver Erwartungshaltung kann es zu längeren Perioden der Unterdeckung kommen. In diesem Abschnitt analysieren wir das Verhalten verschiedener Gewinnsatzsysteme: 30 %, 65 % und 83 % auf der Grundlage von Ergebnissen aus Monte-Carlo-Simulationen, wobei der Schwerpunkt darauf liegt, wie sich Händler psychologisch und strategisch auf den schlimmsten Fall vorbereiten können.

• System mit einer Gewinnrate von 30 %

Die statistischen Ergebnisse der Simulation zeigen, dass ein System mit einer Gewinnrate von 30 % mindestens 10, durchschnittlich 15 und maximal 28 aufeinanderfolgende Verlustgeschäfte aufweisen kann. Es ist von entscheidender Bedeutung, dass man sich mental auf solche lang anhaltenden Rückgänge vorbereitet. Ein Händler, der versteht, dass eine Pechsträhne von 28 Handelsgeschäfte im Bereich des Möglichen liegt, kann emotional geerdet bleiben und vermeiden, das System vorzeitig aufzugeben.

Wenn der Händler diese Realität akzeptiert, kann er ein minimales Risiko pro Handelsgeschäft eingehen, z. B. 1 % des Kontoguthabens, wodurch der mögliche Verlust im schlimmsten Fall auf maximal 28 % reduziert wird. Dies ist zwar ein beträchtlicher Verlust, aber für Händler, die auf die langfristige Rentabilität des Systems setzen, ist er möglicherweise verkraftbar. Wie in Abbildung 6 zu sehen ist, ist der Höchstwert von 28 ein Ausreißer, was bedeutet, dass es statistisch gesehen weniger wahrscheinlich, aber immer noch möglich ist.

Die Händler müssen ehrlich einschätzen, ob sie die emotionale Belastbarkeit und die Kapitaltoleranz haben, um solche tiefen Verlustphasen zu überstehen. Wenn nicht, ist ein System mit einer Gewinnrate von 30 % trotz seiner langfristigen Rentabilität möglicherweise nicht geeignet.

• System mit einer Gewinnrate von 65 %

Für ein System mit einer Gewinnrate von 65 % ergibt die Simulation ein Minimum von 4, einen Median von 5 und ein Maximum von 11 aufeinanderfolgenden Verlustgeschäften. Dieses Profil ist im Vergleich zu Systemen mit niedrigeren Gewinnraten nachsichtiger, birgt aber dennoch potenzielle emotionale Herausforderungen. Ein Händler, der 1 % pro Handel riskiert, könnte im schlimmsten Fall einen Verlust von bis zu 11 % erleiden. Dies ist zwar überschaubarer als das 30 %-System, erfordert aber immer noch psychologische Bereitschaft und angemessene Risikokontrollen, um in Abschwungphasen beständig zu bleiben.

Dieses System kann für Swing- oder Intraday-Händler interessant sein, die ausgewogene Setups und eine solide Gewinnrate mit moderater RRR bevorzugen. Wenn der Händler die Wahrscheinlichkeit von 11 aufeinanderfolgenden Verlusten versteht und akzeptiert, ist es weniger wahrscheinlich, dass er emotional reagiert oder das System aufgibt. Durch diszipliniertes Positionssizing bietet das System mit einer Gewinnrate von 65 % eine glattere Kapitalkurve und erzielt dennoch eine langfristige Rentabilität. Aus Abbildung 6 geht hervor, dass der maximale Verlust von 11 aufeinanderfolgenden Tagen weniger wahrscheinlich ist, da er außerhalb des Bereichs liegt.

• System mit einer Gewinnrate von 83 %

Ein System mit einer Gewinnrate von 83 % wird häufig mit Hochfrequenz- oder Scalping-Strategien in Verbindung gebracht, die auf kleine, konstante Gewinne abzielen. Nach der Simulation kann ein solches System mindestens 2, durchschnittlich 3 und maximal 6 aufeinanderfolgende Verlustgeschäfte aufweisen.

Da die Wahrscheinlichkeit längerer Pechsträhnen gering ist, könnten Händler versucht sein, ihr Risiko pro Handel z. B. auf 5 % zu erhöhen. Auch wenn dies angesichts der hohen Gewinnrate des Systems akzeptabel erscheint, ist es wichtig zu wissen, dass selbst eine Pechsträhne von 6 Handelsgeschäfte bei einem Risiko von 5 % zu einem Drawdown von 30 % führen kann, was einen erheblichen Verlust für das Handelskonto bedeutet.

Um dies in den Griff zu bekommen, müssen die Händler realistische Erwartungen haben und übermäßiges Vertrauen vermeiden. Die Akzeptanz, dass gelegentliche Pechsträhnen vorkommen, selbst bei Systemen mit hoher Wahrscheinlichkeit, kann helfen, emotionale Zusammenbrüche und impulsive Entscheidungen zu vermeiden. Der Aufbau von Widerstandsfähigkeit in Bezug auf diese Zahlen ist für den langfristigen Erfolg entscheidend. Die 6 aufeinanderfolgenden Niederlagen sind weniger wahrscheinlich, da sie außerhalb des Bereichs liegen. Der Python-Code zur Generierung möglicher aufeinanderfolgender Verluste ist diesem Artikel beigefügt.

Die Verwendung des Codes:

Um alternative Ergebnisse zu bewerten, ändern Sie die Parameterwerte im folgenden Abschnitt. Dies ermöglicht ein flexibles Testen unter verschiedenen Bedingungen, wobei der zugrunde liegende analytische Rahmen erhalten bleibt.

import numpy as np
import matplotlib.pyplot as plt

# Systems data: win rates and RRR
win_rates = [0.30, 0.50, 0.65, 0.76, 0.83]
rrrs = [2.6, 1.7, 0.9, 0.6, 0.3]
num_systems = len(win_rates)
num_simulations = 100
num_trades = 500

# Initialize results storage
all_max_consecutive_losses = []

Initialisierung von Variablen und Werten für die Berechnung.

Positionsgröße und die damit verbundenen Drawdowns

Die Positionsgröße spielt eine entscheidende Rolle für die Handelsperformance, insbesondere bei Verlustphasen. Die grundlegende Formel für die Positionsgrößenbestimmung lautet:

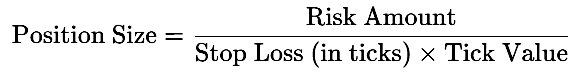
Der Risikobetrag kann entweder als fest (statisch) oder dynamisch (variabel) kategorisiert werden. In diesem Abschnitt untersuchen wir, wie jeder Ansatz die Drawdowns während aufeinanderfolgender Verlustphasen beeinflusst.

Definieren wir:

fraction of Risk% as f,
previous balance as balance j-1,
current balance as balance j
initial balance as balance i
win-rate as P

Die Risikobeträge sind für jeden Fall wie folgt definiert:

Dynamic Risk Amount = Risk% x balance j-1 = f x balance j-1

Fixed Risk Amount = f x balance i

Fall 1: Dynamisches Risiko (Risiko in % des aktuellen Saldos)

Bei diesem Modell wird der Risikobetrag für jeden Handel auf der Grundlage des letzten Kontostands neu berechnet. Dies ermöglicht eine Aufzinsung während Gewinnphasen und einen beschleunigten Rückgang während Drawdowns.

Bei jedem Handel j:

• Wenn das Handelsgeschäft einen Gewinn erzielt:

• Wenn das Handelsgeschäft einen Verlust erzielt:

Kombiniert man beide Ergebnisse probabilistisch, erhält man:

Fall 2: Festes Risiko (Risiko in % des Anfangssaldos)

Bei diesem Modell bleibt der Risikobetrag bei allen Geschäften konstant, unabhängig von der Performance des Kontos. Dies führt zu einem stetigen Wachstum unter günstigen Bedingungen und zu gleichmäßigen Rückgängen in Verlustphasen.

• Wenn das Handelsgeschäft einen Gewinn erzielt:

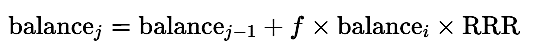
• Wenn das Handelsgeschäft einen Verlust erzielt:

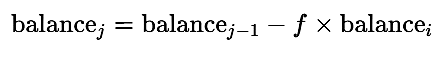
Zusammengenommen ergibt dies:

Ansatz der Simulation

Die Gleichungen (1) und (2) werden in Monte-Carlo-Simulationen umgesetzt, um ein breites Spektrum möglicher Ergebnisse für Kontostand und Drawdown bei jeder Positionsgrößenstrategie zu erzeugen. Durch den Vergleich der Ergebnisse können die Händler besser verstehen, wie sich ein dynamisches gegenüber einem festen Risiko auf das Aktienwachstum, die Volatilität und die Überlebensfähigkeit desHandelssystems auswirkt.

Die beigefügten Charts zeigen die einzelnen Simulationsergebnisse für jedes untersuchte Handelssystem. Jedes System wurde anhand von drei Risikoparametern bewertet: 1 %, 2 % und 5 % des aktuellen Kontosaldos oder des ursprünglichen Kontosaldos. Auf den ersten Blick erscheinen die Kapitalkurven für diesen einzelnen Testlauf sehr vielversprechend – ähnlich wie die Aufregung, die wir empfinden, wenn das Backtesting über einen bestimmten Zeitraum starke Ergebnisse liefert und uns dazu verleitet, zum Live-Handel überzugehen. 

Um die Robustheit und das langfristige Potenzial dieser Systeme zu bewerten, haben wir unsere Analyse durch die Durchführung von 500 Monte-Carlo-Simulationen erweitert, die jeweils aus 1.000 Handelsgeschäften bestehen. Dieser breitere Ansatz ermöglicht es uns, ein breites Spektrum möglicher Aktienkursentwicklungen zu untersuchen und die damit verbundenen Schwankungen und Risiken besser zu verstehen.

Die Simulation wurde für mehrere Systemkonfigurationen wiederholt, darunter:

• Gewinnrate: 30%, RRR: 2.6
• Gewinnrate: 65%, RRR: 0.9
• Gewinnrate: 83%, RRR: 0.3

Indem wir die ausgewählten Handelssysteme unter verschiedenen Risikoniveaus von 1 %, 2 % und 5 % des Kontokapitals bewerten, können wir feststellen, ob es machbar ist, die von professionellen Händlern empfohlenen Risikogrenzen zu überschreiten. Diese spezifischen Risikoniveaus dienen als Maßstab für die Bewertung der Widerstandsfähigkeit und Rentabilität verschiedener Strategien sowohl bei konservativen als auch bei aggressiven Risikopositionen.

Die gewählten Konfigurationen, die in Bezug auf Gewinnrate und RRR variieren, repräsentieren ein Spektrum von Handelsstrategien, das von Setups mit hohem Risiko und hoher Rendite bis zu konservativeren Ansätzen mit hoher Wahrscheinlichkeit reicht. Dies ermöglicht eine gründliche Bewertung der Leistung bei unterschiedlichen Risikoprofilen.

Darüber hinaus werden Forscher und Händler ermutigt, andere Gewinnraten-Szenarien zu erforschen, wie z.B. 50%, 76% oder jede andere Konfiguration von Interesse, um tiefere Einblicke in potenzielle Leistungsergebnisse und Systemstabilität unter verschiedenen Bedingungen zu gewinnen.

Überblick über die Simulationsergebnisse

System 1: Gewinnrate = 30%, RRR = 2,6

Die Abbildungen 7 bis 9 zeigen die Kapitalkurve der Handelsgeschäfte, die mit einem Risikoniveau von 1 %, 2 % und 5 % abgeschlossen wurden. Die beigefügte Tabelle zeigt die aggregierten Ergebnisse von 500 Monte-Carlo-Simulationen, die jeweils 1.000 Handelsgeschäfte mit dem jeweiligen Risikoparameter umfassen. Dieser umfassende Simulationsansatz liefert statistisch signifikante Erkenntnisse über die Leistungsmerkmale des Systems unter kontrollierten Risikobedingungen.

• 1 % Risikoniveau

 

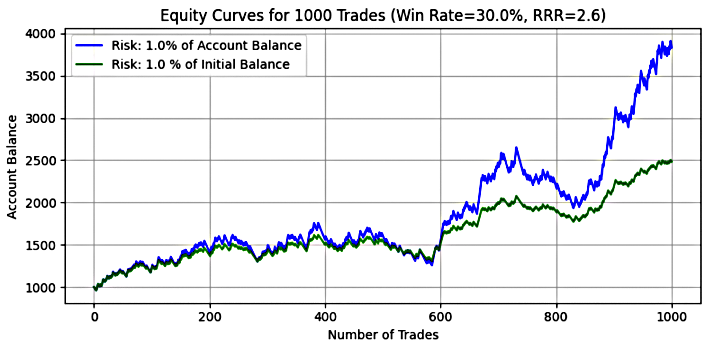
Abbildung 7

Tabelle 2: Monte-Carlo-Simulationsergebnisse für ein System mit Gewinnrate=30%, RRR=2,6, 1% Risiko

Metriken	Dynamisch (1% des aktuellen Saldos)	Fest (1% des Anfangssaldos)
Mittlerer Endsaldo	$2,143.81	$1,778.62
Median Endsaldo	$1,876.43	$1,764.00
Kleinster Endsaldo	$326.01	$0.00
Höchster Endsaldo	$7,831.03	$3,204.00
Mittlerer Drawdown	$649.40	$398.98
Median Drawdown	$584.29	$363.00
Maximaler Drawdown	$1,980.21	$1,278.00
Mittlerer maximaler Drawdown (%)	33.72%	28.47%
Median Max Drawdown (%)	32.02%	25.72%
Maximaler Drawdown (%)	74.91%	114.11%

Wichtige Erkenntnis:

Bei einem Risiko von 1 % weisen die mittleren und mittleren Endsalden auf ein positives Ergebnis hin, was mit der positiven Erwartung des Systems übereinstimmt. Die Kapitalrendite beträgt bei beiden Risikomodellen etwa das Doppelte des ursprünglichen Eigenkapitals, wobei das dynamische Risiko insgesamt eine etwas höhere Rendite erzielt.

In einigen Simulationen führte das dynamische Risiko zu einem maximalen Saldo von etwa dem 8-fachen des Anfangskapitals, verglichen mit dem 3-fachen des festen Risikos. Dies zeigt die Fähigkeit des dynamischen Risikos, Gewinne in Gewinnphasen noch aggressiver zu steigern. Der Preis für eine höhere Rendite ist jedoch eine höhere Volatilität. Der mittlere und der Medianwert des Drawdowns waren beim dynamischen Risiko größer als beim festen Risiko, und während der maximale Drawdown beim dynamischen Risiko etwa 75 % erreichte, kam es beim Modell mit festem Risiko in einigen Fällenzu einem vollständigen Ausbluten des Kontos – mit einem Drawdown von über 114 %, was zu negative Kontostände führt. 

Die Daten zeigen einen klaren Überlebensvorteil für die dynamische Risikodimensionierung (1 % des aktuellen Guthabens) gegenüber dem festen Risiko (1 % des Anfangssaldos) unter ungünstigen Bedingungen.

• 2 % Risikoniveau

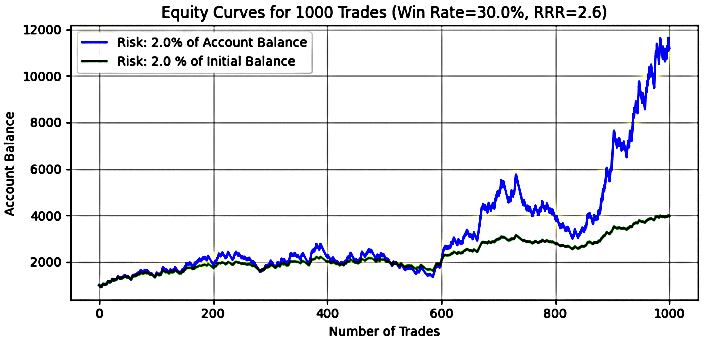
Abbildung 8

Tabelle 3: Monte-Carlo-Simulationsergebnisse für ein System mit Gewinnrate=30%, RRR=2,6, 2% Risiko

Metriken	Dynamisch (2% des aktuellen Saldos)	Fix (2% des Anfangssaldos)
Mittlerer Endsaldo	$4,418.38	$2,557.23
Median Endsaldo	$2,705.11	$2,528.00
Kleinster Endsaldo	$83.85	$-1,000.00
Höchster Endsaldo	$46,107.53	$5,408.00
Mittlerer Drawdown	$2,387.05	$797.95
Median Drawdown	$1,613.94	$726.00
Maximaler Drawdown	$22,972.93	$2,556.00
Mittlerer maximaler Drawdown (%)	57.14%	47.67%
Median Max Drawdown (%)	55.95%	41.85%
Maximaler Drawdown (%)	94.87%	212.80%

Wichtige Erkenntnis:

Bei einem Risiko von 2 % spiegelt das System erneut eine positive Erwartung wider, allerdings mit erhöhter Volatilität und Divergenz zwischen dynamischen und festen Ergebnissen. Der durchschnittliche Endsaldo bei dynamischem Risiko betrug 4.418,38 $ und war damit deutlich höher als die 2.557,23 $ bei festem Risiko. Allerdings war der Median des Endsaldos beim dynamischen Risiko höher als beim festen Risiko, was darauf hindeutet, dass die Kapitalkurve im Vergleich zum festen Risiko nicht stabil ist.

In einigen der Simulationen führte das dynamische Risiko zu einem maximalen Kontowachstum von über dem 46-fachen des Anfangssaldos, während das feste Risiko bei etwa dem 5,4-fachen lag. Dies verdeutlicht das explosive Aufwärtspotenzial des dynamischen Risikos, wenn die Bedingungen günstig sind.

Auf der anderen Seite waren die Rückgänge deutlich stärker. Der Durchschnitt/Median des Drawdowns liegt bei 57%/56%. Einige der Simulationsergebnisse des dynamischen Risikos sahen maximale Ausfälle von fast 95 %, verglichen mit 213 % beim festen Risiko – was nicht nur auf einen vollständigen Kapitalverlust, sondern auch auf eine Verschuldung in extremen Szenarien hindeutet. Ein solches Maß an Volatilität wäre für die meisten Händler ohne strenge Kontrollmechanismen emotional und finanziell nicht tragbar.

• 5% Risikoniveau

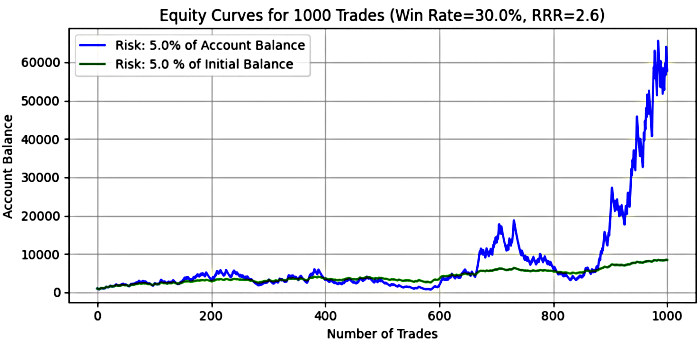
Abbildung 9

Tabelle 4: Monte-Carlo-Simulationsergebnisse für ein System mit Gewinnrate=30%, RRR=2,6, 5% Risiko

Metriken	Dynamisch (5% des aktuellen Saldos)	Fest (5% des Anfangssaldos)
Mittlerer Endsaldo	$25,741.66	$4,893.08
Median Endsaldo	$1,797.64	$4,820.00
Kleinster Endsaldo	$0.37	$-4,000.00
Höchster Endsaldo	$1,857,357.21	$12,020.00
Mittlerer Drawdown	$41,836.96	$1,994.88
Median Drawdown	$5,488.64	$1,815.00
Maximaler Drawdown	$4,836,685.44	$6,390.00
Mittlerer maximaler Drawdown (%)	90.30%	88.15%
Median Max Drawdown (%)	92.07%	72.69%
Maximaler Drawdown (%)	99.99%	532.00%

Wichtige Erkenntnis:

Bei einem Risiko von 5 % zeichnet die Simulation ein Bild von extremer Risiko-Ertrags-Asymmetrie. Der durchschnittliche Endsaldo bei dynamischem Risiko lag bei beeindruckenden 25.741,66 $, verglichen mit 4.893,08 $ bei festem Risiko. Der Median des Endguthabens bei dynamischem Risiko betrug jedoch nur 1.797,64 $, was darauf hindeutet, dass die meisten Simulationen Geld verloren oder kaum überlebt haben, obwohl der hohe Durchschnitt durch einige Ausreißer verzerrt wurde. Der Median für das feste Risiko entsprach in etwa dem mittleren Endsaldo, was darauf schließen lässt, dass die Investitionserträge besser vorhersehbar und beständiger sind, wenn auch nicht unbedingt ertragreich.

In einigen Fällen erreichte das dynamische Risiko einen schwindelerregenden maximalen Endsaldo von mehr als dem 1,857-fachen des Anfangskapitals, was seltene, aber starke Aufzinsungs-Ergebnisse widerspiegelt. Das feste Risiko erreichte seinen Höchststand bei etwa 12x. Dieses Plus war jedoch mit enormen Drawdowns verbunden – der mittlere Drawdown lag beim dynamischen Risiko bei über 92 %, und der maximale Drawdown näherte sich mit 99,99 % dem Totalverlust.

Bei den festen Risiken stieg der maximale Verlust in einigen Fällen auf 532 %, was wiederum auf eine vollständige Zerstörung des Kontos im schlimmsten Fall hindeutet. Das Ertragspotenzial ist zwar gewaltig, aber auch das Risiko – was verdeutlicht, warum eine Positionsgröße von 5 % bei solchen Systemen oft als leichtsinnig angesehen wird, selbst wenn die Erwartung mathematisch positiv ist.

Empfohlenes Risikoniveau für eine Gewinnrate von 30%, RRR = 2,6 System

Zusammenfassend lässt sich sagen, dass für ein Handelssystem mit einer Gewinnrate von 30 % und einem Rendite-zu-Risiko-Verhältnis von 2,6 die Simulationsergebnisse darauf hindeuten, dass das Risiko von 1 % bis 2 % des Kontosaldos der ausgewogenste und nachhaltigste Ansatz ist. Diese Spanne bietet ein gutes Renditepotenzial an günstigen Handelstagen und hält gleichzeitig den mittleren und medianen Drawdown unter 60 %, sodass das Kapital überlebensfähig bleibt.

Andererseits bietet das Risiko von 1 % bis 5 % des anfänglichen Guthabens stabilere und vorhersehbare Ergebnisse – besonders nützlich für Händler, die Beständigkeit suchen. Allerdings ist dieser Ansatz bei längeren Drawdowns immer noch anfällig für einen Totalverlust des Kontos, insbesondere bei höheren Risikoniveaus.

Ein Risiko von 5 % bei einem der beiden Modelle (fest oder dynamisch) sollte generell vermieden werden, es sei denn, der Händler ist sich der Risiken voll bewusst und bereit, das Konto als ein Spiel mit hohem Einsatz zu betrachten. Auch wenn der Aufwärtstrend explosiv sein kann, ist die Wahrscheinlichkeit, dass das Konto explodiert, extrem hoch. In solchen Fällen muss der Händler psychologisch und finanziell darauf vorbereitet sein, jedes Ergebnis zu akzeptieren, auch den vollständigen Verlust des Kapitals.

System 2: Gewinnrate = 65%, RRR = 0,9

Die Abbildungen 10 bis 12 zeigen die Equity-Kurve für Handelsgeschäfte mit einem Risikoniveau von 1%, 2% und 5%. Die nachstehende Tabelle fasst die aggregierten Ergebnisse von 500 Monte-Carlo-Simulationen zusammen, wobei jede Simulation 1.000 Abschlüsse unter bestimmten Risikoparametern durchführt. Dieser umfassende Simulationsrahmen gewährleistet eine statistisch robuste Analyse, die wertvolle Einblicke in die Leistung des Systems unter kontrollierten Risikobedingungen bietet.

• 1 % Risikoniveau

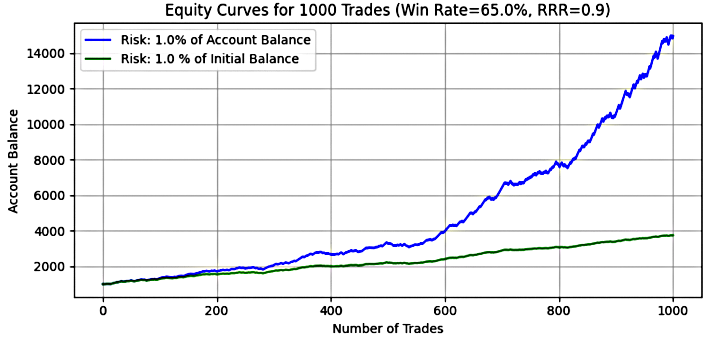
Abbildung 10

Tabelle 5: Monte-Carlo-Simulationsergebnisse für ein System mit Gewinnrate=65%, RRR=0,9, 1% Risiko

Metriken	Dynamisch (1% des aktuellen Saldos)	Fest (1% des Anfangssaldos)
Mittlerer Endsaldo	$10,408.50	$3,348.14
Median Endsaldo	$9,941.86	$3,340.50
Kleinster Endsaldo	$3,879.52	$2,400.00
Höchster Endsaldo	$20,668.22	$4,072.00
Mittlerer Drawdown	$571.54	$92.96
Median Drawdown	$534.55	$88.00
Maximaler Drawdown	$1,567.38	$208.00
Mittlerer maximaler Drawdown (%)	8.98%	5.65%
Median Max Drawdown (%)	8.61%	5.37%
Maximaler Drawdown (%)	18.99%	16.07%

Wichtige Erkenntnis:

Bei einem Risiko von 1 % zeigt die Simulation ein exponentielles Wachstum für das dynamische Risikomodell, während das Modell mit festem Risiko ein linearesund stabiles Wachstum aufweist. Der durchschnittliche Endsaldo für das dynamische Risiko erreichte das 10-fache des Anfangskapitals, während das feste Risiko etwa das 3-fache einbrachte. Die Mediane der Endsalden beider Modelle liegen sehr nahe an ihren jeweiligen Mittelwerten, was auf eine symmetrische Leistung und eine geringe Schiefe in der Verteilung hindeutet.

Bei keinem der simulierten Läufe kam es zu einem vollständigen Blowout, was darauf hindeutet, dass das System bei diesem Risikoniveau robust und nachhaltig ist. Der maximale Drawdown für das dynamische Risiko lag bei etwa 19 %, während das feste Risiko bei etwa 16 % lag. Der mittlere und der mediane Prozentsatz des Drawdowns war bei dem Modell mit festem Risiko niedriger, was auf eine glattere Kapitalkurve mit geringerer Volatilität hindeutet.

Einige Simulationen mit dynamischem Risiko erreichten ein maximales Endsaldo vom 20-fachen des Anfangskapitals, während das feste Risiko einen Spitzenwert von etwa dem 4-fachen erreichte, was den Aufzinsungsvorteil der dynamischen Positionsdimensionierung unterstreicht.

• 2 % Risikoniveau

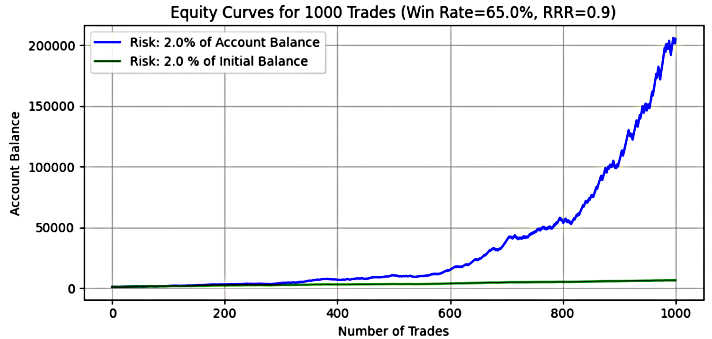
Abbildung 11

Tabelle 6: Monte-Carlo-Simulationsergebnisse für ein System mit Gewinnrate=65%, RRR=0,9, 2% Risiko

Metriken	Dynamisch (2% des aktuellen Saldos)	Fix (2% des Anfangssaldos)
Mittlerer Endsaldo	$107,088.02	$5,696.28
Median Endsaldo	$90,573.24	$5,681.00
Kleinster Endsaldo	$13,775.17	$3,800.00
Höchster Endsaldo	$391,748.08	$7,144.00
Mittlerer Drawdown	$9,787.36	$185.92
Median Drawdown	$8,491.57	$176.00
Maximaler Drawdown	$39,558.61	$416.00
Mittlerer maximaler Drawdown (%)	17.33%	9.48%
Median Max Drawdown (%)	16.71%	8.79%
Maximaler Drawdown (%)	34.71%	31.14%

Wichtige Erkenntnis:

Bei einem Risiko von 2 % zeigt das dynamische Risiko einen deutlichen Sprung im Wachstumspotenzial mit einem durchschnittlichen Endsaldo von über 107.000 $ – das ist das 107-fache des Anfangskapitals. Der Medianwert von etwa 90.573 $ bestätigt ebenfalls ein starkes, stetiges Wachstum. Das feste Risiko führte zu einem mittleren Endsaldo von 5.696 $, also fast dem 6-fachen des Anfangskapitals, und der Median entsprach genau diesem Wert, was auf konsistente und vorhersehbare Ergebnisse hindeutet.

Der maximale Endsaldo bei dynamischem Risiko explodierte auf über 391.000 $, während bei festem Risiko der Höchstbetrag bei nur 7.144 $ lag. Dies unterstreicht das enorme Aufwärtspotenzial des dynamischen Risikos während längerer Gewinnserien.

Auf der anderen Seite stieg der maximale Drawdown beim dynamischen Risiko auf 34,71 %, während das feste Risiko mit 31,14 % relativ kontrolliert blieb. Der mittlere und der mediane Prozentsatz des Drawdowns folgten ebenfalls diesem Muster – das dynamischeRisiko war höher, was ein größeres Volatilitätsrisiko widerspiegelt, während das feste Risiko stabiler, aber weniger lohnend war.

• 5% Risikoniveau

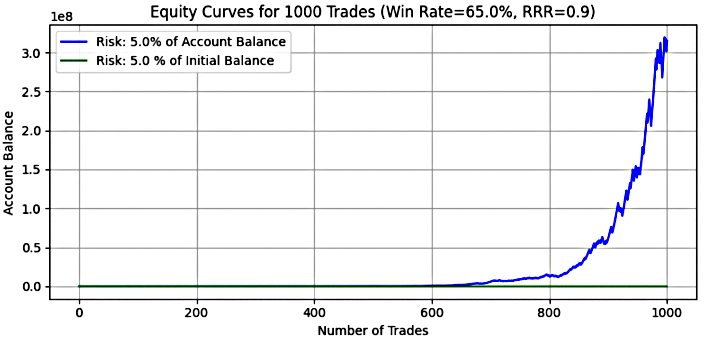
Abbildung 12

Tabelle 7: Monte-Carlo-Simulationsergebnisse für ein System mit Gewinnrate=65%, RRR=0,9, 5% Risiko

Metriken	Dynamisch (5% des aktuellen Saldos)	Fest (5% des Anfangssaldos)
Mittlerer Endsaldo	$106,016,246.65	$12,740.69
Median Endsaldo	$40,611,334.02	$12,702.50
Kleinster Endsaldo	$362,423.53	$8,000.00
Höchster Endsaldo	$1,591,375,537.03	$16,360.00
Mittlerer Drawdown	$18,402,293.20	$464.79
Median Drawdown	$7,730,838.44	$440.00
Maximaler Drawdown	$268,258,572.26	$1,040.00
Mittlerer maximaler Drawdown (%)	38.94%	18.20%
Median Max Drawdown (%)	38.28%	16.16%
Maximaler Drawdown (%)	66.90%	71.24%

Wichtige Erkenntnis:

Bei einem Risiko von 5 % verwandelte sich das dynamische Risiko in eine hochriskante Zinseszinsen-Maschine mit einem astronomischen mittleren Endsaldo von über 106 Millionen Dollar und einem Median von 40 Millionen Dollar. Der maximale Saldo in einer einzigen Simulation erreichte 1,59 Milliarden Dollar, was zeigt, wie die Aufzinsung bei einem starken System außergewöhnliche Ergebnisse hervorbringen kann.

Allerdings geht dieses explosive Wachstum mit extremer Volatilität einher. Der durchschnittliche Verlust lag bei über 18 Mio. $, der maximale Verlust bei über 268 Mio. $, wobei die Verlustquoten zwischen 38 % und 67 % lagen – Werte, die für die meisten Händler ohne strenge Disziplin und Risikopuffer emotional und finanziell untragbar wären.

Das feste Risiko wurde dagegen viel besser kontrolliert. Der Mittelwert und der Median der Endsalden lagen bei etwa 12.700 $, wobei der maximale Saldo bei 16.360 $ lag – etwa das 16-fache des Anfangskapitals. Dieser Ansatz ist zwar im Vergleich bescheiden, bietet aber eine größere Konsistenz, da die maximalen Drawdowns auf 71 % begrenzt sind, und ein realistischeres Volatilitätsniveau für eine langfristige Nachhaltigkeit.

Empfohlene Risikoniveaus für System 3 (65% Gewinnrate, RRR = 0,9)

Auf der Grundlage von Simulationsdaten bietet ein Risiko von 1 bis 2 % des aktuellen Saldos das beste Gleichgewicht zwischen Wachstum und Kapitalschutz. Das dynamische Risiko ermöglicht aufgrund des Zinseszinseffekts einen größeren Wertzuwachs, während das feste Risiko ein gleichmäßigeres, besser vorhersehbares Renditeprofil bietet.

Bei einem Risiko von 5 % kann ein dynamisches Risiko außergewöhnliche Renditen erzielen, allerdings mit so großen Drawdowns, dass es für die meisten Händler ungeeignet ist, es sei denn, sie sind bereit, extreme Volatilität und Kontofluktuationen in Kauf zu nehmen. Das feste Risiko von 5 % schneidet recht gut ab, allerdings mit einem geringeren Aufwärtspotenzial.

In der Praxis wird für dieses System ein dynamisches Risiko von 1 % bis 2 % empfohlen, insbesondere für Händler, die ihr Kapital erhalten und stetig wachsen wollen, ohne unerträglichen emotionalen und finanziellen Schwankungen ausgesetzt zu sein.

Für einige Händler könnte das Risiko von 5 % des anfänglichen Guthabens eine bevorzugte Strategie für dieses System sein, da der mittlere und mediane Drawdown-Prozentsatz niedrig ist und die mittlere Endrendite etwa das 12-fache des anfänglichen Kapitals beträgt, was sowohl beeindruckend als auch statistisch besser vorhersehbar ist. Der maximale Drawdown von 71 % bleibt zwar möglich, wird aber im Rahmen der Simulationen als ein Ereignis mit geringer Wahrscheinlichkeit angesehen, sodass dieser Ansatz für Händler akzeptabel ist, die ein moderates Risiko im Austausch für ein stabiles Wachstumspotenzial tolerieren können.

System 3: Gewinnrate = 83%, RRR = 0,3

Bei diesem System handelt es sich um ein Modell mit hoher Wahrscheinlichkeit und geringer Rendite, das häufig bei Scalping-Strategien oder Systemen mit häufigen kleinen Gewinnen verwendet wird.

In den Abbildungen 13 bis 15 ist die Kapitalkurve für Handelsgeschäfte mit einem Risikoniveau von 1 %, 2 % und 5 % dargestellt. Die nachstehende Tabelle fasst die aggregierten Ergebnisse von 500 Monte-Carlo-Simulationen zusammen, wobei jede Simulation 1.000 Abschlüsse unter bestimmten Risikoparametern durchführt. Durch einen umfassenden Simulationsrahmen erreicht die Analyse statistische Robustheit und liefert wesentliche Erkenntnisse über die Systemleistung unter sorgfältig verwalteten Risikobedingungen.

•  1 % Risikoniveau

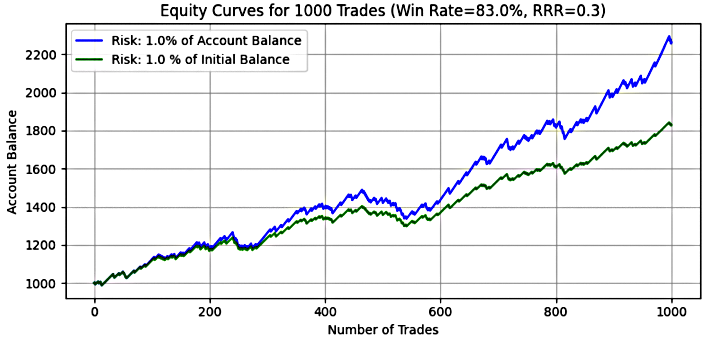
Abbildung 13

Tabelle 8: Monte-Carlo-Simulationsergebnisse für ein System mit Gewinnrate=83%, RRR=0,3, 1% Risiko

Metriken	Dynamisch (1% des aktuellen Saldos)	Fest (1% des Anfangssaldos)
Mittlerer Endsaldo	$2,202.86	$1,790.73
Median Endsaldo	$2,176.49	$1,790.00
Kleinster Endsaldo	$1,452.51	$1,387.00
Höchster Endsaldo	$3,391.51	$2,232.00
Mittlerer Drawdown	$118.36	$72.50
Median Drawdown	$112.90	$68.00
Maximaler Drawdown	$256.29	$143.00
Mittlerer maximaler Drawdown (%)	7.07%	5.50%
Median Max Drawdown (%)	6.71%	5.10%
Maximaler Drawdown (%)	13.55%	11.60%

Wichtigste Einsicht

Bei einem Risiko von 1 % zeigte das System in beiden Modellen ein bescheidenes, aber konsistentes Wachstum. Das durchschnittliche Endsaldo bei dynamischem Risiko betrug 2.202,86 $ – etwa das 2,2-fache des Anfangskapitals – während bei festem Risiko 1.790,73 $ erreicht wurden, also etwa das 1,8-fache. Die Mediane der Endsalden lagen sehr nahe an ihren jeweiligen Mittelwerten, was auf eine enge Verteilung und geringe Volatilität der Ergebnisse hindeutet.

Wichtig ist, dass es bei keiner der Simulationen zu Kontobewegungen kam und dass sich das System als statistisch stabil erwies. Der maximale Drawdown für das dynamische Risiko betrug nur 13,55 %, während das feste Risiko mit 11,60 % sogar noch niedriger lag. Der mittlere und der mediane Prozentsatz des Drawdowns war bei dem festen Modell ebenfalls geringer, was die glattere Kapitalkurve unterstreicht.

In einigen Simulationen erreichte das dynamische Risiko ein maximales Gleichgewicht von 3,4-fachem des ursprünglichen Eigenkapitals, während das feste Risiko bei 2,2-fachem lag, was die begrenzten, aber stabilen Vorteile dieses Systems mit hoher Gewinnrate verdeutlicht.

•  2 % Risikoniveau

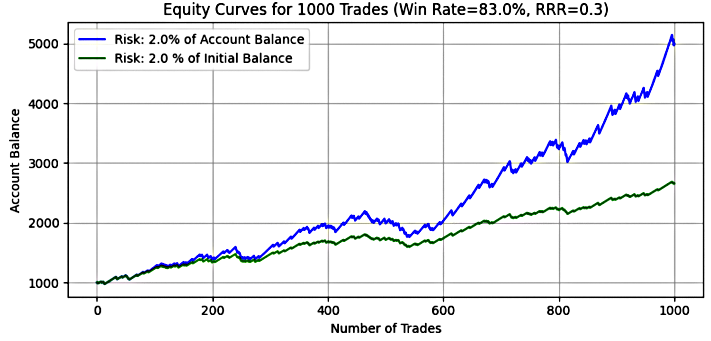
Abbildung 14 

Tabelle 9: Monte-Carlo-Simulationsergebnisse für ein System mit Gewinnrate=83%, RRR=0,3, 2% Risiko

Metriken	Dynamisch (2% des aktuellen Saldos)	Fix (2% des Anfangssaldos)
Mittlerer Endsaldo	$4,842.45	$2,581.46
Median Endsaldo	$4,621.22	$2,580.00
Kleinster Endsaldo	$2,052.24	$1,774.00
Höchster Endsaldo	$11,256.45	$3,464.00
Mittlerer Drawdown	$443.14	$144.99
Median Drawdown	$407.10	$136.00
Maximaler Drawdown	$1,214.00	$286.00
Mittlerer maximaler Drawdown (%)	13.77%	9.42%
Median Max Drawdown (%)	13.13%	8.63%
Maximaler Drawdown (%)	25.67%	21.47%

Wichtige Erkenntnis:

Bei einem Risiko von 2 % werden die Leistungsunterschiede zwischen dynamischen und festen Modellen deutlicher. Das dynamische Risiko führte zu einem durchschnittlichen Endsaldo von 4.842,45 $ (fast das Fünffache des Anfangskapitals), verglichen mit 2.581,46 $ bei festem Risiko (2,6x). Der Median der Endsalden entsprach genau dem Mittelwert, was die Vorhersehbarkeit und die konsistente Leistung bestätigte.

Das maximale Endsaldo bei dynamischem Risiko erreichte 11.256,45 $, was darauf hindeutet, dass einige starke Phasen zu einem beträchtlichen Wachstum führen können, während das feste Risiko mit 3.464 $ seinen Höhepunkt erreichte. Allerdings stiegen auch die maximalen Drawdowns, wobei das dynamische Risiko 25,67 % erreichte und das feste Risiko mit 21,47 % niedriger blieb.

Dieses Szenario spiegelt ein moderates Risiko-Ertrags-Profil wider, bei dem die Aufzinsung unter dynamischem Risiko die Renditen erhöht, während das feste Risiko eine geringere Volatilität mit begrenztem Aufwärtspotenzial bietet.

•  5% Risikoniveau

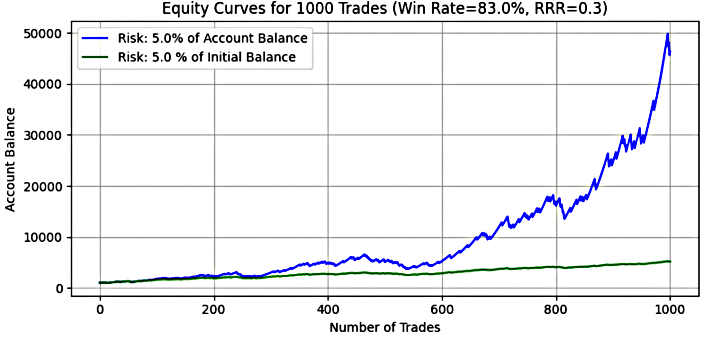
Abbildung 15 

Tabelle 10: Monte-Carlo-Simulationsergebnisse für ein System mit Gewinnrate=83%, RRR=0,3, 5% Risiko

Metriken	Dynamisch (1% des aktuellen Saldos)	Fest (1% des Anfangssaldos)
Mittlerer Endsaldo	$50,642.20	$4,953.64
Median Endsaldo	$38,003.88	$4,950.00
Kleinster Endsaldo	$4,884.41	$2,935.00
Höchster Endsaldo	$360,637.45	$7,160.00
Mittlerer Drawdown	$9,127.86	$362.48
Median Drawdown	$7,201.27	$340.00
Maximaler Drawdown	$62,063.85	$715.00
Mittlerer maximaler Drawdown (%)	31.82%	18.15%
Median Max Drawdown (%)	30.97%	16.25%
Maximaler Drawdown (%)	54.29%	49.28%

Wichtige Erkenntnis:

Bei einem Risiko von 5 % explodiert das Potenzial des Systems unter dynamischem Risiko und führt zu einem mittleren Endsaldo von über 50.000 $ (50-faches Anfangskapital) und einem Median von 38.003 $, was auf eine starke Tendenz zu profitablen Ergebnissen hinweist. Das maximale Endsaldo betrug 360.637 $, was die Fähigkeit des Systems bestätigt, aus kleinen Gewinnen große Gewinne zu erzielen.

Dies wird jedoch durch eine hohe Volatilität erkauft – mit durchschnittlichen Drawdowns von über 9.000 $ und maximalen Drawdowns von über 62.000 $. Der mittlere Drawdown-Prozentsatz lag bei fast 32 %, und das Worst-Case-Szenario erreichte 54,29 %, was für gut kapitalisierte Händler noch tolerierbar sein könnte, aber eine Herausforderung für die psychologische Belastbarkeit darstellt.

Bei den festen Risiken war die Performance verhaltener. Der durchschnittliche Endsaldo betrug 4.953,64 $ (etwa das Fünffache des Kapitals), der Höchstwert lag bei 7.160 $. Die Drawdowns waren deutlich niedriger als die dynamischen, mit einem mittleren maximalen Drawdown von etwa 16 % und einem maximalen Drawdown von 49,28 %.

Empfohlene Risikoniveaus für System 5 (83% Gewinnrate, RRR = 0,3)

Für ein System mit einer so hohen Gewinnrate und einer niedrigen RRR bestätigen die Simulationen, dass es statistisch stabil und widerstandsfähig ist, insbesondere bei konservativem Risiko.

• Ein Risiko von 1 % bis 2 % des aktuellen Kontosaldos ist für die meisten Händler optimal und bietet ein ausgewogenes Verhältnis von Beständigkeit, Wachstum und überschaubaren Rückschlägen.
• Das dynamische Risiko verbessert die Performance durch Aufzinsung, führt aber zu etwas höheren Drawdowns.
• Ein festes Risiko führt zu einer besser vorhersehbaren Kapitalkurve, die sich für Händler eignet, die eine geringe Volatilität bevorzugen.

Bei einem Risiko von 5 % bietet das dynamische Risiko außergewöhnliche Chancen, erfordert aber emotionale Disziplin, um Drawdowns im Bereich von 30-50 % zu ertragen. Ein festes Risiko von 5 % führt zu vorhersehbaren 5-fachen Renditen mit maximalen Drawdowns von unter 50 %, was ihn für Händler attraktiv macht, die stabile Ergebnisse ohne extreme Schwankungen suchen.

Für einige Händler könnte das Risiko von 5 % des anfänglichen Kontostands ein bevorzugter Ansatz für dieses System sein, da der mittlere und mittlere Drawdown-Prozentsatz niedrig ist und ein vorhersehbares Renditepotenzial von etwa dem Fünffachen des Anfangskapitals besteht. Obwohl der Drawdown im schlimmsten Fall 49,28 % erreichte, war dies ein statistisch seltenes Ergebnis in den Simulationen und könnte für Händler, die mit einem moderaten Risiko vertraut sind, tolerierbar sein.

Für andere kann das Risiko von 5 % des aktuellen Saldos (dynamisches Modell) aufgrund seines außergewöhnlichen Renditepotenzials attraktiver sein, mit einem mittleren Endsaldo von mehr als dem 50-fachen und einem Median von 38x des Anfangskapitals. Trotz der aggressiven Risikodimensionierung wies das System ein moderates Drawdown-Verhalten auf, mit einem mittleren und medianen Drawdown von etwa 32 % und einem maximalen Drawdown von 54,29 %. Dieses Volatilitätsniveau ist zwar beträchtlich, hält sich aber in einem akzeptablen Rahmen für erfahrene Händler, die sowohl emotional als auch finanziell auf eine Strategie mit einer hohen Kumulierung und hoher Volatilität vorbereitet sind.

Bei diesem System ist das Risiko, das über die traditionelle 2%-Regel hinausgeht, ein gangbarer Weg, um die Handelsziele zu erreichen, aber es erfordert ein robustes und zuverlässiges Handelssystem, das Sie durch Phasen des Drawdowns trägt und Ihr Ziel erreicht.

Code-Verwendung

Um alternative Ergebnisse zu bewerten, ändern Sie die Parameterwerte im folgenden Abschnitt. Dies ermöglicht ein flexibles Testen unter verschiedenen Bedingungen, wobei der zugrunde liegende analytische Rahmen erhalten bleibt.

# Parameters
win_rate = 0.83
rrr = 0.3
num_trades = 1000
initial_balance = 1000
risk_percent = 0.05  # %

np.random.seed(42)

#The use of a predefined seed (e.g., 42) enables result reproducibility. 
#Users may change this value/deactivate the seeding logic by commenting out the relevant code block.

Schlussfolgerung

In diesem Artikel haben wir Monte-Carlo-Simulationen angewandt, um die Auswirkungen aufeinanderfolgender Pechsträhnen objektiv zu quantifizieren und zu untersuchen, wie sie mit verschiedenen Gewinnraten-Systemen und Positionsgrößenstrategien interagieren. Die Ergebnisse deuten darauf hin, dass Handelssysteme mit niedrigeren Gewinnraten tendenziell längere Pechsträhnen aufweisen, während Systeme mit höheren Gewinnraten kürzere und weniger häufige Pechsträhnen aufweisen.

Trotz der psychologischen Herausforderungen, die mit Systemen mit niedriger Gewinnrate verbunden sind, können Systeme mit positiver Erwartungshaltung (d. h. mit einem ausreichend hohen Verhältnis zwischen Gewinn und Risiko) bei gleichem Risikoniveau deutlich höhere Renditen erzielen. Dies unterstreicht die Tatsache, dass die Gewinnrate allein nicht ausschlaggebend für die Rentabilität ist – Erwartungshaltung und Risikomanagement sind genauso wichtig.

Unsere Analyse ergab auch, dass das Ausmaß des Drawdowns sowohl von der Länge der Verlustphasen als auch von der Höhe des Risikos pro Handel direkt beeinflusst wird. Je höher das Risiko ist, desto größer ist natürlich auch der potenzielle Verlust – aber auch der potenzielle Gewinn, insbesondere bei Systemen mit einem mathematischen Vorteil.

Die traditionelle Risiko-Regel von 1 % – 2 % bleibt zwar eine solide Grundlage, aber unsere Ergebnisse deuten darauf hin, dass Händler mit einem robusten und bewährten System es rechtfertigen können, die 2%-Schwelle zu überschreiten. Das System mit einer Gewinnrate von 83 % und einer RRR von 0,3 zeigte beispielsweise selbst bei einem Risiko von 5 % stabile Drawdowns, insbesondere bei einem festen Risikomodell. Hätte ein solches System eine geringfügig bessere RRR (z. B. 0,5), könnte das Risiko von mehr als 2 % sogar noch tragfähiger sein – dies sollte jedoch mithilfe von Simulationswerkzeugen gründlich getestet werden.

Insgesamt zeigten unsere Simulationen durchweg, dass das dynamische Risiko (auf der Grundlage des aktuellen Saldos) in Bezug auf die langfristigen Renditen das feste Risiko übertraf. Allerdings boten Modelle mit festem Risiko in bestimmten Fällen stabilere und vorhersehbarere Ergebnisse, wie z. B. die 5 %-Risikoeinstellung im System mit 65 % Gewinnrate und RRR = 0,9.

Dies wirft eine umfassendere Frage auf: Können wir uns konkrete Handelsziele setzen und diese mit Hilfe eines klar definierten Handelssystems zuverlässig erreichen?

Wir glauben, dass dies das Herzstück eines erfolgreichen Handels ist – die Umsetzung einer Strategie in gezielte Ergebnisse. Im nächsten Artikel werden wir dieses Konzept weiter vertiefen und zeigen, wie Händler mit simulationsgestützten Strategien realistische Gewinnziele setzen und verfolgen können.