Aufbau eines Handelssystems (Teil 1): Ein quantitativer Ansatz

Einführung

Ein durchweg profitables Handelssystem beruht auf dem Zusammenspiel von drei zentralen Säulen:

1. Gewinnrate
2. Rendite-Risiko-Verhältnis (RRR)
3. Risikoausmaß (über Positionsgröße)

Diese drei Variablen sind die grundlegenden Triebkräfte für wichtige Leistungskennzahlen wie Gewinnfaktor, Erholungsfaktor und Inanspruchnahme. Viele Händler machen jedoch den Fehler, sich fast ausschließlich auf die Gewinnrate zu konzentrieren und dabei die entscheidende Bedeutung von RRR und Positionsgröße bei der Bewertung der Effektivität ihrer (automatischen) Handelssysteme zu übersehen.

Um letztendlich erfolgreich zu sein und auf den Märkten aktiv zu bleiben, müssen Händler die Dynamik ihres Handelsvorteilsverstehen – insbesondere die Gewinnrate, die RRR und die optimale Positionsgröße, die diesen beiden Metriken entspricht.

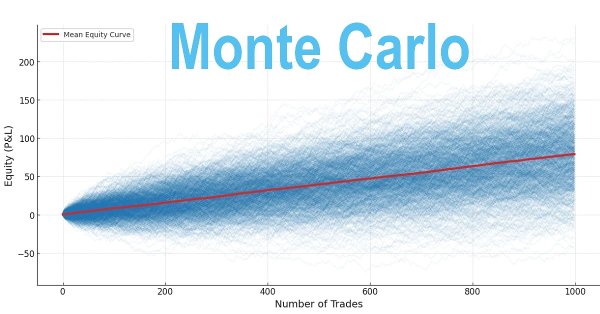
Dieser Artikel soll Händlern helfen, ihre Strategien langfristig zu bewerten, indem sie statistische Ergebnisse aus Backtests in eine Monte-Carlo-Simulation einbeziehen. Dieser Ansatz erzeugt eine breite Palette möglicher Ergebnisse und bietet eine zusätzliche Ebene des Vertrauens, die dem Händler hilft zu entscheiden, ob ein System fortgesetzt, verbessert oder verworfen werden sollte.

Erwartung: Die Mathematik hinter der Rentabilität

Die Rentabilität wird durch die Erwartung quantifiziert – eine Funktion der Gewinnrate und der RRR. Eine positive Erwartungshaltung definiert ein profitables System; eine negative Erwartungshaltung garantiert einen langfristigen Misserfolg, egal wie beeindruckend die Gewinnrate erscheint. Doch selbst bei einer positiven Erwartungshaltung kann eine schlechte Positionsgröße die Rückschläge über die Erholungsphase hinaus verstärken.

Was dieser Artikel behandelt:

• Die mathematischen Grundlagen für profitable Handelssysteme
• Zur Erreichung der Rentabilität erforderliche Mindestschwellen
• Validierung der Leistungsfähigkeit von Strategien mit Hilfe der Monte-Carlo-Simulation in Python

Ziel ist es, den Händlern einen Rahmen an die Hand zu geben, um zu beurteilen, ob ein System statistisch tragfähig ist. Wenn zum Beispiel die Gewinnrate eines Händlers die erforderliche Mindestschwelle für ein bestimmtes RRR nicht übersteigt, kann keine langfristige Rentabilität erwartet werden – unabhängig davon, wie vielversprechend der Backtest auch sein mag.

Mit der Monte-Carlo-Simulation können Händler Tausende von synthetischen Ergebnissen modellieren, die auf unterschiedlichen Kombinationen von Gewinnraten, RRRs und Positionsgrößen basieren. Dies ermöglicht eine bessere Strategieoptimierung, noch bevor die Live-Tests oder historische Backtests beginnt.

Für Händler, die bereits über getestete Ergebnisse verfügen, kann die Simulation verwendet werden, um tatsächliche Gewinnraten, RRRs und Positionsgrößen einzugeben, um die potenzielle zukünftige Performance über eine Reihe von Geschäften zu prognostizieren. Dieser statistische Einblick verschafft mehr Klarheit und Vertrauen in ein System, auf das man sich verlassen kann.

Definitionen und mathematische Konzepte

1. Gewinnrate

Die Gewinnquote ist definiert als der Anteil der gewinnbringenden Geschäfte im Verhältnis zu den gesamten Geschäften in einem bestimmten Zeitraum, ausgedrückt als Prozentsatz oder als Wahrscheinlichkeit für gewinnbringende Geschäfte in einem bestimmten Zeitraum. In diesem Artikel wird die Gewinnquote mit P bezeichnet. 

Beispiel: Bei 40 Gewinnern in 100 Handelsgeschäften beträgt die Gewinnrate 40%.

2. Rendite-Risiko-Verhältnis (RRR)

Verhältnis von Gewinn (Take-Profit) zu Risiko (Stop-Loss):

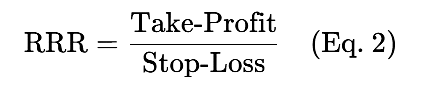
Beispiel: Wenn der Take-Profit bei 100 Pips und der Stop-Loss bei 50 Pips liegt, dann ist RRR = 2.

3. Größenbestimmung von Positionen

Die Positionsgröße bezieht sich darauf, wie viel Kapital pro Handel riskiert wird. Sie kann wie folgt berechnet werden:

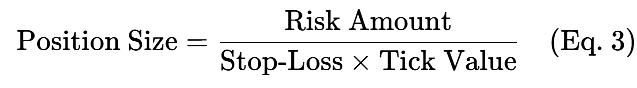
Beispiel: Ein Risiko von 200 $ bei einem Stop-Loss von 50 Pips und einem Tick-Wert von 10 $/Pip,

die Positionsgröße = 0,4 Lose.

4. Erwartung 

Die mit Ev bezeichnete Erwartung stellt die erwartete Rendite pro Handel dar und wird wie folgt berechnet

Ev > 0 : Profitables System (langfristig)

Ev <0 : Unrentables System

Mindestgewinnrate oder RRR-Schwelle, um ein rentables System zu erreichen

Es ist eine mathematische Tatsache, dass Gewinnrate und RRR voneinander abhängig sind. Für jede gegebene Gewinnrate gibt es eine Mindest-RRR, die erforderlich ist, um Rentabilität zu erzielen. Wenn die RRR bekannt ist, ist ebenfalls eine Mindestgewinnrate erforderlich, um rentabel zu sein. Eine hohe Gewinnrate allein bestätigt nicht die Leistung eines automatisierten Systems, es sei denn, sie wird von einem gut definierten Risiko-Ertrags-Verhältnis (RRR) begleitet.

Ein System mit vordefinierten Stop-Loss- und Take-Profit-Einstellungen hat eine feste RRR. Wenn die entsprechende Gewinnquote unter dem erforderlichen Minimum liegt, kann das System langfristig nicht rentabel sein, selbst wenn es kurzfristige Gewinne erzielt, die die Händler in die Irre führen können. Dies führt häufig dazu, dass das Konto am Ende leer ist.

Ableitung der Rentabilitätsbedingung

Gehen wir das mathematische Konzept durch, um es besser zu verstehen

Aus der Formel für die Erwartung 

Ev = (Gewinnrate*Belohnung) – (1 – Gewinnrate)*Risiko

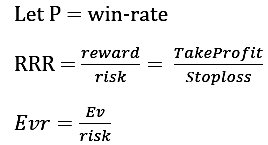
Damit ein System rentabel ist, muss Ev > 0 sein.

Aus Gleichung 5:

Wenn die RRR bekannt ist, ergibt sich die Mindestgewinnrate (P) für ein rentables System wie folgt:

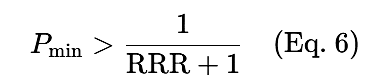
Wenn die Gewinnrate (P) bekannt ist, ergibt sich die Mindest-RRR für ein rentables System wie folgt:

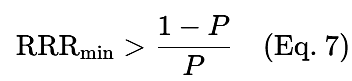
Tabelle 1: Mindestgewinnrate für eine bestimmte RRR

RRR	Minimum P
1.0	> 50.00%
1.5	> 40.00%
2.0	> 33.33%
2.5	> 28.57%
3.0	> 25.00%

Aus Tabelle 1 geht hervor, dass ein System mit einer RRR von 1 eine Gewinnrate von mehr als 50 % benötigt, um langfristig rentabel zu sein. Wenn ein System eine RRR=3,0 hat, dann ist eine Gewinnrate von mehr als 25,00% erforderlich, um langfristig profitabel zu sein. Aus Tabelle 1 geht hervor, dass mit steigender RRR die Mindestgewinnrate sinkt. Wenn die RRR eines Handelssystems seine Mindestgewinnrate übersteigt, ist das System langfristig profitabel.

Tabelle 2: Erforderliche Mindest-RRR für eine bestimmte Gewinnrate

P	Mindest-RRR
30%	> 2.333
40%	> 1.50
50%	> 1.00
60%	> 0.667
70%	> 0.429

Die Gewinnrate eines Systems ist meist nicht bekannt, es sei denn, man testet die Strategie mit historischen Daten mit einer definierten RRR. Tabelle 2 gibt uns eine Vorstellung davon, wie hoch die RRR mindestens sein muss, damit eine bestimmte Gewinnrate rentabel ist. Bei einer Gewinnrate von 30 % sollte die RRR größer als 2,333 sein, um langfristig rentabel zu sein. Ebenso muss bei einer Gewinnrate von 70 % die RRR über 0,429 liegen, um langfristig rentabel zu sein. Mit steigender Gewinnrate sinkt das RRR-Minimum.

Aus diesem Grund sollten Händler nicht blindlings nach hohen Gewinnraten streben, ohne die RRR zu berücksichtigen und umgekehrt.

Da die Gewinnrate einfach das Verhältnis aller Handelsgeschäfte mit Gewinn zu den gesamten Handelsgeschäften ist, ist es wichtig, das System lange genug laufen zu lassen, um genügend Handelsdaten zu sammeln, bevor man Rückschlüsse auf die wahre Gewinnrate zieht. Ein automatisiertes System, das über einen Zeitraum von 6 Monaten nur 30 Handelsgeschäften ausführt und davon 20 gewinnt, würde beispielsweise eine Gewinnrate von 60 % aufweisen. Wenn jedoch dasselbe System – ohne jegliche Änderungen – über einen Zeitraum von 18 Monaten 200 Handelsgeschäfte mit 90 Gewinnern ausführt, sinkt die Gewinnrate auf 45 %. Je mehr Handelsgeschäfte das System abschließt, desto zuverlässiger und repräsentativer wird die Gewinnrate.

Positionsgrößenbestimmung und Risikomanagement

Der Betrag, der zur Bestimmung der Positionsgröße verwendet wird, wird normalerweise als Prozentsatz des Kontostands ausgedrückt. Diese Zahl ist von entscheidender Bedeutung, denn sie bestimmt, ob ein profitables Handelssystem Perioden mit maximalem Drawdown überstehen kann, ohne das Konto zu sprengen und letztendlich die Handelsziele zu erreichen.

Oft riskieren Händler auf der Suche nach schnellen Gewinnen einen zu hohen Prozentsatz ihres Kontos, was dazu führen kann, dass selbst ein profitables System ihr Konto auslöscht. Wenn dies geschieht, kann der Händler den Systementwickler beschuldigen und das System als Betrug bezeichnen. Die Wahrheit ist: egal wie gut oder profitabel ein System ist, solange die Gewinnrate nicht 100% beträgt, wird es Verluste machen. Wenn Sie mehr riskieren, als Ihr Konto verkraften kann, müssen Sie mit Nachschussforderungen rechnen und möglicherweise Ihr Konto komplett auflösen, wenn keine zusätzlichen Mittel zur Verfügung stehen.

In diesem Abschnitt erfahren Sie, wie Sie Ihre Positionen richtig dimensionieren und dabei innerhalb einer sicheren Risikozone bleiben, damit Sie Verlustphasen überstehen und dennoch auf Ihre Gewinnziele hinarbeiten können. Dies ist die Essenz eines soliden Risiko- oder Geldmanagements. Machen wir uns an die Berechnungen:

Definitionen:

•  f: fester Anteil des Kontostandes, der pro Handelsgeschäft riskiert wird.
•  RRRmin = 1,50: Minimales Risiko-Verhältnis
•  P = 0.40: Gewinnquote (40%)

Ergebnis eines erfolgreichen Handelsgeschäfts: 

wenn das Handelsgeschäft gewinnt, ist der Gewinn RRR * Risikobetrag

Neuer Saldo = Aktueller Saldo + 1,50*(f*aktueller Saldo)

Vereinfacht:

Ergebnis eines Handelsgeschäft mit Verlust:

Wenn ein Handelsgeschäft Verluste macht, entspricht der Verlust dem riskierten Betrag:

Erwarteter Multiplikator pro Handel:

Durch Kombination von Gleichung 8 und 9 ergibt sich der erwartete Wachstumsfaktor E[Faktor]:

Substituiert man P=0,4 und vereinfacht, erhält man:

Interpretation: Bei RRRmin = 1,50 beträgt der erwartete Wachstumsfaktor genau 1, d. h. kein langfristiges Wachstum (Breakeven).

Wachstum Bedingung

RRR > RRRmin: Für RRR = 1,70  

Bei positivem Wachstum (Ef > 1) muss f folgende Bedingungen erfüllen 

 

Berechnung des optimalen Risikoanteils (f)

Um das Ziel zu erreichen, sagen wir Ef = 1,002:

Daraus können wir ersehen, dass wir mindestens 2,5 % des Kontosaldos riskieren müssen, um unser Ziel zu erreichen. Wenn wir weniger als 2,5 % riskieren, kann das Konto im Laufe der Zeit gleichmäßiger wachsen. Dies unterstreicht ein wichtiges Konzept, das oft übersehen wird: Für jede gegebene Kombination aus Gewinnrate, Risiko-Ertrags-Verhältnis (RRR) und Gewinnziel gibt es immer ein entsprechendes optimales Risiko pro Handel.

Erwarteter Wachstumsfaktor 

Um den erwarteten Wachstumsfaktor (Ef) zu bestimmen, muss ein Händler zunächst drei Schlüsselparameter definieren:

1. Gewinnziel (P_target)
2. Anzahl der Handelsgeschäfte, um das Ziel zu erreichen (x)
3. Anfangskontostand (Ini_bal)

Ef wird von einer zusammengesetzten Wachstumsgleichung abgeleitet

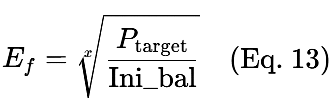
Nehmen wir zum Beispiel folgendes an:

• Gewinnziel (P_target) = $10.000
• Anzahl der Handelsgeschäfte (x) = 300
• Anfangssaldo (Ini_bal) = $1.000

Das Einsetzen der Zahlen ergibt:

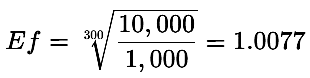
Der erwartete Wachstumsfaktor spiegelt Ihren Handelsstil wider – ob Sie ein konservativer oder aggressiver Händler sind – da er das erforderliche Risiko pro Handel bestimmt, um Ihr Ziel zu erreichen.

Beispiel:

Angenommen, ein Handelssystem hat:

Gewinnquote = 40%

Risiko-Ertrags-Verhältnis (RRR) = 1,7

Ein Händler oder ein automatisiertes System zielt darauf ab, $1000 über 300 Handelsgeschäfte in $10.000 zu verwandeln. Das erforderliche Risiko pro Handelsgeschäft (f) aus Gleichung 12 wird wie folgt berechnet:

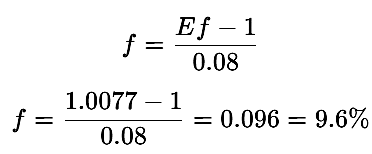
In diesem Fall muss der Händler oder das automatische System mindestens 9,6 % pro Handelsgeschäft riskieren, um das Ziel zu erreichen – ein extrem aggressiver Ansatz.

Wenn nun die Anzahl der Handelsgeschäfte zur Erreichung des Ziels auf x= 700 erhöht wird:

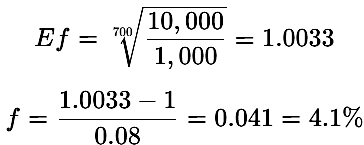
Bei 700 Handelsgeschäften wird das System bzw. der Handel weniger aggressiv und erfordert nur noch ein Risiko von 4,1 % pro Handelsgeschäft, um das gleiche Ziel zu erreichen.

Es ist wichtig zu beachten, dass das Ziel mit einer höheren Gewinnrate und einer höheren RRR besser erreichbar ist.

Beispiel: Bei RRR=2,0 (mit P=40%) ist Ef = 1 + 0,2*f, was f auf 1,54% für Ef=1,0077 reduziert.

Aus diesem mathematischen Modell können wir schließen, dass selbst profitable Systeme eine Optimierung sowohl der Erwartung als auch der Positionsgröße erfordern. Im nächsten Abschnitt werden wir dies anhand von Monte-Carlo-Simulationen weiter veranschaulichen, um eine langfristige Perspektive für das Potenzial des Systems zu bieten.

Monte-Carlo-Simulation

Die Validierung der langfristigen Robustheit eines Handelssystems hängt von der Optimierung von RRR, Gewinnrate und Positionsgröße ab. Monte-Carlo-Simulationen modellieren die Bandbreite möglicher Ergebnisse bei Tausenden von zufälligen Handelssequenzen. Zu optimierende Parameter sind:

1. Gewinnrate
2. RRR 
3. Positionsgrößenbestimmung  

Dies wird berücksichtigt:

• Verlustserien
• Maximaler Drawdown
• Wege einer erwarteten Rendite
• Überlebenswahrscheinlichkeit des Kontos

Ziel ist es jedoch, die erwarteten Erträge und die Wahrscheinlichkeit des Überlebens des Kontos in verschiedenen Szenarien zu prüfen. 

Die Monte-Carlo-Simulation wird mit Hilfe der Python-Programmierung erstellt.

import numpy as np
import matplotlib.pyplot as plt

# Parameters
win_rate = 0.40
reward_risk_ratio = 1.5  # 1.5:1
risk_per_trade = 1  # Risk $1 per trade (normalized)
num_trades = 1000  # Total number of trades to simulate
num_simulations = 1000  # Number of Monte Carlo simulations

# Monte Carlo simulation
equity_curves = []

Wir importieren mathematische Funktionen, mehrdimensionale Arrays und Matrizen, die für Berechnungen mit der NumPy-Bibliothek benötigt werden, und weisen sie als np zu.

Wir importieren auch grafische Funktionen für die Darstellung unserer simulierten Ergebnisse mit dem Modul pyplot von Matplotlib und geben ihm den Alias plt.

Wir initialisieren dann unsere Gewinnrate, das Risiko-Ertrags-Verhältnis, das Risiko pro Handelsgeschäft, die Anzahl der Handelsgeschäfte pro Simulation und die Anzahl der Iterationen. Die Ergebnisse werden in Aktienkurven gespeichert. Die Anzahl der Iterationen kann je nach Präferenz des Nutzers verringert oder erhöht werden.

for _ in range(num_simulations):
    equity = 0
    curve = [equity] # Start curve with initial equity (0)
    peak = equity # Track peak equity for drawdown calculation
   # max_drawdown = 0 # Track max drawdown for this simulation

    for _ in range(num_trades):
        if np.random.rand() < win_rate:
            pnl = risk_per_trade * reward_risk_ratio
        else:
            pnl = -risk_per_trade
        equity += pnl
        curve.append(equity)

    equity_curves.append(curve)

# Convert to numpy array for easier analysis
equity_curves = np.array(equity_curves)

Die Simulation führt 1.000 Iterationen (jeweils 100 Handelsgeschäfte) durch, speichert die Ergebnisse in einer Kapitalkurve und konvertiert sie für die Analyse in ein NumPy-Array.

# Plot results
plt.figure(figsize=(12, 6))
for i in range(min(num_simulations, 100)):
    # Adjust indexing if plotting against trade number (starts from 0)
    plt.plot(range(num_trades + 1), equity_curves[i], alpha=0.2, color='blue')

Die Ergebnisse der einzelnen Simulationen werden in blauer Farbe dargestellt.

# Plot mean curve
mean_curve = equity_curves.mean(axis=0)
plt.plot(range(num_trades + 1), mean_curve, color='red', linewidth=2, label='Mean Equity Curve')

Eine rote Linie markiert den Durchschnitt der simulierten Ergebnisse.

plt.title(f'Monte Carlo Simulation: {num_simulations} Simulations, {num_trades} Trades Each\nWin Rate = {win_rate*100:.1f}%, 
R:R = {reward_risk_ratio}:1')
plt.xlabel('Number of Trades')
plt.ylabel('Equity (P&L)')
plt.legend()
plt.grid(True)
plt.tight_layout() 
plt.show()

Dieses Segment behandelt die Formatierung des Plots: Titel, Achsenbeschriftung (x-label, y-label) und Rasteraktivierung (grid=True).

# Summary statistics
# Final equity is now the last element of the curve, which has num_trades + 1 points
final_equity = equity_curves[:, -1]
mean_final_equity = final_equity.mean()
median_final_equity = np.median(final_equity)
std_final_equity = final_equity.std()
percent_profitable = np.mean(final_equity > 0) * 100

print('mean_final_equity:',mean_final_equity, '\nmedian_final_equity:', median_final_equity,
 '\nstd_final_equity:', std_final_equity,'\npercent_profitable:', percent_profitable,'%')

Der letzte Codeabschnitt berechnet und druckt: durchschnittliches Endkapital, medianes Endkapital, Standardabweichung des Endkapitals und Prozentsatz der profitablen Geschäfte.

Szenario A: Performance einer Handelsstrategie mit 40% Gewinnrate und 1,5 RRR über 1.000 Simulationen

In diesem Szenario wurde eine Handelsstrategie mit einer Gewinnrate von 40 % und einem Rendite-Risiko-Verhältnis (RRR) von 1,5 über 1.000 Handelsgeschäfte pro Simulation getestet. Es wurden insgesamt 1.000 separate Simulationen durchgeführt, um die Leistung und die Risikomerkmale der Strategie zu bewerten. Die Ergebnisse, die in Abbildung 1 zusammengefasst sind, lauten wie folgt:

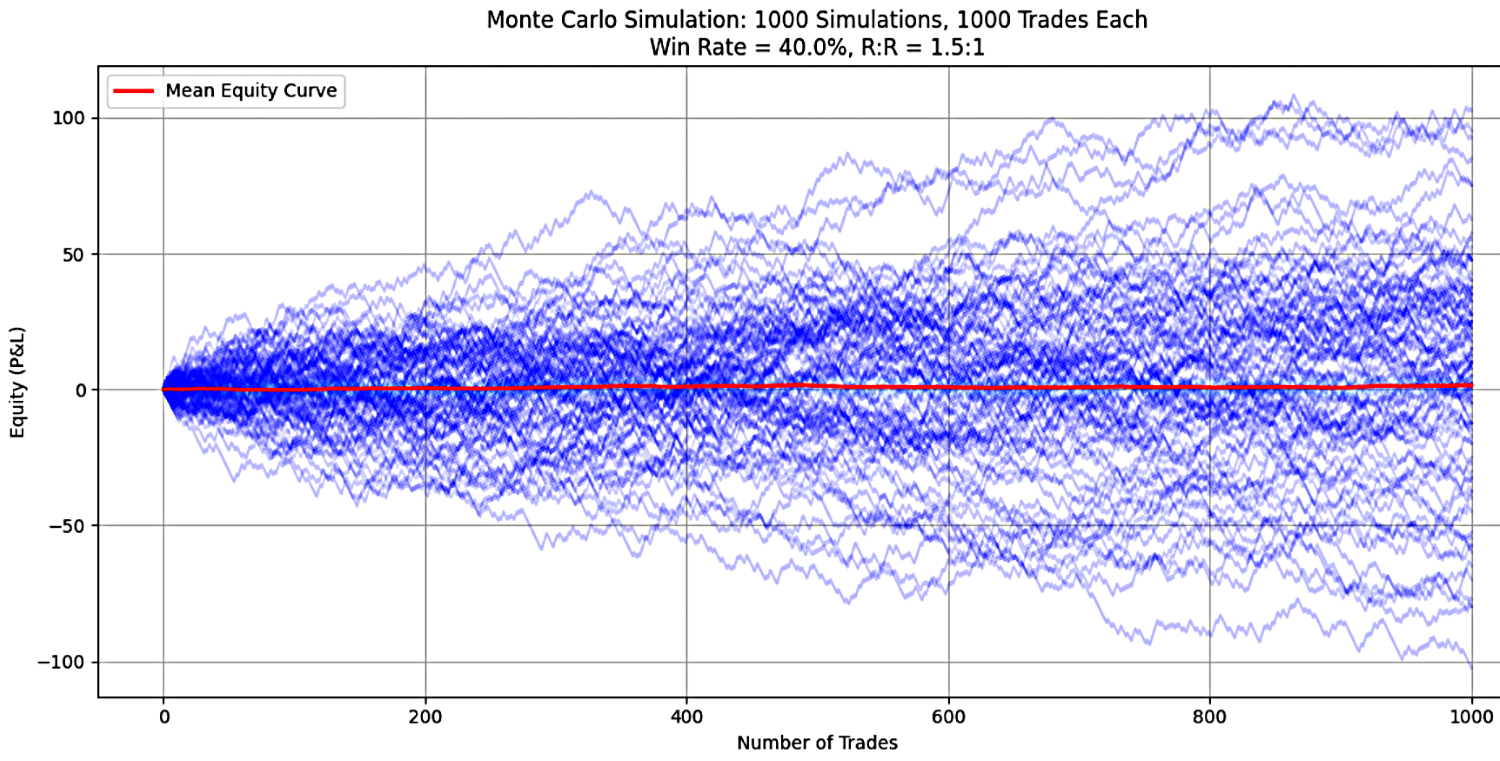
Abbildung 1

Die Simulationsergebnisse für eine Gewinnrate von 40 % und eine RRR von 1,5 lauten wie folgt:

Statistik	Werte
Mittleres endgültiges Eigenkapital	1.44
Median des endgültigen Eigenkapitals	0.0
Standardabweichung des endgültigen Eigenkapitals	37.91
Prozentsatz der gewinnbringenden Simulationen	49.0%

Auswertung der Ergebnisse

1. Mittleres endgültiges Eigenkapital: Der durchschnittliche Endkontostand aller Simulationen war das 1,44-fache des Anfangskapitals. Dies deutet darauf hin, dass die Strategie im Durchschnitt einen bescheidenen Gesamtgewinn erbrachte. Allerdings wird dieser Mittelwert durch einige wenige extrem positive Ergebnisse erheblich beeinflusst, wie in Abbildung 1 dargestellt. Das Vorhandensein dieser Ausreißer verzerrt den Mittelwert nach oben und verschleiert die Häufigkeit der schlechten Ergebnisse.

2. Medianwert des endgültigen Eigenkapitals: Der Medianwert betrug 0,0, was bedeutet, dass mindestens die Hälfte der Simulationen zu einem vollständigen Kapitalverlust führte. Bei mindestens 50 % der Simulationen wird das Konto leergeräumt (wahrscheinlich wurde der Saldo auf 0 gesetzt oder die Marge eingefordert). Diese Strategie birgt ein extremes Risiko des Ruins. Die Hälfte des Szenarios verlor das gesamte Kapital, während die andere Hälfte Gewinne erwirtschaftete, die verzerrt genug waren, dass der Mittelwert auf 1,44 anstieg. Dies zeigt, dass die meisten Ergebnisse schlecht sind und ein rotes Fähnchen für ein nicht tragfähiges Risiko tragen.

3. Standardabweichung: Die Standardabweichung von 37,91 verdeutlicht die extreme Volatilität und Unvorhersehbarkeit der Ergebnisse. Die Standardabweichung ist im Verhältnis zum Mittelwert groß. Die meisten Pfade liegen nahe am Totalverlust (Mittelwert=0). Einige Simulationen endeten mit einem großen positiven Saldo (was den Mittelwert aufbläht), während viele abstürzten.

4. Prozentsatz der gewinnbringenden Simulationen: Nur 49 % der Simulationen endeten mit Gewinn, d. h. das Eigenkapital lag am Ende über dem Anfangsbestand. In 51 % der Fälle hat das System Geld verloren. Dies stimmt mit dem Median=0,0 überein und bestätigt, dass die Verluste katastrophal sind, wenn sie eintreten.

Diese statistischen Werte spiegeln mehrere Schlüsselmerkmale der Leistung des Handelssystems wider: 

• Instabiles System:

Auch wenn der durchschnittliche Endwert positiv ist (1,44x), wird das Ergebnis durch einige „glückliche“ Läufe mit hohen Gewinnen bestimmt. Der Medianwert von Null zeigt deutlich, dass die meisten Läufe schlecht abliefen – mindestens 50 % von ihnen endeten mit einem leergeräumten Konto. Diese Diskrepanz zwischen Mittelwert und Median verdeutlicht ein grundlegend instabiles System – die meisten Läufe schneiden sehr schlecht ab, während nur wenige außergewöhnlich gut abschneiden.

• Hohes Risiko des Ruins:

Ein Median von Null zeigt, dass diese Strategie eine hohe Wahrscheinlichkeit hat, Ihr Konto zu sprengen, wenn nicht sehr strenge Risikokontrollen angewendet werden.

• Hohe Volatilität:

Die hohe Standardabweichung (ca. 37,9) im Vergleich zum Mittelwert (ca. 1,44) deutet darauf hin, dass die Ergebnisse extrem gestreut sind. Einige sind hervorragend, andere katastrophal. Diese Inkonsistenz macht es schwierig, sich auf diese Strategie zu verlassen, wenn es darum geht, stetige Erträge zu erzielen.

• Schwache Rentabilität:

Nur 49 % der Läufe endeten profitabel, obwohl sie einen positiven Mittelwert aufwiesen. Das System erweist sich trotz des positiven Mittelwerts nicht als zuverlässig, da ein stabiles, skalierbares System einen viel höheren Prozentsatz an positiven Ergebnissen aufweisen würde.

Szenario B: Performance einer Handelsstrategie mit 40% Gewinnrate und 1,7 RRR über 1.000 Simulationen

In Szenario B behält die Handelsstrategie eine Gewinnrate von 40 % bei, erhöht aber das Rendite-Risiko-Verhältnis (RRR) auf 1,70 und wurde über 1.000 Handelsgeschäfte pro Simulation bewertet.  Um die Leistungs- und Risikomerkmale gründlich zu bewerten, wurden 1.000 separate Monte-Carlo-Simulationen durchgeführt. Die wichtigsten Ergebnisse, die in Abbildung 2 zusammengefasst sind, lauten wie folgt:

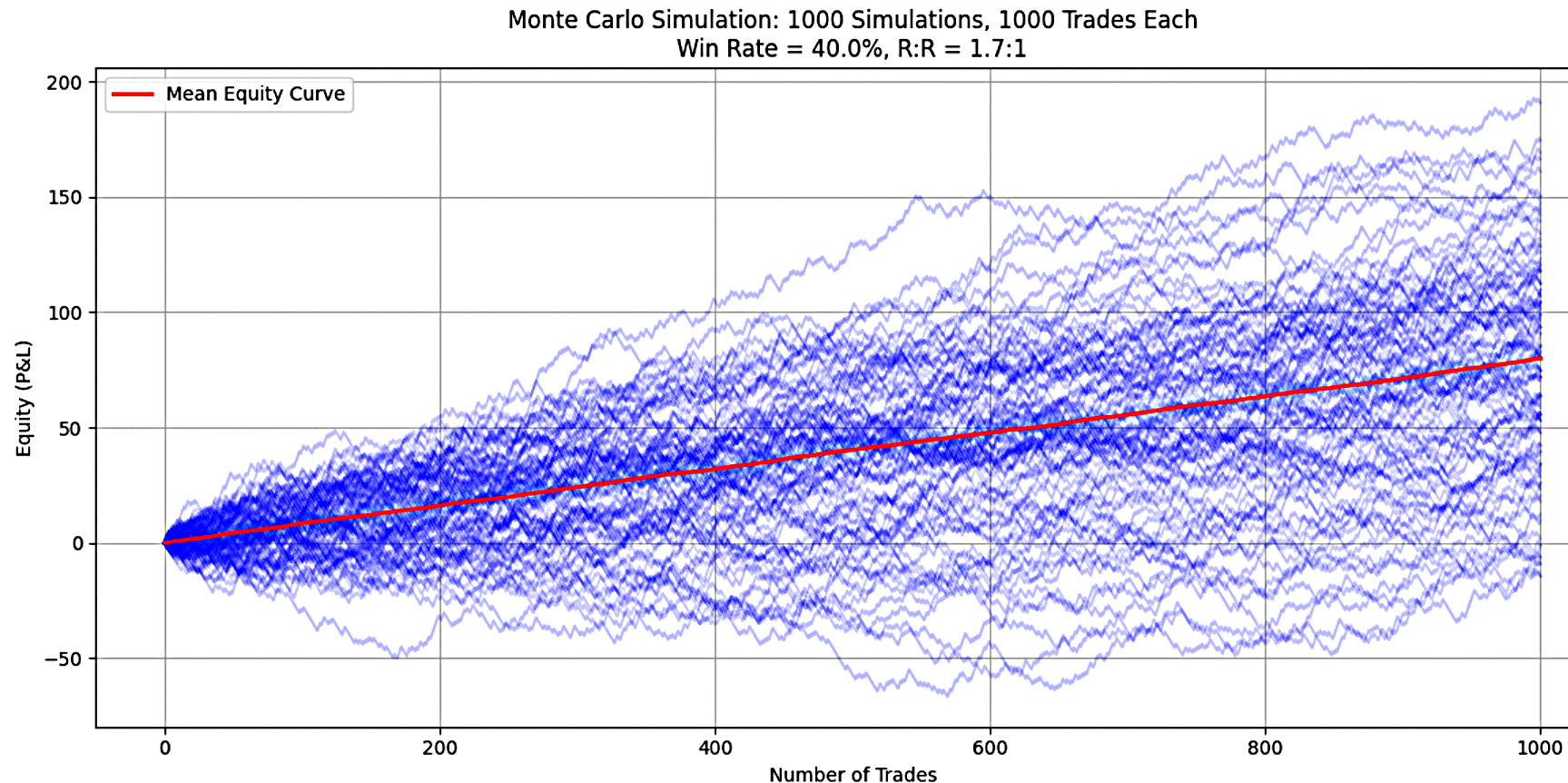
Abbildung 2

Nachfolgend sind die Simulationsergebnisse für eine Gewinnquote von 40 % und ein Risiko-Ertrags-Verhältnis von 1,7 aufgeführt

Statistik	Werte
Mittleres endgültiges Eigenkapital	80.0
Median des endgültigen Eigenkapitals	80.0
Standardabweichung des endgültigen Eigenkapitals	45.82
Prozentsatz der gewinnbringenden Simulationen	96.7%

Auswertung der Ergebnisse

1. Mittleres endgültiges Eigenkapital: Im Durchschnitt wuchs das Anfangskapital während des Simulationszeitraums um das 80-fache. Dies spiegelt ein außerordentliches Wachstumspotenzial wider und bestätigt die hohe Rentabilität der Strategie unter diesen Bedingungen. Eine durchschnittliche Rendite vom 80-fachen des Startguthabens ist ein hervorragendes Ergebnis, das zeigt, dass das System in der Lage ist, erhebliche Gewinne zu erzielen.

2. Median des endgültigen Eigenkapitals: Der Median des Ergebnisses lag ebenfalls beim 80-fachen des Anfangskapitals, was bedeutet, dass mindestens 50 % der Simulationen Renditen auf oder über diesem Niveau erzielten. Die enge Übereinstimmung zwischen Mittelwert und Median deutet auf eine symmetrische Verteilung der Ergebnisse hin, wobei sich die meisten Simulationen um die 80-fache Rendite gruppieren. Dieses Ergebnis unterstreicht nicht nur die hohe Rentabilität, sondern auch die hervorragende Konsistenz zwischen den Simulationsläufen. 

3. Standardabweichung des endgültigen Kapitals: Die Standardabweichung von 45,82 deutet zwar auf eine gewisse Variabilität der Ergebnisse hin, doch ist diese Volatilität im Verhältnis zum beachtlichen Mittelwert relativ bescheiden. Die Standardabweichung liegt bei etwa 57 % des Mittelwerts, was darauf hindeutet, dass die einzelnen Ergebnisse zwar variieren können (wobei einige Läufe z. B. 40- oder 120-fache Renditen erzielen), die Mehrzahl der Ergebnisse jedoch um den 80-fachen Durchschnitt herum liegen. Dies spiegelt ein System mit kontrollierter Volatilität und zuverlässiger Leistung wider.

4. Prozentsatz der gewinnbringenden Simulationen: Beeindruckende 96,7 % der Simulationen endeten mit einem Gewinn, nur 3,3 % endeten mit einem Verlust. Diese sehr hohe Erfolgsquote zeugt von einem System mit außergewöhnlicher Zuverlässigkeit und einem sehr geringen Risiko des Scheiterns. Die überwiegende Mehrheit der Handelsläufe brachte Gewinne, was die Robustheit der Strategie unter diesen simulierten Bedingungen unterstreicht.

Diese statistischen Werte spiegeln mehrere Schlüsselmerkmale der Leistung des Handelssystems wider: 

• Äußerst rentabel:

Die Angleichung von Mittelwert und Median bei 80x in Verbindung mit der engen Clusterung der Ergebnisse zeigt, dass es sich um ein hochprofitables und konsistentes System unter den getesteten Parametern handelt.

• Geringes Risiko des Ruins:

Mit nur 3,3 % der Simulationen, bei denen kein Gewinn erzielt wurde, zeigt das System eine dramatische Verbesserung der Zuverlässigkeit gegenüber dem früheren Szenario mit einer RRR von 1,5. Das Risiko des Ruins ist jetzt außergewöhnlich gering.

• Kontrollierte Volatilität:

Obwohl die absolute Standardabweichung groß erscheint, ist sie im Vergleich zu den sehr hohen Renditen angemessen. Die Ergebnisse deuten darauf hin, dass das System, auch wenn gewisse Abweichungen zu erwarten sind, durchweg gute Ergebnisse liefert.

• Empfindlichkeit gegenüber RRR:

Die auffälligste Beobachtung ist, wie sich die Leistung allein durch die Erhöhung der RRR von 1,5 auf 1,7 verbessert hat, während die Gewinnrate bei 40 % blieb. Dies unterstreicht die Bedeutung der Optimierung des Verhältnisses von Rendite zu Risiko, insbesondere bei Strategien mit geringer Gewinnrate, bei denen selbst kleine Anpassungen die Systemstabilität und Rentabilität erheblich verbessern können.

Schlussfolgerung

Diese Analyse hat sowohl mathematisch als auch durch Monte-Carlo-Simulationen deutlich gezeigt, dass die Optimierung des Rendite-Risiko-Verhältnis (RRR) für eine bestimmte Gewinnrate die Rentabilität und Stabilität eines Handelssystems drastisch verbessern kann. Wie unsere Szenarien zeigen, hat die Erhöhung der RRR von 1,5 auf 1,7 selbst bei einer festen Gewinnrate von 40 % das System von einem System mit hoher Instabilität und erheblichem Risiko des Ruins in ein System verwandelt, das konstante Gewinne mit einer geringen Wahrscheinlichkeit eines Kontenausfalls liefert.

Es ist wichtig zu betonen, dass Gewinnrate und RRR von Natur aus voneinander abhängig sind, wie in Gleichung 6 und 7 dieses Artikels gezeigt wird. Die Bemühungen um eine Optimierung der RRR wirken sich natürlich auf die effektive Gewinnrate aus und umgekehrt. Entscheidend ist, dass jede Gewinnrate eine entsprechende Mindest-RRR hat, die überschritten werden muss, um langfristige Rentabilität zu erreichen. Bei einer Gewinnrate von 40 % muss das System beispielsweise eine RRR-Schwelle von 1,5 überschreiten, um nachhaltig zu sein.

Dies wird auch durch den Erwartungswert verdeutlicht:

Bei RRR=1,5 ist die Erwartung = (0,4*1,50)- (0,6*1) = 0. Vorschlagen einer Gewinnschwelle. Dies erklärt die extreme Divergenz zwischen dem Mittelwert und dem Median.

Bei RRR=1,7 ist die Erwartung = (0,4*1,70)- (0,6*1) = 0,08. Eine positive Erwartung, die zu einem positiven Ergebnis von 96,7 % führt.

Zusammenfassend lässt sich sagen, dass viele Handelssysteme in durchgängig profitable Strategien umgewandelt werden können, indem Gewinnrate und RRR richtig ausbalanciert werden. Der Schlüssel liegt nicht nur darin, eine hohe Gewinnrate zu erzielen, sondern sicherzustellen, dass die RRR die Mindestschwelle überschreitet, die erforderlich ist, um im Laufe der Zeit eine positive Erwartungshaltung zu erzeugen.

Wenn ein Händler sowohl einen Stop-Loss als auch einen Take-Profit definiert, wird die RRR des Systems festgelegt. Damit das System während des Backtests profitabel ist, muss die Gewinnrate den für diese RRR erforderlichen Mindestwert überschreiten. In diesem Artikel finden Sie verschiedene RRR-Werte und die entsprechenden Mindestgewinnquoten. Für andere Kombinationen können die Gleichungen 6 und 7 verwendet werden, um die erforderlichen Rentabilitätsschwellen zu berechnen.

Um die langfristige Rentabilität zu bewerten, können Händler die Monte-Carlo-Simulation nutzen, um die Leistung auf der Grundlage ihrer Backtest-Statistiken zu modellieren. Durch die Simulation tausender möglicher Handelssequenzen unter Verwendung Ihrer bewährten Statistiken (Gewinnrate, RRR, Positionsgröße), Monte-Carlo-Analyse:

• Projiziert die Wahrscheinlichkeit von Erfolg/Misserfolg über längere Zeiträume.
• Ermittelt, ob die Ergebnisse auf Glück oder statistischen Zufall beruhen.
• Gibt Händlern die Möglichkeit, ihrer Strategie zu vertrauen – oder sie zu überarbeiten – bevor sie Kapital riskieren.

Ein System, das in der Simulation durchweg positive Ergebnisse liefert, bietet ein höheres Maß an Vertrauen, das es den Händlern ermöglicht, ihrer Strategie zu vertrauen und Disziplin zu wahren.

Obwohl sich dieser Artikel auf die Erwartungshaltung und die RRR-Optimierung konzentriert hat, ist es wichtig zu betonen, dass die Positionsgrößenbestimmung eine ebenso wichtige Säule der Systemleistung ist. Ohne ein solides Risikomanagement kann selbst ein System mit positiver Erwartungshaltung scheitern. Im nächsten Artikel werden wir untersuchen, wie man eine optimale Positionsgröße anwendet, um die Widerstandsfähigkeit des Systems zu verbessern und einen nachhaltigen Handelserfolg sicherzustellen.