Selbstoptimierende Expert Advisors in MQL5 (Teil 10): Matrix-Faktorisierung

In der Eröffnungsdiskussion dieser Serie, die hier verlinkt ist, haben wir versucht, ein lineares Regressionsmodell zu erstellen, indem wir nur nativen MQL5-Code und Rohdaten von unserem MetaTrader 5-Terminal verwendet haben. Nach dem Lesen der Kommentare und Rückmeldungen zum ersten Artikel haben viele Leser auf Probleme hingewiesen, die sie mit der von uns vorgestellten Lösung hatten. Sie stießen auf zahlreiche Bugs und Fehler, wobei einige darauf hinwiesen, dass das Modell nur eine Art von Position eröffnete. Allgemein wurden von mehreren Nutzern Instabilitätsprobleme in Bezug auf unseren ersten Versuch, ein lineares Modell zu erstellen, angesprochen.

Lineare Modelle sind Vorhersageinstrumente, die es unserer Anwendung ermöglichen, direkt aus Beobachtungen des Marktverhaltens zu lernen und diese Erkenntnisse zu nutzen, um Geschäfte zu platzieren, von denen sie glaubt, dass sie am wahrscheinlichsten erfolgreich sind. Unser Ziel ist es daher, der Anwendung nicht mehr explizit zu sagen, wann sie kaufen oder verkaufen soll. Stattdessen wollen wir, dass es selbständig aus vergangenen Daten lernt.

Dieser Artikel befasst sich mit den Instabilitätsproblemen, auf die die Nutzer in unserer ersten Diskussion gestoßen sind, und zeigt, wie man ebenso leistungsfähige Vorhersagemodelle aus Rohdaten erstellen kann, die einen beliebigen Markt beschreiben, mit dem Sie handeln möchten. Dazu werden wir eine Familie von Algorithmen einführen, die als Matrixfaktorisierung bekannt sind.

Die Matrixfaktorisierung ist ein mathematisches Verfahren, mit dem eine große Matrix in ein Produkt aus kleineren, einfacheren Matrizen zerlegt werden kann. Diese Techniken bringen viele Vorteile mit sich. Bevor wir uns jedoch mit diesen befassen, sollten wir zunächst die Motivation dahinter verstehen.

Im täglichen Leben gibt es bestimmte gemeinsame Erfahrungen, die kulturübergreifend sind. Ich glaube, die meisten Leser sind mit dem Gedanken vertraut, dass wir eine Vorstellung davon bekommen können, wie ein Elternteil sein könnte, wenn wir mit einem Kind sprechen und hören, wie es seine Eltern beschreibt. Diese Beschreibungen können uns sogar dabei helfen zu erraten, wie die Eltern in Situationen handeln würden, die das Kind nicht direkt beschrieben hat. In ähnlicher Weise zerlegt die Matrixfaktorisierung eine große Matrix in kleinere Matrizen – ihre „Kinder“. Diese untergeordneten Matrizen beschreiben jeweils verschiedene Aspekte der ursprünglichen Matrix und helfen uns, die zugrunde liegende Struktur zu verstehen. Genauso wie die Perspektive eines Kindes das Wesen seiner Eltern offenbaren kann, können diese kleineren Matrizen tiefgreifende Erkenntnisse über den von uns analysierten Markt liefern.

Die Ergebnisse der Matrixfaktorisierung liefern häufig numerisch stabile Lösungen für die zuvor vorgestellten linearen Modelle. In diesem Artikel wird auch eine numerische Bibliothek namens OpenBLAS – kurz für Basic Linear Algebra Subprograms – vorgestellt. OpenBLAS ist ein Open-Source-Fork der BLAS-Bibliothek, der so umgestaltet wurde, dass er auf den heutigen Rechnerarchitekturen effizient läuft. BLAS wurde ursprünglich in Fortran und handgeschriebenem Assemblercode geschrieben. 

Ein grundlegendes Konzept der linearen Algebra besagt, dass jeder Datensatz in kleinere Komponenten zerlegt werden kann und diese Komponenten zur Erstellung von Vorhersagemodellen für die ursprünglichen Daten verwendet werden können. Die Darstellungen dieser kleineren Datensätze können auch Merkmale der ursprünglichen Daten offenbaren, die sonst verborgen bleiben würden.

Dieser Artikel führt Sie behutsam in die leistungsstarken Befehle der linearen Algebra ein, mit denen Sie aus Rohdaten Vorhersagemodelle erstellen können. Und das ist erst der Anfang. Diese Matrixfaktorisierungstechniken bieten viel mehr als nur eine reine Vorhersagekraft – sie helfen uns auch, Daten zu komprimieren, verborgene Trends aufzudecken und die Stabilität oder das Chaos des Marktes zu beurteilen. Es ist wirklich bemerkenswert, wie viele Erkenntnisse wir aus jedem Datensatz gewinnen können, indem wir ihn einfach faktorisieren. Fangen wir an.

Erste Schritte in MQL5

Der erste Schritt bei den ersten Schritten mit MQL5 ist die Definition der Systemkonstanten, die wir in dieser Demonstration verwenden werden. Diese Konstanten unterstützen das Skript, das ich erstellt habe, um uns mit der Matrixfaktorisierung vertraut zu machen. 

//+------------------------------------------------------------------+
//|                                                        Solve.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/en/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| System definitions                                               |
//+------------------------------------------------------------------+
#define HORIZON 10
#define START   0

Als Nächstes legen wir die Nutzereingaben für das Skript fest – insbesondere, wie viele Balken wir abrufen möchten. 

//+------------------------------------------------------------------+
//| User inputs                                                      |
//+------------------------------------------------------------------+
input int FETCH =  10;//How many bars should we fetch?

Danach deklarieren wir unsere globalen Variablen, die Trainings- und Testdaten sowie einige andere Variablen enthalten, um die Koeffizienten zu speichern, die von unserer Anwendung aus den von uns bereitgestellten Daten gelernt wurden.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int ROWS        =   5;
//Dependent variable
matrix y,y_test;
//Indenpendent variable
matrix X = matrix::Ones(ROWS,FETCH);
matrix X_test = matrix::Ones(ROWS,FETCH);
//Coefficients
matrix b;
vector temp;
//Row Norms
vector row_norms = vector::Zeros(4);
vector error_vector = vector::Zeros(4);

Zu Beginn drucken wir die Eingabedatenmatrix X in ihrer aktuellen Form aus. Wie in Abbildung 1 dargestellt, ist diese Matrix zunächst mit Einsen gefüllt. Dies ist beabsichtigt: In einem linearen Modell stellt die erste Zeile der Eingaben den Intercept-Term dar. Tatsächliche Marktdaten – wie Eröffnungs-, Höchst-, Tiefst- und Schlusskurse – werden ab der zweiten Zeile in die Matrix eingefügt.

Ein wichtiger Punkt ist die Anordnung der Daten. Wenn Sie unsere Serie verfolgt haben, wie z. B. Reimagining Classic Strategies, in der wir Daten aus MetaTrader 5 extrahieren und in Python verarbeiten, sind Sie vielleicht an das Format gewöhnt, in dem Spalten Marktattribute (Eröffnungs-, Höchst-, Tiefst-, Schlusskurs) und Zeilen die Zeit (z. B. Tage) darstellen. In diesem Fall ist das Layout jedoch vertauscht: Die Zeit läuft entlang der Spalten, während die Marktmerkmale wie Eröffnung, Höchst-, Tiefst- und Schlusskurs entlang der Zeilen laufen.

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Observe the input matrix in its original form
PrintFormat("Input Matrix Gathered From %s",Symbol());
Print(X);

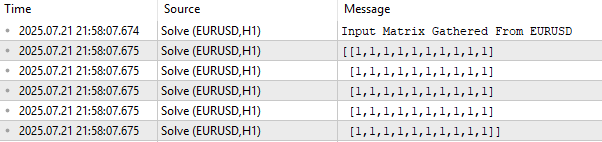
Abbildung 1: Visualisierung unserer aktuellen EURUSD-Eingangsdaten vom Markt

Nachdem dies geklärt ist, gehen wir zu dem Teil des Skripts über, der für das Abrufen historischer Marktdaten zuständig ist. Nach dem Holen speichern wir die Norm jedes Vektors und teilen dann jeden Vektor durch seine Norm. Dieser Normalisierungsschritt stellt sicher, dass jeder Vektor die Länge 1 hat, was eine wichtige Voraussetzung für die Anwendung jeglicher Form der Matrixfaktorisierung ist.

Warum normalisieren? Die Matrixfaktorisierung versucht zu verstehen, in welche Richtung eine Matrix wächst, und vergleicht die Wachstumsraten zwischen Zeilen und Spalten. Um diese Vergleiche fair zu gestalten, wandeln wir jede Zeile in einen Einheitsvektor um, indem wir sie durch ihre Norm dividieren. 

//--- Fetch the data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH*2),FETCH);
row_norms[0] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH*2),FETCH);
row_norms[1] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH*2),FETCH);
row_norms[2] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH*2),FETCH);
row_norms[3] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[3],4);

//--- Fetch the test data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[3],4);

Wenn wir die Eingabedaten für das Training ausdrucken, enthält die erste Zeile Einsen, die den Intercept darstellen, gefolgt von Zeilen für Open, High, Low, Close und schließlich den gleitenden Durchschnitt. Die Daten beginnen wegen der Normalisierung bei 0,3.

//--- The train data
Print("Input");
Print(X);

Abbildung 2: Visualisierung unserer Trainingsdaten nach Normalisierung jeder Zeile durch ihre Vektornorm

Als Nächstes definieren wir unsere Ziele. In diesem Beispiel ist das Ziel der Schlusskurs, den wir in die Matrix y kopieren. Nun enthält X unsere Eingabemerkmale und y die Werte, die wir vorhersagen wollen.

//--- Fill the target 
y.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+(FETCH*2),FETCH);
y_test.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START,FETCH);

Print("Target");
Print(y);

Abbildung 3: Die Ausgabewerte, die wir aus den uns vorliegenden Marktbeobachtungen der Vergangenheit vorherzusagen versuchten

Wie finden wir also Koeffizienten, die X auf y abbilden? Es stellt sich heraus, dass unendlich viele Koeffizientensätze dazu in der Lage sind, sodass wir eine Möglichkeit brauchen, den geeignetsten auszuwählen. In der Regel wählen wir die Koeffizienten aus, die den Fehler zwischen den vorhergesagten und den tatsächlichen Zielwerten minimieren. Eine bekannte Methode, dies zu erreichen, ist die Verwendung der Pseudo-Inverse.

Zur Berechnung der Koeffizienten wird die Pseudo-Inverse von X mit y multipliziert. Diese Matrixmultiplikation ergibt die Best-Fit-Koeffizienten in geschlossener Form. Glücklicherweise bietet MQL5 mit der Funktion PInv() (Pseudo-Inverse) eine eingebaute Funktion dafür.

Lassen Sie sich von der Einfachheit dieser Lösung nicht täuschen. Ich könnte leicht den Rest dieses Artikels damit verbringen, die Bedeutung dieser einen Codezeile zu erklären. Die Lösung der Koeffizienten, die von der MQL5-Funktion PInv() erzeugt wird, soll den RMSE-Fehler zwischen den Vorhersagen und den vergangenen Beobachtungen am besten minimieren. Außerdem ist die Existenz dieser Lösungen garantiert. Der Algorithmus ist numerisch stabil und bietet uns eine kompakte und leicht zu wartende Codebasis für die Erstellung eigener Vorhersagemodelle direkt aus Rohdaten. Dies ist jedoch nicht die empfohlene Lösung, die Sie verwenden sollten.

//--- More Penrose Psuedo Inverse Solution implemented by MQL5 Developers
b = y.MatMul(X.PInv());

Print("Pseudo Inverse Solution: ");
Print(b);

Abbildung 4: Die Koeffizienten, die sich aus der Matrixmultiplikation unseres Ziels und der Psuedo-Inverse unserer Eingaben ergeben, sind die Koeffizienten, die unseren Fehler minimieren

Ziel dieses Artikels ist es, Sie in OpenBLAS und andere Matrixfaktorisierungen einzuführen. Warum sollte man also OpenBLAS lernen, wenn MQL5 bereits eine einfache Möglichkeit bietet, Vorhersagemodelle zu erstellen, indem man einfach die von der Funktion PInv() berechneten Koeffizienten verwendet? Dafür gibt es mehrere zwingende Gründe, allen voran die Schnelligkeit. OpenBLAS ist astronomisch schneller als die eingebaute Pseudo-Inverse von MQL5. Wenn Sie lernen, damit umzugehen, wird sich die Geschwindigkeit Ihrer Backtests drastisch erhöhen.

Unüberwachte Matrixfaktorisierung: Singulärwertzerlegung

Wie in der Einleitung erwähnt, kann jede beliebige Datenmatrix in das Produkt kleinerer Matrizen zerlegt werden. Diese kleineren Matrizen kann man sich als „Kinder“ der ursprünglichen Matrix vorstellen, die jeweils eine einzigartige Beschreibung ihrer „Eltern“ bieten.

Der Algorithmus der Singulärwertzerlegung (SVD) ist eine von vielen Möglichkeiten, eine Matrix zu faktorisieren. SVD – kurz für Singular Value Decomposition – zerlegt jede Matrix in das Produkt dreier kleinerer, elementarer Matrizen. Jede dieser drei Matrizen erfasst ein bestimmtes Merkmal der ursprünglichen Matrix. In diesem Abschnitt werden wir jedes dieser drei „Kinder“ der SVD-Faktorisierung kennenlernen. Wir werden die Motivation hinter SVD erforschen und herausfinden, was jede Komponente über die ursprüngliche Matrix aussagen kann.

Bevor wir uns damit befassen, ist es wichtig, die Terminologie zu klären. Vielleicht haben Sie schon einmal den Begriff unüberwachte Matrixfaktorisierung neben der Matrixfaktorisierung gesehen, aber die beiden Begriffe sind nicht austauschbar. Die unüberwachte Matrixfaktorisierung ist eine spezielle Art der Faktorisierungstechnik. Sie unterscheidet sich von der allgemeinen Faktorisierung dadurch, dass sie sich nur auf die wichtigsten Komponenten der Daten konzentriert.

Die unüberwachte Matrixfaktorisierung gibt uns nicht alle Kinder zurück, sondern nur die wichtigsten. Der Algorithmus zerlegt die Matrix und verwendet dann seine eigenen internen Kriterien, um zu entscheiden, welche Faktoren (oder Kinder) am wertvollsten sind. Diese Entscheidung wird unüberwacht getroffen, d. h. der Algorithmus stützt sich bei der Bestimmung der Relevanz nicht auf gelabelte Ergebnisse oder menschliche Eingaben. Wir wählen nicht aus, welche Kinder wir treffen – der Algorithmus entscheidet für uns.

Wie in Abbildung 5 dargestellt, ist SVD eine solche Matrixfaktorisierungsmethode, die jede Matrix A in die Ausgabe von 3 ihrer „Kinder“ zerlegt. 

OpenBLAS ermöglicht es der SVD-Methode, alle „Kinder“ oder nur die wichtigsten „Kinder“-Matrizen zurückzugeben, dies hängt von den Parametern ab, die dem SVD-Aufruf übergeben werden.

In dieser Diskussion werden wir die OpenBLAS-Bibliothek anweisen, nur die wichtigsten „Kinder“-Matrizen an uns zurückzugeben, daher der Titel unserer Diskussion „Unüberwachte Matrixfaktorisierung“. Wie wir bereits festgestellt haben, zerlegt die SVD unsere ursprüngliche Matrix in das Produkt von 3 einfacheren, elementaren Matrizen. Wir werden nun nacheinander auf jede dieser 3 Komponenten eingehen.

Abbildung 5: Visualisierung der SVD-Faktorisierung

U beschreibt die verborgenen Marktkräfte, die das beobachtete Verhalten unseres Marktes zu „steuern“ scheinen. Diese verborgenen Kräfte sollten besser als Faktoren bezeichnet werden. Die erste Spalte von U informiert uns also über eine marktbestimmende Kraft, die alle 4 OHLC-Preise abwertet, wenn diese Kraft den Markt dominiert. Die zweite Marktkraft wird von positiven Koeffizienten dominiert, was bedeutet, dass sie sich insgesamt positiv auf den Markt auswirkt. Da wir mit historischen Marktdaten arbeiten, können diese Marktkräfte, die wir analysieren, tatsächlich die zugrundeliegende Anlegerstimmung darstellen.

//--- Native MQL5 SVD Solution are also possible without relying on OpenBLAS
Print("Computing Singular Value Decomposition using MQL5");
matrix U,VT;
vector S;
X.SVD(U,VT,S);

Print("U");
Print(U);

Abbildung 6: Die Komponente „U“ der SVD verstehen

V beschreibt uns, wie stark jede der Kräfte in U entlang aller Zeitbeobachtungen im Originaldatensatz ausgeprägt ist. Wenn wir zum Beispiel die erste Zeile von V betrachten, sehen wir, dass der größte Eintrag 0,4262 ist. Dieser Wert steht in der 3. Spalte der ersten Zeile von V, was bedeutet, dass die 3. Spalte von U die Kraft beschreibt, die den Markt am ersten historischen Handelstag beherrschte. Die 3. Spalte von U beschreibt eine gemischte Kraft, die einige Komponenten des Preises negativ und andere positiv beeinflusst. Diese Kräfte können intermittierend oder schwach sein.

Print("VT");
Print(VT);

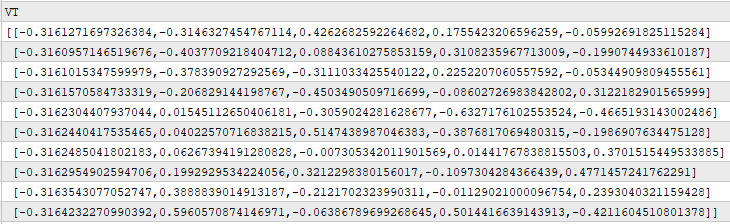
Abbildung 7: Verstehen, wie ausgeprägt die einzelnen treibenden Kräfte des Marktes zu jedem Zeitpunkt sind

Der Sigma-Faktor informiert uns über die Wichtigkeit jeder der in U beschriebenen Marktkräfte. Der Kraft, die unsere historischen Beobachtungen dominiert, wird der größte Wert in Sigma zugewiesen, Kräften, die in den Daten weniger ausgeprägt sind, werden kleinere Werte in Sigma zugewiesen. Wir können also deutlich sehen, dass 3,741 der größte Wert in Sigma ist, und dieser Wert steht in der ersten Spalte von Sigma, was bedeutet, dass die erste Spalte von U die dominanteste Marktkraft beschreibt, die in den Daten beobachtet wurde.

Print("S");
Print(S);

Abbildung 8: Verstehen des Sigma-Faktors aus der SVD-Faktorisierung

Diese Diskussion erhebt keinen Anspruch auf Vollständigkeit, es gibt noch viel mehr, was über die drei Faktoren U, S und V gesagt werden kann. In den Abbildungen 6, 7 und 8 haben wir analysiert, was zurückgegeben wurde, als wir die SVD-Methode aufriefen, die nativ in MQL5 eingebaut ist. Diese Ergebnisse entsprechen weitgehend dem, was beim Aufruf von SingularValueDecompositionDC() aus der OpenBLAS-Bibliothek zurückgegeben wird.

Der Leser kann Abbildung 9 und Abbildung 6 vergleichen, um zu erfahren, dass sowohl die native MQL5-Funktion als auch die OpenBLAS-Funktion ungefähr den gleichen U-Faktor berechnen. Aufgrund von Unterschieden in den Funktionen, die unter der Haube implementiert sind, stimmen die beiden Zahlen nicht bis zur letzten Dezimalstelle überein, aber das ist verständlich.

//--- OpenBLAS SVD Solution, considerably powerful substitute to the closed solution provided by the MQL5 developers 
matrix OB_U,OB_VT,OB_SIGMA;
vector OB_S;

//--- Perform truncated SVD, we will explore what 'truncated' means later.
PrintFormat("Computing Singular Value Decomposition of %s Data using OpenBLAS",Symbol());
X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);

//--- U is a unitary matrix that is of dimension (m,r)
Print("Open BLAS U");
Print(OB_U);

Abbildung 9: Der von OpenBLAS berechnete U-Faktor

In Abbildung 4 oben haben wir gezeigt, dass die MQL5-Funktion PInv() immer die Koeffizienten liefert, die die Eingaben mit dem geringstmöglichen Fehler auf das Ziel abbilden. Ich möchte noch einmal betonen, dass Sie sich von der Einfachheit der in Abbildung 4 dargestellten Lösung nicht täuschen lassen sollten. Es handelt sich um eine mathematisch starke Lösung, die garantiert für jede beliebige Matrix A existiert und auch die L2-Norm der Matrix Ax-b minimiert. 

Was wir in Abbildung 4 nicht erwähnt haben, ist, dass die Funktion PInv() eigentlich nur die Funktion SVD() in Ihrem Namen aufrufen könnte. Mathematisch gesehen wird die Psuedo-Inverse normalerweise anhand der Singulärwertzerlegung der Originaldaten berechnet. Davon können wir uns selbst überzeugen.

In dem nachstehenden Codeschnipsel habe ich die 3 Kindermatrizen genommen, die wir gespeichert haben, als wir SVD() für unsere Marktdaten aufgerufen haben. Wir werden nicht explizit auf alle Regeln der linearen Algebra eingehen, die der Leser verstehen muss, und wir werden auch nicht versuchen, diese Lösung abzuleiten, sondern ich möchte nur zeigen, dass ich lineare Koeffizienten erhalten kann, die meine Eingabedaten und mein Ziel leicht abbilden, indem ich die Kindermatrizen verwende, die SVD mir zurückgegeben hat.

Print("Comparing OLS Solutions");
Print("Native MQL5 Solution");
//--- We will always benchmark the native solution as the truth, the MQL5 developers implemented an extremely performant benchmark for us
Print(b);

//--- The OpenBLAS solution came closest to the native solution implemented for us
Print("OpenBLAS Solution");
matrix ob_solution = y.MatMul(OB_VT.Transpose().MatMul(OB_SIGMA.Inv()).MatMul(OB_U.Transpose()));
Print(ob_solution);

//--- Our manual solution was not even close! We will therefore rely on the OpenBLAS solution.
Print("Manual SVD Solution");
matrix svd_solution = y.MatMul(VT).MatMul(SIGMA.Inv()).MatMul(U.Transpose());
Print(svd_solution);

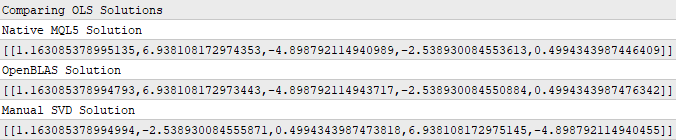
Abbildung 10: Die Koeffizienten, die meine Eingabedaten und meine Ausgabedaten am besten abbilden, können durch SVD ermittelt werden

Aufmerksamen Lesern ist sicherlich aufgefallen, dass keiner der in Abbildung 10 dargestellten Koeffizienten genau übereinstimmt. Dies ist zu erwarten, da wir 3 verschiedene Funktionen verwendet haben, um jeden Satz von Koeffizienten zu erhalten. Das ist so, als hätte man 3 unabhängige Schüler, die ihre Hausaufgaben nach ihren eigenen Methoden erledigen. Was uns jedoch mehr interessiert, ist der Fehler, den diese Koeffizienten verursachen, wenn wir sie verwenden, um Vorhersagen über Daten zu treffen, die wir nicht zum Trainieren des Modells verwendet haben.

Wie in Abbildung 11 zu sehen ist, ergab die OpenBLAS SVD-Lösung den geringsten Fehler bei der Vorhersage der Testdaten. Ich möchte jedoch sicherstellen, dass der Leser Abbildung 11 nicht mit der Motivation für die Einführung von OpenBLAS verwechselt. 

Beachten Sie, dass alle 3 Fehlerniveaus mäßig nahe beieinander liegen. Wenn wir diesen Test also mehrfach wiederholen, und zwar auf verschiedenen Märkten, und bei jeder Testrunde unterschiedliche Datenmengen abrufen, kann es sein, dass OpenBLAS nicht immer den geringsten Fehler produziert. Ich möchte, dass der Leser versteht, dass die OpenBLAS-Bibliothek für uns attraktiv ist, weil sie sorgfältig optimiert ist und aktiv gewartet wird, um schnell und zuverlässig zu sein. Es ist nicht garantiert, dass sie immer den geringsten Fehler produziert, keine einzelne Bibliothek kann einen so umfassenden Anspruch erheben.

//--- Measuring the amount of error
//--- Information lost by MQL5 PsuedoInverse solution
//--- The Frobenius norm squares all 
PrintFormat("Information Loss in Forcasting %s Market : ",Symbol());
Print("PInv: ");
matrix pinv_error = ((b.MatMul(X_test)) - y_test);
Print(pinv_error.Norm(MATRIX_NORM_FROBENIUS));

//--- Let the MQL5 implementation be our benchmark
double benchmark = pinv_error.Norm(MATRIX_NORM_FROBENIUS);

//--- Information lost by Manual SVD solution
Print("Manual SVD: ");
matrix svd_error = ((svd_solution.MatMul(X_test)) - y_test);
Print(svd_error.Norm(MATRIX_NORM_FROBENIUS));

//--- Information lost by OpenBLAS SVD solution
Print("OpenBLAS SVD: ");
matrix ob_error = ((ob_solution.MatMul(X_test)) - y_test);
Print(ob_error.Norm(MATRIX_NORM_FROBENIUS));

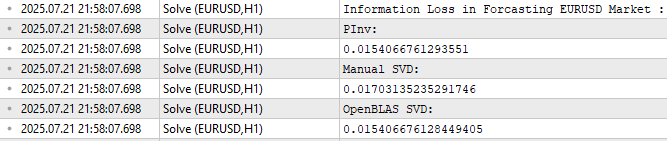
Abbildung 11: Die Höhe des Fehlers, den jeder Satz von Koeffizienten bei der Vorhersage außerhalb des Trainingszeitraums verursacht

Anwendungen der unüberwachten Matrixfaktorisierung über die prädiktive Modellierung hinaus

Ich hoffe, dass ich Ihnen mit meiner einfachen Darstellung eine Vorstellung davon vermitteln konnte, was die Matrixfaktorisierung ist und warum sie bei der Analyse von Finanzmarktdaten nützlich sein kann. Wie ich bereits erwähnt habe, stellen die Vorhersagemodelle, die wir mit Hilfe geeigneter Matrixfaktorisierungen erstellen können, nur einen Bruchteil der nützlichen Aufgaben dar, die wir mit Hilfe der Matrixfaktorisierung bewältigen können. In diesem Abschnitt möchte ich weitere nützliche Anwendungen der Matrixfaktorisierung vorstellen und zeigen, wie wir diese Erkenntnisse in unsere Handelsanwendungen und -strategien einbeziehen können.

Matrixfaktorisierung für unüberwachte Marktfilterung

Ich gehe davon aus, dass der Leser eine gewisse persönliche Erfahrung mit dem Handel hat und dass er aus seiner eigenen Praxis ein gewisses Verständnis für die Frage hat, die ich jetzt stelle. Welche der beiden Anlageklassen, der Devisenmarkt und der Markt für Kryptowährungen, ist Ihrer Meinung nach volatiler? 

Ich hoffe, die Antwort war für uns alle offensichtlich. Kryptowährungen sind weitaus volatiler als traditionelle Währungsmärkte. Für Leser, die sich nicht sicher sind, was die Wahrheit ist, haben wir den Indikator Average True Range (ATR) auf den 1-Minuten-Chart von Bitcoin in Ethereum angewendet (Abbildung 12), und der zweite Chart zeigt den Euro in US-Dollar (Abbildung 13). Der ATR-Indikator misst die Volatilität des Marktes, wobei größere ATR-Werte auf volatilere Marktbedingungen hindeuten. Der ATR-Wert auf dem BTCETH-Chart ist etwa 6000% größer als der ATR-Wert auf dem EURUSD-Chart. Daher hilft dies allen Lesern zu verstehen, warum die Märkte für Kryptowährungen im Allgemeinen als weitaus volatiler gelten als die traditionellen Währungsmärkte.

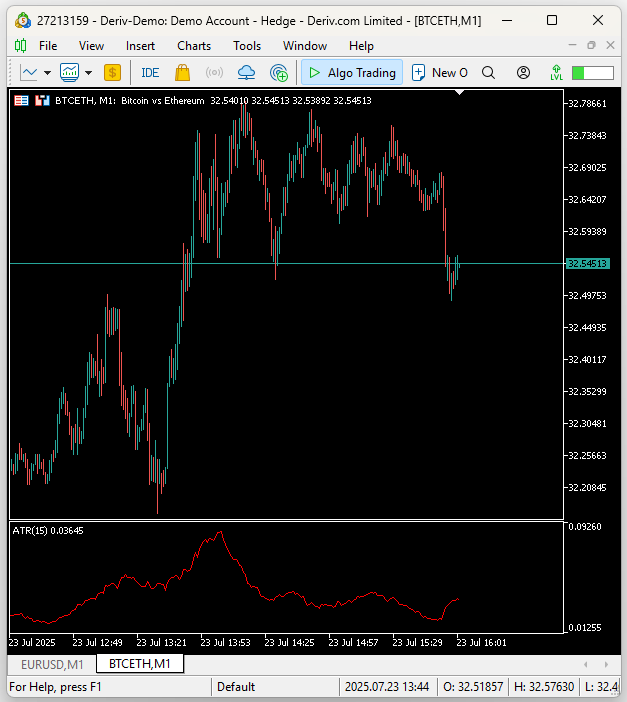
Abbildung 12: Der Volaitlitätswert von BTCETH ist wesentlich volatiler als der von EURUSD

Erinnern Sie sich daran, dass EURUSD das liquideste Währungspaar der Welt ist. EURUSD ist das am aktivsten gehandelte Währungspaar, das der Menschheit bekannt ist, aber sein Volatilitätsniveau ist im Vergleich zu der Volatilität, die wir auf den Kryptowährungsmärkten beobachten, verschwindend gering.

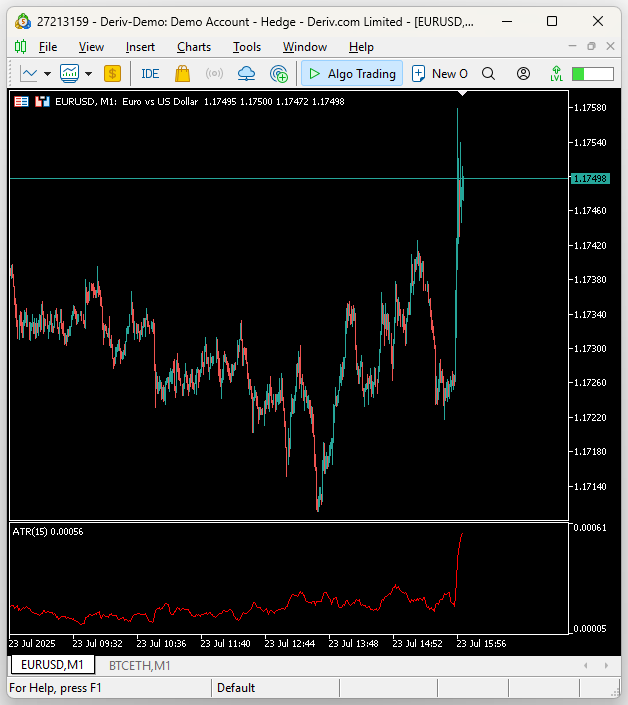
Abbildung 13: Die Volatilität traditioneller Anlageklassen ist kein Vergleich zur Volatilität der Kryptowährungsmärkte

Die Matrixfaktorisierungen, die wir zuvor durchgeführt haben, hätten uns leicht dieselben Informationen liefern können. Wir erinnern daran, dass wir in Abbildung 8 erklärt haben, dass der Faktor Sigma die Bedeutung der einzelnen in den Daten vorkommenden marktbestimmenden Kräfte angibt. Stabile Märkte haben nur einen großen Eintrag im S-Faktor, und alle anderen Einträge liegen nahe bei 0. Je mehr Einträge in S, die weit von 0 entfernt sind, desto chaotischer und volatiler scheint ein Markt den Daten zufolge zu sein.

Wir können unser Skript zweimal anwenden, einmal auf den EURUSD-Markt und das zweite Mal auf den BTCETH-Markt. Die Abbildungen 14 und 15 zeigen jedoch, dass beide Märkte stabil sind. Es scheint, dass beide Märkte nur einen großen Nicht-Null-Eintrag in S haben. Das würde bedeuten, dass BTCETH genauso stabil ist und sich gut verhält wie EURUSD. Dies ist jedoch nicht die ganze Wahrheit. Damit wir uns ein zuverlässiges Bild machen können, müssen wir eine weitere Anwendung der Matrixfaktorisierung lernen.

//+------------------------------------------------------------------+
//| What are we demonstrating here?                                  |
//| 1) We have shown you that any matrix of market data you have,    |
//|    can be analyzed intelligently, to build a linear regression   |
//|    model, using just the raw data.                               |
//| 2) We have demonstrated that the solution to such Linear         |
//|    regression problems, can be obtained through effecient and    |
//|    dedicated functions available in MQL5 or through matrix       |
//|    factorization.                                                |   
//|__________________________________________________________________|
//| I now ask the reader the following question:                     |
//|  "If dedicated functions exist, why bother learning matrix       |
//|   factorization?"                                                |
//+------------------------------------------------------------------+

//--- Matrix factorization gives us a description of the data and it properties
//--- Questions such as: "How stable/chaotic is the market we are in?" can be answered by the factorization we have just performed
//--- Or even questions such as: "How best can I expose the hidden trends in all of this market data?" can still be answered by the factorization we have just performed
//--- I'm only trying to give you a few examples of why you should bother learning these factorizations, even though dedicated functions exist.

//--- Any given matrix A can be represented as the sum of smaller matrices A = USV, this is theorem behind the Singular Value Decomposition.
//--- Each factor is special because each describes different charectersitics of its parent.

//--- Let's get to know Sigma, represented as the S in A = USV.
//--- Sigma technically tells us how many different modes our market appears to exist in, and how important each mode is. 
//--- However, reintepreted in terms of market data, these modes may correspond to investor sentiment.
PrintFormat("Taking a closer look at The Eigenvalues of %s Market Data: ",Symbol());
Print(OB_S/OB_S.Sum());
Print("If sigma has a only few values that are far from 0, then investor's sentiment in this market appears well established and hardly changes");
//--- If Sigma has a lot values that are all far away from 0, then the market is chaotic and it appears investor's sentiment and expectations constantly change
//--- If Sigma has a few, or even just one value that is far away from 0, then investor sentiment in that market appears stable, and hardly changes.
//--- Traders explicitly looking for fast-action scalping oppurtunities may use Sigma as a filter of how much energy the market has. 
//--- Quiet market will have a few dominant values in Sigma, not ideal for scalpers, better suited for long-term trend traders.

Abbildung 14: Visualisierung der Energiemenge auf dem EURUSD-Markt.

Abbildung 15: Visualisierung der Energiemenge auf dem BTCETH-Markt

Matrixfaktorisierung für Datenkomprimierung und Signalextraktion

Die Matrixfaktorisierung kann auch verwendet werden, um Daten zu komprimieren und das dominante Signal in den Daten zu extrahieren. Da die Kind-Matrizen gleichmäßiger sind als ihre Eltern, können diese Algorithmen die Daten effizient verdichten. Diese Eigenschaften der Matrixfaktorisierung sind allen unseren Community-Mitgliedern bekannt, die einen Hintergrund in Bereichen wie Netzwerktechnik, Signalverarbeitung, Elektrotechnik oder anderen verwandten Gebieten haben. Wir können unsere ursprünglichen Daten komprimieren, indem wir die Matrizen S „Kind“ und V „Kind“ multiplizieren. Beachten Sie, dass wir die Methode Diag() für S aufrufen, um es in eine Diagonalmatrix umzuwandeln, bevor wir die Multiplikation durchführen. Das Produkt dieser Multiplikation ist eine neue und kompakte Repräsentation der Muttermatrix.

Der Leser wird mit diesem Algorithmus bereits vertraut sein, er ist gemeinhin als Hauptkomponentenanalyse (PCA) bekannt. Wir werden nicht tief in die PCA eintauchen, sondern ich versuche nur zu zeigen, wie viele nützliche Informationen wir durch die Verwendung der Matrixfaktorisierung gewinnen. Es gibt viele Möglichkeiten, die Hauptkomponenten Ihrer Marktdaten zu berechnen; die Matrixfaktorisierung mit OpenBLAS gehört wahrscheinlich zu den schnellsten Methoden, die Ihnen nativ in MQL5 zur Verfügung stehen.

//--- Fetch the data and prepare to perform PCA
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH*2),FETCH);
row_norms[0] = temp.Mean();
X.Row(temp-row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH*2),FETCH);
row_norms[1] = temp.Mean();
X.Row(temp-row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH*2),FETCH);
row_norms[2] = temp.Mean();
X.Row(temp-row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH*2),FETCH);
row_norms[3] = temp.Mean();
X.Row(temp-row_norms[3],4);

//--- Fetch the test data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[3],4);

//--- Perform truncated SVD, we will explore what 'truncated' means later.
Print("Computing Singular Value Decomposition using OpenBLAS");
X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);

OB_SIGMA.Diag(OB_S);

//--- Calculating Principal Components
Print("Principal Components");
matrix pc = OB_SIGMA.MatMul(OB_VT);
Print(pc);

Abbildung 16: Durch Multiplikation der Faktoren S und V erhalten wir eine kompakte Darstellung unseres ursprünglichen Datensatzes

Über das Produkt, das sich aus der Multiplikation der „Kinder“ von S und V ergibt, kann man noch viel mehr diskutieren. Das Produkt dieser Multiplikation ergibt eine neue Darstellung unseres Datensatzes, die deutlich weniger Korrelation aufweist. Um dies zu beweisen, vergleichen wir die Norm der Korrelationsmatrix aus unserem ursprünglichen Datensatz mit der Korrelationsmatrix aus dem Produkt der Multiplikation von S und V. Erinnern Sie sich daran, dass die Norm in der Linearen Algebra der Frage entspricht, „wie groß“ etwas ist. Wie in Abbildung 17 zu sehen ist, ist die Norm der Korrelationsmatrix nach der Faktorisierung der ursprünglichen Marktdaten erheblich gesunken.

Damit soll dem Leser veranschaulicht werden, dass die Matrixfaktorisierung mit SVD dazu verwendet werden kann, redundante korrelierte Merkmale aus dem ursprünglichen Datensatz zu entfernen, und dass wir dadurch hoffentlich die vorherrschenden Trends und Muster in den Daten besser herausarbeiten können.

//--- PCA reduces the amount of correlation in our dataset 
Print("How correlated is our new representation of the data?");
//--- First we will measure the size of our original correlation matrix
Print(X.Norm(MATRIX_NORM_FROBENIUS));
//--- Then, we will measure the size of our new correlation matrix produced by factorizing the data
Print(pc.CorrCoef().Norm(MATRIX_NORM_FROBENIUS));

Abbildung 17: Die Matrixfaktorisierung kann uns dabei helfen, die Korrelation in unserem Datensatz erheblich zu reduzieren

Mit diesen Informationen können wir ein Marktmodell erstellen, das nur 3 Datenzeilen anstelle der ursprünglichen 5 Datenzeilen verwendet, mit denen wir begonnen haben. Es bleibt zu hoffen, dass diese 3 weniger korrelierten Zeilen die Beziehung zwischen dem Markt und dem Ziel besser erklären als die ursprünglichen Daten. Dies wird als Merkmalsextraktion bezeichnet, da wir neue Merkmale aus den Originaldaten lernen. Aber wie bei den meisten Optimierungsverfahren ist nicht garantiert, dass dies unsere Leistung in Zukunft verbessert, wie in Abbildung 18 zu sehen ist.

//--- Main principal components
matrix mpc;

mpc.Row(pc.Row(0),0);
mpc.Row(pc.Row(1),1);
mpc.Row(pc.Row(2),2);

//--- The factor VT describes the correlational structure across the columns of our data
Print("Performing PCA");
matrix pca_coefs = y.MatMul(mpc.PInv());

//--- Performing PCA on the test data
X_test.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);
Print("Principal Components of Test Data");
pc = OB_SIGMA.MatMul(OB_VT);

Print(pc);

PrintFormat("Most Important Principal Components in %s Market Test Data",Symbol());
Print(OB_S / OB_S.Sum());

//--- Main principal components
mpc.Row(pc.Row(0),0);
mpc.Row(pc.Row(1),1);
mpc.Row(pc.Row(2),2);

matrix pca_error = pca_coefs.MatMul(mpc) - y_test;

Print("PCA Error: ");
Print(pca_error.Norm(MATRIX_NORM_FROBENIUS));

Print("OpenBLAS Error: ");
Print(ob_error.Norm(MATRIX_NORM_FROBENIUS));

Print("Manual Error: ");
Print(svd_error.Norm(MATRIX_NORM_FROBENIUS));

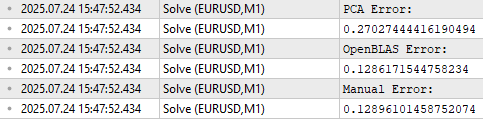
Abbildung 18: Die Merkmalsextraktion ist eine leistungsstarke numerische Methode, die jedoch keine Garantie für eine bessere Leistung bietet.

In den Abbildungen 14 und 15 haben wir versucht zu veranschaulichen, dass die Matrixfaktorisierung genutzt werden kann, um stabile Märkte von volatilen Märkten zu unterscheiden. In unserem ersten Versuch schienen beide Märkte nur einen großen Wert im S-Faktor zu haben. Nach sorgfältiger Prüfung der Daten stellte ich jedoch fest, dass dies nur auf die Zuggarnitur zutraf. Wenn wir den Testsatz unserer Marktdaten faktorisieren und dann den erhaltenen Faktor S analysieren, können wir feststellen, dass BTCETH tatsächlich mehr „Energie“ hat als EURUSD, denn BTCETH hat zwei Einträge in S, die weit von 0 entfernt sind, während EURUSD nur einen hat.

//--- Performing PCA on the test data
X_test.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);
Print("Principal Components of Test Data");
pc = OB_SIGMA.MatMul(OB_VT);


PrintFormat("Most Important Principal Components in %s Market Test Data",Symbol());
Print(OB_S / OB_S.Sum());

Abbildung 19: Analyse der im EURUSD-Markt enthaltenen Energiemenge

Abbildung 19: Analyse der im BTCEHTH-Markt enthaltenen Energiemenge. Es sei daran erinnert, dass der Markt umso chaotischer ist, je mehr einzelne Einträge weit entfernt von 0 zu beobachten sind.

Alles in allem ist dies das MQL5-Skript, das ich für unsere Diskussion über unüberwachte Matrixfaktorisierung vorbereitet habe.

//+------------------------------------------------------------------+
//|                                                        Solve.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/en/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| System definitions                                               |
//+------------------------------------------------------------------+
#define HORIZON 10
#define START   0

//+------------------------------------------------------------------+
//| User inputs                                                      |
//+------------------------------------------------------------------+
input int FETCH =  10;//How many bars should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int ROWS        =   5;
//Dependent variable
matrix y,y_test;
//Indenpendent variable
matrix X = matrix::Ones(ROWS,FETCH);
matrix X_test = matrix::Ones(ROWS,FETCH);
//Coefficients
matrix b;
vector temp;
//Row Norms
vector row_norms = vector::Zeros(4);
vector error_vector = vector::Zeros(4);

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Observe the input matrix in its original form
PrintFormat("Input Matrix Gathered From %s",Symbol());
Print(X);
  
//--- Fetch the data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH*2),FETCH);
row_norms[0] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH*2),FETCH);
row_norms[1] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH*2),FETCH);
row_norms[2] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH*2),FETCH);
row_norms[3] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[3],4);

//--- Fetch the test data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[3],4);

//--- The train data
Print("Input");
Print(X);

//--- Fill the target
y.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+(FETCH*2),FETCH);
y_test.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START,FETCH);

Print("Target");
Print(y);

//--- More Penrose Psuedo Inverse Solution implemented by MQL5 Developers, enterprise level effeciency!
b = y.MatMul(X.PInv());

Print("Pseudo Inverse Solution: ");
Print(b);

//--- Native MQL5 SVD Solution are also possible without relying on OpenBLAS
Print("Computing Singular Value Decomposition using MQL5");
matrix U,VT;
vector S;
X.SVD(U,VT,S);

Print("U");
Print(U);

Print("VT");
Print(VT);

Print("S");
Print(S);
matrix SIGMA;
SIGMA.Diag(S);

//--- OpenBLAS SVD Solution, considerably powerful substitute to the closed solution provided by the MQL5 developers 
matrix OB_U,OB_VT,OB_SIGMA;
vector OB_S;

//--- Perform truncated SVD, we will explore what 'truncated' means later.
PrintFormat("Computing Singular Value Decomposition of %s Data using OpenBLAS",Symbol());
X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);

//--- U is a unitary matrix that is of dimension (m,r)
Print("Open BLAS U");
Print(OB_U);

//--- VT is a mathematically a symmetrical matrix that is (r,r), for effeciency in software it is represented as a vector that is (1,r)
Print("Open BLAS VT");
Print(OB_VT);

//--- We need it in its intended form as an (r,r) matrix, we will explore what this means later. 
Print("Open BLAS S");
Print(OB_S);
OB_SIGMA.Diag(OB_S);

Print("Comparing OLS Solutions");
Print("Native MQL5 Solution");
//--- We will always benchmark the native solution as the truth, the MQL5 developers implemented an extremely performant benchmark for us
Print(b);

//--- The OpenBLAS solution came closest to the native solution implemented for us
Print("OpenBLAS Solution");
matrix ob_solution = y.MatMul(OB_VT.Transpose().MatMul(OB_SIGMA.Inv()).MatMul(OB_U.Transpose()));
Print(ob_solution);

//--- Our manual solution was not even close! We will therefore rely on the OpenBLAS solution.
Print("Manual SVD Solution");
matrix svd_solution = y.MatMul(VT).MatMul(SIGMA.Inv()).MatMul(U.Transpose());
Print(svd_solution);

//--- Measuring the amount of error
//--- Information lost by MQL5 PsuedoInverse solution
//--- The Frobenius norm squares all 
PrintFormat("Information Loss in Forcasting %s Market : ",Symbol());
Print("PInv: ");
matrix pinv_error = ((b.MatMul(X_test)) - y_test);
Print(pinv_error.Norm(MATRIX_NORM_FROBENIUS));

//--- Let the MQL5 implementation be our benchmark
double benchmark = pinv_error.Norm(MATRIX_NORM_FROBENIUS);

//--- Information lost by Manual SVD solution
Print("Manual SVD: ");
matrix svd_error = ((svd_solution.MatMul(X_test)) - y_test);
Print(svd_error.Norm(MATRIX_NORM_FROBENIUS));

//--- Information lost by OpenBLAS SVD solution
Print("OpenBLAS SVD: ");
matrix ob_error = ((ob_solution.MatMul(X_test)) - y_test);
Print(ob_error.Norm(MATRIX_NORM_FROBENIUS));

//+------------------------------------------------------------------+
//| What are we demonstrating here?                                  |
//| 1) We have shown you that any matrix of market data you have,    |
//|    can be analyzed intelligently, to build a linear regression   |
//|    model, using just the raw data.                               |
//| 2) We have demonstrated that the solution to such Linear         |
//|    regression problems, can be obtained through effecient and    |
//|    dedicated functions available in MQL5 or through matrix       |
//|    factorization.                                                |   
//|__________________________________________________________________|
//| I now ask the reader the following question:                     |
//|  "If dedicated functions exist, why bother learning matrix       |
//|   factorization?"                                                |
//+------------------------------------------------------------------+

//--- Matrix factorization gives us a description of the data and it properties
//--- Questions such as: "How stable/chaotic is the market we are in?" can be answered by the factorization we have just performed
//--- Or even questions such as: "How best can I expose the hidden trends in all of this market data?" can still be answered by the factorization we have just performed
//--- I'm only trying to give you a few examples of why you should bother learning these factorizations, even though dedicated functions exist.

//--- Any given matrix A can be represented as the sum of smaller matrices A = USV, this is theorem behind the Singular Value Decomposition.
//--- Each factor is special because each describes different charectersitics of its parent.

//--- Let's get to know Sigma, represented as the S in A = USV.
//--- Sigma technically tells us how many different modes our market appears to exist in, and how important each mode is. 
//--- However, reintepreted in terms of market data, these modes may correspond to investor sentiment.
PrintFormat("Taking a closer look at The Eigenvalues of %s Market Data: ",Symbol());
Print(OB_S/OB_S.Sum());
Print("If sigma has a only few values that are far from 0, then investor's sentiment in this market appears well established and hardly changes");
//--- If Sigma has a lot values that are all far away from 0, then the market is chaotic and it appears investor's sentiment and expectations constantly change
//--- If Sigma has a few, or even just one value that is far away from 0, then investor sentiment in that market appears stable, and hardly changes.
//--- Traders explicitly looking for fast-action scalping oppurtunities may use Sigma as a filter of how much energy the market has. 
//--- Quiet market will have a few dominant values in Sigma, not ideal for scalpers, better suited for long-term trend traders.

//--- Fetch the data and prepare to perform PCA
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH*2),FETCH);
row_norms[0] = temp.Mean();
X.Row(temp-row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH*2),FETCH);
row_norms[1] = temp.Mean();
X.Row(temp-row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH*2),FETCH);
row_norms[2] = temp.Mean();
X.Row(temp-row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH*2),FETCH);
row_norms[3] = temp.Mean();
X.Row(temp-row_norms[3],4);

//--- Fetch the test data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[3],4);

//--- Perform truncated SVD, we will explore what 'truncated' means later.
Print("Computing Singular Value Decomposition using OpenBLAS");
X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);

//--- Calculating Principal Components
Print("Principal Components");
matrix pc = OB_SIGMA.MatMul(OB_VT);
Print(pc);

PrintFormat("Most Important Principal Components of %s Market Data",Symbol());
Print(OB_S / OB_S.Sum());

//--- Main principal components
matrix mpc;

mpc.Row(pc.Row(0),0);
mpc.Row(pc.Row(1),1);
mpc.Row(pc.Row(2),2);

//--- The factor VT describes the correlational structure across the columns of our data
Print("Performing PCA");
matrix pca_coefs = y.MatMul(mpc.PInv());

//--- Performing PCA on the test data
X_test.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);
Print("Principal Components of Test Data");
pc = OB_SIGMA.MatMul(OB_VT);

Print(pc);

PrintFormat("Most Important Principal Components in %s Market Test Data",Symbol());
Print(OB_S / OB_S.Sum());

//--- Main principal components
mpc.Row(pc.Row(0),0);
mpc.Row(pc.Row(1),1);
mpc.Row(pc.Row(2),2);

matrix pca_error = pca_coefs.MatMul(mpc) - y_test;

Print("PCA Error: ");
Print(pca_error.Norm(MATRIX_NORM_FROBENIUS));

Print("OpenBLAS Error: ");
Print(ob_error.Norm(MATRIX_NORM_FROBENIUS));

Print("Manual Error: ");
Print(svd_error.Norm(MATRIX_NORM_FROBENIUS));

}
//+------------------------------------------------------------------+

Aufbau unserer Anwendung

Wir werden damit beginnen, alles, was wir bisher besprochen haben, zu einer einzigen Handelsstrategie zu kombinieren. Unsere Strategie zielt darauf ab, einen fairen Marktpreis zu ermitteln, indem wir den zukünftigen Wert des gleitenden Durchschnittsindikators prognostizieren. Dieser Erwartungswert hilft uns bei der Platzierung unserer Geschäfte in dem Sinne, dass wir bei Kursen, die über unseren Erwartungen liegen, verkaufen, weil wir den Markt für überbewertet halten, während bei unseren Long-Positionen das Gegenteil der Fall ist. 

Wenden wir einen gleitenden 10-Perioden-Durchschnitt auf das EURUSD-Tageschart an und verschieben ihn nach vorne, um uns seinen verschobenen Wert als unsere Vorhersage vorzustellen.

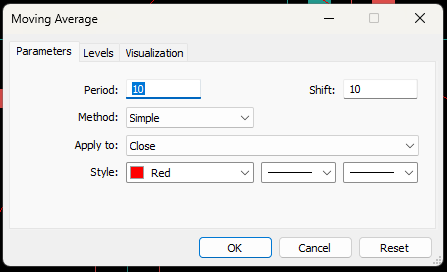
Abbildung 20: Zur Veranschaulichung haben wir den Indikator des gleitenden Durchschnitts einfach um 10 Schritte nach vorne verschoben

Unsere Handelsstrategie geht im Wesentlichen davon aus, dass sich die aktuellen Kursniveaus schließlich dem erwarteten Wert angleichen werden. In dem in Abbildung 21 dargestellten Szenario ist der erwartete Preis niedrig, während der aktuelle Preis hoch ist. Angenommen, Abbildung 21 wurde durch unsere Marktprognose generiert – dies wäre unser Signal.

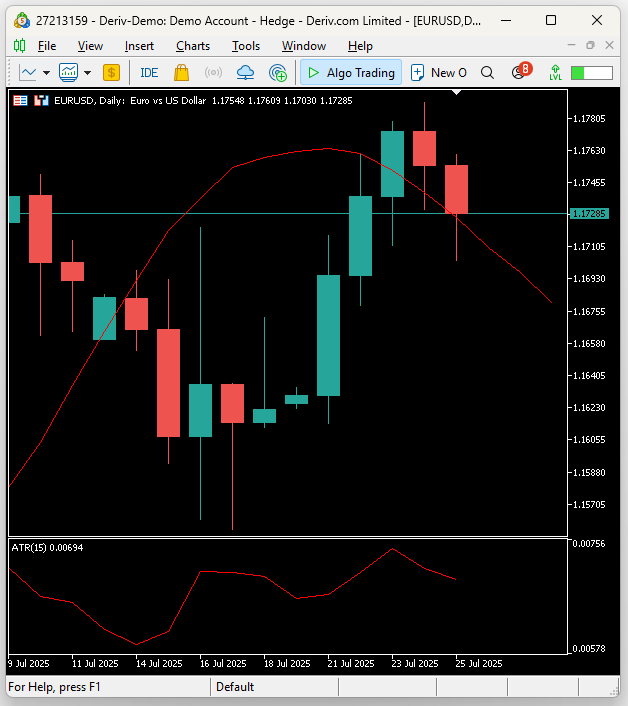
Abbildung 21: Zur Veranschaulichung unserer Handelsstrategie bedeutet der verschobene gleitende Durchschnitt, dass wir auf der Grundlage des von unserem Modell erwarteten Stands des gleitenden Durchschnitts handeln.

Festlegung einer Basislinie

Bevor wir unsere Anwendung entwickeln, müssen wir eine Basislinie erstellen, um die Leistung unseres KI-Modells zu bewerten. Dieser Ausgangswert zeigt das erwartete Ergebnis ohne den Einsatz von AI. Da wir uns in den folgenden Abschnitten mit der vollständigen Implementierung unserer Anwendung befassen werden, möchte ich nun kurz auf die wichtigsten Elemente der Basisanwendung eingehen.

//+------------------------------------------------------------------+
//| Obtain a prediction from our model                               |
//+------------------------------------------------------------------+
void setup(void)
  {
   y.CopyIndicatorBuffer(ma_close_handler,0,0,bars);
   
   Print("Training Target");
   Print(y);

//--- Get a prediction
   prediction = y.Mean();
   Print("Prediction");
   Print(prediction);
  }
//+------------------------------------------------------------------+

Die Basislinie macht ihre Vorhersagen, indem sie gleitende Durchschnittswerte von Indikatoren repliziert, ihren Mittelwert berechnet und auf dieser Grundlage handelt. Wenn der Mittelwert des gleitenden Durchschnittsindikators über dem aktuellen Kurs liegt, kaufen wir, andernfalls verkaufen wir.

if(prediction > c)
  {
   Trade.Buy(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetAsk(),proposed_buy_sl,0);
   state = 1;
  }
if(prediction < c)
  {
   Trade.Sell(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetBid(),proposed_sell_sl,0);
   state = -1;
  }

Wir werden unsere Anwendung nun auf das Paar USD/UL anwenden, wie in Abbildung 22 dargestellt, und dabei zwei Jahre historische Daten von Januar 2023 bis März 2025 verwenden.

Abbildung 22: Testen unserer Basisanwendung anhand historischer Marktdaten

Abbildung 23 zeigt die von uns verwendeten Anwendungseinstellungen. Um faire Vergleiche zu gewährleisten, ist es wichtig, dass diese Eingabeeinstellungen für alle Tests gleich bleiben.

Abbildung 23: Wir werden unsere Benchmark-Parameter beibehalten, um faire Vergleiche zu gewährleisten.

Abbildung 24 zeigt die durch unsere Handelsstrategie erzeugte Aktienkurve. Die Ergebnisse zeigen, dass unser Ansatz solide ist und sich der Kontostand im Laufe der Zeit positiv entwickelt.

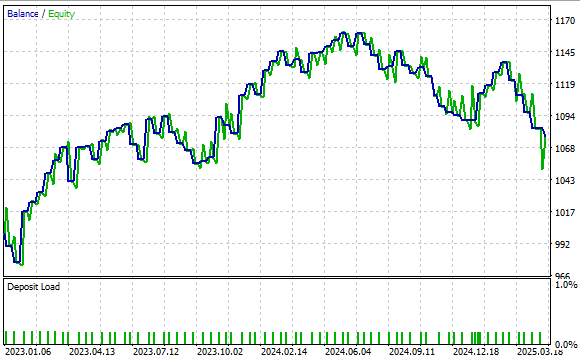
Abbildung 24: Unsere Benchmark-Anwendung hat ein hohes Leistungsniveau festgelegt, das wir mit unserem neuen Verständnis der Matrixfaktorisierung übertreffen können.

Abbildung 25 zeigt detaillierte Leistungskennzahlen. Die Strategie erzielte eine Gewinnquote von 51 % und zeigte eine konstante Rentabilität. Es ergab eine positive Sharpe Ratio von 0,47 – ein gesunder Wert. Auch wenn dieses Verhältnis durch weitere Verfeinerungen noch verbessert werden kann, so stellt das System doch schon jetzt einen starken Maßstab dar. Selbst mit naiven Vorhersagen der zukünftigen gleitenden Durchschnittswerte können wir eine profitable Strategie entwickeln. Lassen Sie uns nun die Vorteile besser informierter Vorhersagen untersuchen.

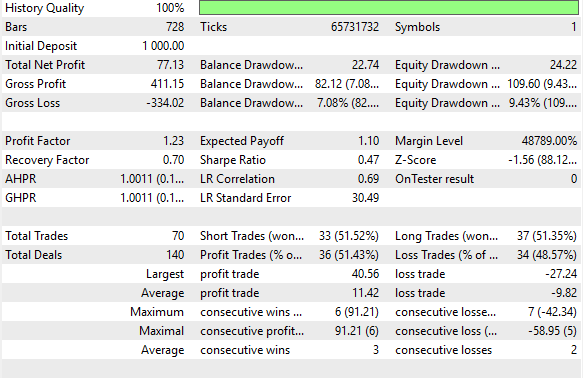
Abbildung 25: Detaillierte Analyse unserer Benchmark-Leistungsniveaus

Verbesserung unserer Ergebnisse

Jetzt können wir mit der Erstellung unserer Anwendung und des MQL5 beginnen. Wir beginnen mit der Definition der wichtigsten Systemkonstanten, die bisher benötigt wurden. Diese Konstanten steuern die technischen Indikatoren, auf die sich unser System stützt, und definieren die Gesamtzahl der für die Anwendung erforderlichen Eingaben.

//+------------------------------------------------------------------+
//|                                            Linear Regression.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/en/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| System constants                                                 |
//+------------------------------------------------------------------+
#define TOTAL_INPUTS 6

Als Nächstes werden wir Systemeingaben definieren, die der Nutzer einstellen kann, um das Verhalten des Systems zu ändern. 

//+------------------------------------------------------------------+
//| System Inputs                                                    |
//+------------------------------------------------------------------+
input int bars = 10;//Number of historical bars to fetch
input int horizon = 10;//How far into the future should we forecast
input int MA_PERIOD = 24; //Moving average period
input ENUM_TIMEFRAMES TIME_FRAME = PERIOD_H1;//User Time Frame

Wir werden auch eine Reihe wichtiger globaler Variablen deklarieren, um alle von unserem linearen Regressionsmodell verwendeten Parameter zu verfolgen.

//+------------------------------------------------------------------+
//| Dependencies                                                     |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
#include <VolatilityDoctor\Time\Time.mqh>
#include <VolatilityDoctor\Trade\TradeInfo.mqh>

Während der Initialisierungssequenz unseres Expert Advisors werden wir alle globalen Variablen mit ihren Standardwerten instanziieren und die relevanten technischen Indikatoren initialisieren. 

//+------------------------------------------------------------------+
//| Global Variables                                                 |
//+------------------------------------------------------------------+
int        ma_close_handler;
double     ma_close[];
Time       *Timer;
TradeInfo  *TradeInformation;
vector     bias,temp,Z1,Z2;
matrix     X,y,prediction,b;
int        time;
CTrade Trade;
int state;
int atr_handler;
double atr[];

In der Deinitialisierungssequenz geben wir den Platz frei, der zuvor globalen Variablen zugewiesen war, einschließlich aller nicht mehr benötigten technischen Indikatoren.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   Timer            = new Time(Symbol(),TIME_FRAME);
   TradeInformation        = new TradeInfo(Symbol(),TIME_FRAME);
   ma_close_handler = iMA(Symbol(),TIME_FRAME,MA_PERIOD,0,MODE_SMA,PRICE_CLOSE);
   bias = vector::Ones(TOTAL_INPUTS);
   Z1 = vector::Ones(TOTAL_INPUTS);
   Z2 = vector::Ones(TOTAL_INPUTS);
   X = matrix::Ones(TOTAL_INPUTS,bars);
   y = matrix::Ones(1,bars);
   time = 0;
   state = 0;
   atr_handler = iATR(Symbol(),TIME_FRAME,14);
//---
   return(INIT_SUCCEEDED);
  }

Wenn unsere Anwendung aktualisierte Preisniveaus erhält, wollen wir die Gewichte der Koeffizienten unseres Modells entsprechend anpassen und sie eng an die aktuellen Marktbedingungen anpassen. Das bedeutet, dass wir die SVD-Faktorisierung während unseres Backtests eine beträchtliche Anzahl von Malen berechnen werden. Dies ist jedoch der Vorteil der einfachen Implementierung, die uns vom OpenBLAS-Team zur Verfügung gestellt wurde. Die zahlreichen Aufrufe, die wir tätigen werden, verlangsamen die Geschwindigkeit unserer historischen Backtests kaum.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
   if(Timer.NewCandle())
     {
      setup();
      double c =  iClose(Symbol(),TIME_FRAME,0);
      CopyBuffer(atr_handler,0,0,1,atr);
      CopyBuffer(ma_close_handler,0,0,1,ma_close);

      if(PositionsTotal() == 0)
        {
         state = 0;
         if(prediction[0,0] > c)
           {
            Trade.Buy(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetAsk(),(TradeInformation.GetBid() - (2 * atr[0])),0);
            state = 1;
           }
         if(prediction[0,0] < c)
           {
            Trade.Sell(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetBid(),(TradeInformation.GetAsk() + (2 * atr[0])),0);
            state = -1;
           }
        }

      if(PositionsTotal() > 0)
        {
         if(((state == -1) && (prediction[0,0] > c)) || ((state == 1)&&(prediction[0,0] < c)))
            Trade.PositionClose(Symbol());
            if(PositionSelect(Symbol()))
               {
                  double current_sl = PositionGetDouble(POSITION_SL);
                  
                  if((state == 1) && ((ma_close[0] - (2 * atr[0]))>current_sl))
                     {
                        Trade.PositionModify(Symbol(),(ma_close[0] - (2 * atr[0])),0);
                     }
                     
                  else if((state == -1) && ((ma_close[0] + (1 * atr[0]))<current_sl))
                     {
                        Trade.PositionModify(Symbol(),(ma_close[0] + (2 * atr[0])),0);
                     }
               }
        }
     }
  }

Schließlich definieren wir die Funktion, die verwendet wird, um Vorhersagen aus unserem linearen Regressionsmodell zu erhalten, indem wir die standardisierten und skalierten Z-Werte verwenden, die in Vektoren mit den Namen Z1 (für den Mittelwert) und Z2 (für die Standardabweichung) verfolgt werden. Jeder dieser skalierten Zeilenvektoren wird in der X_inputs-Matrix gespeichert, und der zugehörige gleitende Durchschnittswert, den wir vorhersagen wollen, wird in Y gespeichert. Anschließend passen wir das Modell mit den zuvor beschriebenen Faktorisierungsmethoden an und verwenden die gelernten Koeffizienten, um Vorhersagen zu treffen.

//+------------------------------------------------------------------+
//| Obtain a prediction from our model                               |
//+------------------------------------------------------------------+
void setup(void)
  {

//--- OpenBLAS SVD Solution, considerably powerful substitute to the closed solution provided by the MQL5 developers 
matrix OB_U,OB_VT,OB_SIGMA;
vector OB_S;

//--- Reshape the matrix
   X = matrix::Ones(TOTAL_INPUTS,bars);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_OPEN,horizon,bars);
   Z1[0] = temp.Mean();
   Z2[0] = temp.Std();
   temp = ((temp - Z1[0]) / Z2[0]);
   X.Row(temp,1);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_HIGH,horizon,bars);
   Z1[1] = temp.Mean();
   Z2[1] = temp.Std();
   temp = ((temp - Z1[1]) / Z2[1]);
   X.Row(temp,2);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_LOW,horizon,bars);
   Z1[2] = temp.Mean();
   Z2[2] = temp.Std();
   temp = ((temp - Z1[2]) / Z2[2]);
   X.Row(temp,3);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_CLOSE,horizon,bars);
   Z1[3] = temp.Mean();
   Z2[3] = temp.Std();
   temp = ((temp - Z1[3]) / Z2[3]);
   X.Row(temp,4);

//--- Store the Z-scores
   temp.CopyIndicatorBuffer(ma_close_handler,0,horizon,bars);
   Z1[4] = temp.Mean();
   Z2[4] = temp.Std();
   temp = ((temp - Z1[4]) / Z2[4]);
   X.Row(temp,5);

   temp.CopyIndicatorBuffer(ma_close_handler,0,0,bars);
   y.Row(temp,0);
   
   Print("Training Input Data: ");
   Print(X);

   Print("Training Target");
   Print(y);

//--- Perform truncated SVD, we will explore what 'truncated' means later.
PrintFormat("Computing Singular Value Decomposition of %s Data using OpenBLAS",Symbol());
X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);
OB_SIGMA.Diag(OB_S);

//--- Fit the model
//--- More Penrose Psuedo Inverse Solution implemented by MQL5 Developers, enterprise level effeciency!
   b = y.MatMul(OB_VT.Transpose().MatMul(OB_SIGMA.Inv()).MatMul(OB_U.Transpose()));
   Print("OLS Solutions: ");
   Print(b);

//--- Prepare to get a prediction
//--- Reshape the data
   X = matrix::Ones(TOTAL_INPUTS,1);

//--- Get a prediction
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_OPEN,0,1);
   temp = ((temp - Z1[0]) / Z2[0]);
   X.Row(temp,1);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_HIGH,0,1);
   temp = ((temp - Z1[1]) / Z2[1]);
   X.Row(temp,2);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_LOW,0,1);
   temp = ((temp - Z1[2]) / Z2[2]);
   X.Row(temp,3);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_CLOSE,0,1);
   temp = ((temp - Z1[3]) / Z2[3]);
   X.Row(temp,4);

   temp.CopyIndicatorBuffer(ma_close_handler,0,0,1);
   temp = ((temp - Z1[4]) / Z2[4]);
   X.Row(temp,5);

   Print("Prediction Inputs: ");
   Print(X);

//--- Get a prediction
   prediction = b.MatMul(X);
   Print("Prediction");
   Print(prediction[0,0]);
  }
//+------------------------------------------------------------------+

Wir sind nun bereit, mit dem Testen der verbesserten Version unseres Handelsalgorithmus zu beginnen. Es sei daran erinnert, dass diese Implementierung dazu dient, den erwarteten Preiswert besser vorherzusagen. Wir werden die Testdaten mit unserem ersten Test übereinstimmen lassen, wie in Abbildung 26 dargestellt. Auch die Anwendungseinstellungen bleiben, wie in Abbildung 23 dargestellt, unverändert. Der Leser kann also mit der gleichen Konfiguration weitermachen.

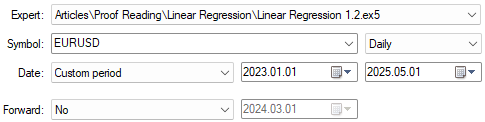
Abbildung 26: Vorbereitung auf den Test der Verbesserungen durch unsere neue Handelsanwendung

Wenn wir die neuen Ergebnisse analysieren, können wir deutliche Verbesserungen feststellen. Die naive Strategie ergab einen Gesamtnettogewinn von 77 $, während unsere verbesserte Strategie einen Nettogewinn von 101 $ erzielte – eine beachtliche Steigerung. Dies entspricht einem Anstieg des gesamten Nettogewinns um 31 %. Darüber hinaus ist die Sharpe Ratio, die bei der ersten Umsetzung 0,47 betrug, auf 0,63 gestiegen. Dies bedeutet eine Verbesserung der risikobereinigten Renditen um 34 %, was auf eine erhebliche Verbesserung der Leistung des Systems hindeutet. 

Auch der Prozentsatz der profitablen Geschäfte stieg von 51,4 % im naiven System auf 51,8 % in der verbesserten Version. Außerdem stieg die Gesamtzahl der platzierten Trades von 70 auf 83, was darauf hindeutet, dass das neue System mehr Handelssignale aufdeckt. 

Während die durchschnittliche Größe sowohl der Gewinn- als auch der Verlustgeschäfte abnahm, ist das System insgesamt aktiver und effektiver. All dies wurde mit nativem MQL5-Code und durch geeignete Anwendung von Matrixfaktorisierungen auf die verfügbaren Daten erreicht.

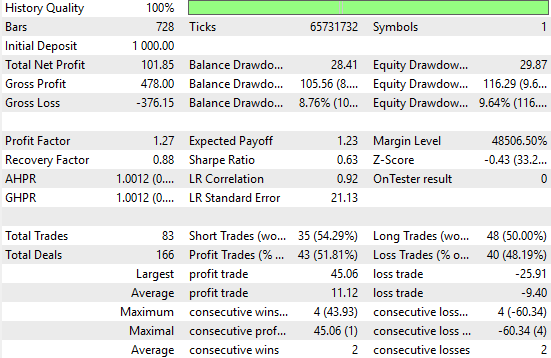
Abbildung 27: Eine detaillierte Analyse des Leistungsniveaus, das durch unsere fundierten Vorhersagen des zukünftigen Preisniveaus erreicht wurde

Wir haben auch die Gewinnkurve aufgenommen, die von unserer verbesserten Version der Handelsanwendung erstellt wurde. Unser neues Handelssystem zeigt einen positiven Trend im Kontostand im Vergleich zu den historischen Daten, was uns ermutigt, weiterhin nach Verbesserungen zu suchen und diese zu realisieren. 

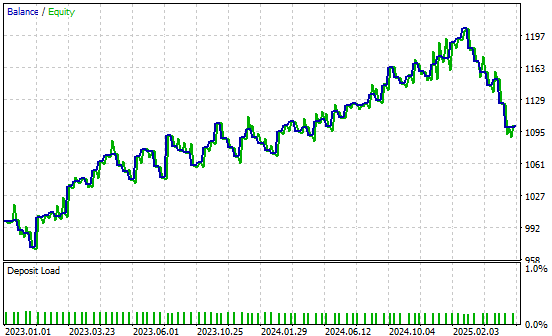
Abbildung 28: Die von unserer verbesserten Handelsanwendung erzeugte Gewinnkurve

Schlussfolgerung

Dieser Artikel hat den Leser mit den vielen Vorteilen der MQL5 Matrix API vertraut gemacht. Die API bietet leistungsstarke mathematische Werkzeuge, die unsere Fähigkeit verbessern, fundierte Handelsentscheidungen zu treffen.

Matrixfaktorisierungen ermöglichen es uns, in korrelierten Daten verborgene Muster aufzudecken – Muster, die mit herkömmlichen Methoden der Marktanalyse möglicherweise nicht zu erkennen sind. Die Leser verfügen nun über solide Alternativen zu den herkömmlichen Zeitreihenansätzen, die in der Finanzwissenschaft gelehrt werden. So beginnt eine typische Zeitreihenanalyse mit der Differenzierung der Daten, um periodische Veränderungen zu messen. Im Gegensatz dazu wurde bei unserem Ansatz auf eine Differenzierung gänzlich verzichtet und stattdessen die Daten faktorisiert.

Dieser Perspektivwechsel öffnet die Tür zu einer Reihe von Anwendungen. Wir haben gezeigt, wie die Matrixfaktorisierung eine schnelle und numerisch stabile statistische Modellierung ermöglicht. Außerdem wird die Dimensionalität der Daten reduziert und sie werden in kompaktere Formen gebracht, die die zugrunde liegenden Trends besser erkennen lassen.

Es kann noch viel mehr über die Vorteile von Matrixfaktorisierungen gesagt werden, aber dieser Artikel bietet eine solide Grundlage. Wichtig ist, dass die Faktorisierungstechniken den Bedarf an explizit definierten Handelsregeln verringern können, sodass das System optimale Strategien direkt aus den Daten lernen kann.

Es ist wirklich bemerkenswert, wie viel wir durch die Integration der MQL5 Matrix API in unsere täglichen Handelsabläufe gewinnen können.