MQL5で自己最適化エキスパートアドバイザーを構築する（第10回）：行列分解

本連載の冒頭の記事では、MetaTrader 5ターミナルから取得した生データとネイティブMQL5コードのみを用いて、線形回帰モデルを構築することを目指しました。初回記事のコメントやフィードバックを読むと、多くの読者が当初示した解法で問題を経験していたことが分かりました。多くのバグやエラーが発生し、中にはモデルが一種類のポジションしか開かないとの指摘もありました。全体として、線形モデルの初回構築に関して、いくつかのユーザーから不安定性に関する問題が報告されています。

復習として、線形モデルは予測ツールであり、アプリケーションが市場の挙動の観測から直接学習し、その洞察を基に最も成功しやすい取引をおこなうことを可能にします。したがって、目標はアプリケーションにいつ買うかやいつ売るかを明示的に指示することではなく、過去のデータから自律的に学習させることです。

本記事では、前回の記事で報告された不安定性の問題に対処し、任意の市場の生データから同等に強力な予測モデルを構築する方法を紹介します。そのために、行列分解(matrix factorization)として知られるアルゴリズム群を取り上げます。

行列分解は、大きな行列をより小さく単純な行列の積に分解する数学的手法です。これらの手法には多くの利点がありますが、利点の説明に入る前に、まず行列分解が生まれた背景を理解しましょう。

日常生活の中には、文化を超えて共通する経験があります。たとえば、子どもに話しかけ、その子どもが親をどのように描写するかを聞くことで、その親の性格や行動の傾向を推測できることに、多くの読者は馴染みがあるでしょう。その描写から、子どもが直接説明していない状況で親がどのように行動するかを推測することもできます。同様に、行列分解は大きな行列を「子行列」に分解します。これらの子行列は、それぞれ元の行列の異なる側面を表しており、構造を理解する手助けとなります。子どもの視点が親の本質を明らかにするように、これらの小さな行列は分析対象の市場に関する深い洞察を提供します。

行列分解の結果は、前述した線形モデルに対して数値的に安定した解をもたらすことがよくあります。本記事では、OpenBLAS（Basic Linear Algebra Subprogramsの略）という数値計算ライブラリも紹介します。 OpenBLASはBLASライブラリのオープンソースフォークで、現代の計算アーキテクチャ上で効率的に動作するよう再設計されています。BLASはもともとFortranと手書きアセンブリコードで作られました。 

線形代数の基本概念として、任意のデータセットは小さな構成要素に分解でき、これらを用いて元のデータの予測モデルを構築できます。これら小さなデータセットから得られる表現は、元のデータの隠れた特性を明らかにする場合もあります。

本記事では、生データから予測モデルを構築するために使用される強力な線形代数コマンドをやさしく紹介します。そしてそれは始まりに過ぎません。行列分解の手法は、単に生データの予測能力を提供するだけでなく、データ圧縮、隠れたトレンドの発見、市場の安定性や混沌の評価にも役立ちます。どんなデータセットからも行列分解するだけでこれほど多くの洞察を得られるのは、まさに驚くべきことです。それでは、始めましょう。

MQL5の始め方

MQL5を使い始める最初のステップは、本デモ全体で使用するシステム定数を定義することです。これらの定数は、行列分解を用いたスクリプトを動かすために作成したサンプルの基盤となります。 

//+------------------------------------------------------------------+
//|                                                        Solve.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/ja/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/ja/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| System definitions                                               |
//+------------------------------------------------------------------+
#define HORIZON 10
#define START   0

次に、スクリプトのユーザー入力、具体的には取得する情報バーの数を定義します。 

//+------------------------------------------------------------------+
//| User inputs                                                      |
//+------------------------------------------------------------------+
input int FETCH =  10;//How many bars should we fetch?

続いて、学習データとテストデータを含むグローバル変数と、提供されたデータからアプリケーションが学習した係数を格納するためのその他の変数を宣言します。

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int ROWS        =   5;
//Dependent variable
matrix y,y_test;
//Indenpendent variable
matrix X = matrix::Ones(ROWS,FETCH);
matrix X_test = matrix::Ones(ROWS,FETCH);
//Coefficients
matrix b;
vector temp;
//Row Norms
vector row_norms = vector::Zeros(4);
vector error_vector = vector::Zeros(4);

まず、入力データ行列Xを現在の状態で出力します。図1に示すように、この行列は初期状態ではすべて1で埋められています。これは意図的なもので、線形モデルにおいて入力行列の最初の行は切片項を表すからです。実際の市場データ、たとえば始値、高値、安値、終値は、2行目以降に格納されます。

ここで重要なポイントは、データのレイアウトです。本連載や「古典的な戦略を再構築する」のような連載を追ってきた読者であれば、MetaTrader 5からデータを抽出してPythonで処理する際、列が市場の属性（始値、高値、安値、終値）を表し、行が時間（例：日単位）を表す形式に慣れているかもしれません。しかし、本例ではレイアウトが転置されています。時間は列方向に沿って進み、市場の属性（始値、高値、安値、終値）は行方向に並んでいます。

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Observe the input matrix in its original form
PrintFormat("Input Matrix Gathered From %s",Symbol());
Print(X);

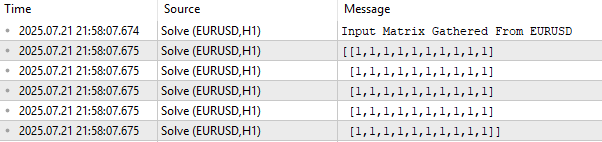
図1：市場からの現在のEURUSD入力データを可視化する

ここまでで前提が整理できたところで、次にスクリプトの、過去の市場データを取得する部分に進みます。データを取得した後は、各ベクトルのノルムを保存し、その後各ベクトルをノルムで割ります。この正規化のステップにより、各ベクトルの長さが1になります。これは、行列分解を適用する前に必須の処理です。

なぜ正規化が必要なのでしょうか。行列分解は、行列がどの方向に成長しているかを理解し、行や列ごとの成長率を比較することを目的としています。この比較を公平に行うために、各行をノルムで割ることで単位ベクトルに変換するのです。 

//--- Fetch the data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH*2),FETCH);
row_norms[0] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH*2),FETCH);
row_norms[1] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH*2),FETCH);
row_norms[2] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH*2),FETCH);
row_norms[3] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[3],4);

//--- Fetch the test data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[3],4);

入力用の学習データを出力すると、最初の行は切片を表すため、すべて1で埋められています。その後に始値、高値、安値、終値、そして移動平均の行が続きます。データは正規化の影響で、概ね0.3前後の値から始まります。

//--- The train data
Print("Input");
Print(X);

図2：各行をベクトルノルムで正規化した後の学習データを視覚化する

次に、目的変数を定義します。本例では、目的変数は終値であり、これを行列「y」にコピーします。これで、Xには入力特徴量が、yには予測したい値が格納されることになります。

//--- Fill the target 
y.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+(FETCH*2),FETCH);
y_test.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START,FETCH);

Print("Target");
Print(y);

図3：過去の市場観測データから予測しようとした出力値

では、どのようにしてXからyへの写像を表す係数を求めるのでしょうか。実は、無限に多くの係数セットが存在するため、最も適切なものを選ぶ必要があります。一般的には、予測値と実際の目的変数との誤差を最小化する係数を選択します。そのためのよく知られた手法のひとつが、擬似逆行列を用いる方法です。

係数を計算するには、Xの擬似逆行列にyを掛けます。この行列積により、最適な係数が閉形式で得られます。幸いなことに、MQL5には擬似逆行列を計算する組み込み関数「PInv()」が用意されています。

この解法の簡潔さに惑わされないでください。この1行のコードの意味を説明するだけで、この記事全体を費やすこともできるほどです。MQL5のPInv()関数で得られる係数は、過去の観測値と予測値の間のRMSE（二乗平均平方根誤差）を最小化することが保証されています。さらに、この解は必ず存在し、数値的に安定しており、生データから直接予測モデルを構築する際に、コンパクトで保守性の高いコードベースを提供してくれます。しかしながら、この方法は必ずしも推奨される解法ではありません。

//--- More Penrose Psuedo Inverse Solution implemented by MQL5 Developers
b = y.MatMul(X.PInv());

Print("Pseudo Inverse Solution: ");
Print(b);

図4：入力行列の擬似逆行列と目的変数の行列積によって得られた係数は、誤差を最小化する係数である

本記事の目的は、OpenBLASやその他の行列分解手法を紹介することにあります。では、MQL5ですでにPInv()関数で計算した係数を用いるだけで予測モデルを構築できる場合、なぜOpenBLASを学ぶ必要があるのでしょうか。 その理由はいくつかありますが、最も重要なのは速度です。OpenBLASはMQL5の組み込み擬似逆行列関数よりも飛躍的に高速です。OpenBLASの使い方を習得することで、バックテストの処理速度を大幅に向上させることができます。

教師なし行列分解：特異値分解(SVD)

序章でも述べた通り、任意のデータ行列は、より小さな行列の積に分解することができます。これらの小さな行列は元の行列の「子行列」と考えることができ、それぞれが親行列の異なる側面を表現します。

特異値分解(SVD: Singular Value Decomposition)アルゴリズムは、行列を分解する多くの方法のひとつです。SVDは任意の行列を、3つのより小さな基本的な行列の積に分解します。これら3つの行列それぞれが、元の行列の異なる特性を捉えています。本セクションでは、SVD分解によって得られる3つの「子行列」について詳しく見ていきます。SVDの目的や、各成分が元の行列に関してどのような情報を提供するかを理解していきましょう。

その前に、用語の整理が重要です。「教師なし行列分解(unsupervised matrix factorization)」という言葉を、単なる行列分解と一緒に目にしたことがあるかもしれませんが、この2つは同義ではありません。教師なし行列分解は、特定の種類の分解手法であり、データの最も重要な成分にのみ着目する点で一般的な行列分解と異なります。

本質的には、教師なし行列分解はすべての子行列を返すわけではなく、最も重要なものだけを返します。アルゴリズムは行列を分解し、内部基準に基づいてどの要素（子行列）が最も価値があるかを判断します。この判断は教師なしでおこなわれるため、ラベル付きの出力や人間による指示に依存せずに行われます。私たちがどの子行列を見るかを選ぶのではなく、アルゴリズムが自動的に決定します。

図5に示す通り、SVDはこのような行列分解の方法の一例であり、任意の行列Aを3つの「子行列」の積に分解します。 

OpenBLASを使用すると、SVDはすべての「子行列」を返すことも、最も重要な「子行列」のみを返すことも可能であり、これはSVD呼び出し時のパラメータに依存します。

本ディスカッションでは、OpenBLASに最も重要な「子行列」のみを返すよう指示します。これが、本セクションのタイトルである「教師なし行列分解」の由来です。前述の通り、SVDによって元の行列は3つのより単純で基本的な行列の積に分解されます。以下では、この3つの成分それぞれについて順に説明します。

図5：SVD分解の可視化

行列Uは、観測された市場の挙動を「駆動」していると考えられる隠れた市場要因を表しています。これらの隠れた要因は、より適切には因子(factor)と呼ばれます。したがって、Uの第1列は、市場全体に影響を与え、ある要因が市場を支配しているときには4つのOHLC価格すべてを下落させる市場駆動要因を示しています。第2の市場要因は正の係数が支配的であり、全体として市場に対して強気の影響を与えます。ここで扱っているのは過去の市場データであるため、分析しているこれらの市場要因は、実際には投資家心理の基盤を反映している可能性があります。

//--- Native MQL5 SVD Solution are also possible without relying on OpenBLAS
Print("Computing Singular Value Decomposition using MQL5");
matrix U,VT;
vector S;
X.SVD(U,VT,S);

Print("U");
Print(U);

図6：SVDの「U」成分の理解

行列「V」は、元のデータセットにおけるすべての時間観測に対して、Uの各市場要因（因子）がどの程度強く現れているかを示しています。たとえば、Vの第1行を考えると、最大値は0.4262であることが分かります。この値は第1行第3列に位置しており、これはUの第3列が、初日の取引で市場を支配していた要因を表していることを意味します。Uの第3列は、価格の一部の要素に対しては負の影響を与え、他の要素には正の影響を与える複合的な要因を表しています。このような要因は、断続的であったり、弱く現れたりすることがあります。

Print("VT");
Print(VT);

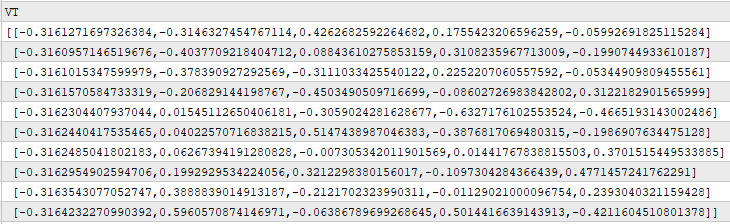
図7：各時間における市場駆動要因の顕著さの理解

Σ因子は、Uで表現された各市場要因の重要度を示します。過去の観測において支配的な要因にはΣの中で最も大きな値が割り当てられ、データ上で顕著でない要因には小さな値が割り当てられます。したがって、Σの中で最大値は3.741であり、この値はΣの第1列に位置しています。これは、Uの第1列がデータ上で観測された最も支配的な市場要因を表していることを意味します。

Print("S");
Print(S);

図8：SSVD分解におけるΣ因子の理解

本解説は網羅的なものを意図したものではなく、U、S、Vの3つの因子についてはさらに多くを語ることができます。図6、7、8では、MQL5に標準で組み込まれたSVDメソッドを呼び出した際に得られた結果を分析しました。これらの結果は、OpenBLASライブラリのSingularValueDecompositionDC()を呼び出した場合に得られる結果とほぼ一致します。

下の図9では、OpenBLASで計算したU因子のスクリーンショットを示しています。読者は図9と図6を比較することで、MQL5のネイティブ関数とOpenBLAS関数がほぼ同じU因子を計算していることが確認できます。関数内部の実装の違いにより、両図が小数点以下の値まで完全に一致するわけではありませんが、これは妥当な差異です。

//--- OpenBLAS SVD Solution, considerably powerful substitute to the closed solution provided by the MQL5 developers 
matrix OB_U,OB_VT,OB_SIGMA;
vector OB_S;

//--- Perform truncated SVD, we will explore what 'truncated' means later.
PrintFormat("Computing Singular Value Decomposition of %s Data using OpenBLAS",Symbol());
X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);

//--- U is a unitary matrix that is of dimension (m,r)
Print("Open BLAS U");
Print(OB_U);

図9：OpenBLASによって計算されたU因子

上記の図4では、MQL5のPInv()関数が、入力を目的変数に写像する際に可能な限り最小の誤差で係数を返すことを示しました。改めて強調しますが、図4の簡潔な解法に惑わされてはいけません。これは数学的に非常に強力な解法であり、任意の行列「A」に対して必ず存在し、さらに行列「Ax-b」のL2ノルムを最小化することが保証されています。 

図4で触れなかった点として、PInv()関数は実際には裏でSVD()関数を呼び出している可能性が高いということがあります。数学的には、擬似逆行列は通常、元のデータの特異値分解を用いて計算されます。ここで、実際に確認してみましょう。

以下のコードスニペットでは、市場データに対してSVD()を呼び出した際に取得した3つの子行列を用いています。線形代数のすべての規則をここで詳述することはしませんし、この解法を導出することも試みません。あくまで、SVDによって返された子行列を使うことで、入力データと目的変数を簡単に写像する線形係数を得られることを示すことが目的です。

Print("Comparing OLS Solutions");
Print("Native MQL5 Solution");
//--- We will always benchmark the native solution as the truth, the MQL5 developers implemented an extremely performant benchmark for us
Print(b);

//--- The OpenBLAS solution came closest to the native solution implemented for us
Print("OpenBLAS Solution");
matrix ob_solution = y.MatMul(OB_VT.Transpose().MatMul(OB_SIGMA.Inv()).MatMul(OB_U.Transpose()));
Print(ob_solution);

//--- Our manual solution was not even close! We will therefore rely on the OpenBLAS solution.
Print("Manual SVD Solution");
matrix svd_solution = y.MatMul(VT).MatMul(SIGMA.Inv()).MatMul(U.Transpose());
Print(svd_solution);

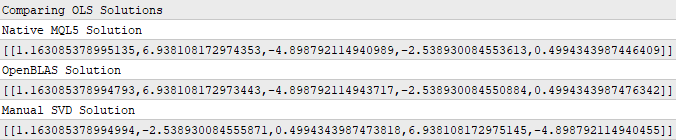
図10：入力データと出力データを最適に結びつける係数はSVDによって得られる

読者が注意深ければ、図10の係数セットがいずれも完全に一致していないことに気づくでしょう。これは当然のことです。思い出してください、各係数セットは異なる3つの関数を用いて取得したものであり、これはあたかも3人の独立した学生が、それぞれの方法で宿題をおこなったようなものです。しかし、私たちにとってより重要なのは、これらの係数を使用して、モデルの学習に使用していないデータに対して予測をおこなった際に生じる誤差です。

図11に示す通り、OpenBLASのSVD解はテストデータの予測において最も低い誤差を示しました。ただし、読者に誤解してほしくないのは、図11がOpenBLAS導入の唯一の動機ではないということです。 

3つの誤差レベルは概ね近い値を示していることに注目してください。したがって、このテストを異なる市場で、異なる量のデータを使用して複数回繰り返した場合、OpenBLASが常に最小の誤差を出すとは限りません。重要なのは、OpenBLASライブラリが魅力的である理由は、慎重に最適化され、活発にメンテナンスされており、高速かつ信頼性が高いことにある、という点です。常に最小の誤差を保証するわけではなく、どのライブラリもそのような広範な主張をおこなうことはできません。

//--- Measuring the amount of error
//--- Information lost by MQL5 PsuedoInverse solution
//--- The Frobenius norm squares all 
PrintFormat("Information Loss in Forcasting %s Market : ",Symbol());
Print("PInv: ");
matrix pinv_error = ((b.MatMul(X_test)) - y_test);
Print(pinv_error.Norm(MATRIX_NORM_FROBENIUS));

//--- Let the MQL5 implementation be our benchmark
double benchmark = pinv_error.Norm(MATRIX_NORM_FROBENIUS);

//--- Information lost by Manual SVD solution
Print("Manual SVD: ");
matrix svd_error = ((svd_solution.MatMul(X_test)) - y_test);
Print(svd_error.Norm(MATRIX_NORM_FROBENIUS));

//--- Information lost by OpenBLAS SVD solution
Print("OpenBLAS SVD: ");
matrix ob_error = ((ob_solution.MatMul(X_test)) - y_test);
Print(ob_error.Norm(MATRIX_NORM_FROBENIUS));

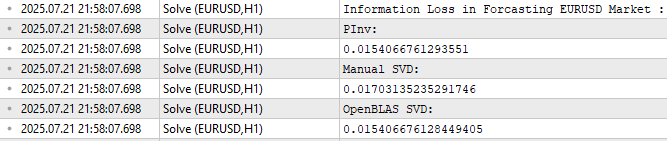
図11：学習期間外のデータを予測した際、各係数セットが生じる誤差の大きさ

予測モデル以外における教師なし行列分解の応用

ここまでの簡単な説明で、行列分解が何であるか、また金融市場データの分析においてなぜ有用であるかについて、読者の皆さんにある程度のイメージをつかんでいただけたと思います。前述の通り、適切な行列分解を用いて構築できる予測モデルは、行列分解を活用して達成できる有用なタスクのほんの一部に過ぎません。本セクションでは、行列分解のその他の有用な応用例を示し、これらの知見をどのように取引アプリケーションや戦略に組み込むことができるかを紹介したいと思います。

行列分解による教師なし市場フィルタリング

読者の皆さんがすでにある程度の取引経験をお持ちであり、独自の取引実践を通じて、これから述べる問いに対してある程度の理解をお持ちであると仮定します。外国為替市場と暗号通貨市場のうち、どちらの資産クラスの方がボラティリティが高いと思いますか。 

その答えは、ほとんどの方にとって明らかであると思います。暗号通貨は、伝統的な通貨市場に比べてはるかにボラティリティが高いのです。もしこの事実に確信が持てない読者の方のために、以下のような検証をおこないました。ビットコインをイーサリアム建てで表示した1分足チャート（図12）と、ユーロを米ドル建てで表示した1分足チャート（図13）に対して、ATR (Average True Range)指標を適用しました。ATRは市場のボラティリティを測定する指標であり、値が大きいほど市場がより活発であることを意味します。その結果、BTCETHチャートのATR値は、EURUSDチャートのATR値に比べておよそ60倍も大きいことが分かりました。したがって、この結果から、暗号通貨市場が一般的に伝統的な通貨市場よりもはるかにボラティリティが高い理由が明確になります。

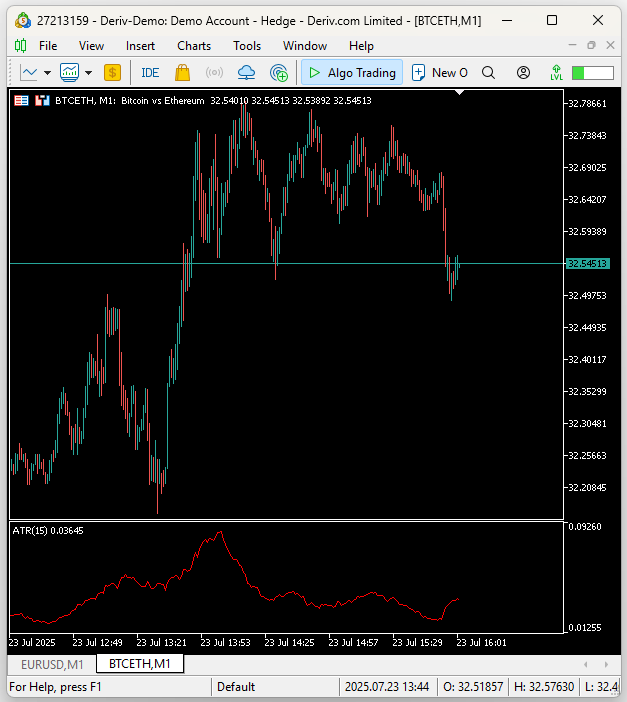
図12：BTC/ETHのボラティリティはEUR/USDよりも著しく高い

ご存知のとおり、EUR/USDは世界で最も流動性が高く、最も取引されている通貨ペアです。しかし、そのボラティリティ水準は、暗号通貨市場で観測されるボラティリティとは比較にならないほど低いのです。

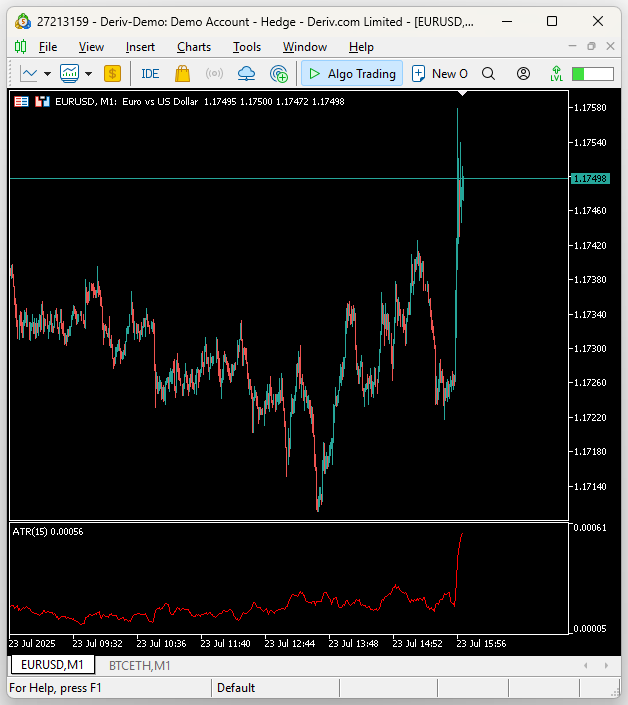
図13：伝統的な資産クラスのボラティリティは、暗号通貨市場のボラティリティには到底及ばない

私たちがこれまでおこなってきた行列分解は、実は同じ情報を示すことができます。図8で説明したように、Σという因子は、データ内に存在する市場の駆動要因の重要度を表しています。安定した市場では、Σの要素のうち大きな値を取るものは1つだけで、その他の値はほぼ0に近くなります。一方で、Σの中に0から大きく離れた値が複数存在する場合、その市場はより混沌としており、ボラティリティが高いことを意味します。

この分析をEUR/USD市場とBTC/ETH市場の両方に適用してみましょう。図14および図15を見ると、どちらの市場も安定しているように見えます。Σの中で大きな非ゼロ値は1つしかありません。これは一見、BTC/ETHがEUR/USDと同じくらい安定していることを示唆しているように見えます。しかし、これは完全な真実ではありません。信頼できる結論を得るためには、行列分解のさらなる応用を学ぶ必要があります。

//+------------------------------------------------------------------+
//| What are we demonstrating here?                                  |
//| 1) We have shown you that any matrix of market data you have,    |
//|    can be analyzed intelligently, to build a linear regression   |
//|    model, using just the raw data.                               |
//| 2) We have demonstrated that the solution to such Linear         |
//|    regression problems, can be obtained through effecient and    |
//|    dedicated functions available in MQL5 or through matrix       |
//|    factorization.                                                |   
//|__________________________________________________________________|
//| I now ask the reader the following question:                     |
//|  "If dedicated functions exist, why bother learning matrix       |
//|   factorization?"                                                |
//+------------------------------------------------------------------+

//--- Matrix factorization gives us a description of the data and it properties
//--- Questions such as: "How stable/chaotic is the market we are in?" can be answered by the factorization we have just performed
//--- Or even questions such as: "How best can I expose the hidden trends in all of this market data?" can still be answered by the factorization we have just performed
//--- I'm only trying to give you a few examples of why you should bother learning these factorizations, even though dedicated functions exist.

//--- Any given matrix A can be represented as the sum of smaller matrices A = USV, this is theorem behind the Singular Value Decomposition.
//--- Each factor is special because each describes different charectersitics of its parent.

//--- Let's get to know Sigma, represented as the S in A = USV.
//--- Sigma technically tells us how many different modes our market appears to exist in, and how important each mode is. 
//--- However, reintepreted in terms of market data, these modes may correspond to investor sentiment.
PrintFormat("Taking a closer look at The Eigenvalues of %s Market Data: ",Symbol());
Print(OB_S/OB_S.Sum());
Print("If sigma has a only few values that are far from 0, then investor's sentiment in this market appears well established and hardly changes");
//--- If Sigma has a lot values that are all far away from 0, then the market is chaotic and it appears investor's sentiment and expectations constantly change
//--- If Sigma has a few, or even just one value that is far away from 0, then investor sentiment in that market appears stable, and hardly changes.
//--- Traders explicitly looking for fast-action scalping oppurtunities may use Sigma as a filter of how much energy the market has. 
//--- Quiet market will have a few dominant values in Sigma, not ideal for scalpers, better suited for long-term trend traders.

図14：EUR/USD市場におけるエネルギー量の可視化

図15：BTC/ETH市場におけるエネルギー量の可視化

データ圧縮と信号抽出のための行列分解

行列分解は、データの圧縮やデータ中に含まれる支配的な信号の抽出にも利用することができます。生成される子行列は親行列よりも小さいため、これらのアルゴリズムはデータを効率的に圧縮することができます。このような行列分解の性質は、ネットワーク工学、信号処理、電気工学などの分野に携わるコミュニティメンバーにとっては、よく知られていることです。元のデータを圧縮するには、子行列であるSとVを掛け合わせます。その際、S行列に対してDiag()メソッドを呼び出し、対角行列に変換してから積を計算します。 この掛け算の結果得られる行列は、元の親行列をよりコンパクトに表現した新しい行列表現となります。

読者の中には、すでにこのアルゴリズムが馴染み深い方もいらっしゃるかもしれません。これは一般的に主成分分析(PCA)として知られています。本記事ではPCAについて詳しく掘り下げることはしませんが、行列分解を用いることで、どれほど多くの有用な情報を得ることができるのかを示したいのです。市場データの主成分を求める方法は多数存在しますが、OpenBLASを利用した行列分解は、MQL5でネイティブに利用可能な手法の中でも最も高速な部類に入るでしょう。

//--- Fetch the data and prepare to perform PCA
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH*2),FETCH);
row_norms[0] = temp.Mean();
X.Row(temp-row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH*2),FETCH);
row_norms[1] = temp.Mean();
X.Row(temp-row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH*2),FETCH);
row_norms[2] = temp.Mean();
X.Row(temp-row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH*2),FETCH);
row_norms[3] = temp.Mean();
X.Row(temp-row_norms[3],4);

//--- Fetch the test data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[3],4);

//--- Perform truncated SVD, we will explore what 'truncated' means later.
Print("Computing Singular Value Decomposition using OpenBLAS");
X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);

OB_SIGMA.Diag(OB_S);

//--- Calculating Principal Components
Print("Principal Components");
matrix pc = OB_SIGMA.MatMul(OB_VT);
Print(pc);

図16：S因子とV因子を掛け合わせることで、元のデータセットをコンパクトに表現できる

SおよびVという「子行列」を掛け合わせて得られる積については、さらに多くのことを議論する余地があります。この乗算によって得られる新しいデータセットの表現は、元のデータセットに比べて相関が大幅に低くなっているのです。このことを証明するために、まず元のデータセットの相関行列のノルムと、SおよびVを乗算した後の相関行列のノルムを比較します。ここで思い出していただきたいのは、線形代数におけるノルムとは、「大きさ」を測る尺度に相当するという点です。図17に示すように、元の市場データを行列分解した後では、相関行列のノルムが大幅に低下していることが確認できます。

この結果は、SVDを用いた行列分解によって、元のデータセットに存在する冗長で相関の高い特徴量を取り除くことができることを示しています。このようにして不要な相関を排除することで、データ中に潜む支配的なトレンドやパターンをより明確に浮かび上がらせることができるのです。

//--- PCA reduces the amount of correlation in our dataset 
Print("How correlated is our new representation of the data?");
//--- First we will measure the size of our original correlation matrix
Print(X.Norm(MATRIX_NORM_FROBENIUS));
//--- Then, we will measure the size of our new correlation matrix produced by factorizing the data
Print(pc.CorrCoef().Norm(MATRIX_NORM_FROBENIUS));

図17：行列分解はデータセット内の相関関係の量を大幅に減らすのに役立つ

この情報を得た上で、私たちは元の5行のデータを使用する代わりに、わずか3行のデータだけを用いた市場モデルを構築することができます。この3行のデータは、相関がより少なくなっているため、元のデータよりも市場と目的変数との関係をより的確に説明できる可能性があります。この手法は「特徴量抽出」と呼ばれます。これは、元のデータから新しい特徴量を学習するという考え方に基づいています。ただし、最適化に関連するほとんどの手法と同様に、この特徴量抽出が将来のパフォーマンスを必ずしも改善するとは限らない点には注意が必要です。この点については、図18に示されているように表されています。

//--- Main principal components
matrix mpc;

mpc.Row(pc.Row(0),0);
mpc.Row(pc.Row(1),1);
mpc.Row(pc.Row(2),2);

//--- The factor VT describes the correlational structure across the columns of our data
Print("Performing PCA");
matrix pca_coefs = y.MatMul(mpc.PInv());

//--- Performing PCA on the test data
X_test.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);
Print("Principal Components of Test Data");
pc = OB_SIGMA.MatMul(OB_VT);

Print(pc);

PrintFormat("Most Important Principal Components in %s Market Test Data",Symbol());
Print(OB_S / OB_S.Sum());

//--- Main principal components
mpc.Row(pc.Row(0),0);
mpc.Row(pc.Row(1),1);
mpc.Row(pc.Row(2),2);

matrix pca_error = pca_coefs.MatMul(mpc) - y_test;

Print("PCA Error: ");
Print(pca_error.Norm(MATRIX_NORM_FROBENIUS));

Print("OpenBLAS Error: ");
Print(ob_error.Norm(MATRIX_NORM_FROBENIUS));

Print("Manual Error: ");
Print(svd_error.Norm(MATRIX_NORM_FROBENIUS));

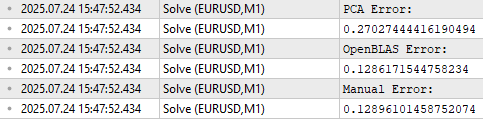
図18：特徴量抽出は強力な数値手法だが、パフォーマンスの向上が保証されるわけではない

図14および図15では、行列分解を用いることで安定した市場とボラティリティの高い市場を区別できることを示そうとしました。最初の試みでは、どちらの市場もS因子に大きな値が1つしか存在しないように見えました。しかし、データを注意深く調べてみると、これは学習データに限って成り立っていたことが分かりました。市場データのテストセットを行列分解し、その際に得られたS因子（Σ行列）を分析すると、確かにBTC/ETHの方がEUR/USDよりも「エネルギー」が大きいことが確認できます。

//--- Performing PCA on the test data
X_test.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);
Print("Principal Components of Test Data");
pc = OB_SIGMA.MatMul(OB_VT);


PrintFormat("Most Important Principal Components in %s Market Test Data",Symbol());
Print(OB_S / OB_S.Sum());

図19：EUR/USD市場に含まれるエネルギー量を分析する

図19：BTC/ETH市場に含まれるエネルギー量を分析する。観測される個々の成分が0から大きく離れている数が多いほど、市場がより混沌としていることを示す

これは、教師なし行列分解の解説のために用意したMQL5スクリプト全体です。

//+------------------------------------------------------------------+
//|                                                        Solve.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/ja/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/ja/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| System definitions                                               |
//+------------------------------------------------------------------+
#define HORIZON 10
#define START   0

//+------------------------------------------------------------------+
//| User inputs                                                      |
//+------------------------------------------------------------------+
input int FETCH =  10;//How many bars should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int ROWS        =   5;
//Dependent variable
matrix y,y_test;
//Indenpendent variable
matrix X = matrix::Ones(ROWS,FETCH);
matrix X_test = matrix::Ones(ROWS,FETCH);
//Coefficients
matrix b;
vector temp;
//Row Norms
vector row_norms = vector::Zeros(4);
vector error_vector = vector::Zeros(4);

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Observe the input matrix in its original form
PrintFormat("Input Matrix Gathered From %s",Symbol());
Print(X);
  
//--- Fetch the data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH*2),FETCH);
row_norms[0] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH*2),FETCH);
row_norms[1] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH*2),FETCH);
row_norms[2] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH*2),FETCH);
row_norms[3] = temp.Norm(VECTOR_NORM_P);
X.Row(temp/row_norms[3],4);

//--- Fetch the test data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp/row_norms[3],4);

//--- The train data
Print("Input");
Print(X);

//--- Fill the target
y.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+(FETCH*2),FETCH);
y_test.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START,FETCH);

Print("Target");
Print(y);

//--- More Penrose Psuedo Inverse Solution implemented by MQL5 Developers, enterprise level effeciency!
b = y.MatMul(X.PInv());

Print("Pseudo Inverse Solution: ");
Print(b);

//--- Native MQL5 SVD Solution are also possible without relying on OpenBLAS
Print("Computing Singular Value Decomposition using MQL5");
matrix U,VT;
vector S;
X.SVD(U,VT,S);

Print("U");
Print(U);

Print("VT");
Print(VT);

Print("S");
Print(S);
matrix SIGMA;
SIGMA.Diag(S);

//--- OpenBLAS SVD Solution, considerably powerful substitute to the closed solution provided by the MQL5 developers 
matrix OB_U,OB_VT,OB_SIGMA;
vector OB_S;

//--- Perform truncated SVD, we will explore what 'truncated' means later.
PrintFormat("Computing Singular Value Decomposition of %s Data using OpenBLAS",Symbol());
X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);

//--- U is a unitary matrix that is of dimension (m,r)
Print("Open BLAS U");
Print(OB_U);

//--- VT is a mathematically a symmetrical matrix that is (r,r), for effeciency in software it is represented as a vector that is (1,r)
Print("Open BLAS VT");
Print(OB_VT);

//--- We need it in its intended form as an (r,r) matrix, we will explore what this means later. 
Print("Open BLAS S");
Print(OB_S);
OB_SIGMA.Diag(OB_S);

Print("Comparing OLS Solutions");
Print("Native MQL5 Solution");
//--- We will always benchmark the native solution as the truth, the MQL5 developers implemented an extremely performant benchmark for us
Print(b);

//--- The OpenBLAS solution came closest to the native solution implemented for us
Print("OpenBLAS Solution");
matrix ob_solution = y.MatMul(OB_VT.Transpose().MatMul(OB_SIGMA.Inv()).MatMul(OB_U.Transpose()));
Print(ob_solution);

//--- Our manual solution was not even close! We will therefore rely on the OpenBLAS solution.
Print("Manual SVD Solution");
matrix svd_solution = y.MatMul(VT).MatMul(SIGMA.Inv()).MatMul(U.Transpose());
Print(svd_solution);

//--- Measuring the amount of error
//--- Information lost by MQL5 PsuedoInverse solution
//--- The Frobenius norm squares all 
PrintFormat("Information Loss in Forcasting %s Market : ",Symbol());
Print("PInv: ");
matrix pinv_error = ((b.MatMul(X_test)) - y_test);
Print(pinv_error.Norm(MATRIX_NORM_FROBENIUS));

//--- Let the MQL5 implementation be our benchmark
double benchmark = pinv_error.Norm(MATRIX_NORM_FROBENIUS);

//--- Information lost by Manual SVD solution
Print("Manual SVD: ");
matrix svd_error = ((svd_solution.MatMul(X_test)) - y_test);
Print(svd_error.Norm(MATRIX_NORM_FROBENIUS));

//--- Information lost by OpenBLAS SVD solution
Print("OpenBLAS SVD: ");
matrix ob_error = ((ob_solution.MatMul(X_test)) - y_test);
Print(ob_error.Norm(MATRIX_NORM_FROBENIUS));

//+------------------------------------------------------------------+
//| What are we demonstrating here?                                  |
//| 1) We have shown you that any matrix of market data you have,    |
//|    can be analyzed intelligently, to build a linear regression   |
//|    model, using just the raw data.                               |
//| 2) We have demonstrated that the solution to such Linear         |
//|    regression problems, can be obtained through effecient and    |
//|    dedicated functions available in MQL5 or through matrix       |
//|    factorization.                                                |   
//|__________________________________________________________________|
//| I now ask the reader the following question:                     |
//|  "If dedicated functions exist, why bother learning matrix       |
//|   factorization?"                                                |
//+------------------------------------------------------------------+

//--- Matrix factorization gives us a description of the data and it properties
//--- Questions such as: "How stable/chaotic is the market we are in?" can be answered by the factorization we have just performed
//--- Or even questions such as: "How best can I expose the hidden trends in all of this market data?" can still be answered by the factorization we have just performed
//--- I'm only trying to give you a few examples of why you should bother learning these factorizations, even though dedicated functions exist.

//--- Any given matrix A can be represented as the sum of smaller matrices A = USV, this is theorem behind the Singular Value Decomposition.
//--- Each factor is special because each describes different charectersitics of its parent.

//--- Let's get to know Sigma, represented as the S in A = USV.
//--- Sigma technically tells us how many different modes our market appears to exist in, and how important each mode is. 
//--- However, reintepreted in terms of market data, these modes may correspond to investor sentiment.
PrintFormat("Taking a closer look at The Eigenvalues of %s Market Data: ",Symbol());
Print(OB_S/OB_S.Sum());
Print("If sigma has a only few values that are far from 0, then investor's sentiment in this market appears well established and hardly changes");
//--- If Sigma has a lot values that are all far away from 0, then the market is chaotic and it appears investor's sentiment and expectations constantly change
//--- If Sigma has a few, or even just one value that is far away from 0, then investor sentiment in that market appears stable, and hardly changes.
//--- Traders explicitly looking for fast-action scalping oppurtunities may use Sigma as a filter of how much energy the market has. 
//--- Quiet market will have a few dominant values in Sigma, not ideal for scalpers, better suited for long-term trend traders.

//--- Fetch the data and prepare to perform PCA
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH*2),FETCH);
row_norms[0] = temp.Mean();
X.Row(temp-row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH*2),FETCH);
row_norms[1] = temp.Mean();
X.Row(temp-row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH*2),FETCH);
row_norms[2] = temp.Mean();
X.Row(temp-row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH*2),FETCH);
row_norms[3] = temp.Mean();
X.Row(temp-row_norms[3],4);

//--- Fetch the test data
temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_OPEN,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[0],1);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_HIGH,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[1],2);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_LOW,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[2],3);

temp.CopyRates(Symbol(),PERIOD_CURRENT,COPY_RATES_CLOSE,START+HORIZON+(FETCH),FETCH);
X_test.Row(temp-row_norms[3],4);

//--- Perform truncated SVD, we will explore what 'truncated' means later.
Print("Computing Singular Value Decomposition using OpenBLAS");
X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);

//--- Calculating Principal Components
Print("Principal Components");
matrix pc = OB_SIGMA.MatMul(OB_VT);
Print(pc);

PrintFormat("Most Important Principal Components of %s Market Data",Symbol());
Print(OB_S / OB_S.Sum());

//--- Main principal components
matrix mpc;

mpc.Row(pc.Row(0),0);
mpc.Row(pc.Row(1),1);
mpc.Row(pc.Row(2),2);

//--- The factor VT describes the correlational structure across the columns of our data
Print("Performing PCA");
matrix pca_coefs = y.MatMul(mpc.PInv());

//--- Performing PCA on the test data
X_test.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);
Print("Principal Components of Test Data");
pc = OB_SIGMA.MatMul(OB_VT);

Print(pc);

PrintFormat("Most Important Principal Components in %s Market Test Data",Symbol());
Print(OB_S / OB_S.Sum());

//--- Main principal components
mpc.Row(pc.Row(0),0);
mpc.Row(pc.Row(1),1);
mpc.Row(pc.Row(2),2);

matrix pca_error = pca_coefs.MatMul(mpc) - y_test;

Print("PCA Error: ");
Print(pca_error.Norm(MATRIX_NORM_FROBENIUS));

Print("OpenBLAS Error: ");
Print(ob_error.Norm(MATRIX_NORM_FROBENIUS));

Print("Manual Error: ");
Print(svd_error.Norm(MATRIX_NORM_FROBENIUS));

}
//+------------------------------------------------------------------+

アプリケーションの構築

これまでに学んできた内容を組み合わせて、1つの取引戦略としてまとめていきます。本戦略の目的は、移動平均インジケーターの将来値を予測することで、公正な市場価格を学習することにあります。この予測値を用いて売買判断をおこないます。すなわち、価格が予測値を上回っている場合は「市場が過大評価されている」と判断して売りポジションを取り、逆に価格が予測値を下回っている場合は「市場が割安である」と判断して買いポジションを取ります。 

ここでは例として、EUR/USDの日足チャートに10期間の移動平均を適用し、それを10ステップ先にシフトさせて、そのシフト後の値を予測値として想定してみます。

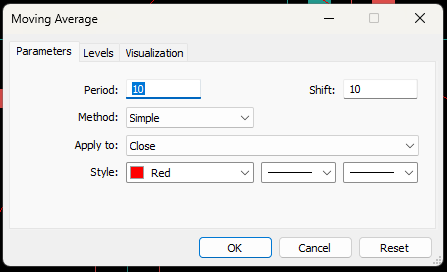
図20：説明目的として、移動平均インジケーターを10ステップ先にシフトした

この取引戦略の本質は、現在の価格レベルはいずれ期待値に収束するという仮定に基づいています。図21に示されたセットアップでは、予測価格が低く、現在価格が高い状態を表しています。仮にこの図21が私たちの市場予測モデルによって生成されたものであれば、これは売買シグナルとなります。

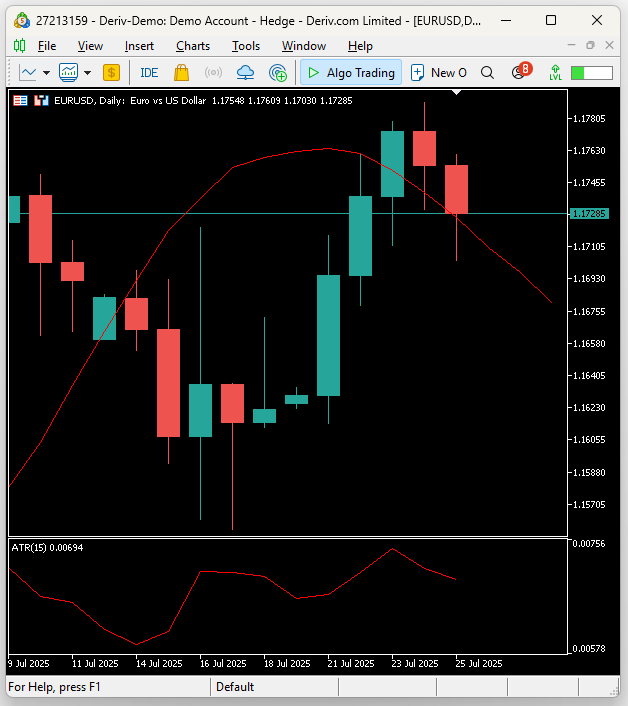
図21：取引戦略の可視化。シフトされた移動平均は、モデルが予測する将来の移動平均の位置に基づいて売買をおこなうことを示している

ベースラインの確立

アプリケーションを構築する前に、まずAIモデルのパフォーマンスを評価するためのベースラインを確立する必要があります。このベースラインは、AIを使用しない場合に期待される結果を示すものです。次のセクションではアプリケーションの完全な実装について詳しく説明しますが、ここではベースラインの主要な要素を簡単に取り上げます。

//+------------------------------------------------------------------+
//| Obtain a prediction from our model                               |
//+------------------------------------------------------------------+
void setup(void)
  {
   y.CopyIndicatorBuffer(ma_close_handler,0,0,bars);
   
   Print("Training Target");
   Print(y);

//--- Get a prediction
   prediction = y.Mean();
   Print("Prediction");
   Print(prediction);
  }
//+------------------------------------------------------------------+

このベースラインモデルは、移動平均インジケーターの値を模倣し、その平均値を計算して取引判断をおこなうという単純な手法を用いています。具体的には、移動平均の平均値が現在の価格より高い場合は買い、低い場合は売る、というロジックです。

if(prediction > c)
  {
   Trade.Buy(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetAsk(),proposed_buy_sl,0);
   state = 1;
  }
if(prediction < c)
  {
   Trade.Sell(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetBid(),proposed_sell_sl,0);
   state = -1;
  }

次に、このベースラインアプリケーションをUSD/UL通貨ペアに適用します。データには、2023年1月から2025年3月までの2年間の過去データを使用します（図22）。

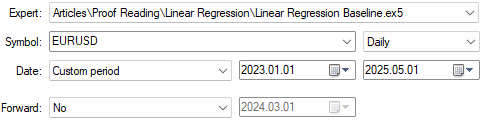
図22：過去の市場データに対してベースラインアプリケーションをテストする

図23には、使用しているアプリケーションの設定を示しています。公平な比較をおこなうため、これらの入力パラメータはすべてのテストで固定しておくことが重要です。

図23：公平な比較をおこなうため、ベンチマークパラメータを固定する

図24では、本取引戦略によって生成された資産曲線を示しています。結果を見ると、口座残高が時間とともに上昇しており、戦略の基本的な有効性が確認できます。

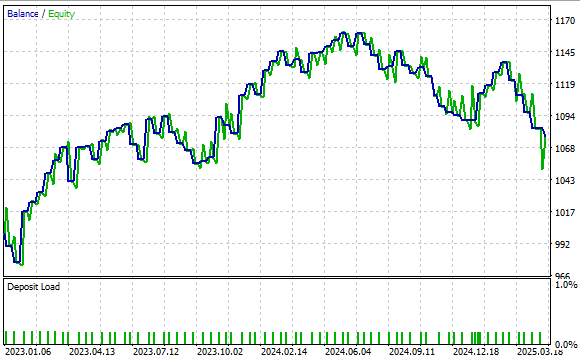
図24：行列分解の新たな理解を用いてこれを上回るための、強力なベースラインパフォーマンスを示している

図25には、詳細なパフォーマンス指標を示しています。この戦略は勝率51%を達成し、一貫した収益性を示しました。また、シャープレシオ0.47という健全な値を記録しています。さらなる改善によってこの比率を高める余地はありますが、すでに堅実なベンチマークシステムとして十分に機能しています。この結果は、単純に移動平均の将来値を予測するだけのナイーブな手法でも、収益性のある戦略を構築できることを示しています。それでは次に、より情報量の多い予測をおこなうことで得られる利点について探っていきましょう。

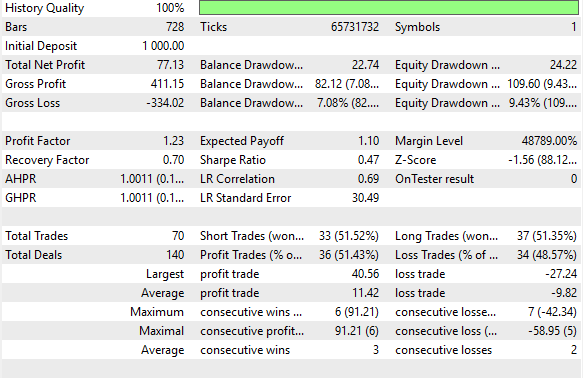
図25：ベンチマークパフォーマンスの詳細分析

結果の改善

ここから、アプリケーションおよびMQL5の実装を本格的に構築していきます。まず、これまでに必要となったシステム定数を定義します。これらの定数は、システムが依存するテクニカル指標を制御するとともに、アプリケーションに必要な総入力数を定義します。

//+------------------------------------------------------------------+
//|                                            Linear Regression.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/ja/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/ja/users/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| System constants                                                 |
//+------------------------------------------------------------------+
#define TOTAL_INPUTS 6

次に、ユーザーがシステムの挙動を調整できるシステム入力値を定義します。 

//+------------------------------------------------------------------+
//| System Inputs                                                    |
//+------------------------------------------------------------------+
input int bars = 10;//Number of historical bars to fetch
input int horizon = 10;//How far into the future should we forecast
input int MA_PERIOD = 24; //Moving average period
input ENUM_TIMEFRAMES TIME_FRAME = PERIOD_H1;//User Time Frame

また、線形回帰モデルで使用するパラメータを追跡するための重要なグローバル変数も宣言します。

//+------------------------------------------------------------------+
//| Dependencies                                                     |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
#include <VolatilityDoctor\Time\Time.mqh>
#include <VolatilityDoctor\Trade\TradeInfo.mqh>

初期化シーケンスでは、これらグローバル変数にデフォルト値を代入し、必要なテクニカル指標を初期化します。 

//+------------------------------------------------------------------+
//| Global Variables                                                 |
//+------------------------------------------------------------------+
int        ma_close_handler;
double     ma_close[];
Time       *Timer;
TradeInfo  *TradeInformation;
vector     bias,temp,Z1,Z2;
matrix     X,y,prediction,b;
int        time;
CTrade Trade;
int state;
int atr_handler;
double atr[];

初期化解除シーケンスでは、不要になったテクニカル指標を含め、以前にグローバル変数に割り当てられたすべてのスペースを解放します。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   Timer            = new Time(Symbol(),TIME_FRAME);
   TradeInformation        = new TradeInfo(Symbol(),TIME_FRAME);
   ma_close_handler = iMA(Symbol(),TIME_FRAME,MA_PERIOD,0,MODE_SMA,PRICE_CLOSE);
   bias = vector::Ones(TOTAL_INPUTS);
   Z1 = vector::Ones(TOTAL_INPUTS);
   Z2 = vector::Ones(TOTAL_INPUTS);
   X = matrix::Ones(TOTAL_INPUTS,bars);
   y = matrix::Ones(1,bars);
   time = 0;
   state = 0;
   atr_handler = iATR(Symbol(),TIME_FRAME,14);
//---
   return(INIT_SUCCEEDED);
  }

価格更新を受け取るたびに、モデルの係数の重みを適切に調整し、現在の市場状況を正確に追跡できるようにします。そのため、バックテスト中にSVD分解を何度も計算しますが、OpenBLASによる高速実装のおかげで、複数回の呼び出しをおこなっても、バックテストの速度はほとんど低下しません。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
   if(Timer.NewCandle())
     {
      setup();
      double c =  iClose(Symbol(),TIME_FRAME,0);
      CopyBuffer(atr_handler,0,0,1,atr);
      CopyBuffer(ma_close_handler,0,0,1,ma_close);

      if(PositionsTotal() == 0)
        {
         state = 0;
         if(prediction[0,0] > c)
           {
            Trade.Buy(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetAsk(),(TradeInformation.GetBid() - (2 * atr[0])),0);
            state = 1;
           }
         if(prediction[0,0] < c)
           {
            Trade.Sell(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetBid(),(TradeInformation.GetAsk() + (2 * atr[0])),0);
            state = -1;
           }
        }

      if(PositionsTotal() > 0)
        {
         if(((state == -1) && (prediction[0,0] > c)) || ((state == 1)&&(prediction[0,0] < c)))
            Trade.PositionClose(Symbol());
            if(PositionSelect(Symbol()))
               {
                  double current_sl = PositionGetDouble(POSITION_SL);
                  
                  if((state == 1) && ((ma_close[0] - (2 * atr[0]))>current_sl))
                     {
                        Trade.PositionModify(Symbol(),(ma_close[0] - (2 * atr[0])),0);
                     }
                     
                  else if((state == -1) && ((ma_close[0] + (1 * atr[0]))<current_sl))
                     {
                        Trade.PositionModify(Symbol(),(ma_close[0] + (2 * atr[0])),0);
                     }
               }
        }
     }
  }

最後に、線形回帰モデルから予測値を取得する関数を定義します。ここでは、平均を格納するZ1ベクトルと標準偏差を格納するZ2ベクトルに追跡される標準化・スケーリング済みの値を使用します。これらのスケーリング済み行ベクトルはX行列に格納され、予測対象である移動平均値はyに格納されます。その後、前述した行列分解手法を用いてモデルを適合させ、学習済みの係数を使用して予測をおこないます。

//+------------------------------------------------------------------+
//| Obtain a prediction from our model                               |
//+------------------------------------------------------------------+
void setup(void)
  {

//--- OpenBLAS SVD Solution, considerably powerful substitute to the closed solution provided by the MQL5 developers 
matrix OB_U,OB_VT,OB_SIGMA;
vector OB_S;

//--- Reshape the matrix
   X = matrix::Ones(TOTAL_INPUTS,bars);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_OPEN,horizon,bars);
   Z1[0] = temp.Mean();
   Z2[0] = temp.Std();
   temp = ((temp - Z1[0]) / Z2[0]);
   X.Row(temp,1);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_HIGH,horizon,bars);
   Z1[1] = temp.Mean();
   Z2[1] = temp.Std();
   temp = ((temp - Z1[1]) / Z2[1]);
   X.Row(temp,2);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_LOW,horizon,bars);
   Z1[2] = temp.Mean();
   Z2[2] = temp.Std();
   temp = ((temp - Z1[2]) / Z2[2]);
   X.Row(temp,3);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_CLOSE,horizon,bars);
   Z1[3] = temp.Mean();
   Z2[3] = temp.Std();
   temp = ((temp - Z1[3]) / Z2[3]);
   X.Row(temp,4);

//--- Store the Z-scores
   temp.CopyIndicatorBuffer(ma_close_handler,0,horizon,bars);
   Z1[4] = temp.Mean();
   Z2[4] = temp.Std();
   temp = ((temp - Z1[4]) / Z2[4]);
   X.Row(temp,5);

   temp.CopyIndicatorBuffer(ma_close_handler,0,0,bars);
   y.Row(temp,0);
   
   Print("Training Input Data: ");
   Print(X);

   Print("Training Target");
   Print(y);

//--- Perform truncated SVD, we will explore what 'truncated' means later.
PrintFormat("Computing Singular Value Decomposition of %s Data using OpenBLAS",Symbol());
X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);
OB_SIGMA.Diag(OB_S);

//--- Fit the model
//--- More Penrose Psuedo Inverse Solution implemented by MQL5 Developers, enterprise level effeciency!
   b = y.MatMul(OB_VT.Transpose().MatMul(OB_SIGMA.Inv()).MatMul(OB_U.Transpose()));
   Print("OLS Solutions: ");
   Print(b);

//--- Prepare to get a prediction
//--- Reshape the data
   X = matrix::Ones(TOTAL_INPUTS,1);

//--- Get a prediction
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_OPEN,0,1);
   temp = ((temp - Z1[0]) / Z2[0]);
   X.Row(temp,1);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_HIGH,0,1);
   temp = ((temp - Z1[1]) / Z2[1]);
   X.Row(temp,2);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_LOW,0,1);
   temp = ((temp - Z1[2]) / Z2[2]);
   X.Row(temp,3);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_CLOSE,0,1);
   temp = ((temp - Z1[3]) / Z2[3]);
   X.Row(temp,4);

   temp.CopyIndicatorBuffer(ma_close_handler,0,0,1);
   temp = ((temp - Z1[4]) / Z2[4]);
   X.Row(temp,5);

   Print("Prediction Inputs: ");
   Print(X);

//--- Get a prediction
   prediction = b.MatMul(X);
   Print("Prediction");
   Print(prediction[0,0]);
  }
//+------------------------------------------------------------------+

これで、改良版取引アルゴリズムのテスト準備が整いました。この実装は、より情報量の多い予測値に基づいて期待価格を算出することを目的としています。テスト期間は初回のテストと同じ設定でおこない（図26）、アプリケーション設定も変更しません（図23）。読者の皆さんは、同じ構成を使用して追試することが可能です。

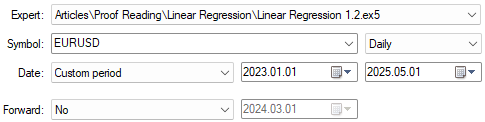
図26：新しい取引アプリケーションによる改善結果をテストする準備

新しい結果を分析すると、明確な改善が確認できます。ナイーブ戦略では総純利益が77ドルであったのに対し、改良戦略では総純利益が101ドルとなり、31%の増加が見られます。また、シャープレシオも初期の0.47から0.63に上昇しており、リスク調整後のリターンが34%改善したことを示しています。これは、システムのパフォーマンスが着実に向上したことを意味します。 

さらに、勝率も51.4%から51.8%に上昇しており、改良版システムがより多くの収益性のある取引を捉えていることが分かります。総取引回数も70回から83回に増加しており、新しいシステムはより多くの取引シグナルを検出していることが示唆されます。 

勝ち取引や負け取引の平均サイズは減少していますが、全体としてシステムはより活発かつ効果的に機能しています。この成果は、ネイティブMQL5コードを使用し、入手可能な市場データに対して行列分解を適切に適用することによって得られたものです。

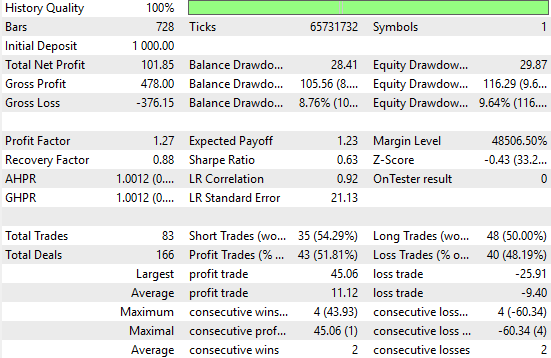
図27：将来の価格レベルに関する情報を反映した予測によって得られたパフォーマンスレベルの詳細分析

また、改良版アプリケーションのによって生成された利益曲線も掲載しています。新しい取引システムは、過去のデータ上で口座残高が上昇傾向を示しており、これにより、さらなる改善を追求して実現していく意欲が高まります。 

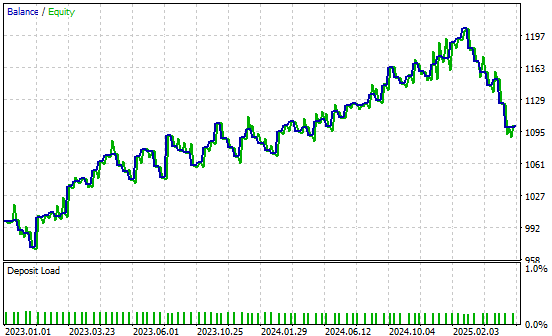
図28：改良版取引アプリケーションによって生成された利益曲線

結論

本記事では、MQL5 Matrix APIの多くの利点を紹介しました。このAPIは強力な数学的ツールを提供し、より情報に基づいた取引判断をおこなう能力を向上させます。

行列分解を用いることで、相関データに隠れたパターンを発見することができます。これらのパターンは、従来の市場分析手法では必ずしも明らかにならない場合があります。読者の皆さんは、従来の金融分野でよく教えられる時系列アプローチに代わる有力な手法を理解できるようになりました。たとえば、典型的な時系列分析では、周期的変化を測定するためにデータを差分化することから始めます。それに対し、私たちの手法では差分化をおこなわず、データを直接行列分解することにより分析をおこないました。

この視点の転換により、多くの応用が可能となります。行列分解を利用することで、高速かつ数値的に安定した統計モデリングが可能になり、データの次元を削減してよりコンパクトな形に簡略化することで、基礎的なトレンドをより明確に把握できます。

行列分解の利点はさらに多くありますが、本記事はその基礎をしっかりと示しています。特に、分解技術を用いることで、明示的に定義された取引ルールの必要性を減らし、システムがデータから直接最適な戦略を学習することが可能になります。

MQL5 Matrix APIを日々の取引ワークフローに統合することで、得られる利点の大きさには驚かされます。