Selbstoptimierende Expert Advisors in MQL5 (Teil 11): Eine sanfte Einführung in die Grundlagen der linearen Algebra

In unserer einleitenden Diskussion über Matrixfaktorisierung haben wir die vielen Vorteile der in der MQL5-API verfügbaren linearen Algebra-Befehle untersucht. Bei dieser ersten Diskussion wurde davon ausgegangen, dass der Leser über ein gewisses Grundwissen verfügt, nämlich über ein grundlegendes Verständnis der Zeitreihenmodellierung und der statistischen Analyse. Im Nachhinein ist jedoch klar, dass diese Annahme nicht für alle Leser gilt.

Wenn Sie zum ersten Mal mit solchen Themen in Berührung kommen, war der Einführungsartikel vielleicht nicht so hilfreich wie beabsichtigt. Der Inhalt schritt schnell voran, wobei viele Konzepte in rascher Folge eingeführt wurden. Daher möchte ich in diesem Artikel den Schwerpunkt auf Leser verlagern, die keinerlei Erfahrung mit den vorgestellten mathematischen Techniken haben.

Ich werde diese Techniken aus einer Perspektive präsentieren, die kein Hintergrundwissen voraussetzt, um sicherzustellen, dass alle Leser folgen können und den Wert der Matrix- und Vektor-API zu schätzen wissen. Die von MQL5 zur Verfügung gestellte Matrix- und Vektor-API ist zwar sehr leistungsfähig, reicht aber allein nicht aus. Sie arbeitet nicht unabhängig. Nur wenn wir die Grundsätze der linearen Algebra verstehen, können wir diese API intelligent und effektiv nutzen.

Dieser Artikel soll als Brücke für Leser ohne formale mathematische Ausbildung dienen. Wir werden einen vergleichenden Unterrichtsstil anwenden: Ich beginne mit der Veranschaulichung von Code, der von einem MQL5-Entwickler ohne Hintergrundwissen in linearer Algebra geschrieben werden könnte, und vergleiche diesen dann mit Code, der von jemandem geschrieben wurde, der die zugrunde liegenden mathematischen Prinzipien versteht. Dieser Ansatz ermöglicht es, die Vorteile der linearen Algebra klar und intuitiv herauszustellen.

Alle vorgestellten theoretischen Konzepte werden direkt mit praktischen Handelsanwendungen verknüpft, die wir hier im MetaTrader 5 Terminal demonstrieren werden. Anhand von realen Marktdaten werden wir die mathematische Theorie praktisch anwenden und so die Vielseitigkeit und den praktischen Wert dieser linearen Algebra-Befehle demonstrieren.

Heute werden wir ein statistisches Modell erstellen, das mehrere Ziele gleichzeitig vorhersagt. In der Regel werden lineare Regressionsmodelle verwendet, um ein einzelnes Ziel zu projizieren, z. B. die zukünftige Preisänderung. In diesem Fall geht es jedoch darum, vier verschiedene Ziele vorherzusagen:

• Der zukünftige gleitende Durchschnitt der Schlusskurse
• Der zukünftige gleitende Durchschnitt der Hochs
  
• Der künftige gleitende Durchschnitt der Tiefs
  
• Der zukünftige Wert der Preise

Wir werden diese Vorhersagen in unsere Handelsstrategie einbeziehen, um sowohl Einstiegs- und Ausstiegsregeln als auch Filter für das Schließen von Positionen zu definieren. Die Matrix- und Vektor-MQL5-API bietet uns leistungsstarke Werkzeuge für die Erstellung moderner Anwendungen für maschinelles Lernen. Um das Potenzial der API auszuschöpfen, müssen Sie jedoch die grundlegenden Regeln der linearen Algebra kennen, die hinter der angemessenen Verwendung dieser speziellen Methoden stehen.

Lineare Algebra ist oft eine abstrakte mathematische Studie. Ich möchte das Thema jedoch für Sie lebendig werden lassen, damit Sie die Vorteile dessen, was wir behandeln werden, klar erkennen können, und dann werden wir die mathematischen Aspekte in der Mitte der Diskussion erörtern. Nachdem die Motivation für unsere Diskussion klar ist und alle erforderlichen mathematischen Notationen erklärt wurden, werden wir ein Beispiel für den Einsatz der linearen Algebra zur Entwicklung numerisch gesteuerter Handelsalgorithmen demonstrieren, die mehrere Ziele gleichzeitig vorhersagen können. 

Wartbare Codebasis

Beim Umgang mit Marktpreisen – z. B. Sammlungen von Eröffnungs-, Höchst-, Tiefst- und Schlusskursen – ist es meist hilfreich, diese Daten in Matrixform zu speichern. In MQL5 werden Matrizen zuerst nach Zeilen und dann nach Spalten indiziert. Daher beginnen wir mit der Definition einer neuen Matrix A, die 3 mal 5 ist und mit Nullen initialisiert wird. Dies bedeutet, dass die Matrix A drei Zeilen und fünf Spalten hat und dass alle Einträge zunächst auf Null gesetzt werden. Wir zeigen dann die Matrix A in ihrem aktuellen Zustand an, die, wie in Abbildung 1 gezeigt, tatsächlich mit Nullen gefüllt ist.

//--- Let's first create an empty matrix
matrix A=matrix::Zeros(3,5);

//--- Peek at the matrix
Print("Original A matrix");
Print(A);

Abbildung 1: Visualisierung unserer leeren Matrix A

Als Nächstes beschriften wir die einzelnen Zeilen: Zeile eins wird mit konstanten Werten von eins gefüllt, Zeile zwei mit Werten von zwei und Zeile drei mit Werten von drei.

Wie der Leser feststellen kann, beginnt die Notation für den Zugriff auf Elemente innerhalb einer Matrix in MQL5 immer mit dem Zeilenindex, gefolgt vom Spaltenindex in eckigen Klammern, der neben dem mit der Matrix verbundenen Bezeichner steht. Wir können die Matrix A noch einmal überprüfen, um sicherzustellen, dass sie korrekt ausgefüllt wurde – Abbildung 2 gibt uns die Gewissheit, dass sie korrekt ausgefüllt wurde.

//--- The notation A[R,C] describes the Row and Column we want to manipulate
//--- We will set all the values in Row 1 to be 1
A[0,0] = 1;
A[0,1] = 1;
A[0,2] = 1;
A[0,3] = 1;
A[0,4] = 1;

//--- We will set all the values in Row 2 to be 2
A[1,0] = 2;
A[1,1] = 2;
A[1,2] = 2;
A[1,3] = 2;
A[1,4] = 2;

//--- We will set all the values in Row 3 to be 3
A[2,0] = 3;
A[2,1] = 3;
A[2,2] = 3;
A[2,3] = 3;
A[2,4] = 3;

Print("Current A matrix");
Print(A);

Abbildung 2: Beschriftung der Zeilen in unserer Matrix A für unsere Übung

Nun wollen wir die Werte in unserer Matrix manipulieren. Angenommen, wir wollen alle Werte in der zweiten Zeile der Matrix A mit fünf multiplizieren. Eine naive Implementierung könnte darin bestehen, eine for-Schleife zu erstellen, die über jeden Eintrag in Zeile zwei iteriert, jeden mit fünf multipliziert und das Ergebnis speichert. Wie wir sehen können, erreicht dieser Ansatz das gewünschte Ergebnis und würde jeden Funktionstest bestehen.

Fallen dem Leser jedoch Gründe ein, warum wir für diese Aufgabe keine for-Schleife verwenden sollten?

//--- Let's multiply all the values of Row 2 by 5 and leave all the other rows the same.

//--- Bad performing code
//--- Copy matrix A
matrix example_1;
example_1.Assign(A);

//--- Loop over matrix A and multiply each element by 5 and then replace the original elements
for(int i =0;i<5;i++)
{
   example_1[1,i] = example_1[1,i] * 5;
}

//--- Done
Print("Example 1: ");
Print(example_1);

Abbildung 3: Die Manipulation der Matrix A mit einer for-Schleife kann zu langsam werden, wenn A größer wird.

Betrachten wir nun einen leicht verbesserten Ansatz. Statt einer Schleife könnten wir die zweite Zeile der Matrix als Zeilenvektor auswählen, sie mit fünf multiplizieren und das Ergebnis dann wieder an seine ursprüngliche Position setzen. Dies hat den gleichen Effekt und ist eleganter. Dennoch frage ich den Leser erneut: Können Sie sich vorstellen, warum selbst dies nicht der bestmögliche Ansatz sein könnte?

//--- Slightly better code
//--- Copy the row, multiply it and then put it back
matrix example_2;
vector copy_vector;

example_2.Assign(A);

copy_vector = example_2.Row(1);

example_2.Row(copy_vector*5,1);

Print("Example 2");
Print(example_2);

Abbildung 4: Die Manipulation der Matrix A mit Vektormethoden ist besser als eine traditionelle for-Schleife, aber nicht optimal

Abschließend möchte ich demonstrieren, was in diesem Zusammenhang als geeigneter Ansatz angesehen wird: Wir beginnen mit der Erstellung eines Skalierungsvektors und wenden diesen Vektor dann mittels Matrixmultiplikation auf die Matrix A an. Wie gezeigt, führen alle drei Codeschnipsel zu demselben Ergebnis. Allerdings sollte der Leser einige wichtige Unterschiede feststellen.

Der dritte Ansatz erfordert die wenigsten Codezeilen. Hier zeigt sich ein wesentlicher Vorteil der Verwendung linearer Algebra für unsere täglichen Handelsaufgaben: Sie ermöglicht es uns, prägnanteren, wartbaren Code zu schreiben. Für die meisten Entwickler sollte dies allein schon ein zwingender Grund sein, Zeit in das Erlernen der linearen Algebra zu investieren. Es gibt jedoch noch viele, weitere Vorteile, die ich im weiteren Verlauf aufzeigen werde. Dies ist einfach ein guter Ausgangspunkt.

//--- Reliable code
matrix example_3,scaler;
vector scale = {1,5,1};

scaler.Diag(scale);
example_3 = scaler.MatMul(A);

//--- Done 
Print("Example 3");
Print(example_3);

Abbildung 5: Es ist immer am besten, geeignete matrix- und vektorbezogene Methoden zu verwenden, wenn es sie gibt.

Nun wollen wir das Beispiel erweitern. Zunächst haben wir nur die zweite Zeile mit fünf multipliziert. Wir multiplizieren nun die erste Zeile mit zwei, die letzte Zeile mit zehn und lassen die mittlere Zeile unverändert. An dieser Stelle werden dem Leser vielleicht die Probleme bei der Verwendung der for-Schleife klar. Mit der Anzahl der Operationen an der Matrix A steigt auch die Länge unserer Schleife und damit die Anzahl der Zeilen, die wir schreiben müssen. Wenn die Matrix A ausreichend groß ist, kann die Iteration über jeden einzelnen Wert – wie in der Schleife vorgeschlagen – die Ausführung erheblich verlangsamen, insbesondere bei den Backtests. 

//--- Now, multiply the first and last rows by 2 and 10, but leave the middle row as it is.

//--- Loops can slow us down during backtests, especially if they must be repeated often.
for(int i =0;i<5;i++)
{
   example_1[0,i] = example_1[0,i] * 2;
   example_1[2,i] = example_1[2,i] * 10;
}

//--- Done
Print("Example 1");
Print(example_1);

Abbildung 6: Wir müssen in unserer for-Schleife mehr Codezeilen schreiben, um den gleichen Effekt zu erzielen

Auch die Methode der Auswahl und Neuzuordnung einzelner Zeilen wird mit zunehmender Anzahl von Vorgängen immer komplexer. Obwohl diese Methode einer einfachen for-Schleife überlegen ist, führt sie dennoch zu aufgeblähtem Code und erhöht die Fehlerwahrscheinlichkeit.

//--- The difference between example 2 and 3 starts to show
//--- Copy the row, multiply it and then put it back
vector copy_vector_2;

copy_vector = example_2.Row(0);
copy_vector_2 = example_2.Row(2);

example_2.Row(copy_vector*2,0);
example_2.Row(copy_vector_2*10,2);

//--- Done
Print("Example 2");
Print(example_2);

Abbildung 7: Die Verkettung allgemeiner Matrix- und Vektormethoden kann die Aufgabe zwar immer noch erfüllen, aber es geht noch besser

Wir können es immer noch besser machen, indem wir uns auf die Matrixmultiplikation verlassen. Bei diesem Ansatz ändern sich nur die Skalierungswerte. Der Rest des Codes bleibt im Wesentlichen gleich, unabhängig von der Anzahl der beteiligten Zeilen. Alle drei Methoden liefern das gleiche Ergebnis – aber nachdem ich sie nebeneinander gesehen habe, frage ich den Leser: Welcher Ansatz scheint bei der Arbeit mit großen Mengen historischer Marktdaten am besten geeignet?

//--- Reliable code
vector scale_2 = {2,1,10};
scaler.Diag(scale_2);
example_3 = scaler.MatMul(example_3);

//--- Done
Print("Example 3");
Print(example_3);

Abbildung 8: Wir können die gleiche Ausgabe mit weniger Codezeilen erreichen, wenn wir präziser programmieren

Erforderliche Zeit für Backtesting

Mit herkömmlichen for-Schleifen können wir möglicherweise nicht alle Datenpunkte effizient verarbeiten, insbesondere bei zeitkritischen Operationen wie den Backtests. Dies bringt uns zu einem zweiten wichtigen Punkt: Unsere Codebasis ist nicht nur einfacher zu pflegen, wenn wir Matrix- und Vektor-APIs angemessen nutzen, sondern auch die Ausführungszeit unserer Handelsstrategien wird effizienter.

Letztendlich sind die meisten Leser wahrscheinlich daran interessiert, leistungsfähige KI-Modelle für den Handel zu entwickeln – Modelle, die in der Lage sind, fundierte Entscheidungen zu treffen. Doch damit Ihr KI-Modell solche Entscheidungen treffen kann, benötigt es Zugang zu großen Datenmengen. Und bevor wir diese Daten in das Modell einspeisen, müssen wir bestimmte Vorverarbeitungsschritte und Manipulationen vornehmen.

Wenn wir diese Operationen ineffizient durchführen, steigt die Anzahl der Zeilen, die für die Erstellung der Anwendung erforderlich sind, rapide an – vor allem, wenn wir uns auf for-Schleifen verlassen. Mit zunehmender Codegröße steigt auch der Zeitaufwand für die Backtests.

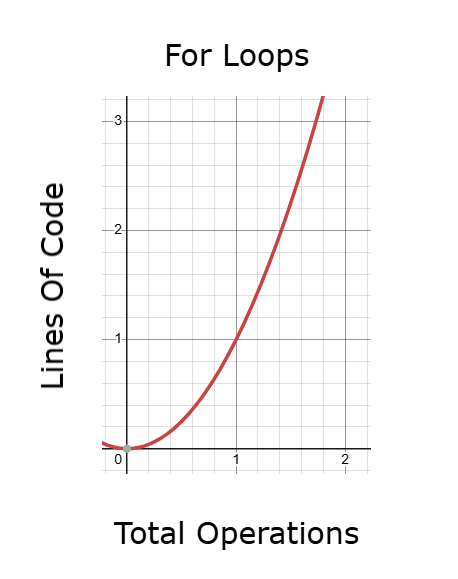
Abbildung 9: For-Schleifen können Code erzeugen, dessen Ausführung bei Backtests zu lange dauert

Eine bessere Alternative ist die Verwendung verketteter Vektor- und Matrixoperationen. Diese Methode ist viel schneller als die traditionelle Schleifenbildung, aber auch sie kann mühsam werden, wenn sie das wiederholte Kopieren, Ändern und Neuzuordnen von Zeilen beinhaltet. Wenn die Anzahl solcher Operationen zunimmt, steigt auch die für die Ausführung des Codes benötigte Zeit, was sich wiederum auf die Backtest-Leistung und die Modelloptimierung auswirkt.

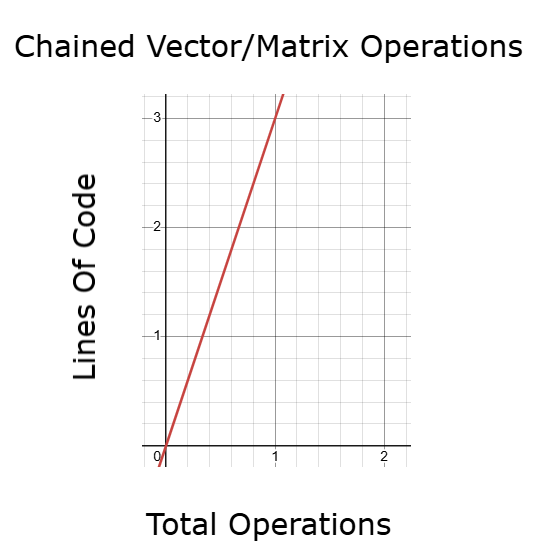
Abbildung 10: Die Verkettung von Matrix- und Vektor-APIs wird schneller sein als eine for-Schleife, aber vielleicht können wir noch mehr erreichen

Andererseits können wir durch die Verwendung geeigneter Vektor- und Matrixoperationen, die auf der linearen Algebra beruhen, die Ausführungszeit kontrollieren und die Codelänge und die Zeit für Backtests konstant halten – selbst wenn die Datengröße zunimmt. Dies ist eine äußerst wünschenswerte Eigenschaft für jede Anwendung. Das bedeutet, dass wir mehr Operationen durchführen können, ohne immer proportional mehr Code zu schreiben und ohne die Ausführungszeit zu verlängern – so können wir Modelle für maschinelles Lernen effektiver iterieren und optimieren. Ich glaube, dass die meisten Leser erstaunt sein werden, wie viele Fortschritte man machen kann, wenn man nur ein paar grundlegende Konzepte der linearen Algebra versteht. Wir brauchen keine fortgeschrittene Theorie, um sinnvolle Verbesserungen bei unseren Anwendungen zu erzielen.

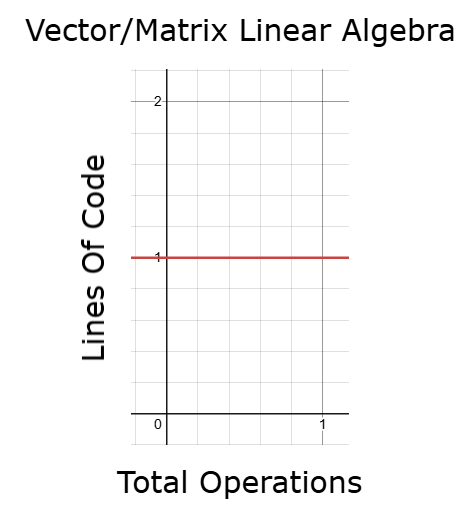
Abbildung 11: Der Einsatz von linearer Algebra kann uns helfen, eine konstante Laufzeit unserer Anwendungen zu erreichen

Precision

Ich möchte auch einen wichtigen Punkt hervorheben, der meines Erachtens in technischen Diskussionen oft übersehen wird: die Präzision. Ich bin der Meinung, dass dieses Thema nicht die Aufmerksamkeit und Prüfung erhält, die es wirklich verdient. Präzision ist eine der wichtigsten Komponenten beim Aufbau einer zuverlässigen Handelsstrategie. Die mit den Backtests erzielten Ergebnisse müssen genau sein, und von den internen Berechnungen und Entscheidungen der Anwendung wird erwartet, dass sie präzise und vertrauenswürdig sind.

Stellen Sie sich folgendes Szenario vor: Im Beispiel-Codeausschnitt führen wir eine einfache Gleitkomma-Subtraktion durch, z. B. 0,3 – 0,1. Der Computer meldet das Ergebnis als 0,199999... anstelle der erwarteten 0,2. Dies ist ein bekanntes Problem in der Informatik im Zusammenhang mit der Fließkommaarithmetik, und es ist nicht nur bei MQL5 der Fall. 

Der Punkt, den ich betonen möchte, ist folgender: Stellen Sie sich vor, Sie führen eine solche Subtraktionsoperation innerhalb einer Schleife durch. Stellen Sie sich nun vor, dass Sie eine Matrix wie A, die über eine Million Zeilen haben kann, in einer Schleife durchlaufen und diese Operation für jede einzelne Zeile durchführen. Es ist leicht zu erkennen, wie sich diese kleinen Fehler in der Genauigkeit akkumulieren und verstärken können und schließlich zu einer erheblichen numerischen Instabilität der Ergebnisse führen.

Arithmetische Berechnungen – wie z. B. direkte Subtraktionen bei großen Matrizen – sind ineffizient und führen nicht zu präzisen oder numerisch stabilen Ergebnissen.

Wenn wir darüber hinaus Algorithmen wie die in früheren Beispielen gezeigten betrachten – bei denen Werte wiederholt von einem Ort zum anderen kopiert werden, neue Objekte erstellt werden, Daten neu zugewiesen werden und Speicher ständig zugewiesen und freigegeben wird – wird das Problem noch dringlicher. Computer haben einen begrenzten Speicher. Wenn wir Matrixoperationen ineffizient durchführen und ständig Objekte erzeugen und zerstören, erhöhen wir den Speicherbedarf unnötig. Der Versuch, das Gedächtnis auf eine solch willkürliche Weise zu verwalten, hat materielle Folgen, die wir oft übersehen.

Darüber hinaus gibt es bekannte Algorithmen – von denen viele bereits in der Matrix- und Vektor-API von MQL5 sowie in unterstützenden Bibliotheken, die wir behandeln werden, implementiert sind – die genau auf diese Probleme ausgerichtet sind. Diese Implementierungen sind optimiert, um Fließkommafehler zu minimieren und die numerische Stabilität zu maximieren. Entscheiden sich Entwickler dagegen für weniger effiziente Methoden – wie manuelle for-Schleifen zur Datenmanipulation – erhöhen sie unwissentlich die Wahrscheinlichkeit, auf diese Probleme zu stoßen.

//--- Why should you care?
//--- Let's start with an often overlooked need, precision!
Print("Our computers have limited memory to store numbers with precision");
Print("What is 0.3 - 0.1");
Print(0.3-0.1);
Print("You and I know the correct answer is 0.2");

Abbildung 12: Die Verwendung der entsprechenden linearen Matrix/Vektor-Algebra kann uns helfen, solche Fehler zu minimieren

Wie können wir als Händler lineare Algebra nutzen?

Nun, da der Leser die Vorteile des Erlernens der linearen Algebra zu schätzen weiß, ist es an der Zeit, einige der grundlegenden Regeln zu betrachten, die bestimmen, wie wir mit Hilfe dieser Algebra Entscheidungen treffen. Die Kenntnis dieser Grundregeln ist eine wertvolle Fähigkeit.

Anmerkung für Anfänger: Mein Ziel ist es nicht, Sie dazu zu bringen, Formeln auswendig zu lernen. Vielmehr geht es darum, Ihnen zu helfen, die Prinzipien so tief zu verstehen, dass sie intuitiv werden – sodass Sie sie sich auf natürliche Weise einprägen, nicht durch Auswendiglernen.

Um die lineare Algebra zu verstehen, benötigen wir zunächst ein solides Verständnis der grundlegenden Algebra. Algebra ist im Wesentlichen die Mathematik der unbekannten Größen. Beginnen wir mit einem einfachen Beispiel, das in Abbildung 13 dargestellt ist: Diese Gleichung besagt, dass ein unbekannter Wert, multipliziert mit 2, 4 ergibt. Um x zu lösen, werden beide Seiten durch 2 geteilt. Wenn wir unsere Lösung testen wollen, ersetzen wir einfach x durch den Wert 2 in der ursprünglichen Gleichung und überprüfen dann, ob 2 multipliziert mit 2 tatsächlich 4 ergibt. Dies mag sich zwar grundlegend anfühlen, bildet aber die Grundlage für weiterführende Konzepte.

Abbildung 13: Veranschaulichung eines einfachen Problems in der Algebra, bei dem der Wert von x gleich 2 ist

Betrachten wir nun eine kleine Abwandlung: Was wäre, wenn in der Gleichung A mit 2 multipliziert würde und 4 ergeben soll? Wir würden beide Seiten durch A dividieren und die Lösung als x ist gleich 4 geteilt durch A angeben. Da uns nicht gesagt wird, was A ist, haben wir die Aufgabe fertig gelöst.

Abbildung 14: Betrachten wir eine etwas kompliziertere Version des in Abbildung 13 dargestellten Problems

Was ist nun, wenn A nicht eine Zahl ist, sondern eine Matrix? Dies ist der Übergang von der in der Schule gelehrten Algebra zur linearen Algebra. Hier ist A eine Matrix. Wir könnten versucht sein, beide Seiten durch A zu teilen, wie wir es bereits getan haben. In der linearen Algebra ist die Division durch eine Matrix jedoch nicht definiert. Stattdessen verwenden wir die Inverse einer Matrix. Wenn die Matrix eine Inverse hat, lösen wir die Gleichung, indem wir beide Seiten mit der Inversen von A multiplizieren.

Abbildung 15: Die lineare Algebra beruht auf der gleichen Logik, die wir für unsere einfachen Beispiele verwendet haben, aber wir ändern nur ein paar Regeln

Was bedeutet das im Zusammenhang mit den Marktdaten? Angenommen, die Matrix A stellt aktuelle Marktdaten dar, z. B. das Preisniveau. Der Vektor y steht für den zukünftigen Preis, den Sie vorhersagen wollen. Sie wollen den Koeffizientenvektor so finden, dass, „wenn ich meine aktuellen Daten mit dem Koeffizientenvektor multipliziere, ich die zukünftigen Preisniveaus erhalten sollte“.

Aber das Problem ist, dass nicht jede Matrix eine Inverse hat. Die Invertierung einer Matrix, die nicht invertierbar ist, kann Ihren Handelsalgorithmus zum Absturz bringen oder unzuverlässige Ergebnisse liefern. Aus diesem Grund invertieren wir nicht „blind“ jede Matrix, die uns begegnet. Stattdessen ist es oft sicherer und stabiler, mit kleineren Untermatrizen von -Anteilen der Daten zu arbeiten, die wir zuverlässig invertieren oder mit anderen numerisch stabilen Techniken wie Matrixfaktorisierungen (z. B. QR, SVD oder Pseudo-Inversen) verarbeiten können.

Abbildung 16: Verallgemeinerung der Lösung eines beliebigen linearen Gleichungssystems

Lineare Algebra zur Verbesserung unseres Handels

Nachdem wir uns nun mit den Grundregeln für das Lösen linearer Gleichungssysteme mit Hilfe der linearen Algebra vertraut gemacht haben, können wir nun damit beginnen, das Gelernte auf das Lösen des Koeffizientenvektors x anzuwenden. Für dieses spezielle Beispiel möchte ich Ihnen zeigen, dass die Formel, die wir besprochen haben, für mehrere Ziele in y genauso einfach gelöst werden kann wie für ein einzelnes Ziel. Beginnen wir also mit der Definition unserer Systemkonstanten. Heute müssen wir angeben, wie viele Eingaben unser Modell benötigt. Dieses spezielle Modell benötigt acht Eingaben.

//+------------------------------------------------------------------+
//|                                            Linear Regression.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/en/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| System constants                                                 |
//+------------------------------------------------------------------+
#define TOTAL_INPUTS 8

Danach müssen wir wichtige Systemparameter festlegen. Zum Beispiel die Anzahl der abzurufenden historischen Balken, wie weit in die Zukunft wir prognostizieren wollen, die verwendeten Zeitrahmen und andere damit verbundene Einstellungen. Alle diese Angaben werden in den Systemparametern gespeichert.

//+------------------------------------------------------------------+
//| System parameters                                                |
//+------------------------------------------------------------------+
int bars = 90;                                        //Number of historical bars to fetch
int horizon = 1;                                      //How far into the future should we forecast
int MA_PERIOD = 2;                                    //Moving average period
ENUM_TIMEFRAMES TIME_FRAME = PERIOD_D1;               //User Time Frame
ENUM_TIMEFRAMES RISK_TIME_FRAME = PERIOD_D1;          //Time Frame for our ATR stop loss
double sl_size = 2;                                   //ATR Stop loss size

Abhängigkeiten sind in jeder Anwendung wichtig, weil sie die Gesamtmenge des Codes reduzieren, die von einem Projekt zum nächsten neu geschrieben werden muss. Daher werden wir mehrere wichtige Abhängigkeiten laden, wie z. B. die Trade Impedance-Abhängigkeit, die bei jeder Version von MetaTrader 5 vorinstalliert ist. Die beiden anderen Abhängigkeiten wurden speziell für unsere Handelsaktivitäten entwickelt.

//+------------------------------------------------------------------+
//| Dependencies                                                     |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
#include <VolatilityDoctor\Time\Time.mqh>
#include <VolatilityDoctor\Trade\TradeInfo.mqh>

Unser System wird auch wichtige globale Variablen definieren, die in verschiedenen Kontexten innerhalb der Anwendung verwendet werden. Wir werden zum Beispiel globale Variablen haben, um die aktuellen Messwerte der Indikatoren zu speichern. In anderen werden Werte gespeichert, die von den Abhängigkeiten verwendet werden, und wieder andere enthalten die Koeffizienten, die wir aus den Daten gelernt haben. Dazu gehören Werte wie der ATR-Wert und viele andere bewegliche Teile unseres Systems.

//+------------------------------------------------------------------+
//| Global Variables                                                 |
//+------------------------------------------------------------------+
int        ma_close_handler,ma_high_handler,ma_low_handler;
double     ma_close[],ma_high[],ma_low[];
Time       *Timer;
TradeInfo  *TradeInformation;
vector     bias,temp,temp_2,temp_3,temp_4,temp_5,Z1,Z2;
matrix     X,y,prediction,b;
int        time;
CTrade Trade;
int state;
int atr_handler;
double atr[];

Bei der Initialisierung erstellt das System neue Objekte für die von uns geladenen nutzerdefinierten Abhängigkeiten. Der Timer ist dafür zuständig, die Bildung neuer Kerzen zu verfolgen. Das Handelsbildungsmodul liefert wichtige Informationen wie das Mindesthandelsvolumen, den Briefkurs (Ask) und den Geldkurs (Bid). Wir werden auch Handler für die Verfolgung unserer gleitenden Durchschnitte erstellen und unsere Matrizen und Vektoren mit Platzhalterwerten von eins initialisieren, nur um den Anfang zu machen.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   Timer                   = new Time(Symbol(),TIME_FRAME);
   TradeInformation        = new TradeInfo(Symbol(),TIME_FRAME);
   ma_close_handler        = iMA(Symbol(),TIME_FRAME,MA_PERIOD,0,MODE_SMA,PRICE_CLOSE);
   ma_high_handler        = iMA(Symbol(),TIME_FRAME,MA_PERIOD,0,MODE_SMA,PRICE_HIGH);
   ma_low_handler        = iMA(Symbol(),TIME_FRAME,MA_PERIOD,0,MODE_SMA,PRICE_LOW);

   bias = vector::Ones(TOTAL_INPUTS);
   Z1 = vector::Ones(TOTAL_INPUTS);
   Z2 = vector::Ones(TOTAL_INPUTS);
   X = matrix::Ones(TOTAL_INPUTS,bars);
   y = matrix::Ones(1,bars);
   time = 0;
   state = 0;
   atr_handler = iATR(Symbol(),RISK_TIME_FRAME,14);
//---
   return(INIT_SUCCEEDED);
  }

Wenn unsere Anwendung nicht mehr in Gebrauch ist, geben wir alle Objekte frei, die an Speicherressourcen gebunden sind. Dies ist eine bewährte Praxis in MQL5 und wir werden sie immer befolgen.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   IndicatorRelease(atr_handler);
   IndicatorRelease(ma_close_handler);
   IndicatorRelease(ma_high_handler);
   IndicatorRelease(ma_low_handler);
  }

Immer wenn aktualisierte Preise in OnTick empfangen werden, prüfen wir zunächst, ob sich eine neue Kerze vollständig gebildet hat. Ist dies der Fall, kopieren wir alle Indikatorwerte in die zugehörigen Arrays und bereiten das Modell für eine Marktprognose vor. Danach verfolgen wir den aktuellen Schlusskurs und berechnen unseren Stop-Loss – sowohl für Verkaufs- als auch für Kaufpositionen.

Von dort aus zeigen wir die voraussichtlichen Preisniveaus, die unser Modell erwartet. Erinnern Sie sich daran, dass wir die gleitenden Durchschnitte der Schlusskurse, der Hochs und der Tiefs und die Preise selbst prognostizieren. Wenn derzeit keine Positionen offen sind, setzen wir zunächst die entsprechenden Zustandsvariablen zurück. Dann prüfen wir die Beziehung zwischen dem erwarteten Schlusskurs und dem erwarteten gleitenden Schlussdurchschnitt in der Zukunft.

Im Allgemeinen wollen wir sehen, dass unser Algorithmus erwartet, dass der gleitende Durchschnitt des Schlusskurses über dem aktuellen Schlusskurs liegt. Dies deutet darauf hin, dass die Preise derzeit unterbewertet sind, da sie unter dem Wert gehandelt werden, den das Modell als fairen Wert ansieht.

Als zusätzliche Bestätigung wollen wir auch sicherstellen, dass unser Stop-Loss wahrscheinlich nicht erreicht wird – sowohl bei Kauf- als auch bei Verkaufspositionen. Im Falle eines Kaufs überprüfen wir, ob der gleitende Durchschnitt der Tiefs nicht unter den Stop-Loss des Kaufs fällt. Bei einem Verkauf prüfen wir, ob der gleitende Durchschnitt der Hochs voraussichtlich nicht über den Verkaufsstopp ansteigt. Wenn eine der beiden Bedingungen verletzt wird, vermeiden wir es, eine Position einzugehen.

Außerdem vergleichen wir jeden einzelnen gleitenden Durchschnitt mit seinem Komplementärpaar. Beim Kauf gehen wir davon aus, dass der zukünftige Wert des unteren gleitenden Durchschnitts höher ist als sein aktueller Wert. Beim Verkauf erwarten wir, dass der künftige Wert des unteren gleitenden Durchschnitts niedriger ist als sein aktueller Wert. In ähnlicher Weise wollen wir beim Kauf, dass der zukünftige hohe gleitende Durchschnitt seinen aktuellen Wert übersteigt.

Wenn es an der Zeit ist, eine Position zu schließen, prüfen wir zunächst, ob sich die Kurse voraussichtlich gegen uns entwickeln werden. Wenn wir davon ausgehen, dass ein gleitender Durchschnitt den Stop-Loss überschreiten könnte, steigen wir sofort aus dem Handel aus. Andernfalls lassen wir den Stop-Loss weiter in ein profitableres Gebiet nachziehen.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
   if(Timer.NewCandle())
     {
      CopyBuffer(atr_handler,0,0,1,atr);
      CopyBuffer(ma_close_handler,0,0,1,ma_close);
      CopyBuffer(ma_low_handler,0,0,1,ma_low);
      CopyBuffer(ma_high_handler,0,0,1,ma_high);

      setup();

      double c =  iClose(Symbol(),TIME_FRAME,0);
      double buy_sl = (TradeInformation.GetBid() - (sl_size * atr[0]));
      double sell_sl = (TradeInformation.GetAsk() + (sl_size * atr[0]));


      Comment("Forecasted MA: ",prediction[0,0],"\nForecasted MA High: ",prediction[1,0],"\nForecasted MA Low: ",prediction[2,0],"\nForecasted Price: ",prediction[3,0]);

      if(PositionsTotal() == 0)
        {
         state = 0;
         if((prediction[0,0] > c) && (prediction[2,0] > buy_sl) && (prediction[3,0] > c) && (prediction[2,0] > ma_low[0]) && (prediction[1,0] > ma_high[0]))
           {
            Trade.Buy(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetAsk(),buy_sl,0);
            state = 1;
           }
         if((prediction[0,0] < c) && (prediction[1,0] < sell_sl) && (prediction[3,0] < c) && (prediction[2,0] < ma_low[0]) && (prediction[1,0] < ma_high[0]))
           {
            Trade.Sell(TradeInformation.MinVolume(),Symbol(),TradeInformation.GetBid(),sell_sl,0);
            state = -1;
           }
        }

      if(PositionsTotal() > 0)
        {
         double current_sl = PositionGetDouble(POSITION_SL);
        
         if(((state == -1) && (prediction[0,0] > c) && (prediction[1,0] > current_sl)) || ((state == 1)&&(prediction[0,0] < c)&& (prediction[2,0] < current_sl)))
            Trade.PositionClose(Symbol());
         if(PositionSelect(Symbol()))
           {
            

            if((state == 1) && ((ma_close[0] - (2 * atr[0]))>current_sl))
              {
               Trade.PositionModify(Symbol(),(ma_close[0] - (2 * atr[0])),0);
              }

            else
               if((state == -1) && ((ma_close[0] + (1 * atr[0]))<current_sl))
                 {
                  Trade.PositionModify(Symbol(),(ma_close[0] + (2 * atr[0])),0);
                 }
           }
        }
     }
  }

Als Nächstes müssen wir auf einige der einzelnen Funktionen eingehen, die für die oben genannten Aufgaben vorbereitet wurden. Die erste Funktion ist prepare_data(). Diese Funktion dient einem einzigen Hauptzweck: Sie kopiert alle benötigten Preisniveaus in die Eingabedatenmatrix x. Es holt den Eröffnungskurs ab, berechnet den Mittelwert und die Standardabweichung des Eröffnungskurses und normalisiert die Daten, indem es den Mittelwert subtrahiert und durch die Standardabweichung dividiert. Dieser Vorgang wird für alle Eingaben wiederholt. Alle Werte des gleitenden Durchschnitts werden ebenfalls kopiert und im Zielfeld y gespeichert.

//+------------------------------------------------------------------+
//| Prepare the training data for our model                          |
//+------------------------------------------------------------------+
void prepare_data(void)
  {
//--- Reshape the matrix
   X = matrix::Ones(TOTAL_INPUTS,bars);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_OPEN,horizon,bars);
   Z1[0] = temp.Mean();
   Z2[0] = temp.Std();
   temp = ((temp - Z1[0]) / Z2[0]);
   X.Row(temp,1);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_HIGH,horizon,bars);
   Z1[1] = temp.Mean();
   Z2[1] = temp.Std();
   temp = ((temp - Z1[1]) / Z2[1]);
   X.Row(temp,2);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_LOW,horizon,bars);
   Z1[2] = temp.Mean();
   Z2[2] = temp.Std();
   temp = ((temp - Z1[2]) / Z2[2]);
   X.Row(temp,3);

//--- Store the Z-scores
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_CLOSE,horizon,bars);
   Z1[3] = temp.Mean();
   Z2[3] = temp.Std();
   temp = ((temp - Z1[3]) / Z2[3]);
   X.Row(temp,4);

//--- Store the Z-scores
   temp.CopyIndicatorBuffer(ma_close_handler,0,horizon,bars);
   Z1[4] = temp.Mean();
   Z2[4] = temp.Std();
   temp = ((temp - Z1[4]) / Z2[4]);
   X.Row(temp,5);

//--- Store the Z-scores
   temp.CopyIndicatorBuffer(ma_high_handler,0,horizon,bars);
   Z1[5] = temp.Mean();
   Z2[5] = temp.Std();
   temp = ((temp - Z1[5]) / Z2[5]);
   X.Row(temp,6);

//--- Store the Z-scores
   temp.CopyIndicatorBuffer(ma_low_handler,0,horizon,bars);
   Z1[6] = temp.Mean();
   Z2[6] = temp.Std();
   temp = ((temp - Z1[6]) / Z2[6]);
   X.Row(temp,7);

//--- Labelling our targets
   temp.CopyIndicatorBuffer(ma_close_handler,0,0,bars);
   temp_2.CopyIndicatorBuffer(ma_high_handler,0,0,bars);
   temp_3.CopyIndicatorBuffer(ma_low_handler,0,0,bars);
   temp_4.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_CLOSE,0,bars);

//--- Reshape y
   y.Reshape(4,bars);

//--- Store the targets
   y.Row(temp,0);
   y.Row(temp_2,1);
   y.Row(temp_3,2);
   y.Row(temp_4,3);
  }

Anschließend definieren wir eine Funktion zur Anpassung des Modells. Diese Funktion beginnt mit der Erstellung der entsprechenden Matrizen und Vektoren. Wir zerlegen (oder faktorisieren) die x-Matrix mithilfe der OpenBlass-Bibliothek und speichern die faktorisierten Matrizen in den Variablen, die wir zuvor eingeführt haben. Mit Hilfe der geschlossenen Lösung können wir B aus x erhalten und dann die gelernten Koeffizienten aus B ausdrucken.

//+------------------------------------------------------------------+
//| Fit our model                                                    |
//+------------------------------------------------------------------+
void fit(void)
  {
//--- Fit the model
   matrix OB_U,OB_VT,OB_SIGMA;
   vector OB_S;

   PrintFormat("Computing Singular Value Decomposition of %s Data using OpenBLAS",Symbol());
   X.SingularValueDecompositionDC(SVDZ_S,OB_S,OB_U,OB_VT);
   OB_SIGMA.Diag(OB_S);
   b = y.MatMul(OB_VT.Transpose().MatMul(OB_SIGMA.Inv()).MatMul(OB_U.Transpose()));
   Print("OLS Solutions: ");
   Print(b);
  }

Um eine Vorhersage zu erstellen, holen wir wieder alle Eingabedaten – genau wie in prepare_data – und führen eine letzte Matrixmultiplikation durch, um unsere Vorhersage von B zu erhalten.

//+------------------------------------------------------------------+
//| Get a prediction from our multiple output model                  |
//+------------------------------------------------------------------+
void predict(void)
  {
//--- Prepare to get a prediction
//--- Reshape the data
   X = matrix::Ones(TOTAL_INPUTS,1);

//--- Get a prediction
   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_OPEN,0,1);
   temp = ((temp - Z1[0]) / Z2[0]);
   X.Row(temp,1);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_HIGH,0,1);
   temp = ((temp - Z1[1]) / Z2[1]);
   X.Row(temp,2);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_LOW,0,1);
   temp = ((temp - Z1[2]) / Z2[2]);
   X.Row(temp,3);

   temp.CopyRates(Symbol(),TIME_FRAME,COPY_RATES_CLOSE,0,1);
   temp = ((temp - Z1[3]) / Z2[3]);
   X.Row(temp,4);

   temp.CopyIndicatorBuffer(ma_close_handler,0,0,1);
   temp = ((temp - Z1[4]) / Z2[4]);
   X.Row(temp,5);
   
   temp.CopyIndicatorBuffer(ma_high_handler,0,0,1);
   temp = ((temp - Z1[5]) / Z2[5]);
   X.Row(temp,6);

   temp.CopyIndicatorBuffer(ma_low_handler,0,0,1);
   temp = ((temp - Z1[6]) / Z2[6]);
   X.Row(temp,7);

   Print("Prediction Inputs: ");
   Print(X);

//--- Get a prediction
   prediction.Reshape(1,4);
   prediction = b.MatMul(X);
   Print("Prediction");
   Print(prediction);
  }

Schließlich rufen wir jedes Mal, wenn wir aktualisierte Preise in OnTick erhalten, eine Funktion namens setup auf. Diese Funktion ruft die drei soeben beschriebenen Hauptfunktionen auf. Es bereitet die Daten auf, passt das Modell an und erstellt eine Vorhersage.

//+------------------------------------------------------------------+
//| Obtain a prediction from our model                               |
//+------------------------------------------------------------------+
void setup(void)
  {
   prepare_data();
   fit();

   Print("Training Input Data: ");
   Print(X);

   Print("Training Target");
   Print(y);

   predict();
  }
//+------------------------------------------------------------------+

#undef TOTAL_INPUTS
//+------------------------------------------------------------------+

Damit sind wir bereit, unsere Anwendung mit historischen Daten zu testen. Wie unten in Abbildung 17 dargestellt, haben wir unsere Anwendung auf den EUR/USD-Markt von 2022 bis 2025 angewandt. Wir führen die Backtests mit historischen Daten aus zwei Jahren durch.

Abbildung 17: Unsere Backtest-Tage umfassen 2 Jahre historischer EURUSD-Marktdaten

Wir haben auch zufällige Verzögerungseinstellungen auf der Grundlage echter Ticks gewählt, um eine möglichst genaue Darstellung der Marktbedingungen zu erhalten. Stellen Sie sicher, dass Sie die gleichen Einstellungen verwenden, wenn Sie eine realistische Emulation der Leistung Ihrer Anwendung wünschen.

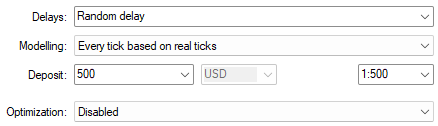
Abbildung 18: Auswahl von zufälligen Verzögerungseinstellungen für den Test unserer Handelsanwendung unter realistischen Marktbedingungen

In Abbildung 18 sehen wir, dass unsere Anwendung erfolgreich vier unabhängige Prognosen erstellt – eine für jedes Preisniveau von Interesse. Es verwendet die im Hauptteil der Anwendung entwickelten Filter, um Positionen auf der Grundlage aller vier Vorhersagen zu eröffnen.

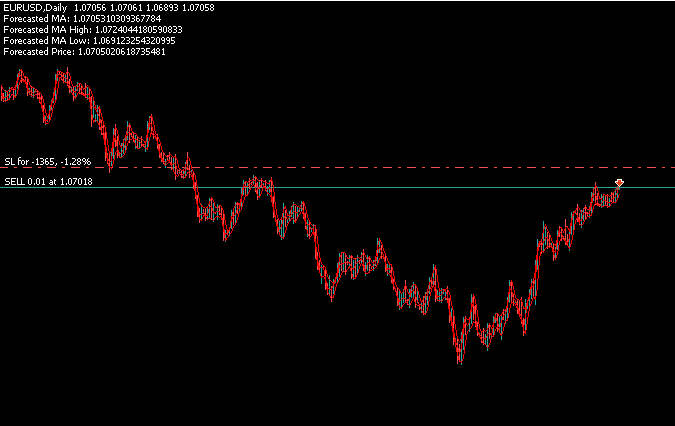
Abbildung 19: Ein Backtest unseres Handelsalgorithmus, um seine Fähigkeit zu testen, 4 verschiedene Ziele gleichzeitig vorherzusagen

Ich habe ein Bildschirmfoto des Terminalprotokolls beigefügt, um zu zeigen, dass unsere Anwendung tatsächlich eine Matrix von Koeffizienten gelernt hat. Wie Sie sehen können, gibt es vier Zeilen in der Lösungsmatrix, was bedeutet, dass unsere Anwendung für jedes der vier Ziele, die wir vorhersagen wollen, einen einzigen Satz von Koeffizienten gelernt hat. Die Anwendung lernt jedes Ziel unabhängig.

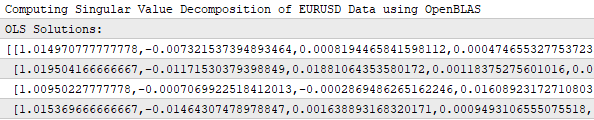
Abbildung 20: Unsere Handelsanwendung lernt für jedes der 4 Ziele, die wir ihr zugewiesen haben, einen eigenen Satz von Koeffizienten

Außerdem zeigt unsere Anwendung im Laufe der Zeit einen positiven Trend beim Kontostand. Obwohl wir die Unregelmäßigkeiten in dieser Bilanz gerne ausgleichen würden, werden wir das System weiter verfeinern, um ein gleichmäßigeres Wachstum zu erreichen.

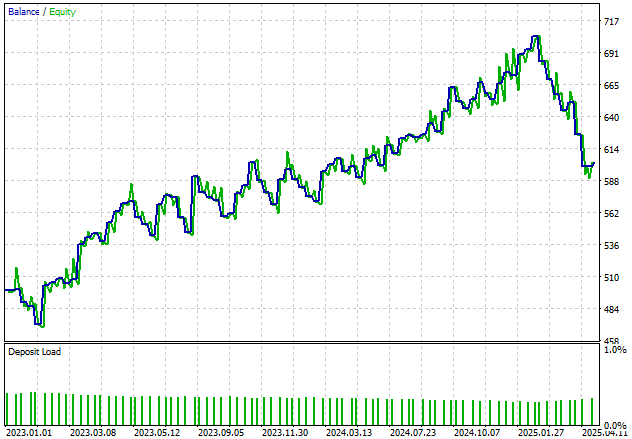
Abbildung 21: Veranschaulichung des Wachstums der Kapitalkurve unseres Kontos über den 2-Jahres-Zeitraum des Backtests.

Wenn wir die Performance des Kontos im Detail analysieren, stellen wir fest, dass 51% unserer Trades profitabel waren. Dies ist zwar ein guter Ausgangspunkt, aber wir wollen diese Zahl in Zukunft auf 55 % oder sogar 60 % erhöhen. Unser durchschnittlicher Gewinn ist größer als unser durchschnittlicher Verlust, und unser größter Gewinn ist fast doppelt so groß wie unser größter Verlust. Das deutet darauf hin, dass das System solide ist, auch wenn wir es noch verbessern wollen.

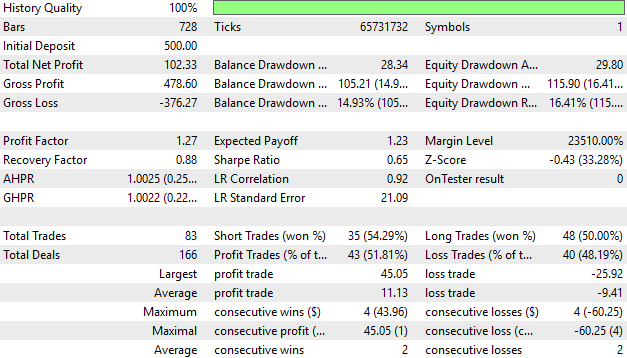
Abbildung 22: Eine detaillierte Analyse der Leistung unserer Handelsanwendung während unseres Backtests

Schlussfolgerung

Abschließend hat dieser Artikel dem Leser gezeigt, wie wichtig es ist, die Konzepte der linearen Algebra zu verstehen – und wie sie sich direkt auf unsere Fähigkeit auswirken, Marktdaten im MetaTrader 5 Terminal zu manipulieren. Ohne dieses Verständnis wird die Analyse großer Mengen von Marktdaten extrem schwierig. Indem wir nur einige wenige Schlüsselprinzipien der linearen Algebra lernen und sehen, wie sie in MQL5 umgesetzt werden, gewinnen wir die Fähigkeit, viel schneller und zuverlässiger Erkenntnisse aus dem Markt zu gewinnen.

Im weiteren Verlauf unserer Diskussion werden wir dem Leser beibringen, wie man die Werkzeuge der linearen Algebra verwendet und sie in MQL5 neu interpretiert, um numerisch stabile und schnelle Handelsalgorithmen zu entwickeln. Nach dieser Lektüre ist der Leser nun in der Lage, Algorithmen zu entwickeln, die in nahezu konstanter Zeit ablaufen und so schnelles Backtests und die Verbesserung seiner Anwendungen ermöglichen, selbst wenn er mehrere Ziele gleichzeitig vorhersagen möchte.