共和分株式による統計的裁定取引（第1回）：エングル=グレンジャーおよびジョハンセンの共和分検定

はじめに

本記事は、統計的裁定取引における共和分の活用方法を示す2回連載の第1回目です。統計的裁定取引は、多くの人に「魔法のようなゼロリスク戦略」と誤解されることがある一方で、「一般の個人トレーダーにはほぼ不可能」と考えられることもあります。この誤解は、一部の大手プレイヤーが得た驚異的な成果の伝説、未経験者による「取引の聖杯探し」、そして統計的裁定取引に関する知識不足に起因しています。

適切に開発され、適切な注文執行インフラに支えられた統計的裁定取引は、長期的には低リスクで安定した収益性を示すことができます。しかし、一般的には、他の取引活動と同様に適切なリスク管理が必要です。改めて強調しますが、統計的裁定取引は魔法のようなゼロリスク戦略ではありません。

前回の記事では、単純な相関に基づくペアトレーディングを実施し、バックテストでは良好な結果を示しました。しかし、リアルタイムのデモ口座で2週間運用したところ、結果は惨憺たるものでした。おそらく、バックテストが戦略の実現可能性を評価する上で有用であることを示す、最も明確で教科書的な証拠であると同時に、現実世界に関してはほとんど示唆を与えないことを意味しています。それ以上に、統計的裁定取引がリスクフリーではないことの明確な証拠でもあります。たとえ有望な戦略であっても、慎重なリスク管理と適切な注文執行環境が不可欠です。本記事では、その基礎となる環境の話を扱います。

なぜ、バックテストと比較してデモ口座での結果がこれほど悪かったのでしょうか。どのようにすれば、2つの資産間の共動を捉える相関係数だけに頼るのではなく、複数の資産における長期的なダイナミクスをより堅牢に検出できるフレームワークを構築できるのでしょうか。また、単純なペアトレーディングを超えて、同一セクターの複数銘柄を組み入れたポートフォリオへと拡張することは可能でしょうか。

バックテストでは成功、リアルタイムでは失敗

最近、私とパートナーは、ブラジル取引所B3でドル建て先物を扱うトレーダーと非公式のミーティングをおこないました。彼女は、農産物で統計的裁定取引を試してみたいと話していました。しかし、従来型の裁量トレーダーで、テクニカル分析やプライスアクション中心の手法を学んでおり、統計や数学のバックグラウンドが乏しかったため、統計的裁定取引は自分には手が届かないと考えていました。これは、冒頭で述べた「個人トレーダーには統計的裁定取引は難しい」という一般的な認識を反映しています。

結論を先に言うと、これが、友人同士で「学習目的で自動化された統計的裁定取引フレームワークを開発してみよう」というチャレンジに変わりました。しかし、私たちは統計学者でも数学者でもなく、巨大プレイヤーに勝てるだけの計算能力もありません。そこで、学習者として通常おこなうことをしました。学術研究を通じて問題を理解し、市場で既に提案されている代替手法を調べ、成功例だけでなく失敗例も研究しました。

私たちの最初の試みは、以前私がここで公開した記事につながります。この記事では、数学者でヘッジファンドマネージャーのジェームズ・シモンズと彼の伝説的なメダリオンファンドを取り上げました。その記事では、簡単なエキスパートアドバイザー(EA)を使用して、XAUEURとXAUUSDの統計的裁定取引を示しました。 

以下のグラフは、以前ここで公開されたバックテストの結果を示しています。

図1：ペアトレーディングEAのバックテスト結果（以前の記事）

次に、実際にゼロスプレッドの手数料ベースのデモ口座で2週間EAを稼働させましたが、結果は惨憺たるものでした。

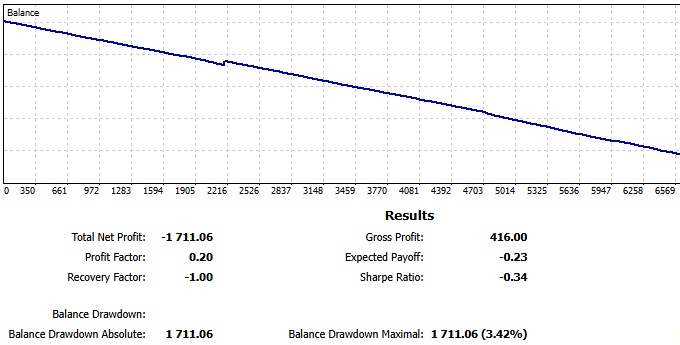
図2：ペアトレーディングEAをデモ口座で2週間稼働させた結果

考えられる原因

取引戦略の失敗原因を探る際、多くの人はパラメータを調整すべきだと考えがちですが、今回はより体系的に原因を分析します。

連続する悪い週？

単に2週連続で市場が不調だったのでしょうか。バックテストでも、損益ゼロの期間や最小ドローダウン期間は存在しました。

もちろんですが、たとえ最悪の週であっても、これほど連続して損失を出したことは一度もありませんでした。しかし、リアルタイムテストでは最大連敗数が42回に達し、最大連勝数はわずか4回でした。平均連勝は1回、平均連敗は5回で、ほとんどの取引で損失を出していました。

図3：デモ口座でのペアトレーディングEAの連敗記録

明らかに、バックテスト環境とは大きく異なる問題がありました。さらに、ペアトレーディングは市場中立戦略であるため、証券リターンに依存しません。

「ペアトレーディングは最も単純な形では市場中立の投資戦略である。」（Gatev et al.,2006)

（単純な統計的裁定取引であるペアトレーディングは市場中立と考えられますが、学術研究によれば、ヘッジ方法によって市場リスクやセクターリスクを負う場合もあります。ヘッジ手法の選択によっては、統計的裁定取引であっても、市場リスクやセクターリスクを負う場合があります。本記事ではリスク管理モジュールで詳しく扱いますが、ここでは単純なペアトレーディングを市場中立と考えます。

ジェームズ・シモンズは、2008年のサブプライム危機で市場が暴落する中でも巨額の利益を上げました。メダリオンファンドに限らず、統計的裁定取引を活用していたヘッジファンドは他にも存在します。では、なぜ彼らは、同業他社が大打撃を受ける中で成功できたのでしょうか。それにもかかわらず、彼らが暴落の最中に利益を上げていたのは、他のファンドにはなかった何かをうまくやっていたからだと考えられます。彼らの運用手法は非常に秘密主義的ですが、今日では当たり前のようでいて、個人投資家が見落としがちな重要な手がかりをいくつか残しています。メダリオンのチームは、莫大な量の高品質なデータによって支えられていました。また、最高レベルの計算能力と注文ルーティングの速度にも投資していました。

したがって、単に「悪い一週間」だったというのが原因ではありません。統計的裁定取引は市場中立的である一方で、データとタイミングに対して非常に敏感であることが分かります。

新しい環境？

ブローカーを変更したことでスプレッドが変わった、という可能性も考えられます。超短期のペアトレードで週に何千回もエントリーするような場合、Bid/Askスプレッドは容易に問題になり得ます。ご存じのとおり、FXブローカーが提供するサービスは通常、Bid/Askスプレッドや、取引量に応じたパーセンテージベースの手数料によって収益化されています。

しかし、今回はスプレッドを原因として除外できます。バックテストでは、意図的に高スプレッドの口座を使用し、ゴールドでは平均約170ピップス、XAUEURでは約50ピップスのスプレッドを設定しました。一方、デモ口座ではスプレッドが狭い「低スプレッド」タイプの手数料制口座に変更し、XAUUSDでは平均約20ピップス、XAUEURでは約10ピップスのスプレッドでした。

したがって、デモ口座の方がBid/Askスプレッドが低かったことを踏まえると、スプレッドが原因である可能性は低いと言えます。

スリッページ？

裁定取引は一般的にタイミングに敏感であり、私たちのペアトレード戦略もタイミングに非常に敏感です。では、CFDブローカーの注文執行ポリシーには、注文タイミングについてどのように記載されているか見てみましょう。

「当社は、ほとんどの注文を自動的に執行しており、手動による介入は最小限です。ただし、市場が変動している場合、注文執行時の価格は、注文入力時に提示されていた買値または売値、あるいは直近の約定価格とは大きく異なる場合があります。」

最後に思い当たるのは、よくある容疑者、つまりスリッページです。私たちは成行注文を即時送信していましたが、誰かがそのギャップを先に埋めていた可能性があります。もしそうだとすれば、特におかしなことではありません。この種の「フロントランニング」は合法的な行為であり、むしろ裁定取引の本質的な要素です。つまり、単に相手の方がより優れたリソースを持っていたということです。たとえば、より高性能なハードウェア、ブローカー近くに設置されたコロケーションサーバー、あるいは単純に高性能に最適化されたソフトウェアなどです。一方、私たちはプロトタイプを使用していました。おそらく、これらの利点を部分的、もしくはすべて備えた複数の競合相手との「スピード競争」に負けていたのでしょう。言い換えれば、大手プレイヤーたちに私たちのささやかなプロトタイプが打ちのめされていたということです。 

Metatrader 5のユーザーガイドを見ると、バックテストで遅延をシミュレーションできることが分かります。 

「ストラテジーテスターでは、EAの動作中にネットワーク遅延をエミュレーションすることで、実際の取引環境に近い条件でテストをおこなうことができます。取引リクエストの送信から執行までの間に一定の時間遅延が挿入され、この間に価格が変化する可能性があります。これにより、取引処理速度が取引結果に与える影響を評価することができます。

即時執行モードでは、ユーザーはさらに、取引サーバーからの「リクオート」に対するEAの応答を確認できます。リクエスト価格と執行価格の差が注文で指定された許容偏差値を超えた場合、EAはリクオートを受け取ります。」

そこで、私たちはランダムな遅延を設定して実行してみました。 

図4：遅延をシミュレーションしたMetaTrader 5テスター設定

すると、スリッページが唯一の原因ではないにせよ、やはり「主犯」である可能性が高いことがわかりました。

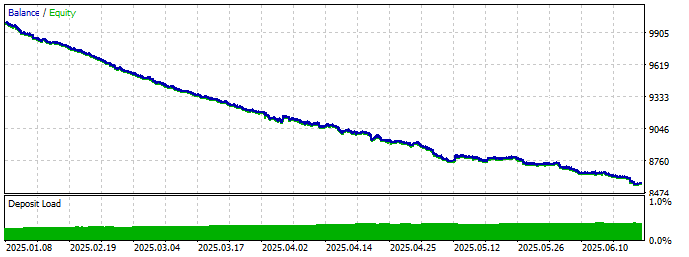
図5：遅延をシミュレーションしたバックテストの結果グラフ 

コード内で最大許容スリッページを設定することも可能ですが、この制限は戦略そのものの本質を損なうことになります。利益を出すためには、ほぼ瞬時に正しい価格を捉える必要があるからです。さらに、通常この最大許容偏差の設定機能はプロフェッショナル口座でのみ利用可能であり、それでは「一般的なリテールトレーダーのための統計的裁定取引フレームワークを開発する」という私たちの本来の目的から外れてしまいます。

主な問題：注文執行

裁定取引は、トースターからトークン、コモディティから通貨まで、あらゆるものの売買で利益を上げるために利用できます。その起源は、人々が今日のような形の「お金」を使う以前、物々交換をしていた時代にまでさかのぼると考えられます。概念自体は非常にシンプルです。たとえば、ある仮想的なトースターがマーケットAでは過小評価されているとします。その場合、そこで安く仕入れ、マーケットBで「適正価格」で売ればよいのです。もしその価格差が取引コストを上回るものであれば、ほとんどリスクを負わずに利益を得ることができます。 

ただし、「低リスクで利益が得られる」という状況は人を引き寄せます。リスクに対してリターンが高ければ高いほど、より多くの人々がその機会を狙うようになります。特に、コモディティや通貨などを扱う金融市場における裁定取引では、潜在的な利益が非常に大きくなるため、過小評価された資産を買おうとする人々が殺到し、誰もが競争相手より先に注文を出そうと必死になります。この「誰よりも早く注文を出し、約定させる」必要性が、高頻度取引(HFT: High-Frequency Trading)のインフラ、手法、そして慣行の発展を促しました。ご存じのとおり、HFTは容易ではなく、また安価でもありません。

ここでの主な問題は、一般的なリテールトレーダーには、スピードで大手プレイヤーに勝つためのリソースがないということです。高度な統計学者や数学者のチーム、高性能な計算環境によるモデル開発能力の欠如を無視したとしても、現実的にはコロケーション環境、高速に最適化されたコード、そして数ミリ秒単位で注文を処理・ルーティングできるブローカーが必要になります。

バックテストの結果は、理想的な注文執行環境においては、この戦略が理論的に成立することを示していました。つまり、実質的には注文が瞬時に執行され、ネットワーク遅延もブローカーのサーバーエラーもない状況です。 

このことからも明らかなように、この戦略は一般的なリテールトレーダー向けではありません。私たちのような謙虚なリテールトレーダーが金融市場で裁定取引から利益を得たいのであれば、単純なペアトレードの試作品を超えた代替手段を模索する必要があります。スピード競争に依存しすぎない、より独自のパターンやアノマリーを発見し、活用する道を探るべきなのです。

相関から共和分へ

前回、私たちはジェームズ・シモンズの言葉を借りて、金融市場を「常に変化し続ける謎」として紹介してきました。この謎を解くには、オペレーターは常に適応を続け、利益を最大化し損失を最小化する必要があります。これまでに、私たちはXAUUSDとXAUEURという2つの資産から成る最小限の「ポートフォリオ」を構築し、それらの米ドル建て価格の平均からの乖離を観察するという統計的関係を用いました。スプレッドが拡大し、その後平均に回帰する局面を、それぞれエントリーおよびエグジットのシグナルとして利用しました。

この段階では、私たちの統計的裁定取引のポートフォリオは非常に限定的であり、統計的関係も限られています。さらに、高速取引のようなスピードの要素は現時点では制御不能であるため、今は「早すぎる最適化」とみなして扱わないことにします。まずは、自分たちが制御できる部分を改善する必要があります。すなわち、ポートフォリオを拡大し、より多様な統計的関係や取引トリガーとなる統計指標を増やす必要があります。

これまで私たちは、相関を基準としてペアを選定してきました。具体的には、主要な為替ペアの中から、特定期間内で最も相関の高いペアを選び出していました。ここからは、ポートフォリオ選定の基準として共和分を導入します。

統計学者によると、 

「相関は短期的な関係を捉え、共和分は長期的な均衡関係を捉える。二つの変数は高い相関を持っていても共和分していない場合があり、その逆もあり得る。」(Alexander, 2001)

相関係数は、XAUUSDとXAUEURの価格が同じ方向にどの程度同時に動くかを示します。一方で、共和分検定は、両資産の間に長期的に成り立つ均衡関係が存在するかどうかを検出します。さらに、相関係数では2資産間の関係しか評価できませんが、共和分検定では複数の資産候補を同時にテストすることが可能です。したがって、共和分検定は本稿の目的に非常に適した手法といえます。

トレーダーやEA開発者としては、共和分検定の数学的背景を詳細に理解する必要はありません。私たちは、MetaTrader 5のPython連携機能を用いてデータ分析やポートフォリオ選定をおこなうため、専門ライブラリが提供する既存のPython関数を活用できます。また、執筆時点で確認したAIアシスタント（MetaTrader 5に組み込まれたGPTなど）も、このような簡単なスクリプト開発を支援してくれます。

トレーダーとして重要なのは、共和分が意味するところと、それをどのように機会発見に活かせるかを理解することです。特に株式市場では、共和分は為替市場よりも有効性が高いことが知られています。一方でEA開発者としては、最適なライブラリを利用し、結果を正しく解釈する能力が求められます。その上で反復的に改善を重ねることが重要です。Pythonのエコシステムには、高品質な数学、統計、機械学習のライブラリが豊富に揃っており、これらを活用することで時間を節約し、エラーを回避し、パフォーマンス向上が期待できます。

さらに深く学びたい場合は、先ほど引用したキャロル・アレクサンダーの著書を参照することをおすすめします。特に第12章は共和分に特化しており、金融分野における共和分の歴史から、外国為替を含むさまざまな市場への応用まで幅広く解説されています。同書はこの分野における標準的なリファレンスとして広く知られています。

次に、代表的な共和分検定であるエングル=グレンジャー検定とジョハンセン検定を、異なる資産クラスに適用する方法と、その結果の読み取り方について見ていきましょう。

エングル=グレンジャー共和分検定

エングル=グレンジャー共和分検定は、2つの資産間の共和分の程度を評価するために用いられる手法です。この検定の目的は、「これら2つの資産は、長期的な均衡関係を共有しているのか」という問いに答えることです。トレーダーやEA開発者にとって、この検定は「2つの資産のスプレッドが平均回帰するかどうか」を示す指標となります。ただし、この検定の結果は「はい」「いいえ」の単純な二択ではありません。先に見たピアソンの相関検定と同様に、相対的な数値（p値）を返します。この数値を他のペアの結果と比較することで、どのペアがより強く共和分しているかを判断できます。 

p値とは、実際には共和分が存在しないという前提のもとで、現在のデータを観測する確率を示します。したがって、p値が小さいほど共和分が強いと判断できます。一般的に使用される基準値は次の通りです。p値 < 0.05は通常、共和分の中程度のシグナルと見なされます。p値 < 0.01は強いシグナルであり、p値 > 0.05は共和分がないシグナルです。ただし、取引戦略においては、これらの閾値をそのまま使用するのではなく、対象市場や取引戦略に応じてファインチューニングすることが推奨されます。

両方の共和分検定（エングル・グレンジャーの検定およびジョハンセンの検定）は、Pythonの有名な統計ライブラリ「statsmodels」を用いて実装できます。 

「statsmodelsは、多様な統計モデルの推定、統計的検定、そしてデータ探索のためのクラスや関数を提供するPythonモジュールです。」

from datetime import datetime, timedelta
import MetaTrader5 as mt5
import pandas as pd
import numpy as np
from statsmodels.tsa.stattools import coint
import matplotlib.pyplot as plt

# connect to MetaTrader 5 terminal
if not mt5.initialize(login=********, server="MetaQuotes-Demo",password="********"):
    print("initialize() failed, error code =",mt5.last_error())
    quit()

# Forex majors - check your Market Watch names
symbols = ['EURUSD', 'GBPUSD', 'USDJPY', 'AUDUSD', 'USDCAD', 'NZDUSD', 'USDCHF']

主要な外国為替ペアの中で、最も共分散の強い組み合わせを探しています。高い共和分係数が見つかることは期待していませんが、これはエングル=グレンジャー検定の仕組みを説明するための例として使用するものです。

# define the timeframe and the number of days
timeframe = mt5.TIMEFRAME_D1  # Daily
n_days = 600
utc_to = datetime.now()
utc_from = utc_to - timedelta(days=n_days)

utc_fromとutc_toの変数を使用して、mt5.copy_rates_rangeにより600取引日の銘柄のレートデータを取得します。1年間にはおおよそ250取引日があります。

# download historical data for each symbol
data = {}

for symbol in symbols:
    # Make sure the symbol is available in Market Watch
    mt5.symbol_select(symbol, True)
    
    # Get historical rates
    rates = mt5.copy_rates_range(symbol, timeframe, utc_from, utc_to)
    
    if rates is None or len(rates) == 0:
        print(f"No data for {symbol}.")
        continue

    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    data[symbol] = df['close']

このforループでは、各銘柄の終値を取得し、それらをPandasのDataFrameに変換したうえで、time配列を表形式データのインデックスとして設定します

その後、複数のDataFrameを連結し、結果を歪める可能性のある欠損値を含む行を削除したうえで、共和分検定を実行します。

# Store cointegration test results
results = []

# Test all unique pairwise combinations for cointegration
pairs = [(a, b) for i, a in enumerate(data.columns) for j, b in enumerate(data.columns) if i < j]

print("Cointegration test results (Engle-Granger):")
for a, b in pairs:
    score, pvalue, _ = coint(data[a], data[b])
    results.append((a, b, pvalue))
    print(f"{a} vs {b} | p-value: {pvalue:.4f}")

Index(['EURUSD', 'GBPUSD', 'USDJPY', 'AUDUSD', 'USDCAD', 'NZDUSD', 'USDCHF'], dtype='object')
Cointegration test results (Engle-Granger):

EURUSD vs GBPUSD | p-value:0.3183
EURUSD vs USDJPY | p-value:0.6990
EURUSD vs AUDUSD | p-value:0.9308
EURUSD vs USDCAD | p-value:0.9206
EURUSD vs NZDUSD | p-value:0.9741
EURUSD vs USDCHF | p-value:0.4342
GBPUSD vs USDJPY | p-value:0.3273
GBPUSD vs AUDUSD | p-value:0.7995
GBPUSD vs USDCAD | p-value:0.6264
GBPUSD vs NZDUSD | p-value:0.7810
GBPUSD vs USDCHF | p-value:0.0238
USDJPY vs AUDUSD | p-value:0.6299
USDJPY vs USDCAD | p-value:0.5620
USDJPY vs NZDUSD | p-value:0.6398
USDJPY vs USDCHF | p-value:0.2377
AUDUSD vs USDCAD | p-value:0.1260
AUDUSD vs NZDUSD | p-value:0.2920
AUDUSD vs USDCHF | p-value:0.5980
USDCAD vs NZDUSD | p-value:0.0052
USDCAD vs USDCHF | p-value:0.8574
NZDUSD vs USDCHF | p-value:0.6384

最も強い共和分関係にあるペア：USDCAD and NZDUSD (p = 0.0052)

2つの最も共和分が強いペアを特定したら、それらをペアトレーディングポートフォリオに組み入れるかどうかを判断できます。下の図を見ると、スプレッドが平均値に回帰している様子がはっきりと分かります。ただし問題は、この取引をおこなう価値があるのかという点です。

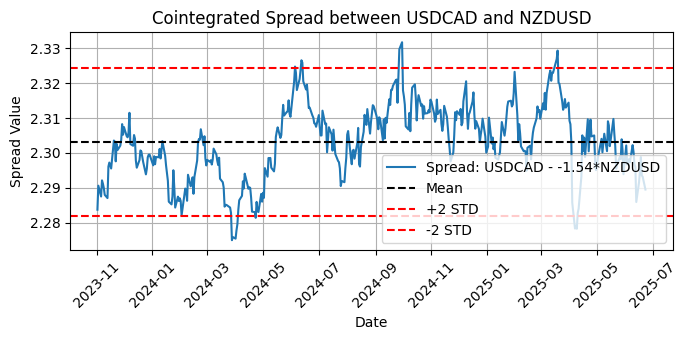
図6：平均および2標準偏差を含むUSDCADとNZDUSD間の共和分スプレッドのプロット

黒の破線はスプレッドの平均値を示しており、これは長期的な均衡水準を意味します。2本の赤い破線は、2標準偏差(STD)のバンドを示します。これらのバンドは、スプレッドが異常に高いまたは低いときに発生する可能性のある取引シグナルを識別するための閾値を定義します。したがって、標準偏差の数は最適化の有力な候補となります。 

ヘッジ比率

長期的スプレッドの計算に使用された「-1.54」という値に注目してください。

スプレッド = USDCAD - (-1.54) * NZDUSD

または

USDCAD + 1.54 * NZDUSD

この値がヘッジ比率を示します。これは線形回帰により統計的に推定された最適比率であり、USDCADとNZDUSDの価格関係を調整してスプレッドが定常的（すなわち一定の平均値の周囲で振動）になるようにします。これは平均回帰戦略において極めて重要な性質です。このヘッジ比率を用いることで、ボラティリティや方向性の違いを補正し、同一スケールで価格を比較できるようになります。

スプレッドは相対的なミスプライシング（誤った価格付け）を捉えます。ペアトレーディングの用語では、スプレッドが平均から2標準偏差上にある場合、統計的に高い水準と見なし、「ショートする」（売る）ことを検討します。逆に、スプレッドが平均から2標準偏差下にある場合、統計的に低い水準と見なし、「ロングする」（買う）ことを検討します。

このデータを基にマーケットニュートラルなペアトレードを構築するには、USDCADを1単位ロングするごとに、NZDUSDを1.54単位ショートします（もしくはシグナルの方向に応じて逆のポジションを取ります）。スプレッドが平均に回帰した時点で、両方のポジションをクローズして取引を終了します。

このコードは、どの市場や資産クラスの銘柄に対しても同様に使用できます。そのまま利用する場合は、上部の銘柄名を希望の銘柄名に置き換えるだけです。

ジョハンセン共和分検定

ジョハンセン共和分検定は、エングル=グレンジャー検定と同じ「これらの資産は長期的な均衡関係を共有しているか」という疑問に答えることを目的としています。実務上、また本記事での目的において、主な違いは次の通りです。ジョハンセン検定は2つ以上の資産を同時に評価できる点であり、これらN資産が共通の平均回帰性スプレッドを持つかどうかを判定できます。たとえば、同じセクターの株式群（石油株、テック株など）の共和分関係を評価する強力なツールとして考えることができます。これにより、3銘柄、4銘柄、あるいはそれ以上の資産が共通の長期均衡関係を持つかどうかを見つけることが可能です。

この検定では、元の時系列が定常でなくても、変数の組み合わせが平均回帰（定常）であるかどうかを確認し、変数間に存在する共和分関係の数を推定します。この数を共和分ランクと呼びます。

検定は主に、トレース統計量と臨界値の2つの統計量を生成します。

トレース統計量は、可能なランクごと（0, 1, 2, …, N−1、Nは時系列の数）に1つずつ計算されます。 統計量が大きいほど、共和分関係の存在を示す証拠が強いことを意味します臨界値はトレース統計量と比較される閾値であり、次の要素によって決まります。

• 評価される変数の数
• サンプルの長さ
• 信頼水準（90%、95%、99%）

本記事の文脈では、変数の数は検定対象の銘柄数と考えることができます。

# Johansen Test
from datetime import datetime, timedelta
import MetaTrader5 as mt5
import pandas as pd
import numpy as np
from statsmodels.tsa.stattools import coint
from statsmodels.tsa.vector_ar.vecm import coint_johansen
import matplotlib.pyplot as plt
# Create a matrix for the test
log_prices = data.apply(np.log)

johansen_result = coint_johansen(log_prices, det_order=0, k_ar_diff=1)

# Trace statistics and critical values
print("\nJohansen Test Results (Trace Statistic):")
for i, stat in enumerate(johansen_result.lr1):
    cv = johansen_result.cvt[i, 1]  # 5% critical value
    print(f"Rank {i}: Trace Stat = {stat:.2f} | 5% CV = {cv:.2f} | {'Significant' if stat > cv else 'Not significant'}")

他の信頼水準での結果は、次のように設定することで確認できます。
johansen_result.cvt[i, 0] for 90%
johansen_result.cvt[i, 2] for 99%

95%信頼水準（5%臨界値）の場合、同じ期間・D1時間足でエングル=グレンジャー検定をおこなった外国為替主要ペアの結果は次の通りです。

Index(['EURUSD', 'GBPUSD', 'USDJPY', 'AUDUSD', 'USDCAD', 'NZDUSD', 'USDCHF'], dtype='object')

Johansen Test Results (Trace Statistic):

Rank 0:Trace Stat = 105.25 | 5% CV = 125.62 | Not significant
Rank 1:Trace Stat = 68.10 | 5% CV = 95.75 | Not significant
Rank 2:Trace Stat = 42.01 | 5% CV = 69.82 | Not significant
Rank 3:Trace Stat = 25.83 | 5% CV = 47.85 | Not significant
Rank 4:Trace Stat = 11.73 | 5% CV = 29.80 | Not significant
Rank 5:Trace Stat = 5.74 | 5% CV = 15.49 | Not significant
Rank 6:Trace Stat = 0.58 | 5% CV = 3.84 | Not significant

予想通り、7つの主要外国為替通貨間には有意な共和分は見られませんでした。

しかし、同じ期間と信頼水準で、H1時間足においてよく知られたGoogle株とNvidia株を検定した場合、有意な共和分結果が得られます（下図参照）。

Index(['NVDA', 'GOOGL'], dtype='object')
Number of observations:5769
Number of variables:2

Johansen Test Results (Trace Statistic):
Rank 0:Trace Stat = 18.71 | 5% CV = 15.49 | Significant
Rank 1:Trace Stat = 0.29 | 5% CV = 3.84 | Not significant

最も強い共和分関係にあるペア（エングル=グレンジャー）：NVDAとGOOGL | p値：0.0824

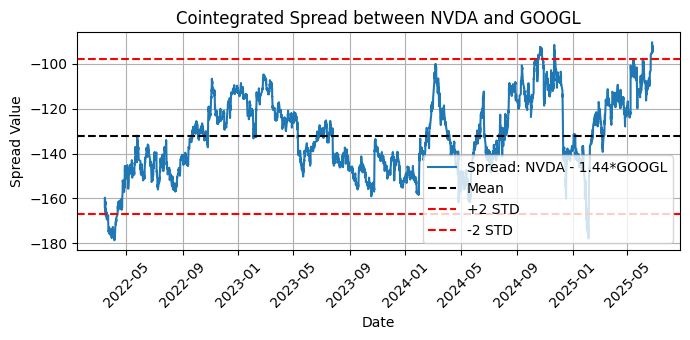
図7：平均および2標準偏差を含むNVDAとGOOGL間の共和分スプレッドのプロット

さて、ジョハンセン検定ではGOOGLとNVDAに対して有意な共和分が確認されましたが、エングル=グレンジャー検定のp値は0.05を上回っており、共和分なしのシグナルとなっています。なぜこのような矛盾した結果になるのでしょうか。これは何を意味するのでしょうか。

ここで、同じスクリプトを銘柄の順序を逆にして実行してみましょう。すると、エングル=グレンジャー検定とジョハンセン検定の間で興味深い違いが見えてきます。

Index(['GOOGL', 'NVDA'], dtype='object')
Number of observations:5769
Number of variables:2

Johansen Test Results (Trace Statistic):
Rank 0:Trace Stat = 18.71 | 5% CV = 15.49 | Significant
Rank 1:Trace Stat = 0.29 | 5% CV = 3.84 | Not significant

最も強い共和分関係にあるペア（エングル=グレンジャー）：GOOGLとNVDA | p値：0.0403

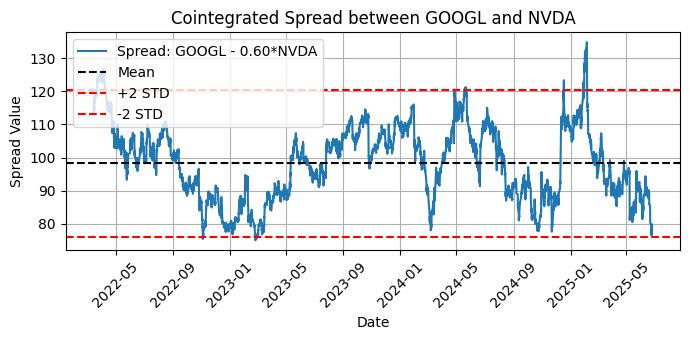
図8：平均および2標準偏差を含むGOOGLとNVDA間の共和分スプレッドのプロット

ご覧の通り、エングル=グレンジャー検定は変数の順序に敏感ですが、ジョハンセン検定は順序の変更による影響を受けませんでした。ジョハンセン検定の詳細を深く理解すると、特にサンプルが短い場合や統計的有意性の境界付近では、まれに順序に対して感度を示すことがあります。しかし、一般的には理論上、順序には不感性です。順序を変えると不一致な結果が返る場合は、まずサンプルサイズを増やすことが推奨されます。これが、D1（1日足）ではなくH1（1時間足）に置き換えて検定をおこなった理由です。より大きなサンプルを提供することで、より安定した結果が得られます。

また、エングル=グレンジャー検定が変数の順序に敏感であることを踏まえると、常に両方向で検定をおこない、プロットを視覚的に確認してスプレッドが平均に回帰しているかを評価することが重要です。

スプレッドの定常性の検定

スプレッドは時系列データであり、平均に回帰しているかどうかを確認するためには定常性を検定する必要があります。定常性とは、平均・分散・共分散が時間とともに変化しない性質を指します。時系列が定常であれば、ARIMAモデルなどの手法を用いたモデリングや予測が容易になります。

これまで共和分の検定に使用してきたPythonライブラリには、定常性を検定するための組み込み関数も用意されています。具体的には、拡張ディッキー＝フラー検定(ADF: Augmented Dickey-Fuller)とKwiatkowski-Phillips-Schmidt-Shin (“KPSS”)検定です。

from statsmodels.tsa.stattools import adfuller

(...)

adf_result = adfuller(spread)

ADF Test on Spread:
 ADF Statistic : -3.0946
 p-value         :0.0270
 Critical Values:
    1%: -3.4315
    5%: -2.8620
    10%: -2.5670

✅ スプレッドは定常です（帰無仮説を棄却します）。

from statsmodels.tsa.stattools import kpss

(...)

def run_kpss(series, regression='c'):
    statistic, p_value, lags, crit_values = kpss(series, regression=regression, nlags='auto')

(...)

# Run KPSS test on the residuals
run_kpss(spread, regression='c')  # 'c' = test for level stationarity (use 'ct' for trend)

KPSS Test on Spread:
 KPSS Statistic :2.2702
 p-value          :0.0100
 Lags Used      :44
 Critical Values:    10% :0.347
    5% :0.463
    2.5% :0.574
    1% :0.739

❌ スプレッドは定常ではありません（定常性の帰無仮説を拒否します）。

今回もまた、矛盾した結果が得られたように見えます。ADF検定ではスプレッドが定常であると示されていますが、KPSS検定では非定常と判断されています。しかし、慌てる必要はありません。statsmodelsライブラリの開発者たちは、この2つの検定結果をどのように解釈すべきかを、すべての組み合わせについて明確に説明してくれています。ここで、より簡潔かつ明確にするのは難しいと思うので、statsmodelsドキュメントを引用します。

「ケース1：ADFとKPSSの両方が「非定常」と結論した場合 → 非定常系列

ケース2：ADFとKPSSの両方が「定常」と結論した場合 → 定常系列

ケース3：KPSSが「定常」、ADFが「非定常」と結論した場合 → トレンド定常系列。トレンドを除去すれば厳密な定常系列になる。除去後の系列で定常性を再確認する。

ケース4：KPSSが「非定常」、ADFが「定常」と結論した場合 → 差分を取ることで定常系列になる。差分系列で定常性を確認する。

つまり、私たちのスプレッドは「差分定常」であり、「厳密な定常系列」ではないことが分かりました。これは何を意味するのでしょうか。このことは、当該時系列がゆるやかな推移を示す可能性はあるものの、その変化の幅が安定していることを意味します。連続する値の差分を取ることで、この時系列を厳密な定常系列へと変換することが可能です。この手法はその名の通り「差分化」と呼ばれ、トレンドや季節性を除去し、より効果的な分析や予測がおこなえるよう時系列を整えるために用いられます。

では、スプレッドを厳密な定常系列に変換する必要があるのでしょうか。多くの時系列モデルではデータが定常であることを前提としていますが、本稿の共和分分析では予測モデルを扱わないため、その必要はありません。 

今回は予測自体をおこないませんが、共和分分析は単なる共和分検定で終わるものではないという点を理解しておくことは、有益であると言えるでしょう。

結論

本記事では、リテールトレーダー向けの統計的裁定取引フレームワークの構築を、さらに一歩進めました。ポートフォリオ構築のための統計ツールとして、エングル=グレンジャー検定およびジョハンセン検定という2つの新しい手法を追加しました。それぞれの検定で何を確認できるのか、また結果をどのように基本的に解釈するのかを学びました。さらに、拡張ディッキー＝フラー(ADF)検定およびKwiatkowski-Phillips-Schmidt-Shin (KPSS)検定を用いて、スプレッドの定常性を確認する方法についても解説しました。

本記事は、基礎的なツールを紹介する 2 部構成の記事のうちの第1部です。次回の記事では、実際の実装、バックテスト、最適化をおこない、共和分関係を持つ為替ペアおよび同一セクター内の株式グループを題材に補足説明をおこないます。

ここで最も重要なのは、ツールや関数、あるいはサンプルコードそのものではありません。最も価値のある知識とは、数学者や統計学者ではないリテールトレーダーとして、扱う資産や市場をどれだけ深く理解しているかという点です。

市場に関するあなた自身の知識こそが、かけがえのない資産です。なぜなら、数学的・統計的な高度な処理はすでに専門家によっておこなわれており、その成果は多くのオープンソースライブラリとして無料で提供されているからです。さらに、Metatrader 5プラットフォーム上のMQL5 ライブラリや、実装を支援するAIアシスタントなども自由に活用することができます。 

今回の教訓：もし限られたリソースの中で戦うリテールトレーダーであるならば、スピードに依存する戦略からは距離を置き、自分の市場知識を活かしてデータを創造的に探求することを目指しましょう。 

参考文献

• Alexander, C.(2001).Market Models:A Guide to Financial Data Analysis, Wiley.
• Engle, R. F., & Granger, C. W.J.(1987).Co-integration and error correction: representation, estimation, and testing.Econometrica.
• Gatev, E., Goetzmann, W. N., & Rouwenhorst, K. G.(2006)."Pairs Trading:Performance of a Relative-Value Arbitrage Rule."Review of Financial Studies.
• Johansen, S.(1988).Statistical analysis of cointegration vectors.Journal of Economic Dynamics and Control.

添付ファイル	説明
coint.ipynb	単一の取引銘柄ペアに対してエングル=グレンジャー共和分検定を実行するための、簡略化されたJupyter Notebookです。
coint_googl_nvda.ipynb	エングル＝グレンジャー検定とジョハンセン検定の両方を、理論上は無制限の数の取引銘柄に対して実行できるように拡張したJupyter Notebookです。また、スプレッドの定常性検定もあわせて実施できるよう設計されています。
helper_quotes_to_db.ipynb	ダウンロードした銘柄のレートデータをsqlite3データベースに保存するための補助ツールです。同じく Jupyter Notebook形式で記述されており、冗長なデータの再ダウンロードを回避し、オフライン環境でも作業を継続できるようにすることを目的としています。