Statistische Arbitrage durch Mean Reversion im Paarhandel: Den Markt mit Mathematik schlagen
117
11
Einführung
„Ich kann die Bewegungen von Himmelskörpern berechnen, aber nicht die Verrücktheit von Menschen.“ (Sir Isaac Newton, in seinen Neunzigern, nachdem er fast seine gesamten Ersparnisse für den Ruhestand durch Investitionen an den Aktienmärkten verloren hatte).
Am 10. Mai letzten Jahres verlor die Welt Jim Simons, den erfolgreichsten Hedgefondsmanager aller Zeiten.
Jim Simons war ein anerkannter Mathematiker, der mehrere Auszeichnungen und akademische Leistungen in den Bereichen Differentialgeometrie und Kryptographie vorweisen konnte. Seine Rolle in der quantitativen Finanzanalyse machte seinen Namen jedoch auch bei Menschen bekannt, die sich nicht für Mathematik oder Finanzen interessieren.
Über ihn wurden mehrere Biografien, Dutzende von Büchern über sein Leben und seine Karriere, Hunderte von Fernsehsendungen und Tausende von Artikeln und Blogbeiträgen in aller Welt verfasst. „The Man Who Solved the Market: How Jim Simons Launched the Quant Revolution“ ist seine sehr berühmte Biographie.
Anfang der achtziger Jahre gründete Simons Renaissance Technologies (RenTech) und begann, ein Team hochqualifizierter „Mathematiker, Physiker, Signalverarbeitungsexperten und Statistiker“ zusammenzustellen. In jahrzehntelanger Zusammenarbeit haben sie bewiesen, dass mit genügend Daten und Rechenleistung, um statistische Muster und Anomalien in diesen Mustern zu finden, der Markt „durch Mathematik geschlagen“ werden kann.
„1988 richtete das Unternehmen sein profitabelstes Portfolio ein, den Medallion Fund, der eine verbesserte und erweiterte Form der mathematischen Modelle von Leonard Baum, verbessert durch den Algebraiker James Ax, nutzte, um Korrelationen zu erkunden, von denen es profitieren konnte.“ (Wikipedia)
Der Medallion Fund erzielte zwischen 1988 und 2018 eine durchschnittliche Rendite von 66 % pro Jahr und erwirtschaftete in diesen drei Jahrzehnten Handelsgewinne in Höhe von mehr als 104 Milliarden Dollar. Der Medallion Fund der RenTech ist auch heute noch aktiv und verdient viel Geld. Wie zu erwarten, möchten viele Leute wissen, wie sie funktionieren, die Details, den geheimen Algorithmus, den Cheat-Code... was auch immer. Aber soweit jeder sterbliche Mensch weiß, wird ihre Geheimsoße als streng geheime Unternehmensvereinbarung aufbewahrt. Auf die Frage des Autors seiner Biografie nach der operativen Strategie von Medallion antwortete Simons mit der gleichen lakonischen Antwort, die er in den kommenden Jahren mehreren Interviewern geben sollte: statistische Arbitrage auf Portfolioebene. Er verriet auch, dass sie von Anfang an „eine Art maschinelles Lernen“ eingesetzt haben, um die Marktanomalien zu finden.
Statistische Arbitrage ist an sich schon ein großes Forschungsgebiet. Wenn wir das maschinelle Lernen hinzufügen, bleibt der durchschnittliche Einzelhändler ohne fundierte Kenntnisse in Mathematik und Statistik außen vor. Ganz zu schweigen von den Anfängern im Handel. Aber wenn es wahr ist, dass es wirklich schwierig ist und viele Ressourcen benötigt werden, um eine voll funktionsfähige, auf maschinellem Lernen basierende statistische Arbitrage auf Portfolioebene ohne all dieses Wissen zu implementieren, dann ist es auch wahr, dass es durchaus möglich ist, zu verstehen, was statistische Arbitrage auf Portfolioebene ist, wie sie funktioniert, und noch wichtiger: Es ist möglich, mit Geduld, harter Arbeit und Zeit, um zu wachsen, klein anzufangen.
Dieser Artikel ist keineswegs ein Versuch, den „Geheimcode“ von RenTech/Jim Simons zu reproduzieren oder, noch schlimmer, zu enthüllen. Wie bereits erwähnt, wäre dies für jeden, der nicht direkt an ihren Aktivitäten beteiligt ist, unmöglich. Es ist ein Versuch, Ihnen mein Verständnis der allgemeinen Prinzipien, die ihren Modellen zugrunde liegen, mitzuteilen. Diese Grundsätze können selbst für den bescheidensten Kleinanleger als Grundlage für sein Handelssystem dienen. Der Unterschied liegt in der Größenordnung der Ergebnisse, die proportional zum Umfang der in das System und den Betrieb investierten Ressourcen ist.
Was Sie also im Folgenden lesen werden, ist das Ergebnis von Recherchen in Büchern, Videodokumentationen und spezialisierten Internet-Communities, kombiniert mit meiner persönlichen Erfahrung aus einigen Jahren im Finanzbereich (mehr auf der Geschäftsseite als auf der Entwicklerseite). Was RenTech betreibt, ist riesig, aber was wir hier sehen werden, ist eine Miniatur, sagen wir mal, eine Actionfigur eines Superhelden, ein maßstabsgetreues Modell eines Wolkenkratzers.
Ziel ist es, mit einer kostengünstigen, leichtgewichtigen und einfach zu entwickelnden Analysemethode beizutragen, die vom durchschnittlichen Einzelhändler getestet und verbessert werden kann, indem er nur die Tools verwendet, die bereits in der MetaTrader 5-Plattform vorhanden sind, die auf einem handelsüblichen Notebook, möglicherweise einem Low-End-Notebook, läuft. Die Methode sollte sowohl für den algorithmischen als auch für den diskretionären Händler nützlich sein. Wir beginnen mit der einfachsten Variante, die gerade ausreicht, um den Prozess zu beschreiben.
Nachdem wir die allgemeinen Konzepte hinter dem Modell verstanden haben, werden wir ein minimales Portfolio für die einfachste Form der statistischen Arbitrage erstellen, es im automatisierten Modus mit einem Expert Advisor handeln, einige Notizen zu den Ergebnissen machen und schließlich über die erforderlichen nächsten Schritte nachdenken. Ich hoffe, dass diese Erfahrung Ihnen helfen kann, mit dieser leistungsstarken Handelstechnik zu beginnen und später in der Lage zu sein, dieses Wissen zu erweitern, indem Sie andere Symbole in das Portfolio aufnehmen und andere Algorithmen als die hier beschriebenen testen, um schrittweise Ihre eigene, voll funktionsfähige StatArb-Strategie aufzubauen, die Ihren Ressourcen und Zielen entspricht.
Allgemeine Konzepte des Modells
Bevor er RenTech gründete, arbeitete Jim Simons während des Kalten Krieges als Codeknacker für den US-Geheimdienst. Als er mit dem Handel an den Finanzmärkten begann, versuchte er, Aktien- und Rohstoffpreise vorherzusagen und scheiterte. Dann änderte er seinen Ansatz. Er ging davon aus, dass er niemals in der Lage sein würde, die Zukunft des Marktes vorauszusehen. Er verstand, dass er akzeptieren musste, dass der Markt ein Rätsel war. Dies ist das erste wichtige Konzept des Modells.
Das andere Konzept besteht darin, dass der Markt einem ständigen Wandel unterworfen ist. Das heißt, es gibt keine steigende oder fallende Märkte, keine Kerzen-/Balkenmuster oder „korrelierte Aktien, die gut zusammenspielen“. Alles ändert sich jetzt und für immer.
Wenn Sie eine Sekunde nachdenken, werden Sie feststellen, dass beide Konzepte übersehen werden.
Der Markt ist ein RätselDer Markt ist ein Rätsel, aber anders als die Enigma-Maschine aus dem Zweiten Weltkrieg, deren Code von Alan Turing und seinem Team geknackt wurde, verfügt das Markträtsel nicht über einen deterministischen Algorithmus, der sich zurückentwickeln und knacken lässt. Zwischen dem Eingang und dem Ausgang können unerwartete Ereignisse auftreten. Während die Anhebung der Zinssätze durch eine Zentralbank den erwarteten Effekt hat, dass die Währung dieses Landes stärker wird, kann der Ausbruch eines politischen Konflikts in einem anderen, weit entfernten Land den gegenteiligen Effekt haben, indem er die Zinserhöhung ausgleicht, indem er ihre Auswirkungen verringert, sie zunichte macht oder die Währung sogar schwächt.
Der Markt ist ein Rätsel, weil zwischen Input und Output die Irrationalität der Wirtschaftsakteure, die Unvorhersehbarkeit der Politik und das chaotische Zusammenspiel der Kräfte, die ihn antreiben, liegen. Zwischen dem einjährigen Aufwärtstrend auf dem Goldmarkt und dem einmonatigen Sturzflug in der nächsten Woche liegt menschliches Verhalten. Nicht umsonst wurde der Psychologe Daniel Kahneman mit dem Nobelpreis für Wirtschaftswissenschaften ausgezeichnet. Denn er geht genau auf diese Frage ein.Obwohl der Markt ein Rätsel ist, das von irrationalen Wirtschaftsakteuren in einem chaotischen Umfeld beherrscht wird, kaufen und verkaufen Investmentbanken Aktien auf der Grundlage von Finanzmodellen, verwenden Hedge-Fonds Black-Scholes, um Optionen zu bewerten, und fast alle großen Marktteilnehmer geben Millionen von Dollar für die Entwicklung von Quantenhandelsstrategien aus. Warum? Weil es funktioniert, versteht sich. Warum funktioniert es, wenn der Markt unvorhersehbar, unberechenbar, irrational und chaotisch ist?
Jim Simons hat zusammen mit Tausenden anderer erfolgreicher Quant-, Algo- und Diskretionärs-Händler die offenste Antwort auf diese Frage. Eine Lektion, die jeder Möchtegern-Händler jeden Morgen vor dem Einstieg in den Markt wie ein Mantra aufsagen sollte:
Aber mit oder ohne den Einsatz von Finanzmodellen kann jede Handelsstrategie für eine gewisse Zeit, eine unbekannte Zeitspanne, recht gut funktionieren. Es kann für einen Tag, einen Monat, ein Jahr... profitabel sein, wir wissen es nicht. Die einzige Garantie ist, dass es in der Vergangenheit funktioniert hat und bei diesen Symbolen, in dieser Periode und in diesem Zeitrahmen mit den im Backtest verwendeten Parameterwerten profitabel war. Es kann sein, dass es in der nächsten Minute nicht mehr rentabel ist, im ersten Durchgang, oder es kann für immer funktionieren. Auch das wissen wir nicht. Wir können es nicht wissen, denn der Markt ist ein Rätsel. Wir können dieses Rätsel nicht lösen. Es gibt keinen Code, der gebrochen werden muss. Es gibt nur einen kontinuierlichen Zustand der Veränderung.
Der Markt befindet sich in einem ständigen Wandel
Der Markt ist in ständiger Bewegung. Die einzige Konstante auf dem Markt ist der Wandel. Die Werte unserer Parameter werden nicht gewählt, weil sie für einen bestimmten Marktzustand am besten geeignet sind, sondern weil sie für eine bestimmte Marktveränderung am besten geeignet waren. Zwischen dem Moment, in dem wir einen Gewinnauftrag erteilten, und dem Moment, in dem der Auftrag geschlossen wurde, veränderte sich der Markt so, wie wir es erwartet hatten. Umgekehrt hat sich der Markt zwischen dem Zeitpunkt, an dem wir einen Verlustauftrag erteilt haben, und dem Zeitpunkt, an dem der Auftrag geschlossen wurde, in einer Weise verändert, die wir nicht erwartet hatten. Dies gilt selbst dann, wenn wir nicht sagen können, welche Veränderung am meisten zum Endergebnis beigetragen hat.
Um es klar zu sagen: Wir werden nie in der Lage sein, die genaue Veränderung zu bestimmen, die eine profitable Strategie in einen Geldfresser verwandelt oder umgekehrt. Um eine Handelsstrategie zu verbessern, müssen wir nach einem Muster suchen, das die Wahrscheinlichkeit erhöht, dass wir die richtigen Entscheidungen wiederholen, wenn wir in der Zukunft mit ähnlichen Veränderungen des Marktzustands konfrontiert werden. Diese Muster zu finden, zu lernen und zu verstehen, ist das, was ein erfahrener Händler in Monaten oder Jahren des Handels mit demselben Vermögenswert oder derselben Gruppe von Vermögenswerten tut. Aus keinem anderen Grund haben wir Handelstagebücher. Es geht darum, unsere Annahmen über die erwarteten Marktveränderungen zu erfassen und sie später zu überprüfen, um unsere Annahmen zu verbessern.
Dank der großen Datenmengen, die heute zur Verfügung stehen, und leistungsfähiger Computer, die diese Daten verarbeiten, können wir diese Jahre des Lernens, um die Muster zu finden, auf Stunden oder sogar Minuten verkürzen. Wir können die Datenerfassung, die Analyse und die Handelsausführung automatisieren. Wir können die Tests und die Berichterstattung automatisieren. Wir können sogar die Auswahl des zu handelnden Symbols/Handelsinstruments und der zu verwendenden Strategie automatisieren, indem wir ein umfassendes maschinelles Lernmodell trainieren, um diese Muster zu lernen. Mit einer angemessenen Menge an Geld, qualifizierten Mitarbeitern und Zeit können wir das tun.
Aber, wie gesagt, der Schwerpunkt dieser Anmerkungen liegt auf dem durchschnittlichen Kleinhändler. Mit diesen beiden einfachen, aber übersehenen Grundsätzen im Hinterkopf, wollen wir sehen, wie wir anfangen können zu verstehen, was StatArb ist und wie es funktioniert.
Aufbau des Portfolios
Da der Markt ein Rätsel ist, das sich ständig verändert, werden wir unser Portfolio ohne Vorurteile aufbauen, wir werden keine Annahmen darüber machen, was wir für wahr halten, und wir werden es regelmäßig aktualisieren. Das Aktualisierungsintervall wird durch die Handelsstrategie bestimmt und durch die Rechenleistung begrenzt.
Wir müssen berücksichtigen, dass die Portfoliobildung bzw. das Portfoliomanagement an sich ein großes Forschungsgebiet ist. Nach einer umfassenden akademischen Literaturübersicht gab es vor zehn Jahren mindestens vier Hauptansätze für den Aufbau eines statistischen Arbitrageportfolios für den Paarhandel: Distanz, Kointegration, Zeitreihen und stochastische Kontrolle. Neben diesen vier Hauptansätzen hat der Autor auch andere Ansätze identifiziert, darunter maschinelles Lernen, kombinierte Prognosen, Copula und Hauptkomponentenanalyse.
Um unseren Fokus auf Einfachheit und Grundlagen zu bewahren, lassen Sie uns mit einem einfachen Paarhandelsportfolio beginnen. Für einige Autoren ist der Paarhandel eine Untergruppe der statistischen Arbitrage, für andere gilt der Paarhandel weithin als „Vorfahre“ der statistischen Arbitrage, wobei der Unterschied in der Portfoliogröße und der Komplexität der statistischen Algorithmen besteht. Wie der Name schon sagt, ist der Paarhandel auf zwei Wertpapiere beschränkt, während die statistische Arbitrage Dutzende oder sogar Hunderte von Symbolen umfassen kann, die verfolgt und schließlich gehandelt werden.
Wie Sie wahrscheinlich bereits wissen, ist der Handel mit Paaren nichts anderes als der gleichzeitige Verkauf von zwei Wertpapieren mit korrelierten oder kointegrierten historischen Kursen und der Kauf des Wertpapiers mit einem Abwärtstrend, wenn der historische Spread zwischen ihren Kursen einen bestimmten Schwellenwert überschreitet. Die zugrunde liegende Annahme ist, dass die Preise „zum Mittelwert zurückkehren“ und sich um die historische Preisspanne herum annähern werden.
Bei einer vollwertigen statistischen Arbitrage beschränken wir uns nicht auf Korrelation oder Kointegration zwischen den Preisen. Da unser Hauptziel in diesem Artikel darin besteht, die Komplexität der statistischen Arbitrage für den durchschnittlichen Einzelhändler zu vereinfachen, werden wir damit beginnen, historische Daten zu sammeln, um ein minimales Paarhandelsportfolio für den Devisenmarkt aufzubauen. Später können Sie auch andere Märkte und andere statistische Beziehungen als die Preiskorrelation einbeziehen.
Wählen Sie eine Gruppe von Wertpapieren, mit der Sie beginnen möchtenZum Zeitpunkt der Erstellung dieses Artikels sind auf meinem Konto des MetaTrader 5-Terminals mehr als zehntausend Symbole verfügbar. Wir werden die Python-Integration für Metatrader 5 in unserer Analyse verwenden.
print("Total symbols =",mt5.symbols_total()) # display all symbols Total symbols = 10563Aus praktischen Gründen müssen wir also zunächst eine Teilmenge aller verfügbaren Symbole auswählen. Beginnen wir mit den XAU-Paaren.
# get symbols containing XAU in their names xau_symbols=mt5.symbols_get("*XAU*") print('len(*XAU*): ', len(xau_symbols)) for s in xau_symbols: print(s.name) len(*XAU*): 6 XAUUSD XAUEUR XAUAUD * XAUG XAUCHF XAUGBP
* Da es sich bei XAUG um einen, ETF, einen börsengehandelten Fonds handelt, können wir ihn vorerst ausschließen und uns auf die anderen fünf Paare konzentrieren. Schauen wir uns an, wie sie jeweils mit dem XAUUSD korrelieren.
Nun müssen wir ihre historische Preiskorrelation berechnen. In einem realen Szenario möchten wir vielleicht alle möglichen Permutationen unter den gewählten Symbolen untersuchen, möglicherweise Hunderte von Aktiensymbolen, da wir von keinerlei Wissen über sie ausgehen. Hier werden wir sie jedoch herausfiltern und nur die Preiskorrelation zwischen der Goldnotierung in US-Dollar (XAUUSD) und der Goldnotierung in Euro, australischen Dollar, Schweizer Franken und britischen Pfund betrachten.Wir benötigen Daten für die täglichen Schlusskurse eines Jahres ab dem aktuellen Tag, was bei Devisenmärkten etwa 250 Handelstagen entspricht.
# get 250 D1 bars from the current day xauusd_rates = mt5.copy_rates_from_pos("XAUUSD", mt5.TIMEFRAME_D1, 0, 250) xaueur_rates = mt5.copy_rates_from_pos("XAUEUR", mt5.TIMEFRAME_D1, 0, 250) xauaud_rates = mt5.copy_rates_from_pos("XAUAUD", mt5.TIMEFRAME_D1, 0, 250) xauchf_rates = mt5.copy_rates_from_pos("XAUCHF", mt5.TIMEFRAME_D1, 0, 250) xaugbp_rates = mt5.copy_rates_from_pos("XAUGBP", mt5.TIMEFRAME_D1, 0, 250) (...) # calculate correlation coefficients import numpy as np usd_eur_corr = np.corrcoef(xauusd_close['close'], xaueur_close['close']) usd_aud_corr = np.corrcoef(xauusd_close['close'], xauaud_close['close']) usd_chf_corr = np.corrcoef(xauusd_close['close'], xauchf_close['close']) usd_gbp_corr = np.corrcoef(xauusd_close['close'], xaugbp_close['close'])
Dies führt zu den folgenden Ergebnissen:
| XAUUSD-Korrelation (Pearson) | |
|---|---|
| XAUEUR | 0.9692368 |
| XAUAUD | 0.96677962 |
| XAUCHF | 0.8418827 |
| XAUGBP | 0.90490282 |
Tabelle 1 - Tägliche Korrelation der Schlusskurse von Gold in US-Dollar (XAUUSD) und Gold in Euro, Australischen Dollar, Schweizer Franken und Britischen Pfund zwischen 2024-04-09 und 2025-03-26.
Die nachstehende Grafik zeigt, wie eine Preiskorrelation von nahezu 0,97 aussehen kann.
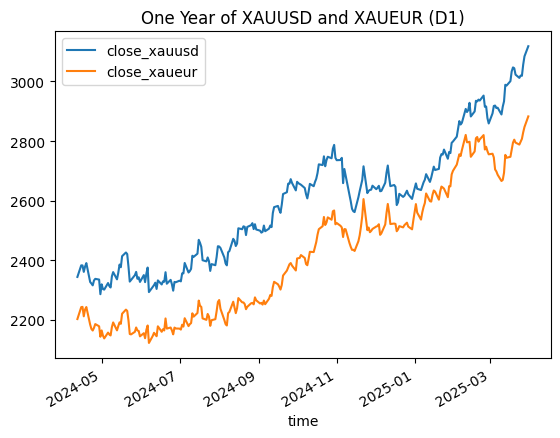
Abb. 1 - Tagesschlusskurse eines Jahres von Gold in US-Dollar und Euro
Beachten Sie, dass die obige Grafik irreführend sein kann. Man könnte versucht sein, den „Spread“ zwischen den Paaren zu handeln, aber das ist nicht der tatsächliche Spread, wenn überhaupt. Konvertieren wir XAUEUR in US-Dollar nach dem Tageskurs.adjusted_for_dollars = pd.concat([xauusd_close, xaueur_close['close'], eurusd_close['close']], join='inner', axis=1) adjusted_for_dollars.columns = ['time', 'xauusd', 'xaueur', 'eurusd'] adjusted_for_dollars['xaueur_dollars'] = adjusted_for_dollars['xaueur'] * adjusted_for_dollars['eurusd'] adjusted_for_dollars['diff'] = abs(adjusted_for_dollars['xauusd'] - adjusted_for_dollars['xaueur_dollars']) print(adjusted_for_dollars) time xauusd xaueur eurusd xaueur_dollars diff 0 2024-04-12 2344.22 2202.92 1.06237 2340.316120 3.903880 1 2024-04-15 2383.10 2242.90 1.06181 2381.533649 1.566351 2 2024-04-16 2382.85 2243.81 1.06720 2394.594032 11.744032 3 2024-04-17 2361.16 2212.14 1.06425 2354.269995 6.890005 4 2024-04-18 2378.86 2234.79 1.06557 2381.325180 2.465180 .. ... ... ... ... ... ... 245 2025-03-25 3019.81 2797.81 1.07918 3019.340596 0.469404 246 2025-03-26 3018.85 2807.50 1.07370 3014.412750 4.437250 247 2025-03-27 3056.42 2829.26 1.07975 3054.893485 1.526515 248 2025-03-28 3084.20 2847.12 1.08276 3082.747651 1.452349 249 2025-03-31 3118.19 2882.78 1.08152 3117.784226 0.405774 [250 rows x 6 columns]
adjusted_for_dollars.plot(title = 'One Year of XAUUSD and XAUEUR in US Dollars (D1)', x='time', y=['xauusd', 'xaueur_dollars']) plt.show()
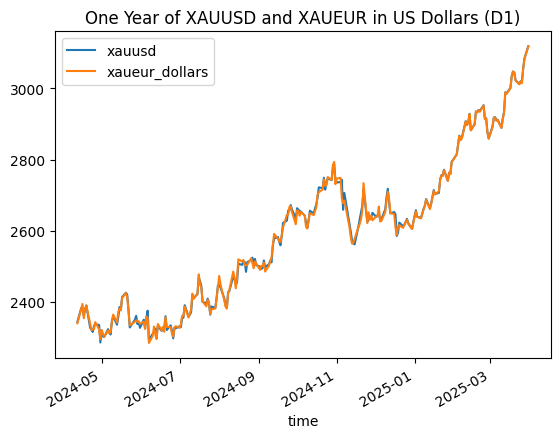
Abb. 2 - Tages-Schlusskurse von Gold in US-Dollar und Euro für ein Jahr, bereinigt um US-Dollar
Betrachtet man die Differenz zwischen der Goldnotierung in USD und der Goldnotierung in Euro...
print("median: ", adjusted_for_dollars['diff'].median()) adjusted_for_dollars['diff'].describe() median: 4.052404150000029 count 250.000000 mean 5.894673 std 6.238511 min 0.050646 25% 1.279615 50% 4.052404 75% 8.587763 max 51.483719 median: 4.052404150000029
... stellen wir fest, dass die tatsächliche durchschnittliche Spanne in diesem Einjahreszeitraum ~5,9 Dollar betrug, mit einer Standardabweichung von ~6,2 Dollar. Wenn wir vereinfachend davon ausgehen, dass die Differenz (Spanne) zwischen den beiden Notierungen nach der Umrechnung mit dem aktuellen Wechselkurs nahe Null liegen sollte, können wir jede Spanne über dem Mittelwert als handelbare Anomalie auf dem Markt betrachten.
Wählen Sie die statistische Beziehung, nach der Sie suchen möchten
Dann beginnen wir mit dem Aufbau unseres statistischen Arbitrageportfolios (stat-arb), das auf der hohen Korrelation zwischen XAUUSD und XAUEUR im letzten Handelsjahr (~250 Tage) beruht. Aber ist die Preiskorrelation die richtige oder gar die bessere statistische Beziehung, nach der man beim Aufbau eines Stat Arb-Portfolios suchen sollte?
Wenn wir über die Korrelation historischer Preise sprechen, besteht die Gefahr, dass wir uns von einigen Unterschieden zwischen der allgemeinen Verwendung des Begriffs und seiner eigentlichen statistischen Bedeutung leiten lassen. Diese Tatsache wird in der Devisenbranche noch deutlicher. Eine einfache Suche nach „forex correlated pairs“ führt uns zu vielen Ressourcen, die die am stärksten/am wenigsten korrelierten Paare zusammen mit Tipps für den Handel mit ihnen auflisten. Es ist nicht unser Ziel, hier zu sagen, dass diese oder jene Ressource, Auflistung oder Handelsempfehlung richtig oder falsch ist. Wir müssen uns vor Augen halten, dass wir die Grundlagen für eine statistische Arbitrage auf Portfolioebene schaffen, die nicht auf Devisenpaare beschränkt sein soll. Stattdessen muss unser System für jede Anlageklasse, jeden Markt und jeden Zeitrahmen verallgemeinert werden können, wobei lediglich die Anforderungen der Marktneutralität und der Überprüfbarkeit erfüllt sein müssen.
Statistiker gehen davon aus, dass die Funktion des Pearson-Korrelationskoeffizienten für stationäre Reihen verwendet wird, aber die Zeitreihe der Preise ist nicht stationär. Bei der Berechnung der Korrelation in einer nicht-stationären Zeitreihe kann es zu so genannten „Scheinkorrelationen“ kommen.
„Nicht-stationäre Daten sind in der Regel unvorhersehbar und können nicht modelliert oder prognostiziert werden. Die Ergebnisse, die durch die Verwendung nicht-stationärer Zeitreihen erzielt werden, können insofern verfälscht sein, als sie eine Beziehung zwischen zwei Variablen anzeigen können, die nicht existiert. Um konsistente, zuverlässige Ergebnisse zu erhalten, müssen die nicht-stationären Daten in stationäre Daten umgewandelt werden.“ (Nason, G. P. (2006). Stationäre und nicht-stationäre Zeitreihen, Investopedia)
Dann müssen wir als Händler, der ein statistisches Arbitrageportfolio aufbauen will, eine Entscheidung treffen: Ist diese „Scheinkorrelation“ ausreichend, oder brauchen wir eine echte Korrelation im statistischen Sinne? Für den Moment akzeptieren wir die erste, nicht perfekte Maßnahme als ausreichend für unser vereinfachtes Modell. Es darf jedoch nicht vergessen werden, dass korrelierte Paare über lange Zeiträume hinweg die Spanne ausweiten können, während sie gleichzeitig steigen oder fallen, d. h. sie können über lange Zeiträume hinweg nicht zum Mittelwert zurückkehren, und dennoch gilt die statistische Korrelation weiterhin. Diese Bedingung ist bei Währungen eher die Ausnahme, bei Rohstoffen, Futures oder Aktienkurszeitreihen jedoch sehr häufig. Daher sind Stop-Loss-Niveaus und Positions-Timing bei Strategien mit „erwarteter Rückkehr zum Mittelwert“ unerlässlich.
Wählen Sie die statistische Kennzahl als HandelsauslöserWarum sollte man den Mittelwert oder den Median als Maß für unsere historische Streuung wählen? Nach Ansicht der Statistiker sollten wir den Mittelwert verwenden, wenn unsere Daten wenige Ausreißer aufweisen, und den Median, wenn der Datensatz extreme Spitzen aufweist, da der Median von diesen Spitzen weniger beeinflusst wird. Wenn Sie beispielsweise die große Streuung herausfiltern wollen, die durch aufsehenerregende Nachrichten verursacht wird, können Sie den Median wählen. Umgekehrt können Sie den Mittelwert wählen, wenn Sie die Auswirkungen dieser wichtigen Nachrichten auf den Spread berücksichtigen wollen.
Es gibt also kein „Rezept“. Sie müssen auf der Grundlage Ihrer Daten und Ihres guten Urteilsvermögens selbst entscheiden. Sie können sich auch dafür entscheiden, weder den Mittelwert noch den Median zu verwenden. Stattdessen können Sie untersuchen und entscheiden, dass eine andere Beziehung für Ihren Anwendungsfall besser geeignet ist.
Ich werde mich auf den Mittelwert stützen und einen Parameter für unsere Handelsstrategie festlegen, der auf der Ausweitung der mittleren Spanne basiert. Angenommen, die Spanne zwischen XAUUSD und XAUEUR weitet sich um mehr als 50 % des Mittelwerts aus, dann lösen wir den Handel aus, indem wir das Symbol kaufen, das das Rennen verliert, und gleichzeitig das Symbol verkaufen, das schneller steigt.
Wie können wir feststellen, welches Symbol steigt und welches fällt? Da wir in unserem speziellen Fall davon ausgehen, dass beide Goldkurse nach der Umrechnung gleich sein sollten, können wir einfach das Symbol mit dem höheren Preis als das steigende Paar und das andere als das fallende Paar nehmen. Wenn wir uns mit der Spanne von Aktienkursen befassen, die zum Mittelwert zurückkehren, könnten wir einen exponentiellen gleitenden Durchschnitt mit einer sehr kurzen Periode verwenden und davon ausgehen, dass das Symbol, das über dem EMA gehandelt wird, steigt und andersherum.
bool IsRising(const int symbol) { switch(symbol) { case BASE_PAIR: //Print("Base pair is rising? ", quotes_base[0] > ema_base[0]); return quotes_base[0] > ema_base[0]; case CORR_PAIR: //Print("Corr pair is rising? ", quotes_corr[0] > ema_corr[0]); return quotes_corr[0] > ema_corr[0]; default: return false; } } bool IsFalling(const int symbol) { switch(symbol) { case BASE_PAIR: //Print("Base pair is falling? ", quotes_base[0] < ema_base[0]); return quotes_base[0] < ema_base[0]; case CORR_PAIR: //Print("Corr pair is falling? ", quotes_corr[0] < ema_corr[0]); return quotes_corr[0] < ema_corr[0]; default: return false; } }Oder wir können die Steigung verwenden.
void CalculateSlopes(double & slope_b[], double & slope_c[]) { slope_b[0] = MathAbs((quotes_base[0] - quotes_base[SlopePeriod]) / SlopePeriod); slope_c[0] = MathAbs((quotes_corr[0] - quotes_corr[SlopePeriod]) / SlopePeriod); }In unserem Fall verwenden wir einfach das Symbol mit dem höchsten Preis.
if(quotes_base[0] > quotes_corr[0])
Handel mit dem Portfolio
Wir haben einen einfachen EA entwickelt, um unsere Hypothese in einem Backtest zu testen.
Wir erhalten die anfänglichen Kurse bei OnInit() und aktualisieren sie in OnTimer(). Das liegt daran, dass wir uns nicht auf die Ereignisbehandlung von OnTick verlassen können, um die Kurse des Paares zu aktualisieren, das nicht das des aktuellen Arbeitscharts ist, da OnTick() nur für das aktuelle Symbol/den aktuellen Chart aufgerufen wird. Siehe Expert Advisors mit mehreren Währungen oder Symbolen.
int OnInit() { ArrayResize(quotes_base, CountQuotes); ArrayResize(quotes_corr, CountQuotes); ArrayResize(quotes_conv, CountQuotes); //--- Get start quotes for both pairs GetQuotes(); //--- EMA indicators EMA_Handle_Base = iMA(BasePair, _Period, EMAPeriod, 0, MODE_EMA, PRICE_CLOSE); EMA_Handle_Corr = iMA(CorrPair, _Period, EMAPeriod, 0, MODE_EMA, PRICE_CLOSE); if(EMA_Handle_Base == INVALID_HANDLE || EMA_Handle_Corr == INVALID_HANDLE) { printf(__FUNCTION__ + ": EMA initialization failed"); return(INIT_FAILED); } //--- create timer EventSetTimer(5); // seconds //--- return(INIT_SUCCEEDED); } bool GetQuotes() { if(CopyClose(BasePair, _Period, 0, CountQuotes, quotes_base) != CountQuotes) { Print(__FUNCTION__ + ": CopyClose failed. No data"); //printf("Size quotes base pair %i ", ArraySize(quotes_base)); return false; } if(CopyClose(CorrPair, _Period, 0, CountQuotes, quotes_corr) != CountQuotes) { Print(__FUNCTION__ + ": CopyClose failed. No data"); //printf("Size quotes corr pair %i ", ArraySize(quotes_corr)); return false; } if(CheckMode == PRICE) { if(CopyClose(ConvPair, _Period, 0, CountQuotes, quotes_conv) != CountQuotes) { Print(__FUNCTION__ + ": CopyClose failed. No data"); //printf("Size quotes conv pair %i ", ArraySize(quotes_conv)); return false; } //--- for(int i = 0; i < CountQuotes; i++) { quotes_corr[i] *= quotes_conv[i]; } } return true; } void OnTimer() { UpdateQuotes(); CalculateMeanSpread(); if(CheckMode == EMA) { GetEMAs(); } } void UpdateQuotes() { ArrayRemove(quotes_base, ArraySize(quotes_base) - 1); double new_quote_base[1]; CopyClose(BasePair, _Period, 0, 1, new_quote_base); ArrayInsert(quotes_base, new_quote_base, 0, 0); //--- ArrayRemove(quotes_corr, ArraySize(quotes_corr) - 1); double new_quote_corr[1]; CopyClose(CorrPair, _Period, 0, 1, new_quote_corr); ArrayInsert(quotes_corr, new_quote_corr, 0, 0); //--- if(CheckMode == PRICE) { ArrayRemove(quotes_conv, ArraySize(quotes_conv) - 1); double new_quote_conv[1]; CopyClose(ConvPair, _Period, 0, 1, new_quote_conv); ArrayInsert(quotes_conv, new_quote_conv, 0, 0); quotes_corr[0] *= quotes_conv[0]; } }
Berechnen wir die mittlere Streuung
bool CalculateMeanSpread() { int sz_base_p = ArraySize(quotes_base); int sz_corr_p = ArraySize(quotes_corr); int sz_conv_p = ArraySize(quotes_conv); if(sz_base_p != sz_corr_p || sz_corr_p != sz_conv_p) { Print(__FUNCTION__ + " Failed: Arrays must be of same size"); return false; } //--- ArrayResize(pairs_spread, CountQuotes); for(int i = 0; i < sz_base_p; i++) { pairs_spread[i] = MathAbs(quotes_base[i] - quotes_corr[i]); } double max_spread = pairs_spread[ArrayMaximum(pairs_spread)]; double min_spread = pairs_spread[ArrayMinimum(pairs_spread)]; mean_spread = MathMean(pairs_spread); //--- //printf("Last quote XAUUSD %f ", quotes_base[0]); //printf("Last quote XAUEUR %f ", quotes_corr[0]); //printf("Last spread %f ", pairs_spread[0]); //printf("Max spread %f ", max_spread); //printf("Min spread %f ", min_spread); //printf("Mean spread %f ", mean_spread); return true; }
Wir prüfen die Handelssignale in OnTick.
void OnTick() { //--- CheckForClose(); CheckForOpen(); }
Wenn die Streuung mindestens um den von uns festgelegten Prozentsatz über dem Mittelwert liegt
bool HasSpreadTrigger() { double trigger_spread = mean_spread + (mean_spread * (PercentTrigger / 100.0)); //printf(" trigger spread %f ", trigger_spread); double current_spread = pairs_spread[0]; //printf(" current spread %f ", current_spread); return current_spread >= trigger_spread; }
Wir kaufen das Symbol, dessen Preis niedrig ist, und verkaufen das Symbol, dessen Preis hoch ist. In unserem Beispiel wird diese Umschaltung für die Enumeration CheckMode (enum) vorgenommen.
void CheckForOpen()
{
if(PositionsTotal() == 0 && HasSpreadTrigger())
{
switch(CheckMode)
{
case EMA:
if(IsRising(BASE_PAIR) && IsFalling(CORR_PAIR))
{
OpenShort(BasePair);
OpenLong(CorrPair);
}
if(IsFalling(BASE_PAIR) && IsRising(CORR_PAIR))
{
OpenLong(BasePair);
OpenShort(CorrPair);
}
break;
case SLOPE:
CalculateSlopes(slope_base, slope_corr);
if(slope_base[0] > slope_corr[0])
{
OpenShort(BasePair);
OpenLong(CorrPair);
}
else
{
OpenLong(BasePair);
OpenShort(CorrPair);
}
break;
case PRICE:
if(quotes_base[0] > quotes_corr[0])
{
OpenShort(BasePair);
OpenLong(CorrPair);
}
else
{
OpenLong(BasePair);
OpenShort(CorrPair);
}
}
}
}
Die Positionen werden durch Stop-Loss/Take-Profit oder durch Mean Reversion bei CheckForClose() geschlossen.
void CheckForClose() { int total = PositionsTotal(); ulong ticket = 0; if(total > 0) { if(PositionSelect(BasePair) || PositionSelect(CorrPair)) { for(int i = 0; i < total; i++) { ticket = PositionGetTicket(i); if(ticket == 0) continue; if(pairs_spread[0] <= mean_spread) { ExtTrade.PositionClose(ticket); } } } } }
Der Backtest bestätigt, dass die Mean-Reversion-Strategie für den Paarhandel praktikabel ist.
Abb. 3. Backtest-Kapitalkurve
Obwohl der Backtest unsere Hypothese bestätigt, können Sie sehen, dass dieser spezielle Algorithmus Verbesserungen benötigt, um die Kapitalkurve zu glätten. Vielleicht eine dynamische Ordergröße (das Handelsvolumen ist hier im Minimum 0,01 - Mikrolot festgelegt) und Optimierungen für das Stop-Loss/Take-Profit-Verhältnis. Aber die Rentabilität ist nicht unser Hauptanliegen in diesem Artikel. Werfen wir nun einen Blick auf einige interessante Ergebnisse, die - einigen Autoren zufolge - bei statistischen Arbitrageoperationen üblich zu sein scheinen.
Abb. 4. Backtest-Ergebnisse
Es gibt eine große Anzahl von Geschäften, das Verhältnis zwischen Gewinnen und Verlusten ist gering (~55/~45), und der maximale Drawdown ist relativ gering.
Abb. 5. Backtest-Handelszeiten
Die Konzentration auf bestimmte Zeiträume (Stunden, Wochentage usw.). In unserem Fall liegt die Konzentration um die Eröffnung der US-Sitzung, mit einem Höhepunkt im April 2024.
Abb. 6. Backtest Positionshaltezeit X Gewinn
Die große Anzahl sehr kurzer Transaktionen zeigt, dass unser System Momente der Marktinstabilität erforscht hat, indem es nach gewonnenen Geschäften wieder eingestiegen ist.
Was könnte besser sein?
Nun möchte ich Ihre Aufmerksamkeit auf den Punkt lenken, dass der Verkäufer einer Handelsstrategie oder eines Setups versuchen wird, Ihnen die bestmöglichen Ergebnisse aus der Vergangenheit zu zeigen, um Ihr Interesse an seinem Produkt zu wecken. Schließlich werden sie nach sorgfältiger Optimierung die leistungsstärksten Parameter auswählen, um die potenziellen Gewinne hervorzuheben und das Risiko von Verlusten zu verringern.
Aber abgesehen von der Idee, dass Sie die Prinzipien verstehen und mit statistischer Arbitrage klein anfangen können, will ich Ihnen hier nichts „verkaufen“. Im Gegenteil, ich würde sagen, ich bin froh, dass der Backtest zeigt, dass wir es mit einem Algorithmus zu tun haben, der verbessert werden muss. Denn dies ist der Grundstein jedes statistischen Arbitrage-Systems.
Das heißt, bisher waren wir bei dieser vereinfachten Automatisierung auf willkürlich gewählte Parameter beschränkt, um das Risiko zu steuern. Was wir stattdessen brauchen, ist:
- Die Kontrolle der Anzahl der zu eröffnenden Positionen in Abhängigkeit vom bewerteten Risiko zu jedem Zeitpunkt.
- Einen veränderlichen Auslöseprozentsatz des Spread, der die Volatilität berücksichtigt.
- Die Entwicklung einer dynamischen Stop-Loss/Take-Profit-Strategie, die die Gewinnwahrscheinlichkeit aus dem Auslösewert des Spread und möglicherweise anderen Variablen ableitet
Dies sind einige mögliche Wege für zukünftige Verbesserungen dieses EA.
Zusammenfassung des Maßstabsmodells
1. Beginnen wir mit einer Hypothese
Die Spanne zwischen korrelierten Paaren tendiert dazu, zum Mittelwert zurückzukehren. Dies ist unsere Hypothese.
Aus der Sicht des Händlers ist das Konzept der Rückkehr zum Mittelwert einfach und intuitiv: Wenn der aktuelle Preis unter dem Durchschnittspreis liegt, kann man erwarten, dass der Preis steigt, und wenn der aktuelle Preis über dem Durchschnittspreis liegt, kann man erwarten, dass der Preis fällt. Wie das Sprichwort sagt, ist der Preis immer auf der Suche nach dem Mittelwert“.
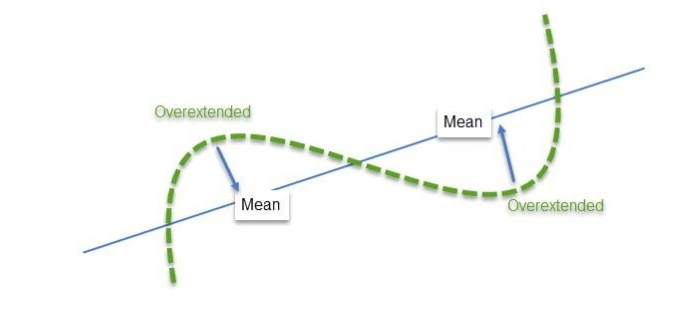
Abb. 7. Überkaufte oder überverkaufte Wertpapiere neigen dazu, zum Durchschnittspreis zurückzukehren (Quelle: ResearchGate CC BY 4.0)
In Trendmärkten wird der Mittelwert zu einer dynamischen Unterstützung für Aufwärtstrends und zu einem dynamischen Widerstand für Abwärtstrends. In sich konsolidierenden Märkten tendiert der Mittelwert dazu, im Kanal zu verlaufen, also in der Mitte zwischen den höchsten Hochs und den tiefsten Tiefs.
Dieses Merkmal ist bei Devisenkursen in kurzen Zeiträumen besser zu beobachten, denn während der Preis jedes anderen Vermögenswerts zumindest theoretisch unbegrenzt steigen oder fallen kann, sind Devisenkurse durch die Regeln des Handels zwischen Nationen „gedeckelt“.
Zum Beispiel: „Apple ging am 12. Dezember 1980 zum Preis von 22,00 Dollar pro Aktie an die Börse. Die Aktie wurde seit dem Börsengang fünfmal gesplittet, sodass der Aktienkurs beim Börsengang auf splitbereinigter Basis bei $,10 lag.“
Zum Zeitpunkt der Erstellung dieses Berichts notiert Apple bei 192,00 US$ (~ 875 %). Und sie steigt weiter an. Es gibt keine theoretische Grenze.
Andererseits kann man nicht einmal mit einer 50%igen Auf- oder Abwertung der Wechselkurse zwischen zwei Währungen rechnen, ohne gleichzeitig an extreme Faktoren wie Hyperinflation oder sogar einen groß angelegten Krieg zu denken. Unter normalen Bedingungen sollte der Wechselkurs, der den „Preis“ des Paares im Devisenhandel bestimmt, viel früher zum Mittelwert zurückkehren.
2. Suche nach Mustern in den Daten, um die Hypothese zu testen
Die Pearson-Korrelation von 0,97 zwischen XAUUSD und XAUEUR verdeutlicht unser Muster: Die Kurse dieser beiden Wertpapiere steigen oder fallen tendenziell gleichzeitig.
3. Überwachung auf Anomalien in den Mustern
Die weit vom Mittelwert abweichende Spanne zwischen XAUUSD und XAUEUR ist unsere Anomalie. Das Aufspüren von Anomalien in Marktmustern ist das A und O der statistischen Arbitrage auf Portfolioebene, wie sie von Simons' Team eingesetzt wurde.
4. Entwicklung einer Automatisierung für den Handel mit Anomalien
Der vereinfachte EA stellt unsere Automatisierung dar, aber wie gesagt, der Algorithmus erfordert viele Verbesserungen, er ist nur ein Werkzeug, das uns hilft, die Prinzipien besser zu verstehen. Außerdem erfordert der EA selbst alle üblichen Fehlerprüfungen.
Schlussfolgerung
Statistische Arbitrage auf Portfolioebene, wie sie von den großen Marktteilnehmern betrieben wird, ist für den durchschnittlichen Kleinhändler praktisch unmöglich. Denn wir müssten im Hochfrequenzhandel (HFT) tätig sein, mit einem hochqualifizierten Team, hochwertigen Big Data und viel Geld. Um unser Modell in etwas zu verwandeln, das der Hedgefonds-Operation von Jim Simons ähnelt oder auch nur nahe kommt, würde ich mit einem Augenzwinkern sagen, dass wir nur in der Lage sein müssen:
- eine Marktanalysen mit einer Granularität von weniger als einer Sekunde für Hunderte von Vermögenssymbolen in jedem Portfolio in Echtzeit zu erstellen, (Irgendwann hatte Simmons' Team mit mehr als achttausend verschiedenen Aktien in einem Dutzend Märkten und Gebieten zu tun).
- Aufträge von einer Million Dollar abzuschicken, die in einer Millionstel Sekunde ausgeführt werden müssten und
- das Modells regelmäßig zu aktualisieren.
Nun, ich nehme an, wir können damit beginnen, das Modell regelmäßig zu aktualisieren. 🙂
Aber im Ernst: Das obige Zitat von Isaac Newton lehrt uns, dass Mathematik allein nicht ausreicht, um auf den Finanzmärkten erfolgreich zu sein. Viele Mathematiker sind dort gescheitert, wo Simons erfolgreich war. Aber Simons ging nicht nur mit Mathematik auf das Schlachtfeld. Er begann seine Karriere im Finanzwesen, indem er wie jeder andere Händler handelte, nach Trends suchte, sich auf technische Analysen und Intuition verließ und Geld verdiente und verlor. Er probierte verschiedene Methoden aus, lernte die Regeln des Handelns, führte Gespräche, ging Partnerschaften ein und arbeitete mit professionellen Händlern zusammen, während er versuchte, einen nachhaltigen Weg des Handels zu finden.
Nichtsdestotrotz ist sein konzeptioneller Rahmen für jeden zugänglich, der bereit ist, die erforderlichen Anstrengungen zu unternehmen, um das richtige Portfolio auszuwählen, die richtigen zu untersuchenden Merkmale auszuwählen, nach Mustern und Anomalien zu suchen, Prototypen mit kostenlosen Daten zu erstellen und hochwertige Daten zu kaufen, wenn der Prototyp vielversprechend genug ist, um das ausgewogenste Modell für ein bestimmtes Portfolio zu finden. Wahrscheinlich zahlen viele Einzelhändler auf der ganzen Welt für diesen Aufwand mit ernsthafter täglicher Arbeit. Die meisten von ihnen werden nicht zu Milliardären, aber viele von ihnen haben ihre Handelstätigkeit zu einem nachhaltigen Geschäft gemacht.
Wir können sogar dem Weg des maschinellen Lernens folgen, um diese Muster und Anomalien zu entdecken. Sie ist für die Sterblichen zugänglich, und es scheint, als sei die Zukunft bereits gegenwärtig, genau hier und jetzt. Es gibt buchstäblich Hunderte von qualitativ hochwertigen Artikeln über den Einsatz von maschinellem Lernen in der MetaTrader 5-Umgebung. Heutzutage ist es NICHT erforderlich, dass wir die einfache Mathematik beherrschen, um maschinelles Lernen in unserem Handelssystem zu nutzen. Wir können MQL5 oder Python verwenden, beide mit eingebauten Batterien, d.h. mit High-Level-Bibliotheken für maschinelles Lernen.
Zusammenfassend lässt sich sagen, dass dieser Artikel Händlern mit begrenzten Ressourcen einen schematischen Weg zum Verständnis der Grundlagen der statistischen Arbitrage auf Portfolioebene aufzeigt.
Wie die Redensart sagt, sind die Ergebnisse der Vergangenheit keine Garantie für zukünftige Ergebnisse. Wir können jedoch fundiertere Entscheidungen treffen, wenn wir diese früheren Ergebnisse mit den richtigen Instrumenten und objektiven Daten analysieren.
| Angehängte Datei | Beschreibung |
|---|---|
| pairs-trading.mq5 | Diese Datei enthält den Beispielcode für den Expert Advisor zur Reproduktion des Experiments. Er benötigt (#<include>) die Datei PairsTradingFunctions.mqh. |
| PairsTradingFunctions.mqh | Diese Datei ist das Include, das von der vorherigen Datei in dieser Liste benötigt wird, und enthält derzeit nur eine Enumeration (enum) des Prüfmodus, der vom EA verwendet wird, um das steigende/fallende Symbol in den Paaren zu identifizieren. |
| pairs-trading.ipynb | Diese Datei ist eine Jupyter-Notebook-Datei, die Python-Code zur Durchführung der statistischen Analyse enthält. |
| stat_arb_pairs_trading_GOLD_XAUEUR.ini | Bei dieser Datei handelt es sich um die Konfigurationseinstellungen des Metratrader 5-Testers zur Reproduktion des Experiments. |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/17735
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 59): Verstärkungslernen (DDPG) mit gleitendem Durchschnitt und stochastischen Oszillatormustern
MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 58): Reinforcement Learning (DDPG) mit gleitendem Durchschnitt und stochastischen Oszillatormustern
Einführung in MQL5 (Teil 15): Ein Anfängerleitfaden zur Erstellung nutzerdefinierter Indikatoren (IV)
Einführung in MQL5 (Teil 14): Ein Anfängerleitfaden zur Erstellung nutzerdefinierter Indikatoren (III)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Hallo. Sehr interessanter Artikel. Ich habe versucht, die Ergebnisse zu replizieren, aber nichts passiert. Was fehlt mir? Ich habe die Dateien pairs-trading.mq5 und PairsTradingFunctions.mqh hochgeladen .
Vielen Dank
XXXUSD = XXXEUR * EURUSD.
XXX = XAU, AUD, ....
Die 5-Sekunden-Intervalle sind an dieser Stelle willkürlich. Es könnte auch 1 Sekunde oder 10 Sekunden sein. Die Idee ist, ein anfängliches Fenster zu haben, um die mittlere Streuung und eventuell andere Statistiken für den von den CountQuotes abgedeckten Zeitraum zu berechnen. Dann wird ein gleitendes Fenster in X-Sekunden-Intervallen aktualisiert, unabhängig vom Zeitrahmen.
Sie haben Recht mit den Balken: Ich interessiere mich nicht für sie oder dafür, sie zu synchronisieren, weil sie in diesem speziellen Fall irrelevant zu sein scheinen. Fast alle Trades dauern ein paar Sekunden und werden innerhalb des Balkens eröffnet und geschlossen.
Abgesehen davon, was halten Sie von diesem Ansatz? Ist er jetzt klarer? Sehen Sie irgendeinen kritischen Fehler, der zu falschen Berechnungen führen oder die Leistung beeinträchtigen könnte, oder ähnliches?
Dann ist der ganze Modus mit iMA falsch, weil er an Balken gebunden ist. Sie müssen den MA anhand von 5-Sekunden-Samples manuell berechnen.
Dann ist der gesamte Modus mit iMA falsch, weil er an Balken gebunden ist. Sie müssen die MA durch 5-Sekunden-Samples manuell berechnen.
Wie
Lesen Sie die Tick-Historie (implementieren Sie sie selbst mit den Funktionen CopyTicks/CopyTickRange oder finden Sie einen fertigen Indikator/Skript in der Codebasis) und berechnen Sie virtuelle 5-Sekunden-Balken als Array. Wenden Sie dann Glättungsalgorithmen aus der Standardbibliothek an (mqh-Dateien, die zusammen mit MT5 bereitgestellt werden).