Statistische Arbitrage durch kointegrierte Aktien (Teil 2): Expert Advisor, Backtests und Optimierung

Einführung

Wir haben die Herausforderung angenommen, einen Rahmen für den statistischen Arbitragehandel zu entwickeln, der von einem durchschnittlichen, einzelnen Händler genutzt werden kann. Die Kernidee besteht darin, eine Reihe von statistischen Funktionen und Analysemethoden zusammenzustellen, die es einem Kleinhändler, der nur ein Notebook und ein normales Maklerkonto besitzt, ermöglichen, mit statistischer Arbitrage für Devisen, Aktien, ETFs und Rohstoffe zu beginnen.

Wir begannen mit einem einfachen korrelationsbasierten Paarhandel, der im Backtest großes Potenzial zeigte, aber im Demokonto kläglich scheiterte. Es war nicht schwer zu erkennen, dass wir unsere Handelsgeschäfte auf der Ebene der Auftragsausführung verloren. Das heißt, unsere Strategie war in hohem Maße von der Geschwindigkeit der Auftragsausführung abhängig, aber unsere Infrastruktur (normales Notebook, langsame Internetverbindung und Standard-Code) entsprach nicht einmal annähernd der erforderlichen Qualität für diese Art von Arbitrage. Unsere Ein- und Ausstiegsregeln waren in hohem Maße vom Timing abhängig, und unsere Arbitragemöglichkeit wurde geschlossen, noch bevor unsere Aufträge auf dem Broker-Server eintrafen. 

Wir könnten versuchen, das Problem der Ausführungszeit zu lösen, zu minimieren oder zu umgehen, indem wir ein VPN einrichten (was wir irgendwann in der Zukunft tun werden), indem wir ein professionelles Konto mit maximal zulässigem Slippage einrichten oder indem wir versuchen, unseren Prototyp-Code zu verbessern. Jede dieser offensichtlichen und relativ billigen Maßnahmen wäre hilfreich gewesen, und beide zusammen würden unsere Strategie sicherlich wieder auf den richtigen Weg bringen. Da wir aber unsere ursprüngliche Vorgabe beibehalten wollen, für den durchschnittlichen Privathändler mit minimalen Ressourcen nützlich zu sein, haben wir uns statt der Ausführungsgeschwindigkeit das Ziel gesetzt, eine Strategie zu entwickeln, die nicht so sehr von der Ausführungsgeschwindigkeit abhängig ist. Die im Folgenden beschriebene Umsetzung ist eine mögliche Antwort auf dieses Ziel.

Im vorigen Artikel haben wir die Kointegrationstests von Engle-Granger und Johansen, ihre Begründung aus der Sicht eines Händlers und ihre grundlegende Interpretation vorgestellt. Jetzt werden wir sie verwenden, um unser kointegriertes Portfolio zu erstellen. 

Aufbau eines Portfolios aus kointegrierten Aktien

Der Betrunkene, der Hund und „Random Walk“*

Bei der Erforschung der Kointegration stößt man häufig auf eine Analogie, die das grundlegende Merkmal kointegrierter Zeitreihen, oder in diesem Fall kointegrierter Aktienkurse, recht gut erklärt. Die Analogie besagt, dass zwei nichtintegrierte Zeitreihen wie ein betrunkener Mann sind, der mit seinem Hund spazieren geht. Ihre Wege trennen sich willkürlich, ohne erkennbare, wahrgenommene oder messbare Logik. Der Mann und der Hund können sogar auf unterschiedlichen Wegen nach Hause kommen, oder der Hund kann sogar für immer verloren gehen.

Aber zwei kointegrierte Zeitreihen wären so, als ob der Hund an einer Hundeleine geführt würde, d.h. der Mann ist immer noch betrunken, seine Schritte taumeln immer noch, aber ihre Wege gehen zusammen weiter, egal was passiert. Kointegrierte Aktien sind so, als ob ihre Preise durch eine „unsichtbare Hundeleine“ gebunden wären. Langfristig kommen sie in der Regel gemeinsam zu Hause an. Das Zuhause ist der gemeinsame Mittelwert, die gemeinsame mittlere Streuung.

Aber wie können wir diese kointegrierten Aktien in einem Universum von Tausenden von Wertpapieren finden? Glücklicherweise wissen wir bereits, dass einige Aktien aus demselben Sektor oder derselben Branche dazu neigen, sich gemeinsam zu bewegen. Mit diesem Wissen lässt sich die ursprüngliche Zahl auf eine überschaubare, aber immer noch große Zahl reduzieren. 

Abb. 1  Anzahl der auf dem MetaQuotes Demo-Server verfügbaren Symbole

Abb. 2 Anzahl der auf einem Demoserver eines kommerziellen Brokers verfügbaren Aktiensymbole nach Land

In der akademischen Literatur wurden bereits mehrere klassische und „neuartige“ Methoden untersucht, um die Aktienkandidaten für den Paarhandel herauszufiltern, aber letztendlich erzielte keine von ihnen bessere Ergebnisse als die Kointegration [Brunetti & De Luca, 2023].

Da es hier nicht um einen akademischen Bericht geht, sondern um einen Backtest und die Beschreibung einer Beispielimplementierung, habe ich eine einfache Heuristik angewandt, um unser kleines Portfolio aufzubauen.

„Heuristik (von altgriechisch εὑρίσκειν heurískein (auffinden, entdecken)) bezeichnet Methoden, die mit begrenztem Wissen (unvollständigen Informationen) und wenig Zeit dennoch zu wahrscheinlichen Aussagen oder praktikablen Lösungen kommen.“ (Wikipedia)

1. Wählen wir einige Nasdaq-Aktien mit hoher Liquidität aus, die alle von Halbleiterunternehmen stammen. Sie können mit ein paar Dutzend beginnen.
2. Wählen Sie unter ihnen diejenigen aus, die auf Tagesbasis in den letzten sechs Monaten oder weniger am stärksten mit Nvidia korreliert haben. Vermeiden Sie längere Rückblickszeiträume, da wir an den jüngsten Bewegungen interessiert sind und wir es mit einem sehr dynamischen Markt zu tun haben (KI und Halbleiter). Außerdem werden wir unser Modell monatlich oder wöchentlich aktualisieren, sodass sechs Monate oder weniger für diesen ersten Filter der richtige Weg sein könnten.
3. Testen Sie die kleine Gruppe – die am stärksten mit Nvidia korreliert – auf Kointegration.
4. Sobald Sie mindestens einen signifikanten Johansen-Vektor gefunden haben, testen Sie der kointegrierte Spread auf Stationarität.
5. Wenn Sie eine kleine Gruppe mit mindestens einem signifikanten Johansen-Vektor mit einem stationären kointegrierten Spread haben, erhalten Sie den ersten Johansen-Eigenvektor, um die relativen Portfolio-Gewichte zu erhalten. 
6. Mit den Portfoliogewichten können Sie einen Backtest des kointegrierten Aktienkorbs durchführen.

Mithilfe der Pearson-Korrelationsmethode, die wir im vorherigen Artikel gesehen haben, haben wir unseren Korb auf die drei unten aufgeführten Aktien eingegrenzt. Alle drei Unternehmen sind von der Nachfrage nach KI-Hardware betroffen und sind direkt oder über angrenzende Märkte Teil der Nvidia-Lieferkette.

Microchip Technology, Inc. (MCHP) – MCHP ist nicht direkt mit Nvidia-GPUs verbunden, profitiert aber vom allgemeinen Halbleitersektor, wenn die Nachfrage nach KI-bezogener Infrastruktur wie Robotik und industrieller KI über OEMs und Systemintegratoren für Nvidia-basierte Systeme steigt.

Monolithic Power System Inc (MPWR) – MPWR liefert integrierte Stromversorgungsschaltungen (PMICs) für Server und Rechenzentren. Diese PMICs werden auch in den Hochleistungs-GPUs von Nvidia eingesetzt, die eine hochspezialisierte Leistungsregelung benötigen, um die thermische und elektrische Stabilität bei hohen Arbeitslasten zu gewährleisten. MPWR profitiert von Nvidias Expansion in die Bereiche Rechenzentren und Inferenz.

Micron Technology Inc. (MU) – MU liefert Speicherprodukte, darunter High-Bandwidth Memory (HBM), das für KI-Beschleuniger wie Nvidias H100 entscheidend ist. Seine Speicherprodukte sind in Nvidia-GPUs und in Lösungen für Rechenzentren integriert. Da Nvidia mehr KI-Chips verkauft, steigt die Nachfrage nach Microns fortschrittlichem Speicher. Micron gab eine starke KI-getriebene Prognose für 2024-2025 bekannt und knüpfte seinen Wachstumsausblick direkt an die Leistung von Nvidia.

Die von uns ausgewählten Aktien sind hier nicht die wichtigsten Informationen. Konzentrieren wir sich stattdessen darauf, das Symbol auszuwählen, das am stärksten mit dem Symbol korreliert, das wir als Referenz, d. h. als Grundlage für unsere Hypothese, verwenden. In unserem Fall war es NVDA, aber es kann jedes Symbol sein, das zu Ihrer Hypothese passt.

Wir wollen KEINE Aktien, die eine außergewöhnlich hohe Korrelation mit NVDA und eine niedrige Korrelation zwischen ihnen aufweisen. Stattdessen suchen wir nach Aktien, die eine hohe Korrelation zu NVDA aufweisen und die auch untereinander eine relativ hohe Korrelation haben. In gewissem Sinne wollen wir eine korrelierte Gruppe von Aktien um unsere Referenz herum, denn diese Eigenschaft passt zu unserer Hypothese, wenn wir mit der Rosinenpickerei beginnen: Wir suchen nach einem korrelierten Korb.

Wir sind auf der Suche nach einer solchen Pearson-Korrelationsmatrix.

	NVDA	MCHP	MPWR	MU
NVDA	1.000000	0.916887	0.894362	0.897219
MCHP	0.916887	1.000000	0.877042	0.941977
MPWR	0.894362	0.877042	1.000000	0.852675
MU	0.897219	0.941977	0.852675	1.000000

Tabelle 1. Pearson-Korrelationsmatrix zwischen NVDA, MCHP, MPWR und MU

Diese Daten lassen sich leichter als Seaborn Heatmap anzeigen.

import seaborn as sns
sns.heatmap(corr_matrix, annot=True, cmap="coolwarm")

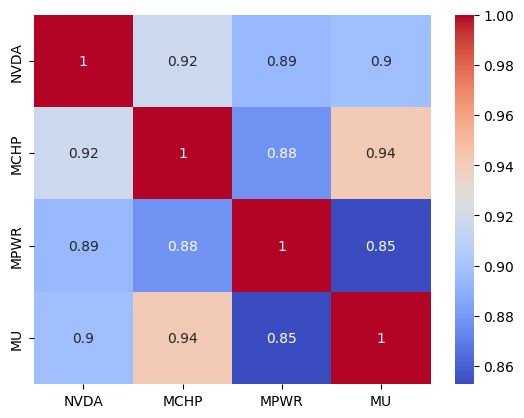
Abb. 3 Pearson-Korrelationsmatrix für NVDA, MCHP, MPWR und MU in Form einer Seaborn-Heatmap

Es ist zu beachten, dass es zwar keine außergewöhnlich hohe Korrelation zwischen MCHP, MPWR und MU mit NVDA gibt, aber alle drei sind mäßig miteinander korreliert.

Beachten Sie, dass wir beim Handel Ticks von vier Vermögenswerten benötigen, um die Spread-Berechnung durchzuführen, die unsere Einstiegs- und Ausstiegspunkte definiert. Das ist der Hauptgrund, warum wir überhaupt erst mit der Auswahl hochliquider Vermögenswerte begonnen haben. Wir wollen keine illiquiden Vermögenswerte, die mehr als ein paar Sekunden lang aus dem Takt geraten oder von unserem OnTick-Ereignishandler abweichen könnten (siehe unten).

Sobald wir diesen korrelierten Korb definiert haben, führen wir den Engle-Granger-Kointegrationstest durch, um das Kointegrationsniveau der Paare zu bewerten, und auch den Johansen-Kointegrationstest, um das Kointegrationsniveau des Korbs, d. h. das Kointegrationsniveau der Gruppe von Vermögenswerten, zu überprüfen. Eine genauere Beschreibung dieser beiden Tests finden Sie im vorangegangenen Artikel.

Aus dem Johansen-Eigenvektor erhält man dann die Portfolio-Hedge-Ratios.

🧮 Portfolio-Gewichte (Johansen-Eigenvektor):

MU 2.699439

NVDA1.000000

MPWR-1.877447

MCHP-2.505294

Der Johansen-Eigenvektor ist eine Liste von Zahlen, eine für jede Aktie in Ihrer Gruppe, die Ihnen das Gewicht oder die Bedeutung jeder Aktie bei der Aufrechterhaltung der durch den Johansen-Test ermittelten stabilen Beziehung angibt. Diese Gewichte sorgen dafür, dass die kombinierten Kursbewegungen der Aktien, wenn Sie sie in einem bestimmten Verhältnis kaufen oder verkaufen, ein einigermaßen vorhersehbares, mehr oder weniger stabiles Muster ergeben.

Diese Werte werden verwendet, um unser Auftragsvolumen auszugleichen und unser Marktrisiko zu minimieren. Denken Sie daran, dass wir bei statistischen Arbitragestrategien immer die Marktneutralität anstreben. Wir können ein gewichtetes Portfolio als eine Verbesserung gegenüber dem einfachen Paarhandel betrachten, bei dem wir von jedem Symbol gleichzeitig eine Einheit kaufen/verkaufen.

Sie finden diese Portfoliogewichte unter den globalen Variablen unseres Beispiel-Expert Advisors.

// Global variables
string symbols[] = {"MU", "NVDA", "MPWR", "MCHP"}; // Asset symbols
double weights[] = {2.699439, 1.000000, -1.877447, -2.505294}; // Johansen eigenvector

NVDA hat den Wert 1.0, weil wir uns für die Normalisierung auf der Symbolliste ersten Vermögenswert in unserem Python-Code (beigefügt), die NVDA ist. Die Normalisierung ermöglicht uns eine relative Interpretation der anderen Werte. Sie können jedes andere Symbol in der Python-Liste normalisieren. Es handelt sich um eine willkürliche Bezugnahme.

# === FIRST COINTEGRATION VECTOR ===
v = johansen_result.evec[:, 0]
# v = v / v[-1]  # Normalize on symbols list last asset
v = v / v[0] # Normalize on symbols list first asset

Nun können wir die multivariate Streuung auf Stationarität testen.

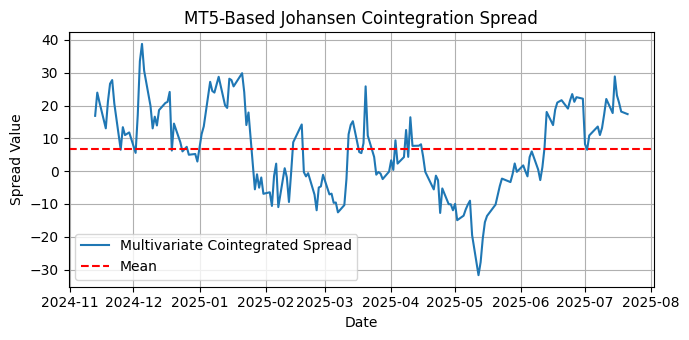
Abb. 4 Darstellung der multivariaten kointegrierten Streuung für NVDA, MCHP, MPWR und MU

Die visuelle Inspektion der multivariaten Streuung ist ein probates Mittel, um ihre Eignung für eine Strategie zur Mittelwertumkehr zu beurteilen. Die visuelle Inspektion ermöglicht eine schnelle Einschätzung der Streuung der Verteilung um den Mittelwert, der Streuung zurück zum Mittelwert und ihrer möglichen Stationarität. Das Fehlen eines sichtbaren Trends ist ein starkes Indiz für Stationarität, ebenso wie das Fehlen von Saisonalität.

Die visuelle Inspektion ist jedoch nicht ausreichend und kann nicht für automatisierte Modelle und Portfolio-Updates verwendet werden. Zum Glück gibt es den Augmented Dickey Fuller („ADF“) und den Kwiatkowski-Phillips-Schmidt-Shin („KPSS“) Test, die uns hier helfen können.

Verwenden Sie die ADF- und KPSS-Tests, um zu bestätigen, dass die Streuung mittelwertumkehrend ist.

# Augmented Dickey-Fuller Test
from statsmodels.tsa.stattools import adfuller

adf_result = adfuller(spread, regression='c')  # 'ct' for trend and constant
print("ADF Test on Spread:")
print(f"  ADF Statistic : {adf_result[0]:.4f}")
print(f"  p-value       : {adf_result[1]:.4f}")
print(f"  Critical Values:")
for key, value in adf_result[4].items():
    print(f"    {key}: {value:.4f}")

if adf_result[1] < 0.05:
    print("\n✅ The cointegrated spread is stationary (reject the null hypothesis).")
else:
    print("\n❌ The cointegrated spread is NOT stationary (fail to reject the null hypothesis).")

ADF-Test auf Streuung:

  ADF-Statistik: -3,2331  

  p-Wert: 0.0181

  Kritische Werte:

    1%: -3.4704    

    5%: -2.8791

    10%: -2.5761

✅ Der kointegrierte Spread ist stationär (Ablehnung der Nullhypothese).

# KPSS Test
from statsmodels.tsa.stattools import kpss

def run_kpss(series, regression='c'):
    statistic, p_value, lags, crit_values = kpss(series, regression=regression, nlags='auto')
    print("KPSS Test on Spread:")

KPSS-Test zur Streuung:

  KPSS-Statistik: 0.4142  

  p-Wert: 0.0710  

  Verwendete Verzögerungen: 8

  Kritische Werte:

    10%: 0.347    

    5%: 0.463    

    2.5%: 0.574

    1%: 0.739

✅ Der kointegrierte Spread ist stationär (keine Ablehnung der Stationarität).

Dieser Schritt ist entscheidend. Ohne ein stationäres Spread fiele unsere Hypothese der mittleren Umkehr in sich zusammen. Ohne ein stationäres Spread können die Preise weiter auseinander gehen, und wir werden mit baumelnden Positionen zurückgelassen, die durch die Mittelwertumkehr nie richtig geschlossen werden. Die Behauptung, dass der Spread stationär ist, ist bei dieser Art von Strategie entscheidend.

Später, wenn unser statistischer Arbitrage-Rahmen sich weiterentwickelt, werden wir unser Portfolio auf automatisierte Weise rotieren. Daher ist es von entscheidender Bedeutung, dass wir diese Stationaritätstests in unserem Instrumentarium haben, da wir uns nicht nur auf die visuelle Beurteilung von Diagrammen verlassen können. 

Die Beispielimplementierung

Unsere Beispielimplementierung beginnt mit der Festlegung von Schwellenwerten für Eintritts- und Austrittspunkte in Form von Standardabweichungen vom Mittelwert.

// Input parameters
input double EntryThreshold = 2.0;      // Entry threshold (standard deviations)
input double ExitThreshold = 0.3;       // Exit threshold (standard deviations)
input double LotSize = 10.0;            // Fixed lot size per leg
input int LookbackPeriod = 252;         // Lookback for moving average/standard deviation
input int Slippage = 3;                 // Max allowed slippage

Die Standard-Losgröße von 10,0 Einheiten sollte die Überprüfung der Portfoliogewichte in den Aufträgen beim Backtesting erleichtern.

Die maximal erlaubte Slippage ist hier fast schon dekorativ, denn wir entwickeln für den durchschnittlichen Einzelhändler, und die maximal erlaubte Slippage ist normalerweise eine Funktion, die nur für professionelle Handelskonten verfügbar ist. Aber es schadet nicht, sie für künftige Verbesserungen bereitzuhalten. Der Parameter wird vom Broker-Server einfach ignoriert, wenn das Handelskonto diese Funktion deaktiviert hat.

Der für die Berechnung des gleitenden Durchschnitts und der Standardabweichungen verwendete Rückblickzeitraum kann derselbe sein, der auch für die Korrelations- und Kointegrationstests verwendet wird, dies ist jedoch keine Voraussetzung. Sobald wir eine Kointegration auf dem täglichen Zeitrahmen für die letzten sechs Monate festgestellt haben, ist es kein Problem, auf dem stündlichen Zeitrahmen für einen zweiwöchigen Rückblick zu operieren, z. B.. Das System ist flexibel genug, um Experimente zuzulassen, und in dieser Flexibilität liegt eine Fülle von Möglichkeiten.

Einige Hinweise zu bestimmten Code-Funktionen.

OnInit()

// Check if all symbols are available
   for(int i = 0; i < ArraySize(symbols); i++)
     {
      if(!SymbolSelect(symbols[i], true))
        {
         Print("Error: Symbol ", symbols[i], " not found!");
         return(INIT_FAILED);
        }
     }

Wir prüfen, ob alle Symbole in unserem Korb auf Market Watch für die Kursanfrage verfügbar sind.

// Set a timer for spread, mean, and stdev calculations
   EventSetTimer(1); // one second

Wir setzen einen Timer für die Berechnung von Spread, Mittelwert und Standardabweichung außerhalb der Funktion OnTick(). Das liegt daran, dass, wie Sie wahrscheinlich wissen, der OnTick-Ereignishandler an das Chart/Symbol gebunden ist, bei dem der EA gestartet wird. Solange es keine Aktualisierungen für dieses Symbol gibt, wird der OnTick nicht ausgelöst. Wir wollen nicht von diesen Aktualisierungen abhängig sein. Durch die Verwendung eines Timers, in diesem Fall mit einem Intervall von einer Sekunde, können wir sicher sein, dass wir in diesem Intervall nach neuen Kursen suchen werden. Wir gehen von einer passiven Kursaktualisierung zu einer aktiven Kursaktualisierung über. 

OnTimer()

void OnTimer(void)
  {
// Calculate current spread value
   currentSpread = CalculateSpread();
// Update spread buffer (rolling window)
   static int barCount = 0;
   if(barCount < LookbackPeriod)
     {
      spreadBuffer[barCount] = currentSpread;
      barCount++;
      return; // Wait until buffer is filled
     }
// Shift buffer (remove oldest value, add newest)
   for(int i = 0; i < LookbackPeriod - 1; i++)
      spreadBuffer[i] = spreadBuffer[i + 1];
   spreadBuffer[LookbackPeriod - 1] = currentSpread;
// Calculate mean and standard deviation using custom functions
   spreadMean = CalculateMA(spreadBuffer, LookbackPeriod);
   spreadStdDev = CalculateStdDev(spreadBuffer, LookbackPeriod, spreadMean);
  }

In der Ereignisbehandlung von OnTimer wird der Rückblickzeitraum des Charts durchlaufen, um die Spanne, den Mittelwert und die Standardabweichung zu berechnen.

OnTick()

void OnTick()
  {
// Trading logic
   if(!tradeOpen)
     {
      // Check for entry signal (spread deviates from mean)
      if(currentSpread > spreadMean + EntryThreshold * spreadStdDev)
        {
         // Short spread (sell MU/NVDA, buy MPWR/MCHP)
         ExecuteTrade(ORDER_TYPE_SELL);
         tradeOpen = true;
        }
      else
         if(currentSpread < spreadMean - EntryThreshold * spreadStdDev)
           {
            // Buy spread (buy MU/NVDA, sell MPWR/MCHP)
            ExecuteTrade(ORDER_TYPE_BUY);
            tradeOpen = true;
           }
     }
   else
     {
      // Check for exit signal (spread reverts to mean)
      if((currentSpread <= spreadMean + ExitThreshold * spreadStdDev) &&
         (currentSpread >= spreadMean - ExitThreshold * spreadStdDev))
        {
         CloseAllTrades();
         tradeOpen = false;
        }
     }
// Display spread in chart
   Comment(StringFormat("Spread: %.2f | Mean: %.2f | StdDev: %.2f", currentSpread, spreadMean, spreadStdDev));
  }

OnTick() enthält nur die Handelslogik. Wenn wir nicht auf dem Markt sind (!tradeOpen()) und ein Handelssignal haben, kaufen oder verkaufen wir entsprechend den Portfoliogewichten, die wir aus dem Johansen-Eigenvektor erhalten haben.

ExecuteTrade(ENUM_ORDER_TYPE orderType)

//+------------------------------------------------------------------+
//| Execute trade with normalized integer lots                |
//+------------------------------------------------------------------+
void ExecuteTrade(ENUM_ORDER_TYPE orderType)
  {
   double volumeArray[];
   ArrayResize(volumeArray, ArraySize(symbols));
   if(!NormalizeVolumeToIntegerLots(volumeArray, symbols, weights, LotSize))
     {
      Print("Volume normalization failed!");
      return;
     }
   for(int i = 0; i < ArraySize(symbols); i++)
     {
      ENUM_ORDER_TYPE legType = (weights[i] > 0) ? orderType :
                                (orderType == ORDER_TYPE_BUY ? ORDER_TYPE_SELL : ORDER_TYPE_BUY);
      trade.PositionOpen(symbols[i], legType, volumeArray[i], 0, 0, 0, "NVDA Coint");
     }
  }

(...)

//+------------------------------------------------------------------+
//| Normalize volumes to integer lots                             |
//+------------------------------------------------------------------+
bool NormalizeVolumeToIntegerLots(double &volumeArray[], const string &symbols_arr[], const double &weights_arr[], double baseLotSize)
  {
   MqlTick tick; // Structure to store bid/ask prices
   double totalDollarExposure = 0.0;
   double dollarExposures[];
   ArrayResize(dollarExposures, ArraySize(symbols_arr));
// Step 1: Calculate dollar exposure for each leg
   for(int i = 0; i < ArraySize(symbols_arr); i++)
     {
      if(!SymbolInfoTick(symbols_arr[i], tick)) // Get latest bid/ask
        {
         Print("Failed to get price for ", symbols_arr[i]);
         return false;
        }
      // Use bid price for short legs, ask for long legs
      double price = (weights_arr[i] > 0) ? tick.ask : tick.bid;
      dollarExposures[i] = MathAbs(weights_arr[i]) * price * baseLotSize;
      totalDollarExposure += dollarExposures[i];
     }
// Step 2: Convert dollar exposure to integer lots
   for(int i = 0; i < ArraySize(symbols_arr); i++)
     {
      double ratio = dollarExposures[i] / totalDollarExposure;
      double targetDollarExposure = ratio * totalDollarExposure;
      // Get min/max lot size and step for the symbol
      double minLot = SymbolInfoDouble(symbols_arr[i], SYMBOL_VOLUME_MIN);
      double maxLot = SymbolInfoDouble(symbols_arr[i], SYMBOL_VOLUME_MAX);
      double lotStep = SymbolInfoDouble(symbols_arr[i], SYMBOL_VOLUME_STEP);
      // Get current price again (for lot calculation)
      if(!SymbolInfoTick(symbols_arr[i], tick))
         return false;
      double price = (weights_arr[i] > 0) ? tick.ask : tick.bid;
      double lots = targetDollarExposure / price;
      lots = MathFloor(lots / lotStep) * lotStep; // Round down to nearest step
      // Clamp to broker constraints using custom Clamp()
      volumeArray[i] = Clamp(lots, minLot, maxLot);
     }
   return true;
  }

Der Backtest

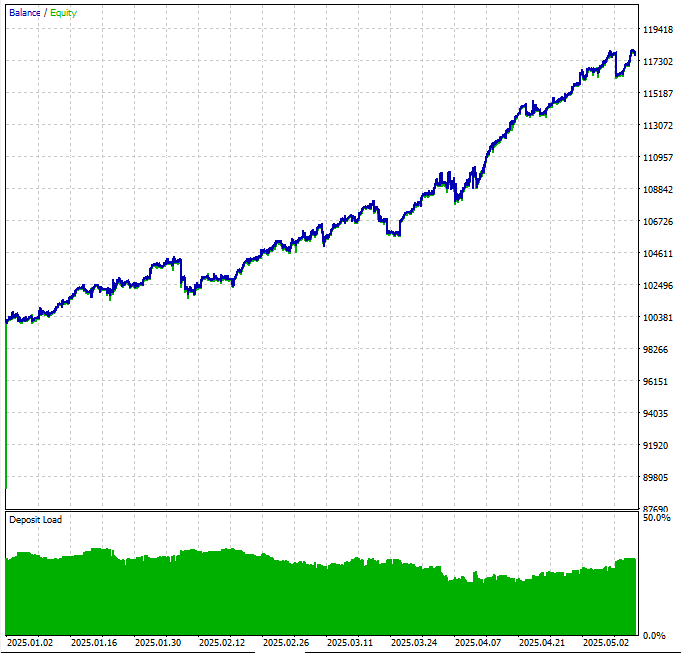
Abb. 5 Kapitalkurve aus dem Backtest des kointegrierten Nasdaq-Korbs für die ersten fünf Monate des Jahres 2025 im täglichen Zeitrahmen

Die Kapitalkurve zeigt, dass unsere Hypothese realisierbar ist, auch wenn sie eine noch nicht umgesetzte Geldmanagementstrategie erfordert, um einige aggressive Drawdowns zu vermeiden.

Abb. 6. Backtest-Zusammenfassung des kointegrierten Nasdaq-Korbs für die ersten fünf Monate des Jahres 2025 im täglichen Zeitrahmen

Wie Sie sehen können, ist die Qualität unserer Preisentwicklung sehr gering, aber das ist das, was wir für diese vier Aktiensymbole kostenlos haben, also arbeiten wir mit dem, was wir haben. Bei der Umsetzung dieser Strategie für den Handel mit echtem Geld wird dringend empfohlen, dass Sie auf mehr Qualität in der Kursentwicklung achten.

Abb. 7. Backtest-Einträge nach Perioden aus dem Backtest des kointegrierten Nasdaq-Korbs für die ersten fünf Monate des Jahres 2025 auf dem täglichen Zeitrahmen

Abb. 8 Haltezeiten aus dem Backtest des kointegrierten Nasdaq-Korbs für die ersten fünf Monate des Jahres 2025 im täglichen Zeitrahmen

Die durchschnittliche Haltedauer der Positionen von ~20 Minuten scheint gut zu sein, da wir die ein- bis zweisekündigen Haltedauern der Positionen aus unserem ersten (und gescheiterten) Versuch, der im ersten Teil dieses Artikels beschrieben wurde, vermeiden können.

Abb. 9 MFE und MAE aus dem Backtest des kointegrierten Nasdaq-Korbs für die ersten fünf Monate des Jahres 2025 im täglichen Zeitrahmen

Kointegration über Aktien hinaus

Dies sind einigermaßen zufriedenstellende Ergebnisse für unseren ersten kointegrierten Aktienkorb für denselben Sektor. Mit einigen Verbesserungen, wie z. B. einer ordnungsgemäßen Geldverwaltung und einer besseren Datenqualität für Optimierungen, können wir davon ausgehen, dass wir einen vernünftigen Kandidaten haben, den wir ein paar Wochen lang in einem Demokonto testen können.

Aber wie Sie wahrscheinlich schon erkannt haben, handelt es sich um eine sehr allgemeine Lösung, bei der wir nur eine sehr kleine Untergruppe von Nasdaq-Aktien in einer noch kleineren Kombination von Rückblickperiode und Zeitrahmen des Kointegrationstests verwenden. Das heißt, wir verwenden vier Symbole, die in den letzten sechs Monaten im täglichen Zeitrahmen auf Kointegration getestet wurden. Wenn Sie beginnen, diese Parameter zu kombinieren, finden Sie möglicherweise Dutzende von Möglichkeiten, die Ihre Aufmerksamkeit verdienen.

Darüber hinaus sind Sie nicht auf Nasdaq-Aktien oder gar auf Aktien beschränkt. Sie können Multi-Asset-Kointegrationstests zwischen Aktien und börsengehandelten Fonds oder Branchenindizes durchführen.

Einige Beispiele

Hier sind einige Beispiele für Kointegration, die für die letzten sechs Monate (180 Tage) im täglichen Zeitrahmen getestet wurden.

Gold-ETFs

symbols = ['AAAU', 'USGO', 'BGLD']

1. AAAU – Goldman Sachs Physical Gold ETF

„AAAU ist ein börsengehandelter Fonds, der die Entwicklung des Goldpreises widerspiegeln soll. Der Fonds hält physische Goldbarren, die in sicheren Tresoren gelagert werden, und die Anleger können ihre Anteile gegen echtes Gold zurückgeben (unter bestimmten Bedingungen). Der AAAU ist so konzipiert, dass er ein direktes Engagement in den Goldpreisen mit minimalem Tracking Error und ohne Derivate bietet.“

2. USGO – Abrdn Physical Gold Shares ETF

„USGO ist ein physisch unterlegter Gold-ETF, der von Aberdeen Investments verwaltet wird. Wie AAAU zielt es darauf ab, den Preis von Goldbarren zu verfolgen, indem es zugewiesenes physisches Gold hält, das in sicheren Tresoren gelagert wird. Es bietet Anlegern eine einfache und kosteneffiziente Möglichkeit, ein Engagement in Gold einzugehen, ohne selbst eine physische Lieferung vorzunehmen.“

3. BGLD – FT Vest Gold Strategy Target Income ETF

„BGLD ist ein aktiv verwalteter Goldstrategie-ETF, der darauf abzielt, Erträge und ein Engagement in Gold zu bieten. Im Gegensatz zu AAAU und USGO hält BGLD nicht direkt physisches Gold. Stattdessen nutzt er eine Kombination aus goldbezogenen Derivaten (wie Futures und Optionen) und einkommensgenerierenden Strategien, um gezielte Renditen mit goldähnlichem Verhalten zu erzielen und sich auf die Erwirtschaftung monatlicher Erträge zu konzentrieren.“

Index(['AAAU', 'USGO', 'BGLD'], dtype='object')

Ergebnisse des Engle-Granger-Kointegrationstests:

AAAU und USGO | p-Wert: 0.1322

AAAU und BGLD | p-Wert: 0.0209

USGO und BGLD | p-Wert: 0.0144

Am meisten kointegriertes Paar (Engle-Granger): USGO und BGLD | p-Wert: 0.0144

Denken Sie daran, dass der Engle-Granger-Test nur paarweise Beziehungen prüft. Dieser Test zeigt nicht die Wechselwirkungen des gesamten Korbes an, die der Johansen-Test erfasst.

Ergebnisse des Johansen-Tests (Trace-Statistik):

Anzahl der Beobachtungen: 119

Anzahl der Variablen: 3

Rang 0: Trace Stat = 30.21 | 5% CV = 29.80 | Signifikant

Rang 1: Trace Stat = 10,65 | 5% CV = 15,49 | Nicht signifikant

Rang 2: Trace Stat = 4,25 | 5% CV = 3,84 | Signifikant

Mit dem Johansen-Test können wir die Anzahl der kointegrierenden Beziehungen im gesamten Korb auf jedem Rang sehen.

Bei Rang 0 übersteigt die Trace-Statistik (30,21) den kritischen Wert von 5 % (29,80), was darauf hindeutet, dass mindestens ein kointegrierender Vektor existiert. Auf Rang 1 ist der Test nicht signifikant, aber auf Rang 2 ist er wieder signifikant (4,25 > 3,84), was auf eine zweite kointegrierende Beziehung hindeutet.

Das Engle-Granger-Ergebnis zeigt, dass AAAU-BGLD (p = 0,0209) und USGO-BGLD (p = 0,0144) beide signifikant stärker kointegriert sind als AAAU-USGO (p = 0,1322), was darauf hindeutet, dass zwei unabhängige kointegrierende Vektoren zwischen den drei Vermögenswerten existieren und wahrscheinlich eine starke und stabile langfristige Gleichgewichtsbeziehung im Korb besteht.

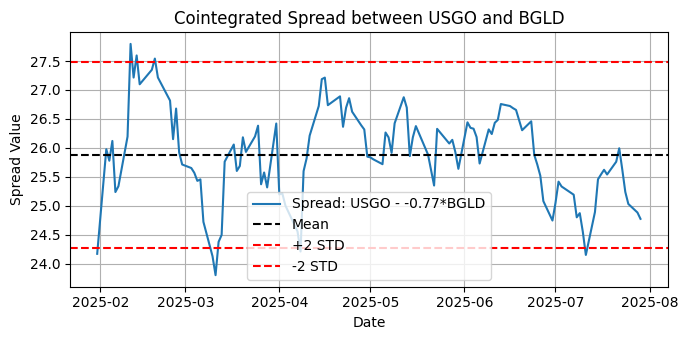
Abb. 10 Darstellung des kointegrierten Spreads zwischen USGO und BGLD für die letzten sechs Monate im täglichen Zeitrahmen

ADF-Test auf Streuung:

  ADF-Statistik: -3,7659 

  p-Wert: 0.0033

  Kritische Werte:

    1%: -3.4870   

    5%: -2.8864

    10%: -2.5800

✅ Der Spread ist stationär (Ablehnung der Nullhypothese).

KPSS-Test zur Streuung:

  KPSS-Statistik: 0.1910 

  p-Wert: 0.1000 Verwendete Verzögerungen: 5

  Kritische Werte:

    10%: 0.347   

    5%: 0.463   

    2.5%: 0.574

    1%: 0.739

✅ Die Streuung ist stationär (keine Ablehnung der Stationarität).

Wir sehen, dass BGLD eine starke kointegrierende Beziehung sowohl zu AAAU als auch zu USGO aufweist, und da sich die Stationarität des Spreads zwischen USGO und BGLD bestätigt, wissen wir, dass wir einen starken Hinweis darauf haben, dass diese Vermögenswerte gute Kandidaten für einen goldbezogenen kointegrierten Korb sind.

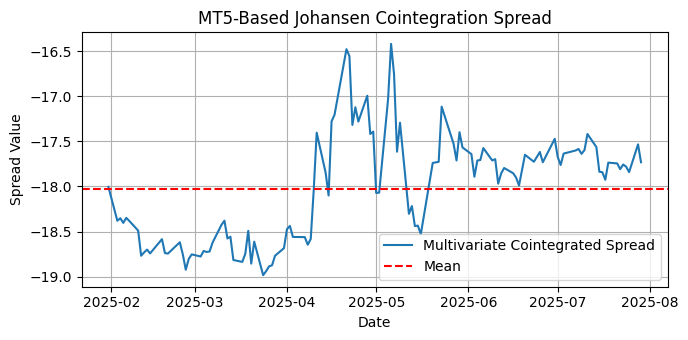
Abb. 11 Darstellung des multivariaten kointegrierten Spreads zwischen AAAU, USGO und BGLD für die letzten sechs Monate im täglichen Zeitrahmen

Deren kointegriertes Spread ist jedoch für diesen Zeitraum und diese Zeitspanne nicht stationär. 

ADF-Test auf Streuung:

  ADF-Statistik: -2,7186 

  p-Wert: 0.0709

  Kritische Werte:

    1%: -3.4870   

    5%: -2.8864

    10%: -2.5800

Der kointegrierte Spread ist NICHT stationär (die Nullhypothese kann nicht zurückgewiesen werden).

KPSS-Test zur Streuung:

  KPSS-Statistik: 0.9687 

  p-Wert: 0,0100 Verwendete Verzögerungen: 6

  Kritische Werte:

    10%: 0.347   

    5%: 0.463   

    2.5%: 0.574

    1%: 0.739

❌ Der kointegrierte Spread ist NICHT stationär (Ablehnung der Stationarität).

Silber-ETFs

symbols = ['CEF', 'SLV', 'SIVR']

1. CEF – Sprott Physical Gold and Silver Trust

„Ein geschlossener Trust, der sowohl physische Gold- als auch Silberbarren hält. Er wird mit einem Auf- oder Abschlag auf seinen Nettoinventarwert gehandelt und ist kein reiner Silberwert, wodurch er sich strukturell von SLV und SIVR unterscheidet.“

2. SLV – iShares Silver Trust

„Ein physisch unterlegter Silber-ETF, der die Entwicklung des Preises von Silberbarren widerspiegeln soll. Er ist einer der größten und liquidesten Silber-ETFs“.

3. SIVR – Aberdeen Physical Silver Shares ETF

„Ähnlich wie SLV ist SIVR ein physisch besicherter Silber-ETF, hat aber in der Regel eine niedrigere Kostenquote, was ihn für kostenbewusste Anleger attraktiv macht.

Index(['CEF', 'SLV', 'SIVR'], dtype='object')

Ergebnisse des Engle-Granger-Kointegrationstests:

CEF und SLV | p-Wert: 0.6092
CEF und SIVR | p-Wert: 0.6109

SLV und SIVR | p-Wert 0.0000

Am meisten kointegriertes Paar (Engle-Granger): SLV und SIVR | p-Wert 0.0000

Ergebnisse des Johansen-Tests (Trace-Statistik):

Anzahl der Beobachtungen: 121

Anzahl der Variablen: 3

Rang 0: Trace Stat = 62,67 | 5% CV = 29,80 | Signifikant

Rang 1: Trace Stat = 7,20 | 5% CV = 15,49 | Nicht signifikant

Rang 2: Trace Stat = 1,95 | 5% CV = 3,84 | Nicht signifikant

Auf Rang 0 (62,67 > 29,80) ist die Trace-Statistik signifikant, was auf das Vorhandensein mindestens eines kointegrierenden Vektors zwischen den drei silberbezogenen ETFs hinweist. Die Ränge 1 und 2 sind jedoch nicht signifikant, was darauf hindeutet, dass es nur eine stabile langfristige Beziehung gibt, die von diesem Korb geteilt wird.

Die Engle-Granger-Ergebnisse zeigen, dass das Paar SLV und SIVR ein starkes Kointegrationssignal aufweist (p = 0,0000). Die CEF scheint weder mit dem SLV noch mit dem SIVR kointegriert zu sein (p > 0,6). Ein erneuter Blick auf das Johansen-Ergebnis lässt den Schluss zu, dass die Kointegration wahrscheinlich auf die enge Beziehung zwischen SLV und SIVR zurückzuführen ist, da es sich bei beiden um nahezu perfekte Substitute handelt, die beide physisch unterlegte Silber-ETFs sind, was ihre Kointegration rechtfertigt. CEF ist auf Silber ausgerichtet, bietet aber auch ein Engagement in Gold und ist ein geschlossener Fonds. Er verhält sich also anders.

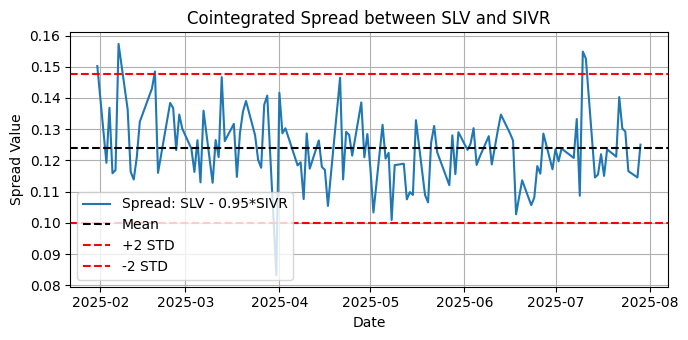
Abb. 12 Darstellung des kointegrierten Spreads zwischen SLV und SIVR für die letzten sechs Monate im täglichen Zeitrahmen

ADF-Test auf Streuung:

  ADF-Statistik: -11,0833 

  p-Wert: 0.0000

  Kritische Werte:

    1%: -3.4861   

    5%: -2.8859

    10%: -2.5798

✅ Der Spread ist stationär (Ablehnung der Nullhypothese).

KPSS-Test zur Streuung:

  KPSS-Statistik: 0.6246 

  p-Wert: 0,0204 Verwendete Verzögerungen: 1

  Kritische Werte:

    10%: 0.347   

    5%: 0.463   

    2.5%: 0.574

    1%: 0.739

❌ Der Spread ist NICHT stationär (Ablehnung der Stationarität).

Hier haben wir festgestellt, dass der kointegrierte Spread zwischen SLV und SIVR nach dem ADF-Test stationär, nach dem KPSS-Test jedoch nicht stationär ist.  Ein ähnliches Beispiel haben wir im vorigen Artikel gesehen, mit der entsprechenden Erklärung in der Dokumentation der Bibliothek von statsmodels, wie diese Art von widersprüchlichen Ergebnissen zu interpretieren ist.

„Fall 1: Beide Tests kommen zu dem Ergebnis, dass die Reihe nicht stationär ist – Die Reihe ist nicht stationär

Fall 2: Beide Tests kommen zu dem Ergebnis, dass die Reihe stationär ist – Die Reihe ist stationär

Fall 3: KPSS weist auf Stationarität und ADF auf Nicht-Stationarität hin – Die Reihe ist trendstabil. Der Trend muss entfernt werden, um die Reihe streng stationär zu machen. Die verzerrte Reihe wird auf Stationarität geprüft.

Fall 4: KPSS weist auf Nicht-Stationarität und ADF auf Stationarität hin – Die Reihe ist differenzstationär. Die Differenzierung ist zu verwenden, um Reihen stationär zu machen. Die Reihe der Differenzen wird auf Stationarität geprüft.“

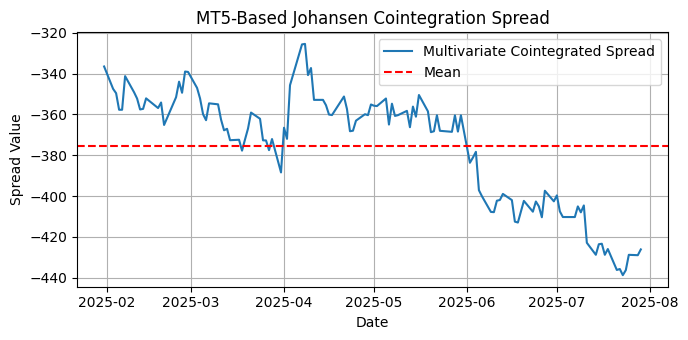
Abb. 13 Darstellung des multivariaten kointegrierten Spreads zwischen CEF, SLV und SIVR für die letzten sechs Monate im täglichen Zeitrahmen

Für den multivariaten kointegrierten Spread, d. h. den gesamten Korb, zeigt die Grafik, dass der Spread für diesen Zeitraum und diesen Zeitrahmen NICHT mittelwertumkehrend ist. Der Stationaritätstest wird dies bestätigen.

ADF-Test auf Streuung:

  ADF-Statistik: -0,8780 

  p-Wert: 0.7951

  Kritische Werte:

    1%: -3.4865   

    5%: -2.8862

    10%: -2.5799

Der kointegrierte Spread ist NICHT stationär (die Nullhypothese kann nicht zurückgewiesen werden).

KPSS-Test zur Streuung:

  KPSS-Statistik: 1.3918 

  p-Wert: 0.0100 

  Verwendete Verzögerungen: 6

  Kritische Werte:

    10%: 0.347   

    5%: 0.463   

    2.5%: 0.574

    1%: 0.739

❌ Der kointegrierte Spread ist NICHT stationär (Ablehnung der Stationarität).

Was bedeutet das? Sicherlich haben wir hier keinen geeigneten Korb von silberbezogenen ETFs, aber wir haben zwei hochgradig kointegrierte ETFs (SLV und SIVR), die für den Paarhandel, der das Thema unseres ersten Artikels dieser Serie ist, einen genauen Blick wert sein könnten.

Diese beiden Beispiele sollen verdeutlichen, dass bei der Suche nach kointegrierten Vermögenswerten für statistische Arbitragemöglichkeiten Experimentieren und Forschung die Schlüsselwörter sind. Außerdem sollten wir nicht vergessen, dass Statistiken allein kein Ersatz für Ihr Verständnis des Sektors und Ihre Marktkenntnisse sind.

Schlussfolgerung

Dieser Artikel beschreibt ein Beispiel für einen Expert Advisor, der mit einer kleinen Gruppe kointegrierter Aktien getestet wird. Es handelt sich um den zweiten von zwei Artikeln, in denen die gebräuchlichsten statistischen Maße für die statistische Arbitrage-Portfolioerstellung beschrieben werden: Korrelationskoeffizienten und Kointegrationsbewertung sowie Spread-Stationaritätstests.

Es ist erwähnenswert, dass diese Art von Strategie, obwohl sie für Währungen (Devisenpaare) aufgrund der seltenen Bedingung, dass mehr als zwei kointegrierte Währungen gefunden werden, fast unmöglich anzuwenden ist, auch für Indizes, ETFs und Rohstoffe gilt. 

Da wir nun über die grundlegenden Instrumente für die kointegrationsbasierte Portfoliobildung verfügen, könnten die logischen nächsten Schritte die Implementierung einer Echtzeit-Portfolio-Rotation sein, die sich in Zukunft zu einem maschinellen Lernansatz weiterentwickeln könnte.

Referenzen

Marianna Brunetti & Roberta De Luca, 2023. „Pre-selection in cointegration-based pairs trading,“ in Statistical Methods & Applications, Springer; Società Italiana di Statistica, vol. 32(5), pages 1611-1640, December.

Hinweis

* Obwohl die Analogie wahrscheinlich von der Pearson'schen Zufallsbewegung abgeleitet ist, sollte sie nicht mit der Pearson'schen Zufallsbewegung verwechselt werden, dem von dem englischen Mathematiker beschriebenen und benannten stochastischen Prozess.

Angehängte Datei	Beschreibung
corr_pearson.ypng	Diese Datei ist ein Jupyter-Notizbuch mit Python-Code. Das Skript führt den Pearson-Korrelationstest durch.
coint_stocks_ETFs.ypnb	Diese Datei ist auch ein Jupyter-Notizbuch, das Python-Code enthält. Das Skript führt die Engle-Granger- und Johansen-Kointegrationstests sowie die ADF- und KPSS-Stationaritätstests durch.
Nasdaq_NVDA_Coint.mql5	Diese Datei enthält den in den Backtests verwendeten Beispiel-Expert Advisor.
Nasdaq_NVDA_Coint.ini	Diese Datei ist eine Konfigurationseinstellungsdatei (.ini), die die im Backtest verwendeten Parameter enthält.
Nasdaq_NVDA_Coint.NVDA.Daily.20250101_20250515.021.ini	Diese Datei ist auch eine Konfigurationseinstellungsdatei (.ini), die die im Backtest verwendeten Optimierungsparameter enthält.