MQL5-Assistenz-Techniken, die Sie kennen sollten (Teil 74): Verwendung von Ichimoku-Mustern und ADX-Wilder mit überwachtem Lernen

Einführung

Im letzten Artikel haben wir uns die Indikatorenkombination Ichimoku und ADX-Wilder als komplementäres S/R- und Trendinstrumentenpaar angesehen. Wie üblich haben wir diese in einem von einem Assistenten zusammengestellten Expert Advisor getestet und uns 10 verschiedene Signalmuster angesehen. Bei dieser Indikatorenkombination waren die meisten von ihnen in der Lage, ein Jahr lang gewinnbringend weiterzugehen, nachdem sie im Vorjahr Tests und Optimierungen durchgeführt hatten. Allerdings gab es 3, die dies nicht zufriedenstellend taten, und zwar Pattern-0, Pattern-1 und Pattern-5. Im Anschluss an diesen Artikel untersuchen wir daher, ob überwachtes Lernen einen Unterschied in ihrer Leistung bewirken kann. Unser Ansatz besteht darin, die Signale jedes dieser Muster als einfachen Eingangsvektor in ein neuronales Netz zu rekonstruieren, wodurch das neuronale Netz im Wesentlichen zu einem zusätzlichen Filter für das Signal wird.

Das Netzwerk

Unsere Wahl für ein überwachtes Lernmodell ist ein Netzwerk, das auf einem Spectral Mixture Kernel basiert. Dies wird durch die folgende Formel definiert:

wobei:

• τ: Zeitunterschied zwischen zwei Punkten.
• Q Anzahl der Spektralkomponenten.
• wi: Gewicht der i-ten Komponente (Amplitude).
• li: Längenskala der i-ten Komponente (steuert das Abklingen).
• fi: Frequenz der i-ten Komponente (Schwingungsrate).

Wir verwenden diesen spektralen Mischungskernel, um eine Eingangsschicht für ein einfaches neuronales Netz zu definieren, dem weitere PyTorch-Linear-Schichten folgen. Die Art von Ebene, die wir erstellen und verwenden, ist eine spektrale Mischungsebene. Wir implementieren diese Schicht und die darauf folgenden Regressornetzwerke in Python wie unten angegeben:

class DeepSpectralMixtureRegressor(nn.Module):
    def __init__(self, input_dim=2, num_components=96):
        super().__init__()
        self.smk = DeepSpectralMixtureLayer(input_dim, num_components)
        feature_dim = input_dim * num_components  # 2 * 96 = 192

        self.head = nn.Sequential(
            nn.Linear(feature_dim, 1024),
            nn.ReLU(),
            nn.Linear(1024, 512),
            nn.ReLU(),
            nn.Linear(512, 256),
            nn.ReLU(),
            nn.Linear(256, 128),
            nn.ReLU(),
            nn.Linear(128, 1)  # <--- Removed sigmoid!
        )

    def forward(self, x):
        features = self.smk(x)
        output = self.head(features)
        return output

Einige Forschungsarbeiten legen nahe, dass unser spezieller Mischungskernel am Eingang dazu dient, Merkmale aus den Eingabedaten zu extrahieren, wobei der Regressionskopf der nachfolgenden Schichten am Ausgang in Fällen geeignet ist, in denen das Modell ein Regressor ist, wie bei unserer Sigmoid-Verwendung gezeigt. Bei unserer Wahl des spektralen Mischungskerns führt die erste Schicht eine periodische Datenmodellierung durch, während die Regressor-/Kopfschichten die Frequenzen, Varianzen und Gewichte des Netzes lernen. Unser Implementierungsansatz ist am besten für Regressionsaufgaben mit oszillierenden Mustern in den Eingabedaten geeignet. Außerdem verbindet es die Flexibilität neuronaler Netze mit den Konzepten des Gaußschen Prozesses.

Unser Netzwerk trägt den Namen „DeepSpectralMixtureRegressor“. Und wir engagieren uns für eine modulare Architektur, die aus zwei Teilen besteht. Merkmalsextraktion und Regression. Der erste Teil der Merkmalsextraktion wird speziell von der Funktion „DeepSpectralMixtureLayer“ durchgeführt, deren Code im Folgenden aufgeführt wird:

class DeepSpectralMixtureLayer(nn.Module):
    def __init__(self, input_dim, num_components):
        super().__init__()
        self.num_components = num_components
        hidden = 512  # Wider hidden layers

        # Go deeper with 4 layers
        def make_subnet():
            return nn.Sequential(
                nn.Linear(input_dim, hidden),
                nn.ReLU(),
                nn.Linear(hidden, hidden),
                nn.ReLU(),
                nn.Linear(hidden, hidden),
                nn.ReLU(),
                nn.Linear(hidden, num_components),
            )

        self.freq_net = make_subnet()
        self.var_net = nn.Sequential(*make_subnet(), nn.Softplus())
        self.weight_net = nn.Sequential(*make_subnet(), nn.Softplus())

    def forward(self, x):
        mu = self.freq_net(x)
        v = self.var_net(x)
        w = self.weight_net(x)

        expanded = x.unsqueeze(2)
        mu = mu.unsqueeze(1)
        v = v.unsqueeze(1)
        w = w.unsqueeze(1)

        x_cos = torch.cos(2 * np.pi * expanded * mu)
        x_exp = torch.exp(-v * expanded**2)
        features = w * x_exp * x_cos

        return features.flatten(start_dim=1)

Unsere obige Funktion lernt Häufigkeiten, Varianzen und Gewichte durch den Einsatz von neuronalen Netzen. Dies gewährleistet die Positivität, da für die Varianzen und Gewichte eine Soft-Plus-Aktivierung verwendet wird. Der Regressionskopf bildet die extrahierten Merkmale auf eine einzelne Ausgabe mit sigmoidaler Aktivierung für begrenzte Regression oder binäre Klassifizierung ab. Das Argument für diese Architektur ist die Anpassungsfähigkeit, wobei sich das Modell an verschiedene Datenmuster anpassen lässt. Dies kann sie für Aufgaben wie die Zeitreihenprognose geeignet machen, insbesondere wenn es periodische Komponenten in den Reihen gibt. Dies führt dazu, dass sowohl das neuronale Netz als auch der kernelbasierte Ansatz genutzt werden.

Wilson et al. (2013) weisen darauf hin, dass spektrale Mischungskerne in Bibliotheken wie GPyTorch als Kovarianzfunktionen für die Verwendung im Gauß-Prozess zur Modellierung periodischer Muster implementiert werden können, wenn sie die Spektraldichte als eine Mischung von Komponenten darstellen. Unser Ansatz adaptiert dieses Konzept in ein neuronales Netz, indem wir die Kernelkomponenten Frequenz, Varianz und Gewichte durch neuronale Netze parametrisieren. Dies ermöglicht eine erlernte, datengesteuerte Merkmalsextraktion, die besonders für Probleme wie Zeitreihenprognosen relevant sein kann, bei denen periodische/oszillatorische Muster in den Daten vorhanden sind. Dies wurde von Sebastian Callh in seinem Blog-Beitrag über spektrale Mischungskerne hervorgehoben. Ein Teil der Inspiration, den Kernel so anzuwenden, wie wir es tun, stammt auch aus dieser GPyTorch Dokumentation. 

Kurz gesagt, statt eines festen Kerns von Parametern verwendet unser Modell neuronale Netze, um Frequenzen zu lernen, die mit mu bezeichnet werden, Varianzen, die wir mit v bezeichnen, und Gewichte, die wir mit w symbolisieren. Dieser Ansatz ermöglicht die Anpassung an verschiedene Datenmuster. Die erste Ebene der Merkmalsextraktion berechnet die Merkmale anhand der Formel „w * exp(-v * x^2) * cos(2πμx)“, die die Periodizität durch Kosinusmodulation mit der Sanftheit eines exponentiellen Abfalls erfasst. Der modulare Aufbau mit der Merkmalsextraktion als eine Schicht über DeepSpectralMixtureLayer und einem Regressionskopf als separate Komponente erhöht die Flexibilität. Der Regressionskopf seinerseits ist ein tiefes, vollständig verbundenes Netz, das mit Hilfe der Sigmoid-Aktivierung Merkmale auf einen einzigen Ausgang abbildet. Dies macht es, wie bereits erwähnt, geeignet für begrenzte Regression oder binäre Klassifizierung.

Lassen Sie uns einen tiefen Einblick in unseren obigen Code nehmen, um zu sehen, wie all das, was wir oben beschrieben haben, umgesetzt wird. Unser Code beginnt mit Standardimporten für PyTorch und verwandte Bibliotheken. Diese Importe bieten Werkzeuge für Tensoroperationen, die Konstruktion neuronaler Netze, Optimierung, Datenverarbeitung und den ONNX-Export des trainierten Modells zur Inferenz in Plattformen von Drittanbietern. Dies ist der Schlüssel zum Aufbau, zur Schulung und zum Einsatz des Modells. Dies ist, wie zu erwarten, nicht nur für die PyTorch-basierte Entwicklung, sondern für das maschinelle Lernen im Allgemeinen von grundlegender Bedeutung. Für die Anleitung ist es wichtig, die Kompatibilität zwischen den Versionen von PyTorch und ONNX zu gewährleisten, um ein effizientes Laden der Daten während des Trainings zu ermöglichen.

Anschließend legen wir die Initialisierung unserer „DeepSpectralMixtureLayer“ fest. Damit werden drei neuronale Netze definiert, nämlich das Frequenznetz, das Varianznetz und das Gewichtsnetz. Jedes der Netze bildet die Eingabe auf die Anzahl der Komponentenausgänge ab, wobei eine Soft-Plus-Aktivierung verwendet wird, die sicherstellt, dass die Varianzen und Gewichte positiv bleiben, wie es die Kernel-Formulierung verlangt. Dies ist wichtig, weil diese Netze den spektralen Mischungskern separat parametrisieren, um die datengesteuerte Merkmalsextraktion mit dem Gauß-Prozess zu ermöglichen. Der Parameter „num_components“ steuert den „Feature-Richness“. Dieser Parameter, num_components, kann je nach Komplexität der Aufgabe angepasst werden. Durch die Verwendung der Soft-Plus-Aktivierung werden negative Werte vermieden, die zu numerischer Instabilität führen können.

Dann legen wir unsere Vorwärtspassfunktion für das Netz fest. Diese Funktion berechnet die spektralen Mischungsmerkmale mit der oben im Text erwähnten Formel. Es formt die Eingaben und Parameter so um, dass sie an den Regressionskopf übertragen werden können. Durch die Anwendung von Kosinus- und Exponentialfunktionen wird die Ausgabe für die Regressionsschichten abgeflacht. Diese Kerntransformation ahmt den spektralen Mischungskern nach. Die Form der Eingabe „x“ sollte dem Format (batch_size, input_dim) entsprechen. Auch die Überprüfung der numerischen Stabilität von „exp“ kann die Begrenzung der Varianz v erfordern. Der Parameter „num_components“ kann auf die gewünschte Merkmalsdimensionalität abgestimmt werden.

Nachdem die Ebene der Merkmalsextraktion oben behandelt wurde, können wir uns nun dem Regressor zuwenden, der Klasse, die bei der Definition des Modells aufgerufen wird. Sein übergeordnetes Ziel ist die Kombination der oben beschriebenen spektralen Mischungsschicht mit einem voll vernetzten Kopf. Dieser Kopf bildet Kernel-Merkmale über Sigmoid auf eine einzelne Ausgabe im Bereich 0-1 ab. Der Architekturkopf kann je nach Komplexität der Aufgabe angepasst werden, indem die Größe/Anzahl der Schichten erhöht wird. Sigmoid kann für unbegrenzte Regressionsaufgaben entfernt werden. Schließlich haben wir auch eine Vorwärtsfunktion, genau wie bei der Spektralschichtfunktion oben. Die Eingaben werden durch die spektrale Mischungsschicht geleitet, um Merkmale zu extrahieren, und dann durch den Kopf, um die endgültige Ausgabe zu erhalten. Diese Vorwärtsfunktion definiert den kompletten Vorwärtsdurchlauf und ermöglicht ein durchgängiges Training und Inferenz.

Die Größe der Eingabe „x“ sollte mit der Eingabegröße übereinstimmen. Eine geeignete Verlustfunktion wie BCE kann angesichts der Verwendung von Sigmoid für die Aktivierung geeignet sein. Der Parameter „num-components“ ist sehr empfindlich für die Leistung des Netzes, und sein Wert bestimmt die Gesamtzahl der Spektralkomponenten. Höhere Werte erhöhen die Aussagekraft, bergen jedoch die Gefahr einer Überanpassung. Es kann sinnvoll sein, mit einem Wert von 64 zu beginnen und ihn dann je nach Komplexität der Daten zu verändern. Die Überwachung der Überanpassung beim Training kann angesichts der übermäßigen Aussagekraft der spektralen Mischungsschicht entscheidend sein. Regulierung und frühzeitiges Aufhören können dazu beitragen, dies zu mildern.

Die Analyse der gelernten Parameter mu, v und w kann helfen, periodische Muster zu verstehen, wie sie in diesen GPyTorch-Beispielen zu sehen sind. Im Vergleich zu typischen Gauß“schen Prozessmodellen fehlt es unserem Ansatz an Unsicherheitsschätzungen. Zusätzliche Maßnahmen, die dies quantifizieren, könnten ergänzt werden. Schließlich kann ein Vorwärtsdurchlauf rechenintensiv sein, insbesondere wenn der Parameter „num-components“ sehr groß ist oder hochdimensionale Eingaben verwendet werden. Dies ist eine zusätzliche Überlegung, die bei der Feinabstimmung und Optimierung dieses Modells berücksichtigt werden muss.

Indikator-Implementierungen

Von den Signalmustern, die wir im letzten Artikel getestet haben, waren die meisten in der Lage, einigermaßen gut vorwärts zu gehen, mit Ausnahme von Pattern-0, Pattern-1 und Pattern-5. Zur Erinnerung: Wir haben 10 Signalmuster für das Symbol GBP USD für das Jahr 2023 getestet/optimiert. Wir haben den 30-Minuten-Zeitrahmen verwendet, im Gegensatz zu unserem typischen 4-Stunden-Zeitrahmen, da die Signale des Ichimoku auf großen Zeitrahmen normalerweise nicht so häufig auftreten. Unser Vorwärtsgang war wie immer auf das Jahr 2024 gerichtet. Obwohl 7 der 10 Muster in der Lage waren, im Jahr 2025 den Vorwärtstest mit Gewinn zu bestehen, lief unser Test nur über 2 Jahre, sodass weitere Sorgfalt und Tests auf längere Zeiträume der historischen Preise ist immer für den Leser empfohlen, bevor das, was hier vorgestellt wird, kann auf eine Live-Handelsumgebung genommen werden.

Vor diesem Hintergrund wollen wir uns nun ansehen, wie die Indikatorfunktionen von Ichimoku und ADX Wilder in Python implementiert sind und wie ihre Funktionen zur Extraktion von Merkmalen für die Pattern-0, -1 und -5 aussehen.

Ichimoku in Python

Wir implementieren die Ichimoku-Funktion in Python wie folgt:

def Ichimoku(df, tenkan_period: int = 9, kijun_period: int = 26, senkou_span_b_period: int = 52, displacement: int = 26) -> pd.DataFrame:
    """
    Calculate Ichimoku Kinko Hyo components and append them to the input DataFrame.

    The components are:
        - Tenkan-sen (Conversion Line)
        - Kijun-sen (Base Line)
        - Senkou Span A (Leading Span A)
        - Senkou Span B (Leading Span B)
        - Chikou Span (Lagging Span)

    Args:
        df (pd.DataFrame): DataFrame with 'high', 'low', and 'close' columns.
        tenkan_period (int): Lookback period for Tenkan-sen (default 9).
        kijun_period (int): Lookback period for Kijun-sen (default 26).
        senkou_span_b_period (int): Lookback period for Senkou Span B (default 52).
        displacement (int): Forward displacement of Senkou spans and backward shift of Chikou span (default 26).
        
    Returns:
        pd.DataFrame: Input DataFrame with added Ichimoku columns.
    """
    # Input validation
    required_cols = {'high', 'low', 'close'}
    if not required_cols.issubset(df.columns):
        raise ValueError("DataFrame must contain 'high', 'low', and 'close' columns")
    if not all(p > 0 for p in [tenkan_period, kijun_period, senkou_span_b_period, displacement]):
        raise ValueError("All period values must be positive integers")

    result_df = df.copy()

    # Tenkan-sen (Conversion Line)
    high_tenkan = result_df['high'].rolling(window=tenkan_period).max()
    low_tenkan = result_df['low'].rolling(window=tenkan_period).min()
    result_df['Tenkan_sen'] = (high_tenkan + low_tenkan) / 2

    # Kijun-sen (Base Line)
    high_kijun = result_df['high'].rolling(window=kijun_period).max()
    low_kijun = result_df['low'].rolling(window=kijun_period).min()
    result_df['Kijun_sen'] = (high_kijun + low_kijun) / 2

    # Senkou Span A (Leading Span A)
    result_df['Senkou_Span_A'] = ((result_df['Tenkan_sen'] + result_df['Kijun_sen']) / 2).shift(displacement)

    # Senkou Span B (Leading Span B)
    high_span_b = result_df['high'].rolling(window=senkou_span_b_period).max()
    low_span_b = result_df['low'].rolling(window=senkou_span_b_period).min()
    result_df['Senkou_Span_B'] = ((high_span_b + low_span_b) / 2).shift(displacement)

    # Chikou Span (Lagging Span)
    result_df['Chikou_Span'] = result_df['close'].shift(-displacement)

    return result_df

Unsere oben kodierte Funktion berechnet die Indikatorkomponenten und fügt sie dem Eingabedatenrahmen mit den Standardperioden 9 für Tenkan-sen, 26 für Kijun-sen, 26 für die Verschiebung und 52 für die Senkou-Spanne B hinzu. Die erste Zeile unseres Codes zielt darauf ab, unsere Eingabe zu überprüfen. Dadurch wird sichergestellt, dass der Datenrahmen die erforderlichen Preisspalten enthält und dass die Periodenparameter positiv sind, um Berechnungsfehler zu vermeiden. Dieser Schritt ist entscheidend für die Datenintegrität und die Vermeidung von Laufzeitfehlern. Unsere Indikatorfunktion muss mit gültigen Laufzeitdaten arbeiten. Es ist immer die beste Praxis, Eingaben vor der Verarbeitung zu validieren, um fehlende Daten oder ungültige Parameter ordnungsgemäß zu behandeln.

Nachdem die Validierung abgeschlossen ist, fahren wir mit der Berechnung des Tenkan-sen fort. Unser Code berechnet den Durchschnitt des höchsten Hochs und des niedrigsten Tiefs der vergangenen „Tenkan-Periode“. In der Regel verwenden wir die Periodenlänge 9, die als kurzfristiger Trendindikator dient. Dieser Puffer hilft bei der Signalisierung potenzieller Umkehrungen, wenn der Kijun-sen überschritten wird, und er kann bei kurzfristigen Handelsentscheidungen hilfreich sein, da er die jüngsten Kursbewegungen widerspiegelt. Die „Tenkan-Periode“ kann angepasst werden, um die gewünschte Empfindlichkeit gegenüber kurzfristigen Kursbewegungen zu erreichen. Bei kürzeren Zeiträumen ist die Empfindlichkeit größer, bei längeren Zeiträumen geringer.

Als Nächstes berechnen wir den Kijun-sen-Puffer. Ähnlich wie der Tenkan-sen wird er über einen längeren Zeitraum berechnet, normalerweise 26. Dies stellt einen mittelfristigen Trendindikator dar. Der Kijun-sen ist wichtig, weil er die Trendrichtung bestätigt und als Unterstützung/Widerstand dient. Im Vergleich zum Tenkan-sen vermittelt er eine etwas stabilere Sicht auf die Märkte. Er ist für die mittelfristige Analyse nützlich, und in der Tat können Überkreuzungen mit dem Tenkan-sen als Handelssignale dienen.

Dann berechnen wir die Senkou-Spanne A. Dies ist einfach der Durchschnitt von Tenkan-sen und Kijun-sen, der um die Verschiebungsperiode nach vorne verschoben wird. Diese Verschiebung beträgt in der Regel 26. Dieser Puffer bildet eine Begrenzung der Kumo-Wolke. Sie ist von entscheidender Bedeutung, da sie künftige Unterstützungen/Widerstände anzeigt und eine vorausschauende Sicht auf die Trendanalyse ermöglicht, wie unter hier dargelegt. Es ist wichtig, die relative Position der Wolke zum Kurs zu beobachten, wobei ein Kurs oberhalb der Wolke auf eine Aufwärtstrend hindeutet, während ein Kurs unterhalb der Wolke ein Aufwärtstrend bedeuten würde.

Als Nächstes folgt die Berechnung der Senkou-Spanne B. Hier wird einfach der Mittelwert des höchsten Hochs und des niedrigsten Tiefs über einen Zeitraum von normalerweise 52 Jahren gebildet und nach vorne verschoben, wodurch die zweite Grenze der Kumo-Wolke gebildet wird. Der Senkou B bietet eine längerfristige Sicht auf Unterstützung/Widerstand und verbessert die Trenderkennung, insbesondere in größeren Zeitrahmen. Als Orientierungshilfe kann die Wolkendicke, der Abstand zwischen Senkou A und B, als Indikator für die Volatilität dienen. Daher können dickere Wolken auf stärkere Unterstützung/Widerstand hindeuten.

Schließlich berechnen wir den letzten Puffer, die Chikou-Spanne. Bei diesem Puffer handelt es sich einfach um den Schlusskurs, der um einen Zeitraum (in der Regel 26 Balken) nach hinten verschoben wird, um die aktuellen Preise mit denen der Vergangenheit vergleichen zu können. Er dient somit als Trendbestätigung dafür, ob die aktuellen Preise über oder unter den vergangenen Preisen liegen, was für die Bestätigung oder Validierung eines Trends nützlich ist. Der Hauptzweck des Chikou besteht also in der Bestätigung, und dazu ist es oft erforderlich, dass genügend historische Daten vorhanden sind, da Verschiebungen und lange Mittelungszeiträume verwendet werden.

ADX-Wilder in Python

Nachdem der Ichimoku in Python definiert wurde, wenden wir uns nun dem ADX Wilder zu. Diese Funktion berechnet den ADX nach der Methode von Wilder. Wie beim Ichimoku fügen wir dem Eingabepreisrahmen zusätzliche Puffer für ADX, +DI und -DI hinzu. Dieser Indikator verwendet eine Standardperiodenlänge von 14, die zur Anpassung an das Ichimoku oder zur Erzielung einer höheren Preissensibilität angepasst werden kann; wir verwenden diese 14 Standardperiode dennoch. Wir implementieren dies in Python wie folgt:

def ADX_Wilder(df, period: int = 14) -> pd.DataFrame:
    """
    Calculate the Average Directional Index (ADX) using Wilder's method and 
    append the ADX, +DI, and -DI columns to the input DataFrame.

    ADX measures trend strength, while +DI and -DI measure trend direction.
    
    Args:
        df (pd.DataFrame): DataFrame with 'high', 'low', and 'close' columns.
        period (int): The lookback period to use. Default is 14.
        
    Returns:
        pd.DataFrame: Input DataFrame with 'ADX', '+DI', and '-DI' columns.
    """
    if not all(col in df.columns for col in ['high', 'low', 'close']):
        raise ValueError("DataFrame must contain 'high', 'low', and 'close' columns")
    if period <= 0:
        raise ValueError("Period must be a positive integer")

    result_df = df.copy()

    # Calculate directional movements
    up_move = result_df['high'].diff()
    down_move = result_df['low'].diff()

    plus_dm = np.where((up_move > down_move) & (up_move > 0), up_move, 0)
    minus_dm = np.where((down_move > up_move) & (down_move > 0), down_move, 0)

    # Calculate True Range (TR)
    high_low = result_df['high'] - result_df['low']
    high_close = np.abs(result_df['high'] - result_df['close'].shift(1))
    low_close = np.abs(result_df['low'] - result_df['close'].shift(1))
    tr = np.maximum(high_low, np.maximum(high_close, low_close))

    # Apply Wilder's smoothing
    atr = pd.Series(tr).rolling(window=period).mean()
    plus_di = 100 * pd.Series(plus_dm).rolling(window=period).sum() / atr
    minus_di = 100 * pd.Series(minus_dm).rolling(window=period).sum() / atr
    dx = 100 * np.abs(plus_di - minus_di) / (plus_di + minus_di)
    adx = dx.rolling(window=period).mean()

    result_df['+DI'] = plus_di
    result_df['-DI'] = minus_di
    result_df['ADX'] = adx

    return result_df

Das erste, was wir tun, ist, die Eingabe der Funktion zu überprüfen. Damit ist wie immer sichergestellt, dass die notwendigen Kursspalten vorhanden sind und auch der Indikatorzeitraum gültig ist, um Berechnungsfehler zu vermeiden. Dies alles ist wichtig für die Datenintegrität und den Betrieb mit gültigen Daten. Auch sollten Fälle fehlender Daten angemessen behandelt werden. Nach der Validierung werden als Nächstes die Berechnungen zur Bewegungsrichtung durchgeführt. Dies sind die Unterschiede in den Hochs und Tiefs, die die Plus-DM- und Minus-DM-Bewegungen bestimmen. Sie markieren die Stärke von Aufwärts- und Abwärtstrends, eine Information, die für die Einschätzung/Analyse der Trendrichtung von entscheidender Bedeutung ist. Es ist wichtig, dass genügend historische Daten vorhanden sind, um genaue Richtungsunterschiede berechnen zu können. Die Daten sollten auch auf Lücken überwacht werden.

Anschließend berechnen wir die wahren Reichweiten. Diese werden als der größte Wert des aktuellen Hochs minus des Tiefs oder des Hochs minus des vorherigen Schlusskurses oder des Tiefs minus des vorherigen Schlusskurses berechnet. Die absoluten Werte dieser Unterschiede werden aus Gründen der Konsistenz übernommen. Dieser Bereich normalisiert die Richtungsbewegungen, indem er sie gemäß den Anforderungen der ADX-Berechnung über verschiedene Vermögenswerte hinweg vergleichbar macht. Es ist unbedingt darauf zu achten, dass keine Daten im Preisdatenrahmen fehlen, um Fehler durch „NaN“ in den Berechnungen zu vermeiden.

Anschließend berechnen wir die geglättete wahre Spanne mit Hilfe eines gleitenden Mittelwerts. Wir glätten auch die Puffer für +DM und –DM und normalisieren die positiven und negativen Richtungsindikatoren so, dass sie für eine prozentuale Darstellung auf 100 skaliert werden. Der Richtungsindex DX, ein Maß für die Trendstärke, ist somit die absolute Differenz zwischen +DM und –DM und wird durch deren Summe normalisiert. Der Hauptindikator ADX schließlich ist eine Glättung des DX über den Indikatorzeitraum, der in unserem Fall 14 beträgt. Dieser endgültige Output dient dann als Maß für die Stärke eines vorherrschenden Trends.

Um den letzten Artikel zu rekapitulieren: Der ADX liefert Werte der Trendstärke im Bereich von 0 bis 100, wobei alles über 25 oft als Zeichen für einen starken Trend gilt. Andererseits werden Werte unter 20 als Zeichen für schwache oder junge Trends gewertet. Die Indices +DI und –DI quantifizieren die Stärke von Aufwärts- bzw. Abwärtstrends, wobei die Differenz zwischen den beiden Indizes als Handelssignal dienen kann. Die verwendete Periodenlänge von 14 kann ebenfalls an die erforderliche Empfindlichkeit angepasst werden, wobei kleinere Werte zu einer früheren Erkennung von Signalen und fraktalen Punkten führen, während längere Perioden weniger volatil sind.

Bei der Anwendung des spektralen Mischungskerns über ein regressives Netzwerk, wie wir es nach der Einleitung definiert haben, nehmen wir unsere Eingaben von diesen beiden Indikatoren in Form eines einfachen 2-Dim-Vektors. In einigen früheren Artikeln haben wir die Möglichkeit erwogen und untersucht, die Größe des Eingangsvektors für unsere überwachten Lernnetze zu erhöhen, indem wir die verschiedenen Signale jedes Musters in einen booleschen Wert, 0 oder 1, zerlegen. Dies führte zu besseren Ergebnissen beim Training/Optimierung, die beim Vorwärtsgehen nicht zustande kamen. Derzeit werden also die Signale und Muster eines jeden Indikators zu einem einzigen booleschen Wert kombiniert, nicht seine Bestandteile. Beim 2-dim werden in jeder Dimension Signale von 2 Indikatoren kombiniert. Das erste Dim dient ausschließlich der Bestätigung eines Aufwärtssignals, das zweite der Bestätigung eines Abwärtssignals.

Merkmal-0

Wir wenden die 3 zurückgebliebenen oder schlecht funktionierenden Merkmale auf unser Netzwerk von Merkmal-0, Merkmal-1 und Merkmal-5 an. Wir implementieren Merkmal-0 in Python wie folgt;

def feature_0(df):
    """
    """
    feature = np.zeros((len(df), 2))
    
    feature[:, 0] = ((df['close'].shift(1) < df['Senkou_Span_A'].shift(1)) &
                     (df['close'] > df['Senkou_Span_A']) &
                     (df['ADX'] >= 25.0)).astype(int)
    
    feature[:, 1] = ((df['close'].shift(1) > df['Senkou_Span_A'].shift(1)) &
                     (df['close'] < df['Senkou_Span_A']) &
                     (df['ADX'] >= 25.0)).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Unsere Funktion beginnt mit der Erstellung eines leeren NumPy-Arrays. Dieses Array der Merkmale ist so groß, dass es dem Eingabedatenrahmen in Zeilen entspricht, ihm werden jedoch 2 Spalten zugewiesen. Dies ermöglicht die Erzeugung von Signalen und stellt sicher, dass keine Restwerte die Ausgabe beeinflussen. Dann weisen wir den Wert für die erste Spalte dieses Datenrahmens zu, der eine Prüfung für das Aufwärtssignal darstellt. Gemäß den Bedingungen, die wir im letzten Artikel beschrieben haben, wird jeder Zeile in dieser Spalte des NumPy-Arrays eine 1 zugewiesen, wenn der vorherige Schlusskurs unter der Senkou-Spanne A liegt, der aktuelle Schlusskurs über der aktuellen Senkou-Spanne A liegt und der ADX mindestens 25 beträgt. Das Erkennen eines Aufwärtskreuzes, bei dem der Kurs über die Senkou-Spanne A steigt, deutet häufig auf einen Aufwärtstrend hin. Ein ADX von mindestens 25 stellt sicher, dass das Signal während eines starken Trends auftritt, um Fehlsignale bei schwachen Märkten zu vermeiden.

Diese Zuweisung, die NumPy-Arrays verwendet, bedeutet, dass die Zuweisungen über mehrere Zeilen hinweg gleichzeitig ausgeführt werden. Einer der Hauptgründe, warum die Entwicklung und das Training von Modellen in Python so gut funktioniert. Anschließend weisen wir den Wert für die Abwärts-Spalte allen Zeilen des Arrays zu. Hier setzen wir den Spaltenwert in jeder Zeile auf 1, wenn der vorherige Schlusskurs über der vorherigen Senkou-Spanne A liegt, der aktuelle Schlusskurs unter der aktuellen Senkou-Spanne A liegt und der ADX-Hauptpuffer mindestens 25 beträgt. Er erkennt das Abwärtskreuz, der ein Zeichen für einen potenziellen Abwärtstrend ist. Der ADX-Filter stellt sicher, dass die Trendstärke das Signal unterstützt.

Nachdem wir die Werte für auf- und abwärts zugewiesen haben, erzwingen wir für die ersten beiden Zeilen unseres Merkmalsarrays den Wert Null, da sie keine Werte und somit ein NaN haben. Wir konnten unser Netzwerk nur auf dieses Muster trainieren, exportierten es als „74_0.onnx“ und importierten es in eine nutzerdefinierte Signalklasse eines MQL5 Expert Advisors. Im letzten Artikel konnte dieses spezielle Muster nicht sinnvoll vorwärts laufen, aber wenn wir es jetzt mit dem Netzwerk testen, das als zusätzlicher Filter für die Eingangssignale des Indikators dient, erhalten wir den folgenden Bericht;

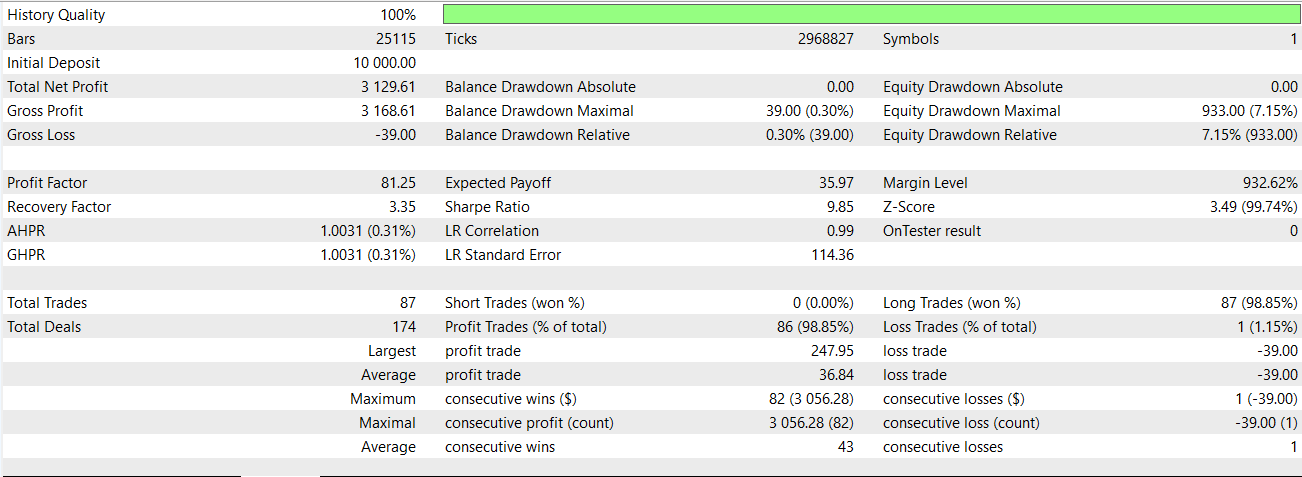
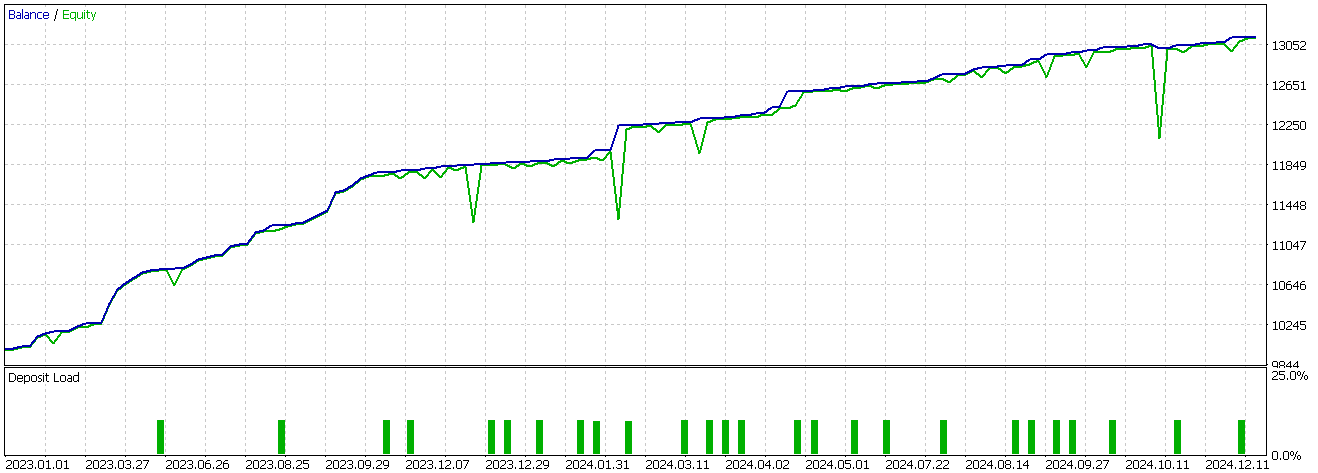
Es scheint eine Trendwende eingetreten zu sein, allerdings nur bei Kaufposition, und wie immer sind unsere Tests vom Datenumfang her sehr begrenzt und haben daher nur explorativen Charakter. Ein charttechnisches Kaufsignal für Merkmal-0 sieht in einem Chart wie folgt aus;

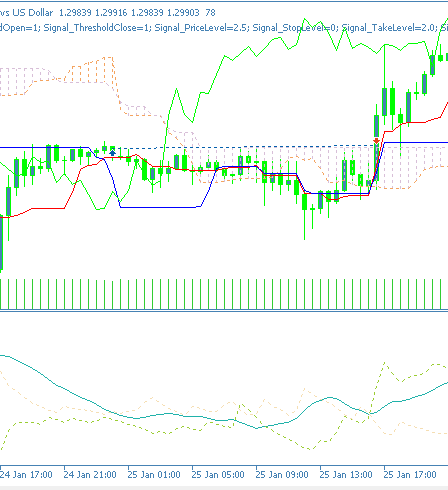
Merkmal-1

Ein weiteres Merkmal/Muster, das im letzten Artikel eine miserable Leistung aufwies, war Merkmal-1. Wir implementieren dies in Python wie folgt:

def feature_1(df):
    """

    """
    feature = np.zeros((len(df), 2))
    
    feature[:, 0] = ((df['Tenkan_sen'].shift(1) < df['Kijun_sen'].shift(1)) &
                     (df['Tenkan_sen'] > df['Kijun_sen']) &
                     (df['ADX'] >= 20.0)).astype(int)
    
    feature[:, 1] = ((df['Tenkan_sen'].shift(1) > df['Kijun_sen'].shift(1)) &
                     (df['Tenkan_sen'] < df['Kijun_sen']) &
                     (df['ADX'] >= 20.0)).astype(int)    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Wir initialisieren unser das Ausgabe-Array für das Ziel, auch feature genannt, wieder mit Nullen und passen die Größe an den Eingabedatenrahmen an. Es gibt 2 Spalten für jeden Datenpunkt in der Zeile, um Auf- und Abwärtssignale zu protokollieren. In der ersten Spalte vergeben wir eine 1 für ein bestätigtes Aufwärtssignal, wenn der vorherige Tenkan-sen unter dem vorherigen Kijun-sen liegt und der aktuelle Tenkan-sen jetzt über dem aktuellen Kijun-sen liegt und der ADX mindestens 20 beträgt. Dieses Signal erfasst das Aufwärtskreuz zwischen Tenkan-sen und Kijun-sen. Es handelt sich um ein mittelfristiges Signal, das den Beginn größerer Trends vorwegnimmt, weshalb der ADX nicht bei 25 liegen muss, sondern auch bei 20 liegen kann.

Das Abwärtssignal, das für die zweite Spalte jeder Zeile des NumPy-Arrays eingegeben wird, wird bei spiegelbildlichen Bedingungen zu unserem Abwärtssignal auf 1 gesetzt. Wenn der vorherige Tenkan-Sen über dem Kijun-Sen lag und der aktuelle Tenkan-Sen unter dem aktuellen Kijun-Sen liegt und der ADX mindestens 20 beträgt und steigt, dann haben wir ein Abwärtssignal. Bei unserem Ansatz müssen mehrere Signalpunkte erfüllt sein, bevor ein Wert ungleich Null zugewiesen wird. Dies ist streng und steht in klarem Gegensatz zu der oben erwähnten Alternative mit größeren Arrays, die einzelne Indikatorsignale als Bits und Eingänge für unser Netzwerk verwenden. Abschließend weisen wir den ersten beiden Zeilen unseres NumPy-Arrays Nullen zu, da wir den Verschiebungsvergleich verwendet haben und einige Datenpunkte NaN-Werte anstelle von Indikatordaten haben. Der Testbericht für Pattern-1 für den GBP USD im 30-Minuten-Zeitrahmen über 2 Jahre, den Zug und den Test, lautet wie folgt;

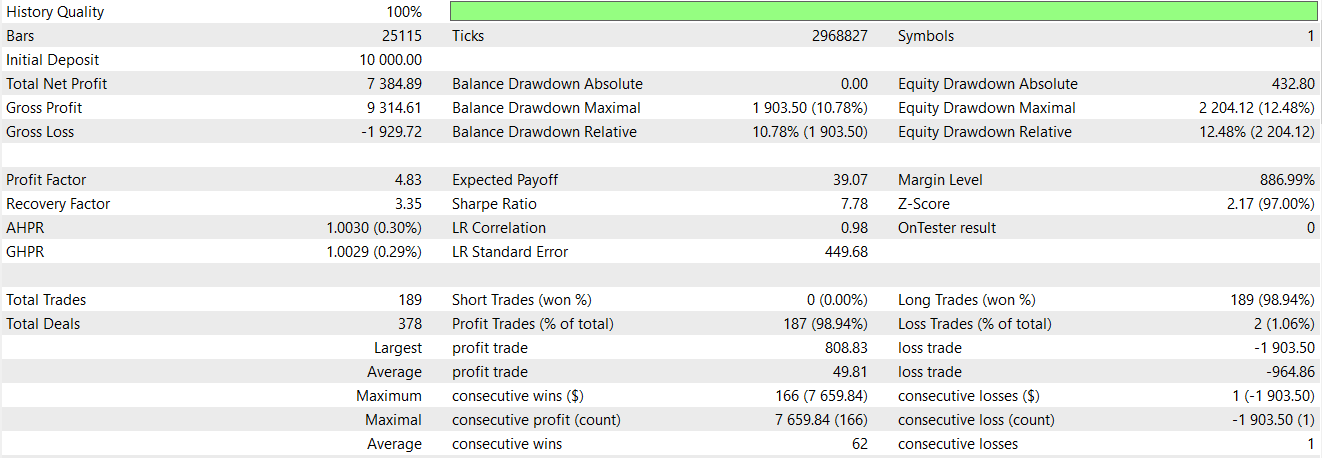
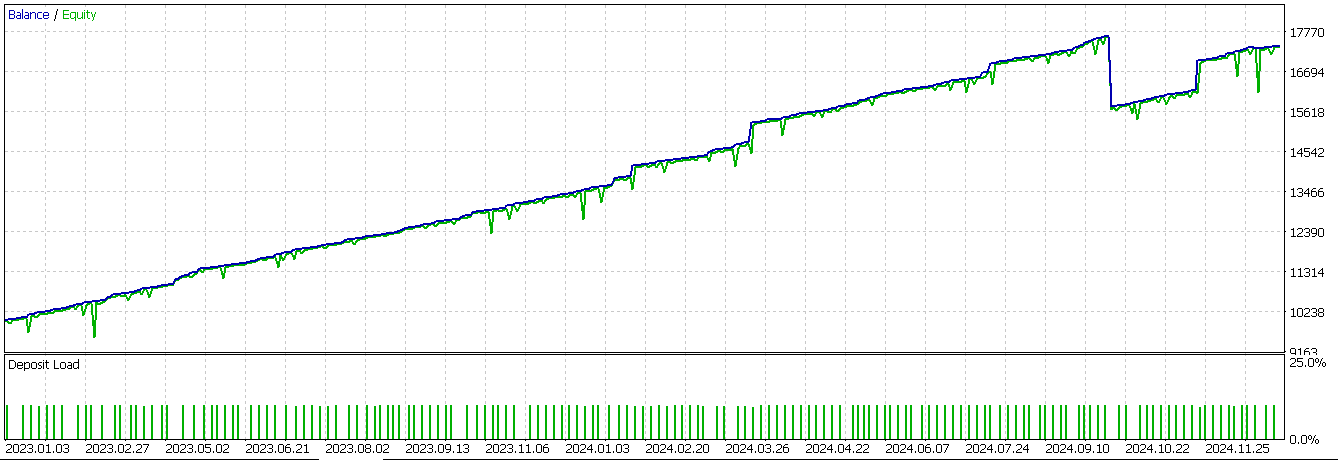
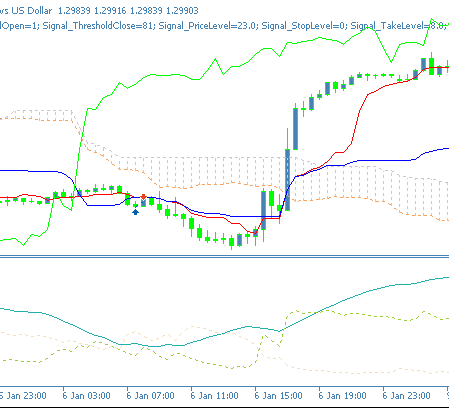
Unser Netzwerk, das die Signalverarbeitung des letzten Artikels als Filter überlagert, scheint wiederum einen Unterschied in der Leistung des vom Assistenten zusammengestellten Expert Advisors zu machen. Ein Aufwärtsmuster auf einem Balken-Chart kann für Merkmal-1 wie folgt aussehen:

Merkmal-5

Das letzte Muster, das wir erneut testen, ist das sechste, Pattern-5. Wir implementieren dies in Python wie folgt:

def feature_5(df):
    """

    """
    feature = np.zeros((len(df), 2))
    
    feature[:, 0] = ((df['close'].shift(2) > df['close'].shift(1)) &
                     (df['close'].shift(1) < df['close']) &
                     (df['close'].shift(2) > df['Tenkan_sen'].shift(2)) &
                     (df['close'] > df['Tenkan_sen']) &
                     (df['close'].shift(1) <= df['Tenkan_sen'].shift(1)) &
                     (df['+DI'] > df['-DI']) &
                     (df['ADX'] >= 25.0)).astype(int)
    
    feature[:, 1] = ((df['close'].shift(2) < df['close'].shift(1)) &
                     (df['close'].shift(1) > df['close']) &
                     (df['close'].shift(2) < df['Tenkan_sen'].shift(2)) &
                     (df['close'] < df['Tenkan_sen']) &
                     (df['close'].shift(1) >= df['Tenkan_sen'].shift(1)) &
                     (df['+DI'] < df['-DI']) &
                     (df['ADX'] >= 25.0)).astype(int)
    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Unser Format ist ähnlich wie bei Pattern-0 und Pattern-1 oben. Auf diese Weise initialisieren wir unser NumPy-Ausgabe-Array und bestimmen seine Größe. Um der ersten Spalte eine 1 zuzuweisen und damit das Aufwärtssignal zu bestätigen, ist es erforderlich, dass der Schlusskurs in einer U-Drehung über den Tenkan-Sen abprallt. Außerdem sollte +DM über –DM liegen und der ADX bei 25 oder mehr. Diese Kursbewegung signalisiert oft eine Trendfortsetzung, und die relative Größe der unterzeichneten Richtungsbewegungspuffer des ADX sowie seine Werte müssen berücksichtigt werden, bevor dies der Fall ist.

Der zweiten Spalte wird eine 1 zugewiesen, um die standardmäßige 0 zu ersetzen, wenn der Kurs am Tenkan-sen von unten abweicht, sodass der aktuelle Schlusskurs darunter liegt, und der ADX ebenfalls mindestens 25 beträgt, wobei die negative Richtungsbewegung größer ist als die positive DM als endgültige Signalbestätigung. Abschließend setzen wir die ersten beiden Zeilen unseres Merkmalsarrays auf Null, um für Verschiebungsberechnungen zu sorgen, die angesichts der Endgültigkeit der Eingabedaten zu NaN-Werten führen. Wir haben auch dieses Muster unter ähnlichen Bedingungen wie die anderen 2 Muster oben getestet, und wir erhielten den folgenden Bericht.

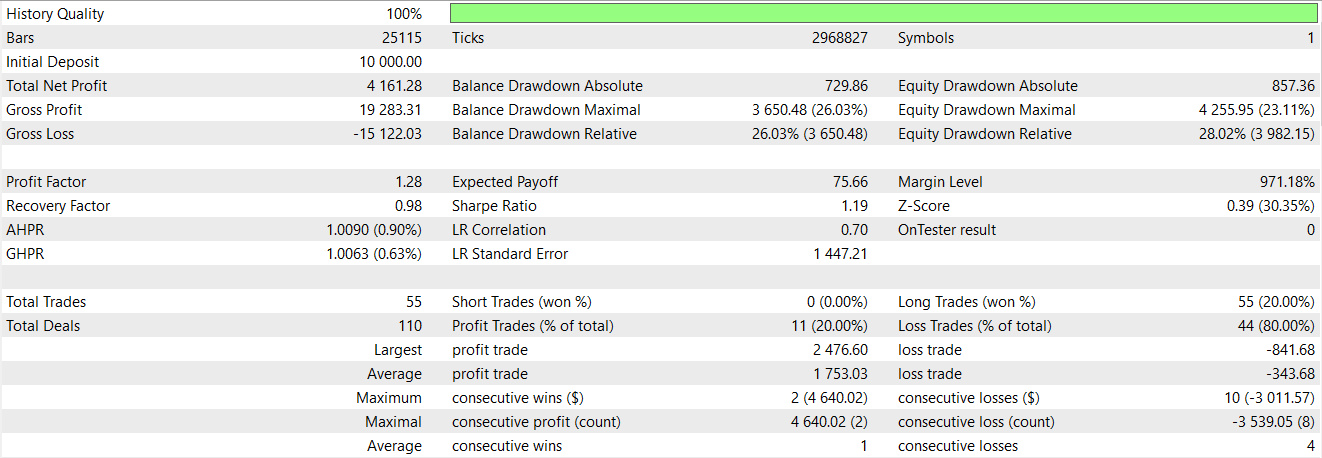
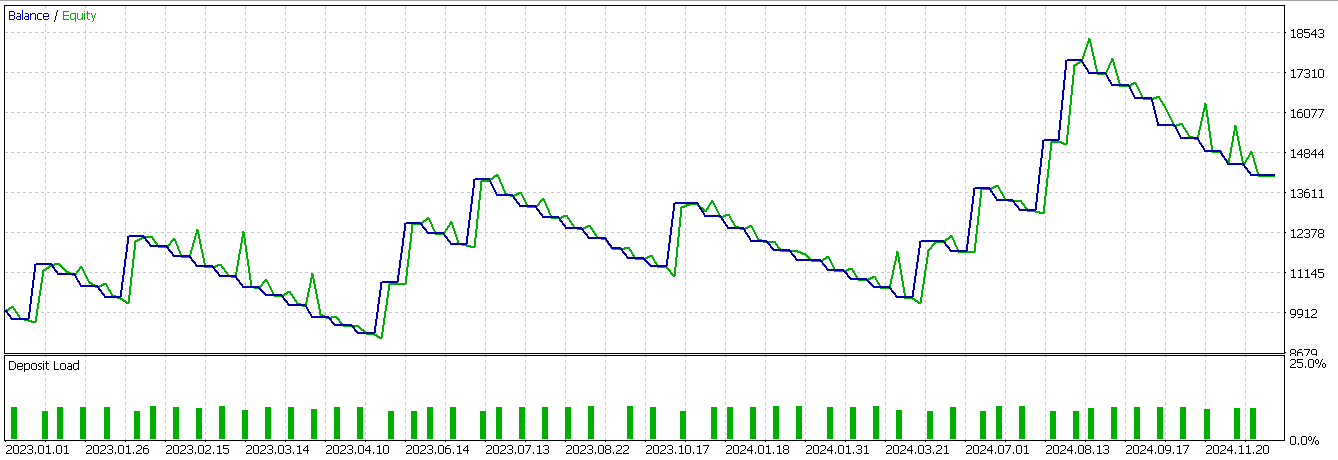
Unser Modell ist profitabel, aber die Entwicklung der Kapitalkurve ist sehr unruhig. Es spricht also einiges dafür, das maschinelle Lernen durch typische Indikatorsignale zu ergänzen. Auch wenn unsere Ergebnisse nicht ideal sind und die Testmöglichkeiten begrenzt sind, könnte man argumentieren, dass die Ergänzung von Indikatorsignalen mit einem spektralen Mischungskernnetz als zusätzlicher Filter eingesetzt werden kann, um den Handelseinstieg zu verbessern und die Leistung zu steigern.

Schlussfolgerung

Wir haben die Verwendung eines neuronalen Netzes untersucht, das nach dem spektralen Mischungskernel für die Feinabstimmung der rohen Handelssignale des Indikatorpaares Ichimoku und ADX-Wilder konzipiert wurde. Das spezielle Netzwerk, das wir eingeführt haben, hat sich als vielversprechend erwiesen, und es ist sicherlich ein Unterschied in der Leistung zu dem, was wir im letzten Artikel hatten, wo wir nur mit den Indikatorsignalen gehandelt haben. Die hier vorgestellten Ergebnisse bedürfen, wie immer, weiterer Sorgfalt seitens des Lesers, bevor sie übernommen oder in bestehende Handelssysteme integriert werden können. Der Gedanke der Einbindung, insbesondere beim Testen, ist etwas, das die mit dem MQL5-Assistenten zusammengestellten Expert Advisors ermöglichen, da mehrere nutzerdefinierte Signale während der Zusammenstellung ausgewählt werden können.

Name	Beschreibung
WZ-74.mq5	Wizard assembliert Expert Advisor, dessen Header die in der Assemblierung verwendeten Dateien anzeigt
SignalWZ-74.mqh	Nutzerdefinierte Signalklassendatei
74-5.onnx	ONNX-Netzwerk für Signal-Pattern-5
74-1.onnx	ONNX-Netzwerk für Signal-Pattern-1
74-0.onnx	ONNX-Muster für Signal-Pattern-0