Bivariate Copulae in MQL5 (Part 1): Implementing Gaussian and Student's t-Copulae for Dependency Modeling

Introduction

Copula-based trading strategies offer an interesting alternative approach to statistical arbitrage by modeling the dependence between two assets using a copula function. Traditional pairs trading relies on temporary divergences from an expected long-term relationship, and a copula can be used to model this relationship to identify trading opportunities. The theoretical advantage of using copulae lies in their ability to capture non-linear and asymmetric dependencies between assets.

With that in mind, this article marks the beginning of a series on the implementation of tools for copula-based trading strategies. In this first installment, we explore the fundamentals of statistical copulae in the context of pairs trading and dependency modeling. We also present MQL5 code for preprocessing datasets before fitting copula models. The broader focus of the series will be a library that implements commonly used copula models. To begin, this article introduces implementations of the Gaussian and Student's t copulae.

Key fundamentals for Copula theory

To work with copulas, three related concepts must be understood.

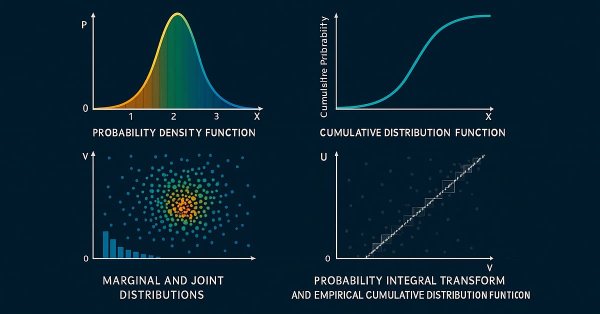
The Probability Density Function. In the study of statistical distributions, the Probability Density Function (PDF) describes the likelihood of a continuous random variable X taking on a particular value x. Unlike a discrete probability mass function, the PDF does not assign probabilities directly to specific values. Instead, it represents a density, such that the probability of X falling within a specific interval [a,b] is given by the integral of the PDF over that range.

The Cumulative Distribution Function. Building upon the PDF, the Cumulative Distribution Function (CDF), provides the probability that a random variable X will take a value less than or equal to x. The CDF is a non-decreasing function, ranging from 0 to 1, and it provides a complete description of the probability distribution of a random variable.

Marginal and joint distributions. When working with multiple random variables, it becomes necessary to distinguish between marginal distributions and joint distributions. A marginal distribution describes the probability distribution of a single variable within a larger set, effectively ignoring the influence of the other variables. In contrast, a joint distribution characterizes the collective probability distribution of all variables in a dataset.  

The Probability Integral Transform (PIT). The PIT is a foundational concept in probability theory and a critical building block for understanding copulae. It states that if X is a continuous random variable with CDF = F​(X), then the transformed variable U=F​(X) is uniformly distributed on the interval [0,1]. In other words, regardless of whether X follows a normal, exponential, or any other continuous distribution, applying its own CDF transforms it into a variable with a uniform distribution on [0,1].

The PIT enables the mapping of any continuous random variable to the unit interval, effectively standardizing it while preserving its probabilistic structure. By transforming marginals to uniform distributions, we can analyze how variables are linked without the influence of their individual distributions. This uniform space is precisely where copulae operate, they capture the dependence structure among variables once the marginals have been transformed in this way.

Empirical Cumulative Distribution Function. When the true underlying distribution of a variable is unknown, we can use the Empirical Cumulative Distribution Function (ECDF) as an estimate for the true CDF. For a sample of N observations, x1​,x2​,…,xN​, the ECDF is defined as:

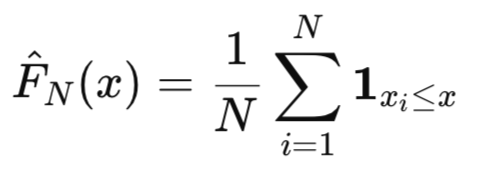
which specifies a function that equals 1 if x_i <= x and 0 otherwise.

Using the ECDF to perform the PIT is often called the non-parametric approach to estimation, as it does not assume a specific distribution shape for the marginals. The transformed data points, are the inputs used to fit the copula itself.

The file linear_cdf.mqh contains the definition of the CLinearCDF class used to estimate the ECDF of a dataset. The class generates an ECDF with linear interpolation applied between the steps of the standard ECDF. This effectively smooths the result while maintaining agreement with the standard ECDF at the sample points.

//+------------------------------------------------------------------+
//|                                                   linear_cdf.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Arrays/ArrayDouble.mqh>
#include<Arrays/ArrayObj.mqh>
#include "ecdf.mqh"
//+------------------------------------------------------------------+
//|CArray objects                                                    |
//+------------------------------------------------------------------+
class CArrayDoubles:public CArrayObj
  {
   virtual bool      CreateElement(const int index)
     {
      m_data[index] = new CArrayDouble();
      return m_data[index]!=NULL;
     }
  };
//+------------------------------------------------------------------+
//| ecdf quantile transformer                                        |
//+------------------------------------------------------------------+
class CLinearCDF
  {
protected:
   CSpline1DInterpolantShell* m_shells[];
   CArrayDoubles      m_internal;
   CArrayDouble      *m_arrays[];
   double            m_ub,m_lb;
   ulong             m_cols;
   void              clean_up(void)
     {

      for(uint i = 0; i<m_shells.Size(); i++)
         delete m_shells[i];
      for(uint i = 0; i<m_arrays.Size(); i++)
         delete m_arrays[i];
      m_internal.Clear();
     }
public:
                     CLinearCDF(void)
     {
      m_cols = 0;
     }
                    ~CLinearCDF(void)
     {
      clean_up();
     }
   bool              save(const int filehandle)
     {
      if(!m_cols)
         return false;
      return m_internal.Save(filehandle);
     }
   bool              load(const int filehandle)
     {
      if(m_cols)
        {
         clean_up();
         m_cols = 0;
        }

      if(m_internal.Load(filehandle))
        {
         int n_arrays = m_internal.Total();
         m_cols = ulong((n_arrays-1)/2);
         ArrayResize(m_shells,int(m_cols));
         ArrayResize(m_arrays,int(m_cols*2)+1);
         double xa[],ya[];
         m_arrays[0] = m_internal.At(0);
         m_ub = m_arrays[0].At(0);
         m_lb = m_arrays[0].At(1);
         for(int i = 0; i<int(m_cols); i++)
           {
            m_arrays[i*2+1] = m_internal.At(i*2+1);
            m_arrays[i*2+2] = m_internal.At(i*2+2);
            ArrayResize(xa,m_arrays[i*2+1].Total());
            for(int j = 0; j<m_arrays[i*2+1].Total(); j++)
               xa[j] = m_arrays[i*2+1][j];
            ArrayResize(ya,m_arrays[i*2+2].Total());
            for(int j = 0; j<m_arrays[i*2+2].Total(); j++)
               ya[j] = m_arrays[i*2+2][j];
            m_shells[i] = new CSpline1DInterpolantShell();
            CAlglib::Spline1DBuildLinear(xa,ya,m_shells[i]);
           }
         return true;
        }
      else
         return false;
     }
   bool              fit(matrix &data,double upper_bound = 1.0-1.e-5,double lower_bound = 1.e-5)
     {
      if(upper_bound<=lower_bound)
        {
         Print(__FUNCTION__, " invalid inputs ");
         return false;
        }

      if(m_cols)
        {
         clean_up();
         m_cols = 0;
        }

      m_ub = upper_bound;
      m_lb = lower_bound;
      m_cols = data.Cols();
      vector v;
      double xa[],ya[];
      vector slopes;
      vector slope_samples;
      CECDF m_ecdf;
      ArrayResize(m_shells,int(m_cols));
      ArrayResize(m_arrays,int(m_cols*2)+1);
      m_arrays[0] = new CArrayDouble();
      if(!m_arrays[0].Add(m_ub) || !m_arrays[0].Add(m_lb) || !m_internal.Add(m_arrays[0]))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }
      for(uint i = 0; i<m_shells.Size(); i++)
        {
         v = data.Col(i);
         if(!m_ecdf.fit(v))
           {
            Print(__FUNCTION__, " error ");
            return false;
           }

         np::quickSort(v,true,0,long(v.Size()-1));
         slopes = np::unique(v);
         slope_samples = m_ecdf.ecdf(slopes);
         m_shells[i] = new CSpline1DInterpolantShell();
         if(!np::vecAsArray(slopes,xa) || !np::vecAsArray(slope_samples,ya))
           {
            Print(__FUNCTION__, " error ");
            return false;
           }
         m_arrays[i*2+1] = new CArrayDouble();
         m_arrays[i*2+2] = new CArrayDouble();
         if(!m_arrays[i*2+1].AddArray(xa) || !m_arrays[i*2+2].AddArray(ya) ||!m_internal.Add(m_arrays[i*2+1])||!m_internal.Add(m_arrays[i*2+2]))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }
         CAlglib::Spline1DBuildLinear(xa,ya,m_shells[i]);
        }

      return true;
     }

   matrix            to_quantile(matrix &in)
     {
      if(in.Cols()!=m_cols)
        {
         Print(__FUNCTION__, " invalid input ");
         return matrix::Zeros(0,0);
        }

      vector temp;
      matrix out(in.Rows(),m_cols);
      for(ulong i = 0; i<m_cols; ++i)
        {
         temp  = in.Col(i);
         for(ulong j = 0; j<in.Rows(); ++j)
            out[j][i] = MathMax(MathMin(CAlglib::Spline1DCalc(m_shells[i],temp[j]),m_ub),m_lb);
        }

      return out;
     }
  };
//+------------------------------------------------------------------+

The fit() method takes a matrix with any number of columns assumed to be variables of a multivariate dataset. The optional upper_bound and lower_bound input parameters define constraints preventing values of exactly 0 or 1. Internally, the standard ECDF is sampled at unique sorted sample points. A one-dimensional linear interpolation model is then created based on these points and their corresponding ECDF values. 

//+------------------------------------------------------------------+
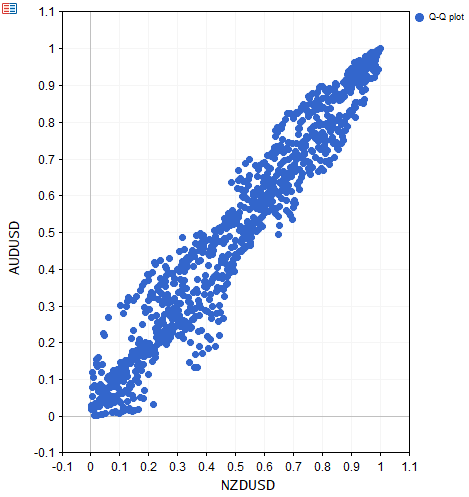
//|                                                    ECDF_Demo.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<ECDF/linear_cdf.mqh>
//--- input parameters
input string   FirstSymbol = "NZDUSD";
input string   SecondSymbol = "AUDUSD";
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2024.01.01 00:00:01';
input ulong HistoryLength = 1000;
input bool Use_Returns = false;
input int DisplayDuration = 30;//display duration in seconds
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---download symbol data
   vector syA,syB;
   if(!syA.CopyRates(FirstSymbol,TimeFrame,COPY_RATES_CLOSE,StartDate,HistoryLength) ||
      !syB.CopyRates(SecondSymbol,TimeFrame,COPY_RATES_CLOSE,StartDate,HistoryLength) ||
      syA.Size()!=syB.Size())
     {
      Print("Error downloading price data ", ::GetLastError());
      return;
     }
//---optionally transform to returns
   if(Use_Returns)
     {
      syA = np::diff(log(syA));
      syB = np::diff(log(syB));
     }
//---create matrix container and fill it
   matrix xy(syA.Size(),2);
   if(!xy.Col(syA,0) || !xy.Col(syB,1))
     {
      Print(" column insertion error ", GetLastError());
      return ;
     }
//---build ECDF model
   CLinearCDF qd;
   if(!qd.fit(xy))
     {
      Print(" CLinearCDF failure ");
      return;
     }
//---transform raw values to quantiles
   matrix yx = qd.to_quantile(xy);
//---display QQ plot
   np::scatter_plot(yx.Col(0),yx.Col(1),"Q-Q plot",FirstSymbol,SecondSymbol,true,0,0,0,0,500,500,true,30);
//---
  }
//+------------------------------------------------------------------

The script ECDF_Demo.ex5 demonstrates the use of the CLinearCDF class, by applying it to a bivariate dataset of prices. The transformed values are then used to display the Quantile-to-Quantile, (Q-Q) plot of the data. 

Defining a copula

A copula is a multivariable cumulative distribution function that captures the dependency structure between random variables, independently of their marginal distributions. In simpler terms, a copula is a mathematical mechanism that allows us to decouple the dependence between variables from the individual behavior of each variable.

Given random variables, each with its own marginal distribution, a copula binds these marginals together into a joint distribution by describing how the variables relate to each other, regardless of the shape of their individual distributions. This separation of marginals and dependence is central to modern multivariate analysis, particularly when the assumption of normality or linear dependence is inappropriate. This is mathematically formalized by Sklar’s Theorem. Sklar's Theorem states that for any continuous joint distribution function F, there exists a unique copula C such that:

where F1​(x1​) and F2​(x2​) are the marginal CDFs of X1​ and X2​, respectively.

The ability of a copula to encapsulate the dependency of two or more random variables can be likened to a measure of association, such as the correlation coefficient. The difference is that a copula provides additional information about the nature of the association between variables, as opposed to the limitation of a single number.

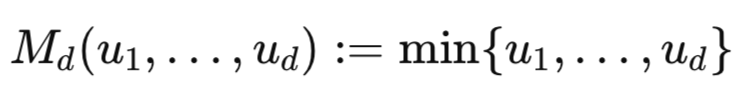
In the same way that the correlation coefficient is bounded between −1 and 1, copulae are characterized by similar bounds called the Fréchet–Hoeffding bounds. The lower and upper Fréchet–Hoeffding bounds are functions that define the most negative and positive dependence that can be captured by a particular copula. The Fréchet–Hoeffding bounds are copulae themselves, where d corresponds to the dimensionality or number of variables.

Tail dependence

The unique nature of individual copula functions allows them to capture different kinds of dependency structures. A property of a copula that is usually of interest in financial applications is its ability to model tail dependence. Tail dependence is a measure of the comovement between random variables when they are at extreme values. The type of tail dependence a copula can model determines how the structure handles joint extreme events. The upper tail refers to extremely high values in a distribution, whereas the lower tail corresponds to extremely low values. Tail dependence is quantified by the Tail Dependence Coefficient (λ), which is calculated as a limit of a conditional probability. Tail dependency is difficult to quantify without expressing it in terms of a copula.

Lower tail dependence measures the probability of one variable being extremely low given that the other variable is also extremely low.

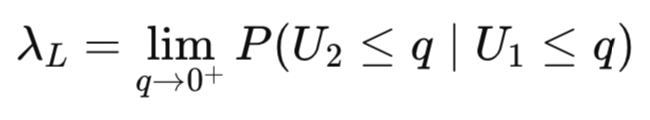
Upper tail dependence measures the probability of one variable being extremely high given that the other variable is also extremely high.

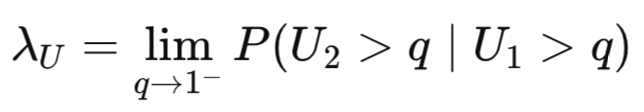
Copula types

Copulae can be categorized into broad classes and families that define specific functional forms. The type of copulae we will describe in this series of articles are parametric. These are copulae that are characterized by parameters that quantify the dependency traits they capture.

Elliptical copulae are a class of multivariate copulae derived from elliptical distributions, such as the multivariate Normal (Gaussian) and Student's t distributions. They are primarily parameterized by some measure of association, which captures the linear dependence structure between the variables. The two most common elliptical copulae are the Gaussian and Student's t copulae. In the next section, we delve into the implementation of bivariate elliptical copulae, beginning with the bivariate Gaussian copula.

Bivariate Gaussian Copula

The bivariate Gaussian copula is derived from the standard bivariate normal distribution. It is characterized by a single parameter: the linear correlation coefficient (ρ) of the underlying bivariate normal distribution. This parameter dictates the strength and direction of the dependence between the two random variables. The Gaussian copula is radially symmetric and is popular for its computational tractability, though it exhibits weak tail dependence. This means it does not adequately capture strong, simultaneous extreme events in the variables.

The header file gaussian.mqh lists the CGaussian class, which implements a bivariate Gaussian copula. CGaussian is a descendant of the abstract CBivariateCopula class defined in base.mqh and is the basis for all the bivariate copulae implementations we will describe.

//+------------------------------------------------------------------+
//| base copula class                                                |
//+------------------------------------------------------------------+
class CBivariateCopula:public CObject
  {
private:
   int               m_len;
protected:
   double            m_eps;
   double            m_theta;
   double            m_rho;
   double            m_nu;
   double            m_threshold;
   ENUM_COPULA_TYPE  m_copula_type;
   vector            m_bounds;
   double            m_tau;
   matrix            m_cov;
   virtual bool      check_theta(void) 
     {
       return (m_theta>m_bounds.Min() < m_theta < m_bounds.Max());  
     }
   virtual double    pdf(double u,double v) { return EMPTY_VALUE; }
   virtual double    cdf(double u,double v) { return EMPTY_VALUE; }
   virtual double    condi_cdf(double u,double v) { return EMPTY_VALUE; }
   virtual vector    pdf(vector& u,vector& v){ return vector::Zeros(0); }
   virtual vector    cdf(vector& u,vector& v){ return vector::Zeros(0); }
   virtual vector    condi_cdf(vector& u,vector& v){ return vector::Zeros(0); }
   virtual double    theta_hat(const double tau){ return EMPTY_VALUE; }
   void              preprocess(double &u, double &v)
     {
      u = MathMin(MathMax(m_eps,u),1.0-m_eps);
      v = MathMin(MathMax(m_eps,v),1.0-m_eps);
     }
   void              preprocess(vector &u, vector &v)
     {
      u.Clip(m_eps,1.0-m_eps);
      v.Clip(m_eps,1.0-m_eps);
     }
   double            kendalTau(const vector &vec1,const vector &vec2)
     {
      double tau = double("nan");
      ulong size=vec1.Size();
      if(size==0 || vec2.Size()!=size)
        {
         Print(__FUNCTION__, " size of input vectors donot match ");
         return(tau);
        }
      //---
      long cnt1=0,cnt2=0,cnt=0;
      //---
      for(long i=0; i<long(size); i++)
        {
         for(long j=i+1; j<long(size); j++)
           {
            double delta1=vec1[i]-vec1[j];
            double delta2=vec2[i]-vec2[j];
            double delta=delta1*delta2;
            if(delta==0)
              {
               if(delta1!=0)
                  cnt1++;
               if(delta2!=0)
                  cnt2++;
              }
            else
              {
               cnt1++;
               cnt2++;
               if(delta>0.0)
                  cnt++;
               else
                  cnt--;
              }
           }
        }
      //--- calculate Kendall tau
      long den=cnt1*cnt2;
      if(den==0)
        {
         Print(__FUNCTION__, " failed zero check at line 76");
         return tau;
        }
      tau=double(cnt)/MathSqrt(den);
      //---
      return(tau);
     }

public:
                     CBivariateCopula(void)
     {
      m_len = 6;
      m_eps = 1.e-5;
      m_theta = m_rho = m_nu = EMPTY_VALUE;
      m_copula_type = WRONG_VALUE;
      m_cov  = matrix::Zeros(0,0);
      m_bounds = vector::Zeros(2);
      m_bounds[0] = -DBL_MIN;
      m_bounds[1] = DBL_MAX;
     }
                    ~CBivariateCopula(void)
     {
     }
   double            Get_theta(void)  { return m_theta; }
   double            Get_tau(void)    { return m_tau;   }
   double            Get_rho(void)    { return m_rho;   }
   matrix            Get_covar(void)  { return m_cov;   }
   double            Get_nu(void)     { return m_nu;    }
   double            Get_threshold(void) { return m_threshold; }
   double            Get_eps(void)    { return m_eps;   }
   virtual void              Set_theta(double theta) {  m_theta = theta; }
   virtual void              Set_tau(double tau) { m_tau = tau; }
   virtual void              Set_threshold(double threshold) { m_threshold = threshold; }
   virtual void              Set_nu(double nu) { m_nu = nu; }
   virtual void              Set_rho(double rho) { m_rho = rho; }
   virtual void              Set_eps(double eps) { m_eps = eps; }
   virtual matrix            Sample(ulong num_samples) { return matrix::Zeros(0,0); }
   virtual void              Set_covariance(matrix &cov)
     {
      m_cov = cov;
      m_rho = m_cov[0][1] / (sqrt(m_cov[0][0]) * sqrt(m_cov[1][1]));
     }
   virtual double    Fit(vector &u, vector&v)
     {
      if(u.Max()>1.0 || v.Max()>1.0 || v.Min()<0.0 ||u.Min()<0.0)
       {
        Print(__FUNCTION__, " Invalid input variable(s) ");
        return EMPTY_VALUE;
       }
      m_tau = kendalTau(u,v);
      m_theta = theta_hat(m_tau);
      if(!check_theta())
        Print(__FUNCTION__, " Invalid theta " );
      return  m_theta;
     }
   double            Log_likelihood(vector &u, vector &v)
     {
      if(u.Size()!=v.Size())
        {
         Print(__FUNCTION__, " vectors are not of equal length ");
         return EMPTY_VALUE;
        }
      
      vector ll = pdf(u,v);

      return (log(ll)).Sum();
     }
   double            Copula_PDF(double u, double v)
     {
      preprocess(u,v);
      return pdf(u,v);
     }
   double            Copula_CDF(double u, double v)
     {
      preprocess(u,v);
      return cdf(u,v);
     }
   double            Conditional_Probability(double u, double v)
     {
      preprocess(u,v);
      return condi_cdf(u,v);
     }
   vector            Copula_PDF(vector& u, vector& v)
     {
      preprocess(u,v);
      return pdf(u,v);
     }
   vector            Copula_CDF(vector& u, vector& v)
     {
      preprocess(u,v);
      return cdf(u,v);
     }
   vector            Conditional_Probability(vector& u, vector& v)
     {
      preprocess(u,v);
      return condi_cdf(u,v);
     }
   double            Theta(double tau = 0.0)
     {
      if(!tau && m_tau)
         return theta_hat(m_tau);
      else
         if(tau)
            return theta_hat(tau);
         else
           {
            Print(__FUNCTION__ " invalid input parameter 'tau' ");
            return EMPTY_VALUE;
           }
     }

   virtual bool      Save(const int file_handle)
     {
      if(file_handle!=INVALID_HANDLE)
        {
         //---
         if(FileWriteLong(file_handle,-1)==sizeof(long))
           {
            //---
            if(FileWriteInteger(file_handle,int(m_copula_type),INT_VALUE)!=INT_VALUE)
               return(false);
            //---
            if(FileWriteInteger(file_handle,m_len,INT_VALUE)!=INT_VALUE)
               return(false);
            //---
            if(FileWriteDouble(file_handle,m_eps)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_theta)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_tau)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_rho)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_nu)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_threshold)!=sizeof(double))
               return false;
            return true;
           }
        }
      return false;
     }
   virtual bool      Load(const int file_handle)
     {
      if(file_handle!=INVALID_HANDLE)
        {
         //---
         if(FileReadLong(file_handle)==-1)
           {
            //---
            m_copula_type = ENUM_COPULA_TYPE(FileReadInteger(file_handle,INT_VALUE));

            if(FileReadInteger(file_handle,INT_VALUE)!=m_len)
               return false;

            ResetLastError();
            m_eps=FileReadDouble(file_handle);
            m_theta=FileReadDouble(file_handle);
            m_tau=FileReadDouble(file_handle);
            m_rho=FileReadDouble(file_handle);
            m_nu=FileReadDouble(file_handle);
            m_threshold=FileReadDouble(file_handle);
            if(GetLastError())
              {
               Print(__FUNCTION__, " possible read error ", GetLastError());
               return false;
              }
            return true;
           }
        }
      return false;
     }
   virtual int       Type(void)
     {
      return int(m_copula_type);
     }
  };

It enables the specification of copula models in one of two ways. A model can be explicitly defined by using the accessor methods to set relevant copula parameters. Alternatively, a model can be built by fitting it to a bivariate dataset of uniform variables (the marginal CDFs of the raw values) via the Fit() method. If successful, the method will return any value other than the EMPTY_VALUE constant.

A copula's density is evaluated by calling the Copula_PDF() method, while Copula_CDF() evaluates the joint cumulative distribution function of the copula. The conditional CDF of the copula is calculated by calling the Conditional_Probability() method. All the methods just mentioned are overloaded to accept scalar and vector inputs. The Sample() method is used to generate synthetic datasets that conform to a copula's model parameters. Finally, Load() and Save() enable the serialization and deserialization of copula models for persistence.

Creating an explicit bivariate Gaussian copula requires the specification of a two-by-two covariance matrix.

virtual void Set_covariance(matrix& cov) override
     {
      if(cov.Rows()!=2 || cov.Cols()!=2)
       {
        Print(__FUNCTION__," invalid input: expecting 2x2 matrix ");
        return;
       }
      m_cov = cov;
      m_rho = m_cov[0][1] / (sqrt(m_cov[0][0]) * sqrt(m_cov[1][1]));
      m_tau = (2.0/M_PI) * MathArcsin(m_rho);
      m_theta = theta_hat(m_tau);
     }

The script SampleEllipticCopula.ex5 tests whether the synthetic data sampled from an Elliptic copula conforms to the specified model parameters. The user-configurable inputs prefixed by Covar specify the elements of a covariance matrix. The Degree_Of_Freedom parameter is not relevant to testing a Gaussian copula. The Size parameter defines the number of samples to generate.

//+------------------------------------------------------------------+
//|                                         SampleEllipticCopula.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Copulas/Bivariate/gaussian.mqh>
#include<Copulas/Bivariate/t.mqh>
//+------------------------------------------------------------------+
//|  enum                                                            |
//+------------------------------------------------------------------+
enum ENUM_ELPT_COPULA
 {
  GAUSSIAN=0,//Gaussian
  STUDENT//Student
 };
//--- input parameters
input ENUM_ELPT_COPULA copula_to_sample_from = GAUSSIAN;
input double Covar_0_0_ = 2.0;
input double Covar_0_1_ = 0.5;
input double Covar_1_0_ = 0.5;
input double Covar_1_1_ = 2.0;
input double Degrees_Of_Freedom = 5.0;
input ulong Size = 1000;

The program uses the Sample() method to generate synthetic data, which is later displayed in a scatter plot. The inverse CDF function of the standard Gaussian distribution is then applied to the dataset before the correlation matrix is estimated.

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix covar(2,2);
//---
   covar[0,0] = Covar_0_0_;
   covar[0,1] = Covar_0_1_;
   covar[1,0] = Covar_1_0_;
   covar[1,1] = Covar_1_1_;
//---
   CBivariateCopula *copula = NULL;
//---
   double set_theta = 0.0;
   switch(copula_to_sample_from)
    {
     case GAUSSIAN:
       copula = (CBivariateCopula*)new CGaussian();
       copula.Set_covariance(covar);
       break;
     case STUDENT:
       copula = (CBivariateCopula*)new CStudent();
       copula.Set_covariance(covar);
       copula.Set_nu(Degrees_Of_Freedom);
       break;
    }
//---
   Print("Specified correlation parameter of ", EnumToString(copula_to_sample_from)," copula :",copula.Get_rho());
   matrix samples = copula.Sample(Size);
   matrix inv_samples = samples;
   
   for(ulong i = 0; i<inv_samples.Rows(); ++i)
     for(ulong j =0; j<inv_samples.Cols(); ++j)
          inv_samples[i,j] = copula_to_sample_from == GAUSSIAN?CAlglib::InvNormalCDF(inv_samples[i,j]):studentTQuantile(inv_samples[i,j],Degrees_Of_Freedom);
          
   Print("Correlation of matrix of variable sampled from  ", EnumToString(copula_to_sample_from)," copula :\n", inv_samples.CorrCoef(false));      
   string cname = EnumToString((ENUM_COPULA_TYPE)copula.Type());
//---
   delete copula;
//---display scatter plot
   np::scatter_plot(inv_samples.Col(0),inv_samples.Col(1),cname+" Scatter plot","X","Y",true,0,0,0,0,500,300,true,10);  
//---
  }

Here is the output from two runs. The expected output is a matrix with off diagonal elements that are around the same as the correlation parameter of the copula model. Note that the number of samples specified will affect the result. The larger the number of samples, the closer the output will be to the specified correlation parameter.

CQ      0       14:06:16.963    SampleEllipticCopula (XAUEUR,D1)        Specified correlation parameter of GAUSSIAN copula :0.24999999999999994
DJ      0       14:06:17.021    SampleEllipticCopula (XAUEUR,D1)        Correlation of matrix of variable sampled from  GAUSSIAN copula :
DG      0       14:06:17.022    SampleEllipticCopula (XAUEUR,D1)        [[1,0.2497651923653427]
RK      0       14:06:17.022    SampleEllipticCopula (XAUEUR,D1)         [0.2497651923653427,1]]

In the next section, we turn our attention to the other elliptical copula: Student's t-copula.

Bivariate Student's t-copula

The bivariate Student's t-copula is one of the more prominent alternatives to the Gaussian copula because it captures tail dependence that the Gaussian copula cannot. The Student's t-copula is defined by two parameters: the correlation coefficient and the degrees of freedom, usually called ρ and ν, respectively. Unlike the Gaussian copula, the t-copula exhibits non-zero tail dependence, meaning that extreme events in one variable make extremes in the other more likely.

where:

• t ρ , ν tρ,ν​ = CDF of the bivariate Student’s t-distribution with correlation ρ ρ and ν ν degrees of freedom,
• t ν − 1 tν−1​ = inverse CDF (quantile function) of the univariate t-distribution with ν ν degrees of freedom,
• u , v ∈ [ 0 , 1 ] u,v∈[0,1].

Dependence in the t-copula is stronger in the tails than in the center—unlike the Gaussian copula, which has uniform dependence across the distribution. This makes it particularly suitable for modeling financial returns, where joint crashes or booms occur more often than Gaussian models would predict. As the degrees of freedom parameter (ν) increases, upper and lower tail dependence decreases. In fact, the student's t-copula converges to a Gaussian copula as degrees of freedom approach infinity. Conversely, the lower the degrees of freedom, the higher the tail dependence will be.

The student's t-copula is implemented in t.mqh as the CStudent class, which is also a subclass of CBivariateCopula.

//+------------------------------------------------------------------+
//|                                                            t.mqh |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "base.mqh"
#ifndef _NP_
#include<np.mqh>
#endif
#include<Math/Stat/T.mqh>
//+------------------------------------------------------------------+
//|utilities for Student's t distribution: Cheng Algorithm           |
//+------------------------------------------------------------------+
double            chengFuAlgo(double probability,double df)
  {
   double k = ceil(df*0.5);
   double a = 1.0 - probability;
   double qi = EMPTY_VALUE;
   if(a!=0.5)
     {
      qi = sqrt(2.0*pow(1.0-2.0*a,2.0)/(1.0 - pow(1.0-2.0*a,2.0)));
      double i = 0.0;
      double gy,j;
      while(i<20.0)
        {
         gy = 0.0;
         j = 0.0;
         while(j<=k-1.0)
           {
            gy+=MathFactorial(int(2*j))/pow(2.0,2.0*j)/pow(MathFactorial(int(j)),2.0)*pow(1.0+pow(qi,2.0)/(2.0*k),-j);
            j+=1.0;
           }
         qi = 1.0/sqrt(1.0/(2.0*k)*(pow(gy/1.0-2.0*a,2.0) - 1.0));
         i+=1.0;
        }
      if(a>0.5)
         return -qi;
      else
         return qi;
     }
   else
      return 0.0;
  }
//+------------------------------------------------------------------+
//| Hills algorithm                                                  |
//+------------------------------------------------------------------+
double            hillsAlgo(double probability,double df)
  {
   double z,a,b,c,x,y,d;
   z = a = b = c = x = y = d = EMPTY_VALUE;
   bool neg = false;
   if(probability>0.5)
     {
      z = 2.0*(1.0-probability);
     }
   else
     {
      neg = true;
      z = 2.0*probability;
     }
   a = 1.0/(df - 0.5);
   b = 48.0/(a*a);
   c = ((20700.0*a/b - 98.0)*a - 16.0)*a + 96.36;
   d = ((94.5/(b + c) - 3.0)/b + 1.0)*sqrt(a*M_PI/2.0)*df;
   x = z*d;
   y = pow(x,(2.0/df));

   if(y>0.05 + a)
     {
      x = CAlglib::InvNormalCDF(z*0.5);
      y = x*x;
      if(df<5.0)
         c = c+0.3*(df-4.5)*(x+0.6);
      c = c + (((0.05*d*x - 5.0)*x - 7.0)*x - 2.0)*x + b;
      y = (((((0.4*y + 6.3)*y + 36.0)*y + 94.5)/c - y - 3.0)/b + 1.0)*x;
      y = a*y*y;
      if(y > 0.002)
         y = exp(y) - 1.0;
      else
         y = y + 0.5*y*y;
     }
   else
      y = ((1.0/(((df + 6.0)/(df*y) - 0.089*d - 0.822)*(df + 2.0)*3.0) + 0.5/(df + 4.0))*y - 1.0)*(df + 1.0)/(df + 2.0) + 1.0/y;
   double q = sqrt(df*y);
   return (neg)?-1.0*q:q;
  }
//+------------------------------------------------------------------+
//| Student's t Inverse CDF                                          |
//+------------------------------------------------------------------+
double            studentTQuantile(double probability, double df)
  {
   if(df == 1.0)
      return tan(M_PI*(probability-1.0/2.0));
   else
      if(df == 2.0)
         return (2.0*probability-1.0)*sqrt(2.0/(4.0*probability*(1.0-probability)));
      else
         if(df == 4.0)
           {
            double a = 4.0*probability*(1.0 - probability);
            double q = cos(1.0/3.0*acos(sqrt(a)))/sqrt(a);
            return np::sign(probability - 0.5)*2.0*sqrt(q-1.0);
           }
         else
            if(!MathMod(df,2.0))
               return chengFuAlgo(probability,df);
            else
               return hillsAlgo(probability,df);
  }
//+------------------------------------------------------------------+
//| Student T Probability Density Function                           |
//+------------------------------------------------------------------+
double studentTDensity(double x, double df)
  {
   return CAlglib::GammaFunction((df + 1.0)/2.0)/(sqrt(df*M_PI)*CAlglib::GammaFunction(df/2.0))*pow((1.0 + pow(x,2.0)/df),(-((df + 1.0)/2.0)));
  }
//+------------------------------------------------------------------+
//| Bivariate Student Copula                                         |
//+------------------------------------------------------------------+
class CStudent : public CBivariateCopula
  {
private:
   virtual double    theta_hat(const double tau) override
     {
      return sin(tau*M_PI/2.0);
     }
   matrix            generate_corr_student(ulong num, matrix& cov, double nu_)
     {
      vector means = vector::Zeros(2);
      matrix normal = np::multivariate_normal(means,cov,num);

      double chi[];
      if(!MathRandomChiSquare(nu_,int(num),chi))
        {
         Print(__FUNCTION__, " Math random chisquare error ", GetLastError());
         return matrix::Zeros(0,0);
        }

      matrix out = matrix::Zeros(num,2);

      for(ulong i = 0; i<out.Rows(); i++)
        {
         double chisqrt = sqrt(chi[i]/nu_);
         out[i,0] = normal[i,0]/chisqrt;
         out[i,1] = normal[i,1]/chisqrt;
        }
      return out;
     }
   double            bvtdist(double z1,double z2, vector& mu, matrix& cov, double df)
     {
      double x1 = z1 - mu[0];
      double x2 = z2 - mu[1];
      double det_cov = cov[0,0]*cov[1,1]-cov[0,1]*cov[1,0];

      double xt = (-2.0*cov[0,1]*x1*x2+cov[0,0]*(pow(x1,2.0)+pow(x2,2.0)))/det_cov;
      double numerator = CAlglib::GammaFunction((2.0+df)/2.0);
      double denominator = (CAlglib::GammaFunction(df/2.0)*df*M_PI*sqrt(det_cov)*pow(1.0+xt/df,(2.0+df)/2.0));
      return numerator/denominator;
     }
   //+------------------------------------------------------------------+
   //|  inner integral function object                                  |
   //+------------------------------------------------------------------+
   class CInnerInt : public CIntegrator1_Func
     {
   private:
      double            m_x;
      double            m_rho;
      matrix            m_corr;
      vector            m_mu;
      double            m_nu;
   public:
      //---
                     CInnerInt(void)
        {
         m_mu = vector::Zeros(2);
        }
                    ~CInnerInt(void) {}
      void              Set(double x, double rho, double nu)
        {
         m_x = x;
         m_nu = nu;
         m_rho = rho;
         matrix crr = {{1.0, m_rho}, {m_rho, 1.0}};
         m_corr = crr;
        }
      virtual void      Int_Func(double x,double xminusa,double bminusx,double &y,CObject &obj)
        {
         double x1 = m_x - 0.0;
         double x2 = x - 0.0;
         double det_cov = m_corr[0,0]*m_corr[1,1]-m_corr[0,1]*m_corr[1,0];

         double xt = (-2.0*m_corr[0,1]*x1*x2+m_corr[0,0]*(pow(x1,2.0)+pow(x2,2.0)))/det_cov;
         double numerator = CAlglib::GammaFunction((2.0+m_nu)/2.0);
         double denominator = (CAlglib::GammaFunction(m_nu/2.0)*m_nu*M_PI*sqrt(det_cov)*pow(1.0+xt/m_nu,(2.0+m_nu)/2.0));
         y =  numerator/denominator;
        }
     };
   //+------------------------------------------------------------------+
   //|  outer integral function object                                  |
   //+------------------------------------------------------------------+
   class COuterInt : public CIntegrator1_Func
     {
   public:
      double            ay_limit;
      double            by_limit;
      double            nu;
      double            rho;
      //---
                     COuterInt(void) {}
                    ~COuterInt(void) {}
      virtual void      Int_Func(double x,double xminusa,double bminusx,double &y,CObject &obj)
        {
         CInnerInt fint;
         //---
         fint.Set(x,rho,nu);
         //---
         CAutoGKStateShell s;
         //---
         double integral;
         //---
         CObject ob;
         //---
         CAutoGKReportShell rep;
         //---
         CAlglib::AutoGKSmooth(ay_limit,by_limit,s);
         //---
         CAlglib::AutoGKIntegrate(s,fint,ob);
         //---
         CAlglib::AutoGKResults(s,integral,rep);
         //---
         CAutoGKReport report = rep.GetInnerObj();
         //---
         if(report.m_terminationtype<0.0)
            Print(__FUNCTION__, " integration error ",report.m_terminationtype);
         //---
         y = integral;
        }
     };
protected:
   virtual double    pdf(double u,double v) override
     {
      double y1,y2;
      y1 = studentTQuantile(u,m_nu);
      y2 = studentTQuantile(v,m_nu);
      vector means = vector::Zeros(2);
      matrix corr = {{1.0,m_rho},{m_rho,1.0}};
      double numerator = bvtdist(y1,y2,means,corr,m_nu);
      double denominator,pdf1,pdf2;
      pdf1 = studentTDensity(y1,m_nu);
      pdf2 = studentTDensity(y2,m_nu);
      denominator = pdf1*pdf2;
      return numerator/denominator;
     }
   virtual double    cdf(double u,double v) override
     {
      double uu,vv;
      uu = MathMax(u,1.e-6);
      vv = MathMax(v,1.e-6);
      //---
      int errcode = 0;
      //---
      COuterInt fout;
      fout.rho = m_rho;
      fout.nu = m_nu;
      fout.ay_limit = double(LONG_MIN);
      fout.by_limit = studentTQuantile(vv,m_nu);
      double ax_limit = double(LONG_MIN);
      double bx_limit = studentTQuantile(uu,m_nu);
      //---
      CObject obj;
      CAutoGKStateShell ss;
      //---
      double outer_integral;
      CAutoGKReportShell repp;
      //---
      CAlglib::AutoGKSmooth(ax_limit,bx_limit,ss);
      //---
      CAlglib::AutoGKIntegrate(ss,fout,obj);
      //---
      CAlglib::AutoGKResults(ss,outer_integral,repp);
      //---
      CAutoGKReport report = repp.GetInnerObj();
      //---
      if(report.m_terminationtype<0.0)
         Print(__FUNCTION__, " integration error ",report.m_terminationtype);
      //---
      return MathMax(MathMin(outer_integral,1.0),0.0);
     }
   virtual double    condi_cdf(double u,double v) override
     {
      double inv_u,inv_v;
      int errcode = 0;
      inv_u = studentTQuantile(u,m_nu);
      inv_v = studentTQuantile(v,m_nu);
      double numerator,denominator;
      numerator = (inv_u-m_rho*inv_v)*sqrt(m_nu+1.0);
      denominator = sqrt((1.0-pow(m_rho,2.))*(pow(inv_v,2.0)+m_nu));
      double tcdf = MathCumulativeDistributionT(numerator/denominator,m_nu+1.0,errcode);
      if(errcode)
        {
         Print(__FUNCTION__, " mathcdf error ", errcode);
         return EMPTY_VALUE;
        }
      return tcdf;
     }
   virtual vector    pdf(vector &u,vector &v) override
     {
      vector out(u.Size());
      for(ulong i = 0; i<u.Size(); ++i)
         out[i] = pdf(u[i],v[i]);
      return out;
     }
   virtual vector    cdf(vector &u,vector &v) override
     {
      vector out(u.Size());
      for(ulong i = 0; i<u.Size(); ++i)
         out[i] = cdf(u[i],v[i]);
      return out;
     }
   virtual vector    condi_cdf(vector &u,vector &v) override
     {
      vector out(u.Size());
      for(ulong i = 0; i<u.Size(); ++i)
         out[i] = condi_cdf(u[i],v[i]);
      return out;
     }
public:
                     CStudent(void)
     {
      m_copula_type = STUDENT_COPULA;
     }
                    ~CStudent(void)
     {
     }

   virtual matrix    Sample(ulong num_samples) override
     {
      matrix spairs = generate_corr_student(num_samples,m_cov,m_nu);
      matrix out = spairs;
      int err1,err2;
      err1 = err2 = 0;
      for(ulong i = 0; i<spairs.Rows(); ++i)
        {
         out[i,0] = MathCumulativeDistributionT(spairs[i,0],m_nu,err1);
         out[i,1] = MathCumulativeDistributionT(spairs[i,1],m_nu,err2);
         if(err1 || err2)
           {
            Print(__FUNCTION__, " mathcdf error ", err1?err1:err2);
            return matrix::Zeros(0,0);
           }
        }
      return out;
     }
   virtual double    Fit(vector &u, vector&v) override
     {
      if(u.Max()>1.0 || v.Max()>1.0 || v.Min()<0.0 ||u.Min()<0.0)
        {
         Print(__FUNCTION__, " Invalid input variable(s) ");
         return EMPTY_VALUE;
        }
      m_tau = kendalTau(u,v);
      m_theta = theta_hat(m_tau);
      if(m_nu == EMPTY_VALUE)
         m_nu = fit_nu(u,v);
      matrix vals = matrix::Zeros(u.Size(),2);
      for(ulong i = 0; i<vals.Rows(); ++i)
        {
         vals[i,0] = studentTQuantile(u[i],m_nu);
         vals[i,1] = studentTQuantile(v[i],m_nu);
        }
      m_cov = vals.Cov(false);
      m_rho = m_cov[0,1]/(sqrt(m_cov[0,0])*sqrt(m_cov[1,1]));
      return m_rho;
     }
  };

//+------------------------------------------------------------------+

Below is the output from two runs of SampleEllipticCopula.ex5, with the corresponding t-copula option selected.

IM      0       14:07:00.097    SampleEllipticCopula (XAUEUR,D1)        Specified correlation parameter of STUDENT copula :0.24999999999999994
NQ      0       14:07:00.295    SampleEllipticCopula (XAUEUR,D1)        Correlation of matrix of variable sampled from  STUDENT copula :
GF      0       14:07:00.295    SampleEllipticCopula (XAUEUR,D1)        [[1,0.2441795870726779]
MJ      0       14:07:00.295    SampleEllipticCopula (XAUEUR,D1)         [0.2441795870726779,1]]

Testing and Validation

To test the rest of the methods of both copula implementations, we have the TestBivariateGaussianCopula.ex5 and TestBivariateStudentTCopula.ex5 scripts. Both scripts create specific copula models and evaluate the PDF, CDF, and conditional CDF code. These tests were reproduced from the unit tests of the ArbitrageLab Python package, which is what the presented MQL5 code is based on. This allows us to check if the MQL5 code works in the same manner as the original Python implementation.

//+------------------------------------------------------------------+
//|                                  TestBivariateGaussianCopula.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
//--- input parameters
#include<Copulas/Bivariate/gaussian.mqh>
//---
 double Covar_0_0_ = 2.0;
 double Covar_0_1_ = 0.5;
 double Covar_1_0_ = 0.5;
 double Covar_1_1_ = 2.0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix covar(2,2);
//---
   covar[0,0] = Covar_0_0_;
   covar[0,1] = Covar_0_1_;
   covar[1,0] = Covar_1_0_;
   covar[1,1] = Covar_1_1_;
//---   
   CGaussian norm_copula;
   norm_copula.Set_covariance(covar);
//---   
   Print("Rho ", norm_copula.Get_rho());
   Print("Joint cdf(0.7,0.0001) ",norm_copula.Copula_CDF(0.7,0.0001));
   Print("Joint cdf(0.0001,0.7) ",norm_copula.Copula_CDF(0.0001,0.7));
   Print("Joint cdf(0.7,1.0) ",norm_copula.Copula_CDF(0.7,1.0));
   Print("Joint cdf(0.5,0.7) ",norm_copula.Copula_CDF(0.5,0.7));
//---   
   Print("Joint pdf(0.5,0.7) ",norm_copula.Copula_PDF(0.5,0.7));
   Print("Joint pdf(0.7,0.5) ",norm_copula.Copula_PDF(0.7,0.5));
   Print("Joint pdf(0.6,0.7) ",norm_copula.Copula_PDF(0.6,0.7));
//---   
   Print("Conditional CDF (U<=0.5|V=0.7) ",norm_copula.Conditional_Probability(0.5,0.7));
  }
//+------------------------------------------------------------------+

Here are the results for the test of the CGaussian methods.

KR      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Rho 0.24999999999999994
JR      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.7,0.0001) 0.00009407442939459683
JG      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.0001,0.7) 0.00009407442939459683
KK      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.7,1.0) 0.6999973036455064
FL      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.5,0.7) 0.38494413131861455
IR      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint pdf(0.5,0.7) 1.0233716657780745
KG      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint pdf(0.7,0.5) 1.0233716657780745
LK      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint pdf(0.6,0.7) 1.0580116369285744
EP      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Conditional CDF (U<=0.5|V=0.7) 0.4461479582632463

For comparison, here is the Python code for the unit test pertaining to the Gaussian copula.

def test_gaussian(self):
        """
        Test Gaussian copula class.
        """

        cov = [[2, 0.5], [0.5, 2]]
        cop = GaussianCopula(cov=cov)
        # Check describe
        descr = cop.describe()
        self.assertEqual(descr['Descriptive Name'], 'Bivariate Gaussian Copula')
        self.assertEqual(descr['Class Name'], 'Gaussian')
        self.assertEqual(descr['cov'], cov)
        self.assertAlmostEqual(descr['rho'], 0.25, delta=1e-5)

        # Check copula joint cumulative density C(U=u,V=v)
        self.assertAlmostEqual(cop.C(0.7, 1e-4), cop.C(1e-4, 0.7), delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1), cop.C(1, 0.7), delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1e-8), 0, delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1), 0.7, delta=1e-4)
        self.assertAlmostEqual(cop.C(0.5, 0.7), 0.384944, delta=1e-4)

        # Check copula joint probability density c(U=u,V=v)
        self.assertAlmostEqual(cop.c(0.5, 0.7), cop.c(0.7, 0.5), delta=1e-8)
        self.assertAlmostEqual(cop.c(0.5, 0.7), 1.023371665778, delta=1e-4)
        self.assertAlmostEqual(cop.c(0.6, 0.7), 1.058011636928, delta=1e-4)

        # Check copula conditional cdf Prob(U<=u|V=v)
        self.assertAlmostEqual(cop.condi_cdf(0.5, 0.7), 0.446148, delta=1e-4

Next, we have the results for the CStudent class.

ER      0       14:40:34.138    TestBivariateStudentTCopula (XAUEUR,D1) Rho 0.24999999999999994
JG      0       14:40:35.369    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.0,0.2) 0.000006839679521344817
JD      0       14:40:36.613    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.2,0.0) 0.000006839679521344818
HK      0       14:40:38.041    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.7,1.0) 0.6999969941893684
PO      0       14:40:39.584    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(1.0,0.7) 0.6999969941893683
OR      0       14:40:41.280    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(1.0,1.0) 0.9999810861796908
RF      0       14:40:42.452    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.0,0.0) 0.0000010861794979038194
HJ      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.3,0.7) 0.23534922600994124
DL      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint pdf(0.5,0.7) 1.0915055449624917
FP      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint pdf(0.7,0.5) 1.0915055449624917
MD      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint pdf(0.6,0.7) 1.1416004955531887
DD      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Conditional CDF (U<=0.5|V=0.7) 0.441518430406228
MG      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Loglikelihood 2.135711666815534

Unit test for Student's t-copula.

def test_student(self):
        """
        Test Student copula class (Student-t).
        """

        cov = [[2, 0.5], [0.5, 2]]
        nu = 5
        cop = StudentCopula(cov=cov, nu=nu)
        # Check describe
        descr = cop.describe()
        self.assertEqual(descr['Descriptive Name'], 'Bivariate Student-t Copula')
        self.assertEqual(descr['Class Name'], 'Student')
        self.assertEqual(descr['cov'], cov)
        self.assertEqual(descr['nu (degrees of freedom)'], nu)
        self.assertAlmostEqual(descr['rho'], 0.25, delta=1e-5)
        # More to be added here for test on C(U<=u, V<=v)

        # Check copula joint probability density c(U=u,V=v)
        self.assertAlmostEqual(cop.c(0.5, 0.7), cop.c(0.7, 0.5), delta=1e-8)
        self.assertAlmostEqual(cop.c(0.5, 0.7), 1.09150554, delta=1e-4)
        self.assertAlmostEqual(cop.c(0.6, 0.7), 1.1416005, delta=1e-4)

        # Check copula joint cumulative density C(U=u,V=v)
        self.assertAlmostEqual(cop.C(0, 0.2), cop.C(0.2, 0), delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1), cop.C(1, 0.7), delta=1e-4)
        self.assertAlmostEqual(cop.C(1, 1), 1, delta=1e-4)
        self.assertAlmostEqual(cop.C(0, 0), 0, delta=1e-4)
        self.assertAlmostEqual(cop.C(0.3, 0.7), 0.23534923332657925, delta=1e-4)

        # Check copula conditional cdf Prob(U<=u|V=v)
        self.assertAlmostEqual(cop.condi_cdf(0.5, 0.7), 0.4415184293094455, delta=1e-4)

        # Check theta(tau)
        self.assertAlmostEqual(cop.theta_hat(2 * np.arcsin(0.2) / np.pi), 0.2, delta=1e-4)

        # log_ml function in ccalc
        u = np.array([0.1, 0.21, 0.5, 0.8])
        v = np.array([0.01, 0.25, 0.4, 0.7])
        new_cop = StudentCopula(nu=5)
        new_cop.fit(u, v)
        ll = new_cop.get_log_likelihood_sum(u=u,
                                            v=v)
        self.assertAlmostEqual(ll, 2.1357117471178584, delta=1e-5

As can be seen from the output, the library seems to be functioning correctly.

Concluding Remarks

Comparing the elliptical copulae implemented so far, the t-copula may be better suited for modeling joint extreme events. However, it cannot capture asymmetric tail dependence. This occurs when dependence is stronger in one tail than the other. For that, Archimedean copulae like Clayton or Gumbel would be more useful.

In the next installment in this series of articles, we will be discussing Archimedean copulae and their implementation in MQL5. Once we have a good number of copulae implemented, we will start to look at how to apply copulae to pairs trading.

File or folder	Description
MQL5/include/np.mqh	A header file of various vector and matrix utility functions.
MQL5/include/Copulas/Bivariate	This folder contains all the header files of coplulae implementations.
MQL5/include/ECDF	This folder contains the header files for the empirical CDF implementation described in the article.
MQL5/script/ECDF_Demo.mq5	This script demonstrated the application of the empirical CDF implementation described in the article.
MQL5/script/TestBivariateGaussianCopula.mq5	This script demonstrates the use of the CGaussian class.
MQL5/script/TestBivariateStudentTCopula.mq5	This script demonstrates the use of the CStudent class.
MQL5/script/SampleEllipticCopula.mq5	This script demonstrates sampling from an elliptical copula.