MQL5における二変量コピュラ（第1回）：依存関係モデリングのための正規コピュラおよびtコピュラの実装

はじめに

コピュラを用いた取引戦略は、資産間の依存関係をコピュラ関数によってモデル化することで、統計的裁定取引に対する有力な代替アプローチを提供します。従来のペア取引は、長期的な関係性からの一時的な乖離を前提としていますが、コピュラを用いることで、この関係性をより柔軟にモデル化することで、取引機会を識別することが可能になります。コピュラを利用する理論的な利点は、資産間の非線形かつ非対称な依存関係を捉えられる点にあります。

このような背景を踏まえ、本記事はコピュラベースの取引戦略を実装するためのツールを紹介する連載の始まりとなります。本記事では、ペア取引および依存関係モデリングの文脈において、統計的コピュラの基礎を解説します。また、コピュラモデルを適合する前段階として必要となる、データセットの前処理に関するMQL5コードも紹介します。連載全体を通じての主な目的は、一般的に使用されるコピュラモデルを実装したライブラリを構築することです。その第一歩として、本記事では正規コピュラとtコピュラの実装を紹介します。

コピュラ理論の基礎要素

コピュラを扱うためには、以下の3つの関連概念を理解する必要があります。

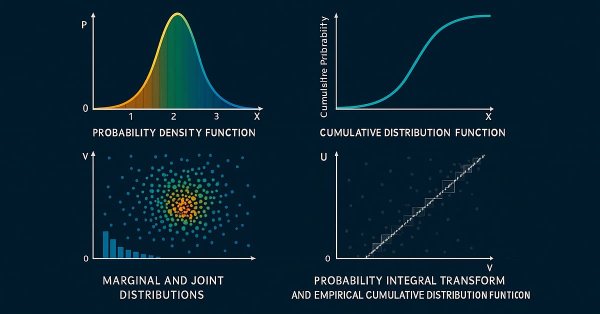
確率密度関数：統計分布の研究において、確率密度関数(PDF)は、連続確率変数Xが特定の値xを取る「起こりやすさ」を記述します。離散型の確率質量関数とは異なり、PDFは特定の値に直接確率を割り当てるものではありません。その代わりに密度を表し、Xが区間[a,b]に含まれる確率は、その区間におけるPDFの積分として与えられます。

累積分布関数：PDFを基礎として構築される累積分布関数(CDF)は、確率変数Xがx以下の値を取る確率を表します。CDFは0から1の範囲を取る単調非減少関数であり、確率変数の分布を完全に記述します。

周辺分布と同時分布：複数の確率変数を扱う場合、周辺分布と同時分布を区別する必要があります。周辺分布は、他の変数の影響を無視して、集合内の単一変数の確率分布を記述します。一方、同時分布は、データセットに含まれるすべての変数の結合的な確率分布を特徴付けます。  

確率積分変換(PIT)：確率積分変換(PIT)は確率論における基本概念であり、コピュラを理解するための重要な構成要素です。これは、連続確率変数Xが累積分布関数F(X)を持つ場合、変換後の変数U=F(X)は区間[0,1]上の一様分布に従うことを示します。つまり、Xが正規分布、指数分布、またはその他の連続分布に従うかに関わらず、自身のCDFを適用することで[0,1]上の一様分布を持つ変数に変換されます。

PITは、任意の連続確率変数を単位区間に写像し、確率構造を保持したまま標準化することを可能にします。周辺分布を一様分布に変換することで、各変数固有の分布形状の影響を受けずに変数間の結びつき（依存構造）を分析できます。この一様空間こそがコピュラが機能する領域であり、コピュラはこの変換後の空間において変数間の依存関係を捉えます。

経験累積分布関数：変数の真の基礎分布が不明な場合、経験累積分布関数(ECDF: Empirical Cumulative Distribution Function)を用いて真のCDFを推定できます。N個の観測値x₁,x₂,…,xₙからなるサンプルに対して、ECDFは次のように定義されます。​

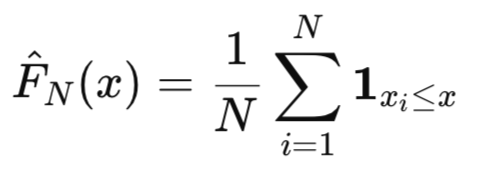
ここで用いられる指示関数は、xᵢ≤xの場合に1、それ以外の場合に0を取ります。

ECDFを用いてPITを実行する方法は、特定の分布形状を仮定しないため、ノンパラメトリック推定と呼ばれます。変換後のデータポイントは、コピュラ自体をフィッティングする際の入力として使用されます。

linear_cdf.mqhファイルには、データセットのECDFを推定するためのCLinearCDFクラスの定義が含まれています。このクラスは、標準的なECDFの段差の間に線形補間を適用したECDFを生成します。これにより、サンプル点では標準ECDFと一致しつつ、全体として滑らかな結果が得られます。

//+------------------------------------------------------------------+
//|                                                   linear_cdf.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Arrays/ArrayDouble.mqh>
#include<Arrays/ArrayObj.mqh>
#include "ecdf.mqh"
//+------------------------------------------------------------------+
//|CArray objects                                                    |
//+------------------------------------------------------------------+
class CArrayDoubles:public CArrayObj
  {
   virtual bool      CreateElement(const int index)
     {
      m_data[index] = new CArrayDouble();
      return m_data[index]!=NULL;
     }
  };
//+------------------------------------------------------------------+
//| ecdf quantile transformer                                        |
//+------------------------------------------------------------------+
class CLinearCDF
  {
protected:
   CSpline1DInterpolantShell* m_shells[];
   CArrayDoubles      m_internal;
   CArrayDouble      *m_arrays[];
   double            m_ub,m_lb;
   ulong             m_cols;
   void              clean_up(void)
     {

      for(uint i = 0; i<m_shells.Size(); i++)
         delete m_shells[i];
      for(uint i = 0; i<m_arrays.Size(); i++)
         delete m_arrays[i];
      m_internal.Clear();
     }
public:
                     CLinearCDF(void)
     {
      m_cols = 0;
     }
                    ~CLinearCDF(void)
     {
      clean_up();
     }
   bool              save(const int filehandle)
     {
      if(!m_cols)
         return false;
      return m_internal.Save(filehandle);
     }
   bool              load(const int filehandle)
     {
      if(m_cols)
        {
         clean_up();
         m_cols = 0;
        }

      if(m_internal.Load(filehandle))
        {
         int n_arrays = m_internal.Total();
         m_cols = ulong((n_arrays-1)/2);
         ArrayResize(m_shells,int(m_cols));
         ArrayResize(m_arrays,int(m_cols*2)+1);
         double xa[],ya[];
         m_arrays[0] = m_internal.At(0);
         m_ub = m_arrays[0].At(0);
         m_lb = m_arrays[0].At(1);
         for(int i = 0; i<int(m_cols); i++)
           {
            m_arrays[i*2+1] = m_internal.At(i*2+1);
            m_arrays[i*2+2] = m_internal.At(i*2+2);
            ArrayResize(xa,m_arrays[i*2+1].Total());
            for(int j = 0; j<m_arrays[i*2+1].Total(); j++)
               xa[j] = m_arrays[i*2+1][j];
            ArrayResize(ya,m_arrays[i*2+2].Total());
            for(int j = 0; j<m_arrays[i*2+2].Total(); j++)
               ya[j] = m_arrays[i*2+2][j];
            m_shells[i] = new CSpline1DInterpolantShell();
            CAlglib::Spline1DBuildLinear(xa,ya,m_shells[i]);
           }
         return true;
        }
      else
         return false;
     }
   bool              fit(matrix &data,double upper_bound = 1.0-1.e-5,double lower_bound = 1.e-5)
     {
      if(upper_bound<=lower_bound)
        {
         Print(__FUNCTION__, " invalid inputs ");
         return false;
        }

      if(m_cols)
        {
         clean_up();
         m_cols = 0;
        }

      m_ub = upper_bound;
      m_lb = lower_bound;
      m_cols = data.Cols();
      vector v;
      double xa[],ya[];
      vector slopes;
      vector slope_samples;
      CECDF m_ecdf;
      ArrayResize(m_shells,int(m_cols));
      ArrayResize(m_arrays,int(m_cols*2)+1);
      m_arrays[0] = new CArrayDouble();
      if(!m_arrays[0].Add(m_ub) || !m_arrays[0].Add(m_lb) || !m_internal.Add(m_arrays[0]))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }
      for(uint i = 0; i<m_shells.Size(); i++)
        {
         v = data.Col(i);
         if(!m_ecdf.fit(v))
           {
            Print(__FUNCTION__, " error ");
            return false;
           }

         np::quickSort(v,true,0,long(v.Size()-1));
         slopes = np::unique(v);
         slope_samples = m_ecdf.ecdf(slopes);
         m_shells[i] = new CSpline1DInterpolantShell();
         if(!np::vecAsArray(slopes,xa) || !np::vecAsArray(slope_samples,ya))
           {
            Print(__FUNCTION__, " error ");
            return false;
           }
         m_arrays[i*2+1] = new CArrayDouble();
         m_arrays[i*2+2] = new CArrayDouble();
         if(!m_arrays[i*2+1].AddArray(xa) || !m_arrays[i*2+2].AddArray(ya) ||!m_internal.Add(m_arrays[i*2+1])||!m_internal.Add(m_arrays[i*2+2]))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }
         CAlglib::Spline1DBuildLinear(xa,ya,m_shells[i]);
        }

      return true;
     }

   matrix            to_quantile(matrix &in)
     {
      if(in.Cols()!=m_cols)
        {
         Print(__FUNCTION__, " invalid input ");
         return matrix::Zeros(0,0);
        }

      vector temp;
      matrix out(in.Rows(),m_cols);
      for(ulong i = 0; i<m_cols; ++i)
        {
         temp  = in.Col(i);
         for(ulong j = 0; j<in.Rows(); ++j)
            out[j][i] = MathMax(MathMin(CAlglib::Spline1DCalc(m_shells[i],temp[j]),m_ub),m_lb);
        }

      return out;
     }
  };
//+------------------------------------------------------------------+

fit()メソッドは、多変量データセットの変数として解釈される任意の列数を持つ行列を受け取ります。オプションの入力パラメータであるupper_boundおよびlower_boundは、値がちょうど0または1になることを防ぐための制約を定義します。内部処理では、標準的なECDFが一意にソートされたサンプル点で評価されます。その後、これらのサンプル点と対応するECDF値を基に、一次元の線形補間モデルが構築されます。 

//+------------------------------------------------------------------+
//|                                                    ECDF_Demo.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<ECDF/linear_cdf.mqh>
//--- input parameters
input string   FirstSymbol = "NZDUSD";
input string   SecondSymbol = "AUDUSD";
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2024.01.01 00:00:01';
input ulong HistoryLength = 1000;
input bool Use_Returns = false;
input int DisplayDuration = 30;//display duration in seconds
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---download symbol data
   vector syA,syB;
   if(!syA.CopyRates(FirstSymbol,TimeFrame,COPY_RATES_CLOSE,StartDate,HistoryLength) ||
      !syB.CopyRates(SecondSymbol,TimeFrame,COPY_RATES_CLOSE,StartDate,HistoryLength) ||
      syA.Size()!=syB.Size())
     {
      Print("Error downloading price data ", ::GetLastError());
      return;
     }
//---optionally transform to returns
   if(Use_Returns)
     {
      syA = np::diff(log(syA));
      syB = np::diff(log(syB));
     }
//---create matrix container and fill it
   matrix xy(syA.Size(),2);
   if(!xy.Col(syA,0) || !xy.Col(syB,1))
     {
      Print(" column insertion error ", GetLastError());
      return ;
     }
//---build ECDF model
   CLinearCDF qd;
   if(!qd.fit(xy))
     {
      Print(" CLinearCDF failure ");
      return;
     }
//---transform raw values to quantiles
   matrix yx = qd.to_quantile(xy);
//---display QQ plot
   np::scatter_plot(yx.Col(0),yx.Col(1),"Q-Q plot",FirstSymbol,SecondSymbol,true,0,0,0,0,500,500,true,30);
//---
  }
//+------------------------------------------------------------------

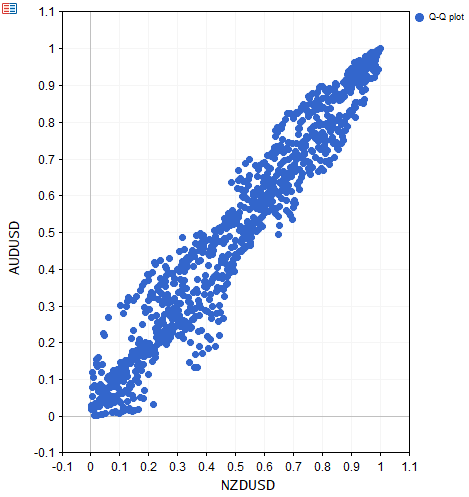
ECDF_Demo.ex5スクリプトは、価格の二変量データセットにCLinearCDFクラスを適用することで、その使用方法を示しています。変換後の値は、データの分位点同士を比較するためのQ-Qプロットを表示するために使用されます。 

コピュラの定義

コピュラとは、周辺分布とは独立して、確率変数間の依存構造を捉える多変量の累積分布関数です。より平易に言えば、コピュラは、各変数固有の挙動から変数間の依存関係を切り離して扱うことを可能にする数学的な仕組みです。

それぞれ独自の周辺分布を持つ複数の確率変数が与えられたとき、コピュラは、個々の分布形状に依存することなく、変数同士がどのように関係しているかを記述することで、これらの周辺分布を結合し、同時分布を構成します。このように、周辺分布と依存構造を分離できる点は、特に正規性や線形依存の仮定が適切でない場合において、現代の多変量解析の中核となる考え方です。この性質は、スコラーの定理(Sklar’s Theorem)によって数学的に定式化されています。スコラーの定理によれば、任意の連続な同時分布関数Fに対して、次の関係を満たす一意なコピュラCが存在します。

ここで、F₁(x₁)およびF₂(x₂)は、それぞれ確率変数X₁およびX₂の周辺累積分布関数です。

コピュラが2つ以上の確率変数間の依存関係を包含できる点は、相関係数のような連関の指標に例えることができます。ただし、相関係数が単一の数値に依存関係を要約するのに対し、コピュラは変数間の結びつきの性質について、より豊富な情報を提供します。

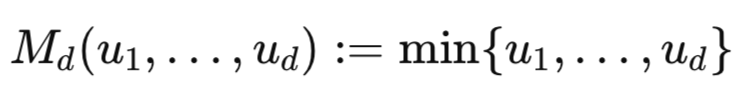
相関係数が−1から1の範囲に制約されているのと同様に、コピュラにもFréchet–Hoeffding境界と呼ばれる対応する上限および下限が存在します。下側および上側のFréchet–Hoeffding境界は、特定のコピュラが表現可能な最も負の依存関係および最も正の依存関係を定義する関数です。Fréchet–Hoeffding境界自体もコピュラであり、ここでのdは次元数、すなわち変数の個数を表します。

裾従属性

各コピュラ関数は固有の性質を持ち、それぞれ異なる種類の依存構造を表現できます。金融分野の応用において特に重要なコピュラの特性の一つが、裾従属性をモデル化する能力です。裾従属性とは、確率変数が分布の裾、すなわち極端な値の領域にあるときに、変数同士がどの程度同時に振る舞うかを測る指標です。コピュラが持つ裾従属性の種類によって、同時に発生する極端事象をどのように表現できるかが決まります。分布において、上側裾は非常に大きな値の領域を指し、下側裾は非常に小さな値の領域を指します。裾従属性は、裾従属性係数λによって定量化され、これは条件付き確率の極限として定義されます。裾従属性は、コピュラを用いて表現しない限り、定量的に評価することが困難な概念です。

下側裾従属性は、一方の変数が分布の下側裾に位置する、すなわち極端に小さい値を取っているときに、もう一方の変数も同様に下側裾に位置する確率を測定します。

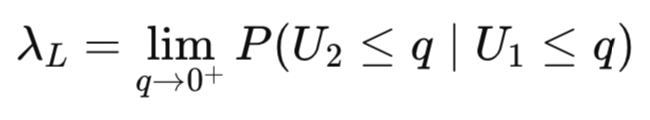
上側裾従属性は、一方の変数が分布の上側裾に位置する、すなわち極端に大きい値を取っているときに、もう一方の変数も同様に上側裾に位置する確率を測定します。

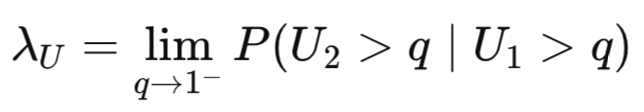
コピュラの種類

コピュラは、その関数形を定義する広範なクラスやファミリーに分類できます。本連載で取り上げるコピュラは、いずれもパラメトリックコピュラです。これらは、捉える依存特性を定量化するパラメータによって特徴付けられるコピュラです。

楕円コピュラは、多変量正規分布（ガウス分布）や多変量スチューデントt分布などの楕円分布から導かれる多変量コピュラのクラスです。これらは主に、変数間の線形依存構造を捉える連関の指標によってパラメータ化されます。最も一般的な楕円コピュラは、正規コピュラとtコピュラです。次のセクションでは、二変量楕円コピュラの実装について詳しく説明し、まず二変量正規コピュラから取り上げます。

二変量正規コピュラ

二変量正規コピュラは、標準的な二変量正規分布から導かれます。このコピュラは、基礎となる二変量正規分布の線形相関係数ρという単一のパラメータによって特徴付けられます。このパラメータが、2つの確率変数間の依存の強さと方向を決定します。正規コピュラは放射対称であり、計算上扱いやすい点から広く利用されています。ただし、裾従属性は弱く、変数間で同時に極端な値が発生する場合を十分に捉えることはできません。

ヘッダファイルgaussian.mqhには、二変量正規コピュラを実装するCGaussianクラスが定義されています。CGaussianは、base.mqhで定義されている抽象クラスCBivariateCopulaを継承しており、以降で説明するすべての二変量コピュラの実装の基盤となっています。

//+------------------------------------------------------------------+
//| base copula class                                                |
//+------------------------------------------------------------------+
class CBivariateCopula:public CObject
  {
private:
   int               m_len;
protected:
   double            m_eps;
   double            m_theta;
   double            m_rho;
   double            m_nu;
   double            m_threshold;
   ENUM_COPULA_TYPE  m_copula_type;
   vector            m_bounds;
   double            m_tau;
   matrix            m_cov;
   virtual bool      check_theta(void) 
     {
       return (m_theta>m_bounds.Min() < m_theta < m_bounds.Max());  
     }
   virtual double    pdf(double u,double v) { return EMPTY_VALUE; }
   virtual double    cdf(double u,double v) { return EMPTY_VALUE; }
   virtual double    condi_cdf(double u,double v) { return EMPTY_VALUE; }
   virtual vector    pdf(vector& u,vector& v){ return vector::Zeros(0); }
   virtual vector    cdf(vector& u,vector& v){ return vector::Zeros(0); }
   virtual vector    condi_cdf(vector& u,vector& v){ return vector::Zeros(0); }
   virtual double    theta_hat(const double tau){ return EMPTY_VALUE; }
   void              preprocess(double &u, double &v)
     {
      u = MathMin(MathMax(m_eps,u),1.0-m_eps);
      v = MathMin(MathMax(m_eps,v),1.0-m_eps);
     }
   void              preprocess(vector &u, vector &v)
     {
      u.Clip(m_eps,1.0-m_eps);
      v.Clip(m_eps,1.0-m_eps);
     }
   double            kendalTau(const vector &vec1,const vector &vec2)
     {
      double tau = double("nan");
      ulong size=vec1.Size();
      if(size==0 || vec2.Size()!=size)
        {
         Print(__FUNCTION__, " size of input vectors donot match ");
         return(tau);
        }
      //---
      long cnt1=0,cnt2=0,cnt=0;
      //---
      for(long i=0; i<long(size); i++)
        {
         for(long j=i+1; j<long(size); j++)
           {
            double delta1=vec1[i]-vec1[j];
            double delta2=vec2[i]-vec2[j];
            double delta=delta1*delta2;
            if(delta==0)
              {
               if(delta1!=0)
                  cnt1++;
               if(delta2!=0)
                  cnt2++;
              }
            else
              {
               cnt1++;
               cnt2++;
               if(delta>0.0)
                  cnt++;
               else
                  cnt--;
              }
           }
        }
      //--- calculate Kendall tau
      long den=cnt1*cnt2;
      if(den==0)
        {
         Print(__FUNCTION__, " failed zero check at line 76");
         return tau;
        }
      tau=double(cnt)/MathSqrt(den);
      //---
      return(tau);
     }

public:
                     CBivariateCopula(void)
     {
      m_len = 6;
      m_eps = 1.e-5;
      m_theta = m_rho = m_nu = EMPTY_VALUE;
      m_copula_type = WRONG_VALUE;
      m_cov  = matrix::Zeros(0,0);
      m_bounds = vector::Zeros(2);
      m_bounds[0] = -DBL_MIN;
      m_bounds[1] = DBL_MAX;
     }
                    ~CBivariateCopula(void)
     {
     }
   double            Get_theta(void)  { return m_theta; }
   double            Get_tau(void)    { return m_tau;   }
   double            Get_rho(void)    { return m_rho;   }
   matrix            Get_covar(void)  { return m_cov;   }
   double            Get_nu(void)     { return m_nu;    }
   double            Get_threshold(void) { return m_threshold; }
   double            Get_eps(void)    { return m_eps;   }
   virtual void              Set_theta(double theta) {  m_theta = theta; }
   virtual void              Set_tau(double tau) { m_tau = tau; }
   virtual void              Set_threshold(double threshold) { m_threshold = threshold; }
   virtual void              Set_nu(double nu) { m_nu = nu; }
   virtual void              Set_rho(double rho) { m_rho = rho; }
   virtual void              Set_eps(double eps) { m_eps = eps; }
   virtual matrix            Sample(ulong num_samples) { return matrix::Zeros(0,0); }
   virtual void              Set_covariance(matrix &cov)
     {
      m_cov = cov;
      m_rho = m_cov[0][1] / (sqrt(m_cov[0][0]) * sqrt(m_cov[1][1]));
     }
   virtual double    Fit(vector &u, vector&v)
     {
      if(u.Max()>1.0 || v.Max()>1.0 || v.Min()<0.0 ||u.Min()<0.0)
       {
        Print(__FUNCTION__, " Invalid input variable(s) ");
        return EMPTY_VALUE;
       }
      m_tau = kendalTau(u,v);
      m_theta = theta_hat(m_tau);
      if(!check_theta())
        Print(__FUNCTION__, " Invalid theta " );
      return  m_theta;
     }
   double            Log_likelihood(vector &u, vector &v)
     {
      if(u.Size()!=v.Size())
        {
         Print(__FUNCTION__, " vectors are not of equal length ");
         return EMPTY_VALUE;
        }
      
      vector ll = pdf(u,v);

      return (log(ll)).Sum();
     }
   double            Copula_PDF(double u, double v)
     {
      preprocess(u,v);
      return pdf(u,v);
     }
   double            Copula_CDF(double u, double v)
     {
      preprocess(u,v);
      return cdf(u,v);
     }
   double            Conditional_Probability(double u, double v)
     {
      preprocess(u,v);
      return condi_cdf(u,v);
     }
   vector            Copula_PDF(vector& u, vector& v)
     {
      preprocess(u,v);
      return pdf(u,v);
     }
   vector            Copula_CDF(vector& u, vector& v)
     {
      preprocess(u,v);
      return cdf(u,v);
     }
   vector            Conditional_Probability(vector& u, vector& v)
     {
      preprocess(u,v);
      return condi_cdf(u,v);
     }
   double            Theta(double tau = 0.0)
     {
      if(!tau && m_tau)
         return theta_hat(m_tau);
      else
         if(tau)
            return theta_hat(tau);
         else
           {
            Print(__FUNCTION__ " invalid input parameter 'tau' ");
            return EMPTY_VALUE;
           }
     }

   virtual bool      Save(const int file_handle)
     {
      if(file_handle!=INVALID_HANDLE)
        {
         //---
         if(FileWriteLong(file_handle,-1)==sizeof(long))
           {
            //---
            if(FileWriteInteger(file_handle,int(m_copula_type),INT_VALUE)!=INT_VALUE)
               return(false);
            //---
            if(FileWriteInteger(file_handle,m_len,INT_VALUE)!=INT_VALUE)
               return(false);
            //---
            if(FileWriteDouble(file_handle,m_eps)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_theta)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_tau)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_rho)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_nu)!=sizeof(double) ||
               FileWriteDouble(file_handle,m_threshold)!=sizeof(double))
               return false;
            return true;
           }
        }
      return false;
     }
   virtual bool      Load(const int file_handle)
     {
      if(file_handle!=INVALID_HANDLE)
        {
         //---
         if(FileReadLong(file_handle)==-1)
           {
            //---
            m_copula_type = ENUM_COPULA_TYPE(FileReadInteger(file_handle,INT_VALUE));

            if(FileReadInteger(file_handle,INT_VALUE)!=m_len)
               return false;

            ResetLastError();
            m_eps=FileReadDouble(file_handle);
            m_theta=FileReadDouble(file_handle);
            m_tau=FileReadDouble(file_handle);
            m_rho=FileReadDouble(file_handle);
            m_nu=FileReadDouble(file_handle);
            m_threshold=FileReadDouble(file_handle);
            if(GetLastError())
              {
               Print(__FUNCTION__, " possible read error ", GetLastError());
               return false;
              }
            return true;
           }
        }
      return false;
     }
   virtual int       Type(void)
     {
      return int(m_copula_type);
     }
  };

CGaussianクラスでは、コピュラモデルを2通りの方法で指定できます。1つは、アクセサメソッドを使用して関連するコピュラパラメータを明示的に設定する方法です。もう1つは、Fit()メソッドを使って二変量の一様分布データ（元の値の周辺CDFに変換したデータ）にモデルを適合させる方法です。適合に成功すると、EMPTY_VALUE定数以外の値が返されます。

コピュラの密度関数はCopula_PDF()メソッドで評価でき、Copula_CDF()メソッドではコピュラの同時累積分布関数を計算できます。条件付き累積分布関数はConditional_Probability()メソッドで求められます。これらのメソッドはすべて、スカラー入力およびベクトル入力に対応しています。Sample()メソッドを使用すると、コピュラのモデルパラメータに従った合成データセットを生成できます。さらに、Load()およびSave()メソッドを使うことで、コピュラモデルのシリアライズとデシリアライズによる永続化が可能です。

明示的に二変量正規コピュラを作成する場合は、2×2の共分散行列を指定する必要があります。

virtual void Set_covariance(matrix& cov) override
     {
      if(cov.Rows()!=2 || cov.Cols()!=2)
       {
        Print(__FUNCTION__," invalid input: expecting 2x2 matrix ");
        return;
       }
      m_cov = cov;
      m_rho = m_cov[0][1] / (sqrt(m_cov[0][0]) * sqrt(m_cov[1][1]));
      m_tau = (2.0/M_PI) * MathArcsin(m_rho);
      m_theta = theta_hat(m_tau);
     }

SampleEllipticCopula.ex5スクリプトは、楕円コピュラから生成した合成データが、指定したモデルパラメータに従っているかをテストします。ユーザーが設定可能な入力パラメータで、Covarで始まるものは共分散行列の各要素を指定します。Degree_Of_Freedomパラメータは、正規コピュラのテストには関係ありません。Sizeパラメータは、生成するサンプルの数を定義します。

//+------------------------------------------------------------------+
//|                                         SampleEllipticCopula.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Copulas/Bivariate/gaussian.mqh>
#include<Copulas/Bivariate/t.mqh>
//+------------------------------------------------------------------+
//|  enum                                                            |
//+------------------------------------------------------------------+
enum ENUM_ELPT_COPULA
 {
  GAUSSIAN=0,//Gaussian
  STUDENT//Student
 };
//--- input parameters
input ENUM_ELPT_COPULA copula_to_sample_from = GAUSSIAN;
input double Covar_0_0_ = 2.0;
input double Covar_0_1_ = 0.5;
input double Covar_1_0_ = 0.5;
input double Covar_1_1_ = 2.0;
input double Degrees_Of_Freedom = 5.0;
input ulong Size = 1000;

プログラムでは、Sample()メソッドを使用して合成データを生成し、その後散布図として表示します。その後、標準正規分布の逆累積分布関数（逆CDF）をデータセットに適用し、相関行列を推定します。

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix covar(2,2);
//---
   covar[0,0] = Covar_0_0_;
   covar[0,1] = Covar_0_1_;
   covar[1,0] = Covar_1_0_;
   covar[1,1] = Covar_1_1_;
//---
   CBivariateCopula *copula = NULL;
//---
   double set_theta = 0.0;
   switch(copula_to_sample_from)
    {
     case GAUSSIAN:
       copula = (CBivariateCopula*)new CGaussian();
       copula.Set_covariance(covar);
       break;
     case STUDENT:
       copula = (CBivariateCopula*)new CStudent();
       copula.Set_covariance(covar);
       copula.Set_nu(Degrees_Of_Freedom);
       break;
    }
//---
   Print("Specified correlation parameter of ", EnumToString(copula_to_sample_from)," copula :",copula.Get_rho());
   matrix samples = copula.Sample(Size);
   matrix inv_samples = samples;
   
   for(ulong i = 0; i<inv_samples.Rows(); ++i)
     for(ulong j =0; j<inv_samples.Cols(); ++j)
          inv_samples[i,j] = copula_to_sample_from == GAUSSIAN?CAlglib::InvNormalCDF(inv_samples[i,j]):studentTQuantile(inv_samples[i,j],Degrees_Of_Freedom);
          
   Print("Correlation of matrix of variable sampled from  ", EnumToString(copula_to_sample_from)," copula :\n", inv_samples.CorrCoef(false));      
   string cname = EnumToString((ENUM_COPULA_TYPE)copula.Type());
//---
   delete copula;
//---display scatter plot
   np::scatter_plot(inv_samples.Col(0),inv_samples.Col(1),cname+" Scatter plot","X","Y",true,0,0,0,0,500,300,true,10);  
//---
  }

ここでは、2回の実行結果を示します。期待される出力は、コピュラモデルの相関パラメータとほぼ同じ値の非対角要素を持つ行列です。指定するサンプル数によって結果は変わることに注意してください。サンプル数が多いほど、出力は指定した相関パラメータに近づきます。

CQ      0       14:06:16.963    SampleEllipticCopula (XAUEUR,D1)        Specified correlation parameter of GAUSSIAN copula :0.24999999999999994
DJ      0       14:06:17.021    SampleEllipticCopula (XAUEUR,D1)        Correlation of matrix of variable sampled from  GAUSSIAN copula :
DG      0       14:06:17.022    SampleEllipticCopula (XAUEUR,D1)        [[1,0.2497651923653427]
RK      0       14:06:17.022    SampleEllipticCopula (XAUEUR,D1)         [0.2497651923653427,1]]

次のセクションでは、他の楕円コピュラであるt-コピュラに注目します。

二変量tコピュラ

二変量tコピュラは、正規コピュラの代替としてよく用いられる手法の一つです。その理由は、正規コピュラでは捉えられない裾従属性を表現できるためです。tコピュラは、相関係数ρと自由度νの2つのパラメータによって定義されます。正規コピュラとは異なり、tコピュラは非ゼロの裾従属性を持ち、ある変数で極端な値が発生すると、もう一方の変数でも極端な値が生じやすくなります。

ここで

• tρ,ν​ ：相関係数ρおよび自由度νを持つ二変量t分布の累積分布関数(CDF)
• tν−1 ：自由度νの一変量t分布の逆累積分布関数（分位関数）
• u , v ∈ [ 0 , 1 ] u,v∈[0,1]

tコピュラでは、裾従属性は分布の裾の方が中心よりも強くなります。これは、分布全体で均一な依存関係を持つ正規コピュラとは異なる特徴です。そのため、金融リターンのモデリングに特に適しており、同時に発生する暴落や急騰といった極端事象をより現実的に表現できます。自由度パラメータνが大きくなると、上側および下側の裾従属性は減少します。自由度が無限大に近づくと、tコピュラは正規コピュラに収束します。逆に、自由度が小さいほど裾従属性は強くなります。

tコピュラは、t.mqhファイル内のCStudentクラスとして実装されており、CBivariateCopulaのサブクラスです。

//+------------------------------------------------------------------+
//|                                                            t.mqh |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "base.mqh"
#ifndef _NP_
#include<np.mqh>
#endif
#include<Math/Stat/T.mqh>
//+------------------------------------------------------------------+
//|utilities for Student's t distribution: Cheng Algorithm           |
//+------------------------------------------------------------------+
double            chengFuAlgo(double probability,double df)
  {
   double k = ceil(df*0.5);
   double a = 1.0 - probability;
   double qi = EMPTY_VALUE;
   if(a!=0.5)
     {
      qi = sqrt(2.0*pow(1.0-2.0*a,2.0)/(1.0 - pow(1.0-2.0*a,2.0)));
      double i = 0.0;
      double gy,j;
      while(i<20.0)
        {
         gy = 0.0;
         j = 0.0;
         while(j<=k-1.0)
           {
            gy+=MathFactorial(int(2*j))/pow(2.0,2.0*j)/pow(MathFactorial(int(j)),2.0)*pow(1.0+pow(qi,2.0)/(2.0*k),-j);
            j+=1.0;
           }
         qi = 1.0/sqrt(1.0/(2.0*k)*(pow(gy/1.0-2.0*a,2.0) - 1.0));
         i+=1.0;
        }
      if(a>0.5)
         return -qi;
      else
         return qi;
     }
   else
      return 0.0;
  }
//+------------------------------------------------------------------+
//| Hills algorithm                                                  |
//+------------------------------------------------------------------+
double            hillsAlgo(double probability,double df)
  {
   double z,a,b,c,x,y,d;
   z = a = b = c = x = y = d = EMPTY_VALUE;
   bool neg = false;
   if(probability>0.5)
     {
      z = 2.0*(1.0-probability);
     }
   else
     {
      neg = true;
      z = 2.0*probability;
     }
   a = 1.0/(df - 0.5);
   b = 48.0/(a*a);
   c = ((20700.0*a/b - 98.0)*a - 16.0)*a + 96.36;
   d = ((94.5/(b + c) - 3.0)/b + 1.0)*sqrt(a*M_PI/2.0)*df;
   x = z*d;
   y = pow(x,(2.0/df));

   if(y>0.05 + a)
     {
      x = CAlglib::InvNormalCDF(z*0.5);
      y = x*x;
      if(df<5.0)
         c = c+0.3*(df-4.5)*(x+0.6);
      c = c + (((0.05*d*x - 5.0)*x - 7.0)*x - 2.0)*x + b;
      y = (((((0.4*y + 6.3)*y + 36.0)*y + 94.5)/c - y - 3.0)/b + 1.0)*x;
      y = a*y*y;
      if(y > 0.002)
         y = exp(y) - 1.0;
      else
         y = y + 0.5*y*y;
     }
   else
      y = ((1.0/(((df + 6.0)/(df*y) - 0.089*d - 0.822)*(df + 2.0)*3.0) + 0.5/(df + 4.0))*y - 1.0)*(df + 1.0)/(df + 2.0) + 1.0/y;
   double q = sqrt(df*y);
   return (neg)?-1.0*q:q;
  }
//+------------------------------------------------------------------+
//| Student's t Inverse CDF                                          |
//+------------------------------------------------------------------+
double            studentTQuantile(double probability, double df)
  {
   if(df == 1.0)
      return tan(M_PI*(probability-1.0/2.0));
   else
      if(df == 2.0)
         return (2.0*probability-1.0)*sqrt(2.0/(4.0*probability*(1.0-probability)));
      else
         if(df == 4.0)
           {
            double a = 4.0*probability*(1.0 - probability);
            double q = cos(1.0/3.0*acos(sqrt(a)))/sqrt(a);
            return np::sign(probability - 0.5)*2.0*sqrt(q-1.0);
           }
         else
            if(!MathMod(df,2.0))
               return chengFuAlgo(probability,df);
            else
               return hillsAlgo(probability,df);
  }
//+------------------------------------------------------------------+
//| Student T Probability Density Function                           |
//+------------------------------------------------------------------+
double studentTDensity(double x, double df)
  {
   return CAlglib::GammaFunction((df + 1.0)/2.0)/(sqrt(df*M_PI)*CAlglib::GammaFunction(df/2.0))*pow((1.0 + pow(x,2.0)/df),(-((df + 1.0)/2.0)));
  }
//+------------------------------------------------------------------+
//| Bivariate Student Copula                                         |
//+------------------------------------------------------------------+
class CStudent : public CBivariateCopula
  {
private:
   virtual double    theta_hat(const double tau) override
     {
      return sin(tau*M_PI/2.0);
     }
   matrix            generate_corr_student(ulong num, matrix& cov, double nu_)
     {
      vector means = vector::Zeros(2);
      matrix normal = np::multivariate_normal(means,cov,num);

      double chi[];
      if(!MathRandomChiSquare(nu_,int(num),chi))
        {
         Print(__FUNCTION__, " Math random chisquare error ", GetLastError());
         return matrix::Zeros(0,0);
        }

      matrix out = matrix::Zeros(num,2);

      for(ulong i = 0; i<out.Rows(); i++)
        {
         double chisqrt = sqrt(chi[i]/nu_);
         out[i,0] = normal[i,0]/chisqrt;
         out[i,1] = normal[i,1]/chisqrt;
        }
      return out;
     }
   double            bvtdist(double z1,double z2, vector& mu, matrix& cov, double df)
     {
      double x1 = z1 - mu[0];
      double x2 = z2 - mu[1];
      double det_cov = cov[0,0]*cov[1,1]-cov[0,1]*cov[1,0];

      double xt = (-2.0*cov[0,1]*x1*x2+cov[0,0]*(pow(x1,2.0)+pow(x2,2.0)))/det_cov;
      double numerator = CAlglib::GammaFunction((2.0+df)/2.0);
      double denominator = (CAlglib::GammaFunction(df/2.0)*df*M_PI*sqrt(det_cov)*pow(1.0+xt/df,(2.0+df)/2.0));
      return numerator/denominator;
     }
   //+------------------------------------------------------------------+
   //|  inner integral function object                                  |
   //+------------------------------------------------------------------+
   class CInnerInt : public CIntegrator1_Func
     {
   private:
      double            m_x;
      double            m_rho;
      matrix            m_corr;
      vector            m_mu;
      double            m_nu;
   public:
      //---
                     CInnerInt(void)
        {
         m_mu = vector::Zeros(2);
        }
                    ~CInnerInt(void) {}
      void              Set(double x, double rho, double nu)
        {
         m_x = x;
         m_nu = nu;
         m_rho = rho;
         matrix crr = {{1.0, m_rho}, {m_rho, 1.0}};
         m_corr = crr;
        }
      virtual void      Int_Func(double x,double xminusa,double bminusx,double &y,CObject &obj)
        {
         double x1 = m_x - 0.0;
         double x2 = x - 0.0;
         double det_cov = m_corr[0,0]*m_corr[1,1]-m_corr[0,1]*m_corr[1,0];

         double xt = (-2.0*m_corr[0,1]*x1*x2+m_corr[0,0]*(pow(x1,2.0)+pow(x2,2.0)))/det_cov;
         double numerator = CAlglib::GammaFunction((2.0+m_nu)/2.0);
         double denominator = (CAlglib::GammaFunction(m_nu/2.0)*m_nu*M_PI*sqrt(det_cov)*pow(1.0+xt/m_nu,(2.0+m_nu)/2.0));
         y =  numerator/denominator;
        }
     };
   //+------------------------------------------------------------------+
   //|  outer integral function object                                  |
   //+------------------------------------------------------------------+
   class COuterInt : public CIntegrator1_Func
     {
   public:
      double            ay_limit;
      double            by_limit;
      double            nu;
      double            rho;
      //---
                     COuterInt(void) {}
                    ~COuterInt(void) {}
      virtual void      Int_Func(double x,double xminusa,double bminusx,double &y,CObject &obj)
        {
         CInnerInt fint;
         //---
         fint.Set(x,rho,nu);
         //---
         CAutoGKStateShell s;
         //---
         double integral;
         //---
         CObject ob;
         //---
         CAutoGKReportShell rep;
         //---
         CAlglib::AutoGKSmooth(ay_limit,by_limit,s);
         //---
         CAlglib::AutoGKIntegrate(s,fint,ob);
         //---
         CAlglib::AutoGKResults(s,integral,rep);
         //---
         CAutoGKReport report = rep.GetInnerObj();
         //---
         if(report.m_terminationtype<0.0)
            Print(__FUNCTION__, " integration error ",report.m_terminationtype);
         //---
         y = integral;
        }
     };
protected:
   virtual double    pdf(double u,double v) override
     {
      double y1,y2;
      y1 = studentTQuantile(u,m_nu);
      y2 = studentTQuantile(v,m_nu);
      vector means = vector::Zeros(2);
      matrix corr = {{1.0,m_rho},{m_rho,1.0}};
      double numerator = bvtdist(y1,y2,means,corr,m_nu);
      double denominator,pdf1,pdf2;
      pdf1 = studentTDensity(y1,m_nu);
      pdf2 = studentTDensity(y2,m_nu);
      denominator = pdf1*pdf2;
      return numerator/denominator;
     }
   virtual double    cdf(double u,double v) override
     {
      double uu,vv;
      uu = MathMax(u,1.e-6);
      vv = MathMax(v,1.e-6);
      //---
      int errcode = 0;
      //---
      COuterInt fout;
      fout.rho = m_rho;
      fout.nu = m_nu;
      fout.ay_limit = double(LONG_MIN);
      fout.by_limit = studentTQuantile(vv,m_nu);
      double ax_limit = double(LONG_MIN);
      double bx_limit = studentTQuantile(uu,m_nu);
      //---
      CObject obj;
      CAutoGKStateShell ss;
      //---
      double outer_integral;
      CAutoGKReportShell repp;
      //---
      CAlglib::AutoGKSmooth(ax_limit,bx_limit,ss);
      //---
      CAlglib::AutoGKIntegrate(ss,fout,obj);
      //---
      CAlglib::AutoGKResults(ss,outer_integral,repp);
      //---
      CAutoGKReport report = repp.GetInnerObj();
      //---
      if(report.m_terminationtype<0.0)
         Print(__FUNCTION__, " integration error ",report.m_terminationtype);
      //---
      return MathMax(MathMin(outer_integral,1.0),0.0);
     }
   virtual double    condi_cdf(double u,double v) override
     {
      double inv_u,inv_v;
      int errcode = 0;
      inv_u = studentTQuantile(u,m_nu);
      inv_v = studentTQuantile(v,m_nu);
      double numerator,denominator;
      numerator = (inv_u-m_rho*inv_v)*sqrt(m_nu+1.0);
      denominator = sqrt((1.0-pow(m_rho,2.))*(pow(inv_v,2.0)+m_nu));
      double tcdf = MathCumulativeDistributionT(numerator/denominator,m_nu+1.0,errcode);
      if(errcode)
        {
         Print(__FUNCTION__, " mathcdf error ", errcode);
         return EMPTY_VALUE;
        }
      return tcdf;
     }
   virtual vector    pdf(vector &u,vector &v) override
     {
      vector out(u.Size());
      for(ulong i = 0; i<u.Size(); ++i)
         out[i] = pdf(u[i],v[i]);
      return out;
     }
   virtual vector    cdf(vector &u,vector &v) override
     {
      vector out(u.Size());
      for(ulong i = 0; i<u.Size(); ++i)
         out[i] = cdf(u[i],v[i]);
      return out;
     }
   virtual vector    condi_cdf(vector &u,vector &v) override
     {
      vector out(u.Size());
      for(ulong i = 0; i<u.Size(); ++i)
         out[i] = condi_cdf(u[i],v[i]);
      return out;
     }
public:
                     CStudent(void)
     {
      m_copula_type = STUDENT_COPULA;
     }
                    ~CStudent(void)
     {
     }

   virtual matrix    Sample(ulong num_samples) override
     {
      matrix spairs = generate_corr_student(num_samples,m_cov,m_nu);
      matrix out = spairs;
      int err1,err2;
      err1 = err2 = 0;
      for(ulong i = 0; i<spairs.Rows(); ++i)
        {
         out[i,0] = MathCumulativeDistributionT(spairs[i,0],m_nu,err1);
         out[i,1] = MathCumulativeDistributionT(spairs[i,1],m_nu,err2);
         if(err1 || err2)
           {
            Print(__FUNCTION__, " mathcdf error ", err1?err1:err2);
            return matrix::Zeros(0,0);
           }
        }
      return out;
     }
   virtual double    Fit(vector &u, vector&v) override
     {
      if(u.Max()>1.0 || v.Max()>1.0 || v.Min()<0.0 ||u.Min()<0.0)
        {
         Print(__FUNCTION__, " Invalid input variable(s) ");
         return EMPTY_VALUE;
        }
      m_tau = kendalTau(u,v);
      m_theta = theta_hat(m_tau);
      if(m_nu == EMPTY_VALUE)
         m_nu = fit_nu(u,v);
      matrix vals = matrix::Zeros(u.Size(),2);
      for(ulong i = 0; i<vals.Rows(); ++i)
        {
         vals[i,0] = studentTQuantile(u[i],m_nu);
         vals[i,1] = studentTQuantile(v[i],m_nu);
        }
      m_cov = vals.Cov(false);
      m_rho = m_cov[0,1]/(sqrt(m_cov[0,0])*sqrt(m_cov[1,1]));
      return m_rho;
     }
  };

//+------------------------------------------------------------------+

以下は、SampleEllipticCopula.ex5を実行し、tコピュラオプションを選択した場合の2回の実行結果です。

IM      0       14:07:00.097    SampleEllipticCopula (XAUEUR,D1)        Specified correlation parameter of STUDENT copula :0.24999999999999994
NQ      0       14:07:00.295    SampleEllipticCopula (XAUEUR,D1)        Correlation of matrix of variable sampled from  STUDENT copula :
GF      0       14:07:00.295    SampleEllipticCopula (XAUEUR,D1)        [[1,0.2441795870726779]
MJ      0       14:07:00.295    SampleEllipticCopula (XAUEUR,D1)         [0.2441795870726779,1]]

テストと検証

両方のコピュラ実装の残りのメソッドをテストするために、TestBivariateGaussianCopula.ex5およびTestBivariateStudentTCopula.ex5スクリプトを用意しています。これらのスクリプトでは、特定のコピュラモデルを作成し、PDF、CDF、および条件付きCDFのコードを評価します。これらのテストは、MQL5コードの元となったArbitrageLab Pythonパッケージのユニットテストを再現したものです。これにより、MQL5コードが元のPython実装と同じ方法で動作するかどうかを確認できます。

//+------------------------------------------------------------------+
//|                                  TestBivariateGaussianCopula.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
//--- input parameters
#include<Copulas/Bivariate/gaussian.mqh>
//---
 double Covar_0_0_ = 2.0;
 double Covar_0_1_ = 0.5;
 double Covar_1_0_ = 0.5;
 double Covar_1_1_ = 2.0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix covar(2,2);
//---
   covar[0,0] = Covar_0_0_;
   covar[0,1] = Covar_0_1_;
   covar[1,0] = Covar_1_0_;
   covar[1,1] = Covar_1_1_;
//---   
   CGaussian norm_copula;
   norm_copula.Set_covariance(covar);
//---   
   Print("Rho ", norm_copula.Get_rho());
   Print("Joint cdf(0.7,0.0001) ",norm_copula.Copula_CDF(0.7,0.0001));
   Print("Joint cdf(0.0001,0.7) ",norm_copula.Copula_CDF(0.0001,0.7));
   Print("Joint cdf(0.7,1.0) ",norm_copula.Copula_CDF(0.7,1.0));
   Print("Joint cdf(0.5,0.7) ",norm_copula.Copula_CDF(0.5,0.7));
//---   
   Print("Joint pdf(0.5,0.7) ",norm_copula.Copula_PDF(0.5,0.7));
   Print("Joint pdf(0.7,0.5) ",norm_copula.Copula_PDF(0.7,0.5));
   Print("Joint pdf(0.6,0.7) ",norm_copula.Copula_PDF(0.6,0.7));
//---   
   Print("Conditional CDF (U<=0.5|V=0.7) ",norm_copula.Conditional_Probability(0.5,0.7));
  }
//+------------------------------------------------------------------+

CGaussianメソッドのテストの結果は次のとおりです。

KR      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Rho 0.24999999999999994
JR      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.7,0.0001) 0.00009407442939459683
JG      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.0001,0.7) 0.00009407442939459683
KK      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.7,1.0) 0.6999973036455064
FL      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint cdf(0.5,0.7) 0.38494413131861455
IR      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint pdf(0.5,0.7) 1.0233716657780745
KG      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint pdf(0.7,0.5) 1.0233716657780745
LK      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Joint pdf(0.6,0.7) 1.0580116369285744
EP      0       14:40:26.403    TestBivariateGaussianCopula (XAUEUR,D1) Conditional CDF (U<=0.5|V=0.7) 0.4461479582632463

比較のために、正規コピュラに関する単体テストのPythonコードを次に示します。

def test_gaussian(self):
        """
        Test Gaussian copula class.
        """

        cov = [[2, 0.5], [0.5, 2]]
        cop = GaussianCopula(cov=cov)
        # Check describe
        descr = cop.describe()
        self.assertEqual(descr['Descriptive Name'], 'Bivariate Gaussian Copula')
        self.assertEqual(descr['Class Name'], 'Gaussian')
        self.assertEqual(descr['cov'], cov)
        self.assertAlmostEqual(descr['rho'], 0.25, delta=1e-5)

        # Check copula joint cumulative density C(U=u,V=v)
        self.assertAlmostEqual(cop.C(0.7, 1e-4), cop.C(1e-4, 0.7), delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1), cop.C(1, 0.7), delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1e-8), 0, delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1), 0.7, delta=1e-4)
        self.assertAlmostEqual(cop.C(0.5, 0.7), 0.384944, delta=1e-4)

        # Check copula joint probability density c(U=u,V=v)
        self.assertAlmostEqual(cop.c(0.5, 0.7), cop.c(0.7, 0.5), delta=1e-8)
        self.assertAlmostEqual(cop.c(0.5, 0.7), 1.023371665778, delta=1e-4)
        self.assertAlmostEqual(cop.c(0.6, 0.7), 1.058011636928, delta=1e-4)

        # Check copula conditional cdf Prob(U<=u|V=v)
        self.assertAlmostEqual(cop.condi_cdf(0.5, 0.7), 0.446148, delta=1e-4

次に、CStudentクラスの結果を示します。

ER      0       14:40:34.138    TestBivariateStudentTCopula (XAUEUR,D1) Rho 0.24999999999999994
JG      0       14:40:35.369    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.0,0.2) 0.000006839679521344817
JD      0       14:40:36.613    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.2,0.0) 0.000006839679521344818
HK      0       14:40:38.041    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.7,1.0) 0.6999969941893684
PO      0       14:40:39.584    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(1.0,0.7) 0.6999969941893683
OR      0       14:40:41.280    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(1.0,1.0) 0.9999810861796908
RF      0       14:40:42.452    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.0,0.0) 0.0000010861794979038194
HJ      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint cdf(0.3,0.7) 0.23534922600994124
DL      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint pdf(0.5,0.7) 1.0915055449624917
FP      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint pdf(0.7,0.5) 1.0915055449624917
MD      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Joint pdf(0.6,0.7) 1.1416004955531887
DD      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Conditional CDF (U<=0.5|V=0.7) 0.441518430406228
MG      0       14:40:43.757    TestBivariateStudentTCopula (XAUEUR,D1) Loglikelihood 2.135711666815534

tコピュラの単体テストのPythonコードを次に示します。

def test_student(self):
        """
        Test Student copula class (Student-t).
        """

        cov = [[2, 0.5], [0.5, 2]]
        nu = 5
        cop = StudentCopula(cov=cov, nu=nu)
        # Check describe
        descr = cop.describe()
        self.assertEqual(descr['Descriptive Name'], 'Bivariate Student-t Copula')
        self.assertEqual(descr['Class Name'], 'Student')
        self.assertEqual(descr['cov'], cov)
        self.assertEqual(descr['nu (degrees of freedom)'], nu)
        self.assertAlmostEqual(descr['rho'], 0.25, delta=1e-5)
        # More to be added here for test on C(U<=u, V<=v)

        # Check copula joint probability density c(U=u,V=v)
        self.assertAlmostEqual(cop.c(0.5, 0.7), cop.c(0.7, 0.5), delta=1e-8)
        self.assertAlmostEqual(cop.c(0.5, 0.7), 1.09150554, delta=1e-4)
        self.assertAlmostEqual(cop.c(0.6, 0.7), 1.1416005, delta=1e-4)

        # Check copula joint cumulative density C(U=u,V=v)
        self.assertAlmostEqual(cop.C(0, 0.2), cop.C(0.2, 0), delta=1e-4)
        self.assertAlmostEqual(cop.C(0.7, 1), cop.C(1, 0.7), delta=1e-4)
        self.assertAlmostEqual(cop.C(1, 1), 1, delta=1e-4)
        self.assertAlmostEqual(cop.C(0, 0), 0, delta=1e-4)
        self.assertAlmostEqual(cop.C(0.3, 0.7), 0.23534923332657925, delta=1e-4)

        # Check copula conditional cdf Prob(U<=u|V=v)
        self.assertAlmostEqual(cop.condi_cdf(0.5, 0.7), 0.4415184293094455, delta=1e-4)

        # Check theta(tau)
        self.assertAlmostEqual(cop.theta_hat(2 * np.arcsin(0.2) / np.pi), 0.2, delta=1e-4)

        # log_ml function in ccalc
        u = np.array([0.1, 0.21, 0.5, 0.8])
        v = np.array([0.01, 0.25, 0.4, 0.7])
        new_cop = StudentCopula(nu=5)
        new_cop.fit(u, v)
        ll = new_cop.get_log_likelihood_sum(u=u,
                                            v=v)
        self.assertAlmostEqual(ll, 2.1357117471178584, delta=1e-5

出力からわかるように、ライブラリは正常に機能しているようです。

結論

これまでに実装した楕円コピュラを比較すると、tコピュラは同時に発生する極端事象のモデリングにより適していると言えます。ただし、非対称な裾従属性、すなわち一方の裾で依存が強く、もう一方では弱い場合を捉えることはできません。そのような場合には、クレイトンやグンベルのようなアルキメデスコピュラの方が有用です。

次回の記事では、アルキメデスコピュラとそのMQL5での実装について解説します。十分な数のコピュラが実装できた段階で、コピュラをペア取引への応用にどのように活かすかについても見ていきます。

ファイルまたはフォルダ	詳細
MQL5/include/np.mqh	各種ベクトルおよび行列のユーティリティ関数をまとめたヘッダファイル
MQL5/include/Copulas/Bivariate	二変量コピュラの実装に関するすべてのヘッダファイルが含まれるフォルダ
MQL5/include/ECDF	記事で解説した経験累積分布関数(ECDF)実装用ヘッダファイルが含まれるフォルダ
MQL5/script/ECDF_Demo.mq5	記事で解説したECDFの実装を適用するデモ用スクリプト
MQL5/script/TestBivariateGaussianCopula.mq5	CGaussianクラスの使用方法を示すテストスクリプト
MQL5/script/TestBivariateStudentTCopula.mq5	CStudentクラスの使用方法を示すテストスクリプト
MQL5/script/SampleEllipticCopula.mq5	楕円コピュラからのサンプリングを示すスクリプト