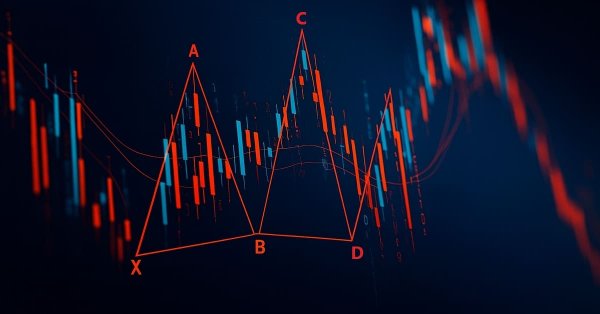
Einführung in MQL5 (Teil 21): Automatisiertes Erkennen von harmonischen Mustern
Einführung
Willkommen zurück zu Teil 21 der Serie Einführung in MQL5! In Teil 20 habe ich Ihnen harmonische Muster vorgestellt und die mathematischen Konzepte hinter Fibonacci-Retracements und -Extensions sowie deren Implementierung in MQL5 erläutert. In diesem Artikel gehen wir einen Schritt weiter und konzentrieren uns auf die Automatisierung der Erkennung des harmonischen Musters von Gartley.
Sie werden lernen, wie Sie mögliche Gartley-Muster programmatisch auf Ihren Charts erkennen können, indem Sie Fibonacci-Levels, Preisausschläge und Chart-Objekte verwenden. Die Logik und die Methoden, die wir hier erörtern, lassen sich auch auf andere harmonische Muster wie Fledermaus, Schmetterling, Krabbe und tiefe Krabbe anwenden, auch wenn wir uns der Einfachheit halber auf das Gartley-Muster konzentrieren werden.
Die Besonderheit dieses Artikels besteht darin, dass er sich an Anfänger wendet und schwierige Sachverhalte in überschaubaren Schritten vereinfacht. Anstatt Sie mit Theorie zu überladen, werden wir an einer projektbasierten Strategie arbeiten, bei der wir einen Expert Advisor (EA) erstellen, der das Gartley-Muster automatisch erkennt.
Einrichten des Projekts
Das Ziel dieses Projekts ist es, einen Expert Advisor (EA) zu erstellen, der automatisch das harmonische Muster von Gartley in einem Chart erkennen kann. Auf der Grundlage vorher festgelegter Kriterien bewertet der EA Kursschwankungen, berechnet wichtige Fibonacci-Retracement- und Extension-Levels und erkennt mögliche Gartley-Formationen.
Vier große Kanten (XA, AB, BC und CD) und bestimmte Fibonacci-Beziehungen definieren das Gartley-Muster: Punkt B muss etwa 78,6 Prozent der XA-Kante zurückgehen, Punkt C muss zwischen 38,2 und 88,6 Prozent der AB-Kante zurückgehen, und Punkt D muss etwa 78,6 Prozent der XA-Kante zurückgehen. Der EA ist anpassungsfähig und auch für Anfänger leicht zu bedienen, da er es den Händlern ermöglicht, die Fibonacci-Retracement- und Erweiterungsbereiche an ihren eigenen Handelsstil anzupassen.
Logik für Kaufen
Um ein Aufwärtsmuster von Gartley zu erkennen, geht der EA wie folgt vor:
- Identifiziere X als einen Tiefpunkt.
- Erkenne A als einen signifikanten hohen Umkehrpunkt nach X.
- Lokalisiere B, der innerhalb des angegebenen Bereichs der XA-Kante zurückgehen muss.
- Bestätige C, der sich innerhalb der angegebenen Spanne der AB-Kante zurückbewegt.
- Berechne den potenziellen D-Punkt, der innerhalb eines bestimmten Bereichs des Retracements der XA-Kante liegen sollte.
- Stell sicher, dass alle Kanten der erforderlichen Fibonacci-Ausrichtung für eine gültige Gartley-Struktur entsprechen.
- Sobald Punkt D bestätigt wird, erzeugt der EA ein Kaufsignal und erwartet, dass der Kurs von diesem Niveau aus nach oben dreht.
- Darüber hinaus ermöglicht der EA den Nutzern, alle Fibonacci-Retracement- und Extensions-Prozentsätze über die Eingabeeinstellungen anzupassen, was Flexibilität auf der Grundlage unterschiedlicher Marktbedingungen bietet.
Sobald der EA ein gültiges Aufwärtsmuster von Gartley bestätigt:
- Eröffnung: Ein Kaufgeschäft wird bei Punkt D eröffnet, gleich nachdem das Muster abgeschlossen ist.
- Stop Loss (SL): Auf dem Tief des Umkehrpunktes, der den Punkt D bildete, platziert.
- Gewinnmitnahme (TP): Die Einstellung erfolgt mit einem Risiko-Ertrags-Verhältnis von 1:3, d.h. der TP-Abstand ist dreimal so groß wie der SL.
Logik für einen Verkauf
Um ein Abwärtsmuster von Gartley zu erkennen, geht der EA folgendermaßen vor:
- Identifiziere X als einen hohen Umkehrpunkt.
- Erkenne A als einen signifikanten tiefen Umkehrpunkt nach X.
- Lokalisiere B, der innerhalb des angegebenen Bereichs der XA-Kante zurückgehen muss.
- Bestätige C, der zwischen den angegebenen Bereich AB Bein zurückgeht.
- Berechne den potenziellen D-Punkt, der in einem Bereich der XA-Kante liegen sollte.
- Stell sicher, dass alle Kanten der erforderlichen Fibonacci-Ausrichtung für eine gültige Gartley-Struktur entsprechen.
- Sobald Punkt D bestätigt wird, erzeugt der EA ein Verkaufssignal und erwartet, dass der Kurs von diesem Niveau aus nach unten dreht.
- Darüber hinaus ermöglicht der EA den Nutzern, alle Fibonacci-Retracement- und Extensions-Prozentsätze über die Eingabeeinstellungen anzupassen, was Flexibilität auf der Grundlage unterschiedlicher Marktbedingungen bietet.
Sobald der EA ein gültiges Abwärtsmuster Gartley bestätigt:
- Eröffnung: Bei Punkt D, unmittelbar nach Abschluss des Musters, wird ein Verkaufsgeschäft eröffnet.
- Stop Loss (SL): Platziert auf dem hohen Umkehrpunkt, der Punkt D bildete.
- Gewinnmitnahme (TP): Die Einstellung erfolgt mit einem Risiko-Ertrags-Verhältnis von 1:3, d.h. der TP-Abstand ist dreimal so groß wie der SL.
Abwärtsmuster von Gartley erkennen
Im letzten Artikel habe ich den Unterschied zwischen steigenden und fallenden harmonischen Mustern im Detail erklärt. Wie ich immer sage, wenn Sie mit Chartmustern arbeiten, brauchen Sie Kerzendaten, und Sie müssen in der Lage sein, hohe und tiefe Umkehrpunkte zu erkennen. Der Anfangspunkt X für ein Abwärtsmuster von Gartley muss ein hoher Umkehrpunkt sein. Die Struktur folgt dann den notwendigen Fibonacci-Retracement- und Extension-Levels, während sie sich in die XA-, AB-, BC- und CD-Kanten bewegt. Der EA kann die XABCD-Struktur abbilden und feststellen, ob sie den Parametern eines fallenden Gartley entspricht, indem er diese Ausschläge genau identifiziert.
Beispiel:
input ENUM_TIMEFRAMES timeframe = PERIOD_CURRENT; // TIMEFRAME double open[]; double close[]; double low[]; double high[]; datetime time[]; datetime time_bar; int bars_check = 500; int total_symbol_bars; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { total_symbol_bars = Bars(_Symbol, timeframe); time_bar = iTime(_Symbol, timeframe, 0); CopyOpen(_Symbol, timeframe, time_bar, bars_check, open); CopyClose(_Symbol, timeframe, time_bar, bars_check, close); CopyLow(_Symbol, timeframe, time_bar, bars_check, low); CopyHigh(_Symbol, timeframe, time_bar, bars_check, high); CopyTime(_Symbol, timeframe, time_bar, bars_check, time); } //+------------------------------------------------------------------+ //| FUNCTION FOR SWING LOW | //+------------------------------------------------------------------+ bool IsSwingLow(const double &low_price[], int index, int lookback) { for(int i = 1; i <= lookback; i++) { if(low_price[index] > low_price[index - i] || low_price[index] > low_price[index + i]) return false; } return true; } //+------------------------------------------------------------------+ //| FUNCTION FOR SWING HIGH | //+------------------------------------------------------------------+ bool IsSwingHigh(const double &high_price[], int index, int lookback) { for(int i = 1; i <= lookback; i++) { if(high_price[index] < high_price[index - i] || high_price[index] < high_price[index + i]) return false; // If the current high is not the highest, return false. } return true; }
Erläuterung:
Der erste Schritt besteht darin, den Zeitrahmen des Expert Advisors so einzustellen, dass er mit dem Chart übereinstimmt, auf dem er arbeitet. Für die Aufzeichnung historischer Kerzendaten, einschließlich Eröffnungs-, Schluss-, Hoch- und Tiefstkursen sowie der Uhrzeit, stehen Arrays bereit. Der Zeitstempel des letzten Balkens, die Gesamtzahl der verfügbaren Balken und die Anzahl der zu analysierenden Balken werden durch andere Variablen verfolgt. Später werden die Marktdaten in diesen Arrays gespeichert, um eine detaillierte Analyse der Preisschwankungen zu ermöglichen.
Das Programm sammelt die Zeit des letzten Balkens und bestimmt, wie viele Balken für jede Marktaktualisierung zur Verfügung stehen. Um zu gewährleisten, dass die Analyse immer auf dem aktuellen Stand des Marktes ist, werden die neuesten Preis- und Zeitdaten gesammelt. Dies bietet eine solide Grundlage für weitere Berechnungen sowie für das Aufspüren technischer Trends in den Kursdaten.
Durch den Vergleich der einzelnen Balken mit ihren Nachbarn ermitteln nutzerdefinierte Funktionen signifikante Höchst- und Tiefstwerte. Eine Funktion prüft ein klares Tief, eine andere ein klares Hoch. Steigende und fallende Gartley-Setups sind Beispiele für harmonische Muster, die der Computer konsequent erkennt, indem er diese Punkte nur überwacht, wenn sich ein neuer Balken bildet.
Identifizierung von X
Das Auffinden des Punktes X ist der erste Schritt zur Identifizierung eines fallenden Gartley-Musters. Punkt X muss ein hoher Umkehrpunkt auf dem Chart sein, damit das Setup abwärts zeigt. Dies bedeutet, dass es sich um eine Spitze handeln sollte, bei der der Preis ansteigt, bevor er zurückgeht.
Beispiel:
double X; datetime X_time; string X_letter; int z = 4; long chart_id = ChartID();
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { total_symbol_bars = Bars(_Symbol, timeframe); time_bar = iTime(_Symbol, timeframe, 0); CopyOpen(_Symbol, timeframe, time_bar, bars_check, open); CopyClose(_Symbol, timeframe, time_bar, bars_check, close); CopyLow(_Symbol, timeframe, time_bar, bars_check, low); CopyHigh(_Symbol, timeframe, time_bar, bars_check, high); CopyTime(_Symbol, timeframe, time_bar, bars_check, time); if(total_symbol_bars >= bars_check) { for(int i = z ; i < bars_check - z; i++) { if(IsSwingHigh(high, i, z)) { X = high[i]; X_time = time[i]; X_letter = StringFormat("X %d",i); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); } } } }
Erläuterung:
Um sicherzustellen, dass genügend Kerzen für die Untersuchung zur Verfügung stehen, beginnt das Programm mit einem Sicherheitscheck. Er stellt sicher, dass mindestens 500 Balken im Chart vorhanden sind, bevor er fortfährt, da er diese Anzahl benötigt. So werden Fehler vermieden, und der Expert Advisor kann sicher sein, dass er nur umfassende Marktdaten verwendet, wenn er diese Vorsicht walten lässt. Nach dieser Prüfung geht die Software in einer Schleife und mit einer Rückblickzeit (z) über die Kerzen und vergleicht jede einzelne mit ihren Nachbarn. Zur Vermeidung von Fehlern, die außerhalb des Bereichs liegen, und zur genauen Bestimmung von Umkehrpunkten wird z beispielsweise auf 4 gesetzt, sodass jede Kerze mit den vier Kerzen verglichen wird, die ihr vorausgingen und folgten.
Der Algorithmus legt den Punkt X, den ersten Anker des fallende Gartley-Musters, innerhalb dieser Schleife fest, indem er nach einem hohen Umkehrpunkt sucht. Preis, Zeit und Index werden beibehalten, wenn ein legitimer hoher Umkehrpunkt identifiziert wird, und das Chart wird sofort mit einer Textbeschriftung versehen, die „X“ lautet. Diese visuelle Markierung hebt nicht nur den entscheidenden Umkehrpunkt hervor, sondern bietet auch eine klare Referenz für die nachfolgenden Phasen bei der Bestimmung des restlichen Gartley-Musters.
Identifizierung von A
Der nächste Schritt ist die Suche nach dem Punkt A, nachdem X korrekt als rechtmäßiger hoher Umkehrpunkt markiert wurde. A ist in der Regel einen tiefen Umkehrpunkt, der sich im Anschluss an X in einem fallenden harmonischen Muster entwickelt. Der EA bewegt sich von dem Balken, an dem X entdeckt wurde, vorwärts, um diesen zu lokalisieren. Ähnlich wie bei der Verwendung von IsSwingHigh für X wird mit der Funktion IsSwingLow nach einem tiefen Umkehrpunk gesucht, indem jeder Balken im Bereich überprüft wird.
Beispiel:
double A; datetime A_time; string A_letter; string xa_line;
if(total_symbol_bars >= bars_check) { for(int i = z ; i < bars_check - z; i++) { if(IsSwingHigh(high, i, z)) { X = high[i]; X_time = time[i]; X_letter = StringFormat("X %d",i); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); for(int j = i; j < bars_check - z; j++) { if(IsSwingLow(low, j, z) && low[j] < X) { A = low[j]; A_time = time[j]; A_letter = StringFormat("A %d",j); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); xa_line = StringFormat("XA Line %d",i); ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A); break; } } } } }
Ausgabe:
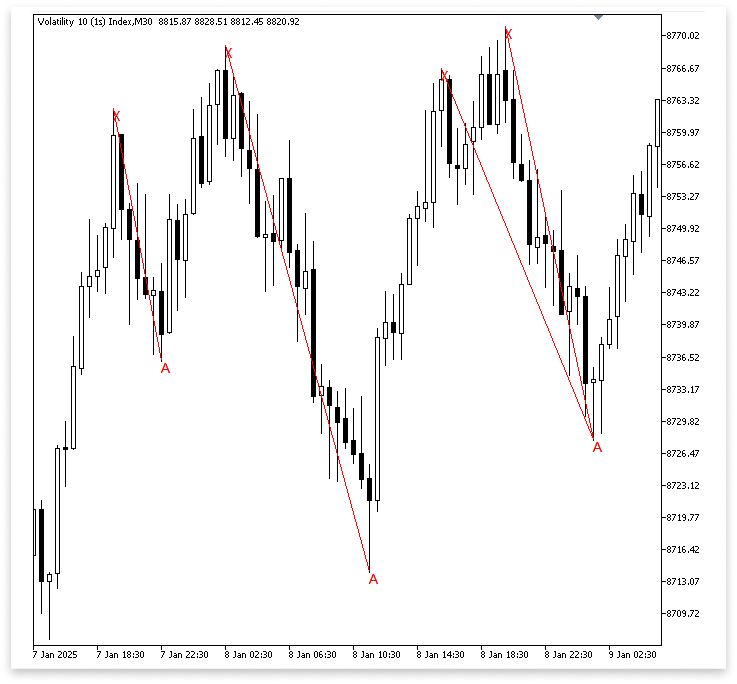
Erläuterung:
Nachdem der Expert Advisor festgestellt hat, dass Punkt X ein legitimer hoher Umkehrpunkt ist, beginnt er schnell mit der Suche nach Punkt A, dem nächsten entscheidenden Punkt des Musters. Es beginnt an der Position X und betrachtet jeden darauf folgenden Balken, um ein Tief zu bestimmen, das sich als tiefer Umkehrpunkt eignet. Um sicherzugehen, dass die Struktur zu einem fallenden harmonischen Muster passt, prüft das Programm während dieser Suche, ob das neue Tief tatsächlich unter dem zuvor angezeigten Hoch liegt. Wenn ein Balken diese Anforderungen erfüllt, markiert die Software dieses entscheidende Niveau auf dem Chart mit einer Kennzeichnung und protokolliert den Preis und die Zeit als Punkt A.
Der EA zeichnet mit ObjectCreate eine Textbeschriftung „A“ an den ausgewählten Punkt, um die Kennzeichnung im Chart zu verdeutlichen. Als Nächstes wird mit Hilfe des OBJ_TREND-Objekts eine Trendlinie von X nach A erstellt. Diese Linie verbindet den ersten hohen Umkehrpunkt mit dem nachfolgenden tiefe und stellt die XA-Kante des harmonischen Musters grafisch dar. Um sicherzustellen, dass der Computer den nächstgelegenen und relevantesten Punkt A nach X festhält, anstatt nach weiteren zu suchen, wird die Suche mit der Anweisung break; beendet, wenn der erste gültige tiefe Umkehrpunkt gefunden ist.
Die äußere Schleife (for(int i = z; i < bars_check – z; i++)) durchläuft jeden Balken im Bereich, wenn der EA nach X (dem hohen Umkehrpunkt) sucht. Um mögliche Anfangspunkte für ein harmonisches Muster zu identifizieren, muss der EA jeden der möglichen hohen Umkehrpunkt der Daten untersuchen. Der EA würde andere legitime X-Punkte übersehen, die später im Chart Muster entwickeln könnten, wenn hier ein Durchbruch eingeleitet würde, weil die Schleife nach der Identifizierung des ersten hohen Umkehrpunkts stoppen würde.
Auf der anderen Seite wird der EA sofort nach dem Auffinden eines X nach einem vergleichbaren A (einen tiefen Umkehrpunkt, der auf X folgt) suchen. In diesem Fall benötigt das Programm, da es die XA-Kante definiert, nur der erste gültige tiefe Umkehrpunkt nach X. Diese Unterbrechung stellt sicher, dass der EA nicht weiter nach Tiefs nach dem ersten legitimen A sucht, was zu Verwirrung oder Überschneidung mit der Kante XA führen könnte. Die Antwort ist, das X zu finden, das A am nächsten liegt, wobei darauf zu achten ist, dass jedes A mit dem nächstgelegenen legitimen X gepaart wird. Auf diese Weise bleibt die XA-Kante konstant und vermeidet überlappende Erkennungen.
Beispiel:if(total_symbol_bars >= bars_check) { for(int i = z ; i < bars_check - z; i++) { if(IsSwingHigh(high, i, z)) { for(int j = i; j < bars_check - z; j++) { if(IsSwingLow(low, j, z) && low[j] < high[i]) { A = low[j]; A_time = time[j]; A_letter = StringFormat("A %d",j); for(int a = j; a >= i; a--) { if(IsSwingHigh(high, a, z) && high[a] > A) { X = high[a]; X_time = time[a]; X_letter = StringFormat("X %d",a); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); xa_line = StringFormat("XA Line %d",i); ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A); break; } } break; } } } } } } } }
Ausgabe:
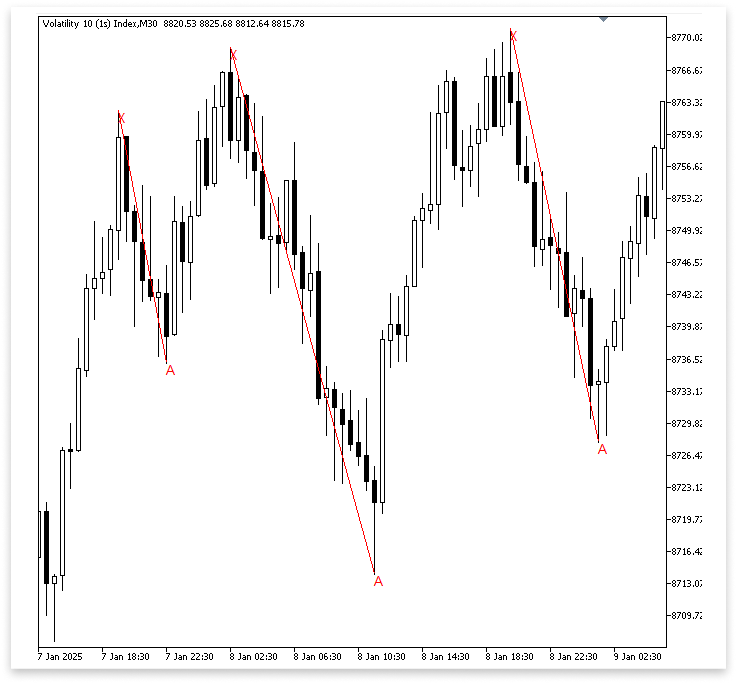
Erläuterung:
Wir verwenden high[i] nur als vorübergehende Referenz, wenn wir zuerst die Bedingung low[j] < high[i] verwenden, um auf einen tiefen Umkehrpunkt zu prüfen. Welcher hoher Umkehrpunkt als X ausgewählt werden soll, ist noch in der Schwebe. Die Struktur eignet sich immer noch für den Beginn einer XA-Kante, da die Verwendung von high[i] lediglich garantiert, dass A (der tiefe Umkehrpunkt) niedriger ist als mindestens ein hoher Umkehrpunkt davor. Anders ausgedrückt: high[i] dient als Platzhalterprüfung zum Ausschluss der Tiefs, die nicht mit A vereinbar sind.
Da dieser hohe Umkehrpunkt möglicherweise nicht der stärkste oder nächstgelegene Kandidat vor A ist, können wir nicht einfach high[i] als X wählen, sobald ein legitimes A ermittelt wurde. Um dies zu verbessern, wurde die Rückwärtsschleife for(int a = j; a >= i; a--) eingeführt. Diese Schleife bewegt sich von der Position A aus rückwärts in Richtung des Anfangshochs. Sie ist die sinnvollste Option für X, da sie versucht, den hohen Umkehrpunkt zu identifizieren, das A am nächsten liegt und höher ist als A. Dies garantiert, dass unsere XA-Kante sicher und angemessen generiert wird und nicht auf einem willkürlichen, vorherigen Hoch basiert.
Da wir diese Elemente erst zeichnen wollen, nachdem wir überprüft haben, dass X gültig ist, übertragen wir schließlich den Prozess der Objekterzeugung (Markierung von X, Markierung von A und Zeichnen der Linie XA) innerhalb dieser Rückwärtsschleife. Ein zu frühes Einzeichnen von X und A, möglicherweise mit dem falschen hohen Umkehrpunkt, wäre die Folge davon, dass die Objekte außerhalb des Bereichs erstellt werden. Wir stellen sicher, dass der Chart die XA-Kante erst dann anzeigt, wenn der gültige, nächstgelegene hohe Umkehrpunkt verifiziert wurde, indem wir dies innerhalb der Schleife tun.
Identifizierung von BC
Die Suche nach der BC-Kante folgt nach der Fertigstellung der XA-Kante. Zwei Punkte, B und C, bilden diesen Abschnitt der Struktur in einem fallenden Gartley-Muster. Punkt C muss sich als tiefer Umkehrpunkt bilden, das auf Punkt B folgt, und Punkt B muss als hoher Umkehrpunkt erscheinen, das auf Punkt A folgt. Wir beginnen mit der Skizzierung des zweiten Teils des harmonischen Musters, indem wir diese beiden Positionen festlegen.
Derzeit werden keine Fibonacci-Retracement- oder Extension-Bedingungen eingeführt. Der Schwerpunkt liegt stattdessen auf der Bestimmung der natürlichen Umkehrpunkte der Kursbewegung.
Beispiel:double B; datetime B_time; string B_letter; double C; datetime C_time; string C_letter; string ab_line; string bc_line;
for(int k = j; k < bars_check - z; k++) { if(IsSwingHigh(high, k, z) && high[k] > A) { B = high[k]; B_time = time[k]; B_letter = StringFormat("B %d",k); for(int l = k; l < bars_check - z; l++) { if(IsSwingLow(low, l, z) && low[l] < B) { C = low[l]; C_time = time[l]; C_letter = StringFormat("C %d",l); ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,B_time,B); ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B"); ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,C_time,C); ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C"); ab_line = StringFormat("AB Line %d",i); ObjectCreate(chart_id,ab_line,OBJ_TREND,0,A_time,A,B_time,B); bc_line = StringFormat("BC Line %d", i); ObjectCreate(chart_id,bc_line,OBJ_TREND,0,B_time,B,C_time,C); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); xa_line = StringFormat("XA Line %d",i); ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A); i = l+1; break; } } break; } }
Ausgabe:
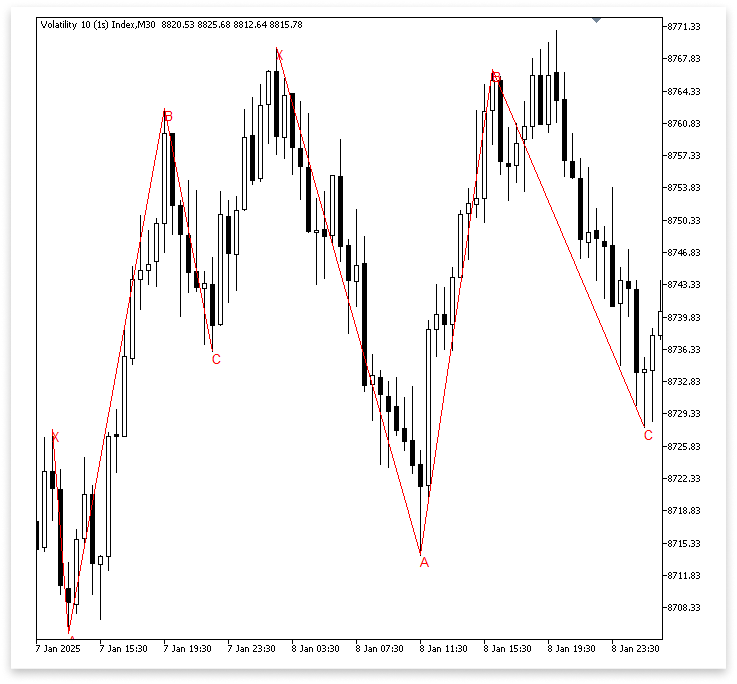
Erläuterung:
Ausgehend vom Punkt A beginnt die erste Schleife, for(int k = j; k < bars_check – z; k++), mit der Suche nach B. Die Software verwendet IsSwingHigh, um innerhalb dieser Schleife nach einem hohen Umkehrpunkt zu suchen. Außerdem wird überprüft, ob high[k] > A ist, was bedeutet, dass der hohe Umkehrpunkt über Punkt A liegt, um sicherzustellen, dass B als Bestandteil der Struktur sinnvoll ist. Die Software protokolliert den Wert, die Zeit und die Bezeichnung für B, nachdem diese Bedingung erfüllt ist.
Zur Bestimmung von C, das ein tiefer Umkehrpunk sein muss, das nach B auftritt, wird dann eine zweite Schleife, for(int l = k; l < bars_check – z; l++), eingesetzt. Die korrekte Abwärtsstruktur des fallenden Gartley wird durch das Kriterium low[l] < B aufrechterhalten, das garantiert, dass C tatsächlich niedriger ist als der hohe Umkehrpunkt B. Details (Preis, Zeit und Etikett) werden gespeichert, wenn ein gültiges C entdeckt wird. Das Programm zeichnet X und A neu, um die Klarheit des Musters zu erhalten, nachdem es die Punkte B und C identifiziert und im Chart beschriftet hat.
Der Algorithmus überspringt die Zeit und vermeidet es, immer wieder die gleichen Stellen zu finden, indem er den Ausdruck i = l+1; verwendet, um die äußere Schleife voranzutreiben. Der Algorithmus kann viele legitime Gartley-Signale verpassen, wenn i = l+1 nach der Identifizierung von C verwendet wird. Er verpasst mögliche Umkehrpunkte, weil er zu weit nach vorne springt. Diese Strategie sollte vermieden werden, indem man die Schleifen normal funktionieren lässt oder die Signale mit Hilfe von Filtertechniken verfeinert, um Chancen zu wahren.
Identifizierung von D
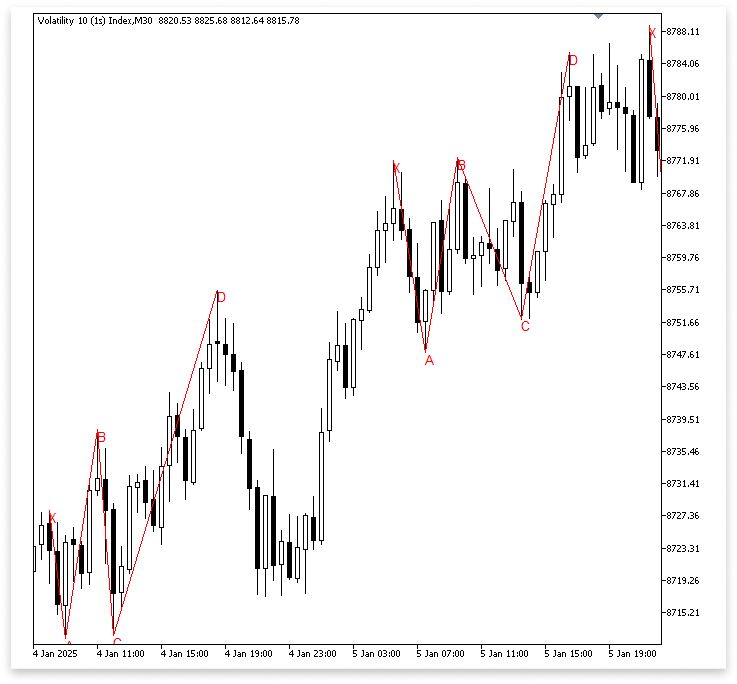
Die Suche nach dem Punkt D ist der nächste Schritt zur Fertigstellung des Gartley-Musters, nachdem X, A, B und C erfolgreich ermittelt wurden. Da es sich bei Punkt D um die mögliche Einstiegszone handelt, ist dies der letzte Abschnitt der Konstruktion und von entscheidender Bedeutung. Wir suchen nach einem hohen Umkehrpunkt, das sich nach Punkt C entwickelt, um D zu identifizieren. Um die CD-Kante zu vervollständigen, sollte dieser Swing vorzugsweise in die entgegengesetzte Richtung von BC laufen.
Beispiel:
double D; datetime D_time; string D_letter; string cd_line;
for(int m = l; m < bars_check - z; m++) { if(IsSwingHigh(high, m, z) && high[m] > B) { D = high[m]; D_time = time[m]; D_letter = StringFormat("D %d",m); ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D); ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D"); cd_line = StringFormat("CD Line %d",i); ObjectCreate(chart_id,cd_line,OBJ_TREND,0,C_time,C,D_time,D); ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,B_time,B); ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B"); ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,C_time,C); ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C"); ab_line = StringFormat("AB Line %d",i); ObjectCreate(chart_id,ab_line,OBJ_TREND,0,A_time,A,B_time,B); bc_line = StringFormat("BC Line %d", i); ObjectCreate(chart_id,bc_line,OBJ_TREND,0,B_time,B,C_time,C); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); xa_line = StringFormat("XA Line %d",i); ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A); i = m+1; break; } }
Ausgabe:
Erläuterung:
Die Schleife beginnt mit dem Scannen des Charts ab dem Index von Punkt C (l) und sucht nach möglichen hohen Umkehrpunkten, die Punkt D sein könnten. Die Bedingung IsSwingHigh(high, m, z) && high[m] > B garantiert, dass der ausgewählte Punkt D höher ist als Punkt B und nicht einfach irgendein hoher Umkehrpunkt. Da Punkt D bei einem fallenden Gartley das Niveau B übertreffen muss, um die richtige Struktur zu erhalten, ist diese Regel von entscheidender Bedeutung.
Nachdem ein solcher hoher Umkehrpunkt identifiziert wurde, erstellt der Code die CD-Linie, um es mit Punkt C zu verbinden, kennzeichnet es als „D“ auf dem Chart und gibt seine Preis- und Zeitdaten in die D-Variablen ein. Der Code zeichnet gleichzeitig die Linien neu, die den anderen signifikanten Punkten entsprechen.
Der nächste Schritt ist die Bestätigung, dass jeder Punkt den dominanten Umkehrpunkt in jeder Kante korrekt wiedergibt, nachdem die Umkehrpunkte effektiv identifiziert wurden. Die Markierung von Höchst- und Tiefstwerten ist unzureichend, da schon kleine Anpassungen den Rahmen unübersichtlich werden lassen können. Es müssen strenge Richtlinien für die Überprüfung der Legitimität jedes Umkehrpunktes eingeführt werden, um falsche Signale zu vermeiden.
Erstens muss der Punkt C zwischen C und D der tiefste Punkt sein. Auf diese Weise ist gewährleistet, dass die CD-Strecke bei einen echten tiefen Umkehrpunkt beginnt und nicht von einem kurzen Einbruch. Um sicherzustellen, dass die BC-Kante von einem legitimen dominanten Hochpunkt ausgeht, muss Punkt B auch das höchste Hoch zwischen B und C sein.
Ebenso sollte überprüft werden, dass der Punkt A der tiefste Tiefpunkt zwischen den Punkten A und B ist. Diese Bedingung bestätigt, dass die Kante AB nicht an einer zufälligen Schwankung, sondern am richtigen Tiefpunkt beginnt. Schließlich muss zwischen X und A der Punkt X der höchste Punkt sein. Die XA-Kante wird dank dieser Prüfung mit dem stärksten hohen Umkehrpunkt in diesem Bereich beginnen.
Beispiel:
int x_a_bars; int x_highest_index; double x_a_hh; datetime x_a_hh_t; int a_b_bars; int a_lowest_index; double a_b_ll; datetime a_b_ll_t; int b_c_bars; int b_highest_index; double b_c_hh; datetime b_c_hh_t; int c_d_bars; int c_lowest_index; double c_d_ll; datetime c_d_ll_t;
for(int m = l; m < bars_check - z; m++) { if(IsSwingHigh(high, m, z) && high[m] > B) { D = high[m]; D_time = time[m]; D_letter = StringFormat("D %d",m); c_d_bars = Bars(_Symbol,PERIOD_CURRENT,C_time,D_time); c_lowest_index = ArrayMinimum(low,l,c_d_bars); c_d_ll = low[c_lowest_index]; c_d_ll_t = time[c_lowest_index]; b_c_bars = Bars(_Symbol, PERIOD_CURRENT, B_time, c_d_ll_t); b_highest_index = ArrayMaximum(high, k, b_c_bars); b_c_hh = high[b_highest_index]; b_c_hh_t = time[b_highest_index]; a_b_bars = Bars(_Symbol,PERIOD_CURRENT,A_time,b_c_hh_t); a_lowest_index = ArrayMinimum(low,j,a_b_bars); a_b_ll = low[a_lowest_index]; a_b_ll_t = time[a_lowest_index]; x_a_bars = Bars(_Symbol, PERIOD_CURRENT, X_time, a_b_ll_t); x_highest_index = ArrayMaximum(high, a, x_a_bars); x_a_hh = high[x_highest_index]; x_a_hh_t = time[x_highest_index]; ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D); ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D"); cd_line = StringFormat("CD Line %d",i); ObjectCreate(chart_id,cd_line,OBJ_TREND,0,c_d_ll_t,c_d_ll,D_time,D); ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,b_c_hh_t,b_c_hh); ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B"); ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,c_d_ll_t,c_d_ll); ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C"); ab_line = StringFormat("AB Line %d",i); ObjectCreate(chart_id,ab_line,OBJ_TREND,0,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh); bc_line = StringFormat("BC Line %d", i); ObjectCreate(chart_id,bc_line,OBJ_TREND,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,x_a_hh_t,x_a_hh); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,a_b_ll_t,a_b_ll); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); xa_line = StringFormat("XA Line %d",i); ObjectCreate(chart_id,xa_line,OBJ_TREND,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll); i = m+1; break; } }
Erläuterung:
Die Überprüfung der Genauigkeit der gefundenen Umkehrpunkte und die Sicherstellung, dass die Gartley-Struktur von den bemerkenswertesten Hochs und Tiefs in jeder Kante abgeleitet wird, sind die Hauptziele dieses Abschnitts des Codes. Wenn nach Punkt C ein neuer hoher Umkehrpunkt entdeckt wird, das höher ist als Punkt B, beginnt der Prozess. Obwohl Punkt D diesem hohem Umkehrpunkt zugeordnet wird, überprüft der Code zunächst alle früheren Punkte, bevor er das Muster abschließt.
Der C-D-Bereich ist der Bereich, in dem die Validierung beginnt. Der Code in diesem Teil sucht nach dem tiefsten Tief, um sicherzustellen, dass Punkt C das tatsächliche Tief zwischen diesen beiden Punkten ist und nicht nur ein vorübergehender Abfall. Um den höchsten Wert zu ermitteln, wird dann der Bereich zwischen B und C untersucht. Dadurch wird sichergestellt, dass Punkt B der stärkste Peak in diesem Abschnitt ist und nicht eine kleine Unebenheit, die das Muster verzerren kann.
Um zu überprüfen, ob Punkt A tatsächlich der markanteste Tiefpunkt der Kante ist, wird der Bereich zwischen A und B auf den tiefsten Tiefpunkt hin untersucht. Um zu bestätigen, dass X die stärkste Spitze vor dem Rückgang zu A ist, wird schließlich der Bereich zwischen X und A auf den höchsten Wert untersucht. Der Code stellt sicher, dass alle Punkte X, A, B und C die richtigen Strukturschwingungen für die Erstellung des harmonischen Musters sind, indem er diese Prüfungen durchführt.
Fibonacci-Retracement
Nach der Identifizierung und Validierung der Umkehrpunkte folgt die Feststellung, ob die Struktur tatsächlich die Kriterien für ein Gartley-Muster erfüllt. Da nicht jede Ansammlung von Umkehrpunkten ein legitimes harmonisches Muster ergibt, reicht es nicht aus, die Punkte X, A, B, C und D auf dem Chart anzugeben. Zur Unterscheidung zwischen den verschiedenen strukturellen Kanten müssen wir die Kriterien des Fibonacci-Retracements und der Extension anwenden.
Die „Filter“, die überprüfen, ob die Kursbewegungen den für ein Gartley-Muster erforderlichen Verhältnissen entsprechen, sind diese Fibonacci-Messungen. Beispielsweise müssen bestimmte Fibonacci-Spannen durch die Ausdehnung des Punktes D im Verhältnis zu den anderen Ausschlägen, die Rückführung des Punktes B von XA und die Rückführung des Punktes C von AB erfüllt werden. Die Struktur kann als legitimes Gartley-Muster eingestuft werden, wenn diese Anforderungen erfüllt sind.
Beispiel:
input double b_xa_max = 78.6; // MAX B RETRACEMENT LEVEL FOR XA input double b_xa_min = 61.8; // MIN B RETRACEMENT LEVEL FOR XA input double c_ab_max = 88.6; // MAX C RETRACEMENT LEVEL FOR AB input double c_ab_min = 38.2; // MIN C RETRACEMENT LEVEL FOR AB input double d_xa_max = 76.0; // MAX D RETRACEMENT LEVEL FOR XA input double d_xa_min = 80.0; // MIN D RETRACEMENT LEVEL FOR XA double lvl_max_b; double lvl_min_b; double lvl_max_c; double lvl_min_c; double lvl_max_d; double lvl_min_d;
if(IsSwingHigh(high, m, z) && high[m] > B) { D = high[m]; D_time = time[m]; D_letter = StringFormat("D %d",m); c_d_bars = Bars(_Symbol,PERIOD_CURRENT,C_time,D_time); c_lowest_index = ArrayMinimum(low,l,c_d_bars); c_d_ll = low[c_lowest_index]; c_d_ll_t = time[c_lowest_index]; b_c_bars = Bars(_Symbol, PERIOD_CURRENT, B_time, c_d_ll_t); b_highest_index = ArrayMaximum(high, k, b_c_bars); b_c_hh = high[b_highest_index]; b_c_hh_t = time[b_highest_index]; a_b_bars = Bars(_Symbol,PERIOD_CURRENT,A_time,b_c_hh_t); a_lowest_index = ArrayMinimum(low,j,a_b_bars); a_b_ll = low[a_lowest_index]; a_b_ll_t = time[a_lowest_index]; x_a_bars = Bars(_Symbol, PERIOD_CURRENT, X_time, a_b_ll_t); x_highest_index = ArrayMaximum(high, a, x_a_bars); x_a_hh = high[x_highest_index]; x_a_hh_t = time[x_highest_index]; lvl_min_b = a_b_ll + ((b_xa_min / 100) * (x_a_hh - a_b_ll)); lvl_max_b = a_b_ll + ((b_xa_max / 100) * (x_a_hh - a_b_ll)); lvl_min_c = b_c_hh - ((c_ab_min / 100) * (b_c_hh - a_b_ll)); lvl_max_c = b_c_hh - ((c_ab_max / 100) * (b_c_hh - a_b_ll)); lvl_min_d = a_b_ll + ((d_xa_min / 100) * (x_a_hh - a_b_ll)); lvl_max_d = a_b_ll + ((d_xa_max / 100) * (x_a_hh - a_b_ll)); if(b_c_hh >= lvl_min_b && b_c_hh <= lvl_max_b && c_d_ll <= lvl_min_c && c_d_ll >= lvl_max_c && D >= lvl_min_d && D <= lvl_max_d) { ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D); ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D"); cd_line = StringFormat("CD Line %d",i); ObjectCreate(chart_id,cd_line,OBJ_TREND,0,c_d_ll_t,c_d_ll,D_time,D); ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,b_c_hh_t,b_c_hh); ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B"); ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,c_d_ll_t,c_d_ll); ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C"); ab_line = StringFormat("AB Line %d",i); ObjectCreate(chart_id,ab_line,OBJ_TREND,0,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh); bc_line = StringFormat("BC Line %d", i); ObjectCreate(chart_id,bc_line,OBJ_TREND,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,x_a_hh_t,x_a_hh); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,a_b_ll_t,a_b_ll); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); xa_line = StringFormat("XA Line %d",i); ObjectCreate(chart_id,xa_line,OBJ_TREND,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll); } // i = m+1; break; } }
Erläuterung:
Wir beginnen mit den Eingabeparametern. Um festzustellen, ob die Struktur von X, A, B, C und D ein gültiges Gartley-Muster ist, verwendet der Expert Advisor diese nutzerdefinierten Fibonacci-Retracement-Levels. Je nach den Eingaben sollte beispielsweise Punkt B zwischen dem angegebenen Retracement der XA-Kante, Position C auf dem angegebenen Retracement der AB-Kante und Punkt D auf dem angegebenen Fibonacci-Retracement der XA-Kante liegen.
Die tatsächlichen Kursniveaus, bei denen sich jeder Umkehrpunkt bilden sollte, werden durch die berechneten Variablen dargestellt. Sie werden auf der Grundlage der in den Inputs festgelegten Fibonacci-Prinzipien aus den Höchst- und Tiefstkursen der Kanten XA und AB berechnet. So wird z. B. durch das Retracement der Kante XA die regelgerechte Spanne für den Punkt B festgelegt, und die gleiche Methode wird zur Berechnung der Spanne für die Punkte C und D im Verhältnis zu AB und XA verwendet.
Bei der letzten Bedingungsprüfung wird überprüft, ob jeder Musterpunkt innerhalb der erforderlichen Fibonacci-Spanne liegt. Er bestätigt, dass die Bedingungen für die Rückwärtsbewegung der Punkte B, C und D erfüllt sind. Wenn alle diese Anforderungen erfüllt sind, erzeugt das Programm Chart-Objekte, um das erkannte Gartley-Muster visuell darzustellen, indem es die Punkte X, A, B, C und D identifiziert und die Verbindungslinien zeichnet.
Ausführung des Handels
Die Handelsausführung erfolgt nach der erfolgreichen Identifizierung eines legitimen Gartley-Musters. Um sicherzustellen, dass die Struktur den Gartley-Formationsrichtlinien entspricht, hat sich der Expert Advisor bisher auf die Untersuchung der Kursdaten, die Identifizierung von hohen und tiefen Umkehrpunkten und die Überprüfung der Fibonacci-Verbindungen konzentriert. Die bloße Identifizierung des Musters bietet dem Händler jedoch nur eine mögliche Handelsmöglichkeit, nicht aber die Möglichkeit, Gewinne zu erzielen. Wenn der EA mit diesem Wissen auf dem Markt handelt, beginnt die eigentliche Aktion.
In der Praxis bedeutet dies, dass der EA nun entscheiden muss, wo er einsteigt, wo er den Take-Profit platziert und wo er den Stop-Loss setzt. Zum Beispiel würde der EA normalerweise einen Verkaufsauftrag am Punkt D in einem fallenden Gartley-Muster auslösen. Zum Schutz vor einer Entwertung des Musters würde der Stop-Loss leicht über dem hohen Umkehrpunkt bei D platziert werden. Der Take-Profit könnte anhand von Fibonacci-Erweiterungszielen oder einem Risiko-Ertrags-Verhältnis wie 1:3 bestimmt werden. Der EA garantiert eine konsistente Leistung ohne Zögern oder emotionale Voreingenommenheit, indem er diesen Prozess automatisiert.
Beispiel:
#include <Trade/Trade.mqh> CTrade trade; input int MagicNumber = 61626; input double lot_size = 0.1; double ask_price; datetime time_price[]; double take_p; string XAB; string BCD; datetime lastTradeBarTime = 0; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- trade.SetExpertMagicNumber(MagicNumber); ArraySetAsSeries(time_price,true); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- ObjectsDeleteAll(chart_id); }
CopyTime(_Symbol, timeframe, 0, 2, time_price); ask_price = SymbolInfoDouble(_Symbol,SYMBOL_ASK); datetime currentBarTime = iTime(_Symbol,timeframe,0); if(b_c_hh >= lvl_min_b && b_c_hh <= lvl_max_b && c_d_ll <= lvl_min_c && c_d_ll >= lvl_max_c && D >= lvl_min_d && D <= lvl_max_d) { ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D); ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D"); cd_line = StringFormat("CD Line %d",i); ObjectCreate(chart_id,cd_line,OBJ_TREND,0,c_d_ll_t,c_d_ll,D_time,D); ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,b_c_hh_t,b_c_hh); ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B"); ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,c_d_ll_t,c_d_ll); ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C"); ab_line = StringFormat("AB Line %d",i); ObjectCreate(chart_id,ab_line,OBJ_TREND,0,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh); bc_line = StringFormat("BC Line %d", i); ObjectCreate(chart_id,bc_line,OBJ_TREND,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,x_a_hh_t,x_a_hh); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,a_b_ll_t,a_b_ll); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); xa_line = StringFormat("XA Line %d",i); ObjectCreate(chart_id,xa_line,OBJ_TREND,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll); XAB = StringFormat("XAB TRIANGLE %d", i); BCD = StringFormat("BCD TRIANGLE %d", i); ObjectCreate(chart_id,XAB,OBJ_TRIANGLE,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh); ObjectSetInteger(chart_id,XAB,OBJPROP_FILL,true); ObjectSetInteger(chart_id,XAB,OBJPROP_COLOR,clrPink); ObjectSetInteger(chart_id,XAB,OBJPROP_BACK,true); ObjectCreate(chart_id,BCD,OBJ_TRIANGLE,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll,D_time,D); ObjectSetInteger(chart_id,BCD,OBJPROP_FILL,true); ObjectSetInteger(chart_id,BCD,OBJPROP_COLOR,clrPink); ObjectSetInteger(chart_id,BCD,OBJPROP_BACK,true); if(time[m+z] == time_price[1] && currentBarTime != lastTradeBarTime) { take_p = ask_price - (MathAbs(D - ask_price) * 3); trade.Sell(lot_size,_Symbol,ask_price,D,take_p); lastTradeBarTime = currentBarTime; } }
Ausgabe:
Erläuterung:
Dieser Teil des Programms verwaltet die visuelle Darstellung des Gartley-Musters auf dem Chart sowie die Handelslogik. Die Standard-MQL5-Handelsbibliothek wird zunächst mit #include <Handel/Handel.mqh> eingebunden. Aus dieser Bibliothek wird ein CTrade-Objekt namens Trade erstellt, das alle handelsbezogenen Aufgaben, einschließlich des Öffnens und Schließens von Positionen, verwaltet. Ein Eingabeparameter namens MagicNumber wird deklariert und bei Transaktionen verwendet, um die von diesem Expert Advisor getätigten Trades von anderen zu unterscheiden: MagicNumber; SetExpertMagicNumber.
Die Menge des auszutauschenden Volumens wird durch andere entscheidende Faktoren wie die Losgröße bestimmt. Um den Marktpreis, die Zeitdaten und die berechneten Gewinnmitnahmen zu speichern, werden unterstützende Variablen wie ask_price, time_price[] und take_p deklariert. Als Vorsichtsmaßnahme wird die Variable lastTradeBarTime verwendet, um sicherzustellen, dass eine neue Transaktion nicht mehr als einmal auf demselben Balken eröffnet wird.
Das jüngste Element wird bei Index Null gehalten, indem ArraySetAsSeries(time_price, true); angewendet wird, um zu gewährleisten, dass die Preisdaten angemessen behandelt werden. Die Eröffnungszeitpunkte der letzten beiden Balken werden dann mit der Methode CopyTime(_Symbol, timeframe, 0, 2, time_price) in das Array time_price kopiert. Ask_price = SymbolInfoDouble(_Symbol, SYMBOL_ASK); liefert den aktuellen Briefkurs, und currentBarTime = iTime(_Symbol, timeframe, 0); speichert den Zeitstempel des letzten Balkens.
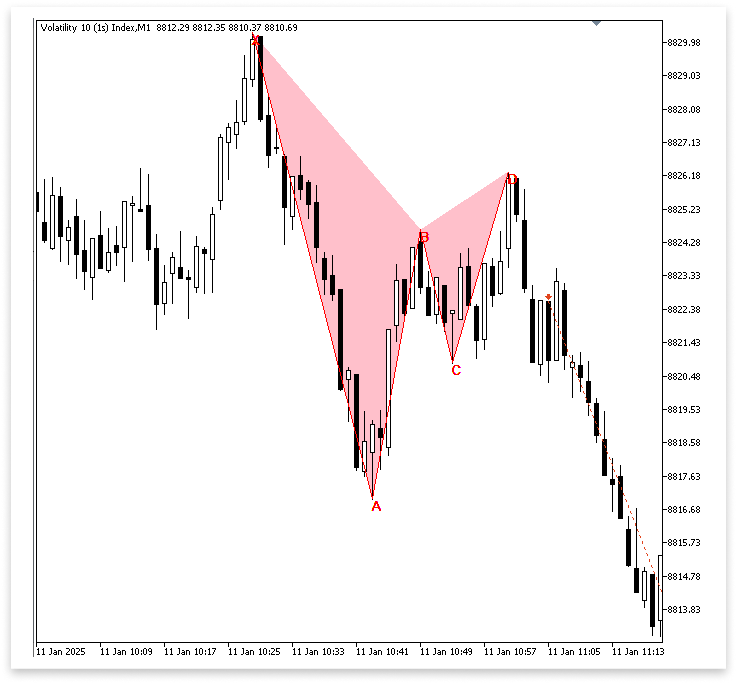
Anhand dieser Angaben kann der Computer den genauen Zeitpunkt bestimmen, an dem die Anforderungen des Handels erfüllt sind. Durch den Vergleich der Balkenzeiten stellt die bedingte Prüfung sicher, dass das Programm nur einmal pro Balken reagiert. Wenn alles so gültig ist, wird ein Verkaufsauftrag ausgeführt und Take-Profit wird mit take_p = ask_price – (MathAbs(D – ask_price) * 3); bestimmt. Sell(lot_size, D, take_p, ask_price, _Symbol);. Um zu verhindern, dass derselbe Balken eine weitere Transaktion auslöst, wird lastTradeBarTime geändert.
Das Programm veranlasst nicht nur Handelsgeschäfte, sondern zeigt auch das Gartley-Muster direkt auf dem Chart an. Zum Beispiel sind XAB = StringFormat(“XAB TRIANGLE %d“, i); und BCD = StringFormat(“BCD TRIANGLE %d“, i); Zeichenketten, die mit Hilfe von StringFormat konstruiert werden, um die grafischen Objekte eindeutig zu benennen. ObjectCreate wird dann verwendet, um zwei dreieckige Formen mit diesen Bezeichnern zu zeichnen. Der XAB-Teil des Musters wird durch das erste Dreieck dargestellt, der BCD-Teil durch das zweite. Anhand der zuvor in der Software gefundenen entsprechenden Umkehrpunkte werden deren Koordinaten ermittelt.
Die Eigenschaften der Dreiecke werden mit ObjectSetInteger festgelegt, wobei sie gefüllt, rosa eingefärbt und auf den Hintergrund übertragen werden, um diese Muster hervorzuheben. Das Programm reagiert nicht nur auf erkannte Gartley-Muster, sondern macht sie dem Händler durch die Kombination von automatischer Handelsausführung und verständlicher grafischer Visualisierung auch zur Überprüfung zugänglich.
Schlussfolgerung
In diesem Artikel haben wir untersucht, wie man das Gartley-Muster in MQL5 erstellt und handelt. Wir begannen mit der Identifizierung der Umkehrpunkte (X, A, B, C und D), wendeten Fibonacci-Retracement- und Extension-Levels an, um die Struktur zu bestätigen, und führten den Handel automatisch aus, sobald das Muster gültig war. Schließlich haben wir Chart-Objekte zur übersichtlichen Visualisierung hinzugefügt, die es einfacher machen, das sich bildende Muster zu erkennen. Dieses Projekt zeigt, wie komplexe harmonische Muster kodiert und automatisch gehandelt werden können. Auf dieser Grundlage können Sie die Regeln verfeinern, Bestätigungen hinzufügen oder die Logik auf andere harmonische Muster erweitern.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/19331
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung des Price Action Analysis Toolkit (Teil 41): Aufbau eines statistischen Preis-Level EA in MQL5
Entwicklung des Price Action Analysis Toolkit (Teil 41): Aufbau eines statistischen Preis-Level EA in MQL5
 Vom Neuling zum Experten: Implementierung von Fibonacci-Strategien im Post-NFP-Handel
Vom Neuling zum Experten: Implementierung von Fibonacci-Strategien im Post-NFP-Handel
 Die Grenzen des maschinellen Lernens überwinden (Teil 4): Überwindung des irreduziblen Fehlers durch mehrere Prognosehorizonte
Die Grenzen des maschinellen Lernens überwinden (Teil 4): Überwindung des irreduziblen Fehlers durch mehrere Prognosehorizonte
 Automatisieren von Handelsstrategien in MQL5 (Teil 32): Erstellung eines Price Action 5 Drives des harmonischen Mustersystems
Automatisieren von Handelsstrategien in MQL5 (Teil 32): Erstellung eines Price Action 5 Drives des harmonischen Mustersystems
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.