Datenwissenschaft und ML (Teil 45): Forex Zeitreihenprognosen mit dem Modell PROPHET von Facebook
145
0
Inhalt
- Was ist das Modell Prophet?
- Das Modell Prophet verstehen
- Implementierung von Prophetin Python
- Hinzufügen von Feiertage zum Modell
- Herstellung des Handelsroboters für MetaTrader 5 auf der Grundlage des Prophet-Modells
- Schlussfolgerung
Was ist das Modell Prophet?
Das Modell Prophet ist ein von Meta (ehemals Facebook) entwickeltes Open-Source-Tool für Zeitreihenprognosen. Es wurde entwickelt, um genaue und nutzerfreundliche Prognosen für geschäftliche und analytische Zwecke zu erstellen, insbesondere für Zeitreihendaten mit starken Saisonalitäten und Trends.
Dieses Modell wurde von Facebook eingeführt (S. J. Taylor & Letham, 2018), ursprünglich für die Vorhersage täglicher Daten mit wöchentlicher und jährlicher Saisonalität sowie den Effekten von Feiertage. Später wurde es erweitert, um weitere Arten von saisonalen Daten zu erfassen. Es funktioniert am besten mit Zeitreihen, die eine starke Saisonalität und mehrere Saisons historischer Daten aufweisen.
Gebräuchliche Begriffe:
- Trend. Der Trend zeigt die Tendenz der Daten, über einen langen Zeitraum zu steigen oder zu fallen, und filtert die saisonalen Schwankungen heraus.
- Saisonabhängigkeit. Unter Saisonalität versteht man die Schwankungen, die über einen kurzen Zeitraum auftreten und nicht deutlich genug sind, um als „Trend“ bezeichnet zu werden.
In diesem Artikel werden wir dieses Modell anhand von Forex-Daten verstehen und implementieren und sehen, wie es uns helfen kann, den Markt zu schlagen, aber nehmen wir uns zunächst einen Moment Zeit, um dieses Modell im Detail zu verstehen.
Das Modell Prophet verstehen
Das Prophet-Modell kann als ein nicht-lineares Regressionsmodell betrachtet werden, das durch die folgende Formel beschrieben wird:
Abbildung 01
wobei:
-
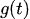einen stückweise linearen Trend (oder „Wachstumsterm“) beschreibt -
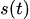die verschiedenen saisonalen Muster beschreibt -
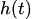die Feiertagseffekte, und 
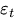ist ein Fehlerterm des weißen Rauschens erfasst.
01: Die Trend-Komponente
Die Trendkomponente 
erlaubt es, dass Änderungspunkte automatisch ausgewählt werden, wenn sie nicht manuell festgelegt wurden. Diese Änderungspunkte repräsentieren Orte im Zeitverlauf, an denen sich der Trend ändern kann (z. B. plötzlicher Anstieg oder Rückgang).
Sie können auch optional ein logistisches Wachstumsmodell anstelle eines linearen Modells verwenden, das einen Kapazitätsparameter (Cap) zur Modellierung von Sättigungseffekten einführt. Dies ist nützlich, wenn sich das Wachstum nach Erreichen einer bestimmten natürlichen Grenze verlangsamt.
02: Saisonalität
Im Prophet-Modell wird die Saisonalität 
mit Hilfe von Fourier-Reihen modelliert.
Standardmäßig:
- Eine Größenordnung von 10 wird für die jährliche Saisonalität verwendet.
- Für die wöchentliche Saisonalität wird eine Ordnung 3 verwendet.
Diese Fourier-Terme helfen dem Modell, wiederkehrende saisonale Effekte zu erfassen.
03: Der Feiertagseffekt-Teil
Feiertagseffekte 
werden als Dummy-Variablen (mit einem Punkt kodiert) einbezogen, sodass das Modell seine Vorhersage um besondere Daten herum anpassen kann, die in der Vergangenheit Abweichungen im Verhalten verursacht haben. Zum Beispiel Wirtschaftsnachrichten oder Feiertage.
Das gesamte Modell wird mithilfe eines Bayes'schen Rahmens geschätzt, der eine automatische Auswahl der Änderungspunkte und anderer Modellparameter ermöglicht.
Obwohl dieses grundlegende additive Zerlegungsmodell einfach aussieht, ist die Berechnung der Terme innerhalb dieser Formel sehr mathematisch, sodass dieses Modell zu falschen Prognosen führen kann, wenn man keine Ahnung hat, was man tut.
Prophet bietet uns zwei Modellierungsansätze.
- Stückweise lineares Wachstumsmodell (Standard)
- Logistisches Wachstumsmodell
01. Stückweise lineares Modell
Dies ist das von Prophet verwendete Standardmodell. Dabei wird davon ausgegangen, dass der Trend in den Daten einem linearen Verlauf folgt, sich aber zu bestimmten Zeitpunkten (den so genannten „Changepoints“) ändern kann. Dieses Modell eignet sich für Daten mit stetigen Wachstums- oder Rückgangsmustern, möglicherweise mit abrupten Verschiebungen.
Dieser Modellierungsansatz ist in der Formel in Abbildung 01 dargestellt.
02. Logistisches Wachstumsmodell
Dieses Modell eignet sich für Daten, die ein sättigendes Wachstum aufweisen, d. h., sie wachsen zunächst schnell, verlangsamen sich aber, wenn sie sich einer maximalen Kapazität oder Grenze nähern. Diese Art von Muster ist häufig in realen Systemen mit natürlichen oder unternehmensbedingten Grenzen zu beobachten (z. B. Nutzerakzeptanz in einem gesättigten Markt).
Das logistische Wachstumsmodell enthält einen Kapazitätsparameter, der diese Obergrenze definiert.
Dieser Modellierungsansatz ergibt sich aus der folgenden Formel:
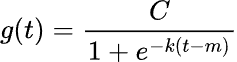
Abbildung 02
wobei:
ist die Tragfähigkeit, 
die Wachstumsrate und 
ein Offset-Parameter.
Implementierung des Prophet-Modells in Python
Anhand der EURUSD-Daten aus dem Stundenchart wollen wir versuchen, den Trend und die Saisonalität zu erkennen und mithilfe dieses Modells zukünftige Werte zu prognostizieren.
Als erstes müssen Sie alle Abhängigkeiten aus der Datei requirements.txt installieren, die am Ende dieses Artikels angehängt ist:
pip install -r requirements.txt
Importieren:
import pandas as pd import numpy as np import MetaTrader5 as mt5 import matplotlib.pyplot as plt import seaborn as sns from prophet import Prophet plt.style.use('fivethirtyeight') sns.set_style("darkgrid")
Holen wir uns die Daten aus dem MetaTrader 5:
if not mt5.initialize(r"c:\Program Files\MetaTrader 5 IC Markets (SC)\terminal64.exe"): print("Failed to initialize MetaTrader5. Error = ",mt5.last_error()) mt5.shutdown() symbol = "EURUSD" timeframe = mt5.TIMEFRAME_H1 rates = mt5.copy_rates_from_pos(symbol, timeframe, 1, 10000) if rates is None: print(f"Failed to copy rates for symbol={symbol}. MT5 Error = {mt5.last_error()}")
Das Modell Prophet stützt sich in hohem Maße auf die Funktion des Zeit- oder Datumsstempels. Diese Funktion ist eine Voraussetzung für das Funktionieren dieses Modells.
Nachdem wir die Daten (Kurse) vom MetaTrader 5 erhalten haben, konvertieren wir sie in ein Pandas-DataFrame-Objekt. Dann konvertieren wir die Spalte time, die die Zeit in Sekunden enthält, in ein Datetime-Format.
rates_df = pd.DataFrame(rates) # we convert rates object to a dataframe rates_df["time"] = pd.to_datetime(rates_df["time"], unit="s") # we convert the time from seconds to datatime rates_df
Ausgabe:
| time | open | high | low | close | tick_volume | spread | real_volume | |
|---|---|---|---|---|---|---|---|---|
| 0 | 2023-11-10 23:00:00 | 1.06849 | 1.06873 | 1.06826 | 1.06846 | 762 | 0 | 0 |
| 1 | 2023-11-13 00:00:00 | 1.06828 | 1.06853 | 1.06779 | 1.06841 | 1059 | 10 | 0 |
| 2 | 2023-11-13 01:00:00 | 1.06854 | 1.06907 | 1.06854 | 1.06906 | 571 | 0 | 0 |
| 3 | 2023-11-13 02:00:00 | 1.06904 | 1.06904 | 1.06822 | 1.06839 | 1053 | 0 | 0 |
| 4 | 2023-11-13 03:00:00 | 1.06840 | 1.06886 | 1.06811 | 1.06867 | 1204 | 0 | 0 |
Das Prophet-Modell ist ein univariates Modell, das nur zwei Merkmale benötigt, um mit einem Pandas-DataFrame zu operieren, nämlich das Datetime-Merkmal ds (Datumsstempel) und die Zielvariable „y“ im DataFrame.
Lassen Sie uns zunächst einen einfachen Datensatz aus dem vom MetaTrader 5 erhaltenen Datensatz mit zwei Merkmalen (Zeit und Volatilität) erstellen. Dies sind die Daten, die wir später im Prophet-Modell einsetzen werden.
prophet_df = pd.DataFrame({
"time": rates_df["time"],
"volatility": rates_df["high"] - rates_df["low"]
}).set_index("time")
prophet_df Die Volatilität (berechnet als Differenz zwischen Höchst- und Tiefstkurs) ist unsere Zielgröße.
Im Gegensatz zu anderen Zeitreihenprognosemodellen wie ARIMA und VAR (siehe oben), bei denen die Zielvariable eine stationäre Variable sein muss, ist das Prophet-Modell nicht auf diese Bedingung beschränkt. Es kann auch mit nicht-stationären Daten arbeiten, aber alle Modelle für maschinelles Lernen neigen dazu, mit stationären Variablen gut zu funktionieren, da sie aufgrund ihrer Beschaffenheit (konstanter Mittelwert, Varianz und Standardabweichung) für Modelle leicht zu lernen sind.
Ich habe mich bei diesem Modell für eine stationäre Zielvariable entschieden, um uns das Leben sehr zu erleichtern.
Stellen wir den DataFrame dar und beobachten wir die Merkmale.
# Color pallete for plotting color_pal = ["#F8766D", "#D39200", "#93AA00", "#00BA38", "#00C19F", "#00B9E3", "#619CFF", "#DB72FB"] prophet_df.plot(figsize=(7,5), color=color_pal, title="Volatility (high-low) against time", ylabel="volatility", xlabel="time")
Ausgabe:
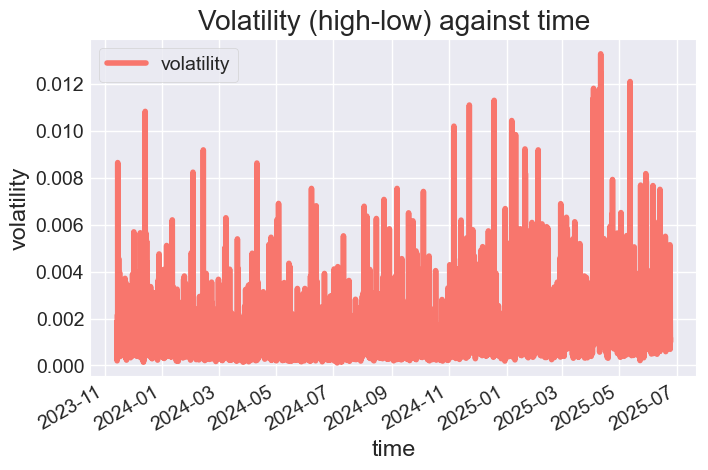
Abbildung 03
Optional können wir X- und Y-Merkmale erstellen, um die Auswirkungen von Zeitmerkmalen auf die Volatilität auf dem Markt zu bewerten.
def create_features(df, label=None): """ Creates time series features from datetime index. """ df = df.copy() df['date'] = df.index df['hour'] = df['date'].dt.hour df['dayofweek'] = df['date'].dt.dayofweek df['quarter'] = df['date'].dt.quarter df['month'] = df['date'].dt.month df['year'] = df['date'].dt.year df['dayofyear'] = df['date'].dt.dayofyear df['dayofmonth'] = df['date'].dt.day df['weekofyear'] = df['date'].dt.isocalendar().week X = df[['hour','dayofweek','quarter','month','year', 'dayofyear','dayofmonth','weekofyear']] if label: y = df[label] return X, y return X X, y = create_features(prophet_df, label='volatility') features_and_target = pd.concat([X, y], axis=1)
Ausgabe:
| hour | dayofweek | quarter | month | year | dayofyear | dayofmonth | weekofyear | volatility | |
|---|---|---|---|---|---|---|---|---|---|
| time | |||||||||
| 2023-11-13 16:00:00 | 16 | 0 | 4 | 11 | 2023 | 317 | 13 | 46 | 0.00122 |
| 2023-11-13 17:00:00 | 17 | 0 | 4 | 11 | 2023 | 317 | 13 | 46 | 0.00179 |
| 2023-11-13 18:00:00 | 18 | 0 | 4 | 11 | 2023 | 317 | 13 | 46 | 0.00186 |
| 2023-11-13 19:00:00 | 19 | 0 | 4 | 11 | 2023 | 317 | 13 | 46 | 0.00125 |
| 2023-11-13 20:00:00 | 20 | 0 | 4 | 11 | 2023 | 317 | 13 | 46 | 0.00150 |
Für die manuelle Analyse können wir diese Merkmale gegen die Volatilität auftragen.
sns.pairplot(features_and_target.dropna(), hue='hour', x_vars=['hour','dayofweek', 'year','weekofyear'], y_vars='volatility', height=5, plot_kws={'alpha':0.45, 'linewidth':0.5} ) plt.suptitle(f"{symbol} close prices by Hour, Day of Week, Year, and Week") plt.show()
Ausgabe:
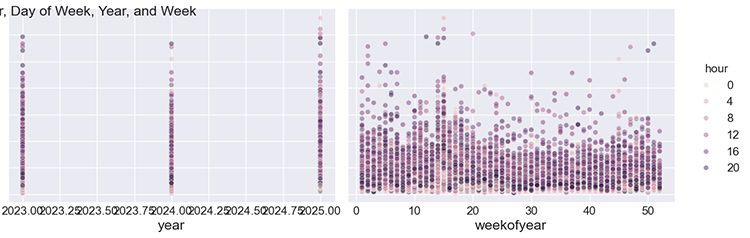
Abbildung 04
Wie Sie aus den Unterdiagrammen ersehen können, haben die Stunde, der Wochentag, das Jahr und die Woche des Jahres alle einen Einfluss auf die Volatilität, die in jeder Stunde des Diagramms auftritt. Dieses Wissen gibt uns die Zuversicht, diese Daten für das Prophet-Modell zu verwenden.
Training des Prophet-Modells
Zunächst werden die Daten anhand eines bestimmten Datums in Trainings- und Testsätze aufgeteilt.
split_date = '01-Jan-2025' # threshold date between training and testing samples, all values after this date are for testing prophet_df_train = prophet_df.loc[prophet_df.index <= split_date].copy().reset_index().rename(columns={"time": "ds", "volatility": "y"}) prophet_df_test = prophet_df.loc[prophet_df.index > split_date].copy().reset_index().rename(columns={"time": "ds", "volatility": "y"})
Wir trainieren das Prophet-Modell anhand der Trainingsdaten.
model = Prophet() model.fit(prophet_df_train)
Nach dem Training des Modells wollen wir oft seine Effektivität an den Daten außerhalb der Stichprobe testen – die Informationen, die das Modell noch nicht gesehen hat. Im Gegensatz zu anderen Modellen liefert das Prophet-Modell die Prognosen auf eine etwas andere Weise.
test_fcst = model.predict(df=prophet_df_test)
Statt eines Vektors mit den Vorhersagen liefert dieses Modell einen ganzen DataFrame mit verschiedenen Merkmalen, die Vorhersagen und den Zustand des Modells darstellen.
test_fcst.head()
Ausgabe:
ds trend yhat_lower yhat_upper trend_lower trend_upper additive_terms additive_terms_lower additive_terms_upper daily daily_lower daily_upper weekly weekly_lower weekly_upper multiplicative_terms multiplicative_terms_lower multiplicative_terms_upper yhat 0 2025-01-02 00:00:00 0.001674 0.000168 0.001993 0.001674 0.001674 -0.000571 -0.000571 -0.000571 -0.000510 -0.000510 -0.000510 -0.000061 -0.000061 -0.000061 0.0 0.0 0.0 0.001102 1 2025-01-02 01:00:00 0.001674 0.000161 0.001977 0.001674 0.001674 -0.000614 -0.000614 -0.000614 -0.000556 -0.000556 -0.000556 -0.000057 -0.000057 -0.000057 0.0 0.0 0.0 0.001060 2 2025-01-02 02:00:00 0.001674 0.000337 0.002123 0.001674 0.001674 -0.000483 -0.000483 -0.000483 -0.000430 -0.000430 -0.000430 -0.000054 -0.000054 -0.000054 0.0 0.0 0.0 0.001191
Die folgende Tabelle enthält die Bedeutung einiger der Spalten (Features), die von der Methode Predict zurückgegeben werden.
| Spalte | Bedeutung |
|---|---|
| ds | Der Zeitpunkt (Zeitstempel) des prognostizierten Punktes |
| yhat | Der endgültige prognostizierte Wert (die Vorhersage von Prophet zu diesem Zeitpunkt) |
| yhat_lower, yhat_upper | Die untere und obere Grenze des 80%- (oder 95%-) Konfidenzintervalls für yhat. |
| trend | Der Wert der Trendkomponente zum Zeitpunkt ds (z. B. langsames Wachstum oder Rückgang im Laufe der Zeit. |
| trend_lower, trend_upper | Konfidenzintervall der Trendkomponente |
| additive_terms | Die Summe aller saisonalen + Feiertagskomponenten zum Zeitpunkt ds (z. B. täglich + wöchentlich + Feiertage) |
| additive_terms_lower, additive_terms_upper | Grenzwerte für additive Komponenten. |
| daily | Der Effekt der täglichen Saisonalität (z. B. stündliche Muster an einem Tag) |
| daily_lower, daily_upper | Konfidenzintervall für die Tageskomponente. |
| weekly | Der wöchentliche Saisonaleffekt (z. B. Wochenenden unterscheiden sich von Wochentagen) |
| weekly_lower, weekly_upper | Konfidenzintervall für die wöchentliche Komponente. |
Was wir am meisten brauchen, sind yhat, yhat_lower, yhat_upper, trend, Saisonmuster (täglich, wöchentlich, jährlich), Feiertage (falls enthalten) und Fehlergrenzen für Komponenten(*_lower und *_upper) Spalten.
Stellen wir die tatsächlichen und die prognostizierten Werte aus der Teststichprobe neben den tatsächlichen Werten aus der Trainingsstichprobe dar.
f, ax = plt.subplots(figsize=(7,5)) ax.scatter(prophet_df_test["ds"], prophet_df_test['y'], color='r') # plot actual values from the testing sample in red fig = model.plot(test_fcst, ax=ax) # plot the forecasts
Ausgangswert.
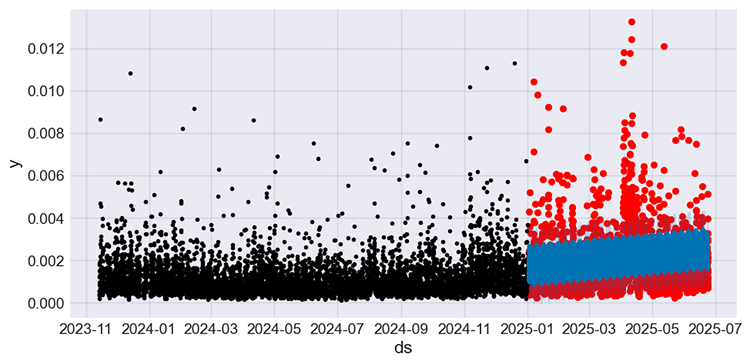
Abbildung 05
Die schwarzen Werte stellen die Trainingsstichprobe dar, die roten Werte sind die tatsächlichen Werte der Teststichprobe und die blauen Werte sind die Vorhersagen des Modells für die Teststichprobe.
Es ist schwierig, die Wirksamkeit des Modells zu verstehen, wenn man sich nur diese Grafik ansieht. Erstellen wir kleine Diagramme, die die tatsächlichen und prognostizierten Werte der Teststichprobe darstellen.
Lassen Sie uns das Modell im Januar 2025, dem ersten Monat der Testdaten, bewerten.
f, ax = plt.subplots(figsize=(7, 5)) ax.scatter(prophet_df_test["ds"], prophet_df_test['y'], color='r') fig = model.plot(test_fcst, ax=ax) ax.set_xbound( lower=pd.to_datetime("2025-01-01"), # starting data on the x axis upper=pd.to_datetime("2025-02-01")) # ending data on the x axis ax.set_ylim(0, 0.005) plot = plt.suptitle("January 2025, Actual vs Forecasts")
Ausgabe:
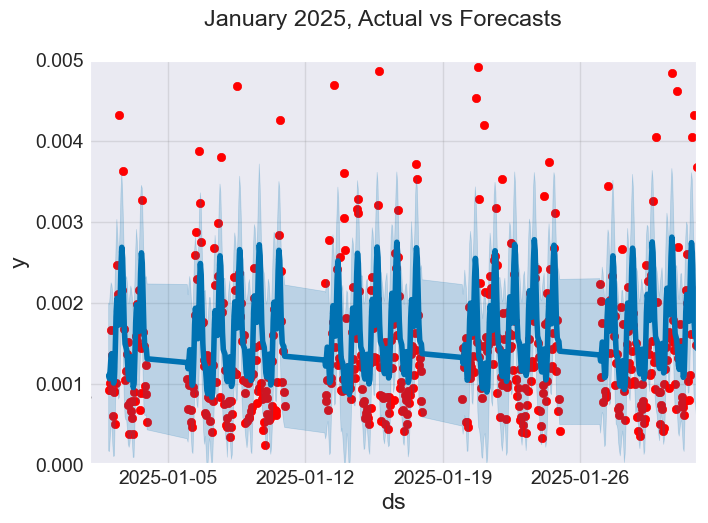
Abbildung 06
Aus der obigen Abbildung geht hervor, dass das Prophet-Modell einige Vorhersagen richtig trifft, und dass es mit Ausreißern in den Daten nicht gut zurechtkommt.
Optional können wir die Vorhersagen weiter untersuchen, indem wir die tatsächlichen Werte mit den Vorhersagen des Modells in der ersten Januarwoche (vom 1. bis 8. Januar) vergleichen.
f, ax = plt.subplots(figsize=(9, 5)) ax.scatter(prophet_df_test["ds"], prophet_df_test['y'], color='r') fig = model.plot(test_fcst, ax=ax) ax.set_xbound( lower=pd.to_datetime("2025-01-01"), upper=pd.to_datetime("2025-01-08")) ax.set_ylim(0, 0.005) plot = plt.suptitle("January 01-08, 2025. Actual vs Forecasts")
Ausgabe:
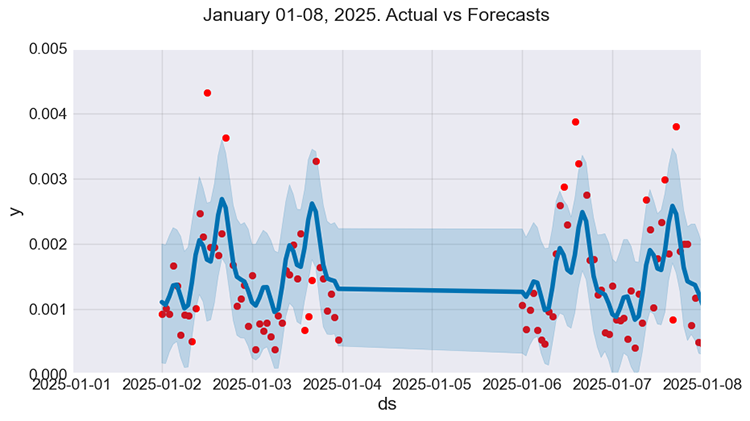
Abbildung 07
Das sieht schon viel besser aus. Das Modell scheint zwar einige Muster zu verstehen, aber seine Prognosen (Vorhersagen) kommen den tatsächlichen Werten nicht sehr nahe, was wir bei der Verwendung von Regressionsmodellen oft anstreben.
Es scheint jedoch eine gute allgemeine Vorhersage zu sein.
Wir wollen sie anhand einiger Bewertungsmaßstäbe bewerten.
import sklearn.metrics as metric def forecast_accuracy(forecast, actual): # Convert to numpy arrays if they aren't already forecast = np.asarray(forecast) actual = np.asarray(actual) metrics = { 'mape': metric.mean_absolute_percentage_error(actual, forecast), 'me': np.mean(forecast - actual), # Mean Error 'mae': metric.mean_absolute_error(actual, forecast), 'mpe': np.mean((forecast - actual) / actual), # Mean Percentage Error 'rmse': metric.root_mean_squared_error(actual, forecast), 'minmax': 1 - np.mean(np.minimum(forecast, actual) / np.maximum(forecast, actual)), "r2_score": metric.r2_score(forecast, actual) } return metrics results = forecast_accuracy(test_pred, prophet_df_test["y"]) for metric_name, value in results.items(): print(f"{metric_name:<10}: {value:.6f}")
Ausgabe:
mape : 0.603277 me : 0.000130 mae : 0.000829 mpe : 0.430299 rmse : 0.001221 minmax : 0.339292 r2_score : -4.547775
Was mich interessiert, ist die MAPE-Kennzahl (Mean Absolute Percentage Error); der Wert von etwa 0,6 bedeutet, dass die Prognosen des Modells im Durchschnitt um 60 % von den tatsächlichen Werten abweichen. Einfach ausgedrückt: Das Modell macht schlechte Vorhersagen und ist fehleranfällig.
Hinzufügen von Feiertage zum Prophet-Modell
Das Prophet-Modell wurde entwickelt, um die Tatsache zu verstehen, dass es in allen Daten Ereignisse geben kann, die ungewöhnliche Veränderungen in den Zeitreihendaten verursachen; diese nennen wir „holidays“ (Feiertage).
In der realen Welt werden Feiertage wahrscheinlich unregelmäßige Auswirkungen auf die Geschäftsdaten haben; diese können sein.
- Feiertage (z. B. Neujahr, Weihnachten)
- Geschäftsveranstaltungen (z. B. Schwarzer Freitag, Produkteinführung)
- Finanzielle Ereignisse (z. B. Ankündigungen der Zentralbank, Quartalsende)
- Lokale Ereignisse (z. B. Wahlen, Wetterkapriolen)
Diese Tage folgen keinem unregelmäßigen saisonalen Muster, sondern sie wiederholen sich, oft jährlich, vierteljährlich, täglich, usw.
Bei Finanzdaten (Handelsdaten) können wir die Wirtschaftsnachrichten als Feiertage betrachten, da sie das beschriebene Szenario verursachen. Auf diese Weise können wir unserem Modell helfen, sein derzeitiges Problem zu lösen – dass es diese extremen Werte nicht erfassen kann.
Wie in Abbildung 01 zu sehen ist, die die Formel des Prophet-Modells zeigt, wird das Modell durch Hinzufügen von Feiertage , falls es welche gibt, vollständig, da Feiertage einer der Hauptbausteine der Formel sind.
Das heißt, wir müssen die Nachrichten in der Sprache MQL5 sammeln.
Dateiname: OHCL + News.mq5
input datetime start_date = D'01.01.2023'; input datetime end_date = D'24.6.2025'; input ENUM_TIMEFRAMES timeframe = PERIOD_H1; MqlRates rates[]; struct news_data_struct { datetime time[]; //News release time double open[]; //Candle opening price double high[]; //Candle high price double low[]; //Candle low price double close[]; //Candle close price string name[]; //Name of the news ENUM_CALENDAR_EVENT_SECTOR sector[]; //The sector a news is related to ENUM_CALENDAR_EVENT_IMPORTANCE importance[]; //Event importance double actual[]; //actual value double forecast[]; //forecast value double previous[]; //previous value void Resize(uint size) { ArrayResize(time, size); ArrayResize(open, size); ArrayResize(high, size); ArrayResize(low, size); ArrayResize(close, size); ArrayResize(name, size); ArrayResize(sector, size); ArrayResize(importance, size); ArrayResize(actual, size); ArrayResize(forecast, size); ArrayResize(previous, size); } } news_data; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- if (!ChartSetSymbolPeriod(0, Symbol(), timeframe)) return; SaveNews(StringFormat("%s.%s.OHLC + News.csv",Symbol(),EnumToString(timeframe))); } //+------------------------------------------------------------------+ //| | //| The function which collects news alongsided OHLC values and | //| saves the data to a CSV file | //| | //+------------------------------------------------------------------+ void SaveNews(string csv_name) { //--- get OHLC values first ResetLastError(); if (CopyRates(Symbol(), timeframe, start_date, end_date, rates)<=0) { printf("%s failed to get price information from %s to %s. Error = %d",__FUNCTION__,string(start_date),string(end_date),GetLastError()); return; } uint size = rates.Size(); news_data.Resize(size-1); //--- FileDelete(csv_name); //Delete an existing csv file of a given name int csv_handle = FileOpen(csv_name,FILE_WRITE|FILE_SHARE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON,",",CP_UTF8); //csv handle if(csv_handle == INVALID_HANDLE) { printf("Invalid %s handle Error %d ",csv_name,GetLastError()); return; //stop the process } FileSeek(csv_handle,0,SEEK_SET); //go to file begining FileWrite(csv_handle,"Time,Open,High,Low,Close,Name,Sector,Importance,Actual,Forecast,Previous"); //write csv header MqlCalendarValue values[]; //https://www.mql5.com/en/docs/constants/structures/mqlcalendar#mqlcalendarvalue for (uint i=0; i<size-1; i++) { news_data.time[i] = rates[i].time; news_data.open[i] = rates[i].open; news_data.high[i] = rates[i].high; news_data.low[i] = rates[i].low; news_data.close[i] = rates[i].close; int all_news = CalendarValueHistory(values, rates[i].time, rates[i+1].time, NULL, NULL); //we obtain all the news with their values https://www.mql5.com/en/docs/calendar/calendarvaluehistory for (int n=0; n<all_news; n++) { MqlCalendarEvent event; CalendarEventById(values[n].event_id, event); //Here among all the news we select one after the other by its id https://www.mql5.com/en/docs/calendar/calendareventbyid MqlCalendarCountry country; //The couhtry where the currency pair originates CalendarCountryById(event.country_id, country); //https://www.mql5.com/en/docs/calendar/calendarcountrybyid if (StringFind(Symbol(), country.currency)>-1) //We want to ensure that we filter news that has nothing to do with the base and the quote currency for the current symbol pair { news_data.name[i] = event.name; news_data.sector[i] = event.sector; news_data.importance[i] = event.importance; news_data.actual[i] = !MathIsValidNumber(values[n].GetActualValue()) ? 0 : values[n].GetActualValue(); news_data.forecast[i] = !MathIsValidNumber(values[n].GetForecastValue()) ? 0 : values[n].GetForecastValue(); news_data.previous[i] = !MathIsValidNumber(values[n].GetPreviousValue()) ? 0 : values[n].GetPreviousValue(); } } FileWrite(csv_handle,StringFormat("%s,%f,%f,%f,%f,%s,%s,%s,%f,%f,%f", (string)news_data.time[i], news_data.open[i], news_data.high[i], news_data.low[i], news_data.close[i], news_data.name[i], EnumToString(news_data.sector[i]), EnumToString(news_data.importance[i]), news_data.actual[i], news_data.forecast[i], news_data.previous[i] )); } //--- FileClose(csv_handle); }
Nach dem Sammeln der Nachrichten in der Funktion SaveNews werden die erhaltenen Daten in einer CSV-Datei im „Common path“ (Ordner) gespeichert.
Innerhalb des Python-Skripts laden wir diese Daten aus demselben Pfad.
from Trade.TerminalInfo import CTerminalInfo import os terminal = CTerminalInfo() data_path = os.path.join(terminal.common_data_path(), "Files") timeframe = "PERIOD_H1" df = pd.read_csv(os.path.join(data_path, f"{symbol}.{timeframe}.OHLC + News.csv")) df
Ausgabe:
| Time | Open | High | Low | Close | Name | Sector | Importance | Actual | Forecast | Previous | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2023.01.02 01:00:00 | 1.06967 | 1.06983 | 1.06927 | 1.06983 | New Year's Day | CALENDAR_SECTOR_HOLIDAYS | CALENDAR_IMPORTANCE_NONE | 0.0 | 0.0 | 0.0 |
| 1 | 2023.01.02 02:00:00 | 1.06984 | 1.07059 | 1.06914 | 1.07041 | New Year's Day | CALENDAR_SECTOR_HOLIDAYS | CALENDAR_IMPORTANCE_NONE | 0.0 | 0.0 | 0.0 |
| 2 | 2023.01.02 03:00:00 | 1.07059 | 1.07069 | 1.06858 | 1.06910 | New Year's Day | CALENDAR_SECTOR_HOLIDAYS | CALENDAR_IMPORTANCE_NONE | 0.0 | 0.0 | 0.0 |
| 3 | 2023.01.02 04:00:00 | 1.06909 | 1.06909 | 1.06828 | 1.06880 | New Year's Day | CALENDAR_SECTOR_HOLIDAYS | CALENDAR_IMPORTANCE_NONE | 0.0 | 0.0 | 0.0 |
| 4 | 2023.01.02 05:00:00 | 1.06881 | 1.07029 | 1.06880 | 1.06897 | New Year's Day | CALENDAR_SECTOR_HOLIDAYS | CALENDAR_IMPORTANCE_NONE | 0.0 | 0.0 | 0.0 |
Da wir in unserem MQL5-Skript die Nachrichten für jede Datenzeile erfasst haben, gibt es in der Spalte Nachrichten einige Zeilen mit dem Namen „null“, was bedeutet, dass es zu dem Zeitpunkt keine Nachrichten gabwir müssen diese Zeilen filtern.
news_df = df[df['Name'] != "(null)"].copy()
Ähnlich wie wir die vorherigen Daten für dieses Modell so strukturiert haben, dass sie zwei Spalten haben – ds und y – müssen wir sicherstellen, dass der Feiertagsdatensatz ebenfalls zwei Spalten hat – ds und Feiertage. Die Spalte holiday dient dazu, den Namen des/der Neuen zu speichern.
holidays = news_df[['Time', 'Name']].rename(columns={ 'Time': 'ds', 'Name': 'holiday' }) holidays['ds'] = pd.to_datetime(holidays['ds']) # Ensure datetime format holidays
Ausgabe:
| ds | holiday | |
|---|---|---|
| 0 | 2023-01-02 01:00:00 | New Year's Day |
| 1 | 2023-01-02 02:00:00 | New Year's Day |
| 2 | 2023-01-02 03:00:00 | New Year's Day |
| 3 | 2023-01-02 04:00:00 | New Year's Day |
| 4 | 2023-01-02 05:00:00 | New Year's Day |
Zusätzlich zu diesen Merkmalen kann der Feiertage-Datenrahmen zwei optionale Spalten haben (lower_window und upper_window). Diese Spalten geben dem Modell Aufschluss über die Auswirkungen der einzelnen Feiertage vor und nach ihrem Auftreten.
Wir wissen, dass jeder Feiertage in der realen Welt nicht nur an dem Tag, an dem er stattfindet, Auswirkungen hat, sondern oft auch davor und danach.
holidays['lower_window'] = 0 holidays['upper_window'] = 1 # Extend effect to 1 hour after
Die Spalte lower_window gibt an, wie stark sich der Feiertage auf die Zeitreihendaten vor seinem Auftreten ausgewirkt hat, während die Spalte upper_window angibt, wie stark sich der Feiertage auf die Zeitreihe nach seinem Auftreten ausgewirkt hat.
- Für die Spalte lower_window können die Werte kleiner oder gleich Null (<=0) sein. Der Standardwert ist Null, was bedeutet, dass der Feiertage keine Auswirkungen auf einen früheren Wert in einer Zeitreihe hat. Ein Wert von -1 zeigt an, dass ein bestimmter Feiertage den vorherigen Einzelwert der Zeitreihe beeinflusst, bevor er auftritt usw.
- Für die Spalte upper_window können die Werte größer oder gleich Null (>=0) sein. Der Standardwert ist Null, was bedeutet, dass der Feiertage keine Auswirkungen auf die Werte in einer Zeitreihe nach seinem Auftreten hat. Ein Wert von 1 bedeutet, dass sich ein bestimmter Feiertage auf den nächsten Einzelwert in der Zeitreihe auswirkt, usw.
Fügen wir nun diese Funktionen wie beschrieben hinzu.
holidays['lower_window'] = -1 # The anticipation of the news affect the volatility 1 bar before it's release holidays['upper_window'] = 1 # The news affects the volatility 1 bar after its release holidays
Unser Feiertags-DataFrame wird nun:
| ds | holiday | lower_window | upper_window | |
|---|---|---|---|---|
| 0 | 2023-01-02 01:00:00 | New Year's Day | -1 | 1 |
| 1 | 2023-01-02 02:00:00 | New Year's Day | -1 | 1 |
| 2 | 2023-01-02 03:00:00 | New Year's Day | -1 | 1 |
| 3 | 2023-01-02 04:00:00 | New Year's Day | -1 | 1 |
| 4 | 2023-01-02 05:00:00 | New Year's Day | -1 | 1 |
| ... | ... | ... | ... | ... |
| 15369 | 2025-06-20 18:00:00 | Eurogroup Meeting | -1 | 1 |
| 15370 | 2025-06-20 19:00:00 | Eurogroup Meeting | -1 | 1 |
| 15371 | 2025-06-20 20:00:00 | Eurogroup Meeting | -1 | 1 |
| 15372 | 2025-06-20 21:00:00 | Eurogroup Meeting | -1 | 1 |
| 15373 | 2025-06-20 22:00:00 | Eurogroup Meeting | -1 | 1 |
Zum Schluss geben wir unserem Prophet-Modell den Feiertags-DataFrame und die Trainingsdaten, die wir zuvor vorbereitet haben.
model_w_holidays = Prophet(holidays=holidays) model_w_holidays.fit(prophet_df_train)
Wir können die Vorhersagen des trainierten Modells mit Feiertage testen, indem wir die vorhergesagten Werte neben den tatsächlichen Werten aufzeichnen, wie wir es zuvor getan haben.
# Predict on training set with model test_fcst = model_w_holidays.predict(df=prophet_df_test) test_pred = test_fcst.yhat # We get the predictions # Plot the forecast with the actuals f, ax = plt.subplots(figsize=(10,5)) ax.scatter(prophet_df_test["ds"], prophet_df_test['y'], color='r') fig = model_w_holidays.plot(test_fcst, ax=ax)
Ausgabe:
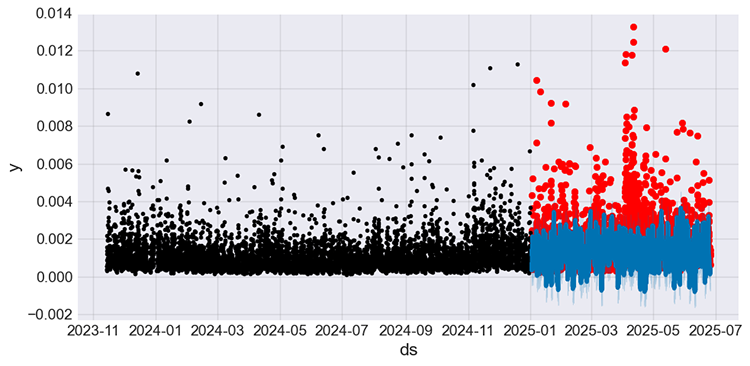
Abbildung 08
Im Gegensatz zu den Vorhersagen des Modells ohne Nachrichten (Feiertage) in Abbildung 05, die statisch zu sein scheinen, scheinen die Vorhersagen dieses neuen Modells mit Nachrichten (Feiertage) einige der Fluktuationen zu erfassen, die dem vorherigen Modell fehlten.
Auch hier bewerten wir das Modell anhand der gleichen Metriken, die wir für das vorherige Modell verwendet haben.
results = forecast_accuracy(test_pred, prophet_df_test["y"]) for metric_name, value in results.items(): print(f"{metric_name:<10}: {value:.6f}")
Ausgabe:
mape : 0.549152 me : -0.000633 mae : 0.000970 mpe : -0.175082 rmse : 0.001487 minmax : 0.461444 r2_score : -2.793478
Die MAPE-Kennzahl zeigt, dass die Vorhersagen des Modells um etwa 10 % verbessert wurden. Das Vorgängermodell wies etwa 60 % Fehler auf, während das neue Modell etwa 55 % Fehler aufwies. Diese Verbesserung lässt sich auch am r2_score ablesen.
Das Modell, das 55 % Fehler macht, ist immer noch nicht gut, ein ideales Modell muss mindestens weniger als 50 % Fehler machen (< 50 %), wir können immer noch etwas über die Feiertage (Nachrichten) tun, um dieses Modell zu verbessern.
In diesem Beispiel haben wir die Werte für lower_window und upper_window als -1 bzw. 1 implementiert, was bedeutet, dass die Nachrichten die Volatilität auf dem Markt einen Balken vor und nach ihrer Veröffentlichung beeinflussen. Dadurch wurde das Modell zwar verbessert, aber ich bezweifle, dass es ideal ist.
Wir wissen, dass verschiedene Nachrichten unterschiedliche Wirkungshorizonte und -stärken haben können, sodass es grundsätzlich falsch ist, diese konstanten Werte für alle Nachrichten anzusetzen. Außerdem haben wir alle Nachrichten verwendet, auch solche mit geringerer Bedeutung, die wir als Händler oft ignorieren, weil solche Nachrichten sehr häufig vorkommen und es schwierig ist, ihre Auswirkungen auf den Chart zu messen und zu beobachten.
Um diese beiden Probleme zu beheben, müssen Sie die Werte für lower_window und upper_window dynamisch entsprechend dem Nachrichtentyp und ihren historisch beobachtbaren Auswirkungen festlegen.
Beispiel Pseudocode.
def get_windows(name): if "CPI" in name: return (-1, 4) # CPI news affects one previous bar volatility, and it affects the volatility of four bars ahead (4 hours impact forward) elif "NFP" in name: return (-1, 2) # NFP news affects one previous bar volatility, and it affects the volatility of two bars ahead (2 hours impact afterward) elif "FOMC" in name or "Rate" in name: return (-2, 6) # NFP news affects two previous bar volatility, and it affects the volatility of six bars ahead (6 hours impact afterward) else: return (0, 1) # Default holidays[['lower_window', 'upper_window']] = holidays['holiday'].apply( lambda name: pd.Series(get_windows(name)) )
In Anbetracht der Zehntausenden von Nachrichtentypen und der Tatsache, dass man sicher sein muss, dass die implementierten Impact-Werte korrekt sind, ist dieser Ansatz sehr schwierig zu implementieren, aber er ist der ideale Weg. Also, machen Sie Ihre Hausaufgaben :).
Das Naheliegendste, was wir jetzt tun können, ist, einige Nachrichten zu filtern, damit wir bei Nachrichten von größerer und mittlerer Bedeutung bleiben können.
news_df = df[ (df['Name'] != "(null)") & # Filter rows without news at all ((df['Importance'] == "CALENDAR_IMPORTANCE_HIGH") | (df['Importance'] == "CALENDAR_IMPORTANCE_MODERATE")) # Filter other news except high importance news ].copy() news_df
Ausgabe:
| Time | Open | High | Low | Close | Name | Sector | Importance | Actual | Forecast | Previous | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 2023.01.02 08:00:00 | 1.06921 | 1.06973 | 1.06724 | 1.06858 | S&P Global Manufacturing PMI | CALENDAR_SECTOR_BUSINESS | CALENDAR_IMPORTANCE_MODERATE | 47.10 | 47.400 | 47.400 |
| 8 | 2023.01.02 09:00:00 | 1.06878 | 1.06909 | 1.06627 | 1.06784 | S&P Global Manufacturing PMI | CALENDAR_SECTOR_BUSINESS | CALENDAR_IMPORTANCE_MODERATE | 47.80 | 47.800 | 47.800 |
| 31 | 2023.01.03 08:00:00 | 1.06636 | 1.06677 | 1.06514 | 1.06524 | Unemployment | CALENDAR_SECTOR_JOBS | CALENDAR_IMPORTANCE_MODERATE | 2.52 | 2.522 | 2.538 |
| 37 | 2023.01.03 14:00:00 | 1.05283 | 1.05490 | 1.05241 | 1.05355 | S&P Global Manufacturing PMI | CALENDAR_SECTOR_BUSINESS | CALENDAR_IMPORTANCE_HIGH | 46.20 | 46.200 | 46.200 |
| 38 | 2023.01.03 15:00:00 | 1.05353 | 1.05698 | 1.05304 | 1.05602 | Construction Spending m/m | CALENDAR_SECTOR_HOUSING | CALENDAR_IMPORTANCE_MODERATE | 0.20 | 0.200 | -0.300 |
Nachdem wir die Spalten Zeit und Name in den Feiertags-DataFrame extrahiert haben, fügen wir die Werte für lower_window und upper_window hinzu.
holidays = news_df[['Time', 'Name']].rename(columns={ 'Time': 'ds', 'Name': 'holiday' }) holidays['ds'] = pd.to_datetime(holidays['ds']) # Ensure datetime format holidays['lower_window'] = 0 holidays['upper_window'] = 1 holidays
Nach dem Training des Modells zeigt das folgende Diagramm die tatsächlichen Werte der Trainings- und Teststichprobe in schwarz bzw. rot und die Vorhersagen der Teststichprobe in blau.
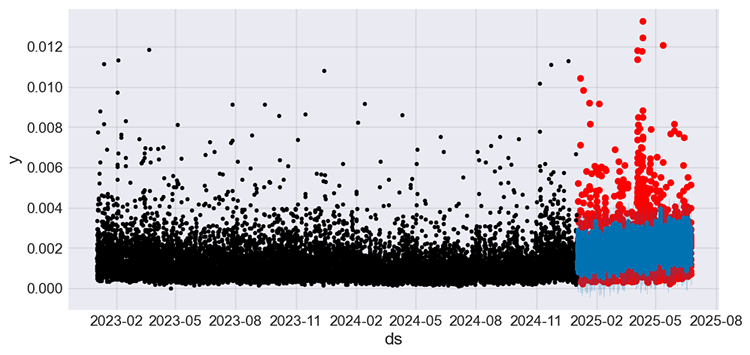
Abbildung 09
Das Modell hat sich erneut verbessert und macht nach der MAPE-Metrik etwa 50 % Fehler. Mit diesem Regressionsmodell können wir nun Vorhersagen treffen.
mape : 0.506827 me : -0.000053 mae : 0.000783 mpe : 0.271597 rmse : 0.001234 minmax : 0.320422 r2_score : -3.318859
Sie haben vielleicht bemerkt, dass wir die Nachrichten separat aus einer CSV-Datei importiert haben, während wir sie zusammen mit den direkt aus MetaTrader 5 importierten Trainingsdaten verwendet haben.
Das Prophet-Modell gleicht die Daten aus dem „Feiertage“-DataFrame mit den Daten in den Haupttrainingsdaten ab, solange die Zeitstempel im Feiertags-DataFrame in den Trainings-/Zukunftsvorhersagezeitraum fallen.
Obwohl dieses Modell in der Lage ist, die Daten zu synchronisieren, müssen Sie ausdrücklich sicherstellen, dass beide Datensätze die gleichen Anfangsdaten haben, um das Beste aus den beiden Datensätzen herauszuholen.
Ich musste zurückgehen und den Prozess des Erhaltens von Preisinformationen von MetaTrader 5 in main.ipynb ändern, Start- und Enddaten stimmen jetzt mit denen überein, die in der Skriptdatei OHLC + News.mq5 verwendet werden.
# set time zone to UTC timezone = pytz.timezone("Etc/UTC") # create 'datetime' objects in UTC-time to avoid the implementation of a local time zone offset utc_from = datetime(2023, 1, 1, tzinfo=timezone) utc_to = datetime(2025, 6, 24, hour = 0, tzinfo=timezone) rates = mt5.copy_rates_range(symbol, timeframe, utc_from, utc_to)
Herstellung des MetaTrader 5-Handelsroboters auf der Grundlage des Prophet-Modells
Um einen Handelsroboter auf der Grundlage des Prophet-Modells zu entwickeln, müssen wir zunächst in der Lage sein, damit Echtzeit-Vorhersagen für die Zielvariable (in diesem Fall die Volatilität) zu treffen.
Um dies zu erreichen, benötigen wir eine Pipeline, um die neuesten Informationen vom Markt (Symbole) zu erhalten, einschließlich der neuesten Nachrichten-Updates auf einmal. Im Trainingsskript main.ipynb haben wir mit dem MetaTrader 5-Python-Paket Daten von MetaTrader 5 gesammelt, aber dieses Paket bietet keine Möglichkeit, Nachrichten zu erhalten, sodass wir definitiv MQL5 für diesen Prozess verwenden müssen.
Die Idee ist, Daten zwischen dem Python-Skript (Handelsroboter) und einem Expert Advisor (EA) in MQL5 auszutauschen.
- Ein EA (Data for Prophet.mq5), der an den MetaTrader 5 Chart angehängt ist, speichert regelmäßig die Daten (News und OHLC-Werte) von MetaTrader 5 in eine CSV-Datei im gemeinsamen Ordner.
- Diese Datei wird dann von dem Python-Skript (Prophet-trading-bot.py) gelesen, um das Prophet-Modell regelmäßig zu trainieren.
- Nach dem Training wird das Modell dann zur Erstellung von Prognosen verwendet, die dann für Handelsentscheidungen innerhalb desselben Python-Skripts genutzt werden.
Dateiname: Data for Prophet.mq5
input uint collect_news_interval_seconds = 60; input uint training_bars = 1000; input ENUM_TIMEFRAMES timeframe = PERIOD_H1; //... other lines of code //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- create timer EventSetTimer(collect_news_interval_seconds); if (!ChartSetSymbolPeriod(0, Symbol(), timeframe)) return INIT_FAILED; //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- destroy timer EventKillTimer(); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- } //+------------------------------------------------------------------+ //| Timer function | //+------------------------------------------------------------------+ void OnTimer() { //--- MqlDateTime time_struct; TimeToStruct(TimeGMT(), time_struct); SaveNews(StringFormat("%s.%s.OHLC.date=%s.hour=%d + News.csv",Symbol(),EnumToString(timeframe), TimeToString(TimeGMT(), TIME_DATE), time_struct.hour)); }
Um sicherzustellen, dass wir mit der richtigen Datei arbeiten, werden das Datum und die aktuelle Stunde (in UTC-Zeit) bei der Benennung der CSV-Datei verwendet.
Dieser Expert Advisor sammelt Nachrichten und andere Werte und speichert sie standardmäßig jede Minute in einer CSV-Datei, entsprechend der Funktion OnTimer.
In einem Python-Skript laden wir die CSV-Datei auf die gleiche Weise aus dem allgemeinen Ordner und importieren die Daten.
Dateiname: Prophet-trading-bot.py
def prophet_vol_predict() -> float: # Getting the data with news now_utc = datetime.utcnow() current_date = now_utc.strftime("%Y.%m.%d") current_hour = now_utc.hour filename = f"{symbol}.{timeframe}.OHLC.date={current_date}.hour={current_hour} + News.csv" # the same file naming as in MQL5 script common_path = os.path.join(terminal.common_data_path(), "Files") csv_path = os.path.join(common_path, filename) # Keep trying to read a CSV file until it is found, as there could be a temporary difference in values for the file due to the change in time while True: if os.path.exists(csv_path): try: rates_df = pd.read_csv(csv_path) rates_df["Time"] = pd.to_datetime(rates_df["Time"], unit="s", errors="ignore") # Convert time from seconds to datetime print("File loaded successfully.") break # Exit the loop once file is read except Exception as e: print(f"Error reading the file: {e}") time.sleep(30) else: print("File not found. Retrying in 30 seconds...") time.sleep(30)
Wir bereiten die Volatilitätsspalte vor und extrahieren die Nachrichtennamen für die Trainingsdaten bzw. die Feiertagsdaten.
# Getting continous variables for the prophet model prophet_df = pd.DataFrame({ "time": rates_df["Time"], "volatility": rates_df["High"] - rates_df["Low"] }).set_index("time") prophet_df = prophet_df.reset_index().rename(columns={"time": "ds", "volatility": "y"}).copy() print("Prophet df\n",prophet_df.head()) # Getting the news data for the model as well news_df = rates_df[ (rates_df['Name'] != "(null)") & # Filter rows without news at all ((rates_df['Importance'] == "CALENDAR_IMPORTANCE_HIGH") | (rates_df['Importance'] == "CALENDAR_IMPORTANCE_MODERATE")) # Filter other news except high importance news ].copy() holidays = news_df[['Time', 'Name']].rename(columns={ 'Time': 'ds', 'Name': 'holiday' }) holidays['ds'] = pd.to_datetime(holidays['ds']) # Ensure datetime format holidays['lower_window'] = 0 holidays['upper_window'] = 1 print("Holidays df\n", holidays)
Am Ende der Funktion prophet_vol_pred wird das Modell mit den erhaltenen Informationen trainiert und ein einzelner prognostizierter Wert zurückgegeben, der die prognostizierte Volatilität darstellt, von der das Modell glaubt, dass sie im nächsten Balken auf dem Markt auftreten wird.
# re-training the prophet model prophet_model = Prophet(holidays=holidays) prophet_model.fit(prophet_df) # Making future predictions future = prophet_model.make_future_dataframe(periods=1) # prepare the dataframe for a single value prediction forecast = prophet_model.predict(future) # Predict the next one value return forecast.yhat[0] # return a single predicted value
Ähnlich wie bei anderen Modellen des maschinellen Lernens, die in der Zeitreihenprognose verwendet werden, müssen wir sie sehr oft aktualisieren, um sicherzustellen, dass sie mit den neuesten Informationen ausgestattet sind, die für zukünftige Prognosen (Vorhersagen) relevant sind. Dies ist der Hauptgrund, warum wir das Modell neu trainieren, bevor wir neue Vorhersagen treffen.
Führen wir die Funktion aus und beobachten wir das Ergebnis.
print("predicted volatility: ",prophet_vol_predict())
Ausgabe:
File loaded successfully. Prophet df ds y 0 2025.04.29 01:00:00 0.00100 1 2025.04.29 02:00:00 0.00210 2 2025.04.29 03:00:00 0.00170 3 2025.04.29 04:00:00 0.00215 4 2025.04.29 05:00:00 0.00278 Holidays df ds holiday lower_window upper_window 8 2025-04-29 09:00:00 GfK Consumer Climate 0 1 14 2025-04-29 15:00:00 Retail Inventories excl. Autos m/m 0 1 31 2025-04-30 08:00:00 Consumer Spending m/m 0 1 33 2025-04-30 10:00:00 Unemployment 0 1 35 2025-04-30 12:00:00 GDP y/y 0 1 .. ... ... ... ... 978 2025-06-24 19:00:00 FOMC Member Williams Speech 0 1 979 2025-06-24 20:00:00 2-Year Note Auction 0 1 982 2025-06-24 23:00:00 Fed Vice Chair for Supervision Barr Speech 0 1 984 2025-06-25 01:00:00 Jobseekers Total 0 1 994 2025-06-25 11:00:00 Bbk Executive Board Member Mauderer Speech 0 1 [186 rows x 4 columns] 16:01:50 - cmdstanpy - INFO - Chain [1] start processing 16:01:50 - cmdstanpy - INFO - Chain [1] done processing predicted volatility: 0.0013592111956094713
Da wir nun in der Lage sind, den vorhergesagten Wert zu erhalten, können wir ihn in unserer Handelsstrategie verwenden.
symbol = "EURUSD" timeframe = "PERIOD_H1" terminal = CTerminalInfo() m_position = CPositionInfo() def main(): m_symbol = CSymbolInfo(symbol=symbol) magic_number = 25062025 slippage = 100 m_trade = CTrade(magic_number=magic_number, filling_type_symbol=symbol, deviation_points=slippage) m_symbol.refresh_rates() # Get recent information from the market # we want to open random buy and sell trades if they don't exist and use the predicted volatility to set our stoploss and takeprofit targets predicted_volatility = prophet_vol_predict() print("predicted volatility: ",prophet_vol_predict()) if pos_exists(mt5.POSITION_TYPE_BUY, magic_number, symbol) is False: m_trade.buy(volume=m_symbol.lots_min(), symbol=symbol, price=m_symbol.ask(), sl=m_symbol.ask()-predicted_volatility, tp=m_symbol.ask()+predicted_volatility) if pos_exists(mt5.POSITION_TYPE_SELL, magic_number, symbol) is False: m_trade.sell(volume=m_symbol.lots_min(), symbol=symbol, price=m_symbol.bid(), sl=m_symbol.bid()+predicted_volatility, tp=m_symbol.bid()-predicted_volatility)
Die obige Funktion holt sich die prognostizierte Volatilität aus dem Prophet-Modell und verwendet sie zum Setzen von Stoploss- und Takeprofit-Zielen in unseren Trades. Bevor ein zufälliger Handel eröffnet wird, wird geprüft, ob eine Position (Handel) desselben Typs noch nicht existiert, bevor eine solche eröffnet wird.
Funktionsaufruf.
main()
Das Ergebnis.
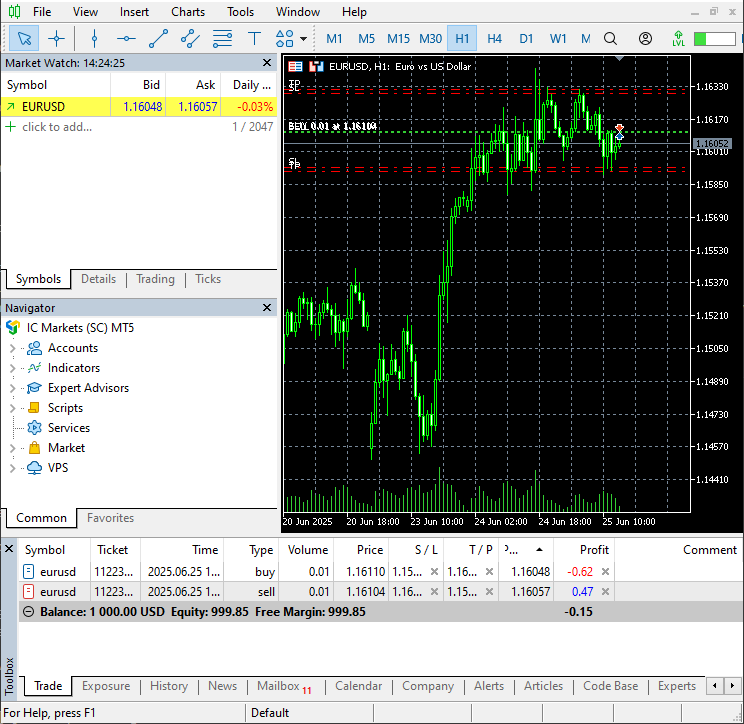
Abbildung 10
Im MetaTrader 5 wurden zwei gegenläufige Handelsgeschäfte mit Stop-Loss- und Take-Profit-Werten eröffnet, die der vom Modell vorhergesagten Volatilität entsprechen.
Wir können diesen Schulungsprozess automatisieren und die Handelsvorgänge und Signale regelmäßig überwachen.
schedule.every(1).minute.do(main) # train and run trading operations after every one minute while True: schedule.run_pending() time.sleep(1)
Schlussfolgerung
Während in einigen Artikeln, Beiträgen und Tutorials im Internet behauptet wird, dass das Prophet-Modell gut für Zeitreihenprognosen geeignet ist, halte ich es für eines der schlechtesten Modelle, die wir in dieser Artikelserie besprochen haben.
Sie könnte sich für die Vorhersage einiger einfacher Zeitreihenprobleme eignen, wie z. B. die Vorhersage der Nachfrage eines Unternehmens, die vom Wetter, von Feiertage oder von saisonalen Mustern abhängt, aber die Finanzmärkte sind sehr viel komplexer, wie aus den Abbildungen (05, 06, 07, 08, 09) ersichtlich ist, die die tatsächlichen und die vorhergesagten Werte für die Teststichproben zeigen. Das Prophet-Modell schafft es nicht, die Mehrzahl der Vorhersagen in die Nähe der tatsächlichen Werte zu bringen.
Ich verstehe, dass es bestimmte Dinge gibt, die man tun kann, um sie zu verbessern, aber ich würde vorschlagen, sie zunächst für einfache Probleme zu verwenden.
Zu den zusammengefassten Einschränkungen dieses Modells gehören.
- Einfache Modellstruktur, die keine komplexen Interaktionen zulässt
- Nicht gut bei Volatilität – wie oben gesehen, funktioniert es nicht gut bei Forex-Daten.
- Keine multivariate Modellierung – Es unterstützt zwei Merkmale: die Zeit und die Zielvariable.
- Keine Möglichkeit zur Kreuzvalidierung oder zur Abstimmung von Hyperparametern, da Sie Trend, Saisonalität und Änderungspunkte selbst kontrollieren müssen.
Mit freundlichen Grüßen.
Quellen und Referenzen
- https://facebook.github.io/prophet/
- https://otexts.com/fpp3/prophet.html
- https://www.geeksforgeeks.org/time-series-analysis-using-facebook-prophet/
- https://www.kaggle.com/code/omegajoctan/time-series-forecasting-with-prophet/edit
Tabelle der Anhänge
| Dateiname | Beschreibung und Verwendung |
|---|---|
| Python code\main.ipynb | Ein Jupyter-Notebook für die Datenanalyse und die Erkundung des Prophet-Modells. |
| Python code\Prophet-trading-bot.py | MetaTrader 5 Handelsroboter auf Python-Basis. |
| Python code\requirementx.txt | Eine Textdatei mit Python-Abhängigkeiten und deren Versionsnummer |
| Python code\error_description.py | Enthält die Beschreibung aller von MetaTrader 5 erzeugten Fehlercodes. |
| Python code\Trade\* | Enthält die Handelsklassen (CTrade, CPositionInfo, etc.) für Python, ähnlich denen, die in der Sprache MQL5 verfügbar sind. |
| Experts\Data for Prophet.mq5 | Ein Expert Advisor, der regelmäßig die Daten für das Training des Prophet-Modells sammelt und in einer CSV-Datei speichert. |
| Scripts\OHLC + News.mq5 | Ein Skript zum Sammeln und Speichern der Daten für das Training des Prophet-Modells in einer CSV-Datei. |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/18549
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
MQL5-Assistenz-Techniken, die Sie kennen sollten (Teil 71): Verwendung der Muster des MACD und des OBV
Vom Neuling zum Experten: Animierte Nachrichtenüberschrift mit MQL5 (II)
Vom Neuling zum Experten: Animierte Nachrichten-Schlagzeile mit MQL5 (III) – Indicator Insights
Datenwissenschaft und ML (Teil 43): Erkennen verborgener Muster in Indikatordaten unter Verwendung Latenter Gaußscher Mischmodelle (LGMM)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.