MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 81): Verwendung von Ichimoku-Mustern und des ADX-Wilder mit Beta-VAE-Inferenzlernen

Einführung

Fast jeder Händler hat erkannt, dass sich die Märkte in Zyklen von Optimismus und Pessimismus bewegen, und dennoch gibt es nur sehr wenige sofort einsetzbare Instrumente, die diese Zyklen mit der für einen profitablen Handel erforderlichen Beständigkeit erfassen. In letzter Zeit tendieren die Märkte weltweit zu einem Abschwung, wobei plötzliche Ausverkäufe und flache Erholungen immer häufiger vorkommen. In einem solchen Umfeld produzieren mechanische Strategien, die auf den Regeln nachlaufender Indikatoren basieren, zwangsläufig Fehlsignale, da die Volatilität Geschäfte zunichte macht, die sonst unter ruhigeren Bedingungen durchgeführt worden wären.

Da es keine Standardlösungen gibt, ist eine individuelle Anpassung erforderlich. Hier zeichnen sich die IDE-gestützten Handelsplattformen aus. Sie bieten nicht nur Ausführung und Charts in institutioneller Qualität, sondern können auch mit Assistenten für die Systemzusammenstellung geliefert werden. Diese Assistenten stellen, wie im Falle von MetaTrader, einen Rahmen dar, der es Händlern ermöglicht, einen Expert Advisor (EA) schnell zusammenzustellen, auch wenn sie keine komplexe Handelslogik von Grund auf programmieren. Die eigentliche Stärke des Assistenten liegt in seiner Fähigkeit, nutzerdefinierte Signalklassen zu integrieren – was bedeutet, dass Händler fortschrittliche maschinelle Lerntechniken direkt in ihre automatisierten Strategien integrieren können.

Unter den verfügbaren modernen Methoden des maschinellen Lernens, Variational Autoencoders (VAEs) haben aufgrund ihrer Fähigkeit, verrauschte, hochdimensionale Daten in strukturierte latente Darstellungen zu komprimieren, Aufmerksamkeit erregt. Im Gegensatz zu einem einfachen Autoencoder führt ein β-VAE eine kontrollierte Strafe ein, die seine verborgene Schicht dazu anregt, entwirrte, bedeutungsvolle Merkmale zu erfassen, anstatt sich rohe Eingaben zu merken. Im Finanzhandel bedeutet dies, dass die Essenz der Muster aus den Strömen der technischen Indikatoren extrahiert wird und die Anfälligkeit für Rauschen verringert wird.

Die wichtigste Erkenntnis – und das Thema dieses Artikels – ist jedoch, dass VAEs besonders leistungsfähig werden, wenn sie mit binär kodierten Merkmalen arbeiten. Anstatt kontinuierliche Indikatorwerte oder skalierte Pipelines einzugeben, definieren wir klare, ereignisgesteuerte Bedingungen. Hat der Ichimoku Tenkan-sen über den Kijun-sen gekreuzt? Wir setzen eine 1, wenn ja, oder 0, wenn nicht. Ist der Schlusskurs unter die Wolke gebrochen? Wieder 1, wenn ja, 0, wenn nicht. Ist der ADX über 25, was einen starken Trend bestätigt? Dito.

Wir arbeiten mit den Mustern 0, 1 und 5 dieses Indikatorpaares, Ichimoku & ADX, und diese können wie folgt auf einem Chart erscheinen.

Muster-0

Abwärtssignal, wenn der Kurs unter die Senkou-Spanne A fällt, was einen Ausbruch unter die Kumo-Wolke bedeutet. Dies wird durch einen ADX-Wert von mindestens 25 bestätigt.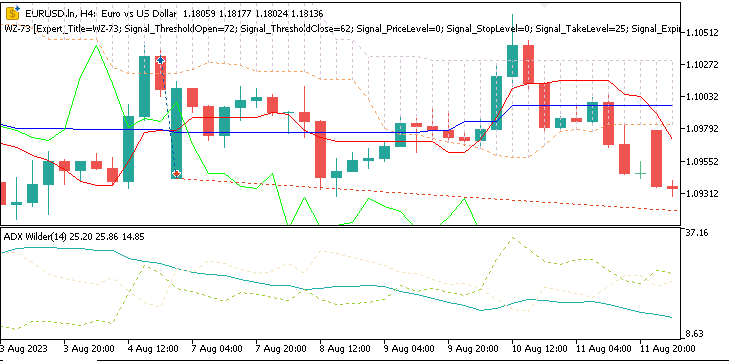

Muster-1

Abwärtssignal, wenn der Tenkan-Sen den Kijun-Sen von oben kreuzt und darunter schließt, was eine kurzfristige Änderung des Momentums in Richtung Verkauf signalisiert. Der ADX sollte mindestens 20 betragen.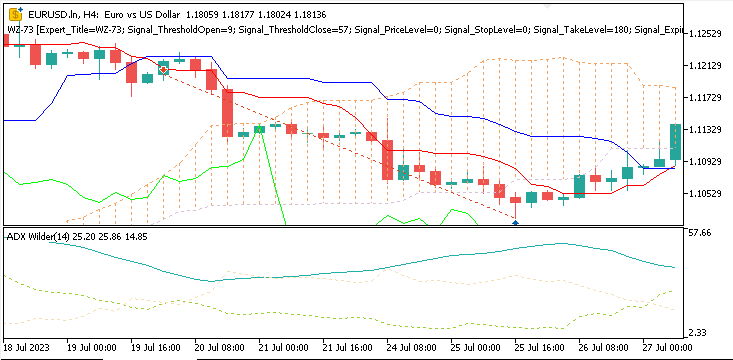

Muster-5

Ein Aufwärtssignal liegt vor, wenn der Kurs vom Tenkan-Sen abprallt und der ADX mindestens den Schwellenwert von 25 erreicht.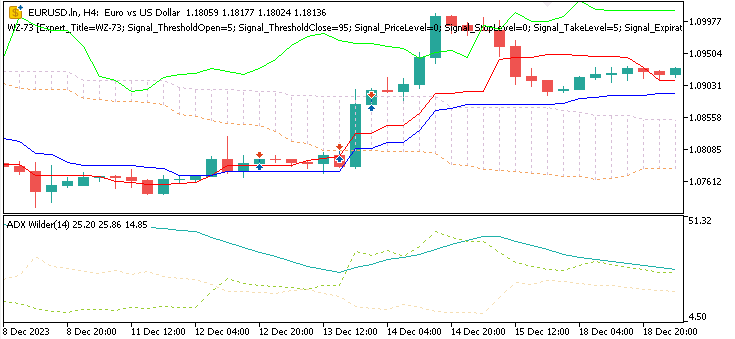

Unsere Prämisse bei der Umsetzung für diesen Artikel ist, dass diese binären Kodierungen kompakte Vektoren bilden, die ausdrücken, ob wichtige Muster zu jedem Zeitpunkt vorhanden oder nicht vorhanden sind. Wenn sie durch den VAE geleitet werden, bieten sie eine viel sauberere Signalstruktur als einige Pipelines mit normalisierten, reellen Zahlen. In unseren Tests hier verbesserte allein diese Anpassung den Trainingsprozess und führte zu stärkeren Signalen während der Tests.

In diesem Artikel erfahren Sie, wie Sie dieses System umsetzen können. Wir werden den Ichimoku-Indikator mit dem ADX von Wilder kombinieren, binäre Merkmalsvektoren erzeugen, einen β-VAE mit historischen Marktdaten trainieren und dann das trainierte Modell in ein ONNX-Format zur Verwendung in MQL5 exportieren. Abschließend werden wir die Ergebnisse der Strategietester überprüfen, um zu zeigen, wie binäre Kodierungen vor dem Hintergrund unserer kürzlich untersuchten Pipelines mit kontinuierlichen Werten abschneiden.

Der MQL5-Assistent

Mit dem MQL5-Assistenten können Händler schnell Expert Advisors aus vordefinierten Blöcken – Signale, Geldmanagement, Ausstiege und Trailing Stops – zusammenstellen, ohne Kesselsteincode schreiben zu müssen. Eine der wichtigsten Funktionen für Händler, die schon etwas weiter fortgeschritten sind, ist das Einfügen von nutzerdefinierten Signalklassen in einen vom Assistenten erstellten Expert Advisor. Für Uneingeweihte: In einer Signalklasse legen Sie die tatsächliche Logik fest, welche Handelsgeschäfte geöffnet werden müssen und wann sie geschlossen werden sollten. MetaQuotes bietet Standardsignale an, die gleitende Durchschnitte oder den RSI beinhalten, aber nutzerdefinierte Signale erweitern die Möglichkeiten des Assistenten erheblich. Mit einer nutzerdefinierten Signalklasse können wir Modelle des maschinellen Lernens, probabilistische Prognosen oder, wie in diesem Fall, einen Beta-VAE mit den eingebauten Standardsignalmustern verbinden, da Händler nicht nur Alpha, sondern auch volatilitätsstabilisierte Portfolios suchen.

Eine wichtige Funktion ist die Möglichkeit, nutzerdefinierte Signalklassen einzufügen. Zu den integrierten Signalen gehören MA oder RSI, während nutzerdefinierte Klassen Modelle des maschinellen Lernens, probabilistische Prognosen oder einen VAE integrieren können. Der Assistent kümmert sich um das Auftragsmanagement und die Positionsgröße, während die nutzerdefinierte Logik für Anpassungsfähigkeit sorgt, falsche Signale herausfiltert und kontextbezogenere Strategien ermöglicht.

Pipelines und binäre Eingaben

Im vorletzten Artikel haben wir untersucht, wie Vorverarbeitungspipelines im Stil von SCIKIT-LEARN bei der Normalisierung von Merkmalen eines Modells vor dem Training und vor der Inferenz von Nutzen sein könnten. Die Idee war einfach: Zuschreibungs-, Skalierungs- und Transformationsschritte systematisch anwenden, sodass alle Indikatorwerte in vergleichbare Bereiche fallen. Methoden wie Min-Max-Skalierung, Standard-Skalierung und robuste Skalierung wurden eingesetzt, um Ichimoku- und ADX-Wilder-Daten aufzubereiten, bevor sie in ein Modell eingespeist wurden. Wie wir jedoch gesehen haben, hatte dieser Ansatz beim Handel ein paar Schwächen.

Erstens war das Signal nicht mehr so klar. Die Skalierung der kontinuierlichen Werte führte zu einer Glättung genau der Bedingungen, die wir hervorheben oder identifizieren wollten. So wurde beispielsweise ein Ausbruch über die Ichimoku-Wolke – ein klarer boolescher/binärer Wert – nach der Normalisierung zu einer Gleitkommadifferenz verwässert. Im Wesentlichen wurde das Modell gezwungen, das neu zu lernen, was die Händler bereits wussten, dass es ziemlich offensichtlich war – der Moment, in dem Kreuzungen oder Breakouts auftreten.

Zweitens hatten wir während des Trainings Probleme mit der Stabilität. Die ausgegebenen, kontinuierlichen Merkmale neigten dazu, das Rauschen zu verstärken. Marktschwankungen, die keine eindeutige Kausalität haben und zufällig sind, spielen in der Praxis keine Rolle, und dennoch wurde ihnen von den Skalentransformatoren die gleiche Bedeutung beigemessen. Dies führte zu einer langsameren Konvergenz beim Training und zu schwächeren Schlussfolgerungen, sobald sie in der Praxis eingesetzt wurden.

Die Lösung scheint darin zu bestehen, dass wir unsere Perspektive ändern. Anstatt von unseren Modellen zu verlangen, dass sie die Größe der Unterschiede interpretieren, haben wir versucht zu markieren, ob bestimmte Bedingungen vorliegen oder nicht. Das ist das Wesentliche bei der Umwandlung von Indikatormustern in boolesche oder binäre Eingaben. Wenn beispielsweise der Tenkan-Sen den Kijun-Sen überquert und der ADX über 20 liegt, würden wir dies als bestätigendes Aufwärtssignal für ein bestimmtes Muster werten und den Wert 1 zuweisen. Alles andere würde eine 0 erhalten. Wenn der Schlusskurs unter die Senkou-Spanne A fällt, der ADX sich jedoch über der 25er-Marke hält, würden wir eine definitive 1 vergeben, während alle anderen Möglichkeiten für dieses spezifische Muster mit 0 bewertet würden.

Diese booleschen Kodierungen wurden für jeden Preisbalken in einem sauberen Signalvektor von Muster-ja/Muster-nein dargestellt. Anstatt also Pipelines zu verwenden, um skalierte Werte zu erzeugen, setzt unsere Funktion GetFeatures aus dem VAE-Python-Code (siehe unten) die booleschen Vektoren direkt zusammen

def GetFeatures(functions, *args, **kwargs) -> np.ndarray:
    features_per_func = []
    n_rows = None
    for f in functions:
        out = f(*args, **kwargs)
        a = np.asarray(out)
        if a.ndim == 1:
            row = SetRow(a)
            block = row
        elif a.ndim == 2:
            rows = [SetRow(a[i, :]) for i in range(a.shape[0])]
            block = np.concatenate(rows, axis=0)
        else:
            raise ValueError("Feature function returned array with ndim "+str(a.ndim))
        if n_rows is None:
            n_rows = block.shape[0]
        elif block.shape[0] != n_rows:
            raise ValueError("Inconsistent number of rows across feature functions.")
        features_per_func.append(block)
    return np.concatenate(features_per_func, axis=1)


def GetStates(df):
    diffs = df['close'].diff()
    df['states'] = np.select(
        condlist=[diffs > 0, diffs < 0],
        choicelist=[1.0, -1.0],
        default=0.0
    )
    return df[['states']]

Es ist bemerkenswert, dass wir im Gegensatz zu früheren Artikeln, in denen wir uns dafür entschieden haben, die Signalmuster nicht zu kombinieren und jedes für sich zu halten, sodass wir am Ende ein Modell für jedes Signalmuster hatten, in diesem Artikel die drei untersuchten Signalmuster zu einem einzigen kombinieren. Nur die drei, nicht die ursprünglichen 10. Das heißt, wir entwickeln und testen nur ein Modell.

Die Auswirkungen waren offenbar sofort spürbar. Der VAE muss nicht mehr herausfinden, welche Teile der numerischen Skala sinnvollen Ereignissen entsprechen und welche Schwachsinn sind. Stattdessen arbeitet sie mit Ein/Aus-Flags, die wohl besser mit der Intuition des Händlers übereinstimmen. Bei den Backtests sorgt diese Designänderung für eine bessere Stabilität und eine bessere Leistung nach dem Test. In einem Marktumfeld wie diesem, in dem ein deutlicher Rücksetzer bei den Kapital bevorsteht, der zwangsläufig mit einer hohen Volatilität einhergeht, kann eine binäre Darstellung die Unterscheidung zwischen Rauschen und gültigen Fortsetzungssignalen besser abbilden. 

Unser Schritt weg von Pipelines und hin zur Binär-Ereignis-Kodierung vereinfacht also nicht nur die eigentliche Vorverarbeitung, sondern gibt unserem Modell, dem beta-VAE, auch die Art von Input, für die es entwickelt wurde, um ihn effektiv zu komprimieren und darzustellen.

Der Beta-Variations-Autoencoder

Sobald wir die booleschen Merkmalsvektoren definiert haben, besteht unser nächster Schritt darin, sie an ein Modell zu übergeben. Die Fähigkeit von Python, diese und ähnliche Schritte in Stapeln zu verarbeiten, ist einer der Gründe, warum es beim Training sehr effizient ist. Hinzu kommt, dass die Verwendung von Tensoren bei der Rückwärtspropagierung zusätzliche Pufferung/Speicherung für registrierte Gradienten bei jedem Vorwärtsdurchlauf mit sich bringt. Unser VAE-Modell ist so konzipiert, dass es in der Lage ist, kompakte Darstellungen von wiederkehrenden Marktstrukturen zu lernen. Dies ist ein wesentliches Erfolgsargument für den beta-VAE.

Ein Standard-Autoencoder komprimiert/zippt seine Eingaben in eine verborgene Schicht. Dies wird oft auch als latenter Raum bezeichnet. Danach werden sie wieder in ihre ursprüngliche Form zurückgebracht. Ein „variativer“ Autoencoder geht noch einen Schritt weiter, indem er den latenten Raum probabilistisch macht. Diese verborgene Schicht wird als Verteilung anstelle von festen Punkten modelliert. Der Encoder erzeugt also beim Training sowohl einen Mittelwert als auch eine Varianz. Aus dieser Verteilung wird eine Zufallsstichprobe ausgewählt, die auch als Umparametrisierung bezeichnet wird.

Der Beta-VAE macht also dort weiter, wo der reguläre VAE aufhört, und fügt noch eine weitere Besonderheit hinzu. Sie multipliziert den KL-Divergenz-Term in der Verlustfunktion mit dem Faktor Beta. Dies hat zur Folge, dass die Regularisierung verstärkt wird, was wiederum das Modell dazu anregt, entflechtete, sinnvolle Merkmale zu lernen, anstatt sich Eingaben zu merken. Für den Handel ist dies von entscheidender Bedeutung, da es dem latenten Raum ermöglicht, Schlüsselmuster, wie z. B. einen Wolkenausbruch oder sogar eine Trendfortsetzung, besser zu kodieren, anstatt sinnlos mit Rauschen „demokratisiert“ zu werden.

Unser Modell gliedert sich in die folgenden Schlüsselkomponenten:

• Kodierer: Diese nimmt den booleschen Eingabe-Merkmalsvektor und leitet ihn durch die dichten Schichten weiter. Das Ergebnis ist eine Verteilungsdarstellung, die einen Mittelwert (z_mean) und den Logarithmus der Varianz (z_logvar) enthält.
• Re-Parametrisierung: Dabei wird z aus der latenten Gauß-Verteilung entnommen. In diesem Fall ist z die „implizite Ausgabe“ der Eingangsmerkmale, und wie bereits erwähnt und allgemein bekannt, trainieren Encoder den Aufbau eines Paares von Gewichtsmatrizen zwischen den sichtbaren und den verborgenen Merkmalen, um die „Standard“-Codierung aller relevanten Eingangsdaten zu ermöglichen.
• Decoder: Anschließend wird versucht, den ursprünglichen booleschen Eingangsvektor aus z zu rekonstruieren. Dadurch wird der latente Raum gezwungen, sich zu konzentrieren oder die Kernstruktur der früheren Eingaben zu erfassen. 
• Latent - y head: Schließlich haben wir einen überwachten Vorhersagekopf, der z auf einen geschätzten Wert, y, abbildet. In unserem Fall bedeutet dies eine Trendprognose für die Preisentwicklung, die entweder nach oben, nach unten oder nach unten gerichtet ist.

Die Verlustfunktion, die wir für diesen VAE einsetzen, fasst drei Verlustwerte zusammen. Erstens, der Rekonstruktionsverlust, der anhand der binären Kreuzentropie zwischen den rekonstruierten Ausgaben und den vorherigen binären Eingabemerkmalen gemessen wird. Zweitens haben wir die KL-Divergenz, die die Abweichung der latenten Verteilungen von der Gaußschen Standardpriorität bestraft. Dies ist der Fall, in dem der Beta-Multiplikator zur Anwendung kommt. Drittens haben wir den Kopf, der den Verlust überwacht. Für unsere Zwecke ist dies einfach ein mittlerer quadratischer Fehler oder MSE-Term zwischen dem vorhergesagten y-Endoutput und dem tatsächlichen y-Output. 

Unsere VAE-Eingabeschicht ist insofern besonders, als wir neben den typischen Indikator-Eingabemerkmalen eine Dimension für den erwarteten Output hinzufügen. Bei der Eingabe weisen wir diesem Dim einen neutralen Wert von 0,5 zu. Nach einem Zyklus zum latenten Raum und zurück zur Eingabe wäre die y-Ausgabe die fehlende nächste Preisaktion, die auf die 6 zuvor bereitgestellten Eingabemerkmale folgt oder mit ihnen gepaart ist. Das bedeutet, dass er in zwei Modi arbeitet, wobei jeder Modus eine andere Leistung erbringt. Unten finden Sie das Verzeichnis der Beta-VAE-Implementierung in Python;

# ----------------------------- β-VAE (inference simplified to VAE-only) -----------------------------
class BetaVAEUnsupervised(nn.Module):
    """
    Encoder: features -> (mu, logvar)
    Decoder: z -> x_hat
    **Inference (now VAE-only):** latent z is mapped to y via an internal head.
    All former infer modes (ridge/knn/kernel/lwlr/mlp) are bypassed.
    """
    def __init__(self, feature_dim, latent_dim, k_neighbors=5, beta=4.0, recon='bce',
                 infer_mode='vae', ridge_alpha=1e-2, kernel_bandwidth=1.0):
        super().__init__()
        self.latent_dim = latent_dim
        self.k_neighbors = k_neighbors
        self.beta = beta
        self.recon = recon
        self.infer_mode = 'vae'  # force VAE-only
        self.ridge_alpha = float(ridge_alpha)
        self.kernel_bandwidth = float(kernel_bandwidth)

        # Encoder
        self.feature_encoder = nn.Sequential(
            nn.Linear(feature_dim, 256), nn.ReLU(),
            nn.Linear(256, 128), nn.ReLU(),
            nn.Linear(128, latent_dim * 2)
        )
        # Decoder
        self.decoder = nn.Sequential(
            nn.Linear(latent_dim, 128), nn.ReLU(),
            nn.Linear(128, 256), nn.ReLU(),
            nn.Linear(256, feature_dim)
        )
        # New: latent→y head (supervised head trained with MSE)
        self.y_head = nn.Sequential(
            nn.Linear(latent_dim, 128), nn.ReLU(),
            nn.Linear(128, 1)
        )

    def encode(self, features):
        h = self.feature_encoder(features)
        z_mean, z_logvar = torch.chunk(h, 2, dim=1)
        return z_mean, z_logvar

    def reparameterize(self, mean, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mean + eps * std

    def decode(self, z):
        return self.decoder(z)

    def predict_from_latent(self, z):
        # VAE-only mapping
        return self.y_head(z)

    def forward(self, features, y=None):
        mu, logvar = self.encode(features)
        z = self.reparameterize(mu, logvar)
        x_logits = self.decode(z)
        y_hat = self.predict_from_latent(z)
        if y is not None:
            return {'z': z, 'z_mean': mu, 'z_logvar': logvar, 'x_logits': x_logits, 'y_hat': y_hat}
        else:
            return {'y': y_hat}

# Reconstruction + KL
def beta_vae_loss(features, x_logits, mu, logvar, beta=4.0, recon='bce'):
    if recon == 'bce':
        recon_loss = F.binary_cross_entropy_with_logits(x_logits, features, reduction='sum') / features.size(0)
    else:
        recon_loss = F.mse_loss(torch.sigmoid(x_logits), features, reduction='mean') * features.size(1)
    kl = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp()) / features.size(0)
    loss = recon_loss + beta * kl
    return loss, recon_loss.detach(), kl.detach()

In der Funktion für den Vorwärtsdurchgang können wir entweder den y-Wert, den nächsten Preisaktionswert, oder diesen Wert plus den Verteilungsvektor erhalten, der den z-Mittelwert und die Varianz erfasst. Für unsere Zwecke beim Export in ONNX, da das Training bereits abgeschlossen ist, geben wir immer nur den y-Wert aus, der auf die nächste Preisaktion hinweist, wobei alles über 0,5f aufwärts und alles unter 0,5f abwärts bedeutet. 

Wenn man zu den drei kombinierten Verlustwerten zurückkehrt und sie beim Training zusammenführt, wird das Modell ermutigt, sowohl binäre Merkmale zu komprimieren als auch eine Vorhersage der Preisrichtung zu treffen. Das Trainingsverfahren wird mit Adam Optimization über mehrere Epochen hinweg durchgeführt. Für unser Modell haben wir 50 Epochen verwendet. Bei jedem Trainingsschritt werden jedoch Merkmale kodiert, wobei die latenten Variablen des Mittelwerts und der Varianz für z abgetastet werden; der Dekoder rekonstruiert die ursprünglichen Merkmale; die latente Schicht gibt an einen Kopf aus, um den nächsten Marktzustand zu prognostizieren; ein Verlust wird für den Fall berechnet, dass eine y-Eingabe bereitgestellt wurde und wir uns daher im Training befinden; und schließlich aktualisiert Backpropagation die Gewichte nicht nur für der VAE, sondern auch für den Kopf.

Die Trainingsschleife, die wir durchführen, verwendet einen Bootstrap, der es uns ermöglicht, effizient über einen Datensatz zu iterieren und gleichzeitig Epoche für Epoche Verlustzusammenfassungen zu drucken. Anhand der Ausdrucke lässt sich beobachten, wie gut der VAE in der Lage ist, ein Gleichgewicht zwischen Kompression und Entflechtung herzustellen, und wie genau sie die nächsten Zustände vorhersagen kann, die der Kopf liefert.

Exportieren nach MQL5

Wie regelmäßige Leser wissen, ist das Training in Python der halbe Weg. Um Modelle, die in dieser Nicht-MQL5-Sprache entwickelt wurden, in einem vom Assistenten zusammengestellten Expert Advisor zu verwenden, benötigen wir eine Brücke. Dabei handelt es sich, wie bereits in früheren Artikeln gezeigt, um ONNX, eine Abkürzung für Open Neural Network Exchange. Diese „Brücke“ gibt uns ein standardisiertes Format für die Darstellung von Modellen, die in Python trainiert wurden, um in einer Vielzahl anderer Plattformen als MetaTrader verwendet werden zu können. Wenn wir sie jedoch nach MQL5 exportieren, kann diese Datei, deren Größe von einigen hundert Kilobyte bis zu 128 MB reichen kann, wie ich bei meinen letzten Tests mit MQL5 festgestellt habe, von verschiedenen Laufzeiten geladen werden. Dazu gehören auch solche, die über das Sandbox-Dateisystem oder die Ressourcenkompilierung zugänglich sind. Unterm Strich bedeutet dies, dass wir fortgeschrittene Modelle effizient mit PyTorch trainieren, sie in Python validieren und sie dann für die Verwendung mit Expert Advisors bereitstellen, ohne die Modelllogik neu zu schreiben. Dieser Vorgang wird hauptsächlich von der Funktion „export_onnx_y“ übernommen. Diese sind wie folgt aufgelistet:

import torch
import torch.nn as nn
import onnx
import onnxruntime as ort

def export_onnx_y(model: nn.Module, feature_dim: int, output_path: str,
                  opset: int = 14):
    """
    Export the VAE so that ONNX takes ONLY `features` and returns the inferred y.
    No latent (z, mu, logvar) are exported. No `y` input is used.
    """
    model.eval()

    # Wrapper that returns a plain tensor (y_hat), suitable for ONNX export
    class _YOnly(nn.Module):
        def __init__(self, m: nn.Module):
            super().__init__()
            self.m = m
        def forward(self, features: torch.Tensor) -> torch.Tensor:
            mu, logvar = self.m.encode(features)
            z = self.m.reparameterize(mu, logvar)
            y_hat = self.m.predict_from_latent(z)
            return y_hat  # shape: [N, 1]

    wrapped = _YOnly(model)

    dummy_features = torch.randn(1, feature_dim, dtype=torch.float32)

    torch.onnx.export(
        wrapped,
        dummy_features,
        output_path,
        input_names=["features"],
        output_names=["y_hat"],
        dynamic_axes={
            "features": {0: "batch_size"},
            "y_hat":    {0: "batch_size"},
        },
        opset_version=opset,
        do_constant_folding=True,
    )

    # Validate and print IO for sanity
    onnx_model = onnx.load(output_path)
    onnx.checker.check_model(onnx_model)
    print(f"ONNX model '{output_path}' exported and validated (features -> y_hat).")

    sess = ort.InferenceSession(output_path)
    for i in sess.get_inputs():
        print(f"input:  {i.name}, shape={i.shape}, type={i.type}")
    for o in sess.get_outputs():
        print(f"output: {o.name}, shape={o.shape}, type={o.type}")

Die obige Exportfunktion konstruiert einen sauberen, arbeitsbereiten ONNX-Kopf. Dies ist bereit für den Vorwärtsdurchlauf, um vorberechnete Merkmale aus unseren beiden Indikatoren zuzuordnen und dann einen Solo-Y-Wert ohne zusätzliche Debug-Ausgaben oder Eingaben auszugeben. Dabei wird zunächst den VAE von PyTorch in den eval-Modus geschaltet, um das Dropout-/Batch-Normalisierungsverhalten einzufrieren. Sobald dies erledigt ist, werden die Merkmale kodiert, um den Mittelwert und die Varianz zu ermitteln, und anschließend wird ein latenter Vektor z mit Hilfe des oben erwähnten Re-Parametrisierungstricks gesampelt. Daraufhin wird z durch die Funktion des Modells zur Vorhersage des latenten Kopfes geleitet, woraufhin der y-Wert in der Form [batch, 1] zurückgegeben wird. Dieser Wrapper wird um das trainierte Modell herum instanziiert, um sicherzustellen, dass der exportierte Graph ein Minimum an Eigenschaften des Vorwärtsdurchlaufs enthält.

Es wird nur ein Dummy-Eingabetensor der Form [1, 6] erstellt, um den Graphen nachzuzeichnen. Das Modul torch.onnx.export wird dann mit expliziter Benennung und mit dynamischen Achsen auf der Batch-Dimension aufgerufen, sodass das exportierte Modell jede Batch-Größe akzeptieren kann. Der Parameter opset ist auf 14 voreingestellt, und auch die konstante Faltung ist aktiviert, damit das Diagramm einfacher zu interpretieren ist. 

In Python müssen wir die Datei auch nach dem Export sofort validieren, indem wir sie erneut importieren und auch die Größe der Eingabe- und Ausgabeschichten überprüfen. Dazu wird die Datei mit dem Modul onnx.load geladen und anschließend mit onnx.checker.check_model überprüft, ob sie gültig ist und in einer geeigneten Inferenzsitzung geöffnet werden kann. Wir drucken die entdeckten Signaturen der Eingangs- und Ausgangsebene aus, die wichtige Eingaben für den MetaTrader sind. Das von uns gewählte Exportmodell vereinfacht das VAE-Modell, sodass es fast wie ein überwachtes Lernnetz aussieht. Wie jedoch bereits oben dargelegt, handelt es sich um ein VAE, das die fehlende y-Eingabe automatisch mit einem neutralen Nullwert eingibt, einen vollständigen Zyklus von der Eingabe bis zum versteckten Wert und zurück durchläuft und dann den fehlenden Wert auf der Grundlage der trainierten Gewichte des VAEs ableitet.

Sobald die ONNX-Datei exportiert wurde, muss sie sofort in MQL5 validiert werden. Anstatt auf eine ONNX-Datei in der Sandbox zu verweisen, entscheiden wir uns wie in der Vergangenheit dafür, diese Datei als Ressource zu importieren. Diese Option hat jedoch Auswirkungen darauf, wie groß ein exportiertes Modell sein kann. Früher lag die Grenze für eine Ressourcendatei bei 256 MB, aber in letzter Zeit scheint sich dieser Wert auf die Hälfte reduziert zu haben und bei etwa 128 MB zu liegen. Ich muss dies noch bestätigen, aber ONNX-Dateien ohne Ressourcen, die sich in einer Sandbox befinden, unterliegen möglicherweise keinen ähnlichen Einschränkungen. Diese Einschränkungen können insbesondere für Händler gelten, die auf die Nutzung des MQL5 VPS zählen.

Rückschlüsse von Teilmerkmalen auf Prognosen ziehen

Das Trainieren eines Modells ist immer nur ein einziger Schritt; es so zu nutzen, wie es im Live-Handel erwartet wird, ist oft ein anderes Unterfangen. Sobald der Beta-VAE in ONNX exportiert ist, wird er, in unserem Fall als Ressource, aufgerufen, um Prognosen zu erstellen. In Python testen wir jedoch, wie diese Inferenz in MQL5 funktionieren wird, indem wir einige synthetische Binärdateien mit der Funktion infer_example ausführen. Dies kann Aufschluss darüber geben, ob die voreingestellten langen oder kurzen Indikatorwerte tatsächlich wie erwartet interpretiert werden.

# ----------------------------- Inference demo (updated) -----------------------------
def infer_example(model, dataloader=None, num_examples=5, prob_one_in_pair=0.6, seed=None, partial_rows=None):
    """
    If partial_rows is provided, we zero-fill missing inputs and run a full VAE cycle
    to produce y that pairs with that incomplete input.
    Otherwise, we keep the previous synthetic-pairs demo using the dataloader.
    """
    model.eval()
    with torch.no_grad():
        if partial_rows is not None:
            device = next(model.parameters()).device
            X = _zero_fill_rows(partial_rows, feature_dim, device)
            preds = model(X)
            print("Inference with partial inputs (zero-filled):")
            for i in range(X.size(0)):
                yhat = float(preds['y'][i].item())
                print(f"X[{i}] first 8: {X[i, :8].tolist()} -> y_hat={yhat:.6f}")
            return
        # ----- legacy synthetic example (kept) -----
        if dataloader is None:
            raise ValueError("dataloader required when partial_rows is None")
        batch = next(iter(dataloader))
        N = min(num_examples, batch["features"].shape[0])
        feat_dim = batch["features"].shape[1]
        assert feat_dim >= 6 and feat_dim % 2 == 0, "feature_dim must be even and >= 6"
        pairs = 3
        device = next(model.parameters()).device
        if seed is not None:
            torch.manual_seed(seed)
        X = torch.zeros((N, feat_dim), device=device)
        any_one = torch.bernoulli(torch.full((N, pairs), float(prob_one_in_pair), device=device)).bool()
        side = torch.bernoulli(torch.full((N, pairs), 0.5, device=device)).long()
        row_idx = torch.arange(N, device=device).unsqueeze(1).expand(N, pairs)
        base = (torch.arange(pairs, device=device).unsqueeze(0).expand(N, pairs) * 2)
        col_idx = base + side
        sel_rows = row_idx[any_one]; sel_cols = col_idx[any_one]
        X[sel_rows, sel_cols] = 1.0
        preds = model(X)
        print(" Example Inference (3 exclusive pairs):")
        for i in range(N):
            yhat = float(preds['y'][i].item())
            print(f"X[{i}]={X[i, :6].int().tolist()}{'...' if feat_dim > 6 else ''} -> ŷ={yhat:.5f}")

Die Märkte bieten selten einen vollständigen Vektor sauberer Signale auf allen Preisbalken. Oft ist es so, dass der Tenkan-Kijun-Kreuzungspunkt offensichtlich ist, aber der Wolkendurchbruch fehlt. Um dies besser zu simulieren, unterstützt unser Inferenzbeispiel partielle Eingaben, wobei Null der Standardwert für fehlende Werte ist. Bemerkenswert ist auch, dass bei unserer Simulation darauf geachtet wird, dass die langen und kurzen Bedingungen nicht gleichzeitig in das Modell eingegeben werden, da dies aufgrund der Definition der Indikatormerkmale nicht möglich ist.

Strategie-Testergebnisse

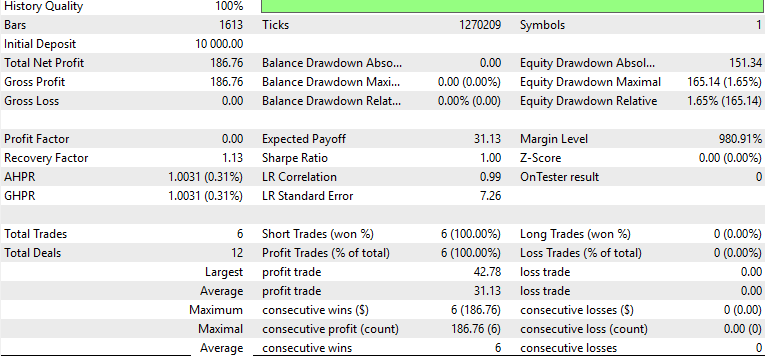
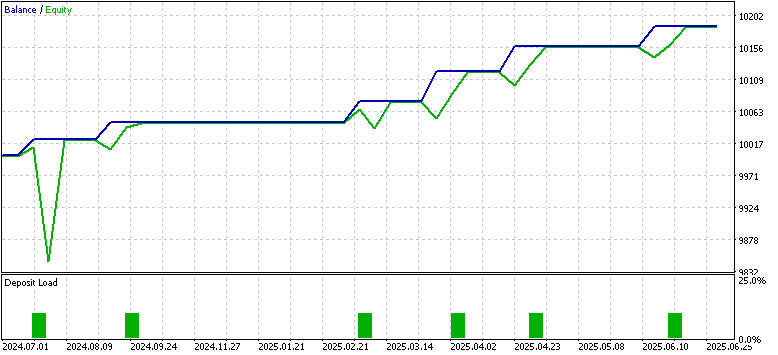
Der Beweis liegt immer im Essen des Puddings, wie sie sagen, und während streng genommen für Händler würde dies Aspekte der Handelskontoverwaltung, die Planung Abhebungen, die MetaTrader simulieren kann, umfassen, für unsere Zwecke werden wir auf die Rentabilität des Modells verweilen, wenn in MQL5 getestet. Nachdem wir den Beta-VAE auf boolesch kodierten Merkmalen aus Indikatorwerten von EUR USD auf dem 4-Stunden-Zeitrahmen von 2023.07.01 bis 2024.07.01 trainiert hatten, exportierten wir diesen für die Vorwärtsbewegung von 2024.07.01 bis 2025.07.01 in MetaTrader. Die Ergebnisse des Vorwärtstests waren besser als die Ergebnisse des letzten Artikels, in dem wir Pipelines in ein Reinforcement-Learning-Modell eingebunden haben. 

Hier gibt es viele bewegliche Teile, die verschiedenen Lerntypen (Inferenz vs. Verstärkung), unterschiedliche Modelltypen (Beta-VAE vs. TD3) und die Tatsache, dass unser Testfenster auf ein Jahr beschränkt ist. Außerdem wurden keine aufwändigeren Regularisierungstechniken eingesetzt, um sicherzustellen, dass das Testfenster ausgewogene Zieldaten mit einer ungefähr gleichen Anzahl von Kursen für Kauf und Verkauf enthält. Deshalb zeigen unsere Berichte nur Käufe an. Diese und andere detailliertere Punkte werden hier nicht richtig behandelt, aber der MQL-Code ist beigefügt und der Gesamtansatz in Python ist skizziert, sodass Händler dies für weitere Entwicklungen nutzen können.

Da wir mit der Testumgebung des letzten Artikels fast gleichauf liegen, könnte es für uns aufschlussreich sein, die Leistung des binären Feature-Input-Modells mit den Ergebnissen des Pipeline-Input-Modells zu vergleichen. Als wir uns auf die SCIKIT-LEARN-Pipelines verließen, erhielt das Modell kontinuierliche Werte aus den Lücken und Differenzen im Ichimoku und dem ADX. Während die Trainingsergebnisse vielversprechend waren und die Verluste zurückgingen, zeigte der Vorwärtstest das Gegenteil. Die Ergebnisse der Aktienkurve waren ebenfalls instabil und wiesen ein schlechtes Risiko-Ertrags-Verhältnis auf. Dasselbe Problem tritt auch bei unseren besseren Ergebnissen mit binären Eingangsvektoren auf, was zum Teil daran liegt, dass wir keinen Stop-Loss verwenden.

Wir hatten auch eine Menge falsch-positiver Signale während abrupter Rebounds mit den 3 Tests der 3 Muster 0, 1 und 5. Diese waren alle unabhängig, anders als in diesem Artikel, in dem wir ihre Indikatorwerte als Input für ein einziges VAE-Modell vereinigt haben. Das ist auch ein weiterer wichtiger Unterschied zu unserem letzten Artikel.

Der binäre Kodierungsansatz hingegen scheint klarere Ergebnisse mit durchweg steigendem Eigenkapital zu liefern, wobei nur sehr wenige Trades ausgeführt wurden, die alle korrekt waren. Dies gilt für das gleiche Testfenster. Auch wenn dieses einjährige Testfenster begrenzt ist und wir ein Handels-Setup ohne ordnungsgemäßes Stop-Management betreiben, zeigt dieser Vergleich zwischen dem Pipeline-Skalierungsmodell und den booleschen Eingaben die Stärken des letzteren auf. Es könnte sein, dass wir die Vorteile des „Entfernens von Rauschen“ in Form von fließenden/kontinuierlichen Eingaben nutzen, wenn wir stattdessen Ja/Nein-Daten verwenden.

Schlussfolgerung

In diesem Artikel haben wir, wie üblich, gezeigt, wie der Assistent über die reguläre eingebaute Signalbibliothek hinaus erweitert werden kann, indem er Inferenzlernen einbezieht – in diesem Fall einen Beta-Variations-Autoencoder, der auf boolesche Indikatormuster trainiert wird. Durch die Kodierung der Ichimoku- und ADX-Wilder-Bedingungen in binäre Ja/Nein-Vektoren haben wir offenbar das Rauschen in den Marktdaten reduziert, während wir es bei der Verwendung von Pipeline-Transformatoren offenbar nur verstärkt haben. In unserem begrenzten Zeitfenster von nur zwei Jahren, einem Trainings- und einem Testjahr, konnten wir einen stabilen Trainingsprozess, sauberere latente Repräsentationen sowie eine verbesserte Leistung im Strategy Tester erzielen. Wie üblich sind Tests in größeren Zeitfenstern und mit echten Tickdaten des Brokers erforderlich, bevor endgültige Schlussfolgerungen gezogen werden können.

Name	Beschreibung
81b.mq5	Mit dem Assistenten erstellter Expert Advisor, dessen Header referenzierte Dateien auflistet
SignalWZ_81b.mqh	Nutzerdefinierte Signalklassendatei, die das Inferenzlernen beinhaltet
81_.onnx	ONNX Exportiertes Modell, als Ressource importiert