MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 82): Verwendung von TRIX- und WPR-Mustern mit DQN-Verstärkungslernen

Einführung

Beim Handel mit Robotern oder Expert Advisors beginnt das Streben nach strukturierten und wiederholbaren Handelsregeln in der Regel mit technischen Indikatoren, die vertraut sind. Die Tendenz geht oft dahin, sich mit Oszillatoren, gleitenden Durchschnitten und preisbasierten Mustern zu beschäftigen, um Strategien zu entwickeln, die wechselnde Marktregimes überdauern können. Der TRIX, auch Triple Smoothed Exponential Moving Average genannt, und der WPR, auch Williams Percent Range genannt, sind ein klassisches Paar. TRIX erfasst in der Regel die Dynamik, indem er das kurzfristige Preisrauschen herausfiltert, während WPR überkaufte oder überverkaufte Situationen aufzeigt. Beide Indikatormuster können sich also, wenn sie kombiniert werden, gegenseitig ergänzen und dabei helfen, Wendepunkte oder Fortsetzungen im Preis zu erkennen.

Die Strategien, die sich aus diesen Indikatoren entwickelt haben, beruhen in der Regel auf festen Regeln. Diese Regeln können z. B. lauten: „Kaufen, wenn der TRIX die Nulllinie überschreitet und der WPR unter -80 liegt“ oder „Verkaufen, wenn der TRIX seinen Höchststand erreicht und der WPR über -20 liegt“. So deterministisch sie auch sein mögen und so leicht sie auch zu überprüfen sind, haben sie doch eine gemeinsame Schwäche, nämlich die Annahme eines statischen Verhältnisses in einem hochdynamischen Markt. Aus diesem Grund kann sich ihre Wahrscheinlichkeit, richtig zu liegen, verschlechtern, wenn sich die vorherrschenden Bedingungen ändern, und diese „absoluten Schwellenwerte“ müssen angepasst werden. 

Dieser Sumpf bildet also die Grundlage für das Reinforcement Learning (RL). RL gehört zu den Techniken des maschinellen Lernens, bei denen versucht wird, aus Erfahrungen oder der Interaktion mit einer Umgebung die passenden Aktionen zu lernen. Anstatt sich ausschließlich auf voreingestellte Indikatorschwellen zu verlassen, kann ein RL-Agent verschiedene Schwellenwerte erkunden und so den Entscheidungsprozess für den Handel anpassen, um die langfristigen Gewinne zu maximieren. Für die meisten Händler würde dies ein System bedeuten, das nicht nur Regeln befolgt, sondern sich anpasst – zumindest auf dem Papier.

Eine der RL-Methoden, die für den Handel vielversprechend erscheint, ist das Deep Q Network (DQN). Im Gegensatz zu überwachten Lernmodellen, die versuchen, Eingaben direkt auf Ausgaben abzubilden, bewerten DQNs den Wert der Durchführung bestimmter Aktionen, wenn bestimmte Zustände vorliegen. Im Zusammenhang mit dem Handel können Zustände Merkmale sein, die von Indikatoren, in einer transformierten Pipeline, im Binärformat oder sogar als Rohwerte vorliegen. Für diesen Artikel sind diese Indikatoren der TRIX und der WPR. Die Handlungen hingegen können einem Kauf, einem Verkauf oder einer neutralen Haltung entsprechen. Der DQN-RL-Rahmen ermöglicht es, diese Handlungen zu bewerten und aus der Erfahrung heraus abzustimmen, im Gegensatz zu festen, willkürlichen Regeln.

Dieser Artikel, der Teil der fortlaufenden Serie „MQL5-Assistententechniken, die Sie kennen sollten“ ist, konzentriert sich daher in diesem Teil-82 auf TRIX- und WPR-Muster mit dem DQN-RL-Algorithmus. Wir beginnen damit, zu untersuchen, was ein DQN ist und wie er in das breitere Terrain der Reinforcement-Learning-Algorithmen passt. Anschließend werden wir die Python-Implementierung eines DQN-Netzwerks mit Quantil-Regression in der Klasse „QuantileNetwork“ untersuchen. Darüber hinaus werden wir die Herausforderungen beim Einsatz von Modellen des Bestärkenden Lernens (Reinforcement Learning) im MetaTrader diskutieren. Abschließend werden wir die Ergebnisse der Strategietester für die drei spezifischen Muster betrachten, die wir auf die Indikatoren TRIX und WPR konzentriert hatten, nämlich 1, 4 und 5. Unser übergeordnetes Thema für diesen Artikel ist die Verknüpfung von Theorie und praktischer Umsetzung unter Verwendung des MQL5-Assistenten, wobei sowohl die Möglichkeiten als auch die Fallstricke dieses hybriden Arbeitsablaufs aufgezeigt werden sollen.

Die Muster 1, 4 und 5 werden wie folgt in einem Chart dargestellt:

Muster-1

Das Abwärtssignal wird registriert, wenn wir eine negative Divergenz im TRIX mit dem WPR im Widerstandsbereich/überkauften Bereich haben.

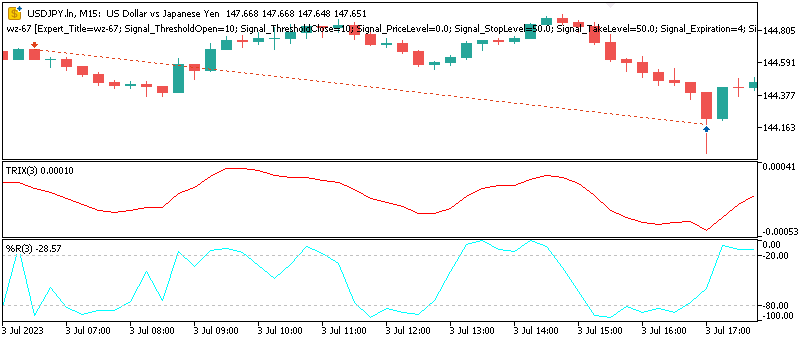
Muster-4

Ein Aufwärtssignal hat der TRIX, wenn er einen Widerstand durchbrochen hat und der WPR zwischen -50 und -20 liegt.

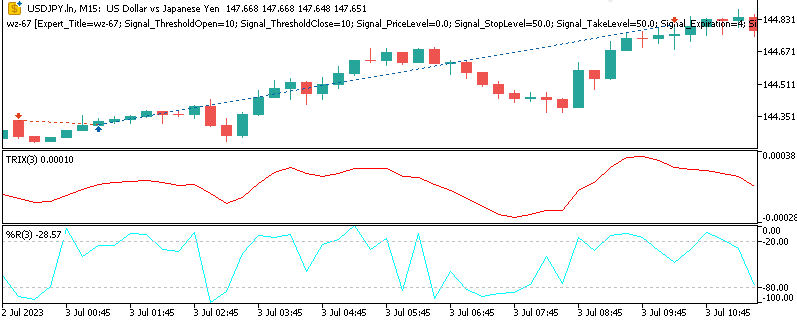
Pattern-5

Ein Abwärtssignal liegt vor, wenn sich der TRIX von einem überverkauften Niveau aus umkehrt und der WPR den überverkauften Bereich verlässt, was auf einen potenziellen Rückfall in einen Abwärtstrend hindeutet.

Tiefe Q-Netze – Wertbasiertes Verstärkungslernen

Um besser zu verstehen, warum DQNs für den Einsatz im Handel gut geeignet sind, könnte es konstruktiv sein, zunächst die Grundlagen des Bestärkenden Lernens zu überdenken. Im Kern ist RL eine systematische Art und Weise, in der ein Agent mit einer bestimmten Umgebung interagiert. In jedem Zeitschritt oder Intervall beobachtet dieser Agent den gegenwärtigen Zustand, ergreift eine Handlung und wird dafür im Verhältnis zu der Erwünschtheit der von ihm durchgeführten Handlung belohnt. Das Endspiel des Agenten besteht darin, im Laufe der Zeit so viel kumulative Belohnung wie möglich zu erhalten; dies kann er erreichen, wenn sich seine Politik, die Zuordnung von Zuständen zu Handlungen, ebenfalls im Laufe der Zeit verbessert. 

Auf den Märkten könnte der Staat, wie oben erwähnt, eine Sammlung von technischen Indikatoren einbeziehen, die von Rohwerten bis hin zu Pipeline-Transformationen reichen könnten. Aktionen, die ebenfalls hervorgehoben werden, können auf Handelsentscheidungen hinweisen, wie z. B. Kaufen, Verkaufen oder neutral bleiben. Die Belohnung, die der Vermittler erhält, wird in der Regel in Form von Gewinn und Verlust ausgedrückt, wobei manchmal Transaktionskosten oder sogar Exkursionsrisiken einberechnet werden. Dabei ist jedoch zu beachten, dass es im Gegensatz zum überwachten Lernen keine einzige richtige Antwort zum Kopieren gibt. Vielmehr ist es die Aufgabe des Agenten, in erster Linie durch Erkundung herauszufinden, welche Entscheidungen durchweg zu mehr Belohnungen führen.

Ein DQN baut auf dem Prinzip des Q-Learning auf. Dies ist einer der etablierteren wertbasierten Algorithmen im Bereich des Bestärkenden Lernens und führt den Begriff der Q-Value-Funktion ein. Dies stellen wir als Q(s, a) dar, wobei die Aufgabe darin besteht, die erwartete zukünftige Belohnung für die Durchführung einer Aktion a zu schätzen, wenn der Agent einen Zustand s beobachtet und sich anschließend an die optimale Strategie hält. Wenn diese Q-Funktion genau ist, wird die am besten geeignete Aktion zu einem bestimmten Zeitpunkt diejenige mit dem höchsten Q-Wert sein. Klassische Q-Learning-Implementierungen speichern diese Q-Werte in einer Tabelle, die erst dann machbar ist, wenn der Aktionsraum und die Zustandsdimensionen machbar sind.

Die Finanzmärkte produzieren jedoch oft kontinuierliche und hochdimensionale Zustände, die tabellarische Methoden nicht sehr praktisch machen. In diesem Punkt erweitert das Deep Learning diese Methode. Anstatt sich auf eine Nachschlagetabelle zu verlassen, schätzt ein tiefes neuronales Netz die Q-Funktion. Es ist diese Symbiose aus Bestärkenden Lernen und Tiefem Lernen (Deep Learning), die den Ursprung des Deep-Q-Network bildet.

Der Prozess der Ausbildung eines DQN spiegelt die iterative und adaptive Natur des Handels selbst wider. Übergänge, die aus dem Zustand, der Aktion, der Belohnung und dem nächsten Zustand, gefolgt von einem Abbruchkennzeichen, bestehen, werden in einem Wiedergabepuffer gespeichert. Das Netz wird dann mit Mini-Batches trainiert, die nach dem Zufallsprinzip aus diesem Puffer entnommen werden. Diese Zufallsstichprobe soll die Korrelation zwischen aufeinanderfolgenden Stichproben verringern und somit den Lernprozess stabilisieren.

Ein weiteres Merkmal dieses Ansatzes ist die Einbeziehung eines Zielnetzes. Dieses Netz, das langsam aktualisiert wird, ist eine Kopie des Q-Netzes. Damit sollen destabilisierende Rückkopplungsschleifen verhindert werden, die zwangsläufig entstehen, wenn das Netz direkt aus seinen eigenen, ständig überarbeiteten Prognosen lernt. Dieser besondere Aktualisierungsmechanismus hängt von der Bellman-Gleichung ab, bei der die Netzwerkparameter angepasst werden, um die Differenz zwischen den Belohnungen und den Schätzungen, die von den zukünftigen Erträgen abgezogen werden, zu minimieren. Die Fähigkeit zur Erkundung wird dadurch erhalten, dass die Entscheidungen des Agenten mit einem gewissen Maß an Zufälligkeit verbunden sind. Dies geschieht häufig in Form einer Epsilon-Greedy-Strategie, die sicherstellen soll, dass das Modell nicht in der vorzeitigen Ausnutzung eines einzigen Musters gefangen ist. Epsilon ist ein gleitender Wert von fast Null, sodass es sich in der Regel um einen sehr kleinen Prozentsatz handelt.

Im Hinblick auf den Handel bedeutet dieser Prozess, dass das Netzwerk langsam in der Lage ist, zu lernen und zu verarbeiten, welche Muster der Indikatoren mit größerer Wahrscheinlichkeit vor bestimmten profitablen Setups auftreten werden. All dies geschieht, während noch alternative Indikatoroptionen getestet werden, um eine Überanpassung an die historischen Daten oder, kurz gesagt, eine Verzerrung aufgrund der Aktualität zu vermeiden.  DQNs haben die Angewohnheit, sich in diesem Umfeld auszuzeichnen, weil sie in der Lage sind, sich auf natürliche Weise in diskrete Aktionsräume einzufügen, wie z. B. mit Kaufen, Verkaufen oder kein Handel. Dabei sind sie in der Lage, adaptiv zu lernen, anstatt sich auf statische Schwellenwerte zu verlassen. Noch wichtiger ist jedoch, dass sie in der Lage sind, die Realität verzögerter Belohnungen einzubeziehen, da die Rentabilität nicht unbedingt immer sofort nach einer Entscheidung eintritt. Durch die Abzinsung künftiger Gewinne neigt der DQN daher dazu, sofortige Auszahlungen gegen langfristige Rentabilität abzuwägen.

In unserer Studie für diesen Artikel werden die Merkmale aus TRIX und WPR entnommen, um den Eingangszustand zu bestimmen. Die einzelnen Aktionen werden den Handelspositionen entsprechen, die ein Händler einnehmen kann. Diese können auch schwebende Aufträge umfassen, wenn man es etwas ausführlicher haben möchte, aber wir beschränken uns auf Kauf, Verkauf und Neutral. Das Training eines DQN mit historischen Daten ermöglicht es dem Modell, die Wechselwirkungen zu erfassen, die zwischen diesen Indikatoren bestehen können und die bei der Anwendung fester Regeln möglicherweise nicht offensichtlich sind. Mit diesem Ansatz wird das Netz in die Lage versetzt, relative Werte im Verhältnis zu Aktionen zuzuweisen. Dies hat den Effekt, dass rohe Signale technischer Indikatoren in umsetzbare Handelsstrategien umgewandelt werden, die Anpassungsfähigkeit und Voraussicht miteinander verbinden.

Wertorientierte RL gegenüber Methoden der Politik und mit Akteur-Kritiker.

Ich dachte, ich würde auch einen Vergleich zwischen diesen beiden einfügen. Tiefe Q-Netze gehören zur Familie der wertbasierten Verstärkungslernalgorithmen, die sich dadurch auszeichnen, dass sie den Schwerpunkt auf die Schätzung des Wertes von Aktionen legen, anstatt eine direkte Pseudoabbildung von Zuständen auf Aktionen zu lernen. Anders ausgedrückt, ein wertorientierter Agent versucht, eine Antwort auf die Frage zu bekommen: „Wenn ich jetzt diese Maßnahme ergreife, wie viel Belohnung kann ich langfristig erwarten“? Im Gegensatz dazu tendieren alternative Methoden des Verstärkungslernens dazu, sich nicht mit der Bewertung von Handlungen zu befassen, sondern eher mit der direkten Gestaltung der Politik oder mit dem Ausgleich zwischen Bewertung und Politiklernen in irgendeiner Form. Diese Unterschiede zu verstehen, kann von entscheidender Bedeutung sein, vor allem, wenn man bedenkt, inwieweit jede Methode den einzigartigen Anforderungen des erfolgreichen Handels an den Märkten gerecht wird. 

Methoden, die auf Richtlinien basieren, wie REINFORCE oder Proximal Policy Optimization (PPO), schätzen die Q-Werte überhaupt nicht. Vielmehr werden sie zu Parametern der Politik selbst, sodass diese zu einer Wahrscheinlichkeitsverteilung über mögliche Aktionen wird. Der Lernprozess passt sich also so an, dass die Aktionen, die zu höheren kumulativen Belohnungen führen, häufiger ausprobiert werden. Ein solcher Ansatz ist besonders vorteilhaft in Umgebungen, in denen die Handlungsräume kontinuierlich sind und in denen es nicht möglich ist, jede mögliche Wahl zu diskretisieren. Für Händler haben politikbasierte Methoden im Prinzip das Potenzial, eine kontinuierliche Bandbreite von Positionsgrößen zu generieren, die sogar mit Vorzeichen (als + oder -) versehen werden können, um Kauf oder Verkauf zu kennzeichnen, im Gegensatz zur Beschränkung auf unseren engen Raum von 3: Kauf, Verkauf oder Neutral. Politische Gradientenverfahren leiden jedoch in der Regel unter einer hohen Varianz bei der Aktualisierung, was im Vergleich zu wertbasierten Verfahren in der Regel mehr Daten zur Stabilisierung erfordert.

Der Ansatz von Akteur und Kritiker versucht, die Stärken der beiden Welten zu vereinen. Bei dieser Mischform bezieht sich der „Akteur“ auf die Politik und kann selbst bestimmen, welche Maßnahmen er ergreift. Der „Kritiker“ hingegen bewertet diese ausgewählten Maßnahmen, indem er eine Einschätzung ihres Wertes abgibt. Indem diese beiden Komponenten zusammenarbeiten, können Algorithmen mit Akteur-Kritiker den Lernprozess stabilisieren und die Aktualisierung von Richtlinien effizienter gestalten. Auf den Finanzmärkten könnten die Ansätze mit Akteur und Kritiker ein Modell in die Lage versetzen, Handelsaktionen in unterschiedlicher Intensität vorzuschlagen, während gleichzeitig der Kritiker diese Aktionsentscheidungen verfeinert. Zu den bewährten Beispielen für diese Paarung gehören „Advantage Actor-Critic“ (A2C), „Deep Deterministic Policy Gradient“ (DDPG) und „Twin Delayed DDPG“ (auch bekannt als TD3, über das ebenfalls kürzlich berichtet wurde).

Der Hauptunterschied zwischen wert- und politikbasierten Methoden liegt also in der Abwägung zwischen Einfachheit und Flexibilität. DQNs, die auf Werten basieren, sind tendenziell einfacher zu implementieren, insbesondere in Fällen, in denen der Aktionsraum von Natur aus diskret ist. Außerdem haben sie die Tendenz, in Umgebungen, in denen verzögerte, aber diskrete Belohnungen üblich sind, viel schneller zu konvergieren. Dies sollte sie für Handelsszenarien attraktiver machen, die als Wahl zwischen einer begrenzten Anzahl von Optionen konfiguriert werden können. Auf dem Papier sind politikbasierte Ansätze und die mit Akteur-Kritiker zwar wirkungsvoll, aber sie bringen auch eine gewisse Komplexität mit sich. Dies wiederum erhöht die Anforderungen an die Rechenressourcen und führt in der Regel zu Implementierungsschwierigkeiten auf Plattformen wie MetaTrader, wo die Rückwärtsdurchläufe von effizient trainierten ONNX-Modellen nicht nativ verarbeitet werden können. Wir werden dies weiter unten erörtern.

Python-Implementierung des Quantilnetzes

Der Code, der für die Untermauerung der These für den Expert Advisor dieses Artikels verantwortlich ist, gibt weitgehend ein solides Beispiel dafür, wie ein Deep Q Network unter Verwendung der Quantilregression an den Handelskontext angepasst werden kann. Diese führen wir wie folgt auf:

# ---------------------------- QR-DQN Core ---------------------------

class QuantileNetwork(nn.Module):
    def __init__(self, state_dim: int, action_dim: int, hidden: int = 256, num_quantiles: int = NUM_QUANTILES):
        super().__init__()
        self.num_quantiles = num_quantiles
        self.action_dim = action_dim
        self.fc1 = nn.Linear(state_dim, hidden)
        self.fc2 = nn.Linear(hidden, hidden)
        self.fc3 = nn.Linear(hidden, hidden)
        self.fc4 = nn.Linear(hidden, action_dim * num_quantiles)
        fanin_init(self.fc1.weight); nn.init.zeros_(self.fc1.bias)
        fanin_init(self.fc2.weight); nn.init.zeros_(self.fc2.bias)
        fanin_init(self.fc3.weight); nn.init.zeros_(self.fc3.bias)
        nn.init.uniform_(self.fc4.weight, -3e-3, 3e-3); nn.init.zeros_(self.fc4.bias)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = F.relu(self.fc3(x))
        q = self.fc4(x)  # [batch, action_dim * num_quantiles]
        # FIX: only one inferred dimension allowed — reshape explicitly
        return q.view(x.size(0), self.num_quantiles, self.action_dim)  # [batch, N, A]

    def q_values(self, x):
        q = self.forward(x)            # [batch, N, A]
        return q.mean(dim=1)           # [batch, A]

Die zentrale Klasse in unserem Python-Programm, QuantileNetwork, ist für die Approximation der Q-Funktion zuständig. Dies ist der Kern des wertorientierten Verstärkungslernens. Auch wenn ein regulärer DQN eine einzelne Q-Wert-Schätzung des Q-Wertes jeder Aktion ausgibt, wird die Erweiterung dieser durch die Quantilvariante bei der Vorhersage einer Verteilung möglicher Ergebnisse ermöglicht. Dies kann insbesondere für den Handel relevant sein, wo die Unsicherheit der Märkte ebenso wichtig ist wie die durchschnittliche Erwartung. Dadurch, dass das Netz in der Lage ist, die gesamte Verteilung zu modellieren, indem es mehr als ein Quantil einbezieht, ist es in der Lage, nicht nur die erwartete Belohnung, sondern auch das damit verbundene Risiko pro Aktion zu erfassen.

Unsere Quantilnetzklasse ist als vollständig verbundenes neuronales Netz mit vier linearen Schichten aufgebaut. Die ersten drei dieser vier Schichten beziehen sich auf Transformationen, denen dann eine geradlinige Aktivierungsfunktion folgt. Dadurch soll das Netz in die Lage versetzt werden, nichtlineare Beziehungen zwischen den Eingabezuständen und den ausgegebenen Aktionen zu erkennen. Die vierte und oberste Schicht ist die Ausgabeschicht, und ihre Dimensionen sind so eingestellt, dass sie denen der Aktionsdimension und der Quantilzahl entsprechen.

Beim Training und bei der Durchführung von Inferenzen wird diese flache Ausgabe in einen Tensor mit Dimensionen umgewandelt, die durch die Quantilzahl bestimmt werden. In der Praxis bedeutet dies, dass das Netz für jeden eingegebenen Zustand eine Reihe von quantilbasierten Q-Werten für alle möglichen Aktionen zur Verfügung haben muss. Wenn wir diese Quantile mitteln, kann das Modell einen konventionellen Q-Wert ermitteln, der sich zwar für die Entscheidungsfindung eignet, aber dennoch die Flexibilität beibehält, die für die Risikoanalyse bei Bedarf wichtig ist.

Die Initialisierung der Gewichte erfolgt sehr behutsam, indem für die Anfangsschichten eine Fan-in-Skalierung vorgenommen wird. Für die letzte Ausgabeschicht werden kleine, gleichmäßige Verteilungen verwendet. Diese Form der Initialisierung ist beim Bestärkenden Lernen unerlässlich, da instabile Gewichtsverteilungen die Tendenz haben können, vorhandenes Rauschen in den Daten zu verstärken. Dies würde den Trainingsprozess destabilisieren. Indem wir also sicherstellen, dass unsere Ausgangsgewichtsparameter eine gewisse Form von Ausgewogenheit aufweisen, ist das Quantilnetz bis zu einem gewissen Grad in der Lage, eine vorzeitige Divergenz zu vermeiden, indem es seine Konvergenz im Optimierungs-/Rückwärtsdurchlaufsprozess verbessert.

Der Agent, den wir mit unserem DQN verwenden, orchestriert den Lernprozess, indem er das Hauptquantilnetz zusammen mit einem Zielnetz unterhält, das einfach eine Kopie unseres Quantilnetzes ist. Diese Kopie wird in regelmäßigen Abständen durch einen Soft Replacement-Mechanismus aktualisiert. Diese verzögerte Aktualisierung sorgt dafür, dass sich die im Training verwendeten Ziele gleichmäßig und nicht sprunghaft entwickeln. Darüber hinaus ist der Agent auch der Schlüssel zum Start eines Optimierers, in unserem Fall Adam. Adam ist gut positioniert, um mit verrauschten Gradientenaktualisierungen umzugehen, die ein Hauptmerkmal des Bestärkenden Lernens sind. Der Code unseres Agentenliste ist wie folgt:

class QRDQNAgent:
    def __init__(self, state_dim: int, action_dim: int, hidden: int = 256):
        self.state_dim = state_dim
        self.action_dim = action_dim
        self.num_quantiles = NUM_QUANTILES

        self.net        = QuantileNetwork(state_dim, action_dim, hidden).to(DEVICE)
        self.target_net = QuantileNetwork(state_dim, action_dim, hidden).to(DEVICE)
        self.target_net.load_state_dict(self.net.state_dict())

        self.optimizer = optim.Adam(self.net.parameters(), lr=LR)
        self.replay_buffer = ReplayBuffer(capacity=100_000, state_dim=state_dim)

        # quantile fractions τ_i (midpoints)
        self.taus = torch.linspace(0.0 + 1.0/(2*self.num_quantiles),
                                   1.0 - 1.0/(2*self.num_quantiles),
                                   self.num_quantiles, device=DEVICE).view(1, -1)  # [1, N]

    @torch.no_grad()
    def act(self, state: torch.Tensor, epsilon: float = 0.1) -> int:
        if np.random.rand() < epsilon:
            return np.random.randint(self.action_dim)
        q_vals = self.net.q_values(state.unsqueeze(0).to(DEVICE))  # [1, A]
        return int(torch.argmax(q_vals, dim=1).item())

    def _quantile_huber_loss(self, preds: torch.Tensor, target: torch.Tensor, taus: torch.Tensor) -> torch.Tensor:
        """
        preds:  [B, N]   (predicted quantiles for chosen action)
        target: [B, N]   (target quantiles)
        taus:   [1, N]
        """
        diff = target.unsqueeze(1) - preds.unsqueeze(2)  # [B, N, N]
        huber = torch.where(diff.abs() <= KAPPA,
                            0.5 * diff.pow(2),
                            KAPPA * (diff.abs() - 0.5 * KAPPA))
        tau = taus.view(1, -1, 1)  # [1, N, 1]
        loss = (torch.abs(tau - (diff.detach() < 0).float()) * huber).mean()
        return loss

    def learn(self, batch_size: int = BATCH_SIZE):
        if self.replay_buffer.size < batch_size:
            return

        s, a, r, ns, d = self.replay_buffer.sample(batch_size)

        with torch.no_grad():
            # Double DQN selection w/ target evaluation (simple variant)
            q_next_online = self.net.q_values(ns)                  # [B, A]
            a_next = q_next_online.argmax(dim=1, keepdim=True)     # [B,1]
            q_next_all = self.target_net(ns)                       # [B, N, A]
            q_next_sel = q_next_all.gather(2, a_next.unsqueeze(1).expand(-1, self.num_quantiles, 1)).squeeze(-1)  # [B, N]
            target = r + (1.0 - d) * GAMMA * q_next_sel            # broadcast [B,1] + [B,N] -> [B,N]

        q_preds_all = self.net(s)                                  # [B, N, A]
        a_expanded  = a.view(-1, 1, 1).expand(-1, self.num_quantiles, 1)  # [B, N, 1]
        q_preds     = q_preds_all.gather(2, a_expanded).squeeze(-1)       # [B, N]

        loss = self._quantile_huber_loss(q_preds, target, self.taus)

        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

        # Soft update target
        with torch.no_grad():
            for tp, sp in zip(self.target_net.parameters(), self.net.parameters()):
                tp.data.mul_(1.0 - TARGET_TAU)
                tp.data.add_(TARGET_TAU * sp.data)

    # -------------------- ONNX Export --------------------
    def export_qnet_onnx(self, path: str):
        """
        Export a wrapper that outputs mean Q-values: [1, action_dim]
        """
        class QValuesHead(nn.Module):
            def __init__(self, net: QuantileNetwork):
                super().__init__()
                self.net = net
            def forward(self, x):
                return self.net.q_values(x)

        wrapper = QValuesHead(self.net).to(DEVICE).eval()
        dummy = torch.zeros(1, self.state_dim, dtype=torch.float32, device=DEVICE)
        torch.onnx.export(
            wrapper, dummy, path,
            export_params=True, opset_version=17, do_constant_folding=True,
            input_names=["state"], output_names=["q_values"], dynamic_axes=None
        )
        return path

Wir brauchen auch eine Implementierung eines Wiedergabepuffers, um unsere Zustandsübergänge zu speichern. Unser Agent ist in der Lage, aus diesem Puffer zufällige kleine Datenstapel zu entnehmen, um die Trainingsdaten zu entkorrelieren, wie bereits oben dargelegt.

Unser Lernprozess umfasst die Berechnung eines Quartil-Huber-Verlusts, einer Metrik für die Differenz zwischen den Prognosquantilen und den Ziel-/Erwartungsquantilen. Dies geschieht unter Wahrung der Robustheit gegenüber Ausreißern. Der bekannte DQN-Ansatz wird verwendet, um die Ziele zu konstruieren, wobei die nächste Aktion in Übereinstimmung mit dem Online-Netzwerk ausgewählt wird. Die Bewertung seines Wertes erfolgt jedoch durch das Zielnetz. Dadurch wird die Verzerrung verringert, die sonst fast immer auftritt, wenn dasselbe Netz sowohl für die Auswahl als auch für die Bewertung verwendet wird. Unser Quantil-Huber-Verlust bestraft nicht nur Prognosen, deren Mittelwerte falsch sind, sondern auch Abweichungen in der gesamten Verteilungsspanne möglicher Renditen. Dies wird das Modell in volatilen und unsicheren Märkten widerstandsfähiger machen.

Unser obiges Listing hat auch eine Umgebungsklasse, CustomDataEnv, deren Zweck es ist, festzulegen, wie der Agent mit historischen Daten interagieren soll. Unsere Umgebung nimmt als Input eine Merkmalsmatrix, die von TRIX- und WPR-Indikatormustern abgeleitet ist, sowie ein Zielfeld, das die nachfolgende Preisaktion zeigt, nachdem die besagten Indikatormuster offensichtlich waren. Für jeden Schritt kann der Agent eine Aktion wählen: kaufen, verkaufen oder neutral. Die Umwelt gibt dann den nächsten Zustand sowie eine Belohnung zurück, die als Produkt aus der Aktion und der beobachteten Rendite berechnet wird, aber mit Transaktionskosten bestraft wird, wenn die Aktion geändert werden muss. Mit dieser Methode können wir die historischen Daten in ein sequenzielles Entscheidungsfindungsumfeld verlagern, in dem wir einige Live-Handelsaktionen nachahmen.

Am Ende muss die Implementierung eine ONNX-Exportfunktion bereitstellen. Bemerkenswert ist jedoch, dass ein Rückwärtsdurchlauf im MetaTrader der exportierten ONNX nicht möglich ist, was leider die einzige Option bei der Verwendung von mit Python trainierten Modellen ist. Sie ist nur für Schlussfolgerungen gedacht. Beim Export wird die Klasse QuantileNetwork jedoch in einen leichtgewichtigen Kopf verpackt, der als Ausgabe mittlere Q-Werte liefert. Dies garantiert, dass das resultierende Modell kompakt und effizient genug ist, um Auswertungen für einen Expert Advisor durchzuführen. Wie bereits in früheren Artikeln erwähnt, ist dieser Schritt, bei dem wir die Größe der Eingabe- und Ausgabeschichten überprüfen und sicher sein müssen, von entscheidender Bedeutung für die Aufrechterhaltung unserer Brücke zwischen schlanken, gut trainierten Modellen und deren Einsatz auf Live-Konten.

Zusammenfassend lässt sich sagen, dass das QuantileNetwork und sein Agenten-Wrapper zeigen, wie Konzepte des Bestärkenden Lernens brauchbaren Code umgesetzt werden können. Die Verwendung der Quantilsregression erhöht die Anpassungsfähigkeit durch die Erfassung von Belohnungsverteilungen, und der Wiederholungspuffer sowie das Zielnetz tragen dazu bei, eine gewisse Stabilität in den Trainingsprozess zu bringen, wobei ONNX eine Möglichkeit zur Integration in die reale Welt bietet. Für uns Händler sind diese Python-Code-Listen, die keinen Anspruch auf Vollständigkeit erheben, ein wichtiger erster Schritt auf dem Weg von indikatorbasierten Signalen zu einer robusten, datengestützten Entscheidungsfindung.

Herausforderungen der Integration von RL und MQL5

Obwohl die Verwendung von Python und die Überbrückung zu MQL5 zeigt, wie Bestärkendes Lernen mit historischen Daten trainiert werden kann, ist die Übertragung solcher Modelle in MetaTrader im Allgemeinen mit einigen Problemen verbunden. Ich habe diese in früheren Artikeln angedeutet, insbesondere in der Schlussfolgerung des letzten Artikels, in dem wir zufällig ein mit Verstärkungslernen trainiertes Modell verwendet haben. Die primäre Einschränkung besteht darin, dass MQL5, und damit jede Plattform, die Rückwärtsdurchläufe von ONNX-Dateien nicht unterstützt. Sie waren/sind nur für Vorwärtsdurchläufe gedacht, zumindest in den letzten Versionen. 

Da wir in Python sowohl den ursprünglichen Netzcode als auch die zweckmäßigen Tensorbibliotheken zur Verfügung haben, sind wir in der Lage, Netze effizient zu trainieren und zurück zu propagieren. Die inhärente Einschränkung von MQL5 besteht derzeit darin, dass es für die effiziente, leichtgewichtige Ausführung von Handelslogik und nicht für massenhafte numerische Berechnungen entwickelt und gebaut wurde. Das bedeutet, dass wir beim Export eines ONNX, der entweder in der Sandbox referenziert oder in den Expert Advisor eingebettet ist, nur eine Vorwärtsinferenz durchführen können. Die Gewichte des exportierten Modells, wie in der letzten und neuesten ONNX-Version, erlauben keine Aktualisierung der Gewichte. 

Dieser Vorbehalt zwingt uns zu einem Kompromiss, der einfach unsere nächstbeste Alternative oder streng genommen unsere einzige Option ist, um die gesamte Ausbildung des exportierten Modells zu nutzen. Dieser Kompromiss verdeutlicht auch, warum wir vorerst nur ein Netzwerkmodell in ONNX exportieren, wenn wir das Bestärkenden Lernen in MQL5 nutzen wollen. In der klassischen Verstärkungslernschleife interagiert der Agent ständig mit der Umwelt, speichert Erfahrungen und passt seine Q-Werte in Echtzeit an. In unserem MQL5-Kontext sollte das Training jedoch vollständig offline in Python erfolgen. Das Modell soll einmal anhand historischer Daten lernen, und sobald es trainiert ist, werden seine Netzgewichte, Schichten und Verzerrungen exportiert und als statischer Akteur eingesetzt.

Aus diesem Grund ist das so genannte Reinforcement-Learning-System im MetaTrader in Wirklichkeit ein überwachtes Lernmodell. Es bildet einfach die Eingabemerkmale der Indikatoren TRIX und WPR auf Ausgabewerte ab, die die relative Erwünschtheit von Handelsaktionen anzeigen. Diese Politik oder Mapping-Beziehung passt sich beim Live-Handel nicht an neue oder entstehende Zustände an, auch nicht beim Vorwärtsgehen.

Ein weiteres, wenn auch überschaubares Problem ist die Anpassung der Erwartungen an die ONNX-Laufzeitumgebung innerhalb der MQL5-Schnittstelle. ONNX-Modelle sind praktisch konstante Variablen, da sie für die jeweiligen Schichten bestimmte Eingabe- und Ausgabeformen erwarten. Diese Formen werden in Python mit Stapeldimensionen und einer bestimmten Fließkommagenauigkeit, 32 oder 64, definiert. Wenn die in MQL5 deklarierten Containerformen bei der Initialisierung der ONNX-Handles nicht mit dem übereinstimmen, was in Python eingestellt wurde, schlägt die Laufzeitinitialisierung fehl. Dies ist oft ein lösbarer, aber dennoch heikler Punkt, denn die meisten Leute, die ihre Modelle exportieren, nehmen sich nicht die Zeit, die tatsächlichen Formen dieser Eingabe- und Ausgabeebenen auszudrucken.

Die gute Nachricht ist jedoch, dass Meta Editor neben dem Ausdruck der tatsächlichen Form dieser Schichten in Python nun auch eine Anwendung zum Betrachten neuronaler Netze im Menü „Extras“ anbietet. Sobald die Anwendung gestartet ist, kann man in einem vom Meta-Editor getrennten Fenster die exportierte ONNX-Datei öffnen und dann ihr detailliertes Layout einschließlich der Größen und Formen der Eingabe- und Ausgabeschichten betrachten.

Kompromiss beim Überwachten Lernen

Mit einem Reinforcement-Learning-Modell, das in Python trainiert und nach ONNX exportiert wurde, ändert sich sein Zweck innerhalb von MQL5 erheblich. Das Modell kann nicht mehr, wie beabsichtigt und konzipiert, es ist kein adaptiver Lerner mehr, sondern eine statische Entscheidungsmaschine. In der Praxis bedeutet dies, dass das exportierte Akteursnetz wie jedes andere prädiktive überwachte Lernnetz verwendet wird. Das bedeutet, dass die Anzahl der Schichten, die Größe der Schichten und andere Details der Architektur nicht so ansprechend sind wie bei vergleichbaren überwachten Lernmodellen, die als solche entworfen und trainiert wurden. Unser kompromisshafter Ansatz erlaubt dennoch die Integration weiterer Logik in MQL5, die zwar ohne Python und ONNX möglich ist, aber nicht so effizient eingebunden werden kann.

Unsere kompromittierte Implementierung beginnt also damit, dass wir die ONNX-Dateien der Akteure direkt in MQL5 als Ressourcen einbetten. Bei diesen ONNX-Dateien handelt es sich im Wesentlichen um die Gewichte, Verzerrungen und Schichtgrößen unseres trainierten Quantilnetzes. Sie wird in ein Format komprimiert, das die MQL5-Laufzeitumgebung effizient verarbeiten kann. In unserer nutzerdefinierten Signalklasse werden die drei Modelle für die Muster 1, 4 und 5 referenziert, wobei jedes einem einzigartigen Satz von Indikatormustern aus den Indikatoren TRIX und WPR entspricht. Bei der Initialisierung erstellt der Expert Advisor ONNX-Handles aus diesen Puffern und sorgt dafür, dass alle Netze bei der Auswertung der Bedingungen für Handelseintritte aufgerufen werden können. Wenn wir hier sind, wird das Modell nicht neu trainiert oder verändert, sondern es wird einfach als Referenzwerkzeug in den Speicher geladen und ist dann einsatzbereit.

Signal-Logik

Sobald ONNX exportiert und in MQL5 eingebettet ist, besteht einer der wichtigsten Schritte darin, den Signalcode und die Bedingungen für die offene Position zusammenzustellen. Dies ist der Code, der die Ergebnisse des Quantilnetzes in sinnvolle Handelsbedingungen umsetzt. Diese Logik, auf die wir uns beziehen, ist in den Funktionen Long-Condition und Short-Condition innerhalb der nutzerdefinierten Signalklasse wie folgt aufgeführt:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalRL_TRX_WPR::LongCondition(void)
{  int result  = 0, results = 0;
   vectorf _x;
   _x.Init(2);
   _x.Fill(0.0);
//--- if the model 1 is used
   if(((m_patterns_usage & 0x02) != 0) && IsPattern_1(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_1;
         results++;
      }
   }
//--- if the model 4 is used
   if(((m_patterns_usage & 0x10) != 0) && IsPattern_4(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_4;
         results++;
      }
   }
//--- if the model 5 is used
   if(((m_patterns_usage & 0x20) != 0) && IsPattern_5(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_5;
         results++;
      }
   }
//--- return the result
//if(result > 0)printf(__FUNCSIG__+" result is: %i",result);
   if(results > 0 && result > 0)
   {  return(int(round(result / results)));
   }
   return(0);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalRL_TRX_WPR::ShortCondition(void)
{  int result  = 0, results = 0;
   vectorf _x;
   _x.Init(2);
   _x.Fill(0.0);
//--- if the model 1 is used
   if(((m_patterns_usage & 0x02) != 0) && IsPattern_1(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_1;
         results++;
      }
   }
//--- if the model 4 is used
   if(((m_patterns_usage & 0x10) != 0) && IsPattern_4(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_4;
         results++;
      }
   }
//--- if the model 5 is used
   if(((m_patterns_usage & 0x20) != 0) && IsPattern_5(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_5;
         results++;
      }
   }
//--- return the result
//if(result > 0)printf(__FUNCSIG__+" result is: %i",result);
   if(results > 0 && result > 0)
   {  return(int(round(result / results)));
   }
   return(0);
}

Unsere Auflistung dieser beiden Methoden oben bestimmt den Kern dessen, wie der Expert Advisor entscheidet, wann er Kauf- oder Verkaufspositionen eröffnet. Dazu wird die Mustererkennung der technischen Indikatoren mit den Entscheidungsergebnissen des Bestärkenden Lernens kombiniert.

Die lange Funktion beginnt mit der Deklaration eines Merkmalsvektors, der für den Eingabezustand steht. Dieser Vektor x wird initialisiert und dann mit Nullen gefüllt. Sobald dies geschehen ist, können wir selektiv einem der beiden Indizes eine 1 zuweisen, je nachdem, welche Muster vom Expert Advisor verwendet werden. Dies ist also die Bedeutung des Eingabeparameters „verwendete Muster“.

Wenn ein Muster beispielsweise den Index 1 hat, müssen wir den Parameter „Patterns-Used“ auf 2 hoch 1 setzen, was 2 ergibt. Wenn der Index 2 ist, dann führt das zu 2 hoch 2, also 4, und so weiter. Der maximale Wert, der diesem Parameter sinnvollerweise zugewiesen werden kann, ist 1023, da wir nur 10 Parameter haben. Jede Zahl zwischen 0 und 1023, die kein reiner Exponent von 2 ist, würde eine Kombination dieser Muster darstellen, und der Leser könnte die Einrichtung des Expert Advisors zur Verwendung mehrerer Muster untersuchen. Auf der Grundlage unserer Argumente und Testergebnisse, die wir in früheren Artikeln dargelegt haben, haben wir uns jedoch entschieden, diesen Weg in dieser Serie vorerst nicht weiter zu verfolgen.

Da wir nur die Muster 1, 4 und 5 verwenden, müssen wir nur auf diese Muster achten. Wenn die Muster-1-Bedingungen erfüllt sind, wird dem ersten Index des Vektors eine 1 zugewiesen. Dies geschieht auch, wenn wir mit Muster 4 oder Muster 5 handeln. Beachten Sie, dass dieser Expert Advisor zwar auf dem Papier die verwendeten Eingabeparameter-Muster so anpassen kann, dass mehrere Muster verwendet werden können (siehe kursive Schrift oben), wir aber immer nur ein Muster verwenden. Die Verwendung von Mehrfachmustern führt zwangsläufig zu sehr unzuverlässigen Testergebnissen, da die Auslöschung von Kreuzsignalen weit verbreitet ist.

Sobald ein verwendetes Muster übereinstimmt, tragen das optimierte Gewicht sowie ein ONNX-Vorwärtspass zum Endergebnis der Bedingung bei. Die Verkaufsbedingung spiegelt diese Logik ebenfalls wider, konzentriert sich aber auf Gelegenheiten von Verkaufsmustern. Der Merkmalsvektor x wird deklariert, und es werden ähnliche Musterprüfungen durchgeführt. Der Hauptunterschied besteht darin, dass wir bei einer Musterübereinstimmung, die durch das Quantilnetz bestätigt wird, die 1 dem zweiten Index zuordnen, nicht dem ersten. Alle anderen Durchschnitte der Gewichte und die Berechnung des Ergebniswerts entsprechen den Angaben in der Bedingung für einen Kauf.

Testergebnisse

Beim Training und bei der Optimierung haben wir das Symbol EUR USD auf dem 4-Stunden-Zeitrahmen vom 2023.07.01 bis 2024.07.01 getestet. Das Zeitfenster für die Vorwärtsbewegung war von 2024.07.01 BIS 2025.07.01, und dies lieferte uns die folgenden Ergebnisse für die drei Muster 1, 4, und 5.

Muster-1

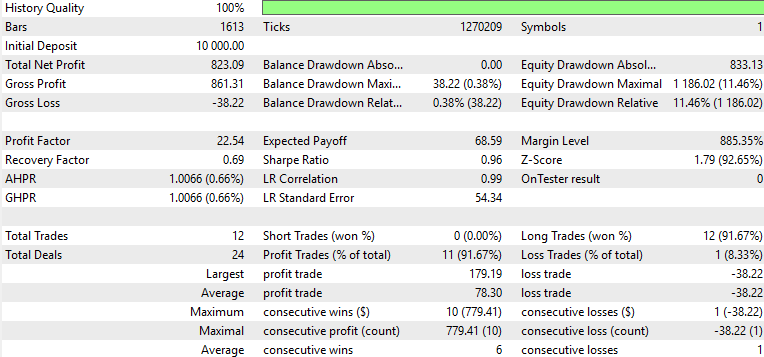
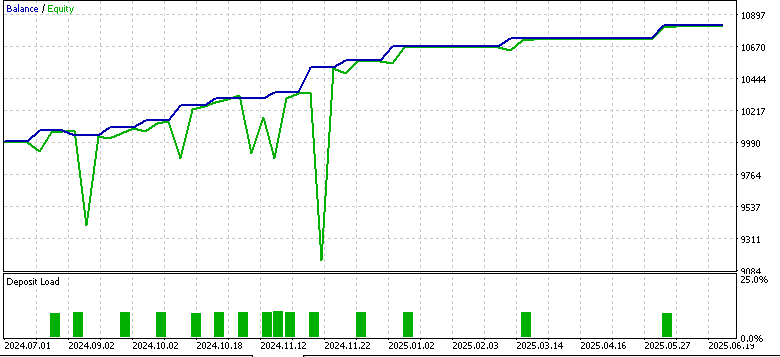
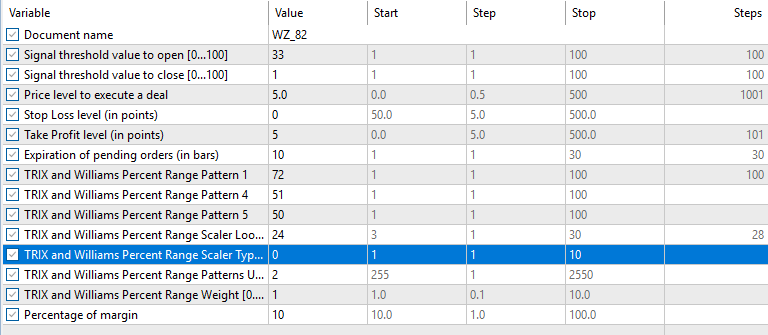
Muster-4

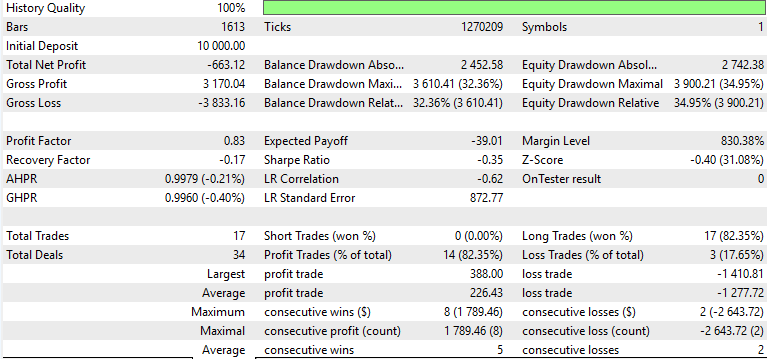
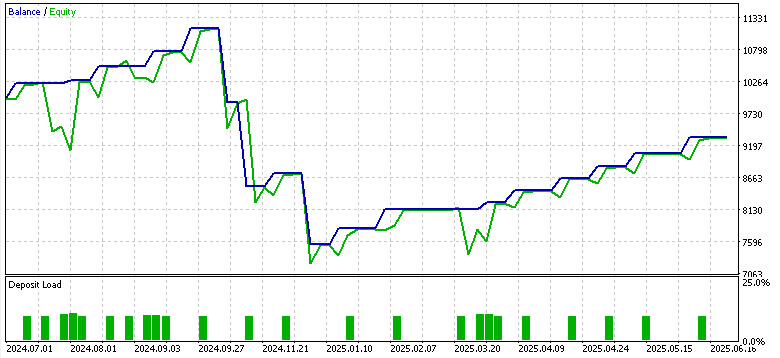
Pattern-5

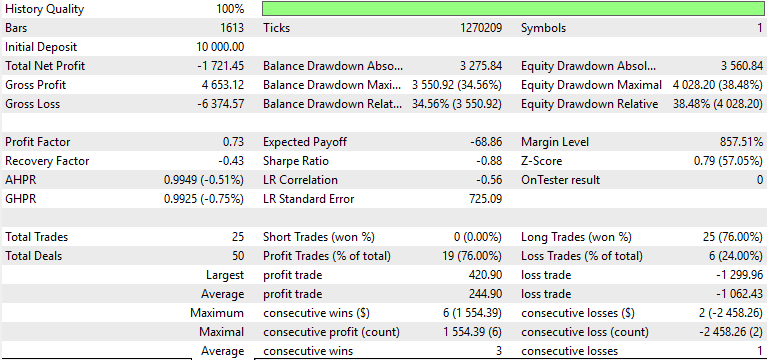
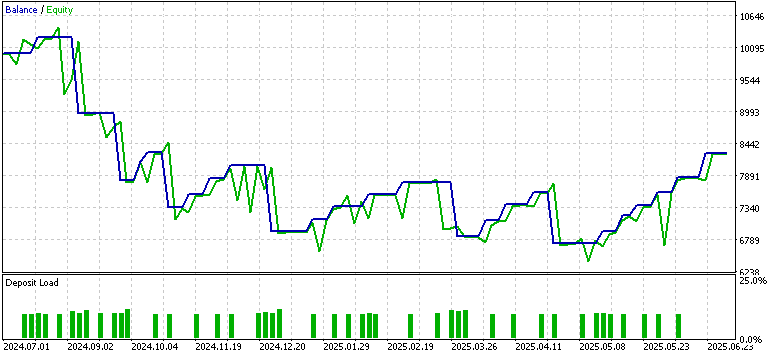
Nur Muster 1 schien den Vorwärtstest mit Gewinn zu bewältigen, während 4 und 5 Schwierigkeiten hatten. Es gilt der übliche Vorbehalt, dass es sich hierbei nicht um eine Finanzberatung handelt, aber die Verwendung von „schwachen“ bzw. unangepassten Akteursnetzwerken als überwachte Lernmodelle könnte daran schuld sein. Unser Ziel ist es wie immer, keine „out of box“-Lösungen anzubieten, sondern vielmehr eine Vielzahl von Möglichkeiten auszuloten und zu zeigen, was möglich ist. Die abschließende Arbeit und wichtige Abgrenzung obliegt immer dem Leser, wenn er sich dafür entscheidet, einige der hier vorgestellten Ideen zu übernehmen.

Schlussfolgerung

Unser Artikel über die TRIX- und WPR-Signalmuster im Rahmen eines Verstärkungslernens hat sowohl das Versprechen als auch die Grenzen von MQL5 aufgezeigt. Python-Module werden ständig aktualisiert, sodass es möglich ist, dass irgendwann in der Zukunft die von ONNX exportierten Netzwerke mit den Fähigkeiten von Rückwärtsdurchläufen aktualisiert werden können. Im Moment ist dies nicht der Fall, sodass dies eine Einschränkung darstellt. Modelle müssen offline trainiert und dann „in Stein gemeißelt“ werden, sodass sie als Inferenzmaschinen funktionieren.

Name	Beschreibung
WZ_82.mq5	Die mit dem Assistenten erstellte Expert-Hauptdatei, deren Header referenzierte Dateien auflistet
SignalWZ_82.mqh	Nutzerdefinierte Signalklasse, die DQNs importiert
82_5_0.onnx	ONNX Exportiertes Modell für Muster-5
82_4_0,onnx	ONNX Exportiertes Modell für Muster-4
82_1_0.onnx	ONNX Exportiertes Modell für Muster-1

Eine Anleitung zur Verwendung der angehängten Dateien finden neue Leser hier.