Kombinatorisch symmetrische Kreuzvalidierung in MQL5
261
1
Einführung
Manchmal beginnen wir bei der Entwicklung einer automatisierten Strategie mit einer Reihe von Regeln, die auf willkürlichen Indikatoren beruhen und die in irgendeiner Weise verfeinert werden müssen. Bei diesem Verfeinerungsprozess werden mehrere Tests mit verschiedenen Parameterwerten der ausgewählten Indikatoren durchgeführt. Auf diese Weise können wir die Indikatorwerte finden, die den Gewinn oder jede andere Kennzahl, die uns wichtig ist, maximieren. Das Problem bei dieser Praxis ist, dass wir aufgrund des in Finanzzeitreihen vorherrschenden Rauschens eine gewisse optimistische Verzerrung einführen. Ein Phänomen, das als Overfitting (Überanpassung) bekannt ist.
Eine Überanpassung lässt sich zwar nicht vermeiden, doch kann das Ausmaß der Überanpassung von einer Strategie zur anderen variieren. Es wäre daher hilfreich, wenn man feststellen könnte, in welchem Umfang dies geschehen ist. Combinatorially Symmetrical Cross Validation (CSCV, kombinatorische symmetrische Kreuzvalidierung) ist eine Methode, die in der wissenschaftlichen Arbeit „The Probability of Backtest Overfitting“, von David H. Bailey et al. vorgestellt wurde. Sie kann verwendet werden, um das Ausmaß der Überanpassung bei der Optimierung der Parameter einer Strategie abzuschätzen.
In diesem Artikel werden wir die Implementierung von CSCV in MQL5 demonstrieren und anhand eines Beispiels zeigen, wie es auf einen Expert Advisor (EA) angewendet werden kann.
Die CSCV-Methode
In diesem Abschnitt wird die genaue CSCV-Methode Schritt für Schritt beschrieben, beginnend mit einleitenden Aspekten bezüglich der Daten, die in Bezug auf die gewählten Leistungskriterien gesammelt werden müssen.
Die CSCV-Methode kann in verschiedenen Bereichen außerhalb der Strategieentwicklung und -analyse angewandt werden, aber in diesem Artikel beschränken wir uns auf den Kontext der Strategieoptimierung. Wir haben eine Strategie, die durch eine Reihe von Parametern definiert ist, die durch zahlreiche Tests mit unterschiedlichen Parameterkonfigurationen feinabgestimmt werden müssen.
Bevor wir mit den Berechnungen beginnen, müssen wir zunächst entscheiden, welche Leistungskriterien wir für die Bewertung der Strategie heranziehen wollen. Die CSCV-Methode ist insofern flexibel, als jede beliebige Leistungskennzahl verwendet werden kann. Vom einfachen Gewinn bis hin zu kennzahlenbasierten Metriken ist es für CSCV unerheblich.
Die gewählten Leistungskriterien bestimmen auch die zugrundeliegenden Daten, die für die Berechnungen verwendet werden, d. h. die granularen Rohdaten, die bei allen Testläufen erfasst werden. Wenn wir uns beispielsweise für die Sharpe Ratio als Erfolgsgröße entscheiden, müssen wir die Ergebnisse Balken für Balken von jedem Testlauf erfassen. Wenn wir den einfachen Gewinn verwenden würden, bräuchten wir den Gewinn oder Verlust für jeden einzelnen Balken. Wichtig ist, dass die Menge der bei jedem Durchlauf gesammelten Daten konsistent ist. Dadurch wird sichergestellt, dass wir für alle Testläufe ein Maß für jeden entsprechenden Datenpunkt haben.
- Der erste Schritt beginnt mit der Datenerfassung während der Optimierung, da die verschiedenen Parametervariationen getestet werden.
- Nach Abschluss der Optimierung fassen wir alle Daten aus den Testläufen in einer Matrix zusammen. Jede Zeile dieser Matrix enthält alle Erfolgswerte, Balken für Balken, die zur Berechnung einer Handelsperformance-Kennzahl für einen entsprechenden Testlauf verwendet werden.
- Die Matrix hat so viele Zeilen, wie Parameterkombinationen getestet wurden, und die Anzahl der Spalten entspricht der Anzahl der Balken, die den gesamten Testzeitraum ausmachen. Diese Spalten werden dann in eine beliebige gerade Anzahl von Sätzen aufgeteilt. Sagen wir, N Sätze.
- Diese Mengen sind Teilmatrizen, die verwendet werden, um Kombinationen von Gruppen der Größe N/2 zu bilden. Kombinatorisch werden insgesamt N Kombinationen geschaffen, die N/2 auf einmal genommen werden, also N Cn/2 . Aus jeder dieser Kombinationen konstruieren wir ein In-Sample-Set (ISS), indem wir N/2 Teilmatrizen zusammenstellen, und auch ein entsprechendes Out-Of-Sample-Set (OOSS) aus den verbleibenden Teilmatrizen, die nicht im ISS enthalten sind.
- Für jede Zeile der ISS- und OOSS-Matrizen berechnen wir die entsprechende Leistungskennzahl und notieren die Zeile in der ISS-Matrix mit der besten Leistung. Das ist die optimale Parameterkonfiguration. Die entsprechende Zeile in der OOSS-Matrix wird zur Berechnung des relativen Rangs verwendet, indem die Anzahl der Out-of-Sample-Parameterversuche mit schlechterer Leistung im Vergleich zu der mit der optimalen Parameterkonfiguration erzielten Leistung gezählt wird. Diese Zahl wird als Bruchteil aller getesteten Parametersätze dargestellt.
- Während wir alle Kombinationen durchgehen, kumulieren wir die Anzahl der relativen Rangwerte, die kleiner oder gleich 0,5 sind. Sie ist die Anzahl der Parameterkonfigurationen außerhalb der Stichprobe, deren Leistung unter derjenigen liegt, die mit dem optimalen Parametersatz beobachtet wurde. Sobald alle Kombinationen verarbeitet sind, wird diese Zahl als Bruchteil aller Kombinationen + 1 dargestellt. Darstellung der Wahrscheinlichkeit von Backtest Overfitting (PBO).
Nachfolgend eine Visualisierung der soeben beschriebenen Schritte für N = 4.
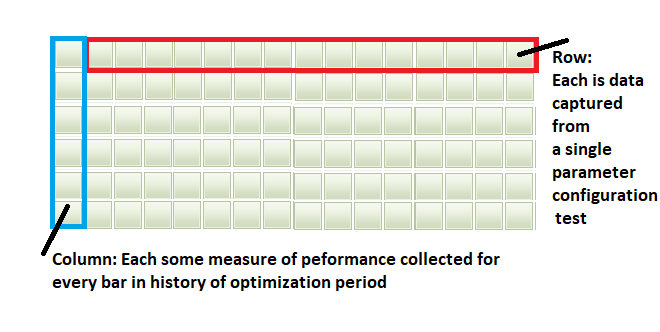
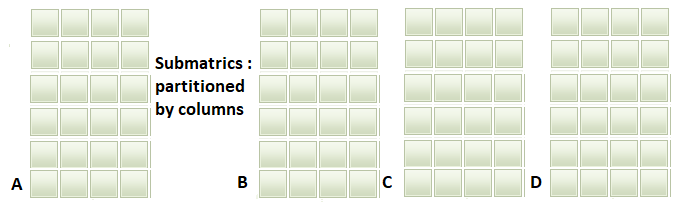
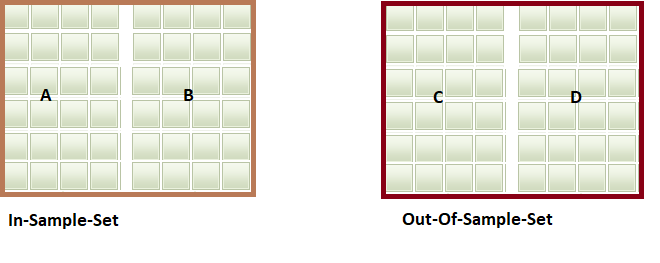
Im folgenden Abschnitt sehen wir uns an, wie wir die soeben beschriebenen Schritte in Code umsetzen können. Wir befassen uns in erster Linie mit dem Kern der CSCV-Methode und überlassen den Code für die Datenerfassung dem Beispiel, das am Ende des Artikels gezeigt wird.
MQL5-Implementierung von CSCV
Die in CSCV.mqh enthaltene Klasse Ccsvc kapselt den CSCV-Algorithmus. CSCV.mqh beginnt mit der Aufnahme der Unterfunktionen der Standardbibliothek für Mathematik von MQL5.
//+------------------------------------------------------------------+ //| CSCV.mqh | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #include <Math\Stat\Math.mqh>
Der Zeiger auf die Funktion Criterion definiert einen Funktionstyp, der zur Berechnung der Leistungskennzahl aus einem Array als Eingabe verwendet wird.
#include <Math\Stat\Math.mqh> typedef double (*Criterion)(const double &data[]); // function pointer for performance criterion
Ccscv hat nur eine Methode, mit der sich die Nutzer vertraut machen müssen. Sie kann aufgerufen werden, nachdem eine Instanz der Klasse initialisiert wurde. Diese Methode „CalculateProbabilty()“ gibt bei Erfolg den PBO-Wert zurück. Wenn ein Fehler auftritt, gibt die Methode -1 zurück. Es folgt eine Beschreibung der Eingabeparameter:
//+------------------------------------------------------------------+ //| combinatorially symmetric cross validation class | //+------------------------------------------------------------------+ class Cscv { ulong m_perfmeasures; //granular performance measures ulong m_trials; //number of parameter trials ulong m_combinations; //number of combinations ulong m_indices[], //array tracks combinations m_lengths[], //points to number measures for each combination m_flags []; //tracks processing of combinations double m_data [], //intermediary holding performance measures for current trial is_perf [], //in sample performance data oos_perf []; //out of sample performance data public: Cscv(void); //constructor ~Cscv(void); //destructor double CalculateProbability(const ulong blocks, const matrix &in_data,const Criterion criterion, const bool maximize_criterion); };
- Der erste Eingabeparameter ist „blocks“. Das entspricht der Anzahl der Sätze (N Sätze), in die die Spalten der Matrix unterteilt werden.
- „in_data“ ist eine Matrix mit so vielen Zeilen wie die Gesamtzahl der für einen Optimierungslauf getesteten Parametervarianten und so vielen Spalten wie Balken, die die Gesamtheit der für die Optimierung ausgewählten Historie ausmachen.
- „criterion“ ist ein Funktionszeiger auf eine Routine, die zur Berechnung der gewählten Leistungskennzahl verwendet wird. Die Routine sollte einen Wert vom Typ double zurückgeben und als Eingabe ein Array vom Typ double annehmen.
- „maximize_criterion“ ist mit „criterion“ insofern verwandt, als es die Angabe ermöglicht, ob die beste der ausgewählten Leistungskennzahlen durch einen Höchst- oder Mindestwert definiert ist. Wird beispielsweise der Drawdown als Leistungskriterium verwendet, wäre der beste Wert der niedrigste, sodass „maximize_criterion“ falsch sein sollte.
double Cscv::CalculateProbability(const ulong blocks, const matrix &in_data,const Criterion criterion, const bool maximize_criterion) { //---get characteristics of matrix m_perfmeasures = in_data.Cols(); m_trials = in_data.Rows(); m_combinations=blocks/2*2; //---check inputs if(m_combinations<4) m_combinations = 4; //---memory allocation if(ArrayResize(m_indices,int(m_combinations))< int(m_combinations)|| ArrayResize(m_lengths,int(m_combinations))< int(m_combinations)|| ArrayResize(m_flags,int(m_combinations))<int(m_combinations) || ArrayResize(m_data,int(m_perfmeasures))<int(m_perfmeasures) || ArrayResize(is_perf,int(m_trials))<int(m_trials) || ArrayResize(oos_perf,int(m_trials))<int(m_trials)) { Print("Memory allocation error ", GetLastError()); return -1.0; } //---
In „ComputeProbability“ ermitteln wir zunächst die Anzahl der Spalten und Zeilen der „in_data“-Matrix und überprüfen „blocks“, um sicherzustellen, dass es sich um eine gerade Zahl handelt. Die Ermittlung der Abmessungen der Eingabematrix ist notwendig, um die Größe der internen Instanzpuffer zu bestimmen.
int is_best_index ; //row index of oos_best parameter combination double oos_best, rel_rank ; //oos_best performance and relative rank values //--- ulong istart = 0 ; for(ulong i=0 ; i<m_combinations ; i++) { m_indices[i] = istart ; // Block starts here m_lengths[i] = (m_perfmeasures - istart) / (m_combinations-i) ; // It contains this many cases istart += m_lengths[i] ; // Next block } //--- ulong num_less =0; // Will count the number of time OOS of oos_best <= median OOS, for prob for(ulong i=0; i<m_combinations; i++) { if(i<m_combinations/2) // Identify the IS set m_flags[i]=1; else m_flags[i]=0; // corresponding OOS set } //---
Sobald der Speicher für die internen Puffer erfolgreich zugewiesen wurde, beginnen wir mit den Vorbereitungen für die Partitionierung der Spalten gemäß „m_combinations“. Das Array „m_indices“ wird mit den Anfangsspaltenindizes für eine bestimmte Partition gefüllt, und „m_lengths“ enthält die entsprechende Anzahl von Spalten, die in jeder Partition enthalten sind. „num_less“ enthält die Anzahl der Fälle, in denen die Out-of-Sample-Leistung des besten Versuchs innerhalb der Stichprobe geringer ist als die Out-of-Sample-Leistung der übrigen Versuche. „m_flags“ ist ein ganzzahliges Array, dessen Werte entweder 1 oder 0 enthalten können. Dies hilft bei der Identifizierung von Teilmengen, die als in-sample und out-of-sample bezeichnet werden, während wir alle möglichen Kombinationen durchgehen.
ulong ncombo; for(ncombo=0; ; ncombo++) { //--- in sample performance calculated in this loop for(ulong isys=0; isys<m_trials; isys++) { int n=0; for(ulong ic=0; ic<m_combinations; ic++) { if(m_flags[ic]) { for(ulong i=m_indices[ic]; i<m_indices[ic]+m_lengths[ic]; i++) m_data[n++] = in_data.Flat(isys*m_perfmeasures+i); } } is_perf[isys]=criterion(m_data); } //--- out of sample performance calculated here for(ulong isys=0; isys<m_trials; isys++) { int n=0; for(ulong ic=0; ic<m_combinations; ic++) { if(!m_flags[ic]) { for(ulong i=m_indices[ic]; i<m_indices[ic]+m_lengths[ic]; i++) m_data[n++] = in_data.Flat(isys*m_perfmeasures+i); } } oos_perf[isys]=criterion(m_data); }
An diesem Punkt beginnt die Hauptschleife, die alle Kombinationen von In-Sample- und Out-of-Sample-Sets durchläuft. Zwei innere Schleifen werden verwendet, um die simulierte In-Sample- und Out-of-Sample-Leistung zu berechnen, indem die Funktion „criterion“ aufgerufen und dieser Wert in den Arrays „is_perf“ bzw. „oos_perf“ gespeichert wird.
//--- get the oos_best performing in sample index is_best_index = maximize_criterion?ArrayMaximum(is_perf):ArrayMinimum(is_perf); //--- corresponding oos performance oos_best = oos_perf[is_best_index];
Der Index des besten Leistungswerts im Array „is_perf“ wird gemäß dem „maximize_criterion“ berechnet. Der entsprechende Wert für die Leistung außerhalb der Stichprobe wird in der Variablen „oos_best“ gespeichert.
//--- count oos results less than oos_best int count=0; for(ulong isys=0; isys<m_trials; isys++) { if(isys == ulong(is_best_index) || (maximize_criterion && oos_best>=oos_perf[isys]) || (!maximize_criterion && oos_best<=oos_perf[isys])) ++count; }
Wir durchlaufen das Array „oos_perf“ und zählen, wie oft „oos_best“ gleich oder besser ist.
//--- calculate the relative rank rel_rank = double (count)/double (m_trials+1); //--- cumulate num_less if(rel_rank<=0.5) ++num_less;
Die Anzahl wird verwendet, um den relativen Rang zu berechnen. Schließlich wird „num_less“ kumuliert, wenn der berechnete relative Rang kleiner als 0,5 ist.
//---move calculation on to new combination updating flags array along the way int n=0; ulong iradix; for(iradix=0; iradix<m_combinations-1; iradix++) { if(m_flags[iradix]==1) { ++n; if(m_flags[iradix+1]==0) { m_flags[iradix]=0; m_flags[iradix+1]=0; for(ulong i=0; i<iradix; i++) { if(--n>0) m_flags[i]=1; else m_flags[i]=0; } break; } } }
Die letzte innere Schleife dient dazu, die Iteration zum nächsten Satz von In-Sample- und Out-of-Sample-Datensätzen zu verschieben.
if(iradix == m_combinations-1) { ++ncombo; break; } } //--- final result return double(num_less)/double(ncombo); }
Der letzte if-Block bestimmt, wann die äußere Hauptschleife verlassen werden soll, bevor der endgültige PBO-Wert durch Division von „num_less“ durch „ncombo“ zurückgegeben wird.
Bevor wir uns ein Beispiel für die Anwendung der Klasse Ccscv ansehen. Wir müssen uns etwas Zeit nehmen, um uns anzusehen, was dieser Algorithmus über eine bestimmte Strategie verrät.
Interpretation der Ergebnisse
Der von uns implementierte CSCV-Algorithmus gibt eine einzige Metrik aus. Nämlich die PBO. Nach David H. Bailey et al. definiert der PBO die Wahrscheinlichkeit, dass der Parametersatz, der während der Optimierung auf einem In-Sample-Datensatz die beste Leistung erbracht hat, auf einem Out-of-Sample-Datensatz eine Leistung erreicht, die unter dem Median der Leistungsergebnisse mit nicht optimalen Parametersätzen liegt.
Je größer dieser Wert ist, desto größer ist das Ausmaß der Überanpassung. Mit anderen Worten, es besteht eine größere Wahrscheinlichkeit, dass die Strategie bei der Anwendung außerhalb der Stichprobe schlechter abschneidet. Ein idealer PBO würde unter 0,1 liegen.
Der erreichte PBO-Wert hängt hauptsächlich von der Vielfalt der während der Optimierung erprobten Parametersätze ab. Es muss sichergestellt werden, dass die gewählten Parametersätze repräsentativ für diejenigen sind, die in der realen Welt angewendet werden könnten. Die absichtliche Einbeziehung von Parameterkombinationen, deren Wahl unwahrscheinlich ist oder die von Kombinationen dominiert werden, die nahe oder weit von ihrem Optimum entfernt sind, verfälscht nur das Endergebnis.
Ein Beispiel
In diesem Abschnitt stellen wir die Anwendung der Ccscv-Klasse auf einen Expert Advisor vor. Der Moving Average Expert Advisor, der mit jeder MetaTrader 5-Installation ausgeliefert wird, wird geändert, um die Berechnung des PBO zu ermöglichen. Um die CSCV-Methode effektiv zu implementieren, werden wir Frames verwenden, um Balken für Balken die Daten zu sammeln. Wenn die Optimierung abgeschlossen ist, werden die Daten aus jedem Durchgang in einer Matrix zusammengefasst. Das bedeutet, dass zumindest die Ereignisbehandlungen von „OnTester()“ und „OnTesterDeinit()“ zum Code des EA hinzugefügt werden sollten. Schließlich sollte der ausgewählte EA einer vollständigen Optimierung unterzogen werden, indem die Option „Langsamer vollständiger Algorithmus“ im Strategy Tester verwendet wird.
//+------------------------------------------------------------------+ //| MovingAverage_CSCV_DemoEA.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include <Returns.mqh> #include <CSCV.mqh> #include <Trade\Trade.mqh>
Wir beginnen mit der Einbindung von CSCV.mqh und Returns.mqh, die die Definition der Klasse CReturns enthält. CReturns ist nützlich für die Sammlung der Ergebnisse Balken für Balken, mit denen wir Sharpe Ratio, die mittlere Rendite oder die Gesamtrendite berechnen können. Wir können eines dieser beiden Kriterien für die Bestimmung der optimalen Leistung verwenden. Wie bereits am Anfang des Artikels erwähnt. Die gewählte Leistungskennzahl spielt keine Rolle, sie kann beliebig verwendet werden.
sinput uint NumBlocks = 4;
Es wird ein neuer, nicht optimierbarer Parameter mit der Bezeichnung „NumBlocks“ hinzugefügt, der die Anzahl der vom CSCV-Algorithmus zu verwendenden Partitionen angibt. Später werden wir sehen, wie sich eine Änderung dieses Parameters auf den PBO auswirkt.
CReturns colrets;
ulong numrows,numcolumns; Eine Instanz von CReturns wird global deklariert. Hier werden auch „numrows“ und „numcolumns“ deklariert, die wir zur Initialisierung einer Matrix verwenden werden.
//+------------------------------------------------------------------+ //| TesterInit function | //+------------------------------------------------------------------+ void OnTesterInit() { numrows=1; //--- string name="MaximumRisk"; bool enable; double par1,par1_start,par1_step,par1_stop; ParameterGetRange(name,enable,par1,par1_start,par1_step,par1_stop); if(enable) numrows*=ulong((par1_stop-par1_start)/par1_step)+1; //--- name="DecreaseFactor"; double par2,par2_start,par2_step,par2_stop; ParameterGetRange(name,enable,par2,par2_start,par2_step,par2_stop); if(enable) numrows*=ulong((par2_stop-par2_start)/par2_step)+1; //--- name="MovingPeriod"; long par3,par3_start,par3_step,par3_stop; ParameterGetRange(name,enable,par3,par3_start,par3_step,par3_stop); if(enable) numrows*=ulong((par3_stop-par3_start)/par3_step)+1; //--- name="MovingShift"; long par4,par4_start,par4_step,par4_stop; ParameterGetRange(name,enable,par4,par4_start,par4_step,par4_stop); if(enable) numrows*=ulong((par4_stop-par4_start)/par4_step)+1; }
Wir fügen die Ereignisbehandlung durch „OnTesterInit()“ hinzu, in die Anzahl der zu testenden Parametersätze gezählt wird.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- colrets.OnNewTick(); //--- if(SelectPosition()) CheckForClose(); else CheckForOpen(); //--- }
In der Ereignisbehandlung von „OnTick()“ rufen wir die Methode „OnNewtick()“ von CReturns auf.
//+------------------------------------------------------------------+ //| Tester function | //+------------------------------------------------------------------+ double OnTester() { //--- double ret=0.0; double array[]; //--- if(colrets.GetReturns(ENUM_RETURNS_ALL_BARS,array)) { //--- ret = MathSum(array); if(!FrameAdd(IntegerToString(MA_MAGIC),long(MA_MAGIC),double(array.Size()),array)) { Print("Could not add frame ", GetLastError()); return 0; } //--- } //---return return(ret); }
Innerhalb von „OnTester()“ sammeln wir das Array der Ergebnisse mit unserer global deklarierten CReturns-Instanz. Und schließlich fügen wir diese Daten mit einem Aufruf von „FrameAdd()“ zu einem Rahmen hinzu.
//+------------------------------------------------------------------+ //| TesterDeinit function | //+------------------------------------------------------------------+ void OnTesterDeinit() { //---prob value numcolumns = 0; double probability=-1; int count_frames=0; matrix data_matrix=matrix::Zeros(numrows,1); vector addvector=vector::Zeros(1); Cscv cscv; //---calculate if(FrameFilter(IntegerToString(MA_MAGIC),long(MA_MAGIC))) { //--- ulong pass; string frame_name; long frame_id; double passed_value; double passed_data[]; //--- while(FrameNext(pass,frame_name,frame_id,passed_value,passed_data)) { //--- if(!numcolumns) { numcolumns=ulong(passed_value); addvector.Resize(numcolumns); data_matrix.Resize(numrows,numcolumns); } //--- if(addvector.Assign(passed_data)) { data_matrix.Row(addvector,pass); count_frames++; } //--- } } else Print("Error retrieving frames ", GetLastError()); //---results probability = cscv.CalculateProbability(NumBlocks,data_matrix,MathSum,true); //---output results Print("cols ",data_matrix.Cols()," rows ",data_matrix.Rows()); Print("Number of passes processed: ", count_frames, " Probability: ",probability); //--- }
In „OnTesterDeinit()“ finden wir den Großteil der am EA vorgenommenen Ergänzungen. Hier deklarieren wir eine Instanz von Ccscv zusammen mit Variablen vom Typ Matrix und Vektor. Wir gehen in einer Schleife durch alle Bilder und übertragen ihre Daten in die Matrix. Der Vektor wird als Vermittler verwendet, um für jedes Bild eine neue Datenzeile hinzuzufügen.
Die Methode „CalculateProbability()“ von Ccscv wird aufgerufen, bevor die Ergebnisse auf der Registerkarte „Experten“ des Terminals ausgegeben werden. In diesem Beispiel haben wir die Funktion „MathSum()“ an die Methode übergeben, was bedeutet, dass die Gesamtrendite zur Bestimmung des optimalen Parametersatzes verwendet wird. Die Ausgabe zeigt auch die Anzahl der verarbeiteten Bilder an, um zu bestätigen, dass alle Daten erfasst wurden.
Hier sind einige Ergebnisse der Ausführung unseres modifizierten EA mit verschiedenen Einstellungen. In unterschiedlichen Zeiträumen. Das PBO-Ergebnis wird auf der Registerkarte Experten des Terminals ausgegeben.
MovingAverage_CSCV_DemoEA (EURUSD,H1) Number of passes processed: 23520 Probability: 0.3333333333333333
| NumBlocks | TimeFrame | Wahrscheinlichkeit einer Backtest-Überanpassung |
|---|---|---|
| 4 | Wöchentlich | 0.3333 |
| 4 | Täglich | 0.6666 |
| 4 | 12 Stündlich | 0.6666 |
| 8 | Wöchentlich | 0.2 |
| 8 | Täglich | 0.8 |
| 8 | 12 Stündlich | 0.6 |
| 16 | Wöchentlich | 0.4444 |
| 16 | Täglich | 0.8888 |
| 16 | 12 Stündlich | 0.6666 |
Das beste Ergebnis, das wir erhalten haben, ist ein PBO von 0,2. Die anderen waren weitaus schlimmer. Dies zeigt, dass es sehr wahrscheinlich ist, dass dieser EA eine schlechtere Leistung erbringt, wenn er auf einen beliebigen Datensatz außerhalb der Stichprobe angewendet wird. Wir können auch sehen, dass diese schlechten PBO-Werte auch über verschiedene Zeiträume hinweg bestehen bleiben. Die Anpassung der Anzahl der in der Analyse verwendeten Partitionen führte nicht zu einer Verbesserung des ursprünglich schlechten Ergebnisses.
Schlussfolgerung
Wir haben die Implementierung der kombinatorisch symmetrischen Kreuzvalidierungstechnik demonstriert, um die Überanpassung nach einem Optimierungsverfahren zu bewerten. Im Vergleich zur Verwendung von MonteCarlo-Permutationen zur Quantifizierung der Überanpassung hat CSCV den Vorteil, dass es relativ schnell ist.
Außerdem werden die verfügbaren historischen Daten effizient genutzt. Wie dem auch sei, es gibt potenzielle Fallstricke, derer sich die Praktiker bewusst sein sollten. Die Zuverlässigkeit dieser Methode hängt allein von den zugrunde liegenden Daten ab.
Insbesondere der Umfang der getesteten Parametervariationen. Die Verwendung weniger Parametervariationen kann zu einer Unterschätzung der Überanpassung führen, während die Einbeziehung einer großen Anzahl unrealistischer Parameterkombinationen zu Überschätzungen führen kann. Zu beachten ist auch der für den Optimierungszeitraum gewählte Zeitrahmen. Dies kann sich auf die Wahl der auf eine Strategie angewandten Parameter auswirken. Das bedeutet, dass der endgültige PBO in verschiedenen Zeiträumen variieren kann. Generell sollten möglichst viele sinnvolle Parameterkonfigurationen in den Test einbezogen werden.
Ein bemerkenswerter Nachteil dieses Tests ist, dass er nicht ohne weiteres auf EAs angewendet werden kann, deren Quellcode nicht zugänglich ist. Theoretisch wäre es möglich, einzelne Backtests für jede mögliche Parameterkonfiguration durchzuführen, aber das führt zu der gleichen Mühsal wie der Einsatz von Monte-Carlo-Methoden.
Für eine gründlichere Beschreibung des CSCV und der Interpretation des PBO sollten die Leser das Originalpapier lesen; der Link ist im zweiten Absatz dieses Artikels angegeben. Die Quellcodes aller im Artikel erwähnten Programme sind unten beigefügt.
| Dateiname | Beschreibung |
|---|---|
| Mql5\Include\Returns.mqh | Definiert die Klasse CReturns zur Erfassung von Ergebnis- oder Kapitaldaten in Echtzeit. |
| Mql5\Include\CSCV.mqh | Enthält die Definition der Klasse Ccscv, die die kombinatorisch symmetrische Kreuzvalidierung implementiert. |
| Mql5\Experts\MovingAverage_CSCV_DemoEA.mq5 | Modifizierter gleitender Durchschnitt EA zur Demonstration der Anwendung der Ccscv-Klasse. |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/13743
Modifizierter Grid-Hedge EA in MQL5 (Teil I): Erstellung eines einfachen Hedge EA
Entwurfsmuster in der Softwareentwicklung und MQL5 (Teil 2): Strukturelle Muster
Wie man einen einfachen Multi-Currency Expert Advisor mit MQL5 erstellt (Teil 5): Die Bollinger Bänder mit dem Keltner-Kanal — Indikatoren Signal
Einführung in MQL5 (Teil 1): Ein Leitfaden für Einsteiger in den algorithmischen Handel
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Sehen Sie sich den neuen Artikel an: Kombinatorisch symmetrische Kreuzvalidierung in MQL5.
Autor: Francis Dube
Nur neugierig, ob jemand Glück mit dieser Methode hatte? Ich habe versucht, es auf einem m5 Backtest über 10 Jahre mit einem Forward bei 1/2 zu implementieren und es ist wahnsinnig langsam, würde gerne wissen, ob jemand einen Weg gefunden hat, es so zu codieren, dass es ein wenig schneller ist? sicher wäre es interessant, diese Methode auszuprobieren.