Combinatorially Symmetric Cross Validation In MQL5

Introduction

Sometimes when creating an automated strategy, we start out with an outline of rules based on arbitrary indicators, that need to be refined in some way. This process of refinement involves running multiple tests with different parameter values of the chosen indicators. By doing so we are able to find the indicator values that maximize profit or any other metric we care about. The problem with this practice is that we introduce a certain amount of optimistic bias because of the prevalent noise in financial time series. A phenomenon known as overfitting.

Whilst overfitting is something that cannot be avoided, the extent to which it manifests can vary from one strategy to another. It would therefore be helpful to be able to determine the degree to which it has occured. Combinatorially Symmetrical Cross Validation (CSCV) is a method presented in an academic paper "The Probability of Backtest Overfitting", written by David H. Bailey et al. It can be used to estimate the extent of overfitting when optimizing parameters of a strategy.

In this article we will demonstrate the implementation of CSCV in MQL5 and show how it can be applied to an Expert Advisor (EA) through an example.

The CSCV method

In this section we describe the precise method of CSCV step by step, starting with preliminary aspects regarding the data that needs to be collected in relation to the performance criteria chosen.

The CSCV method can be applied in different domains outside of strategy development and analysis, but for this article, we stick to the context of strategy optimization. Where we have a strategy defined by a set of parameters that need to be fine tuned, by running numerous tests with varying parameter configurations.

Before embarking on any calculations we first need to make a decision in terms of what performance criteria we will use to asses the strategy. The CSCV method is flexible in that any performance metric can be used. From simple profit to ratio based metrics, it is of no consequence to CSCV.

The chosen performance criteria will also determine the underlying data that will be used in the calculations, this is the raw granular data that will be collected from all test runs. For example, if we decide to use the Sharpe ratio as our chosen performance measure, we would need to collect the bar by bar returns from each test run. If we were using simple profit, we would need the bar by bar profit or loss. Whats important, is to make sure that the amount of data collected for each run is consistent. There by ensuring we have a measure for each corresponding data point for all test runs.

1. The first step begins with data collection during optimization, as the different parameter variations are tested. 
   
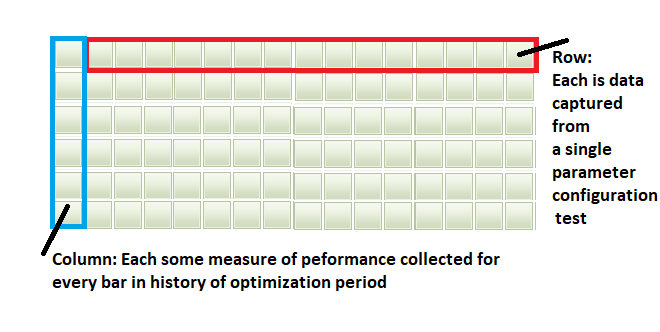
2. After optimization is completed, we pool all the data collected from the test runs into a matrix. Each row of this matrix will contain all the bar by bar performance values that will be used to calculate some trading performance metric for a corresponding test run.
   
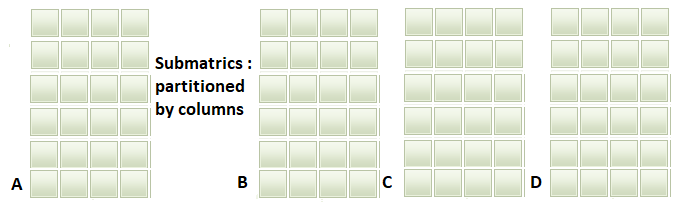
3. The matrix will have as many rows as parameter combinations trialed and the number of columns equal to the bars that make up the entire test period. These columns are then divided up into an arbitrary even number of sets. Say, N sets.
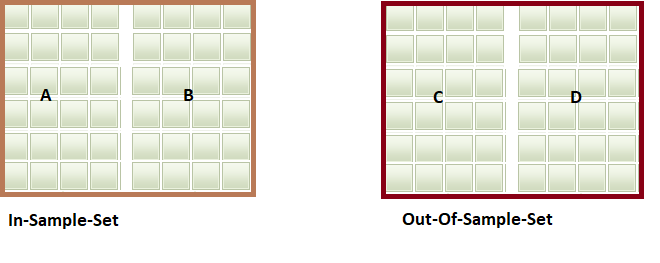
4. These sets are submatrices, that will be used to form combinations of groups of size N/2. Combinatorially, creating a total of N combinations taken N/2 at a time, ie N C n/2  . From each of these combinations we construct an In-Sample-Set (ISS) by putting together N/2 submatrices and also a corresponding Out-Of-Sample-Set (OOSS) from the remaining submatrices not included in the ISS.
   
5. For each row of the ISS and OOSS matrices we calculate the corresponding performance metric. And note the row in the ISS matrix with the best performance. Which represents the optimal parameter configuration. The corresponding row in the OOSS matrix is used to compute the relative rank by counting the number of out-of-sample parameter trials with inferior performance relative to that attained using the optimal parameter configuration. And presenting this count as a fraction of all parameter sets tested.
   
6. As we traverse all combinations we cumulate the number of relative rank values less than or equal to 0.5. It is the number of out-of-sample parameter configurations whose performance is below that observed using the optimal parameter set. Once all combinations are processed this number is presented as a fraction of all combinations + 1. Representing the Probability of Backtest Overfitting (PBO).
   

 Below is a visualization of the steps just described when N = 4.

In the section that follows, take a look at how we can implement the steps just described in code. We deal primarily with the core CSCV method and leave the code relating to data collection to the example that will be demonstrated towards the end of the article.

MQL5 Implementation of CSCV

The Ccsvc class contained in CSCV.mqh encapsulates the CSCV algorithm. CSCV.mqh begins with the inclusion of the subfunctions of MQL5's Mathematics standard library.

//+------------------------------------------------------------------+
//|                                                         CSCV.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include <Math\Stat\Math.mqh>

The Criterion function pointer defines a function type used to calculate the performance metric given an array as input.

#include <Math\Stat\Math.mqh>
typedef double (*Criterion)(const double &data[]); // function pointer for performance criterion

Ccscv only has one method that users need to familiarize themselves with. It can be called after an instance of the class is initialized. This method, "CalculateProbabilty()" returns the PBO value on success. If an error is encountered the method returns -1. A description of its input parameters follows:

//+------------------------------------------------------------------+
//| combinatorially symmetric cross validation class                 |
//+------------------------------------------------------------------+
class Cscv
  {
   ulong             m_perfmeasures;         //granular performance measures
   ulong             m_trials;               //number of parameter trials
   ulong             m_combinations;         //number of combinations

   ulong  m_indices[],           //array tracks combinations
          m_lengths[],           //points to number measures for each combination
          m_flags  [];           //tracks processing of combinations
   double m_data   [],           //intermediary holding performance measures for current trial
          is_perf  [],           //in sample performance data
          oos_perf [];           //out of sample performance data


public:
                     Cscv(void);                   //constructor
                    ~Cscv(void);                  //destructor

   double            CalculateProbability(const ulong blocks, const matrix &in_data,const Criterion criterion, const bool maximize_criterion);
  };

• The first input parameter is "blocks". It corresponds to the number of sets (N sets), that the columns of the matrix will be partitioned into.

• "in_data" is a matrix with as many rows as the total number of parameter variations trialed for an optimization run and as many columns as bars that make up the entirety of the history selected for optimization.

• "criterion" is a function pointer to a routine that will be used to calculate the chosen performance metric. The routine should return a value of type double and take as input an array of type double.
•  "maximize_criterion" is related to "criterion" in that  it allows specifying whether the best of the selected performance metric is defined by a maximum or minimum value. For example if using drawdown as a performance criteria, the best would be the lowest value, so "maximize_criterion" should be false.

double Cscv::CalculateProbability(const ulong blocks, const matrix &in_data,const Criterion criterion, const bool maximize_criterion)
  {
//---get characteristics of matrix
   m_perfmeasures = in_data.Cols();
   m_trials = in_data.Rows();
   m_combinations=blocks/2*2;
//---check inputs
   if(m_combinations<4)
      m_combinations = 4;
//---memory allocation
   if(ArrayResize(m_indices,int(m_combinations))< int(m_combinations)||
      ArrayResize(m_lengths,int(m_combinations))< int(m_combinations)||
      ArrayResize(m_flags,int(m_combinations))<int(m_combinations)   ||
      ArrayResize(m_data,int(m_perfmeasures))<int(m_perfmeasures)    ||
      ArrayResize(is_perf,int(m_trials))<int(m_trials)               ||
      ArrayResize(oos_perf,int(m_trials))<int(m_trials))
     {
      Print("Memory allocation error ", GetLastError());
      return -1.0;
     }
//---

In "ComputeProbability" we begin by getting the number of columns and rows of "in_data" matrix and checking "blocks" to ensure that it is an even number. Getting the dimensions of the input matrix is necessary so as to determine the size of internal instance buffers.

   int is_best_index ;               //row index of oos_best parameter combination
   double oos_best, rel_rank ;   //oos_best performance and relative rank values
//---
   ulong istart = 0 ;
   for(ulong i=0 ; i<m_combinations ; i++)
     {
      m_indices[i] = istart ;        // Block starts here
      m_lengths[i] = (m_perfmeasures - istart) / (m_combinations-i) ; // It contains this many cases
      istart += m_lengths[i] ;       // Next block
     }
//---
   ulong num_less =0;                    // Will count the number of time OOS of oos_best <= median OOS, for prob
   for(ulong i=0; i<m_combinations; i++)
     {
      if(i<m_combinations/2)        // Identify the IS set
         m_flags[i]=1;
      else
         m_flags[i]=0;               // corresponding OOS set
     }
//---

Once memory is successfully allocated for the internal buffers we begin to prepare for the partitioning of colums according to "m_combinations". The "m_indices" array is filled with starting column indexes for a particular partition and "m_lengths" will hold the corresponding number of columns contained in each one. "num_less" maintains the count of the number of times the out-of-sample performance of the in-sample best trial is less than the out-of-sample performance of the rest.  "m_flags"  is an integer array whose values can contain either 1 or 0. This helps to identify subsets designated as in-sample and out-of-sample as we iterate through all possible combinations.

ulong ncombo;
   for(ncombo=0; ; ncombo++)
     {
      //--- in sample performance calculated in this loop
      for(ulong isys=0; isys<m_trials; isys++)
        {
         int n=0;
         for(ulong ic=0; ic<m_combinations; ic++)
           {
            if(m_flags[ic])
              {
               for(ulong i=m_indices[ic]; i<m_indices[ic]+m_lengths[ic]; i++)
                  m_data[n++] = in_data.Flat(isys*m_perfmeasures+i);
              }
           }
         is_perf[isys]=criterion(m_data);
        }
      //--- out of sample performance calculated here
      for(ulong isys=0; isys<m_trials; isys++)
        {
         int n=0;
         for(ulong ic=0; ic<m_combinations; ic++)
           {
            if(!m_flags[ic])
              {
               for(ulong i=m_indices[ic]; i<m_indices[ic]+m_lengths[ic]; i++)
                  m_data[n++] = in_data.Flat(isys*m_perfmeasures+i);
              }
           }
         oos_perf[isys]=criterion(m_data);
        }

At this point the main loop that iterates through all combinations of in-sample and out-of-sample sets begins. Two inner loops are used to calculate the simulated in-sample and out-of-sample performance by calling the "criterion" function and saving this value in "is_perf" and "oos_perf" arrays respectively.

//--- get the oos_best performing in sample index
      is_best_index = maximize_criterion?ArrayMaximum(is_perf):ArrayMinimum(is_perf);
      //--- corresponding oos performance
      oos_best = oos_perf[is_best_index];

The index of the best performance value in "is_perf" array is calculated according to  "maximize_criterion". The corresponding out-of-sample performance value is saved to the "oos_best" variable.

//--- count oos results less than oos_best
      int count=0;
      for(ulong isys=0; isys<m_trials; isys++)
        {
         if(isys == ulong(is_best_index) || (maximize_criterion && oos_best>=oos_perf[isys]) || (!maximize_criterion && oos_best<=oos_perf[isys]))
            ++count;
        }

We loop through the "oos_perf" array and count the number of times "oos_best" is equal or better.

//--- calculate the relative rank
      rel_rank = double (count)/double (m_trials+1);
      //--- cumulate num_less
      if(rel_rank<=0.5)
         ++num_less;

The count is used to calculate the relative rank. Finally "num_less" is cumulated if the computed relative rank is less than 0.5.

//---move calculation on to new combination updating flags array along the way
      int n=0;
      ulong iradix;
      for(iradix=0; iradix<m_combinations-1; iradix++)
        {
         if(m_flags[iradix]==1)
           {
            ++n;
            if(m_flags[iradix+1]==0)
              {
               m_flags[iradix]=0;
               m_flags[iradix+1]=0;
               for(ulong i=0; i<iradix; i++)
                 {
                  if(--n>0)
                     m_flags[i]=1;
                  else
                     m_flags[i]=0;
                 }
               break;
              }
           }
        }

The final inner loop is used to move the iteration to the next set of in-sample and out-of-sample data sets.

if(iradix == m_combinations-1)
        {
         ++ncombo;
         break;
        }
     }
//--- final result
   return double(num_less)/double(ncombo);
  }

The last if block determines when to break out of the main outer loop before returning the final PBO value by dividing "num_less" by "ncombo".

Before we look at an example of how to apply the Ccscv class. We need to take some time to go over what this algorithm reveals about a particular strategy.

Interpreting the results

The CSCV algorithm we have implemented outputs a single metric. Namely the PBO. According to David H. Bailey et al, the PBO, defines the probability that the parameter set that produced the best the performance during optimization on an in-sample data set will attain performance that is below the median of performance results using non optimal parameter sets on an out-of-sample data set.

The larger this value is the more significant the degree to which overfitting has occured. In other words, there is a greater possibility that the strategy will underperform when applied out-of-sample. An ideal PBO would be below 0.1.

The PBO value attained will mainly depend on the variety of parameter sets trialed during optimization. It is important to ensure that the parameter sets chosen are representative of those that could be realistically applied in real world use. Deliberately including parameter combinations that are unlikely to be chosen, or are dominated by combinations close or far away from their optimal will only taint the final result.

An example

In this section we present the application of the Ccscv class to an Expert Advisor. The Moving Average Expert Advisor shipped with every MetaTrader 5 install will be modified to enable the calculation of PBO. To effectively implement the CSCV method we will employ frames to collect  bar-by-bar data. When optimization is completed data from each pass will be collated into a matrix. This means that at the very least , the handlers and "OnTesterDeinit()" should be added to the EA's code. Lastly, the selected EA should be subjected to full optimization using the slow complete algorithm option in the Strategy Tester.  

//+------------------------------------------------------------------+
//|                                    MovingAverage_CSCV_DemoEA.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <Returns.mqh>
#include <CSCV.mqh>
#include <Trade\Trade.mqh>

We begin by including CSCV.mqh and Returns.mqh which contains the definition of the CReturns class. CReturns will be useful for the collection of bar by bar returns, with which we can compute the Sharpe Ratio, mean return or the total return. We can use either of these as the criteria used to determine optimal performance. As already mentioned early on in the article. The performance metric chosen does not matter, any can be used.

sinput uint  NumBlocks          = 4;

A new non-optimizable parameter is added, called "NumBlocks", which specifies the number of partitions to be employed by the CSCV algorithm. Later on we will see a change to this parameter impacts the PBO.  

CReturns colrets;
ulong numrows,numcolumns;

An instance of CReturns is declared globally. "numrows" and "numcolumns" are declared here as well, which we will use to initialize a matrix.

//+------------------------------------------------------------------+
//| TesterInit function                                              |
//+------------------------------------------------------------------+
void OnTesterInit()
  {
   numrows=1;
//---
   string name="MaximumRisk";
   bool enable;
   double par1,par1_start,par1_step,par1_stop;
   ParameterGetRange(name,enable,par1,par1_start,par1_step,par1_stop);
   if(enable)
      numrows*=ulong((par1_stop-par1_start)/par1_step)+1;

//---
   name="DecreaseFactor";
   double par2,par2_start,par2_step,par2_stop;
   ParameterGetRange(name,enable,par2,par2_start,par2_step,par2_stop);
   if(enable)
      numrows*=ulong((par2_stop-par2_start)/par2_step)+1;

//---
   name="MovingPeriod";
   long par3,par3_start,par3_step,par3_stop;
   ParameterGetRange(name,enable,par3,par3_start,par3_step,par3_stop);
   if(enable)
      numrows*=ulong((par3_stop-par3_start)/par3_step)+1;

//---
   name="MovingShift";
   long par4,par4_start,par4_step,par4_stop;
   ParameterGetRange(name,enable,par4,par4_start,par4_step,par4_stop);
   if(enable)
      numrows*=ulong((par4_stop-par4_start)/par4_step)+1;
  }

We add the  "OnTesterInit()" handler, within which we count the number of parameter sets that will be tested.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
   colrets.OnNewTick();
//---
   if(SelectPosition())
      CheckForClose();
   else
      CheckForOpen();
//---
  }

In the "OnTick()" event handler we call the "OnNewtick()" method of CReturns.

//+------------------------------------------------------------------+
//| Tester function                                                  |
//+------------------------------------------------------------------+
double OnTester()
  {
//---
   double ret=0.0;
   double array[];
//---
   if(colrets.GetReturns(ENUM_RETURNS_ALL_BARS,array))
     {
      //---
      ret = MathSum(array);
      if(!FrameAdd(IntegerToString(MA_MAGIC),long(MA_MAGIC),double(array.Size()),array))
        {
         Print("Could not add frame ", GetLastError());
         return 0;
        }
      //---
     }
//---return
   return(ret);
  }

Inside  "OnTester()" we gather the array of returns with our globally declared CReturns instance. And finally add this data to a frame with a call to "FrameAdd()".

//+------------------------------------------------------------------+
//| TesterDeinit function                                            |
//+------------------------------------------------------------------+
void OnTesterDeinit()
  {
//---prob value
   numcolumns = 0;
   double probability=-1;
   int count_frames=0;
   matrix data_matrix=matrix::Zeros(numrows,1);
   vector addvector=vector::Zeros(1);
   Cscv cscv;
//---calculate
   if(FrameFilter(IntegerToString(MA_MAGIC),long(MA_MAGIC)))
     {
      //---
      ulong pass;
      string frame_name;
      long frame_id;
      double passed_value;
      double passed_data[];
      //---
      while(FrameNext(pass,frame_name,frame_id,passed_value,passed_data))
        {
         //---
         if(!numcolumns)
           {
            numcolumns=ulong(passed_value);
            addvector.Resize(numcolumns);
            data_matrix.Resize(numrows,numcolumns);
           }
         //---
         if(addvector.Assign(passed_data))
           {
            data_matrix.Row(addvector,pass);
            count_frames++;
           }
         //---
        }
     }
   else
      Print("Error retrieving frames ", GetLastError());
//---results
   probability = cscv.CalculateProbability(NumBlocks,data_matrix,MathSum,true);
//---output results
   Print("cols ",data_matrix.Cols()," rows ",data_matrix.Rows());
   Print("Number of passes processed: ", count_frames, " Probability: ",probability);
//---
  }

It is in "OnTesterDeinit()" that we find the bulk of the additions made to the EA. This is where we declare an instance of Ccscv along with matrix and vector type variables. We loop through all the frames and pass their data into the matrix. The vector is used as an intermediary to add a new row of data for each frame.

The "CalculateProbability()" method of Ccscv is called before outputing the results to the terminal's Experts tab. In this example we passed the "MathSum()" function to the method, meaning that the total return is used to determine the optimal parameter set. Output also gives an indication of the number of frames that were processed, to confirm that all the data was captured.

Here are some results from running our modified EA, with various settings. On different timeframes. The PBO result is output to the terminal's Experts tab.

MovingAverage_CSCV_DemoEA (EURUSD,H1)   Number of passes processed: 23520 Probability: 0.3333333333333333

NumBlocks	TimeFrame	Probability of Backtest Overfitting
4	Weekly	0.3333
4	Daily	0.6666
4	12 Hourly	0.6666
8	Weekly	0.2
8	Daily	0.8
8	12 Hourly	0.6
16	Weekly	0.4444
16	Daily	0.8888
16	12 Hourly	0.6666

The best result we got is a PBO of 0.2. The rest were far worse. This shows that it is very likely this EA will produce worse performance when applied on any out-of-sample data set. We can also see that these poor PBO scores persist across different timeframes as well. Adjusting the number of partitions used in the analysis did not improve the initially bad score.

Conclusion

We have demonstrated the implementation of the Combinatorially Symmetrical Cross Validation technique, for the evaluation of overfitting after an optimization procedure. Compared to using MonteCarlo permutations to quantify overfitting, CSCV  
has the advantage of being relatively quick. It also makes efficient use of available historical data. Be that as it may, there are potential pitfalls that practioners should be aware of. The reliability of this method depends solely on the undelying data used.

Particularly, the extent of parameter variations trialed. Using fewer parameter variations can lead to the under estimation of overfitting, at the same time including a large number of unrealistic parameter combinations can produce over estimates. Also something to take note of, is the timeframe selected for the optimization period. This can affect the choice of parameters applied to a strategy. Implying that the final PBO can vary across different timeframes. Generally speaking, as many viable parameter configurations as possible should be considered in the test.

One notable drawback of this test is that it cannot be easily applied to EA's whose source code is inaccessible. Theoretically it could be possible to run individual backtests for each possible parameter configuration, but that introduces the same tedium of employing Monte Carlo methods.
 
For a more thorough description of CSCV and the intepretation of the PBO, readers should see the original paper, the link is given in second paragraph of this article. The source code for all programs mentioned in the article is attached below.

File Name	Description
Mql5\Include\Returns.mqh	Defines CReturns class for collecting returns or equity data in real time
Mql5\Include\CSCV.mqh	Contains definition of Ccscv class which implements Combinatorially Symmetrical Cross Validation
Mql5\Experts\MovingAverage_CSCV_DemoEA.mq5	Modified Moving Average EA demonstrating the application of Ccscv class