Interessante Ideen, etwas, mit dem man arbeiten kann. :)
Danke für den Artikel!
Das ist seltsam, es stimmt nicht mit
überein.
Indikator hier
Vielleicht habe ich etwas missverstanden.
der Median stimmt nicht immer mit dem gleitenden Durchschnitt überein... vielmehr stimmen sie meistens nicht überein. Der Median ist eine starre Struktur (wenn Sie zum Beispiel Trendlinien entlang des Medians ziehen, erhalten Sie ein völlig anderes Bild).
Und die Nichtübereinstimmung kommt genau deshalb zustande, weil der Median sehr stabil ist, selbst bei kurzen Zeiträumen.... Versuchen Sie, Ihren Indikator mit der Bayesschen Glättung zu vergleichen
der Median ist nicht immer mit dem gleitenden Durchschnitt identisch.... vielmehr stimmen sie meistens nicht überein. Der Median der Mediane ist eine starre Struktur (wenn man z. B. Trendlinien entlang des Medians zeichnet, ergibt sich ein völlig anderes Bild)
Und die Nichtübereinstimmung kommt gerade deshalb zustande, weil der Median sehr stabil ist, selbst bei kurzen Zeiträumen.... Versuchen Sie, Ihren Indikator mit der Bayesschen Glättung zu vergleichen
Oh, ja, ich habe nicht aufgepasst.
Oh, ich sehe
Ich habe in den Code geschaut.
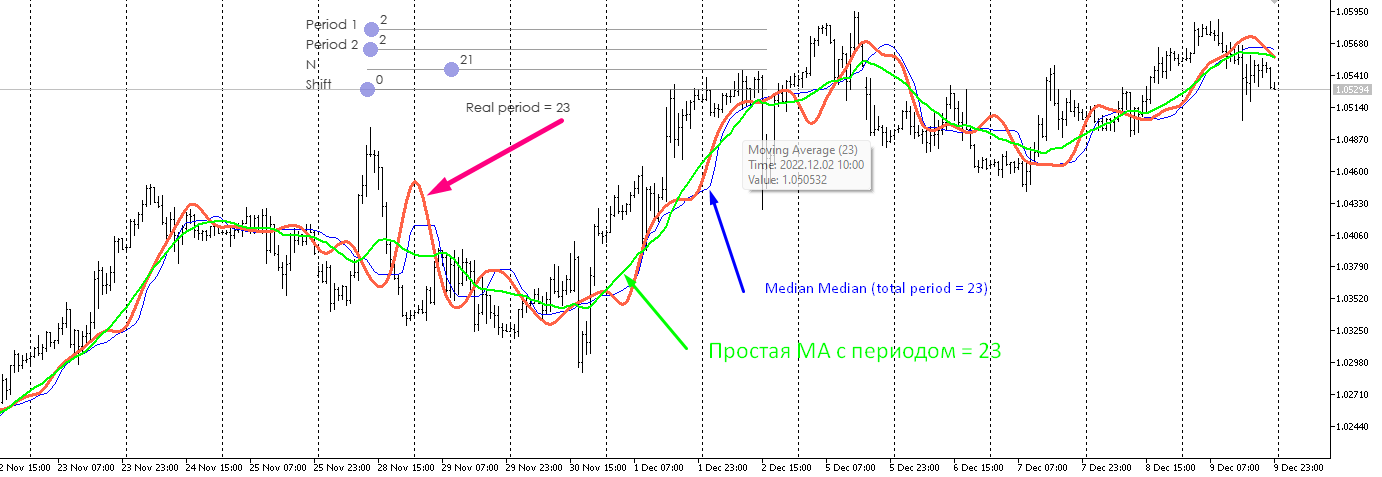
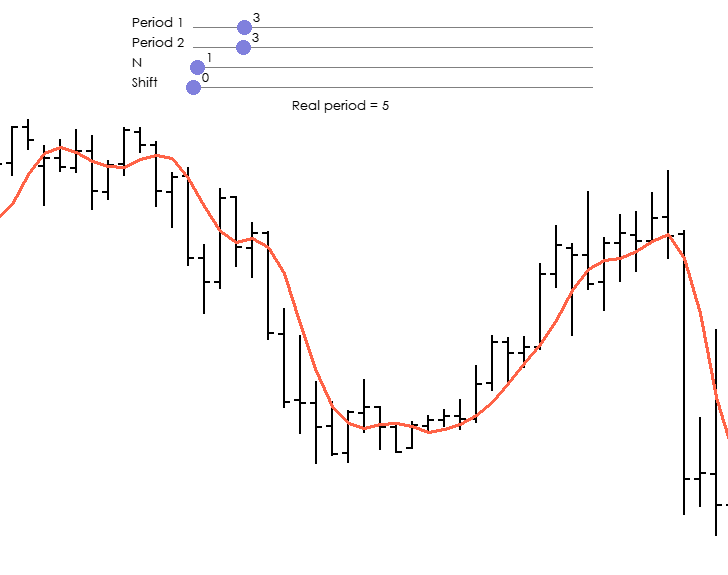
Es sagt eine Sache, aber die Grafik zeigt etwas anderes. Die Periode ist nicht 3 von 3, sondern 14 von 14.
D.h. der Indikator zeigt einen Wert aus den letzten 23 Werten an.
Ich habe ihn analysiert und mit anderen gleitenden Typen verglichen. Leider konnte ich keine Vorteile feststellen, trotz des deutlich höheren Rechenaufwands durch die Sortierung.
Die Schlussfolgerung ist dieselbe.
Alle Versuche irgendwelcher Manipulationen mit den vorangegangenen Daten einer bestimmten Größe (Periode) - addieren, multiplizieren, dividieren, gradieren, logarithmieren usw., um eine neue Linie zu erhalten - sind derzeit sinnlos, denn all diese zahlreichen Indikatoren (Linien) sagen das weitere Kursverhalten auf dem nächsten Balken (nach unten oder oben) mit einer Wahrscheinlichkeit voraus, die der Wahrscheinlichkeit von Kopf oder Zahl einer geworfenen Münze nahe kommt. Dies lässt sich leicht überprüfen und beweisen.
ah, ich sehe
Ich habe mir den Code angesehen.
Er sagt das eine, aber auf dem Chart sieht es ganz anders aus. Der Zeitraum ist nicht 3 von 3, sondern 14 von 14.
D.h. der Indikator zeigt einen Wert aus den letzten 23 Werten an.
Ich habe es analysiert und mit anderen Folien verglichen. Leider habe ich keine Vorteile gefunden, trotz der deutlich höheren Rechenlast durch die Sortierung.
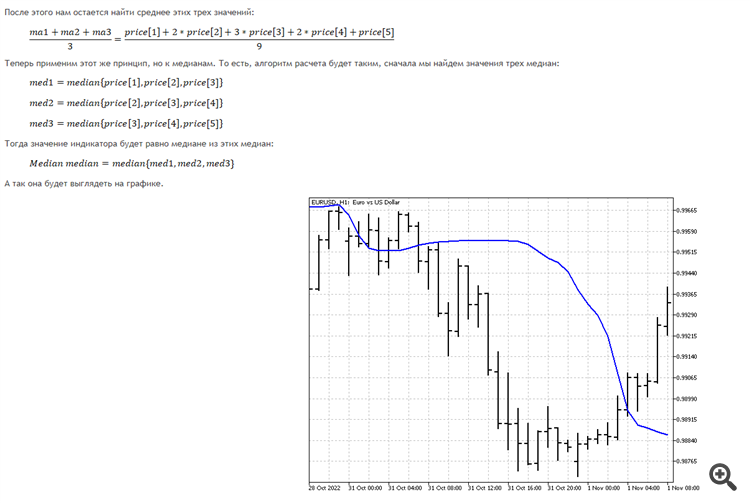
Besser ist es, den Median in dieser Form mit einem dreieckigen Fenster zu vergleichen. Die "schmackhafteste" Situation dafür ist ein Wechsel der Trendrichtung in die entgegengesetzte. Wenn Sie eine empfindlichere Variante benötigen, ist es besser, dies so zu tun. Zuerst wird der Median aus einem letzten Kurs ermittelt, dann der Median aus zwei Kursen, dann aus drei usw. Am Ende finden wir den Median aller zuvor gefundenen Preise. Wir erhalten das Analogon eines linear gewichteten Durchschnitts. Dadurch wird der Hauptnachteil des Medians - der Verlust von Informationen an den Rändern - nicht beseitigt, aber der Indikator reagiert empfindlicher auf aktuelle Veränderungen.
Der Median der Mediane in dieser Form ist besser als ein dreieckiges Fenster. Die "schmackhafteste" Situation dafür ist eine Änderung der Trendrichtung in die entgegengesetzte Richtung. Wenn Sie eine empfindlichere Variante benötigen, ist es besser, es so zu machen. Zuerst wird der Median aus einem letzten Kurs ermittelt, dann der Median aus zwei Kursen, dann aus drei usw. Am Ende finden wir den Median aller zuvor gefundenen Preise. Wir erhalten das Analogon eines linear gewichteten Durchschnitts. Dadurch wird der Hauptnachteil des Medians - der Verlust von Informationen an den Rändern - nicht beseitigt, aber der Indikator reagiert empfindlicher auf aktuelle Veränderungen.
Genauso wie alle meine früheren Versuche vor vielen Jahren, verschiedene Methoden des Clustering und der Mittelwertbildung zu entwickeln und Hunderte von Robotern mit ihrer Anwendung zu erstellen, vergeblich waren. Glauben Sie mir, ich habe viel mehr Erfolg damit gehabt. Es gibt keine weißen Flecken mehr auf diesem Gebiet.
Es bleibt nur noch die KI mit Muster- und Prozesserkennung.
Sie werden sowieso dazu kommen, wenn Sie den Boden nicht betreten.
Oh, ja, ich habe nicht aufgepasst.
Wenn man den Lag bekämpfen will, muss man ein geeignetes Modell verwenden. Wir zeichnen zum Beispiel ein Polynom dritten Grades um 20 Punkte vor. Wir erhalten die Koeffizienten {4979,3264,1904,864,109,-396,-686,-796,-761,-616,-396,-136,129,364,534,604,539,304,-136,-816} /8855 - ein solcher Indikator wird nicht lag
Wenn wir mit der Verzögerung zu kämpfen haben, müssen wir ein geeignetes Modell wählen. Zum Beispiel konstruieren wir ein Polynom dritten Grades vorwärts durch 20 Punkte. Wir erhalten die Koeffizienten {4979,3264,1904,864,109,-396,-686,-796,-761,-616,-396,-136,129,364,534,604,539,304,-136,-816} /8855 - ein solcher Indikator wird nicht hinterherhinken
Längst ist alles implementiert, geprüft, erneut geprüft, getestet, erneut getestet. Es gibt keinen Fisch. Genauer gesagt, die Existenz von Fischen ist immer vorübergehend, und der Rest der Zeit Nivellierung vorübergehenden Erfolg.
Wenn wir mit der Verzögerung zu kämpfen haben, müssen wir ein geeignetes Modell wählen. Zum Beispiel konstruieren wir ein Polynom dritten Grades vorwärts durch 20 Punkte. Wir erhalten die Koeffizienten {4979,3264,1904,864,109,-396,-686,-796,-761,-616,-396,-136,129,364,534,604,539,304,-136,-816} /8855 - ein solcher Indikator wird nicht hinterherhinken
Das Polynom selbst wird neu gezeichnet, so dass der Wert seine Spur ist, die eine nicht gezeichnete gleitende Linie bildet.
In der Tat ist es möglich, eine minimale Verzögerung zu erreichen, aber es beginnen andere Probleme.
Forum zum Thema Handel, automatisierte Handelssysteme und Testen von Handelsstrategien.
Nikolai Semko, 2020.02.01:09
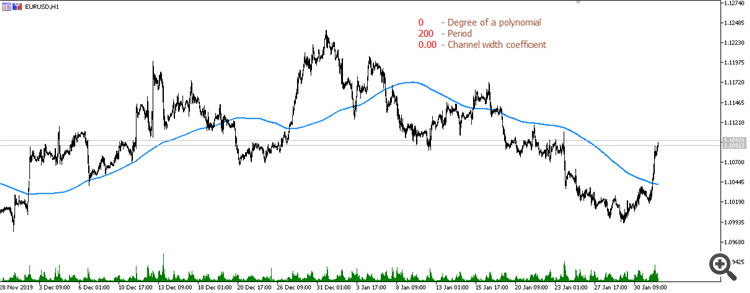
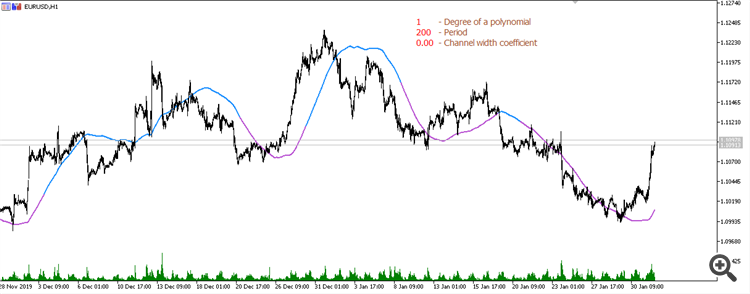
Einfacher gleitender Durchschnitt (Periode 200):
Gleitender Durchschnitt aus linearer Regression (Periode 200):
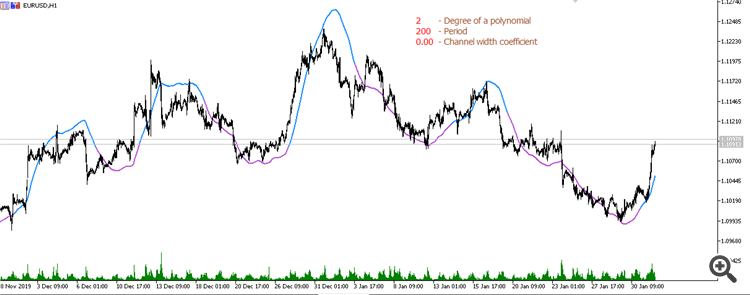
Gleitender Durchschnitt aus einer parabolischen Regression (Periode 200):
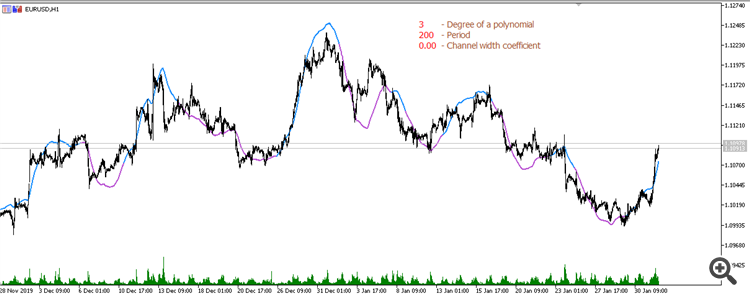
Gleitender Durchschnitt aus einem Polynom 3. Grades (Periode 200):
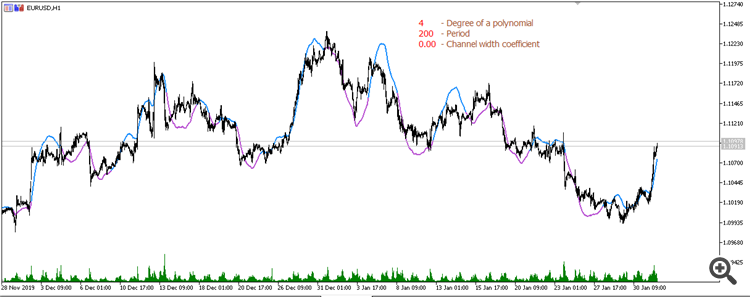
Gleitender Durchschnitt aus einem Polynom 4. Grades (Zeitraum 200):
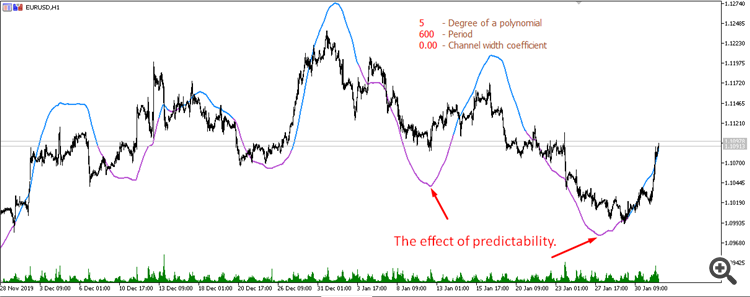
Gleitender Durchschnitt aus einem Polynom 5. Grades (Periode 600):
usw.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Nicht-lineare Indikatoren :
In diesem Artikel werde ich versuchen, einige Möglichkeiten zur Erstellung nichtlinearer Indikatoren und deren Verwendung im Handel zu besprechen. In der MetaTrader-Handelsplattform gibt es eine ganze Reihe von Indikatoren, die nicht-lineare Ansätze verwenden.
Der Modus ist der Wert, der in der Datenstichprobe am häufigsten vorkommt. Zum Beispiel ist in der Stichprobe 1, 6, 9, 3, 3, 7, 8 die häufigste Zahl 3. Es wird der Modus der Serie sein. Bei der Analyse von Preisen kann jedoch jeder Wert nur einmal vorkommen. Um den Modus zu berechnen, können wir die empirische Gleichung von Pearson verwenden:
Gemäß der Gleichung ist der Modus ein instabiler Indikator (die Koeffizienten gehen über die Grenzen des Intervalls -1...+1 hinaus). Er kann jedoch als Ergänzung zu anderen Indikatoren nützlich sein.
Ein weiteres zentrales Maß kann als die Mitte des Spektrums angesehen werden. Um ihn zu berechnen, müssen wir die Halbsumme der Höchst- und Mindestwerte der Zeitreihe ermitteln. Obwohl der mittlere Bereich empfindlich auf Ausschläge reagiert und nicht sehr zuverlässig ist, wird er in einigen Indikatoren verwendet.
So sehen alle vier Maße der zentralen Trendberechnung im Chart aus.
Autor: Aleksej Poljakov