模式搜索的暴力方法（第六部分）：循环优化

MetaTrader 5 — 示例 | 7 三月 2024, 10:11

970

Evgeniy Ilin

概述

考虑到我上一篇文章中的材料，我可以说这只是我在算法中引入的所有函数的肤浅描述。它们不仅涉及EA创建的完全自动化，还涉及诸如结果优化和选择的完全自动化以及随后用于自动交易，或者我稍后将展示的更先进的EA的创建等重要函数。

由于交易终端、通用EA和算法本身的共生关系，您可以完全摆脱手动开发，或者在最坏的情况下，只要您具备必要的计算能力，就可以将可能改进的劳动强度降低一个数量级。在这篇文章中，我将开始描述这些创新最重要的方面。

常规过程

对我来说，随着时间的推移，创建和随后修改此类解决方案的最重要因素是了解确保常规操作最大限度自动化的可能性。在这种情况下，常规操作包括所有非必要的人工工作：

想法的产生。
创造一个理论。
根据理论编写代码。
代码修改。
持续的EA重新优化。
持续的EA选择。
EA维护。
使用终端。
实验和实践。
其它。

正如你所看到的，这个常规过程的范围相当广泛。我把这当成一种常规过程，因为我能够证明所有这些事情都是自动化的。我提供了一份总清单。你是谁并不重要——算法交易者、程序员，或者两者兼而有之。你是否了解如何编程并不重要。即使你不了解，那么在任何情况下，你都会遇到这个列表中的至少一半。我不是说当你在市场上购买EA，在图表上运行它，然后按下一个按钮就万事大吉了。当然，这种情况会发生，尽管极为罕见。

了解了这一切，首先我必须将最明显的事情自动化。我在上一篇文章中从概念上描述了所有这些优化。然而，当你做这样的事情时，你开始了解如何在已经实现的功能的基础上改进整个事情。对我来说，这方面的主要想法如下：

完善优化机制。
创建用于合并 EA（合并机器人）的机制。
所有组件的交互路径的正确体系结构。

当然，这只是一个非常简短的列举，我会更详细地描述每件事。我所说的优化是指同时包含几个因子的集合。所有这些都是在构建整个系统的选定范式中经过深思熟虑的：

通过消除分时加快优化速度。
通过消除交易决策点之间的利润曲线控制来加速优化。
通过引入自定义优化标准来提高优化质量。
最大限度地提高远期效率。

在这个论坛网站上，你仍然可以找到关于是否需要优化以及优化的好处的争论。此前，我对这一行为的态度相当明确，很大程度上是由于个人论坛和网站用户的影响。现在这种观点一点也不困扰我。至于优化，这完全取决于你是否知道如何正确使用它以及你的目标是什么。如果使用正确，此行动将产生所需的结果。总的来说，事实证明，这一行动非常有用。

许多人不喜欢优化，这有两个客观原因：

缺乏对基本知识的理解（为什么、做什么和如何做，如何选择结果以及与此相关的一切，包括缺乏经验）。
优化算法的缺陷。

事实上，这两个因素相辅相成。公平地说，MetaTrader 5优化器在结构上执行得无可挑剔，但在优化标准和可能的过滤器方面仍需要许多改进。到目前为止，所有这些功能都类似于儿童沙箱。很少有人考虑如何实现正向的前瞻时间段，最重要的是，如何控制这一过程。我想了很久了。事实上，当前文章中有相当一部分将专门讨论这个主题。

新的优化算法

除了任何回溯测试的基本已知评估标准外，我们还可以提出一些组合特征，这些特征可以帮助任何算法的值相乘，从而更有效地选择结果并随后应用设置。这些特性的优点是可以加快查找优化设置的过程。为此，我创建了一个类似于MetaTrader的策略测试报告：

图1

详细报告

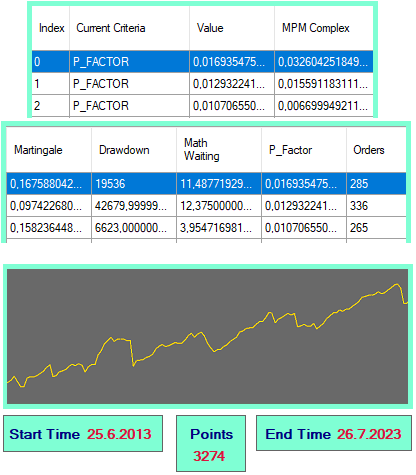
有了这个工具，我只需点击一下就可以选择我喜欢的选项。通过点击，生成了一个设置，我可以立即将其移到终端中的适当文件夹中，以便通用EA可以读取并开始在其上进行交易。如果我愿意，我也可以点击按钮生成一个EA，在我需要一个单独的EA，里面有固定的设置时，它将被构建。还有一条利润曲线，当您从表中选择下一个选项时会重新绘制。

让我们计算一下表中的数字。计算这些特性的主要元素是以下数据：

Points：对应资产在整个回测中的利润点数（“_Points”）。
Orders：完全打开和关闭的订单的数量（它们按照严格的顺序相互遵循，根据规则“只能有一个打开的订单”）。
Drawdown：余额的回撤。

基于这些值，计算出以下交易特征：

Math Waiting: 数学期望点数。
P Factor：类似于利润因子，标准化为范围[-1…0…1]（我的标准）。
Martingale：马丁格尔应用（我的标准）。
MPM Complex：上述三项的综合指标（我的标准）。

现在让我们看看这些标准是如何计算的：

等式1

优化标准

正如你所看到的，我创建的所有标准都非常简单，最重要的是易于理解。由于每个标准的增加表明回溯测试结果在概率论方面更好，因此可以将这些标准相乘，就像我在MPM综合标准中所做的那样。通用度量将更有效地根据结果的重要性对结果进行排序。在进行大规模优化的情况下，它将允许您分别保留更多高质量的选项和删除更多低质量的选项。

此外，请注意，在这些计算中都是使用点数。这对优化过程有积极影响。对于计算，使用严格正的主量，这些主量总是在开始时计算。其余的都是根据它们来计算的。我认为，值得列出表中未列出的主量：

Points Plus: 每个盈利订单或零盈利订单的利润总和（以点数为单位）
Points Minus: 每个不盈利订单的损失模之和（以点为单位）
Drawdown: 余额的回撤（我用自己的方式计算）

这里最有趣的是如何计算回撤。在我们的案例中，这是最大的相对余额回撤。考虑到我的测试算法拒绝监控资金曲线，其他类型的回撤无法计算。然而，我认为应该展示一下我是如何计算这一回撤的：

图2

最大相对余额回撤

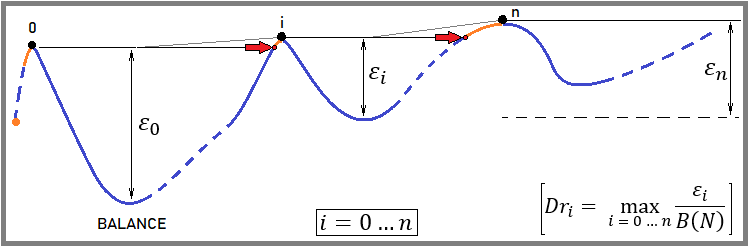
它的定义非常简单：

计算回测的起始点（第一次回撤计数的开始）。
如果交易以盈利开始，那么我们会随着余额的增长将这一点向上移动，直到出现第一个负值（这标志着回撤计算的开始）。
等待，直到余额达到参考点的水平。之后，将其设置为新的参考点。
我们返回到回撤搜索的最后一部分，并在上面寻找最低点（该部分的回撤量是从这一点计算得出的）。
对整个回溯测试或交易曲线重复整个过程。

最后一个周期将永远是未完成的状态，然而，它的回撤也被考虑在内，尽管如果测试继续下去，它有可能增加。但这在这里并不是一件特别重要的事情。

最重要的优化标准

现在让我们来谈谈最重要的过滤器。事实上，在选择优化结果时，这个标准是最重要的。这个标准没有包含在MetaTrader 5优化器的功能中，这是一个遗憾。所以让我提供一些理论材料，让每个人都能在自己的代码中重现这种算法。事实上，这一标准适用于任何类型的交易，适用于任何利润曲线，包括体育博彩、加密货币和你能想到的任何其他东西。标准如下：

等式2

线性系数

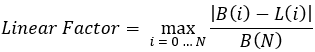
让我们看看这个等式里面有什么：

N - 在整个回溯测试或交易部分中完全开放和关闭的交易头寸的数量。
B(i) — 对应平仓“i”之后的余额线的值。
L(i) — 从零到余额最后一点的直线（最终余额）。

我们需要执行两次回溯测试来计算这个参数。第一次回溯测试将计算最终余额。之后，可以通过保存每个余额点的值来计算相应的指标，从而无需进行不必要的计算。然而，这种计算可以称为重复回溯测试。这个等式可以在自定义测试器中使用，这些测试器可以构建到您的EA中。

重要的是要注意，这一指标作为一个整体可以进行修改，以便更好地理解。例如，如下所示：

等式3

修改版线性系数

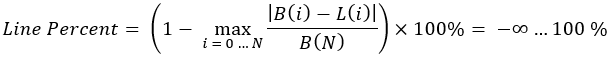
这个等式在感知和理解方面更困难。但从实际角度来看，这样的标准很方便，因为它的值越高，我们的余额曲线就越像一条直线。我在以前的文章中谈到了类似的问题，但没有解释它们背后的含义。我们先来看下图：

图3

线性系数和曲线系数

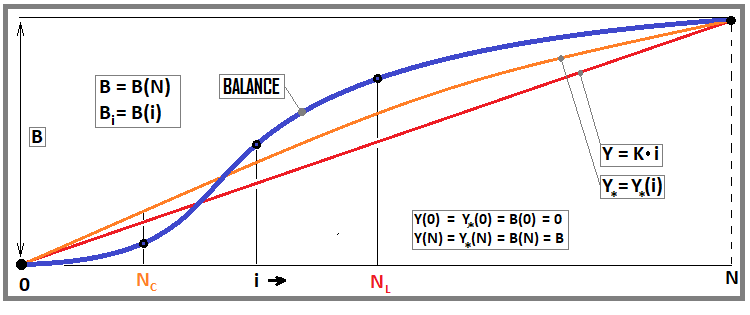
该图显示了一条余额线和两条曲线：其中一条与我们的等式（红色）有关，第二条与以下修改标准有关（方程11）。我将进一步展示，但现在让我们专注于等式。

如果我们把我们的回溯测试想象成一个简单的有平衡的点阵列，那么我们可以把它表示为一个统计样本，并将概率论公式应用于它。我们将把直线视为我们正在努力的模型，而利润曲线本身就是为我们的模型而努力的真实数据流。

重要的是要理解，线性系数表示整个可用交易标准集的可靠性。反过来，更高的数据可靠性可能表明可能有更长更好的远期（未来可以获利的交易）。严格地说，一开始我应该考虑随机变量来考虑这些事情，但在我看来，这样的演示应该更容易理解。

考虑到可能的随机尖峰，让我们创建一个线性因子的替代模拟。要做到这一点，我们需要引入一个方便我们的随机变量及其平均值，用于后续的离散度计算：

等式4

随机变量及其均值

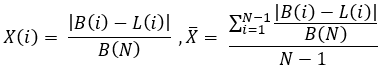
为了更好地理解，应该澄清的是，我们有“N”个完全开启又关闭的仓位，它们严格遵循一个接一个的顺序。这意味着我们有“N+1”个点连接余额线的这些部分。所有线的零点都是常见的，所以它的数据会像最后一个点一样，朝着改进的方向扭曲结果。因此，我们将它们排除在计算之外，剩下的是“N-1”个点，我们将对其进行计算。

将两行的值数组转换为一行的表达式的选择非常有趣。请注意以下分数：

等式5

重要的分数

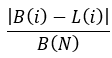
这里重要的是，在所有情况下，我们都要用最终的余额来除所有的数字。因此，我们将所有内容都减少到一个相对值，这确保了所有测试策略的计算特性的等效性，无一例外。在线性因子的第一个简单标准中存在相同的分数并非巧合，因为它是基于相同的考虑。但让我们完成我们的替代标准的构建。要做到这一点，我们可以使用一个众所周知的概念，即离散度：

等式6

相对偏差离散度

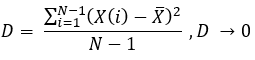
离散度只不过是整个样本平均值的平方偏差的算术平均值。我立即在那里代入了我们的随机变量，上面定义了它们的表达式。理想曲线的平均偏差为零，因此，给定样本的离散度也将为零。基于这些数据，很容易猜测，由于其结构——所使用的随机变量或样本（如您所愿）——这种离散度可以用作替代线性因子。此外，这两个标准可以同时使用，以更有效地约束样本参数，尽管老实说，我只使用第一个标准。

让我们来看一个类似的、更方便的标准，它也是基于我们定义的一个新的线性因子：

等式7

正如我们所看到的，它与类似的标准相同，该标准是建立在第一个标准（等式2）的基础上的。然而，这两个标准远远超出了我们所能想到的极限。支持这种考虑的一个明显事实是，这一标准过于理想化，更适合理想模型，而且调整EA以实现或多或少的显著对应将极其困难。我认为，值得列出应用等式后一段时间内显而易见的负面因素：

交易数量的大幅减少（降低结果的可靠性）
拒绝最大数量的有效场景（取决于策略，曲线并不总是倾向于直线）

这些缺点是非常关键的，因为目标不是放弃好的策略，而是找到没有这些缺点的新的和改进的标准。这些缺点可以通过同时引入几个优选线路来完全或部分消除，每个线路都可以被认为是可接受的或优选的模型。要理解新的改进标准，在没有这些缺点的情况下，您只需要理解相应的替换：

等式8

几条曲线

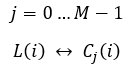
然后，我们可以从列表中计算每条曲线的拟合因子：

等式9

族中每条曲线的匹配系数

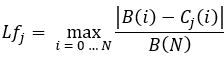
类似地，我们也可以计算一个替代标准，该标准考虑了每条曲线的随机尖峰：

等式10

各曲线对应因素对离散度的影响

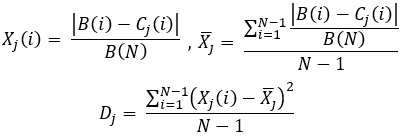
然后我们需要计算以下内容：

等式11

曲线族因子

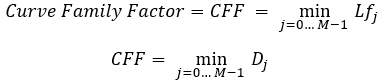
这里我介绍一个标准，称为曲线族因子。事实上，通过这个行动，我们同时找到了与交易曲线最相似的曲线，并立即找到了与之对应的因子。匹配因子最小的曲线最接近真实情况。我们将其值作为修改后的标准的值，当然，计算可以通过两种方式进行，这取决于我们更喜欢这两种变化中的哪一种。

这一切都很酷，但正如许多人所注意到的，在这里，选择这样一组曲线有一些细微差别。为了正确地描述这样一组曲线，可以考虑各种因素，但以下是我的想法：

所有曲线都不应该有拐点（每个后续的中间点都应该严格高于前一个）。
曲线应该是凹形的（曲线的陡峭度可以是恒定的，也可以只增加）。
曲线的凹度应该是可调整的（例如，应使用一些相对值或百分比来调整偏转量）。
曲线模型的简单性（最好将模型建立在最初简单易懂的图形模型上）。

这只是该曲线族的初始变化。可以在考虑所有所需配置的情况下进行更广泛的更改，这可以完全避免我们丢失质量设置。稍后我将承担这项任务，但目前我只涉及凹曲线族的原始策略。利用我的数学知识，我能够很容易地创建这样一个曲线族。让我立即向您展示这个曲线族的最终外观：

图4

曲线族

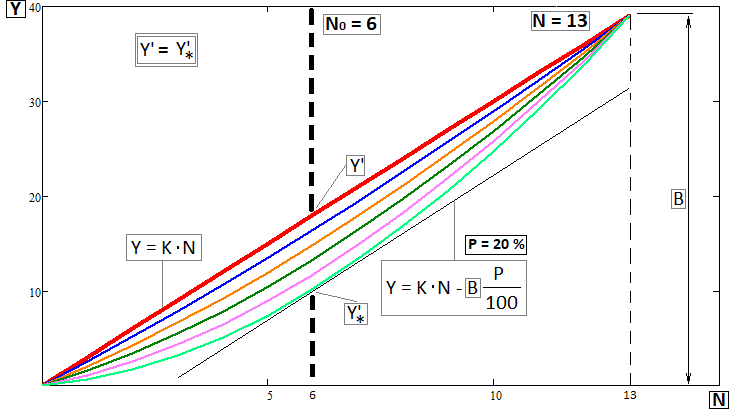
在建造这样一个族时，我使用了一个位于垂直支架上的弹性杆的抽象概念。这种杆的偏转程度取决于力的施加点及其大小。很明显，这只是在某种程度上类似于我们在这里处理的问题，但这足以开发某种视觉上相似的模型。当然，在这种情况下，我们首先应该确定极值的坐标，它应该与回测图上的一个点重合，X轴由从零开始的交易指数表示。我是这样计算的：

等式12

余额曲线的条件中点

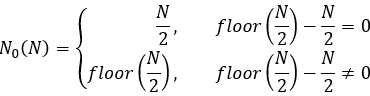
这里有两种情况：对于偶数和奇数“N”。如果“N”是偶数，那么不可能简单地将其除以2，因为索引应该是一个整数。顺便说一句，我在最后一张图片中准确地描述了这种情况。在那里，施力的点离开始有点近。当然，你可以做相反的事情，在接近结束的时候做一点，但正如我在图中所描绘的那样，这只对少数交易有意义。随着交易数量的增加，所有这些都不会对优化算法起到任何重要作用。

在设置了以百分比表示的“P”偏转值和回溯测试的“B”最终余额后，在之前确定了极值的坐标后，我们可以开始顺序计算进一步的分量，以构建每个可接受的曲线族的表达式。接下来，我们需要连接回溯测试的开始和结束的直线的陡峭度：

等式13

回测开始和结束之间的直线倾角的切线

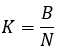
这些曲线的另一个特征是，在横坐标为“N0”的点处，每条曲线的切线角度与“K”相同。在构造等式时，我从任务中要求这个条件。这也可以在最后一张图中以图形方式看到（图4），其中也有一些等式和恒等式。让我们继续。现在我们需要计算以下值：

等式

K delta

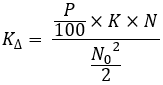
请记住，“P”是为族中的每条曲线设置的。严格地说，这些是从一个族中构造一条曲线的等式。应该对族中的每条曲线重复这些计算。然后我们需要计算另一个重要的比率：

等式15

没有必要探究这些结构的含义。创建它们只是为了简化构建曲线的过程。还有待计算最后一个辅助比率：

等式16

K epsilon

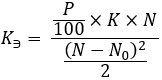
现在，基于所获得的数据，我们可以获得用于计算所构建的曲线的点的数学表达式。然而，首先需要澄清的是，曲线不是由单个等式描述的。在“N0”点的左边，我们有一个等式，而另一个等式在右边。为了更容易理解，我们可以执行以下操作：

等式17

现在我们可以看到最后的等式：

等式18

描述曲线左右部分的两个方程

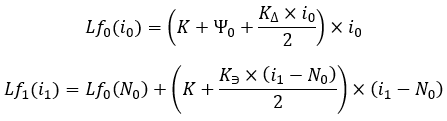
我们还可以显示如下：

等式19

插值函数的严格数学描述

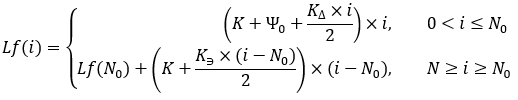
严格地说，这个函数应该被用作一个离散的辅助函数。然而，它允许我们计算分数为“i”的值。当然，就我们的问题而言，这不太可能对我们有任何有益的好处。

由于我给出了这样的数学，我有义务提供算法实现的示例。我认为，每个人都会对获得更容易适应其系统的现成代码感兴趣。让我们从定义主要变量和方法开始，这些变量和方法将简化必要量的计算：

//+------------------------------------------------------------------+
//| Number of lines in the balance model                             |
//+------------------------------------------------------------------+
#define Lines 11 

//+------------------------------------------------------------------+
//| Initializing variables                                           |
//+------------------------------------------------------------------+
double MaxPercent = 10.0;
double BalanceMidK[,Lines];
double Deviations[Lines];
int Segments;
double K;

//+------------------------------------------------------------------+
//| Method for initializing required variables and arrays            |
//| Parameters: number of segments and initial balance               |
//+------------------------------------------------------------------+
void InitLines(int SegmentsInput, double BalanceInput) 
{
  Segments = SegmentsInput;
  K = BalanceInput / Segments;
  ArrayResize(BalanceMidK,Segments+1);
  ZeroStartBalances();
  ZeroDeviations();
  BuildBalances();
}

//+------------------------------------------------------------------+
//| Resetting variables for incrementing balances                    |
//+------------------------------------------------------------------+
void ZeroStartBalances()
{
  for (int i = 0; i < Lines; i++ ) 
  {
      for (int j = 0; j <= Segments; j++)
      {
          BalanceMidK[j,i] = 0.0;
      }
  }
}

//+------------------------------------------------------------------+
//| Reset deviations                                                 |
//+------------------------------------------------------------------+
void ZeroDeviations()
{
  for (int i = 0; i < Lines; i++)
  {
      Deviations[i] = -1.0;
  }
}

该代码被设计为可重复使用。在下一次计算之后，您可以通过首先调用InitLines方法来计算不同余额曲线的指标。你需要给它回测和交易数量的最终余额，之后你可以开始根据这些数据构建我们的曲线：

//+------------------------------------------------------------------+
//| Constructing all balances                                        |
//+------------------------------------------------------------------+
void BuildBalances()
{
   int N0 = MathFloor(Segments / 2.0) - Segments / 2.0 == 0 ? Segments / 2 : (int)MathFloor(Segments / 2.0);//calculate first required N0
   for (int i = 0; i < Lines; i++)
   {
       if (i==0)//very first and straight line 
       {
           for (int j = 0; j <= Segments; j++)
           {
               BalanceMidK[j,i] = K*j;
           }
       }
       else//build curved lines
       {
           double ThisP = i * (MaxPercent / 10.0);//calculate current line curvature percentage
           double KDelta = ( (ThisP /100.0) * K * Segments) / (MathPow(N0,2)/2.0 );//calculation first auxiliary ratio
           double Psi0 = -KDelta * N0;//calculation second auxiliary ratio
           double KDelta1 = ((ThisP / 100.0) * K * Segments) / (MathPow(Segments-N0, 2) / 2.0);//calculate last auxiliary ratio
           //this completes the calculation of auxiliary ratios for a specific line, it is time to construct it

           for (int j = 0; j <= N0; j++)//construct the first half of the curve 
           {
               BalanceMidK[j,i] = (K + Psi0 + (KDelta * j) / 2.0) * j;
           }
           for (int j = N0; j <= Segments; j++)//construct the second half of the curve 
           {
               BalanceMidK[j,i] = BalanceMidK[i, N0] + (K + (KDelta1 * (j-N0)) / 2.0) * (j-N0);
           }
       }
   }
}

请注意，“Lines”决定了我们的族中将有多少条曲线。凹度从零（直线）逐渐增加到MaxPercent，正如我在相应的图中所示。然后，您可以计算每条曲线的偏差，并选择最小的一条：

//+------------------------------------------------------------------+
//| Calculation of the minimum deviation from all lines              |
//| Parameters: initial balance passed via link                      |
//| Return: minimum deviation                                        |
//+------------------------------------------------------------------+
double CalculateMinDeviation(double &OriginalBalance[])
{
   //define maximum relative deviation for each curve 
   for (int i = 0; i < Lines; i++)
   {
       for (int j = 0; j <= Segments; j++)
       {
          double CurrentDeviation = OriginalBalance[Segments] ? MathAbs(OriginalBalance[j] - BalanceMidK[j, i]) / OriginalBalance[Segments] : -1.0;
          if (CurrentDeviation > Deviations[i])
          {
              Deviations[i] = CurrentDeviation;
          }           
       }
   }
    
   //determine curve with minimum deviation and deviation itself 
   double MinDeviation=0.0;
   for (int i = 0; i < Lines; i++)
   {
       if ( Deviations[i] != -1.0 && MinDeviation == 0.0)
       {
           MinDeviation = Deviations[i];
       }
       else if (Deviations[i] != -1.0 && Deviations[i] < MinDeviation)
       {
           MinDeviation = Deviations[i];
       }
   }
   return MinDeviation;
}

这就是我们应该如何使用它：

OriginalBalance 原始余额数组的定义。
确定其长度SegmentsInput和最终余额BalanceInput，以及调用InitLines方法。
然后，我们通过调用BuildBalances方法来构建曲线。
由于绘制了曲线，我们可以考虑为曲线族改进CalculateMinDeviation标准。

这就完成了标准的计算。我认为曲线族系数（Curve Family Factor）的计算不会造成任何困难。没有必要在这里介绍它。

自动搜索交易配置

整个想法中最重要的元素是终端和我的程序之间的交互系统。事实上，它是一个具有高级优化标准的循环优化器。上一节介绍了最重要的问题。为了使整个系统正常工作，我们首先需要一个报价来源，这是MetaTrader 5终端之一。正如我在上一篇文章中所展示的，报价是以一种对我来说很方便的格式写入文件的。这是使用EA完成的，乍一看功能相当奇怪：

. EA撰写报价的概念

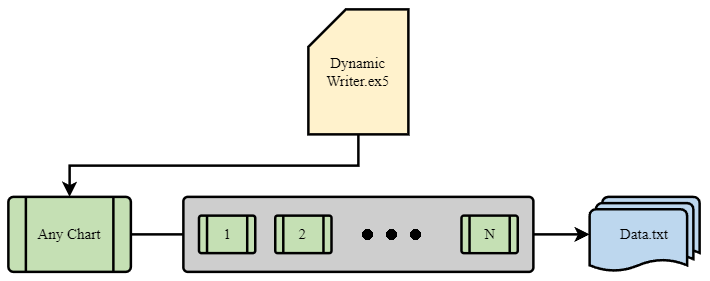
我发现使用我独特的EA功能方案是一种非常有趣和有益的体验。这里只是我需要解决的问题的演示，但所有这些也可以用于交易EA：

使用EA编写报价的示例

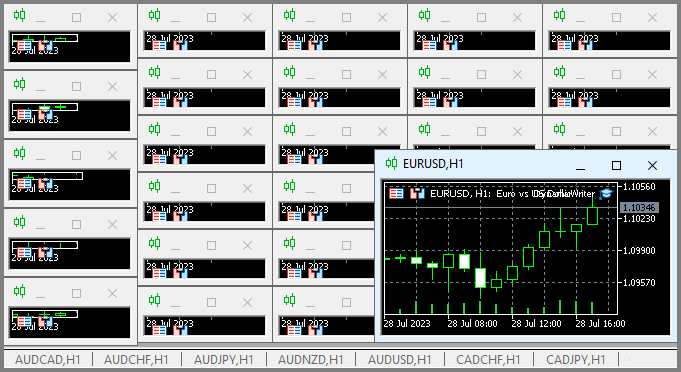
这个方案的特点是我们可以从任何图中进行选择。为了避免数据重复，它不会被用作交易工具，但它只会充当分时处理程序或计时器。图表的其余部分代表了我们需要生成报价的工具期。

写引号是通过使用随机数生成器随机选择报价的形式完成的。如果需要，我们可以优化这个过程。使用以下基本函数在一段时间后进行书写：

//+------------------------------------------------------------------+
//| Function to write data if present                                |
//| Write quotes to file                                             |
//+------------------------------------------------------------------+
void WriteDataIfPresent()
{
    // Declare array to store quotes 
    MqlRates rates[];
    ArraySetAsSeries(rates, false);

    // Select a random chart from those we added to the workspace 
    ChartData Chart = SelectAnyChart();
    
    // If the file name string is not empty 
    if (Chart.FileNameString != "")
    {
        // Copy quotes and calculate the real number of bars
        int copied = CopyRates(Chart.SymbolX, Chart.PeriodX, 1,
                        int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX))),
                        rates);
        
        // Calculate ideal number of bars
        int ideal = int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX)));
        
        // Calculate percentage of received data 
        double Percent = 100.0 * copied / ideal;
        
        // If the received data is not very different from the desired data, 
        // then we accept them and write them to a file
        if (Percent >= 95.0)
        {
            // Open file (create it if it does not exist, 
            // otherwise, erase all the data it contained)
            OpenAndWriteStart(rates, Chart, CommonE); 
            WriteAllBars(rates); // Write all data to file
            WriteEnd(rates); // Add to end
            CloseFile(); // Close and save data file
        }
        else 
        {
            // If there are much fewer quotes than required for calculation 
            Print("Not enough data"); 
        }
    }
}

如果复制的数据至少是基于指定参数计算的理想条形数的95%，则WriteDataIfPresent函数会将有关所选图表中引号的信息写入文件。如果复制的数据小于95%，该功能将显示消息“数据不足”。如果具有给定名称的文件不存在，则函数将创建该文件。

为了使此代码发挥作用，应额外描述以下内容：

//+------------------------------------------------------------------+
//| ChartData structure                                              |
//| Objective: Storing the necessary chart data                      |
//+------------------------------------------------------------------+
struct ChartData {
    string FileNameString;
    string SymbolX;
    ENUM_TIMEFRAMES PeriodX;
};

//+------------------------------------------------------------------+
//| Randomindex function                                             |
//| Objective: Get a random number with uniform distribution         |
//+------------------------------------------------------------------+
int Randomindex(int start, int end) {
    return start + int((double(MathRand())/32767.0)*double(end-start+1));
}

//+------------------------------------------------------------------+
//| SelectAnyChart function                                          |
//| Objective: View all charts except current one and select one of  |
//|       them to write quotes                                       |
//+------------------------------------------------------------------+
ChartData SelectAnyChart() {
    ChartData chosenChart;
    chosenChart.FileNameString = "";
    int chartCount = 0;
    long currentChartId, previousChartId = ChartFirst();

    // Calculate number of charts
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;  
        }
        previousChartId = currentChartId;
        
        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }

    int randomChartIndex = Randomindex(0, chartCount - 1);
    chartCount = 0;
    currentChartId = ChartFirst(); 
    previousChartId = currentChartId;
    
    // Select random chart
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;
        }
        
        previousChartId = currentChartId;
        
        // Fill in selected chart data
        if (chartCount == randomChartIndex) {
            chosenChart.SymbolX = ChartSymbol(currentChartId);
            chosenChart.PeriodX = ChartPeriod(currentChartId);
            chosenChart.FileNameString = "DataHistory" + " " + chosenChart.SymbolX + " " + IntegerToString(CorrectPeriod(chosenChart.PeriodX));
        }
        
        if (chartCount > randomChartIndex) {
            break;
        }

        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }
       
    return chosenChart;
}

此代码用于记录和分析当前可以在终端中打开的各种图表中不同货币的历史金融市场数据（报价）。

ChartData结构用于存储每个图表的数据，包括文件名、交易品种（货币对）和时间框架。
Randomindex（start，end）函数生成一个介于“start”和“end”之间的随机数。这用于随机选择一个可用的图表。
SelectAnyChart（）遍历所有打开和可用的图表（不包括当前图表），然后随机选择其中一个进行处理。

生成的报价会被程序自动提取，之后会自动搜索可以获利的配置。整个过程的自动化相当复杂，但我试图将其浓缩为一幅图：

图5

自动化选项卡

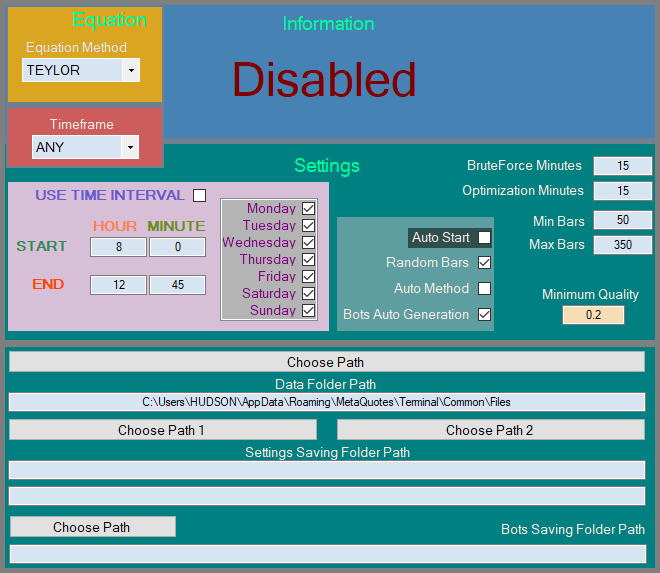
该算法有三种状态：

不活动的。
等待报价中。
活动的。

如果记录报价的EA还没有生成一个文件，或者我们已经从指定的文件夹中删除了所有报价，那么算法只需等待它们出现并暂停一段时间。至于我们改进的标准，我以MQL5风格为您实现了它，它也用于暴力和优化：

图6

线性因子和曲线族因子

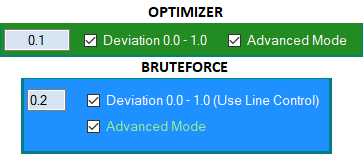
高级模式操作曲线族因子，而标准算法仅使用线性因子。剩下的改进太过广泛，无法纳入本文。在下一篇文章中，我将展示基于通用多货币模板的将 EA 交易粘合在一起的新算法。该模板在一个图表上启动，但处理所有合并的交易系统，而不要求每个EA在自己的图表上启动。它的一些功能已在这篇文章中使用。

结论

在本文中，我们更详细地研究了自动化开发和优化交易系统过程领域的新机遇和想法。主要成果是开发了一种新的优化算法，创建了终端同步机制和自动优化器，以及一个重要的优化标准——曲线因子和曲线族。这使我们能够减少开发时间并提高所获得结果的质量。

一个重要的补充也是凹曲线族，它代表了在反向正向周期的背景下更现实的余额模型。通过计算每条曲线的拟合因子，我们可以更准确地选择自动交易的最佳设置。

链接

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/9305

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.