формулы 2
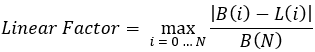
让我们来了解一下这个公式的含义:
- N - 整个回溯测试或交易部分中完全打开和关闭的交易头寸数量。
- B(i) - 相应平仓头寸 "i "后的平衡线数值。
- L(i) - 从零开始到最近的平衡点(最终平衡点)之间的连线。
似乎与夏普 差不多:
//--- 计算权益数组中增量的对数 for(int i = 1; i < m_bars_counter; i++) { //--- 仅在权益发生变化时添加 if(m_equities[i] != prev_equity) { log_return = MathLog(m_equities[i] / prev_equity); // 增量的对数 aver += log_return; // 增量的平均对数 AddReturn(log_return); // 从增量中填充对数数组 counter++; // 生成计数器 } prev_equity = m_equities[i]; } //--- 如果没有足够的值来计算夏普比率,则返回 0 if(counter <= 1) return(0); //--- 增量对数的平均值 aver /= counter; //--- 计算标准偏差 for(int i = 0; i < counter; i++) std += (m_returns[i] - aver) * (m_returns[i] - aver); std /= counter; std = MathSqrt(std); //--当前时间框架下的夏普比率 double sharpe = aver / std;

- www.mql5.com
有相似之处,但只是乍一看。每个人都会怀念余额增长模式。如果平衡增长的斜率持续下降(平衡曲线的二阶导数为负),那么这种模式就不可取,因为它可能很快就会进入负值。关键是要选择那些从图形上看最有希望的曲线。
针对下降曲线的夏普算法会给出一个负值。我给你的只是类比,没有必要讨论夏普....。
我的经验之谈。
- 美丽曲线 "标准 - 不通过 OOS。
- 丑陋曲线 "标准 - 通过 OOS,而曲线本身却很美。
- 零佣金 - 不通过 OOS。
- 佣金已设定 - 通过 OOS。
也就是说,当优化的目的是为了美观时,拟合的成分会很高。当发现有价值的东西时,它看起来就很美。
这就是为什么我自己不追求美。我更依赖于交易数量和 TS 核心的算法。我们的目标是在没有美感标准的情况下获得美感。通常,这种变体会通过 OOS。
ZY 有佣金的变体更有趣(但一般来说,反之亦然:佣金越少,找到模式的可能性越大)。它实际上减少了交易次数(统计意义),但增加了搜索成功的概率。
下行曲线的夏普算法会产生一个负值。我给出它只是为了类比,讨论夏普算法没有意义.....。
我的经验举例。
- 美丽的曲线 "标准 - 不能通过 OOS。
- "丑陋曲线 "标准 - 通过 OOS,但曲线本身很美。
- 零佣金 - 不通过 OOS。
- 佣金设置 - 通过 OOS。
也就是说,当优化的目的是为了美观时,拟合的成分会很高。当发现有价值的东西时,它看起来就很美。
这就是为什么我自己不追求美。我更依赖于交易数量和 TS 核心的算法。我们的目标是在没有 "美 "的标准的情况下获得 "美"。通常,这种变体会通过 OOS。
ZY 有佣金的变体更有趣(但通常反之亦然:佣金越少,发现模式的概率越高)。它实际上减少了交易数量(统计意义),但增加了搜索成功的概率。
很明显,这仍然有局限性。例如,我是这样做的:
- 我以点数为单位设定最低期望值(只考虑点差,我还会加上佣金和掉期,大约是这样)。
- 设置最低交易次数要求,考虑到所考虑部分的长度
- 调整曲线匹配系数
我不这样做。市场规律并不取决于经纪人的交易条件。我倾向于这样做。
fxsaber, 2023.08.19 11:10 AM
通过历史数据选择潜在利润最高的经纪商。例如,EURUSD_Broker1 的潜在利润高于 EURUSD_Broker2。那么就选择 EURUSD_Broker1。
主要货币和交叉货币都可以剥头皮。但不是全部。只需在每种情况下进行训练,看看结果如何。我大致就是这么做的。
也就是说,搜索 "石头中的黄金 "浓度较高的地方是合乎逻辑的。
- 考虑到相关区域的长度,我设定了所需的最低交易次数。
- 调整曲线拟合系数。
我不明白 TS 与传播的关系。
- Например, можно обучить ТС, чтобы выдавал PF>2.5. При должном количестве сделок это почти автоматом выдаст красивую кривую
我同意其他观点。
。
- 我不明白 TS 与价差的关系
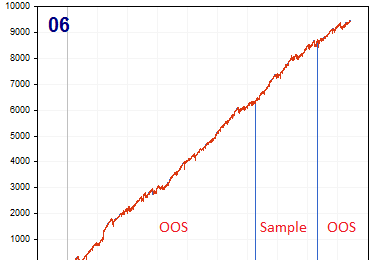

新文章 模式搜索的暴力方法(第六部分):循环优化已发布:
在这篇文章中,我将展示改进的第一部分,这些改进不仅使我能够使MetaTrader 4和5交易的整个自动化链闭环,而且还可以做一些更有趣的事情。从现在起,这个解决方案使我能够完全自动化创建EA和优化,并最大限度地降低寻找有效交易配置的劳动力成本。
整个想法中最重要的元素是终端和我的程序之间的交互系统。事实上,它是一个具有高级优化标准的循环优化器。上一节介绍了最重要的问题。为了使整个系统正常工作,我们首先需要一个报价来源,这是MetaTrader 5终端之一。正如我在上一篇文章中所展示的,报价是以一种对我来说很方便的格式写入文件的。这是使用EA完成的,乍一看功能相当奇怪:
.
我发现使用我独特的EA功能方案是一种非常有趣和有益的体验。这里只是我需要解决的问题的演示,但所有这些也可以用于交易EA:
作者:Evgeniy Ilin