패턴 검색에서 무자비 대입 방식(6부): 주기적 최적화

콘텐츠

• 소개
• 루틴
• 새로운 최적화 알고리즘
• 가장 중요한 최적화 기준
• 트레이딩 구성 자동 검색
• 결론
• 링크

소개

제가 쓴 이전 글의 내용들을 고려해보면 이것은 제가 알고리즘에 도입한 모든 함수에 대한 피상적인 설명에 불과하다고 할 수 있습니다. 이 함수들은 EA 생성의 완전한 자동화 뿐만 아니라 자동 거래 최적화의 자동화와 앞으로 다룰 내용인 보다 진보적인 EA의 생성과 같은 중요한 기능에 관한 것입니다.

트레이딩 터미널, 범용 EA 및 알고리즘 덕분에 수동 개발의 과정 없이 프로그램을 개선하기 위한 노동 강도를 크게 줄일 수 있습니다. 이 글에서는 이러한 혁신의 가장 중요한 측면에 대해 설명하겠습니다.

루틴

이러한 솔루션을 만들고 이후 수정하는 데 있어 가장 중요한 것은 일상적인 작업을 최대한 자동화할 수 있는 가능성에 대해 이해하는 것이었습니다. 이 경우 루틴이란 필수적으로 필요하지 않은 사람이 하는 모든 작업이 포함됩니다:

• 아이디어 생성.
• 이론 만들기.
• 이론에 따라 코드를 작성하기.
• 코드 수정.
• 지속적인 EA 재최적화.
• 지속적인 EA 선택.
• EA 유지 관리.
• 터미널로 작업하기.
• 실험과 연습.
• 기타.

보시다시피 이 루틴의 범위는 상당히 넓습니다. 이 작업들이 저에게는 대수롭지 않습니다. 이 모든 것이 자동화될 수 있다는 것을 증명할 수 있었기 때문입니다. 일반적인 목록을 제공했습니다. 여러분이 알고리즘 트레이더, 프로그래머 또는 두 가지 모두에 해당하던지 상관없습니다. 여러분이 프로그래밍을 할 줄 아는지 여부는 중요하지 않습니다. 그렇지 않더라도 여러분은 어떤 경우에도 이 목록의 절반 이상을 맞닥들이게 될 것입니다. 시장에서 EA를 구입하여 차트에서 실행하고 버튼 하나만 누르고 편히 쉰 경우에 대해 말하는 것이 아닙니다. 물론 극히 드물기는 하지만 이런 일이 발생하기도 합니다.

이 모든 것을 이해하기 위해 저는 먼저 가장 분명한 것들을 자동화해야 했습니다. 이전 글에서 이 모든 최적화에 대해 개념적으로 설명한 적이 있습니다. 하지만 이런 작업을 수행하면 여러분은 이미 구현된 기능을 기반으로 전체 기능을 개선하는 방법을 이해할 수 있을 것입니다. 이와 관련하여 제가 생각한 주요 아이디어는 다음과 같습니다:

• 최적화 메커니즘 개선.
• EA 병합(봇 병합)을 위한 메커니즘 생성.
• 모든 컴포넌트의 상호 작용 경로의 올바른 아키텍처.

물론 이것은 매우 간단한 열거입니다. 모든 것을 더 자세히 설명해 드리겠습니다. 최적화를 개선한다는 것은 여러 가지 요소를 한꺼번에 개선하는 것을 의미합니다. 이 모든 것은 전체 시스템 구축을 위해 선택한 패러다임 내에서 고려되어야 합니다:

• 틱을 제거하여 최적화 속도를 높입니다.
• 거래 결정 시점 사이에서 수익 곡선 제어를 제거하여 최적화를 가속화합니다.
• 사용자 지정 최적화 기준을 도입하여 최적화 품질을 개선합니다.
• 기간의 효율성을 극대화합니다.

이 웹사이트의 포럼에서 최적화가 필요한지 여부와 최적화의 이점에 대한 지속적인 토론을 찾아볼 수 있을 것입니다. 저는 이전에는 개별 포럼 및 웹사이트 사용자의 성격 때문에 이 포럼에 대해 다소 부정적인 태도를 가지고 있었습니다. 이제 이 의견은 문제 되지 않습니다. 최적화의 경우에는 여러분이 포럼을 사용 방법과 포럼을 사용하는 목표가 무엇인지 여러분이 알고 있는지에 따라 달라집니다. 최적화를 올바르게 사용하면 이를 통해 원하는 결과를 얻을 수 있습니다. 일반적으로 최적화는 매우 유용합니다.

많은 사람들이 최적화를 좋아하지 않습니다. 여기에는 두 가지 객관적인 이유가 있습니다:

• 기본 사항(왜, 무엇을, 어떻게 해야 하는지, 결과를 선택하는 방법 및 이와 관련된 모든 것, 경험 부족 등)에 대한 이해 부족.
• 최적화 알고리즘의 불완전성.

사실 이 두 가지 요소는 서로를 강화하는 역할을 합니다. MetaTrader 5 최적화 도구는 구조적으로 흠잡을 데 없지만 최적화 기준과 가능한 필터의 측면에서 보면 여전히 많은 개선이 필요합니다. 지금까지 이 모든 기능은 어린이용 샌드박스와 비슷합니다. 포지티브 포워드 기간을 달성하는 방법 그리고 가장 중요한 이 과정을 통제하는 방법에 대해 생각하는 사람은 거의 없습니다. 저는 이 문제에 대해 오랫동안 생각해 왔습니다. 실제로 현재 기사의 상당 부분을 이 주제에 할애하고 있습니다.

새로운 최적화 알고리즘

우리는 백테스트에서 알려진 평가 기준 외에도 보다 효율적인 결과를 선택하고 후속적인 설정을 적용 하기 위해 알고리즘의 가치를 배가하는 데 도움이 되는 몇 가지 결합된 특성을 생각해낼 수 있습니다. 이러한 특성의 특징은 작업 설정을 찾는 프로세스의 속도를 높일 수 있다는 것입니다. 이를 위해 저는 MetaTrader에서와 유사한 일종의 전략 테스터 보고서를 만들었습니다:

그림 1

이 도구를 사용하면 저는 클릭 한 번으로 원하는 옵션을 선택할 수 있습니다. 클릭하면 설정이 생성되고 저는 즉시 터미널의 해당 폴더로 이동해서 범용 EA가 이를 읽고 이 설정에서 거래를 할 수 있습니다. 원하는 경우 버튼을 클릭하여 EA를 생성할 수도 있으며 별도의 EA가 필요한 경우 내부에 설정이 고정된 EA가 생성됩니다. 표에서 다음 옵션을 선택하면 다시 그려지는 수익 곡선도 있습니다.

표에서 무엇이 계산되는지 알아봅시다. 이러한 특성을 계산하기 위한 주요 요소로 다음과 같은 데이터입니다:

1. Points: 해당 상품의 "_Point"로 표시된 전체 백테스트의 수익입니다.
2. Orders: 완전히 체결된 주문과 체결되지 않은 주문의 수("체결된 주문은 하나만 있을 수 있다"는 규칙에 따라 엄격한 순서로 서로 뒤따릅니다).
3. Drawdown: 잔액 저감.

이러한 값들을 기반으로 다음과 같은 거래 특성이 계산됩니다:

• Math Waiting: 포인트 단위의 수학적 기대치입니다.
• P Factor: [-1 ...] 범위로 정규화 된 수익 계수의 아날로그입니다. 0 ... 1] (제 기준).
• Martingale: 마틴 게일 적용 가능성(제 기준).
• MPM Complex: 앞의 세 가지 지표(제 기준)를 종합한 지표입니다.

이제 이러한 기준이 어떻게 계산되는지 살펴보겠습니다:

방정식 1

보시다시피, 제가 만든 모든 기준은 매우 간단하고 이해하기 쉽습니다. 각각의 기준이 증가하는 것은 확률 이론의 측면에서 백테스트 결과가 더 좋다는 것을 의미하기 때문에 제가 MPM 복합 기준에서 한 것과 같이 이러한 기준을 곱하는 것이 가능해집니다. 공통 메트릭을 사용하면 중요도에 따라 결과를 더 효과적으로 정렬할 수 있습니다. 이렇게 하면 대규모 최적화의 경우 각각 더 많은 고품질 옵션을 유지하고 더 많은 저품질 옵션을 제거할 수 있습니다.

또한 이러한 계산에서는 모든 것이 포인트 단위로 이루어집니다. 이는 최적화 프로세스에 긍정적인 영향을 미칩니다. 계산에는 항상 처음에 계산되는 양의 기본 수량이 사용되며 나머지는 모두 이를 기준으로 계산됩니다. 표에는 없는 주요 수량을 나열해 볼 필요가 있습니다.

• Points Plus: 각 수익 또는 영점 주문의 수익 합계(포인트)
• Points Minus: 수익성이 없는 각 주문의 손실 모듈을 포인트로 환산한 합계
• Drawdown: 잔액 기준 드로다운(저만의 방식으로 계산)

여기서 가장 흥미로운 점은 드로다운이 계산되는 방식입니다. 우리의 경우 이것은 최대 상대적 잔액 감소입니다. 저의 테스트 알고리즘이 자금 곡선을 모니터링 하는 것이 불가능 하다는 사실을 고려할 때 다른 유형의 드로다운은 계산될 수 없습니다. 하지만 제가 이 삭감액을 어떻게 계산했는지 그 방법을 보여드리면 유용할 것 같습니다:

그림 2

매우 간단하게 정의됩니다:

1. 백테스트의 시작점(첫 번째 드로다운 카운트다운의 시작)을 계산합니다.
2. 만약 거래가 수익인것으로 시작되면 잔액이 증가함에 따라 첫 번째 음수 값이 나타날 때까지 이 지점을 위로 이동합니다(드로다운 계산의 시작을 표시합니다).
3. 잔액이 기준점 수준에 도달할 때까지 기다립니다. 그런 다음 새 기준점으로 설정합니다.
4. 드로다운 검색의 마지막 섹션으로 돌아가서 가장 낮은 지점을 찾습니다(이 섹션의 드로다운 양은 이 지점부터 계산됩니다).
5. 전체 백테스트 또는 트레이딩 곡선에 대해 전체 프로세스를 반복합니다.

마지막 주기는 항상 미완성 상태로 유지됩니다. 그러나 테스트가 계속 진행되면 더 늘어날 가능성이 있다는 점도 고려해야 합니다. 그러나 이것은 여기서 특별히 중요한 것은 아닙니다.

가장 중요한 최적화 기준

이제 가장 중요한 필터에 대해 이야기해 보겠습니다. 실제로 이 기준은 최적화 결과를 선택할 때 가장 중요한 기준입니다. 이 기준이 MetaTrader 5 최적화 도구의 기능에 포함되어 있지 않다는 사실은 아쉽습니다. 누구나 자신의 코드에서 이 알고리즘을 재현할 수 있도록 제가 그 이론적인 자료를 제공하겠습니다. 실제로 이 기준은 모든 유형의 트레이딩에 적용되며 스포츠 베팅, 암호화폐 등 모든 수익 곡선에 적용될 수 있습니다. 기준은 다음과 같습니다:

방정식 2

이 방정식 안에 무엇이 있는지 살펴봅시다:

• N - 전체 백테스트 또는 트레이딩 구간에서 진입 및 청산된 거래 포지션 수입니다.
• B(i) - 청산 포지션 "i" 이후의 밸런스 라인 값입니다.
• L(i) - 0에서 잔액의 마지막 지점(최종 저울)까지 그려진 직선입니다.

이 매개 변수를 계산하려면 우리는 두 가지 백 테스트를 수행해야 합니다. 첫 번째 백테스트는 최종 잔액을 계산합니다. 그 후에는 각 잔액 포인트의 값을 저장하여 해당 지표를 계산할 수 있으므로 불필요한 계산을 할 필요가 없습니다. 그럼에도 불구하고 이 계산은 반복 백테스트라고 할 수 있습니다. 이 방정식은 사용자 지정 테스터에서 사용할 수 있으며 EA에 내장될 수 있습니다.

이 지표는 이해를 돕기 위해 전체적으로 수정될 수 있다는 점을 알아 두세요. 예를 들면 다음과 같습니다:

방정식 3

이 방정식은 인식과 이해의 측면에서 더 어렵습니다. 그러나 실용적인 관점에서 볼 때 이러한 기준은 높을수록 편리해집니다. 왜냐하면 균형 곡선이 직선과 비슷해지기 때문입니다. 저는 이전 글에서 비슷한 문제에 대해 언급했지만 그 이면의 의미에 대해서는 설명하지 않았습니다. 먼저 다음 그림을 살펴보겠습니다:

그림 3

이 그림은 균형선과 두 개의 곡선을 보여줍니다. 하나는 방정식(빨간색)과 관련된 곡선이고, 다른 하나는 다음과 같은 수정된 기준(방정식 11)에 대한 곡선입니다. 더 자세히 보여드리겠지만 지금은 방정식에 좀더 집중해 보겠습니다.

백테스트를 잔액이 있는 단순한 점의 배열로 상상하면 이를 통계적 표본으로 표현하고 여기에 확률 이론 방정식을 적용할 수 있습니다. 직선을 우리가 추구하는 모델로, 수익 곡선 자체를 우리 모델이 추구하는 실제 데이터 흐름으로 각각 간주합니다.

여기서 선형성 계수는 사용 가능한 전체 거래 기준 세트의 신뢰성을 나타낸다는 점을 이해하는 것이 중요합니다. 결과적으로 데이터의 신뢰도가 높을수록 선물환 기간이 길어지고 수익성이 좋아질 수 있습니다(향후 수익성 있는 거래). 엄밀히 말하면 처음에는 무작위 변수를 고려하면서 그런 것들을 고려하기 시작 했어야 했습니다. 그러나 이런 표현이 더 이해하기 쉬울 것 같았습니다.

무작위 스파이크 가능성을 고려하여 선형성 계수의 대체 아날로그를 만들어 보겠습니다. 이를 위해서는 이후 분산을 계산하기 위해 우리에게 편리한 무작위 변수와 그 평균을 도입해야 합니다:

방정식 4

이해를 돕기 위해 우리에게 "N"개의 진입 포지션과 청산 포지션이 있으며 이는 엄격하게 차례로 이어진다고 가정합니다. 즉 이는 우리에게 균형선의 이러한 세그먼트를 연결하는 "N+1" 포인트가 있다는 것입니다. 모든 선의 영점은 공통적이므로 마지막 점과 마찬가지로 결과가 개선되는 방향으로 왜곡됩니다. 따라서 이러한 영점을 계산에서 제외하면 계산을 수행할 "N-1" 포인트만 남게 됩니다.

두 줄의 값 배열을 하나로 변환하기 위한 표현식의 선택은 매우 흥미로웠습니다. 다음 부분을 참고하세요:

방정식 5

여기서 중요한 것은 모든 경우에 모든 것을 최종 잔액으로 나눈다는 것입니다. 따라서 모든 것을 상대적인 값으로 환원하고 모든 테스트된 전략에 대해 계산된 특성의 동등성을 보장합니다. 선형성 계수의 첫 번째와 간단한 기준에 동일한 분수가 존재하는 것은 우연이 아니며 이는 동일한 고려 사항을 기반으로 구축되었기 때문입니다. 하지만 대체 기준의 구성을 완료해 보겠습니다. 이를 위해 우리는 분산과 같은 잘 알려진 개념을 사용할 수 있습니다:

방정식 6

분산은 전체 샘플의 평균에서 제곱 편차의 산술 평균에 불과합니다. 저는 즉시 위에 정의된 식에 무작위 변수를 대입했습니다. 이상적인 곡선의 평균 편차는 0이며 결과적으로 주어진 샘플의 분산도 0이 됩니다. 이러한 데이터를 기반으로 생각해 보면 사용된 무작위 변수 또는 샘플(원하는 대로)의 구조로 인해 이 분산을 대체 선형성 인자로 사용할 수 있다는 것을 쉽게 알 수 있습니다. 또한 두 가지 기준을 함께 사용하여 샘플 매개변수를 보다 효과적으로 제한할 수도 있지만 솔직히 저는 첫 번째 기준만 사용합니다.

우리가 정의한 새로운 선형성 계수를 기반으로 하는 유사하고 더 편리한 기준을 살펴보겠습니다:

방정식 7

보시다시피 이는 첫 번째 기준(방정식 2)을 기반으로 만들어진 유사한 기준과 동일합니다. 그러나 이 두 가지 기준은 우리가 생각할 수 있는 범위의 한계와는 거리가 있습니다. 이 부분을 옹호하는 것은 이 기준이 너무 이상적으로 되어 있어 이상적인 모델에 더 적합하며 어느 정도 EA를 조정하는 것이 매우 어렵다는 것입니다. 이제 방정식을 적용한 후 언젠가는 분명하게 드러날 부정적인 요소들을 알아볼 필요가 있습니다.

1. 거래 횟수 대폭 감소(결과의 신뢰성 감소)
2. 효율적인 시나리오의 최대 수 거부 (전략에 따라 곡선이 항상 직선으로 향하는 것은 아님)

이러한 단점은 매우 중요한데 목표는 좋은 전략을 폐기하는 것이 아니라 반대로 이러한 단점이 없는 새롭고 개선된 기준을 찾는 것이기 때문입니다. 이러한 단점은 여러 가지 선호 라인을 한 번에 도입하여 완전히 또는 부분적으로 중성화 될 수 있으며 각 라인은 수용 가능하거나 선호하는 모델로 간주될 수 있습니다. 이러한 단점이 없는 새로운 개선된 기준을 이해하려면 여러분은 해당되는 대체 항목만 이해하면 됩니다:

방정식 8

그런 다음 목록에서 각 곡선에 대한 맞춤 계수를 계산할 수 있습니다:

방정식 9

마찬가지로 각 곡선에 대해 무작위 스파이크를 고려하는 대체 기준을 계산할 수도 있습니다:

방정식 10

그런 다음 다음을 계산해야 합니다:

방정식 11

여기서는 곡선 패밀리 계수라는 기준을 소개합니다. 실제로 이 작업을 통해 우리는 거래 곡선과 가장 유사한 곡선을 동시에 찾고 이에 대응하는 계수를 즉시 찾습니다. 최소 매칭 계수를 가진 곡선이 실제에 가장 가까운 곡선입니다. 물론 우리는 이 값을 수정된 기준의 값으로 사용하며 두 가지 변형 중 어느 것이 더 마음에 드는지에 따라 계산은 두 가지 방법으로 수행될 수 있습니다.

이 모든 것이 매우 멋지지만 많은 분들이 이미 알아 차렸 듯이 여기에는 그러한 곡선 제품군의 선택과 관련된 뉘앙스가 있습니다. 이러한 패밀리를 올바르게 설명하기 위해 다양한 고려 사항을 따를 수 있지만 제 생각은 다음과 같습니다:

• 모든 곡선에는 변곡점이 없어야 합니다(이후의 각 중간 지점은 이전 지점보다 엄격하게 높아야 합니다).
• 곡선은 오목해야 합니다(곡선의 가파른 정도는 일정하거나 증가만 할 수 있습니다).
• 곡선의 오목함이 조정될 수 있어야 합니다(예: 상대 값 또는 백분율을 사용하여 편향의 양을 조정해야 함).
• 곡선 모델 단순성(처음에는 단순하고 이해하기 쉬운 그래픽 모델을 기반으로 모델을 만드는 것이 좋습니다).

이것은 이 곡선 계열의 초기 변형일 뿐입니다. 원하는 모든 구성을 고려하여 더 광범위한 변형을 할 수 있으므로 품질 설정이 손실되는 것을 완전히 방지할 수 있습니다. 이 작업은 나중에 다룰 예정이지만 지금은 오목 곡선 계열의 원래 전략에 대해서만 다루겠습니다. 저는 수학에 대한 지식을 활용해 아주 쉽게 그런 패밀리를 만들 수 있었습니다. 이 곡선 계열이 궁극적으로 어떤 모습인지 바로 보여드리겠습니다:

그림 4

이러한 제품군을 구성할 때 저는 수직 지지대 위에 놓인 탄성 막대를 추상화 하는 방식을 이용했습니다. 이러한 막대의 휨 정도는 힘의 적용 지점과 크기에 따라 달라집니다. 이것은 우리가 여기서 다루고 있는 것과 다소 유사하지만 시각적으로 유사한 모델을 개발하는 것으로도 충분히 가치 있는 일입니다. 물론 이 상황에서 우리는 우선 백 테스트 차트의 포인트 중 하나와 일치해야 하는 극한의 좌표를 결정해야 하며 여기서 X축은 0에서 시작하는 거래 지수로 표시됩니다. 이렇게 계산합니다:

방정식 12

여기에는 짝수인 경우와 홀수인 경우의 두 가지 경우가 있습니다. "N"이 짝수로 밝혀지면 인덱스가 정수여야 하므로 단순히 2로 나누는 것은 불가능합니다. 그건 그렇고 저는 마지막 사진에서 이 경우를 정확히 묘사했습니다. 사진에서 힘을 가하는 지점은 처음에 조금 더 가깝습니다. 물론 여러분은 반대로 할 수도 있고 마지막에 조금 더 가까워 질 수도 있지만 이는 그림에서 묘사한 것처럼 적은 수의 거래에서만 중요 할 것입니다. 거래 수가 증가하면 이 모든 것이 최적화 알고리즘에 큰 역할을 하지 못합니다.

백테스트의 "P" 편향 값과 "B" 최종 균형을 백분율로 설정하고 극값의 좌표를 미리 결정한 후 허용되는 각 곡선 패밀리에 대한 식을 구성하기 위해 추가 구성 요소를 순차적으로 계산하기 시작할 수 있습니다. 다음으로 백테스트의 시작과 끝을 연결하는 직선의 가파른 정도가 필요합니다:

방정식 13

이 곡선의 또 다른 특징은 "N0"의 횡좌표가 있는 지점에서 각 곡선에 접하는 각도가 "K"와 동일하다는 사실입니다. 저는 방정식을 만들 때 작업에서 이 조건이 필요했습니다. 이는 마지막 그림(그림 4)에서도 그래픽으로 확인할 수 있으며 거기에도 몇 가지 방정식과 아이덴티티가 있습니다. 계속 진행하겠습니다. 이제 다음 값을 계산해야 합니다:

방정식 14

 

"P"는 패밀리 곡선마다 다르게 설정된다는 점에 유의하세요. 엄밀히 말하면 이들은 패밀리에서 하나의 곡선을 구성하기 위한 방정식들입니다. 이러한 계산은 계열의 각각의 곡선에 대해 반복해야 합니다. 그런 다음 또 다른 중요한 비율을 계산해야 합니다:

방정식 15

이러한 구조의 의미를 자세히 살펴볼 필요는 없습니다. 이들은 곡선을 만드는 과정을 단순화하기 위해 만들어졌습니다. 마지막 보조 비율을 계산하는 것이 남아 있습니다:

방정식 16

이제 얻은 데이터를 기반으로 구성된 곡선의 점을 계산하기 위한 수학적 표현식을 얻을 수 있습니다. 그러나 먼저 곡선이 단일 방정식으로 설명되지 않는다는 점을 명확히 할 필요가 있습니다. "N0" 점의 왼쪽에는 하나의 방정식이 있고 오른쪽에는 다른 방정식이 있습니다. 이해하기 쉽도록 다음과 같이 설명할 수 있습니다:

방정식 17

이제 우리는 최종 방정식을 볼 수 있습니다:

방정식 18

이를 다음과 같이 표시할 수도 있습니다:

방정식 19

엄밀히 말하면 이 함수는 개별적이고 보조적인 기능으로 사용되어야 합니다. 하지만 그럼에도 불구하고 우리는 분수 'i'로 값을 계산할 수 있습니다. 물론 이것은 문제의 맥락에서 우리에게 유용한 이점을 가져다 주지는 않을 것입니다.

저는 이러한 수학에 대해 설명하는 것으로 알고리즘 구현의 예시를 제공해야 할 의무가 있습니다. 누구나 자신의 시스템에 쉽게 적용할 수 있는 기성 코드를 얻는 데 관심이 있을 것이라고 생각합니다. 이제 필요한 수량의 계산을 단순화하는 주요 변수와 방법을 정의하는 것부터 시작하겠습니다:

//+------------------------------------------------------------------+
//| Number of lines in the balance model                             |
//+------------------------------------------------------------------+
#define Lines 11 

//+------------------------------------------------------------------+
//| Initializing variables                                           |
//+------------------------------------------------------------------+
double MaxPercent = 10.0;
double BalanceMidK[,Lines];
double Deviations[Lines];
int Segments;
double K;

//+------------------------------------------------------------------+
//| Method for initializing required variables and arrays            |
//| Parameters: number of segments and initial balance               |
//+------------------------------------------------------------------+
void InitLines(int SegmentsInput, double BalanceInput) 
{
  Segments = SegmentsInput;
  K = BalanceInput / Segments;
  ArrayResize(BalanceMidK,Segments+1);
  ZeroStartBalances();
  ZeroDeviations();
  BuildBalances();
}

//+------------------------------------------------------------------+
//| Resetting variables for incrementing balances                    |
//+------------------------------------------------------------------+
void ZeroStartBalances()
{
  for (int i = 0; i < Lines; i++ ) 
  {
      for (int j = 0; j <= Segments; j++)
      {
          BalanceMidK[j,i] = 0.0;
      }
  }
}

//+------------------------------------------------------------------+
//| Reset deviations                                                 |
//+------------------------------------------------------------------+
void ZeroDeviations()
{
  for (int i = 0; i < Lines; i++)
  {
      Deviations[i] = -1.0;
  }
}

이 코드는 재사용할 수 있도록 설계되었습니다. 다음 계산 후에는 먼저 InitLines 메서드를 호출하여 다른 밸런스 곡선에 대한 지표를 계산할 수 있습니다. 백테스트의 최종 잔액과 거래 횟수를 입력한 후 이 데이터를 기반으로 곡선의 구성을 시작할 수 있습니다:

//+------------------------------------------------------------------+
//| Constructing all balances                                        |
//+------------------------------------------------------------------+
void BuildBalances()
{
   int N0 = MathFloor(Segments / 2.0) - Segments / 2.0 == 0 ? Segments / 2 : (int)MathFloor(Segments / 2.0);//calculate first required N0
   for (int i = 0; i < Lines; i++)
   {
       if (i==0)//very first and straight line 
       {
           for (int j = 0; j <= Segments; j++)
           {
               BalanceMidK[j,i] = K*j;
           }
       }
       else//build curved lines
       {
           double ThisP = i * (MaxPercent / 10.0);//calculate current line curvature percentage
           double KDelta = ( (ThisP /100.0) * K * Segments) / (MathPow(N0,2)/2.0 );//calculation first auxiliary ratio
           double Psi0 = -KDelta * N0;//calculation second auxiliary ratio
           double KDelta1 = ((ThisP / 100.0) * K * Segments) / (MathPow(Segments-N0, 2) / 2.0);//calculate last auxiliary ratio
           //this completes the calculation of auxiliary ratios for a specific line, it is time to construct it

           for (int j = 0; j <= N0; j++)//construct the first half of the curve 
           {
               BalanceMidK[j,i] = (K + Psi0 + (KDelta * j) / 2.0) * j;
           }
           for (int j = N0; j <= Segments; j++)//construct the second half of the curve 
           {
               BalanceMidK[j,i] = BalanceMidK[i, N0] + (K + (KDelta1 * (j-N0)) / 2.0) * (j-N0);
           }
       }
   }
}

'Lines'는 패밀리에서 곡선의 개수를 결정합니다. 오목한 부분은 해당 그림에 표시된 것처럼 0(직선)에서 최대 퍼센트까지 점차적으로 증가합니다. 그런 다음 각 곡선의 편차를 계산하고 최소값을 선택할 수 있습니다:

//+------------------------------------------------------------------+
//| Calculation of the minimum deviation from all lines              |
//| Parameters: initial balance passed via link                      |
//| Return: minimum deviation                                        |
//+------------------------------------------------------------------+
double CalculateMinDeviation(double &OriginalBalance[])
{
   //define maximum relative deviation for each curve 
   for (int i = 0; i < Lines; i++)
   {
       for (int j = 0; j <= Segments; j++)
       {
          double CurrentDeviation = OriginalBalance[Segments] ? MathAbs(OriginalBalance[j] - BalanceMidK[j, i]) / OriginalBalance[Segments] : -1.0;
          if (CurrentDeviation > Deviations[i])
          {
              Deviations[i] = CurrentDeviation;
          }           
       }
   }
    
   //determine curve with minimum deviation and deviation itself 
   double MinDeviation=0.0;
   for (int i = 0; i < Lines; i++)
   {
       if ( Deviations[i] != -1.0 && MinDeviation == 0.0)
       {
           MinDeviation = Deviations[i];
       }
       else if (Deviations[i] != -1.0 && Deviations[i] < MinDeviation)
       {
           MinDeviation = Deviations[i];
       }
   }
   return MinDeviation;
}

이렇게 사용해야 합니다:

1. OriginalBalance 원본 잔액 배열의 정의입니다.
2. 길이 SegmentsInput과 최종 잔액 BalanceInput을 결정하고 InitLines 메서드를 호출합니다.
3. 그런 다음 BuildBalances 메서드를 호출하여 곡선을 빌드합니다.
4. 곡선이 플롯되었으므로 곡선 계열에 대한 개선된 CalculateMinDeviation 기준을 고려할 수 있습니다.

이것으로 기준 계산이 완료되었습니다. 곡선 패밀리 팩터 계산에 어려움이 없을 것이라고 생각합니다. 여기에 제시할 필요는 없습니다.

트레이딩 구성 자동 검색 

전체 아이디어에서 가장 중요한 요소는 터미널과 내 프로그램 간의 상호 작용 시스템입니다. 실제로 이것은 고급 최적화 기준을 갖춘 순환 최적화 프로그램입니다. 가장 중요한 것은 이전 섹션에서 다루었습니다. 전체 시스템이 작동하려면 먼저 MetaTrader 5 터미널 중 하나인 호가 소스가 필요합니다. 이전 글에서 이미 설명했듯이 호가는 내게 편리한 형식으로 파일에 기록됩니다. 이것은 언뜻 보기에 다소 이상하게 작동하는 EA를 사용하여 수행됩니다:

.

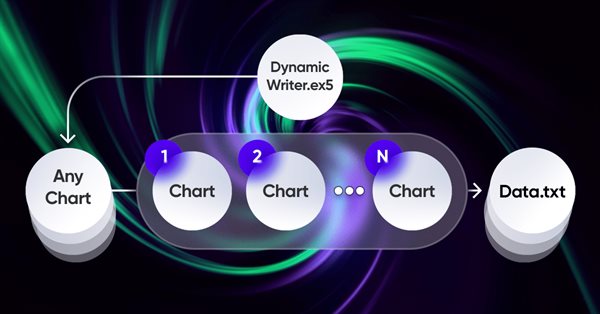
EA의 기능에 저만의 독특한 체계를 사용하는 것은 꽤 흥미롭고 유익한 경험이었습니다. 여기서 다룬것은 제가 해결해야 했던 문제의 데모 일뿐이지만 이 모든 것은 EA를 사용한 거래에서도 사용될 수 있습니다:

 

이 구성표의 특징은 우리가 선택할 그래프에서 그래프를 선택한다는 것이며 데이터 중복을 피하기 위해 트레이딩 도구로 사용되지 않고 틱 핸들러 또는 타이머로만 작동합니다. 나머지 차트는 우리가 시세를 생성해야 하도록 하는 상품 기간을 나타냅니다.

호가 작성은 난수 생성기를 사용하여 호가를 무작위로 선택하는 방식으로 이루어집니다. 필요한 경우 이 프로세스를 최적화할 수 있습니다. 이 기본 함수를 사용하면 일정 시간이 지난 후에 쓰기가 이루어집니다:

//+------------------------------------------------------------------+
//| Function to write data if present                                |
//| Write quotes to file                                             |
//+------------------------------------------------------------------+
void WriteDataIfPresent()
{
    // Declare array to store quotes 
    MqlRates rates[];
    ArraySetAsSeries(rates, false);

    // Select a random chart from those we added to the workspace 
    ChartData Chart = SelectAnyChart();
    
    // If the file name string is not empty 
    if (Chart.FileNameString != "")
    {
        // Copy quotes and calculate the real number of bars
        int copied = CopyRates(Chart.SymbolX, Chart.PeriodX, 1,
                        int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX))),
                        rates);
        
        // Calculate ideal number of bars
        int ideal = int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX)));
        
        // Calculate percentage of received data 
        double Percent = 100.0 * copied / ideal;
        
        // If the received data is not very different from the desired data, 
        // then we accept them and write them to a file
        if (Percent >= 95.0)
        {
            // Open file (create it if it does not exist, 
            // otherwise, erase all the data it contained)
            OpenAndWriteStart(rates, Chart, CommonE); 
            WriteAllBars(rates); // Write all data to file
            WriteEnd(rates); // Add to end
            CloseFile(); // Close and save data file
        }
        else 
        {
            // If there are much fewer quotes than required for calculation 
            Print("Not enough data"); 
        }
    }
}

WriteDataIfPresent 함수는 복사된 데이터가 지정된 매개변수에 따라 계산된 이상적인 막대 수의 95% 이상인 경우 선택한 차트에서 호가에 대한 정보를 파일에 기록합니다. 복사된 데이터가 95% 미만인 경우 '데이터 부족' 메시지가 표시됩니다. 지정된 이름의 파일이 존재하지 않으면 함수가 파일을 만듭니다.

이 코드가 작동하려면 다음 사항들이 추가로 설명되어야 합니다:

//+------------------------------------------------------------------+
//| ChartData structure                                              |
//| Objective: Storing the necessary chart data                      |
//+------------------------------------------------------------------+
struct ChartData {
    string FileNameString;
    string SymbolX;
    ENUM_TIMEFRAMES PeriodX;
};

//+------------------------------------------------------------------+
//| Randomindex function                                             |
//| Objective: Get a random number with uniform distribution         |
//+------------------------------------------------------------------+
int Randomindex(int start, int end) {
    return start + int((double(MathRand())/32767.0)*double(end-start+1));
}

//+------------------------------------------------------------------+
//| SelectAnyChart function                                          |
//| Objective: View all charts except current one and select one of  |
//|       them to write quotes                                       |
//+------------------------------------------------------------------+
ChartData SelectAnyChart() {
    ChartData chosenChart;
    chosenChart.FileNameString = "";
    int chartCount = 0;
    long currentChartId, previousChartId = ChartFirst();

    // Calculate number of charts
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;  
        }
        previousChartId = currentChartId;
        
        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }

    int randomChartIndex = Randomindex(0, chartCount - 1);
    chartCount = 0;
    currentChartId = ChartFirst(); 
    previousChartId = currentChartId;
    
    // Select random chart
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;
        }
        
        previousChartId = currentChartId;
        
        // Fill in selected chart data
        if (chartCount == randomChartIndex) {
            chosenChart.SymbolX = ChartSymbol(currentChartId);
            chosenChart.PeriodX = ChartPeriod(currentChartId);
            chosenChart.FileNameString = "DataHistory" + " " + chosenChart.SymbolX + " " + IntegerToString(CorrectPeriod(chosenChart.PeriodX));
        }
        
        if (chartCount > randomChartIndex) {
            break;
        }

        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }
       
    return chosenChart;
}

이 코드는 현재 단말기에서 열 수 있는 다양한 차트에서 다양한 통화에 대한 과거 금융 시장 데이터(시세)를 기록하고 분석하는 데 사용됩니다.

• ChartData 구조는 파일 이름, 심볼(통화쌍), 기간 등 각 차트의 데이터를 저장하는 데 사용됩니다. 
• "Randomindex(start, end)" 함수는 "시작"과 "끝" 사이에 임의의 숫자를 생성하며 사용 가능한 차트 중 하나를 무작위로 선택하는 데 사용됩니다.
• SelectAnyChart()는 현재 차트를 제외한 열려 있고 사용 가능한 모든 차트를 반복한 다음 처리할 차트 중 하나를 임의로 선택합니다.

생성된 견적은 프로그램에 의해 자동으로 선택되며 그 후 수익성 있는 구성이 자동으로 검색됩니다. 전체 프로세스를 자동화하는 것은 상당히 복잡하지만 저는 이를 하나의 그림으로 나타냈습니다:

그림 5

이 알고리즘에는 세 가지 상태가 있습니다:

1. 비활성화됨.
2. 호가를 기다리는 중입니다.
3. 활성.

호가 기록용 EA가 아직 단일 파일을 생성하지 않았거나 지정된 폴더에서 모든 호가를 삭제한 경우 알고리즘은 호가가 나타날 때까지 기다렸다가 잠시 일시 중지합니다. MQL5 스타일로 구현한 개선된 기준의 경우 무차별 대입과 최적화 모두에 대해 구현되었습니다:

그림 6

표준 알고리즘은 선형성 계수만 사용하는 반면 고급 모드는 곡선 패밀리 계수를 사용합니다. 나머지 개선 사항은 너무 광범위하여 이 글에 모두 담을 수 없습니다. 다음 글에서는 범용 다중 통화 템플릿을 기반으로 EA를 하나로 묶는 새로운 알고리즘을 보여드리겠습니다. 템플릿은 하나의 차트에서 실행되지만 각 EA가 자체 차트에서 실행할 필요 없이 병합된 모든 트레이딩 시스템을 처리합니다. 이 글에서는 일부 기능이 사용되었습니다.

결론

이 기사에서는 트레이딩 시스템 개발 및 최적화 프로세스 자동화 분야의 새로운 기회와 아이디어를 더 자세히 살펴봤습니다. 주요 성과는 새로운 최적화 알고리즘 개발, 터미널 동기화 메커니즘 및 자동 최적화 도구의 생성, 중요한 최적화 기준인 곡선 계수 및 곡선 패밀리입니다. 이를 통해 우리는 개발 시간을 단축하고 결과물의 품질을 개선할 수 있습니다.

역방향 기간의 맥락에서 보다 현실적인 균형 모델을 나타내는 오목 곡선 제품군도 중요한 추가 기능입니다. 각 곡선에 대한 적합도를 계산하면 자동매매를 위한 최적의 설정을 보다 정확하게 선택할 수 있습니다.

링크

• 패턴 검색에 대한 무자비 대입 방식(5부): 신선한 관점
  
• 패턴 검색에서 무자비 대입 방식(4부): 최소한의 기능
• 패턴 검색에서 무자비 대입 방식(3부): 새로운 지평
  
• 패턴 검색에서 무자비 대입 방식(2부): 몰입도
  
• 패턴 검색에서 무자비 대입 방식