
MQL5中使用坐标下降法的弹性网络回归
概述
弹性网络回归(Elastic net regression)结合岭(ridge)和拉索(lasso)技术的最佳品质来构建一般线性模型。应用它可以最大限度地减少回归的一个主要缺点,即过拟合。众所周知,这与交易策略的发展尤其相关,这是表现不佳或策略失败的最常见原因。这是由于在训练过程中将噪音误认为模式的结果。在这篇文章中,我们将介绍弹性网络回归的实现,它在纯MQL5中使用优化的坐标下降方法。在文章的最后,我们将通过开发一个简单的基于移动平均的预测策略来演示该技术的实际应用。
正则化
在构建预测模型时,目标是创建一个能够辨别一些独特模式的样本,这些模式可以用于现实世界。为了有效地做到这一点,我们必须确保模型从训练数据中“学习”相关模式。这显然说起来容易做起来难。通常情况下,模型最终会拾取不相关的信息(噪声),这最终会在使用时损害其性能。正则化是一个用于最小化过拟合影响的过程。
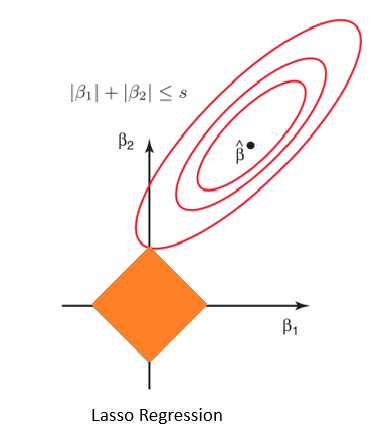
当模型由太多可优化变量定义时,拉索技术通过抑制冗余预测因子来帮助减少训练偏差,从而简化了模型。
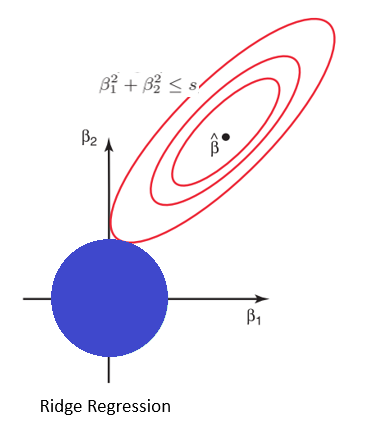
在岭回归中,回归方程的系数被最小化,从而使它们远离最佳值。这有助于在保留所有预测因子的同时泛化模型。
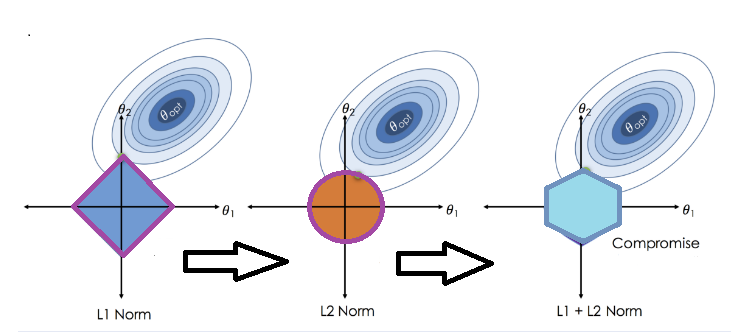
拉索和岭的区别在于所用罚项的性质。弹性净回归惩罚项是系数的绝对值和平方的组合,由两个超参数 alpha 和 lambda 加权。
通过这种方式,alpha控制正则化的类型。当 alpha 为零时,惩罚项减少到l2范数,或者,当alpha为1时,惩罚函数变成l1范数。alpha 在0和1之间的指定使得可以建立线性模型,该线性模型在一定程度上结合了岭回归和拉索回归的性质,如控制正则化程度的lambda超参数所控制的。
当应用于交易策略开发时,这样的模型可能是一个福音,因为我们经常发现自己盲目地应用许多预测因素,希望找到一些能产生利润的组合。使用弹性网络回归,我们可以最大限度地减少过度拟合,同时也能够将无用的指标与具有显著预测潜力的指标区分开来。我们可以做到这一点,而不必担心指标之间的关系。这似乎太好了,不可能是真的。
坐标下降
坐标下降是一种非常适合于多变量优化的优化方法。将复杂的多维优化问题简化为一维问题的集合。通过迭代最小化函数的每个单独维度,同时保持其他维度中函数的值不变来实现。互联网上有许多资源可以为感兴趣的人提供更详细的解释。在这里,我们感兴趣的是它在策略开发中的应用
出于我们的目的,坐标下降法将以两种方式用于实现弹性网络回归。首先,它将用于根据用户指定的固定alpha来确定最佳lambda。一旦完成,就再次调用优化方法来计算回归方程的 beta 系数。让我们深入研究一些代码,看看这是如何实现的。
CoordinateDescent类
//+------------------------------------------------------------------+ //| Coordinate Descent optimization class | //+------------------------------------------------------------------+ class CCoordinateDescent { private: bool m_initialized; // Was everything legal and allocs successful? double m_beta[]; // Beta coefs (m_nvars of them) double m_explained; // Fraction of variance m_explained by model; computed by Train() double m_xmeans[]; // Mean of each X predictor double m_xscales[]; // And standard deviation double m_ymean; // Intercept (mean of Y) double m_yscale; // Standard deviation of Y int m_nvars ; // Number of variables int m_observs ; // Number of cases bool m_covarupdates ; // Does user want (often faster) covariance update method? int m_nlambda ; // Reserve space for this many m_beta sets for saving by TrainLambda() (may be zero) double m_lambdabeta_matrix[]; // Saved m_beta coefs (m_nlambda sets of m_nvars of them) double m_lambdas[]; // Lambdas tested by TrainLambda() double m_x_matrix[]; // Normalized (mean=0, std=1) X; m_observs by m_nvars double m_y[]; // Normalized (mean=0, std=1) Y double m_resid[]; // Residual double m_xinner_matrix[]; // Nvars square inner product matrix if m_covarupdates double m_yinner[]; // Nvars XY inner product vector if m_covarupdates public: //constructor CCoordinateDescent(const int num_predictors, const int num_observations, const bool use_covariance_updates, const int num_lambdas_to_trial) ; //desctructor ~CCoordinateDescent(void) ; //Accessor methods for private properties double GetYmean(void) { return m_ymean; } double GetYscale(void) { return m_yscale;} double GetExplainedVariance(void) { return m_explained;} double GetXmeansAt(const int index) { if(index>=0 && index<ArraySize(m_xmeans)) return m_xmeans[index]; else return 0;} double GetXscalesAt(const int index) { if(index>=0 && index<ArraySize(m_xscales)) return m_xscales[index]; else return 0;} double GetBetaAt(const int index) { if(index>=0 && index<ArraySize(m_beta)) return m_beta[index]; else return 0;} double GetLambdaAt(const int index) { if(index>=0 && index<ArraySize(m_lambdas)) return m_lambdas[index]; else return 0;} double GetLambdaBetaAt(const int index) { if(index>=0 && index<ArraySize(m_lambdabeta_matrix)) return m_lambdabeta_matrix[index]; else return 0;} double GetLambdaThreshold(const double alpha) ; //Set model parameters and raw input data bool SetData(const int begin, const int num_observations, double &xx_matrix[], double &yy[]) ; //Training routines void Train(const double alpha, const double lambda, const int maxits, const double convergence_criterion, const bool fast_test, const bool warm_start) ; void TrainLambda(const double alpha, const int maxits, const double convergence_criterion, const bool fast_test, const double maxlambda, const bool print_steps) ; } ;
CCordinateDescent.mqh文件中定义了CCordinatedDescent类。它的构造函数是参数化的,用于指定模型的重要特征,但在我们深入讨论之前,关于要使用的特定数据构造,还有一些相关的问题。
我们将指定的库不会使用任何唯一的数据类型,例如MQL5的新矩阵和向量类型。这是为了确保与mql4的兼容性。由于无法动态定义多维数组,因此矩阵将表示为正则平面数组。举例说明这个结构是最好的方法
假设我们想要定义一个4行3列的矩阵。我们将创建一个大小为4乘以3的数组,即12。如果使用内置矩阵数据类型,则此数组的成员将按照其显示的方式排列。也就是说,使用我们的示例,首先指定第一行成员,然后指定第二行成员,依此类推。下面的代码片段演示了4乘3矩阵的创建,其中列中的每个值都是相同的。
int rows=4, columns=3; double our_matrix[]; ArrayResize(our_matrix,rows*columns); /* Creating matrix with columns of 1s,2s,3s */ for(int i = 0; i<rows; i++) for(int j=0; j<columns; j++) our_matrix[i*columns+j]=j+1; ArrayPrint(our_matrix);
ArrayPrint的输出。
KP 0 13:01:32.445 Construct(GBPUSD,D1) 1.00000 2.00000 3.00000 1.00000 2.00000 3.00000 1.00000 2.00000 3.00000 1.00000 2.00000 3.00000
当以矩阵方式遍历数组时,我们有行索引*列数+列索引。需要此类数组构造的实例都由类变量名或函数参数名的_matrix后缀表示。
使用这种构造意味着,当将匹配传递给函数时,必须保留一些函数参数来指定特定矩阵的维数。我相信,一旦我们在文章的末尾了解到类的应用程序,它将变得更加直观。如果用户对跨平台可移植性不感兴趣,可以自由派生库。回到类的描述。
//+------------------------------------------------------------------+ //|Constructor | //+------------------------------------------------------------------+ CCoordinateDescent::CCoordinateDescent( const int num_predictors, // Number of predictor variables const int num_observations, // Number of cases we will be training const bool use_covariance_updates, // Use fast covariance updates rather than slow naive method const int num_lambdas_to_trial // Number of m_lambdas we will be using in training )
参数化构造函数需要4个参数:
- num_predictors 设置变量的数量,这是预测器或指标的数量,每组指标将占据内部数据矩阵中的一列。
- num_observations指定对象应该期望的数据量,这将是每一组变量/预测因子/指标中可用的行数或确切的元素数。
- use_covariance_updates是一个布尔选项,理想情况下,当num_observation多于num_predictors时应使用该选项。将其设置为true可显著改善相对于备选方案的执行时间。只有在num_observations>num_predictors时才应考虑此选项。
- num_lambdas_to_trial设置将在训练过程中测试的lambda变化的最大数量。
构造函数只是准备内部数据结构来接收所有所需的数据。
{
m_nvars = num_predictors ;
m_observs = num_observations ;
m_covarupdates = use_covariance_updates ;
m_nlambda = num_lambdas_to_trial ;
m_initialized=true;
m_ymean=m_yscale=m_explained=0;
if(m_nvars<0 || m_observs<0 || m_nlambda<0)
{
m_initialized=false;
Print("Invalid parameter value, neither num_predictors ,num_observations, nor num_lambdas_to_trial can be negative");
return;
}
if(ArrayResize(m_x_matrix,m_observs*m_nvars)<m_observs*m_nvars ||
ArrayResize(m_y,m_observs)<m_observs ||
ArrayResize(m_xmeans,m_nvars)<m_nvars ||
ArrayResize(m_xscales,m_nvars)<m_nvars ||
ArrayResize(m_beta,m_nvars)<m_nvars ||
ArrayResize(m_resid,m_observs)<m_observs)
m_initialized=false;
//---conditional allocation
if(m_covarupdates)
{
if(ArrayResize(m_xinner_matrix,m_nvars*m_nvars)<m_nvars*m_nvars||
ArrayResize(m_yinner,m_nvars)<m_nvars)
m_initialized=false;
}
//---
if(m_nlambda>0)
{
if(ArrayResize(m_lambdabeta_matrix,m_nlambda*m_nvars)<m_nlambda*m_nvars ||
ArrayResize(m_lambdas,m_nlambda)<m_nlambda)
m_initialized=false;
}
//---return immediately if any error
if(!m_initialized)
Print("Memory allocation error ", GetLastError());
}
一旦创建了一个CCordinateDescent实例,我们就必须收集所有的预测因子和目标值进行预处理。这是通过SetData方法完成的。它的第一个参数是一个起始索引,显示要提供给该方法的数组中开始收集数据的位置。这样做有助于以后进行交叉验证。
//+------------------------------------------------------------------+ //|Get and standardize the data | //| Also compute inner products if covar_update | //+------------------------------------------------------------------+ bool CCoordinateDescent::SetData( const int begin, // Starting index in full database for getting m_observs of training set const int num_observations,// Number of cases in full database (we wrap back to the start if needed) double &xx_matrix[], // Full database (num_observations rows, m_nvars columns) double &yy[] // Predicted variable vector, num_observations long )
num_observations是构造函数中已经遇到的参数名称,这里它的使用有点不同。如果此处设置的值小于对象实例化时使用的值,那么一旦达到该索引位置,就可以恢复到数组中的第一个值。如果不需要这样的功能,则将其设置为与构造函数调用中使用的值相同的值。只是不要将其设置为零或更低,因为这会导致错误。
下一个所需的参数xx_matrix是具有所讨论的特殊矩阵排列的阵列。这是我们输入原始指标的地方。它应该是构造函数调用中指定的大小,即num_observations*num_predictors。
最后一个参数yy是相应目标值的数组。
该方法在将两个输入数组复制到内部对象缓冲区之前对其进行标准化。
{
if(!m_initialized)
return false;
// parameter checks
if(begin<0 || num_observations<0)
{
Print("Invalid parameter value: neither begin nor num_observations can be negative");
return false;
}
//--- invalid a
if(ArraySize(xx_matrix)<(m_observs*m_nvars) || ArraySize(yy)<m_observs)
{
Print("Insufficient data supplied relative to object specification");
return false;
}
//---
int icase, ivar, jvar, k,xptr;
double sum, xm, xs, diff;
/*
Standardize X
*/
for(ivar=0 ; ivar<m_nvars ; ivar++)
{
xm = 0.0 ;
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
xm += xx_matrix[k*m_nvars+ivar] ;
}
xm /= m_observs ;
m_xmeans[ivar] = xm ;
xs = 1.e-60 ; // Prevent division by zero later
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
diff = xx_matrix[k*m_nvars+ivar] - xm ;
xs += diff * diff ;
}
xs = sqrt(xs / m_observs) ;
m_xscales[ivar] = xs ;
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
m_x_matrix[icase*m_nvars+ivar] = (xx_matrix[k*m_nvars+ivar] - xm) / xs ;
}
}
/*
Standardize Y
*/
m_ymean = 0.0 ;
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
m_ymean += yy[k] ;
}
m_ymean /= m_observs ;
m_yscale = 1.e-60 ; // Prevent division by zero later
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
diff = yy[k] - m_ymean ;
m_yscale += diff * diff ;
}
m_yscale = sqrt(m_yscale / m_observs) ;
for(icase=0 ; icase<m_observs ; icase++)
{
k = (icase + begin) % num_observations ;
m_y[icase] = (yy[k] - m_ymean) / m_yscale ;
}
/*
If user requests covariance updates, compute required inner products
We store the full m_xinner_matrix matrix for faster addressing later,
even though it is symmetric.
We handle both unweighted and weighted cases here.
*/
if(m_covarupdates)
{
for(ivar=0 ; ivar<m_nvars ; ivar++)
{
xptr = ivar ;
// Do XiY
sum = 0.0 ;
for(icase=0 ; icase<m_observs ; icase++)
sum += m_x_matrix[xptr+icase*m_nvars] * m_y[icase] ;
m_yinner[ivar] = sum / m_observs ;
// Do XiXj
for(jvar=0 ; jvar<m_nvars ; jvar++)
{
if(jvar == ivar)
m_xinner_matrix[ivar*m_nvars+jvar] = 1.0 ; // Recall that X is standardized
else
if(jvar < ivar) // Matrix is symmetric, so just copy
m_xinner_matrix[ivar*m_nvars+jvar] = m_xinner_matrix[jvar*m_nvars+ivar] ;
else
{
sum = 0.0 ;
for(icase=0 ; icase<m_observs ; icase++)
sum += m_x_matrix[xptr+icase*m_nvars] * m_x_matrix[icase*m_nvars+jvar] ;
m_xinner_matrix[ivar*m_nvars+jvar] = sum / m_observs ;
}
}
} // For ivar
}
//---
return true;
} 如果SetData通过返回true成功完成,则用户可以自由调用Train()或TrainLambda(),具体取决于他们想要做什么。
//+------------------------------------------------------------------+ //|Core training routine | //+------------------------------------------------------------------+ void CCoordinateDescent::Train( const double alpha, // User-specified alpha, (0,1) (0 problematic for descending lambda) const double lambda, // Can be user-specified, but usually from TrainLambda() const int maxits, // Maximum iterations, for safety only const double convergence_criterion, // Convergence criterion, typically 1.e-5 or so const bool fast_test, // Base convergence on max m_beta change vs m_explained variance? const bool warm_start // Start from existing m_beta, rather than zero? )
Train()方法是进行核心优化的地方。这里指定了正则化的类型(alpha)和正则化的程度(lambda)。连同要进行的收敛测试的类型(fast_test)和要获得的收敛所需的精度(convergence_criterion)。
- maxits参数是一个故障保护参数,可以防止例程花费不合理的时间来完成,它应该设置为一个相当大的值,比如1000或更多。
- warm_start 指示是否以初始化为零的 beta 权重开始训练。
{
if(!m_initialized)
return;
if(alpha<0 || alpha>1)
{
Print("Invalid parameter value: Legal values for alpha are between 0 and 1 inclusive");
return;
}
if(lambda<0)
{
Print("Invalid parameter value: lambda accepts only positive values");
return;
}
if(maxits<=0)
{
Print("Invalid parameter value: maxist accepts only non zero positive values");
return;
}
int i, iter, icase, ivar, kvar, do_active_only, active_set_changed, converged,xptr ;
double residual_sum, S_threshold, argument, new_beta, correction, update_factor ;
double sum, explained_variance, crit, prior_crit, penalty, max_change, Xss, YmeanSquare ;
/*
Initialize
*/
S_threshold = alpha * lambda ; // Threshold for the soft-thresholding operator S()
do_active_only = 0 ; // Begin with a complete pass
prior_crit = 1.0e60 ; // For convergence test
if(warm_start) // Pick up with current betas?
{
if(! m_covarupdates) // If not using covariance updates, must recompute residuals
{
for(icase=0 ; icase<m_observs ; icase++)
{
xptr = icase * m_nvars ;
sum = 0.0 ;
for(ivar=0 ; ivar<m_nvars ; ivar++)
sum += m_beta[ivar] * m_x_matrix[xptr+ivar] ;
m_resid[icase] = m_y[icase] - sum ;
}
}
}
else // Not warm start, so initial betas are all zero
{
for(i=0 ; i<m_nvars ; i++)
m_beta[i] = 0.0 ;
for(i=0 ; i<m_observs ; i++) // Initial residuals are just the Y variable
m_resid[i] = m_y[i] ;
}
// YmeanSquare will remain fixed throughout training.
// Its only use is for computing m_explained variance for the user's edification.
YmeanSquare = 1.0 ;
/*
Outmost loop iterates until converged or user's maxits limit hit
*/
for(iter=0 ; iter<maxits ; iter++)
{
/*
Pass through variables
*/
active_set_changed = 0 ; // Did any betas go to/from 0.0?
max_change = 0.0 ; // For fast convergence test
for(ivar=0 ; ivar<m_nvars ; ivar++) // Descend on this m_beta
{
if(do_active_only && m_beta[ivar] == 0.0)
continue ;
Xss = 1 ; // X was standardized
update_factor = Xss + lambda * (1.0 - alpha) ;
if(m_covarupdates) // Any sensible user will specify this unless m_observs < m_nvars
{
sum = 0.0 ;
for(kvar=0 ; kvar<m_nvars ; kvar++)
sum += m_xinner_matrix[ivar*m_nvars+kvar] * m_beta[kvar] ;
residual_sum = m_yinner[ivar] - sum ;
argument = residual_sum + Xss * m_beta[ivar] ; // Argument to S() [MY FORMULA]
}
else
// Use slow definitional formula (okay if m_observs < m_nvars)
{
residual_sum = 0.0 ;
xptr = ivar ; // Point to column of this variable
for(icase=0 ; icase<m_observs ; icase++)
residual_sum += m_x_matrix[xptr+icase*m_nvars] * m_resid[icase] ; // X_ij * RESID_i
residual_sum /= m_observs ;
argument = residual_sum + m_beta[ivar] ; // Argument to S() ; (Eq 8)
}
// Apply the soft-thresholding operator S()
if(argument > 0.0 && S_threshold < argument)
new_beta = (argument - S_threshold) / update_factor ;
else
if(argument < 0.0 && S_threshold < -argument)
new_beta = (argument + S_threshold) / update_factor ;
else
new_beta = 0.0 ;
// Apply the update, if changed, and adjust the residual if using naive or weighted updates
// This is also used to update the fast convergence criterion
correction = new_beta - m_beta[ivar] ; // Will use this to adjust residual if using naive updates
if(fabs(correction) > max_change)
max_change = fabs(correction) ; // Used for fast convergence criterion
if(correction != 0.0) // Did this m_beta change?
{
if(! m_covarupdates) // Must we update the residual vector (needed for naive methods)?
{
xptr = ivar ; // Point to column of this variable
for(icase=0 ; icase<m_observs ; icase++) // Update residual for this new m_beta
m_resid[icase] -= correction * m_x_matrix[xptr+icase*m_nvars] ;
}
if((m_beta[ivar] == 0.0 && new_beta != 0.0) || (m_beta[ivar] != 0.0 && new_beta == 0.0))
active_set_changed = 1 ;
m_beta[ivar] = new_beta ;
}
} // For all variables; a complete pass
/*
A pass (complete or active only) through variables has been done.
If we are using the fast convergence test, it is simple. But if using the slow method...
Compute m_explained variance and criterion; compare to prior for convergence test
If the user requested the covariance update method, we must compute residuals for these.
*/
if(fast_test) // Quick and simple test
{
if(max_change < convergence_criterion)
converged = 1 ;
else
converged = 0 ;
}
else // Slow test (change in m_explained variance) which requires residual
{
if(m_covarupdates) // We have until now avoided computing residuals
{
for(icase=0 ; icase<m_observs ; icase++)
{
xptr = icase * m_nvars ;
sum = 0.0 ;
for(ivar=0 ; ivar<m_nvars ; ivar++)
sum += m_beta[ivar] * m_x_matrix[xptr+ivar] ; // Cumulate predicted value
m_resid[icase] = m_y[icase] - sum ; // Residual = true - predicted
}
}
sum = 0.0 ; // Will cumulate squared error for convergence test
for(i=0 ; i<m_observs ; i++)
sum += m_resid[i] * m_resid[i] ;
crit = sum / m_observs ; // MSE component of optimization criterion
explained_variance = (YmeanSquare - crit) / YmeanSquare ; // Fraction of Y m_explained
penalty = 0.0 ;
for(i=0 ; i<m_nvars ; i++)
penalty += 0.5 * (1.0 - alpha) * m_beta[i] * m_beta[i] + alpha * fabs(m_beta[i]) ;
penalty *= 2.0 * lambda ; // Regularization component of optimization criterion
crit += penalty ; // This is what we are minimizing
if(prior_crit - crit < convergence_criterion)
converged = 1 ;
else
converged = 0 ;
prior_crit = crit ;
}
/*
After doing a complete (all variables) pass, we iterate on only
the active set (m_beta != 0) until convergence. Then we do a complete pass.
If the active set does not change, we are done:
If a m_beta goes from zero to nonzero, by definition the active set changed.
If a m_beta goes from nonzero to another nonzero, then this is a theoretical flaw
in this process. However, if we just iterated the active set to convergence,
it is highly unlikely that we would get anything other than a tiny move.
*/
if(do_active_only) // Are we iterating on the active set only?
{
if(converged) // If we converged
do_active_only = 0 ; // We now do a complete pass
}
else // We just did a complete pass (all variables)
{
if(converged && ! active_set_changed)
break ;
do_active_only = 1 ; // We now do an active-only pass
}
} // Outer loop iterations
/*
We are done. Compute and save the m_explained variance.
If we did the fast convergence test and covariance updates,
we must compute the residual in order to get the m_explained variance.
Those two options do not require regular residual computation,
so we don't currently have the residual.
*/
if(fast_test && m_covarupdates) // Residuals have not been maintained?
{
for(icase=0 ; icase<m_observs ; icase++)
{
xptr = icase * m_nvars ;
sum = 0.0 ;
for(ivar=0 ; ivar<m_nvars ; ivar++)
sum += m_beta[ivar] * m_x_matrix[xptr+ivar] ;
m_resid[icase] = m_y[icase] - sum ;
}
}
sum = 0.0 ;
for(i=0 ; i<m_observs ; i++)
sum += m_resid[i] * m_resid[i] ;
crit = sum / m_observs ; // MSE component of optimization criterion
m_explained = (YmeanSquare - crit) / YmeanSquare ; // This variable is a member of the class
} 当我们迭代观察时,我们还计算解释的目标方差的分数。当使用慢收敛测试时(fast_test设置为false),当从一次迭代到下一次迭代的变化小于指定的收敛标准值时,即可实现收敛。
否则,如果使用快速方法,则当所有 beta 中 beta 调整的最大变化小于收敛标准时,实现收敛。
//+------------------------------------------------------------------+ //|Compute minimum lambda such that all betas remain at zero | //+------------------------------------------------------------------+ double CCoordinateDescent::GetLambdaThreshold(const double alpha) { if(!m_initialized) return 0; if(alpha>1 || alpha<0) { Print("Invalid parameter for Alpha, legal values are between 0 and 1 inclusive"); return 0; } int ivar, icase,xptr ; double thresh, sum; thresh = 0.0 ; for(ivar=0 ; ivar<m_nvars ; ivar++) { xptr = ivar ; sum = 0.0 ; for(icase=0 ; icase<m_observs ; icase++) sum += m_x_matrix[xptr+icase*m_nvars] * m_y[icase] ; sum /= m_observs ; sum = fabs(sum) ; if(sum > thresh) thresh = sum ; } return thresh / (alpha + 1.e-60) ; }
GetLambdaThreshold()需要一个指定正则化类型的输入参数。此方法返回lambda的计算值,所有对应的 beta 都为零。其想法是,这样的值将是开始搜索给定 alpha 的最佳 lambda 超参数的好地方。
lambda的实际优化是由TrainLambda()完成的。它的函数参数与Train()类似。用户可以通过 maxlambda 指定起始 lambda 值。将其设置为0或更小会自动使用 GetlambdaThreshold()来设置真正的起始值。主循环重复调用Train(),并为每个 lambda 保存 beta,以便在构造函数调用中指定最多m_nlambda迭代。
//+----------------------------------------------------------------------------------------+ //| Multiple-lambda training routine calls Train() repeatedly, saving each m_beta vector | | //+----------------------------------------------------------------------------------------+ void CCoordinateDescent::TrainLambda( const double alpha, // User-specified alpha, (0,1) (0 problematic for descending lambda) const int maxits, // Maximum iterations, for safety only const double convergence_criterion, // Convergence criterion, typically 1.e-5 or so const bool fast_test, // Base convergence on max m_beta change vs m_explained variance? const double maxlambda, // Starting lambda, or negative for automatic computation const bool print_steps // Print lambda/m_explained table? ) { if(!m_initialized) return; int ivar, ilambda, n_active ; double lambda, min_lambda, lambda_factor,max_lambda=maxlambda; string fprint ; if(m_nlambda <= 1) return ; /* Compute the minimum lambda for which all m_beta weights remain at zero This (slightly decreased) will be the lambda from which we start our descent. */ if(max_lambda <= 0.0) max_lambda = 0.999 * GetLambdaThreshold(alpha) ; min_lambda = 0.001 * max_lambda ; lambda_factor = exp(log(min_lambda / max_lambda) / (m_nlambda-1)) ; /* Repeatedly train with decreasing m_lambdas */ if(print_steps) { fprint+="\nDescending lambda path..."; } lambda = max_lambda ; for(ilambda=0 ; ilambda<m_nlambda ; ilambda++) { m_lambdas[ilambda] = lambda ; // Save in case we want to use later Train(alpha, lambda, maxits, convergence_criterion, fast_test,(bool)ilambda) ; for(ivar=0 ; ivar<m_nvars ; ivar++) m_lambdabeta_matrix[ilambda*m_nvars+ivar] = m_beta[ivar] ; if(print_steps) { n_active = 0 ; for(ivar=0 ; ivar<m_nvars ; ivar++) { if(fabs(m_beta[ivar]) > 0.0) ++n_active ; } fprint+=StringFormat("\n %8.4lf %4d %12.4lf", lambda, n_active, m_explained) ; } lambda *= lambda_factor ; } if(print_steps) Print(fprint); }
我们的坐标下降类已经完整了,我们接下来需要的是一个进行交叉验证的工具,以便调整lambda超参数。
OptimizeLambda 函数
//+------------------------------------------------------------------------------------------+ //| Cross-validation training routine calls TrainLambda() repeatedly to optimize lambda | //+------------------------------------------------------------------------------------------+ double OptimizeLambda( int n_observations, // Number of cases in full database int n_predictors, // Number of variables (columns in database) int n_folds, // Number of folds bool covar_updates, // Does user want (usually faster) covariance update method? int n_lambda, // This many out_lambdas tested by lambda_train() (must be at least 2) double alpha, // User-specified alpha, (0,1) (0 problematic for descending lambda) int maxits, // Maximum iterations, for safety only double convergence_criterion, // Convergence criterion, typically 1.e-5 or so bool fast_test, // Base convergence on max beta change vs explained variance? double &in_matrix[], // Full database (n_observations rows, n_predictors columns) double &in_targets[], // Predicted variable vector, n_observations long double &out_lambdas[], // Returns out_lambdas tested by lambda_train() double &out_lambda_OOS[], // Returns OOS explained for each of above out_lambdas bool print_output = false // show full output )
其主要目的是实现交叉验证训练,以自动选择lambda超参数。它的大多数输入参数都有熟悉的名称,因为例程使用坐标下降优化。
当用户不确定要使用哪个lambda值时,可以选择使用此函数。交叉验证是调整超参数的常用技术。要使用它,我们显然会传递相同的训练数据,这些数据最终将用于构建完整的回归模型。
in_matrix是预测器矩阵的输入,in_targets是对应目标的输入。除了这些输入数组,我们还必须提供另外两个数组。out_lambdas 和 out_lambda_OOS 是将保存交叉验证过程的更精细细节的数组。
最后一个参数指示是否将处理结果打印到终端。
{
int i_IS, n_IS, i_OOS, n_OOS, n_done, ifold ;
int icase, ivar, ilambda, ibest, k,coefs ;
double pred, sum, diff, max_lambda, Ynormalized, YsumSquares, best,work[] ;
CCoordinateDescent *cd ;
if(n_lambda < 2)
return 0.0 ;
/*
Use the entire dataset to find the max lambda that will be used for all descents.
Also, copy the normalized case weights if there are any.
*/
cd = new CCoordinateDescent(n_predictors, n_observations, covar_updates, n_lambda) ;
cd.SetData(0, n_observations, in_matrix, in_targets) ; // Fetch the training set for this fold
max_lambda = cd.GetLambdaThreshold(alpha) ;
delete cd ;
if(print_output)
PrintFormat("%s starting for %d folds with max lambda=%.9lf",__FUNCTION__, n_folds, max_lambda) ;
i_IS = 0 ; // Training data starts at this index in complete database
n_done = 0 ; // Number of cases treated as OOS so far
for(ilambda=0 ; ilambda<n_lambda ; ilambda++)
out_lambda_OOS[ilambda] = 0.0 ; // Will cumulate across folds here
YsumSquares = 0.0 ; // Will cumulate to compute explained fraction
/*
Process the folds
*/
for(ifold=0 ; ifold<n_folds ; ifold++)
{
n_OOS = (n_observations - n_done) / (n_folds - ifold) ; // Number OOS (test set)
n_IS = n_observations - n_OOS ; // Number IS (training set)
i_OOS = (i_IS + n_IS) % n_observations ; // OOS starts at this index
// Train the model with this IS set
cd = new CCoordinateDescent(n_predictors, n_IS, covar_updates, n_lambda) ;
cd.SetData(i_IS, n_observations, in_matrix, in_targets) ; // Fetch the training set for this fold
cd.TrainLambda(alpha, maxits, convergence_criterion, fast_test, max_lambda,print_output) ; // Compute the complete set of betas (all out_lambdas)
// Compute OOS performance for each lambda and sum across folds.
// Normalization of X and Y is repeated, when it could be done once and saved.
// But the relative cost is minimal, and it is simpler doing it this way.
for(ilambda=0 ; ilambda<n_lambda ; ilambda++)
{
out_lambdas[ilambda] = cd.GetLambdaAt(ilambda) ; // This will be the same for all folds
coefs = ilambda * n_predictors ;
sum = 0.0 ;
for(icase=0 ; icase<n_OOS ; icase++)
{
k = (icase + i_OOS) % n_observations ;
pred = 0.0 ;
for(ivar=0 ; ivar<n_predictors ; ivar++)
pred += cd.GetLambdaBetaAt(coefs+ivar) * (in_matrix[k*n_predictors+ivar] - cd.GetXmeansAt(ivar)) / cd.GetXscalesAt(ivar) ;
Ynormalized = (in_targets[k] - cd.GetYmean()) / cd.GetYscale() ;
diff = Ynormalized - pred ;
if(ilambda == 0)
YsumSquares += Ynormalized * Ynormalized ;
sum += diff * diff ;
}
out_lambda_OOS[ilambda] += sum ; // Cumulate for this fold
} // For ilambda
delete cd ;
n_done += n_OOS ; // Cumulate OOS cases just processed
i_IS = (i_IS + n_OOS) % n_observations ; // Next IS starts at this index
} // For ifold
/*
Compute OOS explained variance for each lambda, and keep track of the best
*/
best = -1.e60 ;
for(ilambda=0 ; ilambda<n_lambda ; ilambda++)
{
out_lambda_OOS[ilambda] = (YsumSquares - out_lambda_OOS[ilambda]) / YsumSquares ;
if(out_lambda_OOS[ilambda] > best)
{
best = out_lambda_OOS[ilambda] ;
ibest = ilambda ;
}
}
if(print_output)
PrintFormat("\n%s ending with best lambda=%9.9lf explained=%9.9lf",__FUNCTION__, out_lambdas[ibest], best) ;
return out_lambdas[ibest] ;
}
//+------------------------------------------------------------------+
该函数使用CCordinateDescent的本地实例来测试一组 lambda。测试 lambda 的数量由函数的 n_lambda 参数设置。测试的 lambda 从调用 GetLambdaThreshold()计算的最大值开始。在每次测试迭代之后,先前的 lambda 值会稍微减小。每个 lambda 检验生成新的 beta 系数,用于计算解释的方差的分数。所有这些都是针对每个折叠完成的。对所有折叠的结果进行检查,并选择最佳折叠。给出最佳结果的 lambda 将作为最佳 lambda 返回。
有了所有描述的代码实用程序,是时候让它们发挥作用了。
示例
为了演示这种方法的实际应用,我们将使用它来构建一个模型,该模型基于一组长短移动平均线来预测下一个小节的价格变化。我们想找到一组移动平均线,这些移动平均线对预测下一小节的价格变化最有用。
为了实现这一点,我们为模型提供了基于对数转换的原始价格计算的指标,目标是对数差异。我们需要一个记录原始价格的指标,以便其他指标(在这种情况下是移动平均值)可以参考它。记录价格指标如下所示。
//+------------------------------------------------------------------+ //| LogPrices.mq5 | //| Copyright 2023, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #property indicator_separate_window #property indicator_buffers 1 #property indicator_plots 1 //--- plot Log #property indicator_label1 "Log" #property indicator_type1 DRAW_LINE #property indicator_color1 clrTurquoise #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- indicator buffers double LogBuffer[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,LogBuffer,INDICATOR_DATA); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- for(int i=(prev_calculated>0)?prev_calculated-1:0; i<rates_total; i++) LogBuffer[i]=(price[i]>0)?log(price[i]):0; //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
训练程序将以脚本形式实施。我们首先指定基本的包含文件和脚本的输入。这些输入允许用户调整程序的各个方面以适应他们的需要。这包括设置训练和测试时间跨度的日期的能力。
//+------------------------------------------------------------------+ //| ElasticNetRegressionModel_MA.mq5 | //| Copyright 2023, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #resource "\\Indicators\\LogPrices.ex5" #include<CoordinateDescent.mqh> #include<ErrorDescription.mqh> #property script_show_inputs //--- input parameters input uint MA_period_inc=2; //MA lookback increment input uint Num_MA_periods=30; //Num of lookbacks input double Alpha=0.5; input int AppliedPrice=PRICE_CLOSE; input ENUM_MA_METHOD MaMethod=MODE_EMA; input ENUM_TIMEFRAMES tf=PERIOD_D1; //time frame input uint BarsLookAhead=1; input uint Num_Folds = 10; //Num of Folds for cross validation input uint MaximumIterations=1000; input datetime TrainingSampleStartDate=D'2019.12.31'; input datetime TrainingSampleStopDate=D'2022.12.31'; input datetime TestingSampleStartDate=D'2023.01.02'; input datetime TestingSampleStopDate=D'2023.06.30'; input string SetSymbol=""; input bool UseCovarUpdates=true; input bool UseFastTest=true; input bool UseWarmStart=false; input int NumLambdasToTest=50; input bool ShowFullOutPut=false; //print full output to terminal
重要的用户输入选项是设置周期增量的MA_period_inc输入参数。Num_Ma_reperiods 定义将提供给算法的移动平均数。用作预测因子的指标值将是长移动平均值和短移动平均值之间的差值。短移动平均线被计算为所得到的长移动平均线的周期的一半。通过增加MA_period_inc,Num_MA_period时间来确定长移动平均值。
Num_Folds规定了交叉验证期间Optimizelambda函数要使用的折叠数。
其他输入参数是不言自明的。
脚本首先枚举训练和测试数据集。本地缓冲区的大小将根据所选的用户输入参数进行调整。
//+------------------------------------------------------------------+ //|global integer variables | //+------------------------------------------------------------------+ int size_insample, //training set size size_outsample, //testing set size size_observations, //size of of both training and testing sets combined size_lambdas, //number of lambdas to be tested size_predictors, //number of predictors maxperiod, //maximum lookback price_handle=INVALID_HANDLE, //log prices indicator handle long_ma_handle=INVALID_HANDLE, //long moving average indicator handle short_ma_handle=INVALID_HANDLE;//short moving average indicator handle //+------------------------------------------------------------------+ //|double global variables | //+------------------------------------------------------------------+ double prices[], //array for log transformed prices targets[], //differenced prices kept here predictors_matrix[], //flat array arranged as matrix of all predictors_matrix ie size_observations by size_predictors longma[], //long ma indicator values Lambdas[], //calculated lambdas kept here Lambdas_OOS[], //calculated out of sample lambdas are here shortma[], //short ma indicator values Lambda; //initial optimal lambda value //+------------------------------------------------------------------+ //| Coordinate descent pointer | //+------------------------------------------------------------------+ CCoordinateDescent *cdmodel; //coordinate descent pointer //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //get relative shift of is and oos sets int teststart,teststop,trainstart,trainstop; teststart=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TestingSampleStartDate); teststop=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TestingSampleStopDate); trainstart=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStartDate); trainstop=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStopDate); //check for errors from ibarshift calls if(teststart<0 || teststop<0 || trainstart<0 || trainstop<0) { Print(ErrorDescription(GetLastError())); return; } //---set the size of the sample sets size_observations=(trainstart - teststop) + 1 ; size_outsample=(teststart - teststop) + 1; size_insample=(trainstart - trainstop) + 1; maxperiod=int(Num_MA_periods*MA_period_inc); size_insample-=maxperiod; size_lambdas=NumLambdasToTest; size_predictors=int(Num_MA_periods); //---check for input errors if(size_lambdas<=0 || size_insample<=0 || size_outsample<=0 || size_predictors<=0 || maxperiod<=0 || BarsLookAhead<=0) { Print("Invalid inputs "); return; } //--- Comment("resizing buffers...");
准备并填充将传递给CCordinateDescent实例的数组,这是目标数组和预测器矩阵。
//---allocate memory if(ArrayResize(targets,size_observations)<(int)size_observations || ArrayResize(predictors_matrix,size_observations*size_predictors)<int(size_observations*size_predictors) || ArrayResize(Lambdas,size_lambdas)<(int)size_lambdas || ArrayResize(Lambdas_OOS,size_lambdas)<(int)size_lambdas || ArrayResize(shortma,size_observations)<(int)size_observations || ArrayResize(longma,size_observations)<(int)size_observations || ArrayResize(prices,size_observations+BarsLookAhead)<int(size_observations+BarsLookAhead)) { Print("ArrayResize error ",ErrorDescription(GetLastError())); return; } //--- Comment("getting price predictors_matrix..."); //---set prices handle price_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,tf,"::Indicators\\LogPrices.ex5",AppliedPrice); if(price_handle==INVALID_HANDLE) { Print("invalid logprices handle ",ErrorDescription(GetLastError())); return; } //--- Comment("getting indicators..."); //----calculate the full collection of predictors_matrix int longmaperiod,shortmaperiod,prevshort,prevlong; int k=0; //--- prevlong=prevshort=0; //--- for(uint iperiod=0; iperiod<Num_MA_periods; iperiod++) { longmaperiod=(int)(iperiod+1)*int(MA_period_inc); shortmaperiod = (longmaperiod>=2)?int(longmaperiod/2):longmaperiod; ResetLastError(); int try=10; while(try) { long_ma_handle=iMA(SetSymbol!=""?SetSymbol:NULL,tf,longmaperiod,0,MaMethod,price_handle); short_ma_handle=iMA(SetSymbol!=""?SetSymbol:NULL,tf,shortmaperiod,0,MaMethod,price_handle); if(long_ma_handle==INVALID_HANDLE || short_ma_handle==INVALID_HANDLE) try--; else break; } Comment("copying buffers for short ",shortmaperiod," long ",longmaperiod); if(CopyBuffer(long_ma_handle,0,teststop,size_observations,longma)<=0 || CopyBuffer(short_ma_handle,0,teststop,size_observations,shortma)<=0) { Print("error copying to ma buffers ",GetLastError()); return; } for(int i=0 ; i<int(size_observations) ; i++) predictors_matrix[i*size_predictors+k] = shortma[i]-longma[i]; ++k ; if(long_ma_handle!=INVALID_HANDLE && short_ma_handle!=INVALID_HANDLE && IndicatorRelease(long_ma_handle) && IndicatorRelease(short_ma_handle)) { long_ma_handle=short_ma_handle=INVALID_HANDLE; prevlong=longmaperiod; prevshort=shortmaperiod; } } //--- Comment("filling target buffer..."); //--- ResetLastError(); if(CopyBuffer(price_handle,0,teststop,size_observations+BarsLookAhead,prices)<int(size_observations+BarsLookAhead)) { Print("error copying to price buffer , ",ErrorDescription(GetLastError())); return; } //--- for(int i=0 ; i<int(size_observations); i++) targets[i] = prices[i+BarsLookAhead]-prices[i]; //---
Lambda调整取决于Alpha的值。当alpha小于或等于零时,不会计算出最佳lambda。结果将是一个类似于标准线性回归的模型,没有任何正则化。
//--- Comment("optional lambda tuning..."); //--- if(Alpha<=0) Lambda=0; else //train Lambda=OptimizeLambda(size_insample,size_predictors,(int)Num_Folds,UseCovarUpdates,size_lambdas,Alpha,(int)MaximumIterations,1.e-9,UseFastTest,predictors_matrix,targets,Lambdas,Lambdas_OOS,ShowFullOutPut); //---
一旦CCordinateDescent对象完成训练,结果可以选择性地输出到终端。
Comment("coordinate descent engagement..."); //---initialize CD object cdmodel=new CCoordinateDescent(size_predictors,size_insample,UseCovarUpdates,0); //--- if(cdmodel==NULL) { Print("error creating Coordinate Descent object "); return; } //---set the parameters and data cdmodel.SetData(0,size_insample,predictors_matrix,targets); //--- Print("optimal lambda ",DoubleToString(Lambda)); //---train the model cdmodel.Train(Alpha,Lambda,(int)MaximumIterations,1.e-7,UseFastTest,UseWarmStart); //--- Print("explained variance ",cdmodel.GetExplainedVariance()); //---optionally output results of training here if(ShowFullOutPut) { k=0; string output; for(uint iperiod=0; iperiod<Num_MA_periods; iperiod++) { longmaperiod=(int)(iperiod+1)*int(MA_period_inc); output+=StringFormat("\n%5d ", longmaperiod) ; shortmaperiod = (longmaperiod>=2)?int(longmaperiod/2):longmaperiod; output+=StringFormat(",%5d ,%9.9lf ", shortmaperiod,cdmodel.GetBetaAt(k)); ++k; } Print(output); } //---
程序输出将按列显示,第一列显示长移动平均周期,第二列显示相应的短移动平均,最后给出特定预测器的 beta 值。如果显示零,则表示该预测器已被丢弃。
double sum=0.0; //cumulated predictions double pred; //a prediction int xptr; k=size_observations - (size_insample+maxperiod) - 1; //--- Comment("test the model..."); //---do the out of sample test for(int i=k ; i<size_observations ; i++) { xptr = i*size_predictors ; pred = 0.0 ; for(int ivar=0 ; ivar<int(size_predictors) ; ivar++) pred += cdmodel.GetBetaAt(ivar) * (predictors_matrix[xptr+ivar] - cdmodel.GetXmeansAt(ivar)) / cdmodel.GetXscalesAt(ivar) ; pred = pred * cdmodel.GetYscale() + cdmodel.GetYmean() ; // Unscale prediction to get it back in original Y domain if(pred > 0.0) sum += targets[i] ; else if(pred < 0.0) sum -= targets[i] ; } //--- PrintFormat("OOS total return = %.5lf (%.3lf percent)",sum, 100.0 * (exp(sum) - 1.0)) ; //--- delete cdmodel; //--- Comment("");
在选定的测试周期内检查性能后,程序结束。用户应该注意,在程序端显示的性能值并不能表示真正的性能,因为有很多没有考虑在内。这些数字应相对于从不同程序参数集获得的其他结果使用。
下面的输出显示Alpha为0时的结果。如前所述,当alpha为0时,不存在正则化,模型是使用所有提供的预测因子构建的,没有遗漏任何预测因子。
DH 0 19:58:47.521 ELN_MA (GBPUSD,D1) optimal lambda 0.00000000 HP 0 19:58:47.552 ELN_MA (GBPUSD,D1) explained variance 0.9914167039554915 ID 0 19:58:47.552 ELN_MA (GBPUSD,D1) FF 0 19:58:47.552 ELN_MA (GBPUSD,D1) 2 , 1 ,1.85143599128379721108e+00 JJ 0 19:58:47.552 ELN_MA (GBPUSD,D1) 4 , 2 ,-2.44139247803866465958e+00 MR 0 19:58:47.552 ELN_MA (GBPUSD,D1) 6 , 3 ,2.32230838054034549600e+00 HF 0 19:58:47.552 ELN_MA (GBPUSD,D1) 8 , 4 ,-2.35763762038486313077e-01 FJ 0 19:58:47.552 ELN_MA (GBPUSD,D1) 10 , 5 ,-5.12822602346063693979e-01 MP 0 19:58:47.552 ELN_MA (GBPUSD,D1) 12 , 6 ,-2.63526268082343251287e-01 CF 0 19:58:47.552 ELN_MA (GBPUSD,D1) 14 , 7 ,-4.66454472659737495732e-02 FN 0 19:58:47.552 ELN_MA (GBPUSD,D1) 16 , 8 ,6.22551516067148258404e-02 KP 0 19:58:47.552 ELN_MA (GBPUSD,D1) 18 , 9 ,9.45364603399752728707e-02 JK 0 19:58:47.552 ELN_MA (GBPUSD,D1) 20 , 10 ,8.71627177974267641769e-02 JM 0 19:58:47.552 ELN_MA (GBPUSD,D1) 22 , 11 ,6.43970377784374714558e-02 CG 0 19:58:47.552 ELN_MA (GBPUSD,D1) 24 , 12 ,3.92137206481772693234e-02 FI 0 19:58:47.552 ELN_MA (GBPUSD,D1) 26 , 13 ,1.74528224486318189745e-02 HS 0 19:58:47.552 ELN_MA (GBPUSD,D1) 28 , 14 ,1.04642691815316421500e-03 PG 0 19:58:47.552 ELN_MA (GBPUSD,D1) 30 , 15 ,-9.98741520244338966406e-03 RM 0 19:58:47.552 ELN_MA (GBPUSD,D1) 32 , 16 ,-1.64348263919291276425e-02 CS 0 19:58:47.552 ELN_MA (GBPUSD,D1) 34 , 17 ,-1.93143258653755492404e-02 QI 0 19:58:47.552 ELN_MA (GBPUSD,D1) 36 , 18 ,-1.96075858211104264717e-02 FO 0 19:58:47.552 ELN_MA (GBPUSD,D1) 38 , 19 ,-1.81510403514190954422e-02 RD 0 19:58:47.552 ELN_MA (GBPUSD,D1) 40 , 20 ,-1.56082180218151990447e-02 PJ 0 19:58:47.552 ELN_MA (GBPUSD,D1) 42 , 21 ,-1.24793265043600110076e-02 HP 0 19:58:47.552 ELN_MA (GBPUSD,D1) 44 , 22 ,-9.12541199880392318866e-03 MF 0 19:58:47.552 ELN_MA (GBPUSD,D1) 46 , 23 ,-5.79584482050124645547e-03 DL 0 19:58:47.552 ELN_MA (GBPUSD,D1) 48 , 24 ,-2.65399377323665905393e-03 PP 0 19:58:47.552 ELN_MA (GBPUSD,D1) 50 , 25 ,2.00883928121427593472e-04 RJ 0 19:58:47.552 ELN_MA (GBPUSD,D1) 52 , 26 ,2.71594753051577000869e-03 IL 0 19:58:47.552 ELN_MA (GBPUSD,D1) 54 , 27 ,4.87097208116808733092e-03 IF 0 19:58:47.552 ELN_MA (GBPUSD,D1) 56 , 28 ,6.66787159270224374930e-03 MH 0 19:58:47.552 ELN_MA (GBPUSD,D1) 58 , 29 ,8.12292277995673578372e-03 NR 0 19:58:47.552 ELN_MA (GBPUSD,D1) 60 , 30 ,9.26111235731779183777e-03 JG 0 19:58:47.568 ELN_MA (GBPUSD,D1) OOS total return = 3.42660 (2977.187 percent)
以下是Alpha为0.1时的输出。感兴趣的是与上一次运行相比的 beta 值。零 beta 值表明相应的预测器已被丢弃。
NP 0 19:53:32.412 ELN_MA (GBPUSD,D1) optimal lambda 0.00943815 HH 0 19:53:32.458 ELN_MA (GBPUSD,D1) explained variance 0.9748473636648924 GL 0 19:53:32.458 ELN_MA (GBPUSD,D1) GN 0 19:53:32.458 ELN_MA (GBPUSD,D1) 2 , 1 ,1.41004781317849103850e+00 MR 0 19:53:32.458 ELN_MA (GBPUSD,D1) 4 , 2 ,-6.98106822708694618740e-01 DJ 0 19:53:32.458 ELN_MA (GBPUSD,D1) 6 , 3 ,0.00000000000000000000e+00 NL 0 19:53:32.458 ELN_MA (GBPUSD,D1) 8 , 4 ,1.30221271072762545540e-01 MG 0 19:53:32.458 ELN_MA (GBPUSD,D1) 10 , 5 ,1.13824982442231326107e-01 DI 0 19:53:32.458 ELN_MA (GBPUSD,D1) 12 , 6 ,0.00000000000000000000e+00 IS 0 19:53:32.458 ELN_MA (GBPUSD,D1) 14 , 7 ,0.00000000000000000000e+00 NE 0 19:53:32.458 ELN_MA (GBPUSD,D1) 16 , 8 ,0.00000000000000000000e+00 GO 0 19:53:32.458 ELN_MA (GBPUSD,D1) 18 , 9 ,0.00000000000000000000e+00 JP 0 19:53:32.458 ELN_MA (GBPUSD,D1) 20 , 10 ,0.00000000000000000000e+00 DH 0 19:53:32.458 ELN_MA (GBPUSD,D1) 22 , 11 ,-3.69006880128594713653e-02 OM 0 19:53:32.458 ELN_MA (GBPUSD,D1) 24 , 12 ,-2.43715386443472993572e-02 LS 0 19:53:32.458 ELN_MA (GBPUSD,D1) 26 , 13 ,-3.50967791710741789518e-03 DK 0 19:53:32.458 ELN_MA (GBPUSD,D1) 28 , 14 ,0.00000000000000000000e+00 LM 0 19:53:32.458 ELN_MA (GBPUSD,D1) 30 , 15 ,0.00000000000000000000e+00 KG 0 19:53:32.458 ELN_MA (GBPUSD,D1) 32 , 16 ,0.00000000000000000000e+00 RI 0 19:53:32.458 ELN_MA (GBPUSD,D1) 34 , 17 ,0.00000000000000000000e+00 ES 0 19:53:32.458 ELN_MA (GBPUSD,D1) 36 , 18 ,0.00000000000000000000e+00 PE 0 19:53:32.458 ELN_MA (GBPUSD,D1) 38 , 19 ,0.00000000000000000000e+00 KO 0 19:53:32.458 ELN_MA (GBPUSD,D1) 40 , 20 ,0.00000000000000000000e+00 NQ 0 19:53:32.458 ELN_MA (GBPUSD,D1) 42 , 21 ,0.00000000000000000000e+00 QK 0 19:53:32.458 ELN_MA (GBPUSD,D1) 44 , 22 ,0.00000000000000000000e+00 PM 0 19:53:32.458 ELN_MA (GBPUSD,D1) 46 , 23 ,0.00000000000000000000e+00 GG 0 19:53:32.458 ELN_MA (GBPUSD,D1) 48 , 24 ,0.00000000000000000000e+00 OI 0 19:53:32.458 ELN_MA (GBPUSD,D1) 50 , 25 ,0.00000000000000000000e+00 PS 0 19:53:32.458 ELN_MA (GBPUSD,D1) 52 , 26 ,0.00000000000000000000e+00 RE 0 19:53:32.458 ELN_MA (GBPUSD,D1) 54 , 27 ,1.14149417738317331301e-03 FO 0 19:53:32.458 ELN_MA (GBPUSD,D1) 56 , 28 ,3.18638349345921325848e-03 IQ 0 19:53:32.458 ELN_MA (GBPUSD,D1) 58 , 29 ,3.87574752936066481077e-03 KK 0 19:53:32.458 ELN_MA (GBPUSD,D1) 60 , 30 ,3.16472282935538083357e-03 QN 0 19:53:32.474 ELN_MA (GBPUSD,D1) OOS total return = 3.40954 (2925.133 percent)
接下来,我们查看Alpha为0.9时的输出,这次我们突出显示LambdaOptimize的输出。第一列是测试的lambda值,第二列显示模型中包括的预测因子的数量,最后一列显示特定倍数的测试解释方差的分数。在脚本中,我们指定了10个折叠,因此有10个表包含这些数据。
ME 0 19:57:21.630 ELN_MA (GBPUSD,D1) OptimizeLambda starting for 10 folds with max lambda=1.048683301 JE 0 19:57:21.833 ELN_MA (GBPUSD,D1) RO 0 19:57:21.833 ELN_MA (GBPUSD,D1) Descending lambda path... RE 0 19:57:21.833 ELN_MA (GBPUSD,D1) 1.0487 0 0.0000 NM 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.9108 1 0.2009 ND 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.7910 1 0.3586 RL 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.6870 1 0.4813 LD 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.5967 1 0.5764 OL 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.5182 1 0.6499 KG 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.4501 1 0.7065 LO 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.3909 1 0.7500 JG 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.3395 1 0.7833 QO 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.2949 1 0.8088 OF 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.2561 1 0.8282 CN 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.2224 1 0.8431 CF 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.1932 1 0.8544 HN 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.1678 1 0.8630 LI 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.1457 1 0.8695 GQ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.1266 1 0.8744 LI 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.1099 2 0.8788 QQ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0955 2 0.8914 PH 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0829 2 0.9019 IP 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0720 2 0.9098 EH 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0625 2 0.9159 RP 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0543 2 0.9205 EK 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0472 3 0.9325 HS 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0410 2 0.9424 NK 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0356 2 0.9467 HS 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0309 2 0.9500 KJ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0268 2 0.9525 JR 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0233 3 0.9556 GJ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0202 3 0.9586 NR 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0176 4 0.9610 CM 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0153 3 0.9635 CE 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0133 4 0.9656 OM 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0115 3 0.9677 PE 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0100 3 0.9689 QL 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0087 5 0.9707 CD 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0075 4 0.9732 RL 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0066 5 0.9745 ND 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0057 5 0.9756 NO 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0049 4 0.9767 HG 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0043 4 0.9776 IO 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0037 5 0.9784 EG 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0032 6 0.9793 KN 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0028 6 0.9808 DF 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0024 8 0.9825 HN 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0021 6 0.9840 PF 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0018 7 0.9847 OQ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0016 7 0.9855 OI 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0014 5 0.9862 DQ 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0012 7 0.9867 MI 0 19:57:21.833 ELN_MA (GBPUSD,D1) 0.0010 8 0.9874 KS 0 19:57:22.068 ELN_MA (GBPUSD,D1) OF 0 19:57:22.068 ELN_MA (GBPUSD,D1) Descending lambda path... OL 0 19:57:22.068 ELN_MA (GBPUSD,D1) 1.0487 0 0.0000 RG 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.9108 1 0.2006 PO 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.7910 1 0.3583 JG 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.6870 1 0.4810 RO 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.5967 1 0.5761 NF 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.5182 1 0.6495 RN 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.4501 1 0.7061 OF 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.3909 1 0.7496 RN 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.3395 1 0.7829 LI 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.2949 1 0.8084 NQ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.2561 1 0.8279 OI 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.2224 1 0.8427 JQ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.1932 1 0.8540 LH 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.1678 1 0.8626 QP 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.1457 1 0.8691 MH 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.1266 1 0.8741 IP 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.1099 3 0.8794 NK 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0955 2 0.8929 PS 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0829 2 0.9029 NK 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0720 2 0.9106 RS 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0625 2 0.9164 JJ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0543 3 0.9225 MR 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0472 3 0.9348 KJ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0410 2 0.9433 MR 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0356 2 0.9474 KM 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0309 2 0.9506 JE 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0268 2 0.9529 FM 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0233 3 0.9559 KE 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0202 3 0.9589 DL 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0176 3 0.9616 CD 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0153 3 0.9636 ML 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0133 3 0.9663 CD 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0115 3 0.9678 KO 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0100 4 0.9691 EG 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0087 5 0.9719 RO 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0075 5 0.9737 KG 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0066 4 0.9751 IN 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0057 5 0.9763 MF 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0049 4 0.9774 FN 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0043 4 0.9784 EF 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0037 5 0.9792 QQ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0032 6 0.9802 NI 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0028 7 0.9818 HQ 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0024 7 0.9834 EI 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0021 5 0.9847 HP 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0018 6 0.9854 KH 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0016 7 0.9861 FP 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0014 5 0.9866 GH 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0012 6 0.9871 PS 0 19:57:22.068 ELN_MA (GBPUSD,D1) 0.0010 7 0.9877 MH 0 19:57:22.318 ELN_MA (GBPUSD,D1) EL 0 19:57:22.318 ELN_MA (GBPUSD,D1) Descending lambda path... CF 0 19:57:22.318 ELN_MA (GBPUSD,D1) 1.0487 1 0.0003 HN 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.9108 1 0.2020 IF 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.7910 1 0.3597 QQ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.6870 1 0.4824 GI 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.5967 1 0.5775 LQ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.5182 1 0.6510 JI 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.4501 1 0.7076 OP 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.3909 1 0.7511 NH 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.3395 1 0.7845 MP 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.2949 1 0.8100 IH 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.2561 1 0.8294 CS 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.2224 1 0.8443 QK 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.1932 1 0.8556 IS 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.1678 1 0.8641 QK 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.1457 1 0.8707 ER 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.1266 1 0.8756 QJ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.1099 2 0.8805 GR 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0955 2 0.8928 LJ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0829 2 0.9032 FE 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0720 2 0.9111 HM 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0625 2 0.9171 LE 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0543 2 0.9217 OM 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0472 3 0.9315 GD 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0410 3 0.9421 EL 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 HD 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 DL 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0268 2 0.9530 OG 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0233 3 0.9558 JO 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0202 3 0.9588 OG 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0176 4 0.9612 CO 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0153 3 0.9638 MF 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0133 4 0.9659 LN 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0115 3 0.9680 FF 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0100 4 0.9694 PN 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0087 5 0.9709 RI 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0075 4 0.9738 JQ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0066 5 0.9751 KI 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0057 5 0.9763 GQ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0049 4 0.9774 MH 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0043 4 0.9783 QP 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0037 4 0.9791 DH 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0032 5 0.9800 QP 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0028 6 0.9812 LK 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 GS 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0021 8 0.9842 OK 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0018 6 0.9853 IS 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0016 7 0.9861 DJ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0014 6 0.9869 RR 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0012 6 0.9874 PJ 0 19:57:22.318 ELN_MA (GBPUSD,D1) 0.0010 7 0.9879 DQ 0 19:57:22.568 ELN_MA (GBPUSD,D1) PK 0 19:57:22.568 ELN_MA (GBPUSD,D1) Descending lambda path... KQ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 1.0487 1 0.0004 FI 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.9108 1 0.2021 IP 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.7910 1 0.3598 KH 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.6870 1 0.4825 LP 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.5967 1 0.5777 RH 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.5182 1 0.6511 IS 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.4501 1 0.7078 KK 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.3909 1 0.7512 JS 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.3395 1 0.7846 OK 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.2949 1 0.8101 KR 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.2561 1 0.8295 CJ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.2224 1 0.8444 CR 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.1932 1 0.8557 FJ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.1678 1 0.8643 QE 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.1457 1 0.8708 GM 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.1266 1 0.8757 OE 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.1099 2 0.8808 NM 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0955 2 0.8931 CD 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0829 2 0.9034 IL 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0720 2 0.9113 KD 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0625 2 0.9173 DL 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0543 2 0.9218 RG 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0472 3 0.9319 IO 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0410 3 0.9424 NG 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0356 2 0.9474 CO 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0309 2 0.9507 OF 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0268 2 0.9532 CN 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0233 3 0.9560 DF 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0202 3 0.9590 PN 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0176 3 0.9613 QI 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0153 3 0.9639 PQ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0133 4 0.9659 JI 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0115 3 0.9681 GQ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0100 4 0.9694 LH 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0087 6 0.9710 LP 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0075 5 0.9738 LH 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0066 4 0.9751 QP 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0057 4 0.9763 MK 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0049 5 0.9774 OS 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0043 5 0.9783 CK 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0037 5 0.9791 JS 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0032 5 0.9801 DJ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0028 7 0.9813 DR 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0024 7 0.9828 HJ 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0021 7 0.9843 NR 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0018 6 0.9853 KM 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0016 7 0.9860 NE 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0014 5 0.9867 IM 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0012 6 0.9872 GE 0 19:57:22.568 ELN_MA (GBPUSD,D1) 0.0010 8 0.9878 JO 0 19:57:22.740 ELN_MA (GBPUSD,D1) RQ 0 19:57:22.740 ELN_MA (GBPUSD,D1) Descending lambda path... PK 0 19:57:22.740 ELN_MA (GBPUSD,D1) 1.0487 1 0.0003 DS 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.9108 1 0.2021 GK 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.7910 1 0.3598 MS 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.6870 1 0.4825 MJ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.5967 1 0.5776 PR 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.5182 1 0.6511 NJ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.4501 1 0.7077 MR 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.3909 1 0.7512 IM 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.3395 1 0.7845 RE 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.2949 1 0.8100 MM 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.2561 1 0.8295 HE 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.2224 1 0.8443 FL 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.1932 1 0.8556 CD 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.1678 1 0.8642 OL 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.1457 1 0.8708 ID 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.1266 1 0.8757 DO 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.1099 2 0.8807 DG 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0955 2 0.8928 GO 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0829 2 0.9032 HG 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0720 2 0.9112 NN 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0625 2 0.9172 FF 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0543 2 0.9218 JN 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0472 3 0.9313 MF 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0410 3 0.9419 RQ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 CI 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 PQ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0268 2 0.9531 LI 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0233 3 0.9558 PP 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0202 4 0.9588 QH 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0176 3 0.9612 PP 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0153 3 0.9638 DH 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0133 4 0.9657 GS 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0115 3 0.9680 IK 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0100 4 0.9694 DS 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0087 5 0.9708 GK 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0075 5 0.9737 MR 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0066 4 0.9750 PJ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0057 4 0.9762 RR 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0049 5 0.9773 RJ 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0043 5 0.9782 FE 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0037 5 0.9790 GM 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0032 5 0.9800 FE 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0028 6 0.9812 OM 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 ID 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0021 7 0.9842 KL 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0018 6 0.9852 ND 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0016 6 0.9860 LL 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0014 5 0.9867 GG 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0012 6 0.9872 IO 0 19:57:22.740 ELN_MA (GBPUSD,D1) 0.0010 7 0.9877 KD 0 19:57:23.052 ELN_MA (GBPUSD,D1) OH 0 19:57:23.052 ELN_MA (GBPUSD,D1) Descending lambda path... RR 0 19:57:23.052 ELN_MA (GBPUSD,D1) 1.0487 1 0.0002 DJ 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.9108 1 0.2019 LR 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.7910 1 0.3596 JM 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.6870 1 0.4823 ME 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.5967 1 0.5775 RM 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.5182 1 0.6509 LE 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.4501 1 0.7076 FL 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.3909 1 0.7510 GD 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.3395 1 0.7844 HL 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.2949 1 0.8099 RD 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.2561 1 0.8293 RO 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.2224 1 0.8442 FG 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.1932 1 0.8555 KO 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.1678 1 0.8641 DG 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.1457 1 0.8706 RN 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.1266 1 0.8755 DF 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.1099 2 0.8804 HN 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0955 2 0.8927 GF 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0829 2 0.9031 OQ 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0720 2 0.9110 MI 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0625 2 0.9170 IQ 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0543 2 0.9216 DI 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0472 3 0.9316 LP 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0410 3 0.9422 OH 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 NP 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 RH 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0268 2 0.9530 ES 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0233 3 0.9558 LK 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0202 3 0.9588 ES 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0176 4 0.9612 DK 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0153 3 0.9637 HR 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0133 4 0.9658 JJ 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0115 3 0.9680 MR 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0100 4 0.9693 CJ 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0087 6 0.9709 RE 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0075 5 0.9737 LM 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0066 4 0.9750 IE 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0057 4 0.9762 OM 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0049 5 0.9773 GD 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0043 5 0.9782 CL 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0037 5 0.9790 CD 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0032 5 0.9799 DL 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0028 7 0.9812 JG 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 HO 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0021 6 0.9843 CG 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0018 5 0.9852 LO 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0016 7 0.9860 EF 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0014 5 0.9867 JN 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0012 6 0.9872 EF 0 19:57:23.052 ELN_MA (GBPUSD,D1) 0.0010 8 0.9877 KM 0 19:57:23.302 ELN_MA (GBPUSD,D1) CG 0 19:57:23.302 ELN_MA (GBPUSD,D1) Descending lambda path... EM 0 19:57:23.302 ELN_MA (GBPUSD,D1) 1.0487 1 0.0003 ID 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.9108 1 0.2021 NL 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.7910 1 0.3598 PD 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.6870 1 0.4825 HL 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.5967 1 0.5776 MG 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.5182 1 0.6511 GO 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.4501 1 0.7077 PG 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.3909 1 0.7512 MO 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.3395 1 0.7846 KF 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.2949 1 0.8100 HN 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.2561 1 0.8295 HF 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.2224 1 0.8444 PN 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.1932 1 0.8557 JI 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.1678 1 0.8642 FQ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.1457 1 0.8708 DI 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.1266 1 0.8757 PQ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.1099 2 0.8804 LH 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0955 2 0.8927 KP 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0829 2 0.9031 DH 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0720 2 0.9111 JP 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0625 2 0.9171 NK 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0543 2 0.9217 PS 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0472 3 0.9316 HK 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0410 3 0.9422 CS 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 JJ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 ER 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0268 2 0.9531 RJ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0233 3 0.9559 GR 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0202 3 0.9589 LM 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0176 3 0.9612 EE 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0153 3 0.9638 LM 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0133 4 0.9658 NE 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0115 3 0.9680 IL 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0100 4 0.9693 OD 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0087 6 0.9709 EL 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0075 4 0.9737 GD 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0066 4 0.9751 NO 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0057 4 0.9763 CG 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0049 5 0.9773 KO 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0043 5 0.9782 PG 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0037 4 0.9790 FN 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0032 5 0.9800 PF 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0028 7 0.9812 NN 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 LF 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0021 7 0.9842 RQ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0018 6 0.9852 HI 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0016 7 0.9860 PQ 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0014 6 0.9867 NI 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0012 6 0.9872 QP 0 19:57:23.302 ELN_MA (GBPUSD,D1) 0.0010 8 0.9877 EK 0 19:57:23.537 ELN_MA (GBPUSD,D1) QM 0 19:57:23.537 ELN_MA (GBPUSD,D1) Descending lambda path... PG 0 19:57:23.537 ELN_MA (GBPUSD,D1) 1.0487 1 0.0002 NO 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.9108 1 0.2019 NG 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.7910 1 0.3596 PO 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.6870 1 0.4823 KF 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.5967 1 0.5775 HN 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.5182 1 0.6509 KF 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.4501 1 0.7075 LN 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.3909 1 0.7510 II 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.3395 1 0.7844 RQ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.2949 1 0.8099 PI 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.2561 1 0.8293 HQ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.2224 1 0.8442 DH 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.1932 1 0.8555 FP 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.1678 1 0.8640 FH 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.1457 1 0.8706 HP 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.1266 1 0.8755 FK 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.1099 2 0.8804 RS 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0955 2 0.8927 IK 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0829 2 0.9031 IS 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0720 2 0.9110 KJ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0625 2 0.9170 OR 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0543 2 0.9216 FJ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0472 3 0.9316 CR 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0410 3 0.9421 QM 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 DE 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 PM 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0268 2 0.9530 KE 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0233 3 0.9558 NL 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0202 3 0.9588 KD 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0176 4 0.9612 FL 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0153 3 0.9637 RD 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0133 4 0.9658 HO 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0115 3 0.9680 CG 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0100 4 0.9693 EO 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0087 6 0.9709 HG 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0075 5 0.9737 NN 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0066 4 0.9750 OF 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0057 4 0.9762 QN 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0049 5 0.9773 QF 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0043 5 0.9782 EQ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0037 5 0.9790 HI 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0032 5 0.9800 FQ 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0028 7 0.9812 PI 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 JP 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0021 6 0.9843 MH 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0018 5 0.9852 MP 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0016 6 0.9860 KH 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0014 5 0.9867 HS 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0012 6 0.9872 KK 0 19:57:23.537 ELN_MA (GBPUSD,D1) 0.0010 8 0.9877 PP 0 19:57:23.880 ELN_MA (GBPUSD,D1) HD 0 19:57:23.880 ELN_MA (GBPUSD,D1) Descending lambda path... GN 0 19:57:23.880 ELN_MA (GBPUSD,D1) 1.0487 1 0.0000 DF 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.9108 1 0.2018 FQ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.7910 1 0.3595 JI 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.6870 1 0.4822 HQ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.5967 1 0.5773 RI 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.5182 1 0.6508 EP 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.4501 1 0.7074 MH 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.3909 1 0.7509 NP 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.3395 1 0.7842 MH 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.2949 1 0.8097 JS 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.2561 1 0.8292 OK 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.2224 1 0.8440 OS 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.1932 1 0.8553 IK 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.1678 1 0.8639 MR 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.1457 1 0.8704 RJ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.1266 1 0.8754 KR 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.1099 2 0.8804 NJ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0955 2 0.8928 PE 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0829 2 0.9031 PM 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0720 2 0.9110 FE 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0625 2 0.9170 GM 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0543 2 0.9215 ID 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0472 3 0.9318 LL 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0410 3 0.9423 HD 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0356 2 0.9472 ML 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0309 2 0.9505 IG 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0268 2 0.9530 FO 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0233 3 0.9558 CG 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0202 3 0.9588 FO 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0176 4 0.9612 KF 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0153 3 0.9637 HN 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0133 4 0.9659 KF 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0115 3 0.9679 NN 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0100 4 0.9693 DI 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0087 6 0.9710 QQ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0075 5 0.9737 CI 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0066 4 0.9750 JQ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0057 4 0.9762 HH 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0049 5 0.9773 HP 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0043 5 0.9782 LH 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0037 5 0.9790 DP 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0032 5 0.9799 KK 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0028 7 0.9812 LS 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0024 7 0.9828 OK 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0021 6 0.9843 DS 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0018 5 0.9852 DJ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0016 6 0.9860 ER 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0014 5 0.9866 RJ 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0012 7 0.9872 OR 0 19:57:23.880 ELN_MA (GBPUSD,D1) 0.0010 7 0.9877 EN 0 19:57:24.130 ELN_MA (GBPUSD,D1) IS 0 19:57:24.130 ELN_MA (GBPUSD,D1) Descending lambda path... EI 0 19:57:24.130 ELN_MA (GBPUSD,D1) 1.0487 1 0.0005 EP 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.9108 1 0.2023 RH 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.7910 1 0.3600 LP 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.6870 1 0.4827 PH 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.5967 1 0.5778 QS 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.5182 1 0.6513 OK 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.4501 1 0.7079 PS 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.3909 1 0.7514 PK 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.3395 1 0.7847 OR 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.2949 1 0.8102 DJ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.2561 1 0.8297 ER 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.2224 1 0.8445 GJ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.1932 1 0.8558 JE 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.1678 1 0.8644 GM 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.1457 1 0.8709 LE 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.1266 1 0.8759 JM 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.1099 2 0.8808 DD 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0955 2 0.8929 OL 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0829 2 0.9033 HD 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0720 2 0.9113 FL 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0625 2 0.9173 FG 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0543 2 0.9219 RO 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0472 3 0.9312 MG 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0410 3 0.9418 JO 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0356 2 0.9473 EF 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0309 2 0.9506 GN 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0268 2 0.9531 QF 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0233 4 0.9559 HN 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0202 4 0.9589 QI 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0176 3 0.9613 HQ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0153 3 0.9639 RI 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0133 4 0.9658 OQ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0115 3 0.9681 JH 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0100 5 0.9695 KP 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0087 4 0.9709 NH 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0075 4 0.9738 CP 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0066 5 0.9752 NK 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0057 5 0.9764 CS 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0049 4 0.9774 RK 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0043 5 0.9783 LS 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0037 4 0.9792 GJ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0032 5 0.9801 NR 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0028 7 0.9812 PJ 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0024 7 0.9827 RR 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0021 7 0.9842 KM 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0018 6 0.9853 EE 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0016 7 0.9861 NM 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0014 6 0.9867 OE 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0012 6 0.9873 KL 0 19:57:24.130 ELN_MA (GBPUSD,D1) 0.0010 7 0.9878 HG 0 19:57:24.146 ELN_MA (GBPUSD,D1) PG 0 19:57:24.146 ELN_MA (GBPUSD,D1) OptimizeLambda ending with best lambda=0.001048683 explained=0.987563916
请注意,当lambda达到最大值时,活动预测器的数量为零,并且该值随着每次迭代中lambda的减少而增加。所选预测器的数量随着算法决定哪个lambda值最好而增加或减少。生成的模型最终会丢弃一些它认为不必要的指标值。
PE 0 19:57:24.177 ELN_MA (GBPUSD,D1) optimal lambda 0.00104868 GM 0 19:57:24.287 ELN_MA (GBPUSD,D1) explained variance 0.9871030095923066 DK 0 19:57:24.287 ELN_MA (GBPUSD,D1) NS 0 19:57:24.287 ELN_MA (GBPUSD,D1) 2 , 1 ,1.70372722883263016946e+00 RG 0 19:57:24.287 ELN_MA (GBPUSD,D1) 4 , 2 ,-1.67483731989555195696e+00 QO 0 19:57:24.287 ELN_MA (GBPUSD,D1) 6 , 3 ,1.07905337481491181428e+00 PQ 0 19:57:24.287 ELN_MA (GBPUSD,D1) 8 , 4 ,0.00000000000000000000e+00 HJ 0 19:57:24.287 ELN_MA (GBPUSD,D1) 10 , 5 ,0.00000000000000000000e+00 LN 0 19:57:24.287 ELN_MA (GBPUSD,D1) 12 , 6 ,-1.81038986082938974098e-01 DF 0 19:57:24.287 ELN_MA (GBPUSD,D1) 14 , 7 ,0.00000000000000000000e+00 OH 0 19:57:24.287 ELN_MA (GBPUSD,D1) 16 , 8 ,0.00000000000000000000e+00 FR 0 19:57:24.287 ELN_MA (GBPUSD,D1) 18 , 9 ,0.00000000000000000000e+00 CE 0 19:57:24.287 ELN_MA (GBPUSD,D1) 20 , 10 ,0.00000000000000000000e+00 FO 0 19:57:24.287 ELN_MA (GBPUSD,D1) 22 , 11 ,0.00000000000000000000e+00 IQ 0 19:57:24.287 ELN_MA (GBPUSD,D1) 24 , 12 ,0.00000000000000000000e+00 HK 0 19:57:24.287 ELN_MA (GBPUSD,D1) 26 , 13 ,0.00000000000000000000e+00 OM 0 19:57:24.287 ELN_MA (GBPUSD,D1) 28 , 14 ,0.00000000000000000000e+00 GG 0 19:57:24.287 ELN_MA (GBPUSD,D1) 30 , 15 ,0.00000000000000000000e+00 HI 0 19:57:24.287 ELN_MA (GBPUSD,D1) 32 , 16 ,0.00000000000000000000e+00 ES 0 19:57:24.287 ELN_MA (GBPUSD,D1) 34 , 17 ,0.00000000000000000000e+00 RE 0 19:57:24.287 ELN_MA (GBPUSD,D1) 36 , 18 ,0.00000000000000000000e+00 CO 0 19:57:24.287 ELN_MA (GBPUSD,D1) 38 , 19 ,0.00000000000000000000e+00 HQ 0 19:57:24.287 ELN_MA (GBPUSD,D1) 40 , 20 ,0.00000000000000000000e+00 IK 0 19:57:24.287 ELN_MA (GBPUSD,D1) 42 , 21 ,0.00000000000000000000e+00 FM 0 19:57:24.287 ELN_MA (GBPUSD,D1) 44 , 22 ,0.00000000000000000000e+00 CG 0 19:57:24.287 ELN_MA (GBPUSD,D1) 46 , 23 ,0.00000000000000000000e+00 LI 0 19:57:24.287 ELN_MA (GBPUSD,D1) 48 , 24 ,0.00000000000000000000e+00 DS 0 19:57:24.287 ELN_MA (GBPUSD,D1) 50 , 25 ,0.00000000000000000000e+00 CE 0 19:57:24.287 ELN_MA (GBPUSD,D1) 52 , 26 ,0.00000000000000000000e+00 JO 0 19:57:24.287 ELN_MA (GBPUSD,D1) 54 , 27 ,0.00000000000000000000e+00 MQ 0 19:57:24.287 ELN_MA (GBPUSD,D1) 56 , 28 ,0.00000000000000000000e+00 HK 0 19:57:24.287 ELN_MA (GBPUSD,D1) 58 , 29 ,0.00000000000000000000e+00 IM 0 19:57:24.287 ELN_MA (GBPUSD,D1) 60 , 30 ,0.00000000000000000000e+00 PD 0 19:57:24.287 ELN_MA (GBPUSD,D1) OOS total return = 3.42215 (2963.528 percent)
结论
弹性网络回归在其能力方面相当显著。但这并不是灵丹妙药,因为有许多关键变量用于定义模型,需要规范。除了需要选择的正则化类型之外,用户还必须处理其他方面,例如收敛标准。尽管有这些缺点,但不可否认的是,它是一个有用的工具。| 文件名 | 描述 |
|---|---|
| MQL5\Indicators\LogPrices.mq5 | 一个记录交易原始价格的指标,其句柄可以传递给其他指标调用。 |
| MQL5\Include\CoordinateDescent.mqh | 包含包含CCordinateDescent类定义以及OptimizeLambda()函数的文件。 |
| MQL5\Scripts\ELN_MA.mq5 | 这是一个应用弹性网络从多个移动平均指标构建预测模型的脚本示例。 |
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/11350
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
我饶有兴趣地阅读了这篇文章,但在结尾处,我感觉作者的键盘上的字母突然用完了,文章也就没有写完。
"在文章快结束时,我们将通过制定一个基于移动平均线 的简单预测策略来演示这种方法的实际应用"。
我还是不明白:
1.什么是预测策略的演示????
2.哪里有什么预测?
//---
我运行了脚本,只更改了设置中的日期和时间范围,日志中出现了以下条目:
请向我解释一下这些数字是要告诉我什么。
该指标的工作看起来很奇怪。
红线建在低价位,黄线建在高价位。
为什么有些地方高价比低价低?
指示器的运行看起来很奇怪。
红线在低价位时出现,黄线在高价位时出现。
为什么有些地方高价比低价低?
你知道一个子窗口中的指标不会被调到相同的刻度,除非你明确设置为相同,对吗?
您知道,除非明确设置为相同比例,否则同一子窗口中的指标不会被调至相同比例,对吗?
是的,这有点蠢。好吧 谢谢 All right.谢谢。