
Investigando las características estacionales de las series temporales financieras con la ayuda de diagramas Boxplot
Tratando de refutar la hipótesis del mercado eficiente y probar la existencia de los ciclos de mercado
En 2013, Gene Fama se convirtió en Premio Nobel de economía, gracias a su hipótesis del mercado eficiente. Esta hipótesis presupone que toda la información sustancial se refleja total e inmediatamente en el mercado de valores. En este caso, además, ninguno de los participantes del mercado tiene ventaja sobre los demás, si bien existen ciertas salvedades, y la eficiencia puede adoptar tres niveles:
- débil, si el coste de un activo de mercado refleja plenamente la información pasada relacionada con este activo;
- media, si refleja, no solo la información pasada, sino también la pública;
- fuerte, si además refleja la información privilegiada, no disponible al público general.
Dependiendo del grado de eficiencia, los mercados poseen un nivel diferente de predictibilidad. Para el análisis técnico, esto significa que en el mercado pueden estar presentes componentes estacionales cíclicos de distinta naturaleza.
Por ejemplo, la actividad del mercado puede cambiar de un año a otro, de un mes a otro, de una sesión comercial a otra, de una hora a otra, etcétera. Lo que es más, estos ciclos, por ejemplo, pueden suponer ciertas secuencias predecibles, dentro y entre las cuales el tráder puede encontrar su alfa. Asimismo, los ciclos pueden superponerse unos a otros, creando diferentes composiciones de patrones que debemos investigar.
Buscando regularidades estacionales en los incrementos de precio
Podemos estudiar tanto los ciclos regulares, como los compuestos. Vamos a analizar un ejemplo de análisis de la oscilaciones mensuales de algún instrumento financiero. Para ello, usaremos el lenguaje IPython combinado con el terminal MetaTrader5.
Para que sea fácil importar las cotizaciones directamente desde el terminal, usaremos el código siguiente:
from MetaTrader5 import * from datetime import datetime import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline import seaborn; seaborn.set() # Initializing MT5 connection MT5Initialize("C:\\Program Files\\MetaTrader 5\\terminal64.exe") MT5WaitForTerminal() print(MT5TerminalInfo()) print(MT5Version())
Aquí, el lector deberá indicar la ruta hasta su terminal, porque esta podría diferenciarse de la nuestra.
Vamos a escribir unas cuentas líneas más, para sumergirnos directamente en el análisis de datos:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_D1, datetime(2010, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]
returns.head(5)
Monthly_Returns = returns.groupby([returns.index.year.rename('year'), returns.index.month.rename('month')]).mean()
Monthly_Returns.boxplot(column='close', by='month', figsize=(15, 8))
La variable rates aplica un frame de datos de la biblioteca pandas con los precios en el intervalo temporal indicado (por ejemplo, 10 años, como en este ejemplo). Supongamos que nos interesan solo los precios de cierre (así, la interpretación resultará más sencilla), para trabajar solo con ellos, eliminamos las columnas de datos sobrantes con la ayuda del método rates.drop().
Dado que los precios tienen un desplazamiento temporal medio y forman tendencias, podemos aplicar el análisis estadístico a estas series brutas. En econometría se usa el cambio porcentual de los precios (incrementos de precio) para que todos se ubiquen más o menos en un mismo intervalo de valores. Obtendremos el cambio porcentual a través de pd.DataFrame(rates['close'].pct_change(1)).
Nos interesan los intervalos medios de precio por meses. Vamos a agrupar el recuadro de tal forma que obtengamos los incrementos mensuales medios por años y podamos representarlos en el gráfico de boxplot (diagramas de caja).
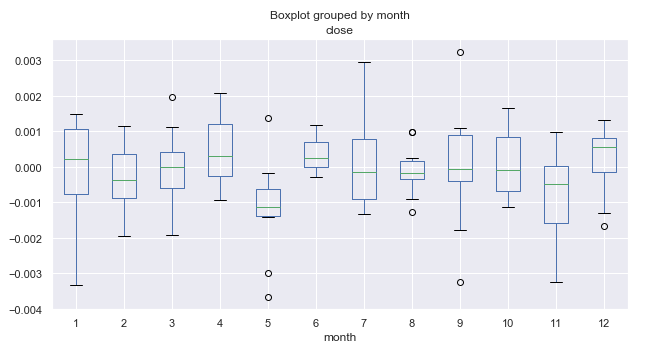
Fig. 1. Intervalos medios de incremento de precio por meses en los últimos diez años.
Qué son los boxplots (o diagramas de caja), y cómo interpretarlos correctamente
Necesitamos disponer de información sobre la variabilidad del mercado o la dispersión de los datos de precio en un cierto periodo. Cada diagrama de caja individual ofrece una buena imagen sobre la distribución de los valores en el conjunto de datos. A pesar de sus similitudes visuales, no debemos confundir el diagrama de caja con el gráfico de velas japonesas. A diferencia de las velas, se trata de un método estandarizado de representación de la distribución de datos, basado en cinco indicadores.
- La mediana, Q2 o percentil 50, muestra el valor medio del conjunto de datos. En el gráfico, se marca con líneas horizontales verdes dentro de las cajas.
- El primer cuartil Q1 (o percentil 25), representa la mediana entre Q2 y el menor valor de la muestra incluido en un intervalo de confianza del 99%. En el gráfico, se marca con el límite inferior del "cuerpo" de la caja.
- El tercer cuartil Q3 (o percentil 75) es la mediana entre Q2 y el valor máximo mostrado como límite superior del "cuerpo" de la caja.
- El cuerpo de la caja forma el rango intercuartílico (entre los percentiles 25 y 75), también llamado RIC.
- Los "bigotes" de la caja complementan la distribución, abarcando el 99% de la dispersión de toda la muestra, mientras que los puntos superior e inferior indican los valores atípicos fuera del intervalo de valores del 99%.
Esta información es suficiente para valorar el intervalo de oscilaciones, así como la dispersión dentro del intervalo.
Continuamos el análisis de las regularidades estacionales
Ahora, vamos a analizar la figura 1 con mayor atención. Podemos ver que la mediana del incremento en el quinto mes (mayo) se ha desplazado hacia abajo con respecto al cero, y que tenemos un valor atípico considerable, que ha superado el cero. De media, el mercado en mayo ha descendido respecto a marzo, hecho destacado por las estadísticas recopiladas en 10 años. Y solo ha habido un año cuando el mercado ha crecido sustancialmente en este periodo. Es información interesante, que se corresponde con el dicho de los tráders: "Sell in may and go away!".
Echamos un vistazo al mes 6 (junio), después de mayo. Prácticamente siempre (salvo un año), el mercado ha crecido en junio con respecto a mayo, lo que constituye una regularidad indudable que se repite cada año. La amplitud de las oscilaciones de junio es bastante pequeña, sin valores atípicos (a diferencia de mayo), lo que indica una buena estabilidad estacional.
Prestemos atención al mes 11 (noviembre): la posibilidad de que el mercado descienda en este periodo es alta, después de lo cual, el mercado ha ascendido en diciembre. Enero (el primer mes), ha destacado por su alta volatilidad y su tendencia al descenso con respecto a diciembre.
Los datos obtenidos pueden resultar útiles como imagen general para tomar decisiones comerciales. Asimismo, las capacidades se pueden incorporar a un sistema comercial, supongamos, para que realice más compras o ventas en los mismos meses.
La información sobre los ciclos mensuales es muy interesante, pero también podemos fijarnos en ciclos más breves, de días.
Echemos un vistazo a la distribución de los incrementos de precio en cada día de la semana por separado, durante los mismos 10 años:
Daily_Returns = returns.groupby([returns.index.week.rename('week'), returns.index.dayofweek.rename('day')]).mean()
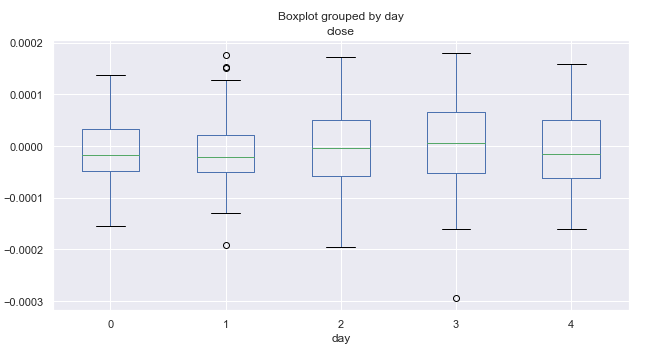
Fig. 2. Intervalos medios de incremento de precio por días comerciales en los últimos diez años.
Aquí, el cero se corresponde con el lunes, y el cuatro con el viernes. A juzgar por la amplitud, la volatilidad por días permanece casi constante, es decir, no podemos afirmar que en un día concreto de la semana las transacciones se den de una forma más activa o más tranquila. De media, los lunes y viernes, el mercado tiende a descender más que a ascender. Quizá en otros meses la distribución por días tenga un aspecto distinto. Vamos a realizar este análisis.
# leave only one month "returns.index[~returns.index.month.isin([1])" returns = returns.drop(returns.index[~returns.index.month.isin([1])])
En el listado adjunto, la unidad se corresponde con el mes de enero. Cambiando este valor, es posible obtener una estadística selectiva por días de cualquier mes, en nuestro caso de 10 años.
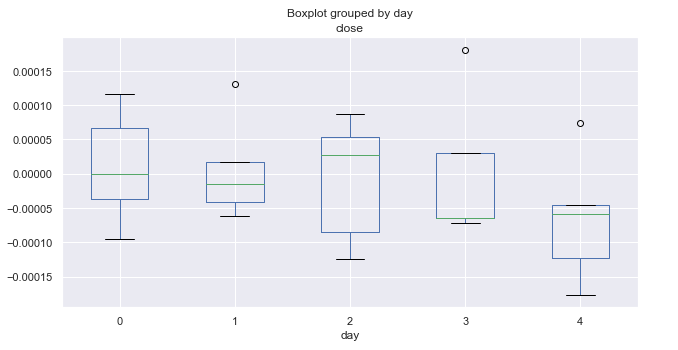
Fig. 3. Intervalos medios del incremento de precio por días comerciales durante 10 años (enero).
En el diagrama de arriba se presentan las distribuciones de los incrementos por días para el mes de enero. El diagrama es ahora más informativo, en comparación con las estadísticas reunidas sobre todos los meses. Se ve perfectamente la tendencia del mercado a descender los viernes: solo una vez la pareja de divisas "EURUSD" no ha descendido (valor atípico por encima de cero, en forma de punto).
Vamos a analizar la misma estadística para el mes de marzo:
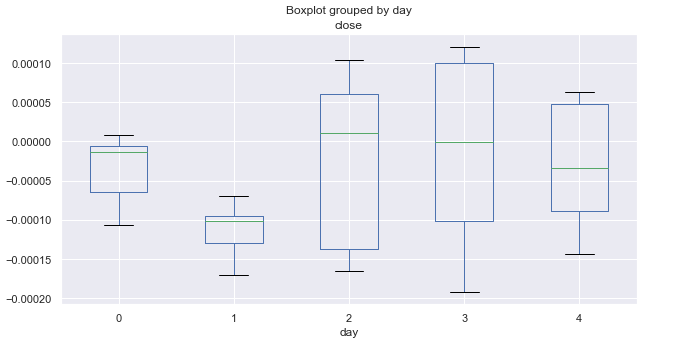
Fig. 4. Intervalos medios del incremento de precio por días comerciales durante 10 años (marzo).
La estadística de marzo se distingue claramente de la de enero. Los lunes y martes (sobre todo los martes) muestran una tendencia bajista. Todos los martes se han cerrado con un descenso considerable, mientras que el resto de días oscilan próximos al cero (de media).
Vamos a analizar ahora el mes de octubre con el mismo método:
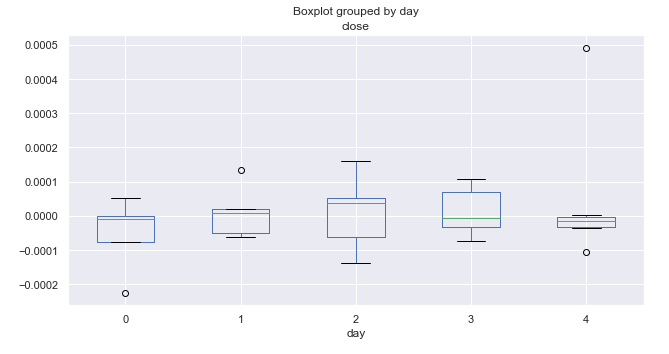
Fig. 5. Intervalos medios del incremento de precio por días comerciales durante 10 años (octubre).
El análisis de la distribución de los incrementos por días en octubre no ha detectado ninguna regularidad destacable. Podemos apenas destacar el miércoles, que tiene la mayor amplitud y potencial de movimiento de precios; por lo demás, los movimientos ascendentes o descendentes son igual de probables, con algún valor atípico.
Análisis de las regularidades estacionales intradía
Con frecuencia, para construir sistemas comerciales, debemos tener en cuenta la distribución dentro del día, supongamos, por horas, como complemento a la mesual y la semanal. Esto se puede hacer con facilidad, vamos a analizar la situación.
Echemos un vistazo a la distribución de los incrementos de precio en cada hora:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]
Hourly_Returns = returns.groupby([returns.index.day.rename('day'), returns.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(10, 5))
Al igual que en el primer caso, obtenemos las cotizaciones de los 10 años, pero ya con un marco temporal de 15 minutos. Existe una segunda diferencia: los datos han sido agrupados por días y horas, para así obtener la mediana de la estadística por horas para todos los días en la submuestra.
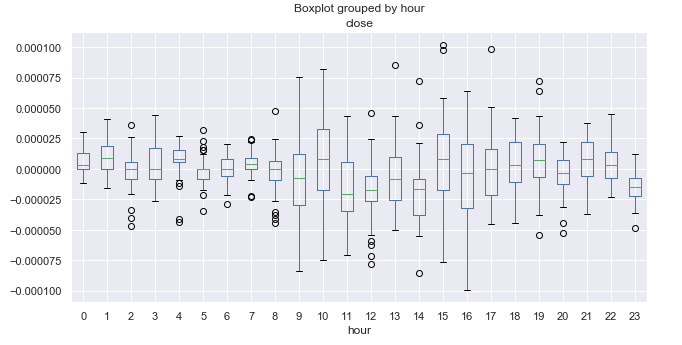
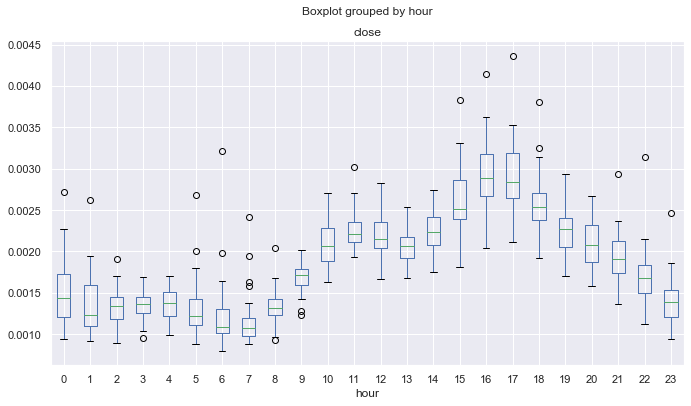
Fig. 6. Intervalos medios de incremento de precio por horas en los últimos diez años.
Para que el lector pueda orientarse en las estadísticas mostradas, deberá conocer el huso horario de su terminal. En nuestro caso, es UTC + 2. Como referencia, escribiremos la hora de comienzo y finalización de las principales sesiones comerciales de FÓREX en el formato UTC + 2.
| Sesión | Comienzo | Finalización |
|---|---|---|
| Pacífica | 21.00 | 08.00 |
| Asiática | 01.00 | 11.00 |
| Europea | 08.00 | 18.00 |
| Americana | 14.00 | 00.00 |
La sesión pacífica es conocida por la transquilidad de sus transacciones. Si miramos la amplitud del diagrama de cajas, notaremos fácilmente que en el intervalo 21.00-08.00, la amplitud es mínima, lo cual se corresponde con el comercio analizado. Después del comienzo de las sesiones europea y americana, la amplitud aumenta, tras lo cual, disminuye paulatinamente. A primera vista, no existe la obvia periodicidad que se observaba en el marco temporal de días. El incremento medio oscila en torno a cero, principalmente, sin mostrar horas de ascenso o descenso claros.
Resulta interesante el periodo de las 23.00 (final de la sesión americana), en el que los precios, de media, descienden con respecto a las 22.00. Esto puede suponer una cierta corrección al final de las transacciones. Al mismo tiempo, a las 00.00, los precios ascienden con respecto a las 23.00, es decir, de media, se observa cierta periodicidad. Resulta complicado detectar algún otro ciclo claro; no obstante, disponemos de una imagen general de las amplitudes de precio, y sabemos qué podemos esperar en este u otro momento.
La eliminación de tendencias con un mismo retraso ocultan ciertas regularidades, por eso, lo razonable será fijarse en la eliminación de tendencias según una media móvil con periodo aleatorio.
Buscando regularidades estacionales con eliminación de tendencias según una media móvil
La correcta detección de la tendencia es casi un arte. A veces, podemos suavizar demasiado una serie temporal y obtener pocas señales para el comercio. Si reducimos el periodo de suavizado, sucederá lo contrario: una alta frecuencia en las transacciones podría no cubrir el spread y la comisión. Vamos a modificar el código, para implementar la eliminación de tendencias según una media móvil:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
rates = rates.set_index('time')
# set the moving average period
window = 25
# detrend tome series by MA
ratesM = rates.rolling(window).mean()
ratesD = rates[window:] - ratesM[window:]
plt.figure(figsize=(10, 5))
plt.plot(rates)
plt.plot(ratesM)
Establecemos un periodo para la media móvil igual a 25. Este parámetro se puede modificar, así como el periodo de los precios de cierre obtenidos. Aquí, hemos tomado el marco temporal de 15 minutos; la promediación conforme al mismo, da como resultado la desviación media de precios de cierre con respecto a una media móvil según el marco temporal de 15 minutos para cada hora. Representamos la serie temporal obtenida:
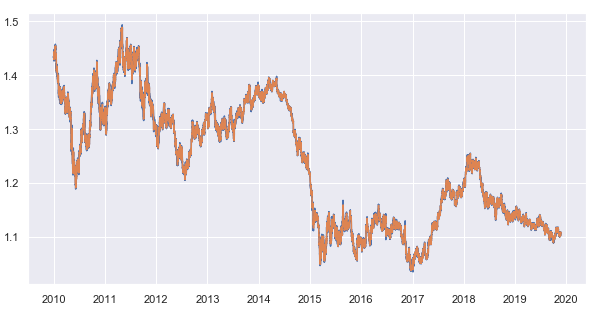
Fig. 7. Precios de cierre con el marco temporal de 15 minutos y una media móvil con un periodo de 25
Vamos a restar la media móvil de los precios de cierre, obteniendo la serie temporal sometida a la eliminación de tendencias (resto):
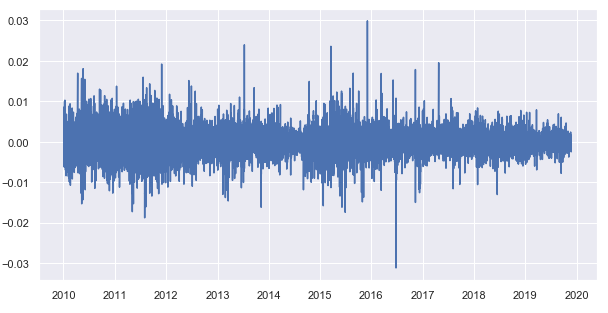
Fig. 8. resto de la sustracción de la media móvil a los precios de cierre
Solo queda obtener la estadística por horas de las distribuciones de los restos según cada hora comercial:
Hourly_Returns = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(15, 8))
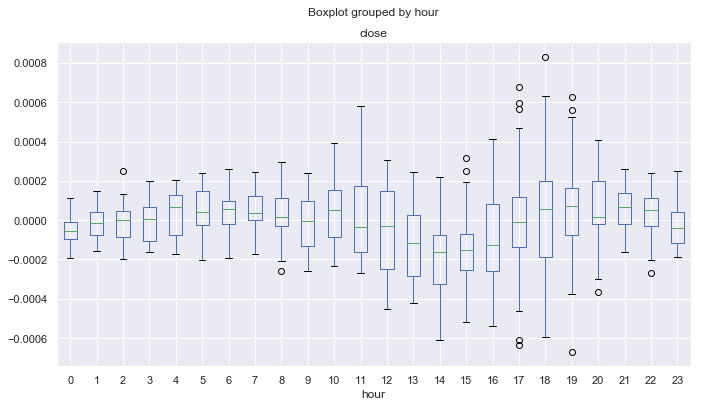
Fig. 9. Intervalos medios de incremento de precio por horas según la eliminación de tendencias conforme a una media móvil de 25 periodos, en diez años.
A diferencia del diagrama en la figura 6, que ha sido construido según los incrementos de precio con retraso único, este diagrama muestra menos valores atípicos, así como una mayor cantidad de regularidades cíclicas. Por ejemplo, ahora se ve que, a partir de las 0.00 y hasta las 08.00 (sesión pacífica), los precios, de media, aumentan paulatinamente con respecto a la media móvil. Desde las 12.00 hasta las 14.00, se detecta una tendencia al descenso, después de lo cual, ya en la sesión americana, los precios ascienden de media. Al inicio de la sesión pacífica, los precios descienden durante 4 horas, a partir de las 21.00.
Como es natural, nos apetece mirar los momentos más importantes en la distribución de este "microcosmos", para realizar una valoración más precisa. Por ejemplo, podemos mostrar las desviaciones estándar para la serie temporal obtenida tras la eliminación de tendencia, en forma de diagrama de cajas:
Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).std()
Fig. 10. Desviación estándar media de precio de los incrementos de precio por horas, según la eliminación de tendencias conforme a una media móvil de 25 periodos, en diez años.
En la fig. 10 podemos ver en qué horas se observa un comportamiento más estable del precio en cuanto a su desviación estándar con respecto a la esperanza matemática. Por ejemplo, las horas 4, 13, 14, 19 tienen una dispersión estable de un día a otro, y pueden resultar más atractivas para las estrategias con mean reversion. Otras horas pueden mostrar valores atípicos y bigotes largos, lo que indica una volatilidad por horas más variable de un día a otro.
Otro momento interesante es el coeficiente de asimetría, vamos a mostrarlo:
Hourly_skew = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).skew()

Fig. 11. Coeficientes medios de asimetría de los incrementos de precio por horas, según la eliminación de tendencias conforme a una media móvil de 25 periodos, en diez años.
La proximidad al cero y la pequeña dispersión indican una distribución más "estándar" de los incrementos. Aquí, de manera visual, el diagrama comienza a adquirir una forma cóncava. Por ejemplo, las oscilaciones en las sesiones europea y americana, aunque tienen una gran amplitud (fig. 9), sus distribuciones por horas son más estables y se encuentran menos desplazadas, a diferencia de las sesiones pacífica y asiática. Esto podría estar condicionado por los grandes saltos de actividad en las dos últimas sesiones, cuando una actividad comercial casi cero alterna con movimientos inesperados, que contribuyen notablemente en la deformación de las distribuciones.
De forma similar se muestra la estadística de curtosis:
Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).apply(pd.DataFrame.kurt)
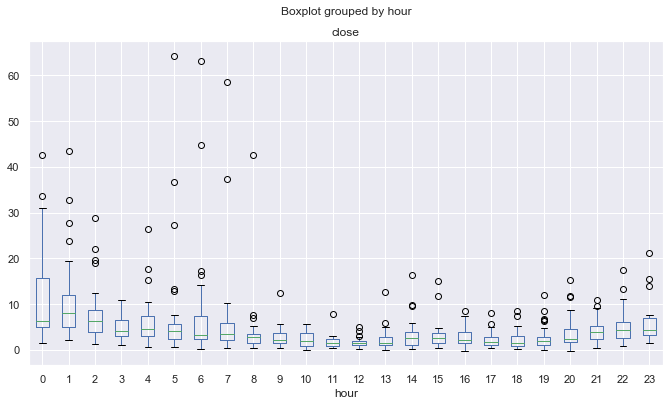
Fig. 12. Coeficientes medios de curtosis de los incrementos de precio por horas, según la eliminación de tendencias conforme a una media móvil de 25 periodos, en diez años.
Debido al efecto descrito más arriba (podemos suponer), las distribuciones muestran picos menos agudos y más "normales" para las sesiones comerciales más volátiles, y más "anormales" para las sesiones comerciales tranquilas. Se da esa paradoja.
Buscando regularidades estacionales con eliminación de tendencias según una media móvil en un mes o día de la semana determinado
Podemos ver la distribución de los precios por horas restándole la tendencia para cada mes por separado, y también para cualquier día de la semana. El código completo se adjunta al final del artículo, aquí solo mostramos la comparación entre marzo y noviembre.
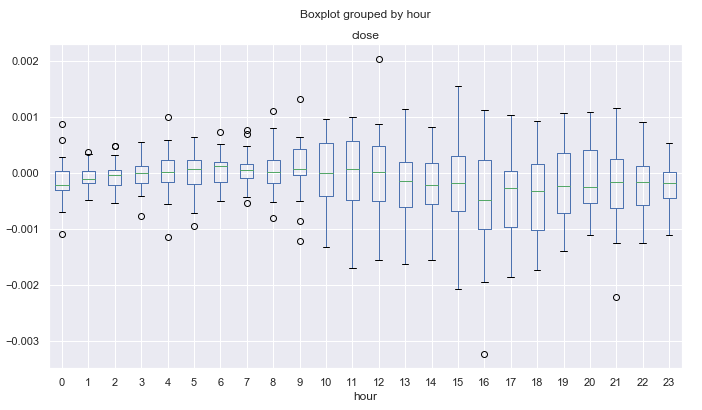
Fig. 13. Intervalos medios de incremento de precio por horas según la eliminación de tendencias conforme a una media móvil de 25 periodos, en diez años, para el mes "marzo".
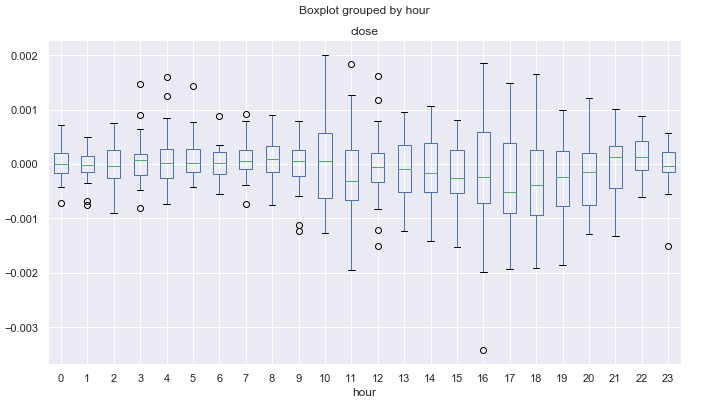
Fig. 14. Intervalos medios de incremento de precio por horas según la eliminación de tendencias conforme a una media móvil de 25 periodos, en diez años, para el mes "noviembre".
También podemos buscar ciclos intradía más pequeños, dentro de los datos de ticks, pero hemos decidido limitarnos a las regularidades estacionales básicas que, en opinión de los tráders, están presentes en la series temporales financieras. Esta información se puede usar para desarrollar sistemas comerciales propios, teniendo en cuenta las "peculiaridades" estacionales de este u otro instrumento financiero.
Comprobando las regularidades de la lógica comercial
Vamos a escribir un sencillo experto comercial que explotará la regularidad encontrada en la fig. 9. Estamos hablando de la suposición de que desde las 0.00 hasta las 04.00 horas de GMT+2, los precios de la pareja EURUSD aumentan con respecto a su media durante las cuatro horas.
//+------------------------------------------------------------------+ //| Seasonal trader.mq5 | //| Copyright 2020, Max Dmitrievsky | //| https://www.mql5.com/ru/users/dmitrievsky | //+------------------------------------------------------------------+ #property copyright "Copyright 2020, Max Dmitrievsky" #property link "https://www.mql5.com/ru/users/dmitrievsky" #property version "1.00" #include <MT4Orders.mqh> #include <Trade\AccountInfo.mqh> #include <Math\Stat\Math.mqh> input int OrderMagic = 666; input double MaximumRisk=0.01; input double CustomLot=0; int hnd = iMA(NULL, 0, 25, 0, MODE_SMA, PRICE_CLOSE); MqlDateTime hours; double maArr[], prArr[]; void OnTick() { //--- CopyBuffer(hnd, 0, 0, 1, maArr); CopyClose(NULL, 0, 0, 1, prArr); double pr = prArr[0] - maArr[0]; TimeToStruct(TimeCurrent(), hours); if(hours.hour >=0 && hours.hour <=4) if(countOrders(0)==0 && countOrders(1)==0) if(pr < -0.0002) OrderSend(Symbol(),OP_BUY,0.01,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN); if(countOrders(0)!=0 && pr >=0) for(int b=OrdersTotal()-1; b>=0; b--) if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) { if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; } } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int countOrders(int a) { int result=0; for(int k=0; k<OrdersTotal(); k++) { if(OrderSelect(k,SELECT_BY_POS,MODE_TRADES)==true) if(OrderType()==a && OrderMagicNumber()==OrderMagic && OrderSymbol() == _Symbol) result++; } return(result); }
Aquí, usaremos la misma media móvil que utilizamos para la valoración estadística con el periodo 25. A continuación, restamos la media al último precio conocido y comprobamos que la hora actual de las transacciones se encuentre en el intervalo entre las cero horas y las cuatro, ambas incluidas. Echando un vistazo a la fig. 9, podemos comprender que la diferencia máxima entre los precios de cierre y las medias móviles en este periodo es de -0.0002 puntos, y que la media se encuentra por encima de cero. Por consiguiente, nuestra lógica comercial consistirá en abrir transacciones de compra al alcanzar esta diferencia, y cerrar la posición cuando alcance cero. Este bot de comprobación no dispone de stops ni de niguna otra otra verificación, ha sido diseñado solo para comprobar la presencia de regularidades. Realizaremos la simulación desde 2015 a 2019 en el marco temporal de 15 minutos (la media móvil en la investigación se construía precisamente con este periodo), con todos los ticks:
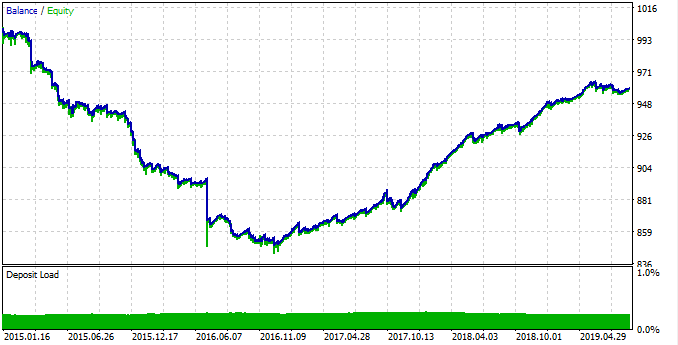
Fig. 15. Simulación de la regularidad encontrada.
De 2015 a 2017, la regularidad ha funcionado mal, y el gráfico ha descendido significativamente, mientras que desde 2017 a 2019, se detecta un crecimiento estable. Vamos a ver por qué ha sucedido así. Para ello, analizaremos estadísticas aparte para cada intervalo temporal.
Para comenzar, vamos a analizar el intervalo comercial rentable:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2017, 1, 1), datetime(2019, 11, 25)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
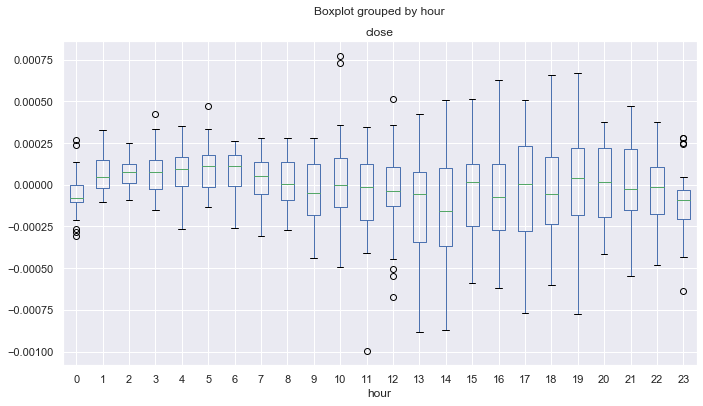
Fig. 16. estadística de los años 2017-19.
Se ve bien que todas las horas (excepto la cero) tienen una media por encima de cero con respecto a la media móvil. De esta forma, alfa se encuentra estadísticamente del lado de nuestro sistema y, de media, el sistema se queda en el beneficio. Ahora, vamos a echar un vistazo a la distribución de los años 2015-17.
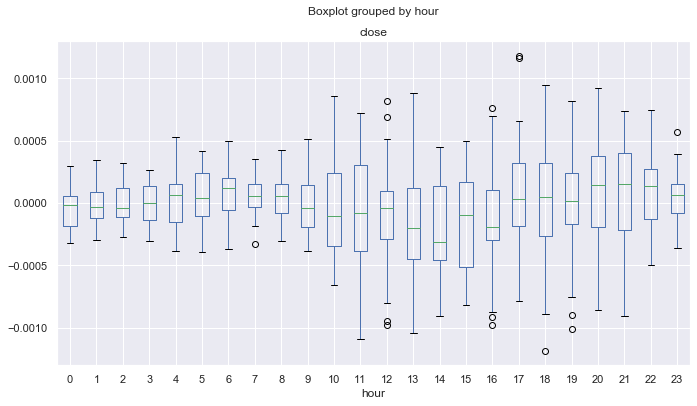
Fig. 17. estadística de los años 2015-17.
En este caso, las distribuciones tienen un desplazamiento de la media (mediana) por debajo o igual a cero para todas las horas, salvo la cuarta, lo que indica una probabilidad menor de obtener beneficios. Además, los diagramas de caja tienen una amplitud media significativamente mayor en comparación con el otro intervalo temporal, en el que el valor mínimo no es inferior a -0.00025, aquí alcanza casi -0.0005. Otra desventaja es que la valoración de las distribuciones se da solo de los precios de cierre, por lo que los valores atípicos en los precios no son tenidos en cuenta. Esto se puede corregir analizando los datos de ticks, pero ese asunto se sale del tema del artículo. La diferencia resulta comprensible, así que podemos intentar afinar el sistema para igualar los resultados de todos los años.
Permitiremos abrir transacciones solo a las horas 0-1, presuponiendo que en las siguientes horas la transacción se cerrará con beneficios a pesar de todo, dado que la desviación con respecto a la media tiende a salir hacia el lado positivo. Asimsimo, aumentaremos el umbral de cierre de transacciones de 0.0 a 0.0003, permitiendo al robot conseguir potencialmente mayores beneficios. Los cambios se muestran en este listado:
TimeToStruct(TimeCurrent(), hours); if(hours.hour >=0 && hours.hour <=1) if(countOrders(0)==0 && countOrders(1)==0) if(pr < -0.0004) OrderSend(Symbol(),OP_BUY,LotsOptimized(), SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN); if(countOrders(0)!=0 && pr >= 0.0003) for(int b=OrdersTotal()-1; b>=0; b--) if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) { if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; }
Vamos a poner a prueba el robot, para sacar las conclusiones definitivas:
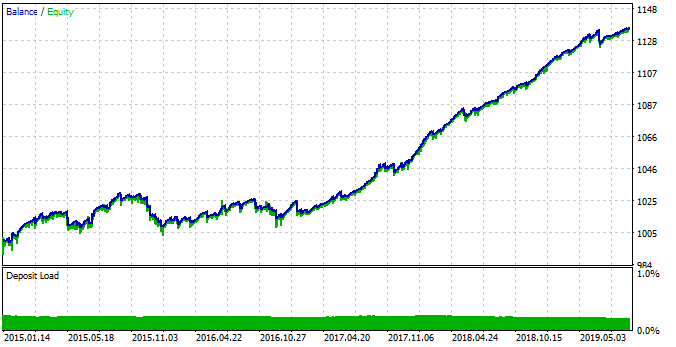
Fig. 18. Simulación de la regularidad encontrada, tras modificar los parámetros del sistema comercial.
Podemos ver que el sistema es ahora más estable en el intervalo de los años 2015-17. Sin embargo, la regularidad estacional cambiada, no le ha permitido comerciar con la misma eficacia que en los años 2017-19. Este comportamiento se puede explicar por los cambios fundamentales en el mercado, que se describen fácilmente con la ayuda de los diagramas boxplot.
Claro que aún quedan muchas regularidades por investigar, pero este ejemplo básico debería darnos una idea de las nuevas posibilidades interesantes que abre el uso de estas técnicas.
Conclusión
En este artículo, hemos ofrecido un método estadístico de búsqueda de regularidades estacionales en las series temporales financieras. Hemos demostrado que en el mercado pueden existir tanto ciclos estacionales mensuales, como ciclos intradía, dependiendo del mes. El análisis por horas ha demostrado que, seleccionando un periodo de suavizado determinado (por ejemplo, el de la media móvil), podemos encontrar ciclos determinados tanto dentro de las sesiones, como al pasar de una sesión comercial a otra.
Entre las ventajas de dicho paso, podemos destacar el trabajo con diferentes regularidades del mercado, así como la práctica inexistencia de reoptimización en cuanto a la iteración de parámetros, gracias a lo cual, el sistema comercial puede poseer una gran estabilidad.
Entre las desventajas, podemos nombrar la laboriosidad del propio proceso de minería de las regularidades estacionales y la iteración de diferentes combinaciones de ciclos.
Todo el análisis se ha realizado con la pareja de divisas EURUSD en un intervalo temporal de 10 años. Los códigos fuente en el lenguaje Python se adjuntan al final del artículo, en el formato .ipynb (Jupyter notebook). El lector podrá analizar por sí mismo cualquier instrumento que le interese con la ayuda de esta biblioteca para el desarrollo de sistemas comerciales propios, o bien mejorar su propio sistema.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/7038
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Hola Maxim,
Ejecuto el código:
rates = pd.DataFrame(mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_D1, datetime(2010, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
y el tiempo que obtengo es algo así como '1262563200' que no tiene sentido, ¿Cómo se puede solucionar esto plz?
Gracias.
Hola, prueba esto
" Por ejemplo, las horas 4, 13, 14 y 19 tienen una varianza estable de un día para otro y pueden ser más atractivas para las estrategias de reversión a la media" .
¿Por qué no se incluye la hora 20? Según el gráfico de varianza, también parece estable.
" Por ejemplo, 4, 13, 14, 19 horas tienen una varianza consistente de un día a otro y pueden ser más atractivas para las estrategias de reversión a la media"
¿Por qué no se incluye la hora 20? Según el gráfico de varianza, también parece estable.
No me acuerdo, era sólo un ejemplo, creo. Por supuesto, usted puede probar otras horas también. Pero lo desarrollé con el MO.
Muestra que la hora 20 es realmente buena.
"Análisis exploratorio para cada hora de negociación" sección.
¡Muy bien!
Muchas gracias.