文章 "ALGLIB 库优化方法（第二部分）"
全表。
如果我没理解错的话，我们想找到希尔函数等于 1 的最大值。
double Core (double x, double y) { double res = 20.0 + x * x + y * y - 10.0 * cos (2.0 * M_PI * x) - 10.0 * cos (2.0 * M_PI * y) - 30.0 * exp (-(pow (x - 1.0, 2) + y * y) / 0.1) + 200.0 * exp (-(pow (x + M_PI * 0.47, 2) + pow (y - M_PI * 0.2, 2)) / 0.1) //全局最大值 + 100.0 * exp (-(pow (x - 0.5, 2) + pow (y + 0.5, 2)) / 0.01) - 60.0 * exp (-(pow (x - 1.33, 2) + pow (y - 2.0, 2)) / 0.02) //全球最小值。 - 40.0 * exp (-(pow (x + 1.3, 2) + pow (y + 0.2, 2)) / 0.5) + 60.0 * exp (-(pow (x - 1.5, 2) + pow (y + 1.5, 2)) / 0.1); return Scale (res, -39.701816104859866, 229.91931214214105, 0.0, 1.0); }
这个函数只有两个参数。
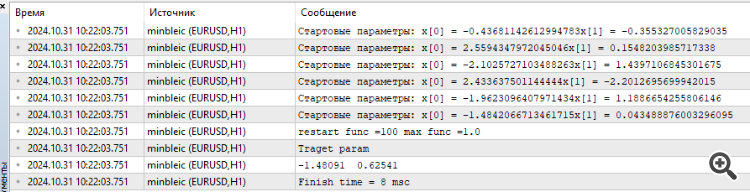
我连接了 MinBleic
在我看来，我们应该计算的不是优化器给出的平均结果，而是最大值。 当然，你也可以看到时间，惊人的 8 毫秒。
1.如果我理解正确的话，我们想要找到希尔函数等于 1 的最大值。
2.这个函数只有两个参数。
3.连接 MinBleic
在我看来，我们应该计算的不是优化器产生的平均结果，而是最大结果。 当然，你也可以看到时间，惊人的 8 毫秒。
感谢您的评论。
1.是的，没错。所有测试函数都是统一的，它们的值都在 [0.0; 1.0] 范围内。
2.所有测试函数都只有两个参数。但在测试算法时，我们通过反复复制一个二维函数，使用多维搜索空间（三种测试类型，5*2=10、25*2=50、500*2=1000 个参数来评估 AO 的扩展能力）。
3.两个参数的问题过于简单，无法充分比较算法之间的差异，几乎所有算法都能立即解决这样的问题，收敛性达到 100%。这些算法在处理多维空间时存在困难。
我们应该取最大结果吗？问题的关键在于，不同算法运行结果的分散性很重要。在所有算法的第一次迭代中，播种点的随机值可能完全随机地非常接近全局极值，在这种情况下，算法会不合理地很快找到最佳结果，因此从运行结果中取平均值更能反映算法的特性，排除随机依赖性对算法 "成功 "的影响。
这与概率论有关。无论目标函数多么复杂，如果只有一个参数，那么即使产生 10 个随机值，其中也会有一个非常接近全局极值。ALGLIB（梯度下降的变体）方法对空间中点的初始位置很敏感，因此这些方法具有确定性。随着搜索空间维度的增加，空间的复杂度也呈指数级增长，没有办法通过生成随机数来达到全局极值。
如果问题的维数增加，这些方法甚至难以收敛于单调、平滑、单峰抛物面，这就是证明。
无论搜索空间的初始值如何，AO 显示的结果越稳定，就越能说明这种方法在解决问题方面是可靠的。这就是我们在测试中选择多次运行 AO 的平均值的原因。
当今的现实情况是，许多任务需要优化数百万甚至数十亿个参数（人工智能、LLM、生成网络、生产和商业中的复杂控制任务），我们无法谈论任务的平滑性和单模性。
感谢您的评论。
1.是的，正确。所有测试函数都是统一的，其值位于 [0.0; 1.0] 范围内。
2.所有测试函数都只有两个参数。但在测试算法时，我们通过反复复制一个二维函数，使用多维搜索空间（三种测试类型，5*2=10、25*2=50、500*2=1000 个参数来评估 AO 的扩展能力）。
3.两个参数的问题过于简单，无法充分比较算法之间的差异，几乎所有算法都能立即解决这样的问题，收敛性达到 100%。这些算法在处理多维空间时存在困难。
我们应该取最大结果吗？问题的关键在于，不同算法运行结果的分散性很重要。在所有算法的第一次迭代中，播种点的随机值，可以完全随机地非常接近全局极值，在这种情况下，算法会不合理地迅速找到最佳结果，因此从运行结果中取平均值更能反映算法的特性，排除随机依赖性对算法 "成功 "的影响。
这与概率论有关。无论目标函数多么复杂，如果只有一个参数，那么即使产生 10 个随机值，其中也会有一个非常接近全局极值。ALGLIB（梯度下降的变体）方法对空间中点的初始位置很敏感，因此这些方法具有确定性。随着搜索空间维度的增加，空间的复杂度也会呈指数增长，因此无法通过生成随机数来达到全局极值。
如果问题的维数增加，这些方法甚至难以收敛于单调、平滑、单峰抛物面，这就是证明。
无论搜索空间的初始值如何，AO 显示的结果越稳定，就越能说明这种方法在解决问题方面是可靠的。这就是我们在测试中选择多次运行 AO 的平均值的原因。
当今的现实情况是，许多任务需要优化数百万甚至数十亿个参数（人工智能、LLM、生成网络、生产和商业中的复杂控制任务），我们无法谈论任务的平滑性和单模性。
你所采用的函数本身就非常复杂。我认为，随着参数数量的增加，为这类函数的总和寻找最佳参数纯粹是理论上的兴趣。对于交易而言，一个预测性数学模型可能有很多参数，但损失函数本身非常简单，因此搜索起来要容易得多。当然，如果我们对 Kurvafitting 不感兴趣的话，也不可能有十亿个参数，只有 10-100 个适中的参数。
如果我们从结果的角度来看。我感兴趣的是能找到函数最大值的参数，为什么需要平均结果？我感兴趣的是最优值以及达到最优值所需的时间。如果这个时间是可以接受的，那么我不在乎计算机花了多少精力来选择起始参数向量，最重要的是我得到了结果。
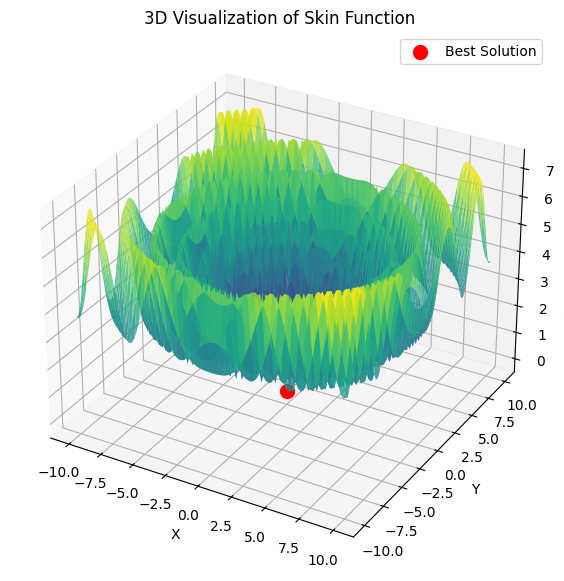
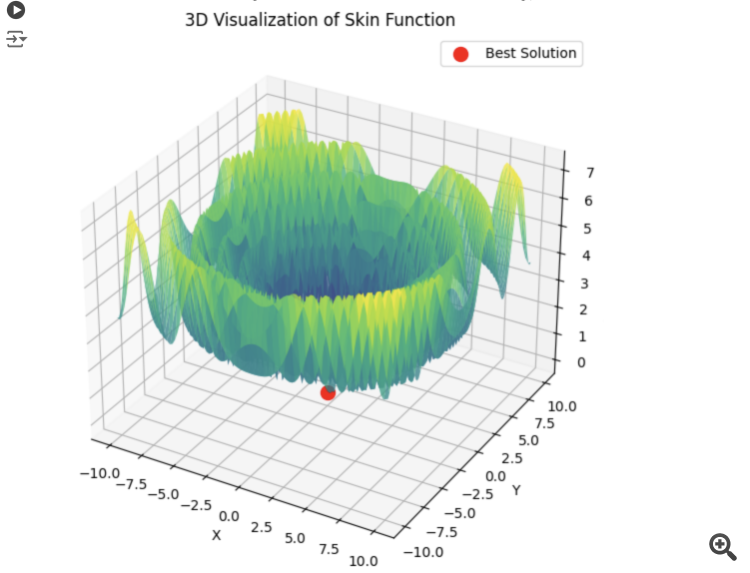
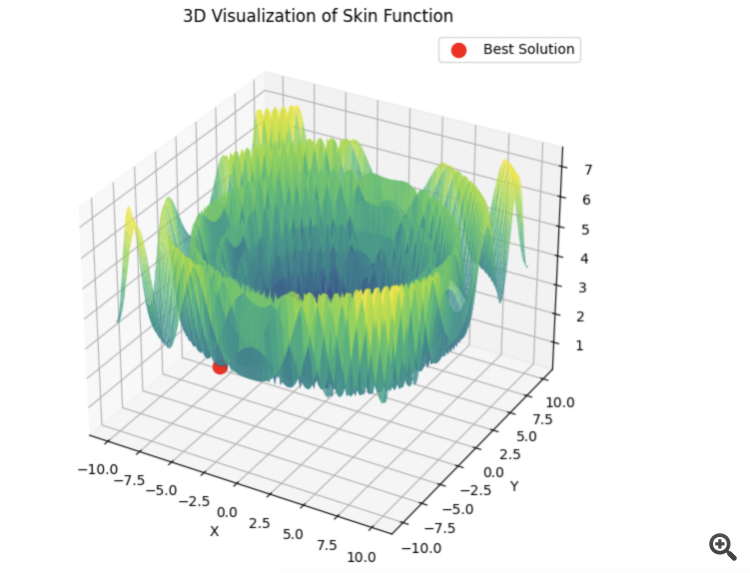
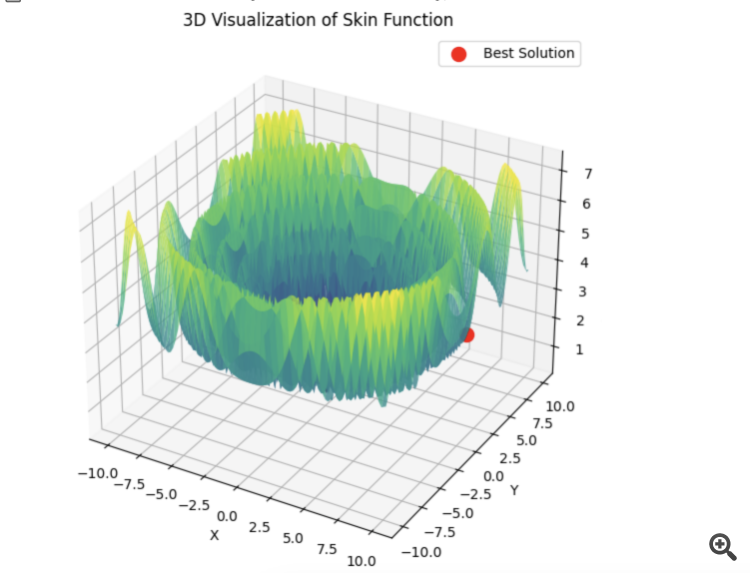
下面是 5 个希利函数之和的示例
15 秒的时间，结果是 0.76。我觉得还不错。特别是考虑到交易主题，我们根本不知道全局最优等于多少，也永远不会知道。
无论如何，感谢你的文章。这里有很多值得思考的地方。我稍后会测试其他算法，并公布结果。
1) 你提出的函数本身非常复杂。我认为，随着参数数量的增加，为这些函数之和寻找最佳参数纯粹是理论上的兴趣。
2）对于交易而言，一个预测性数学模型可能有很多参数，但损失函数本身非常简单，因此寻找起来要容易得多。当然，如果我们对 kurvafitting 不感兴趣的话，也不可能有十亿个参数，只有 10-100 个适中的参数。
3) 如果我们从结果的角度来看。我感兴趣的是能找到函数最大值的参数，为什么需要平均结果？我感兴趣的是最优值和达到最优值所需的时间。如果这个时间是可以接受的，那么我不在乎计算机花了多少精力来选择起始参数向量，最重要的是我得到了结果。
4) 下面是 5 个希利函数之和的示例
15 秒的时间，结果是 0.76。我觉得还不错。特别是考虑到交易主题，我们根本不知道全局最优等于多少，而且永远也不会知道。
5) 总之，感谢您的文章。这里有很多值得思考的地方。我稍后会测试其余的算法，并将结果公布出来。
1) 在文章中，我们并不是把 AEO 本身当作真空中的一匹马（例如 PSO，非常著名，因此很受欢迎，但功能并不强大；同样的 AEO，根本不为人所知，但它在光滑和离散的空间中的切削速度却像芯片飞行一样快），而是在分析它们的逻辑和设备的同时，将它们的搜索能力相互比较。这样，我们就能深入了解它们在实际任务中的潜力。随着维度的增加，算法之间的相互比较才能揭示出真正的可能性。在现实生活中，几乎没有简单的任务，当然，除非我们谈论的是可以通过分析解决的任务。
我在上文解释了为什么在比较算法时必须使用最终结果的平均值--以排除 "随机成功 "的影响，并直接揭示算法的搜索能力。
而当涉及到 AO 的实际应用时（不是为了比较 AO），那么是的，建议使用多次优化运行来选择最佳结果。但是，如果一种弱算法必须反复重启，浪费了宝贵的目标函数运行次数，那么另一种算法就可以用更少的目标函数运行次数获得相同的结果。既然结果是一样的，为什么还要多花钱呢？弱算法会陷入困境，在搜索空间中停滞不前，需要多次重启，而且你永远无法确定你是否在优化的最开始就被卡住了。我想在实践中没有人会对这种情况感兴趣。
2) 尝试在一个实际问题上用一些 Expert Advisor 将损失函数可视化，至少有两个参数，结果会发现表面并不平滑，根本不是单模态的。由于交易任务的离散性，简单平滑的目标根本不存在。因此，即使在光滑抛物面上也有困难的方法在交易中将是无效的。
3）平均结果用于算法之间的比较，而非实际应用（见第 1 点）。如果你不在乎搜索所花费的时间和精力，那就进行完整的搜索，根本没有必要使用 AO。但实际上这种情况很少发生，我们的时间和计算资源总是有限的。
4) 所提供的结果缺乏关于实现指定结果所需的目标函数运行次数的信息。 这一指标是评估自动优化效果的关键。选择自动操作应基于效率最大化（运行次数最小化）和卡住概率最小化，特别是在实际交易任务中。
5) 谢谢，我很高兴文章为推理提供了依据。如果您能提供所做测试的代码就更好了，尽管文章中已经提供了所有代码（显然，您使用了自己的测试方法）。我们会研究并找出答案。
我正在就这次讨论中提出的问题单独撰写一篇文章。
尝试不同的算法，我们已经考虑过很多算法，并对它们进行了比较。Alglib 方法非常快，我认为它们非常适合解决分析式问题（这是另一个话题），但如果不知道分析式，还有其他选择。
对于那些需要解决解析式问题的人来说，这些文章也将非常有用，因为它们描述了使用 ALGLIB 方法的工作原理。
这样比较元求解器和梯度求解器是不正确的。它们应该处于同等条件下。
Metaevr. 已经有了种子点，而梯度解算器是从一个点开始的。
为了创造同等条件，我们需要对后者进行批处理。或者多重初始化。
这就是为什么梯度解算器需要用最佳结果而不是平均结果来评估。这也是它们运行速度更快的原因。这样就能在训练神经网络时兼顾速度和准确性。
如果 PSO 马上就能选出正确的最小值，那么 lbfgs 就会跳转定位点：
那么 lbfgs 就会从一个局部跳到另一个局部，这对它来说是正常行为。但它的速度很快，可以跳转可配置的次数，将优化函数分成若干批次。
# Оптимизация с использованием L-BFGS и батчей def optimize_with_lbfgs_batches(initial_guesses, bounds, batch_size): best_solution = None best_value = float('inf') for batch in generate_batches(initial_guesses, batch_size): for initial_guess in batch: result = minimize(skin_function, initial_guess, method='L-BFGS-B', bounds=bounds) if result.fun < best_value: best_value = result.fun best_solution = result.x return best_solution, best_value # Параметры оптимизации dim = 2 # Размерность пространства решений lower_bound = -10 upper_bound = 10 num_initial_guesses = 100 # Количество начальных приближений batch_size = 10 # Размер батча
新文章 ALGLIB 库优化方法（第二部分）已发布：
在关于MetaTrader 5标准发行版中ALGLIB库优化算法的第一部分研究中，我们详细探究了以下算法：BLEIC（边界、线性等式-不等式约束）、L-BFGS（有限内存Broyden-Fletcher-Goldfarb-Shanno）和NS（盒式/线性/非线性——非光滑约束的非光滑非凸优化）。我们不仅研究了它们的理论基础，还讨论了如何将它们应用于优化问题的简单方法。
在本文中，我们将继续探索ALGLIB库中剩余的方法。特别关注在复杂的多维函数上测试它们，这将使我们能够形成对每种方法效率的全方位观点。最后，我们将对获得的结果进行全面分析，并提出选择特定类型任务的最优算法的实际建议。
作者：Andrey Dik