数据科学和机器学习（第 18 部分）：掌握市场复杂性博弈，截断型 SVD 对比 NMF

MetaTrader 5 — 交易 | 23 九月 2024, 10:22

1 071

Omega J Msigwa

-- 你拥有的越多，你看到的就越少！

内容：

什么是 NMF？

截断型 SVD 对比 NMF，博弈：

降维

根据维基百科，降维是将数据从高维空间转换为低维空间的过程，从而在低维表示中保留原始数据的一些有意义的属性，理想情况下接近其内在维度。

出于多种原因，在高维空间中工作可能并不可取；由于维度诅咒，原始数据通常是稀疏的，并且所分析数据通常计算棘手（难以控制或处理）。降维在处理大量观察和/或大量变量的领域中很常见，例如信号处理、语音识别、神经信息学、和生物信息学，阅读更多。

以下是降维的一些关键点。

高维数据

我们现实一点，在大多数现实世界的应用程序中，许多构建机器学习模型的数据集具有非常多的特征或变量（维度）。高维数据可能会引发各式各样的挑战，例如增加计算复杂性、过度拟合的风险、和可视化困难。您通常用到的的数据集拥有 5 个自变量！这不是 AI 算法交易中的大佬所做的。

假设您收集了所有 MT5（38）内置指标缓冲区。您最终会得到 56 个缓冲区的数据。这个数据集现在很庞大。

维度诅咒

这个诅咒是真实的，对于那些不相信的人，请尝试实现一个包含大量相关自变量的线性回归模型。

高度相关特征的存在可能会导致机器学习模型捕获训练数据中存在噪声和特定形态，而这些形态也许无法很好地推广到新的、尚未见过的数据。

维度诅咒是指在处理高维数据时浮现的问题，例如稀疏数据分布、增加的计算需求、以及模型过度拟合的风险，阅读更多。

利用一个线性回归模型，我仔细演示一下：

由于 CSV 文件中的前 13 个指标是趋势跟踪指标，因此尽管维度不同，但它们最有可能与自身和市场相关。

当在我们的线性回归模型中仅用 10 个趋势跟踪指标来预测 100 根柱线的收盘价时：

 matrix_utils.TrainTestSplitMatrices(data, train_x, train_y, test_x, test_y);
      
 lr.fit(train_x, train_y, NORM_MIN_MAX_SCALER);
   
 vector preds = lr.predict(train_x);
   
 Print("Train acc = ",metrics.r_squared(train_y, preds));

结果是训练阶段的模型准确率达到 92.2%。

IH      0       16:02:57.760    dimension reduction test (EURUSD,H1)    Train acc = 0.9222314640780123

甚至预测也非常准确。

KE      0       07:10:55.652    GetAllIndicators Data (EURUSD,H1)       Actuals
GS      0       07:10:55.652    GetAllIndicators Data (EURUSD,H1)       [1.100686090182938,1.092937381937508,1.092258894809645,1.092946246629209,1.092958015748051,1.093392517797872,1.091850551839335,1.093040013995282,1.10067748979471,1.09836069904319,1.100275794247118,1.09882067865937,1.098572498565924,1.100543446136921,1.093174625248424,1.092435707204331,1.094128601953777,1.094192935809526,1.100305866167228,1.098452358470866,1.093010702771546,1.098612431849777,1.100827466038129,1.092880150279397,1.092600810699407,1.098722104612313,1.100707460497776,1.09582736814953,1.093765475161778,1.098767398966827,1.099091982657956,1.1006214183736,1.100698195592653,1.092047903797313,1.098661598784805,1.098489471676998,1.0997812203466,1.091954251247136,1.095870956581002,1.09306319770129,1.092915244023817,1.09488564050598,1.094171202526975,1.092523345374652,1.100564904733422,1.094200831112628,1.094001716368673,1.098530017588284,1.094081896433971,1.099230887219729,1.092892028948739,1.093709694144579,1.092862170694582,1.09148709705318,1.098520929394599,1.095105152264984,1.094272325978734,1.098468177450342,1.095849714911251,1.097952718476183,1.100746388049607,1.100114369109941,1.10052138086191,1.096938196194811,1.099992890418429,1.093106549957034,1.095523586088275,1.092801661288758,1.095956895328893,1.100419992807803]
PO      0       07:10:55.652    GetAllIndicators Data (EURUSD,H1)       Preds
DH      0       07:10:55.652    GetAllIndicators Data (EURUSD,H1)       [1.10068609018278,1.092937381937492,1.092258894809631,1.09294624662921,1.092958015748061,1.093392517797765,1.091850551839298,1.093040013995258,1.100677489794526,1.098360699043097,1.100275794246983,1.098820678659222,1.09857249856584,1.1005434461368,1.093174625248397,1.09243570720428,1.094128601953754,1.094192935809492,1.100305866167089,1.098452358470756,1.09301070277155,1.098612431849647,1.100827466038003,1.092880150279385,1.092600810699346,1.098722104612175,1.100707460497622,1.095827368149497,1.093765475161723,1.098767398966682,1.099091982657809,1.100621418373435,1.100698195592473,1.092047903797267,1.098661598784675,1.098489471676911,1.099781220346472,1.091954251247108,1.095870956580967,1.09306319770119,1.092915244023811,1.094885640505868,1.094171202526922,1.092523345374596,1.100564904733304,1.094200831112605,1.094001716368644,1.098530017588172,1.094081896433954,1.099230887219588,1.092892028948737,1.093709694144468,1.092862170694582,1.091487097053125,1.098520929394468,1.09510515226494,1.094272325978626,1.098468177450255,1.095849714911142,1.097952718476091,1.100746388049438,1.100114369109807,1.100521380861786,1.096938196194706,1.099992890418299,1.093106549956975,1.09552358608823,1.092801661288665,1.095956895328861,1.100419992807666]

我相信您和我都会同意，这好得令人难以置信。尽管该模型在测试样本中显现出令人印象深刻的 87.5% 准确率，但准确率下降了约 5%。

IJ      0       16:02:57.760    dimension reduction test (EURUSD,H1)    Test acc = 0.8758590697252272

我们可用最流行的降维技术，称为主成分分析（PCA），来减少数据集的维度，现在有 10 列。

//--- Reduce dimension
   
pca = new CPCA(8); //Reduce the dimensions of the data to 8 columns
data = pca.fit_transform(data);
pca.extract_components(data, CRITERION_SCREE_PLOT);

结局是线性回归模型在训练期间准确率为 88.98%，在测试期间准确率为 89.991%，至少可以说准确率并没有下降。

DJ      0       16:03:23.890    dimension reduction test (EURUSD,H1)    Train acc = 0.8898608919375138
RH      0       16:03:23.890    dimension reduction test (EURUSD,H1)    Test acc = 0.8991693574000851

仍然是一个过度拟合模型，但在普适能力方面比 92% 准确率的模型要好得多，这至关重要，对于 ML 模型必须能够做到，您可以进一步降低维度，以便查看数据的哪些维度在样本之外的预测中给出了最佳结果。

降维的动机

计算效率：降低维度数量可以加快机器学习算法的训练和执行速度。
提升普适度：降维有助于提高模型普适到新的、未见数据的能力，就像我们在线性回归模型示例中看到的那样。
可视化：可以更轻松地在低维空间中可视化和解释数据，从而帮助人们理解。

什么是截断型 SVD？

截断型奇异值分解（Truncated SVD）是一种降维技术，与其它降维技术一样，它在保留大部分原始信息的同时，对高维数据进行降维。在数据拥有大量特征的境况下，该技术特别实用，故其在执行高效计算或可视化数据时很吃力。

它是奇异值分解（SVD）的一种变体，它仅保留前 k 个奇异值、及其相应的奇异向量来近似原始矩阵。

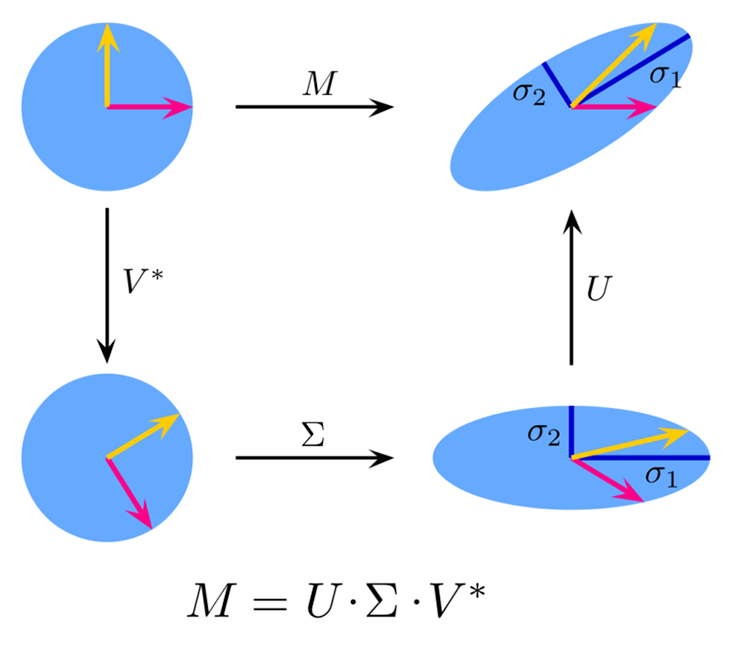
理论：

图片来源：维基百科

给定维度 × 的矩阵，的奇异值分解由下式给出：

其中：

是一个 × 正交矩阵（左奇异向量），

是一个 × 对角矩阵，奇异值位于对角线上，

是一个 × 正交矩阵（右奇异向量）。

截断型 SVD 仅保留前 k 个奇异值、及其相应的向量：

其中：

是一个 × 矩阵，

是 × 对角矩阵，

是一个 × 矩阵。

实现：

matrix CTruncatedSVD::fit_transform(matrix &X)
 {
  n_features = X.Cols();
  
   if (m_components>n_features)
     {
       printf("%s Number of dimensions K[%d] is supposed to be <= number of features %d",__FUNCTION__,m_components,n_features);
       this.m_components = (uint)n_features;
     }
   
    // Center the data (subtract mean)
    matrix X_centered = CDimensionReductionHelpers::subtract(X, X.Mean(0));
        
   // Compute the covariance matrix
    matrix cov_matrix = X_centered.Cov(false);
    
   // Perform SVD on the covariance matrix
    matrix U, Vt;
    vector Sigma;
    
    if (!X_centered.SVD(U,Vt,Sigma))
       Print(__FUNCTION__," Line ",__LINE__," Failed to calculate SVD Err=",GetLastError());    
        
    this.components_ = CDimensionReductionHelpers::Slice(Vt, this.m_components).Transpose();
    
    if (MQLInfoInteger(MQL_DEBUG))
      Print("components\n",CDimensionReductionHelpers::Slice(Vt, this.m_components),"\ncomponents_T\n",this.components_);
    
    this.explained_variance_ = MathPow(CDimensionReductionHelpers::Slice(Sigma, this.m_components), 2) / (X.Rows() - 1);
    
    return X_centered.MatMul(components_);
 }

有一个内置的 MQL5 方法来计算矩阵的 SVD。

// Singular Value Decomposition.

bool matrix::SVD(
  matrix&  U,                   // unitary matrix 
  matrix&  V,                   // unitary matrix 
  vector&  singular_values      // singular values vector
   );

fit_transform 函数执行以下操作：

它通过减去平均值来令数据居中。
它计算居中数据的协方差矩阵（不重要）。
它针对协方差矩阵执行 SVD。
它保留前 k 个奇异值和向量。
它构造原始矩阵的降维表示。

这都能做到，但真正的问题是，我们如何针对所减少的数据，找到最佳 k 个分量数量？

计算可释方差函数

该函数通过对所有奇异值的平方求和来计算总方差。

ulong CTruncatedSVD::_select_n_components(vector &singular_values)
 {
    double total_variance = MathPow(singular_values.Sum(), 2);
    
    vector explained_variance_ratio = MathPow(singular_values, 2).CumSum() / total_variance;
    
    if (MQLInfoInteger(MQL_DEBUG))
      Print(__FUNCTION__," Explained variance ratio ",explained_variance_ratio);
    
    vector k(explained_variance_ratio.Size());
    
    for (uint i=0; i<k.Size(); i++)
      k[i] = i+1;
    
    plt.ScatterCurvePlots("Explained variance plot",k,explained_variance_ratio,"variance","components","Variance");
    
   return explained_variance_ratio.ArgMax() + 1;  //Choose k for maximum explained variance
 }

该函数取奇异值数组（singular_values）作为输入。这些奇异值是从矩阵的奇异值分解（SVD）中获得的。

然后，该函数通过查找并选择方差最大的分量数（k）。这是由以下代码行达成的：

explained_variance_ratio.ArgMax() + 1;

我们需要修改我们的 fit_transform 函数，令其能够检测最佳分量数（当没有给出任何数量时），从而降低数据的维度，并为截断型 SVD 应用分量数。

matrix CTruncatedSVD::fit_transform(matrix &X)
 {
  n_features = X.Cols();
  
   if (m_components>n_features)
     {
       printf("%s Number of dimensions K[%d] is supposed to be <= number of features %d",__FUNCTION__,m_components,n_features);
       this.m_components = (uint)n_features;
     }
   
    // Center the data (subtract mean)
    matrix X_centered = CDimensionReductionHelpers::subtract(X, X.Mean(0));
        
   // Compute the covariance matrix
    matrix cov_matrix = X_centered.Cov(false);
    
   // Perform SVD on the covariance matrix
    matrix U, Vt;
    vector Sigma;
    
    if (!cov_matrix.SVD(U,Vt,Sigma))
       Print(__FUNCTION__," Line ",__LINE__," Failed to calculate SVD Err=",GetLastError());    
        
     if (m_components == 0)
       {
         m_components = (uint)this._select_n_components(Sigma);
         Print(__FUNCTION__," Best value of K = ",m_components);
       }
            
    this.components_ = CDimensionReductionHelpers::Slice(Vt, this.m_components).Transpose();
    
    if (MQLInfoInteger(MQL_DEBUG))
      Print("components\n",CDimensionReductionHelpers::Slice(Vt, this.m_components),"\ncomponents_T\n",this.components_);
    
    this.explained_variance_ = MathPow(CDimensionReductionHelpers::Slice(Sigma, this.m_components), 2) / (X.Rows() - 1);
    
    return X_centered.MatMul(components_);
 }

默认的 k 值现在设为零，以便这一切能毫不费力地发生。

CTruncatedSVD::CTruncatedSVD(uint k=0)
:m_components(k)
 {
 
 }

运用截断型 SVD 降维

现在我们看看如何执行截断型 SVD 降低数据维度：

   truncated_svd = new CTruncatedSVD();
   
   data = truncated_svd.fit_transform(data);
   Print("Reduced matrix\n",data);

//--- 

   matrix train_x, test_x;
   vector train_y, test_y;
   
   data = matrix_utils.concatenate(data, target); //add the target variable to the dataset that is either normalized or not
   
   matrix_utils.TrainTestSplitMatrices(data, train_x, train_y, test_x, test_y, 0.7, 42);
     
   lr.fit(train_x, train_y, NORM_STANDARDIZATION); //training Linear regression model
   
   vector preds = lr.predict(train_x); //Predicting the training data
   
   Print("Train acc = ",metrics.r_squared(train_y, preds)); //Measuring the performance
  
   
   preds = lr.predict(test_x); //predicting the test data 
   
   Print("Test acc = ",metrics.r_squared(test_y, preds)); //measuring the performance

输出：

LH      0       20:13:41.385    dimension reduction test (EURUSD,H1)    CTruncatedSVD::_select_n_components Explained variance ratio [0.2399955100411572,0.3875113031818686,0.3903532427910986,0.3929609228375971,0.3932960517565894,0.3933072531960168,0.3933072531960282,0.3933072531960282,0.3933072531960282,0.3933072531960282]
EH      0       20:13:41.406    dimension reduction test (EURUSD,H1)    CTruncatedSVD::fit_transform Best value of K = 7
...
...
...
MR      0       20:13:41.407    dimension reduction test (EURUSD,H1)    Train acc = 0.8934645199970468
HP      0       20:13:41.407    dimension reduction test (EURUSD,H1)    Test acc = 0.8988671205298875

令人惊叹且稳定的性能：训练准确率 89.3%，测试准确率 89.8%。那 NMF 呢？

什么是 NMF？

NMF 代表非负矩阵分解，它是一种降维技术，可将矩阵分解为两个非负矩阵。NMF 的目标是将原始矩阵表示为两个低维矩阵的乘积，其矩阵中的所有元素都是非负的。

给定维度为 m×n 的输入矩阵 X，NMF 将其分解为两个矩阵 W 和 H，如这般：

其中：

是一个 × 矩阵，其中 k 是分量或特征的数量。

是一个 × 矩阵。

和两者都有非负项，这种非负约束令 NMF 特别适用于数据自然为非负的应用程序，譬如图像数据、文本数据、和频谱图。

因式分解是通过最小化原始矩阵与其近似值 × 之间差值的 Frobenius 范数达成的。数学上，这可以如此表达：

其中表示 Frobenius 范数。

实现：

变换方法

matrix CNMF::transform(matrix &X)
 {
  n_features = X.Cols();
  if (m_components>n_features)
     {
       printf("%s Number of dimensions K[%d] is supposed to be <= number of features %d",__FUNCTION__,m_components,n_features);
       this.m_components = (uint)n_features;
     }
     
  if (this.W.Rows()==0 || this.H.Rows()==0)
    {
      Print(__FUNCTION__," Model not fitted. Call fit method first.");
      matrix mat={};
      return mat;
    }
  
  return X.MatMul(this.H.Transpose());
 }

transform 函数使用已拟合的 NMF 分量变换为新数据 X。

拟合变换方法

matrix CNMF::fit_transform(matrix &X, uint k=2)
 {
  ulong m = X.Rows(), n = X.Cols();
  double best_frobenius_norm = DBL_MIN;
  
   m_components = m_components == 0 ? (uint)n : k;      
   
//--- Initialize Random values 

   this.W = CMatrixutils::Random(0,1, m, this.m_components, this.m_randseed);  
   this.H = CMatrixutils::Random(0,1,this.m_components, n, this.m_randseed);
   
//--- Update factors
      
   vector loss(this.m_max_iter);
    for (uint i=0; i<this.m_max_iter; i++)
      {
        // Update W
         this.W *= MathAbs((X.MatMul(this.H.Transpose())) / (this.W.MatMul(this.H.MatMul(this.H.Transpose()))+ 1e-10));
         
        // Update H
         this.H *= MathAbs((this.W.Transpose().MatMul(X)) / (this.W.Transpose().MatMul(this.W.MatMul(this.H))+ 1e-10));
         
         loss[i] = MathPow((X - W.MatMul(H)).Flat(1), 2);
                    
         // Calculate Frobenius norm of the difference
        double frobenius_norm = (X - W.MatMul(H)).Norm(MATRIX_NORM_FROBENIUS);

         if (MQLInfoInteger(MQL_DEBUG))
           printf("%s [%d/%d] Loss = %.5f frobenius norm %.5f",__FUNCTION__,i+1,m_max_iter,loss[i],frobenius_norm);
         
          // Check convergence
          if (frobenius_norm < this.m_tol)
              break;
      }
  
  return this.W.MatMul(this.H); 
 }

fit_transform 方法针对输入矩阵 X 执行 NMF 因式分解，并返回矩阵 W 和 H 的乘积。

与截断型 SVD 不同，我们能够编写代码来判定分量的数量，并将其应用于自身，如此使用截断型函数库就更容易，NMF 学习算法完全不同，因为它需要迭代 n 次，以便找到算法的最佳值，而在循环期间，k 个分量的数量必须保持不变，这就是为什么 fit_transform 函数将 k 个分量的数值作为其参数之一。

我们可以调用函数 select_best_components 获得非负矩阵分解算法的最佳分量数：

uint CNMF::select_best_components(matrix &X)
{
    uint best_components = 1;
    this.m_components = (uint)X.Cols();
    
    vector explained_ratio(X.Cols());    
    for (uint k = 1; k <= X.Cols(); k++)
    {
       // Calculate explained variance or other criterion 
       matrix X_reduced = fit_transform(X, k);
   
       // Calculate explained variance as the ratio of squared Frobenius norms
       double explained_variance = 1.0 - (X-X_reduced).Norm(MATRIX_NORM_FROBENIUS) / (X.Norm(MATRIX_NORM_FROBENIUS));
        
        if (MQLInfoInteger(MQL_DEBUG))
            printf("k %d Explained Var %.5f",k,explained_variance);
       
       explained_ratio[k-1] = explained_variance;       
    }
    return uint(explained_ratio.ArgMax()+1);
}

由于 Basic 矩阵和 Coefficient 矩阵的随机性，迭代乘法算法的结果也会是随机值，故结局应该是不可预测的，除非将随机状态设置为大于零的值。

class CNMF
  {
protected:
   uint m_components;
   uint m_max_iter;
   int m_randseed;
   ulong n_features;
   matrix W; //Basic matrix
   matrix H; //coefficient matrix
   double m_tol; //loss tolerance
   
public:
                     CNMF(uint max_iter=100, double tol=1e-4, int random_state=-1);
                    ~CNMF(void);
                    
                    matrix fit_transform(matrix &X, uint k=2);
                    matrix transform(matrix &X);
                    uint select_best_components(matrix &X);
                    
  };

运用 NMF 降维

现在我们看看执行非负矩阵分解如何降低数据维度：

   nmf = new CNMF(30);
   
   data = nmf.fit_transform(data, 10);
   Print("Reduced matrix\n",data);

//--- 

   matrix train_x, test_x;
   vector train_y, test_y;
   
   data = matrix_utils.concatenate(data, target); //add the target variable to the dataset that is either normalized or not
      
   matrix_utils.TrainTestSplitMatrices(data, train_x, train_y, test_x, test_y, 0.7, 42);
      
   lr.fit(train_x, train_y, NORM_STANDARDIZATION); //training Linear regression model
   
   vector preds = lr.predict(train_x); //Predicting the training data
   
   Print("Train acc = ",metrics.r_squared(train_y, preds)); //Measuring the performance
   
   preds = lr.predict(test_x); //predicting the test data 
   
   Print("Test acc = ",metrics.r_squared(test_y, preds)); //measuring the performance

结局：

DG      0       11:51:07.197    dimension reduction test (EURUSD,H1)    Best k components = 10
LG      0       11:51:07.197    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [1/30] Loss = 187.40949 frobenius norm 141.12462
EG      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [2/30] Loss = 106.49597 frobenius norm 130.94039
KS      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [3/30] Loss = 84.38553 frobenius norm 125.05413
OS      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [4/30] Loss = 67.07345 frobenius norm 118.96900
OR      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [5/30] Loss = 52.50290 frobenius norm 112.46587
LR      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [6/30] Loss = 40.14937 frobenius norm 105.48081
RR      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [7/30] Loss = 29.79307 frobenius norm 98.11626
IR      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [8/30] Loss = 21.32224 frobenius norm 90.63011
NS      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [9/30] Loss = 14.63453 frobenius norm 83.36462
HL      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [10/30] Loss = 9.58168 frobenius norm 76.62838
NL      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [11/30] Loss = 5.95040 frobenius norm 70.60136
DM      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [12/30] Loss = 3.47775 frobenius norm 65.31931
LM      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [13/30] Loss = 1.88772 frobenius norm 60.72185
EN      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [14/30] Loss = 0.92792 frobenius norm 56.71242
RO      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [15/30] Loss = 0.39182 frobenius norm 53.19791
NO      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [16/30] Loss = 0.12468 frobenius norm 50.10411
NH      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [17/30] Loss = 0.01834 frobenius norm 47.37568
KI      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [18/30] Loss = 0.00129 frobenius norm 44.96962
KI      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [19/30] Loss = 0.02849 frobenius norm 42.84850
MJ      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [20/30] Loss = 0.07289 frobenius norm 40.97668
RJ      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [21/30] Loss = 0.11920 frobenius norm 39.31975
QK      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [22/30] Loss = 0.15954 frobenius norm 37.84549
FD      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [23/30] Loss = 0.19054 frobenius norm 36.52515
RD      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [24/30] Loss = 0.21142 frobenius norm 35.33409
KE      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [25/30] Loss = 0.22283 frobenius norm 34.25183
PF      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [26/30] Loss = 0.22607 frobenius norm 33.26170
GF      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [27/30] Loss = 0.22268 frobenius norm 32.35028
NG      0       11:51:07.201    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [28/30] Loss = 0.21417 frobenius norm 31.50679
CG      0       11:51:07.201    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [29/30] Loss = 0.20196 frobenius norm 30.72260
CP      0       11:51:07.201    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [30/30] Loss = 0.18724 frobenius norm 29.99074
...
...
FS      0       11:51:07.201    dimension reduction test (EURUSD,H1)    Train acc = 0.604329883526616
IR      0       11:51:07.202    dimension reduction test (EURUSD,H1)    Test acc = 0.5115967009955317

函数 select_best_components 发现最佳分量数是 10，与我们给它的数据集中的列数相同，可以公平地说，当应用于线性回归模型时，由 NMF 产生的数据准确性在训练期间产生了 61% 的平均结果，而在测试期间产生了 51% 的平均结果。在我们得出结论之前，TruncatedSVD 在这种情况下显然是赢家，然而，我们需要承认一个事实，即非负矩阵分解（NMF）需要大量编程才能令其工作。如果正确实现，并伴以更好的学习算法，例如随机梯度下降（SGD）、或任何其它智能学习算法，它可以产生更好的数据集，但当下这两种算法只是基本实现！截断型 SVD 获胜（尽管是在纸面上）

我们看看两者在大数据中的性能如何：

我们将整个数据应用于我们的算法，并衡量它们在整个数据集上的费效，这将为我们提供一条线索，即应用该方法能为我们的线性回归模型获取最佳紧缩数据。

截断型 SVD 对比 NMF，博弈：

这一次没有过滤任何数据，我们全力以赴，伴以全部可应用于截断型 SVD 的指标。

void TrainTestLR(int start_bar=1)
 {
   string names;
   matrix data = indicators.GetAllBuffers(names, start_bar, buffer_size);   
   
//--- Getting close values

   MqlRates rates[];
   ArraySetAsSeries(rates, true);
   CopyRates(Symbol(), PERIOD_CURRENT, start_bar, buffer_size, rates);
   
   double targ_Arr[];
   ArrayResize(targ_Arr, buffer_size);
   
   for (int i=0; i<buffer_size; i++)
     targ_Arr[i] = rates[i].close;
   
   vector target = matrix_utils.ArrayToVector(targ_Arr);
      
//--- Dimension reduction process 
   
   switch(dimension_redux)
     {
      case  NMF:
        {
          nmf = new CNMF(nmf_iterations);
         
          uint k = nmf.select_best_components(data);
          //Print("Best k components = ",k);
          data = nmf.fit_transform(data, k);    
        }
        break;
      case TRUNC_SVD:
      
         truncated_svd = new CTruncatedSVD();
         data = truncated_svd.fit_transform(data);  
         
        break;
      case None:
        break;
     }
     
//---

  Print(EnumToString(dimension_redux)," Reduced matrix[",data.Rows(),"x",data.Cols(),"]\n",data);
  
//--- 

   matrix train_x, test_x;
   vector train_y, test_y;
   
   data = matrix_utils.concatenate(data, target); //add the target variable to the dimension reduced data
      
   matrix_utils.TrainTestSplitMatrices(data, train_x, train_y, test_x, test_y, 0.7, 42);
      
   lr.fit(train_x, train_y, NORM_STANDARDIZATION); //training Linear regression model
   
   vector preds = lr.predict(train_x); //Predicting the training data
   
   Print("Train acc = ",metrics.r_squared(train_y, preds)); //Measuring the performance
   
   preds = lr.predict(test_x); //predicting the test data 
   
   Print("Test acc = ",metrics.r_squared(test_y, preds)); //measuring the performance

 }

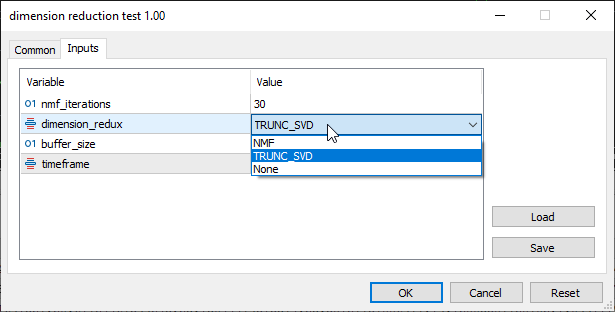
在输入部分中的 TRUNC_SVD，是为了选择截断型 SVD ：

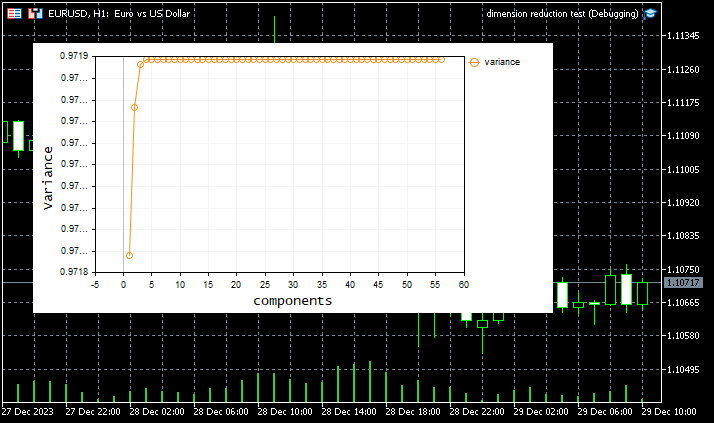
正如预期的那样，截断型 SVD 的结果非常出色。数据在下图的关键点被压缩为 11 个实用的分量

输出：

KI      0       13:35:07.262    dimension reduction test (EURUSD,H1)    [56x56] Covariance
HS      0       13:35:07.262    dimension reduction test (EURUSD,H1)    [[1.659883222775595e-05,0.03248108864728622,0.002260592127494286,0.002331226815118805,0.0473802958063898,0.009411152185446843,-0.0007144995075063451,1.553267567351765e-05,1.94117385500497e-05,1.165361279698562e-05,1.596183979153003e-05,1.56892102141789e-05,1.565786314082391e-05,1.750827764889262e-05,1.568797564383075e-05,1.542116504856457e-05,1.305965012072059e-05,1.184306318548672e-05,0,1.578309112710041e-05,1.620880130984106e-05,3.200794587841053e-07,1.541769717649654e-05,1.582152318930163e-05,5.986572608120619e-07,-7.489818958341503e-07,-1.347949386573036e-07,1.358668593395908,-0.0551110816439555,7.279528408421348e-05,-0.0001838813666139953,5.310112938097826e-07,6.759105066381161e-07,1.755806692036581e-05,-1.448992128283333e-07,0.003656398187537544,-2.423948560741599e-05,1.65581437719033e-05,-0.01251289868226832,-0.007951606834421109,8.315844054428887e-08,-0.02211745766272421,58.3452835083685,-0.004138620879652527,115.0719348800515,0.7113815226449098,-3.467421230325816e-07,1.456828920113124e-05,1.536603660063518e-05,1.576222466715787e-05,6.85495465028602e-07,0,0,1.264184887739262e-06,-8.035590653384948e-05,-6.948836688267333e-07]
DG      0       13:35:07.262    dimension reduction test (EURUSD,H1)     [0.03248108864728622,197.2946284096305,47.5593359902222,-70.84984591299812,113.00968468357,80.50832448214619,-85.73100643892406,0.01887146397983594,0.03089371802428824,0.006849209935383654,0.03467670330041064,0.02416916876582018,0.02412087871833598,0.0345064443900023,0.03070601018237932,0.02036445858890056,0.009641324468627534,0.006973716378187099,0,0.02839705603036633,0.02546230398502955,0.000344615196142723,0.04030780408653764,0.02543558488321825,0.0003508232190957864,0.00918131954773614,0.009950700238139187,18501.50888551419,578.0227911644578,1.963532857377992,7.661630153435527,0.006966837168084083,0.004556433245004339,2.562261625497797,0.002410403923079745,118.382177007498,1.555763207775421,1.620640369180333,97.88352837129584,116.7606184094667,0.0006817870698682788,163.5401896749969,108055.4673427991,140.7005993870342,173684.2642498043,3567.96895955429,0.0026091195479834,0.01088219157686945,0.01632411390047346,0.02372834986595739,0.02071124643451263,0,0,0.003953688163493562,-1.360529605248643,-0.04542261766857811]
IL      0       13:35:07.262    dimension reduction test (EURUSD,H1)     [0.002260592127494286,47.5593359902222,39.19958980374253,-35.49971367926001,7.967839162735706,33.38887983973432,-33.90876164339727,-0.001453063639065681,-0.000297822858867019,-0.002608304419264346,0.002816269112655834,-0.0006711791217058063,-0.0006698381044796457,0.002120545460717355,0.002300146098203005,0.0001826452994732207,-0.0003768483866125172,-0.002445364564315893,0,0.0003665645439668078,-0.003400376924338417,-1.141907378821958e-06,0.006568498854351883,0.0006581929826678372,-0.0005502523415197902,0.00579179204268979,0.006348707171855972,7967.929705662135,452.5996105540225,0.7520153701277594,4.211592829265125,0.001461149548206051,0.0001367863805269901,0.8802824558924612,0.001324363167679062,50.70542641656378,0.6826775813408293,0.5131585731076505,116.3828090044126,97.64469627257866,5.244397974811099e-05,113.6246589165999,13312.60086575102,66.02007474397942,15745.06353439358,3879.735235353455,0.002648988695504766,-0.00244724050922883,-0.00263645588222185,-0.001438073133818628,0.005654239425742305,0,0,-0.000119694862927093,-0.3588916052856576,-0.1059287487094797]
EM      0       13:35:07.262    dimension reduction test (EURUSD,H1)     [0.002331226815118805,-70.84984591299812,-35.49971367926001,60.69058251292376,1.049456584665883,-42.35184208285295,60.90812761343581,0.008675881760275542,0.008620685402656748,0.008731078117894331,-0.000667294720674837,0.005845080481159768,0.005833401998679988,0.002539790385479495,0.001675796458760079,0.00792229604709134,0.01072137357191657,0.01189054942647922,0,0.003518070782066417,0.00809138574827074,0.0002045106345618818,-0.005848319055742076,0.005549764528898804,0.00103946798619902,-0.008604821519805591,-0.007960056731330659,-10509.62154107038,-607.7276555152829,-1.225906326607001,-5.179537786920108,-0.003656220590983723,-0.001714862736227047,-1.657652278786164,-0.001941357854756676,-80.61630801951124,-1.158614351229071,-1.010395372975761,-137.5151461158883,-129.0146405010356,…]
DK      0       13:35:07.264    dimension reduction test (EURUSD,H1)    CTruncatedSVD::_select_n_components Explained variance ratio [0.9718079496976207,0.971876424055512,0.9718966593387935,0.971898669685807,0.9718986697080317,0.9718986697081728,0.9718986697082533,0.9718986697082695,0.9718986697082731,0.9718986697082754,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757]
JJ      0       13:35:07.282    dimension reduction test (EURUSD,H1)    CTruncatedSVD::fit_transform Best value of K = 11
FE      0       13:35:07.282    dimension reduction test (EURUSD,H1)    components
GP      0       13:35:07.282    dimension reduction test (EURUSD,H1)    [[1.187125882554785e-07,1.707109381366902e-07,-2.162493440707256e-08,-3.212808990986057e-07,1.871672229653978e-07,-1.333159242305641e-05,-1.709658791626167e-05,5.106786021196193e-05,2.160157948893384e-05,-1.302989528292599e-06,4.973487699412528e-06,2.354866764130305e-06,0.0001127065022780296,-0.0001141032171988836,-7.674973628685988e-05,4.318893830956814e-06,-8.017085790662858e-05,1.258581118770149e-05,0.001793756756130711,0.0002550931459979332,0.0005154637372606566,0.001801147973070216,0.0001081777898713252,0.1803191282351903,-0.0971245889819613,0.1677985300894154,0.1116153850447159,0.6136670152098842,0.022810600805461,-0.4096528016535661,-0.04163009420605639,-6.077467743293966e-06,-0.01526638316446551,-0.5288520838909793,-0.03965140358106178,-0.1758179670991415,-0.003645717072725773,-0.0587633049540756,0.004124498383003558,-0.1172419838852104,0.06762215235985558,-0.04328191674666172,0.002573659612267772,0.003811049362514162,-0.0659455961610354,-0.02792883463906511,0.008647163802477509,-0.05514899696636823,0.008017364204121686,2.516946811168054e-06,-0.1623798112317545,6.339565837779877e-07,-9.103773865679859e-08,0,0,0]
CH      0       13:35:07.282    dimension reduction test (EURUSD,H1)     [0.000187434605818864,0.002812180913638008,0.000925532096115269,0.003073325320378009,0.009404433538995808,-0.1105512584754667,-0.2590049789665196,0.4726584971639716,0.1447383637844528,-0.05374370025421956,-0.752572111353205,0.04852191253671465,-0.1154729372340165,-0.2700032006603445,0.1267147455792905,-0.04806661586591762,-0.0004106947202907203,-0.001517506503982104,-0.003502569576390078,-0.002616630851275089,-0.0003258690084512006,-1.313122566421376e-05,-0.0009386837340425192,7.909925585103072e-05,-7.798476572374581e-05,-8.126463184191059e-05,5.556082790448295e-05,-2.687039190421141e-05,-6.540787996573879e-06,1.330764390715927e-05,-4.491635420079414e-05,-8.144156726118825e-06,-8.508538790002811e-07,5.307068574641107e-05,8.482440778162809e-06,-2.9724306932086e-05,2.843845070244019e-05,1.220433778827776e-05,4.206331251218703e-06,1.256512854012554e-05,7.365925693883173e-06,-1.116338606511276e-05,-2.071419560390051e-06,-3.218285979262829e-06,-1.138651025910271e-05,-7.728111919788928e-06,-4.653652137908648e-06,-9.580813709785919e-06,-1.028740118967147e-05,-6.979591632948435e-06,8.116615752437345e-06,1.763108270729631e-06,-4.348070304093866e-07,0,0,0]
JR      0       13:35:07.282    dimension reduction test (EURUSD,H1)     [1.848792316776081e-05,0.0008588118715707877,0.001008311173244842,0.002376194713912998,0.03118554398340165,0.07889519945845663,-0.07568381470451135,0.0286506682781276,-0.09873220604411656,-0.09161678196011247,-0.06574722506621368,-0.8477734032486133,-0.2533539865405071,0.01738574140899809,-0.2520128661222155,0.338533576002899,0.03018091859501061,0.03802772499047165,-0.001646103636389454,-0.00230341248842314,0.007310099460075021,-0.006012419384786831,-0.001413152018214914,2.142238614111051e-05,2.944210407515316e-05,-6.521097350129076e-05,4.95794487446122e-05,-8.706533732190571e-06,3.322659358695792e-05,-8.146689287415223e-07,7.338661273889888e-06,6.605547217087068e-06,9.447199984574336e-06,-5.17902002055696e-05,2.513872334761899e-06,-2.256988836110105e-05,-1.911456753589991e-05,-3.264899090321399e-05,-5.800966034108816e-06,1.84157480007614e-05,5.356185659483905e-06,-1.722849771456492e-05,1.407694486288703e-05,-7.853816348797691e-06,-1.555432680785718e-05,1.323568644672602e-05,-6.760913172750632e-06,-1.302135272406512e-05,-3.211793238456227e-06,5.802687671843603e-07,-4.280158053673846e-06,1.549960937140237e-06,-4.919157307518426e-07,0,0,0]
ND      0       13:35:07.282    dimension reduction test (EURUSD,H1)     [4.113935038265459e-05,-0.00163116425762962,-0.0006793200544509552,-0.002550542034446345,-0.0360619764220519,-0.05083503039040507,0.1457232134777539,-0.1319534223026893,-0.1000465688426969,0.03066773678926198,0.211126338548004,0.02610057183969087,-0.4621259104920466,-0.5881871797892803,0.5329599008633419,0.2326293789423069,-0.004192622153062945,-0.05839467173045784,0.002320319216461524,0.007699098543144081,-0.007658991162669676,-0.003166005488782055,-0.002283364895801648,0.0001978857108759482,9.652410400630472e-05,5.391765247424044e-05,-2.114027852314159e-05,-3.571496353187668e-06,6.919610375993553e-06,-2.388732546126286e-05,-1.795211964869842e-05,-4.375012411627235e-05,-6.279526099805299e-05,2.71361750709131e-06,-2.519904126359203e-05,-3.154274545518064e-05,-4.95034356619025e-05,4.982607182957078e-05,2.91223664932767e-05,7.266298957499022e-06,-5.27732883601878e-0…]
QD      0       13:35:07.283    dimension reduction test (EURUSD,H1)    TRUNC_SVD Reduced matrix[100x11]
FJ      0       13:35:07.283    dimension reduction test (EURUSD,H1)    [[3032.510155721446,0.6797958296629614,0.3147476036369294,-1.879105115460979,2.342311343896795,-1.444862488231156,1.72748820545895,9003.45453268309,6583.0037062413,11248.15180107277,7664.89601210886]
QF      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [2613.746957390415,0.8994353272147151,0.2278876639409569,-1.833173521667439,2.422820504229084,-1.194855144516288,1.619766862896731,8730.428168136412,6321.389560496657,10843.26327739175,7319.502533761807]
PE      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [2290.391536977857,0.8379176898463352,0.123448650655239,-1.79572777997295,2.553555290053082,-1.261720012039457,1.872612496522998,9359.431555011421,6628.023623123124,11573.90347441899,7725.564567458286]
MG      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1793.638587775052,0.8840827856664026,-0.009259140368535656,-1.812929578463889,2.752934946133839,-1.194132624145421,2.137669035967074,10045.24774931484,6958.660329797975,12319.85906895874,8090.242616080116]
IG      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1067.248927502046,0.9361386848947133,0.2824462001532311,-2.094258230827017,2.302295904768048,-0.9859566963069195,1.849760818059724,8852.426567434784,5936.081092995532,10850.91447636461,7048.244994007338]
NK      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [875.831228770905,1.10630868463423,0.3875078994082357,-2.07189694520072,2.003365098290179,-0.8110375102176066,1.363090061871958,7086.981018896034,4689.12320342304,8755.082428498208,5718.774787652458]
GK      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [750.5105412678478,1.58876151742295,0.4277968820488219,-2.495434492237099,2.546292376170158,-0.5828893757361142,1.468026541982692,8457.543559890122,5579.75159746014,10352.91442474459,6691.476688344664]
EK      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1028.864261893481,1.737564309663063,0.6859148896559381,-2.576387294650619,2.22158096752311,-0.3483142589026745,0.9424367352835165,7447.770506698205,5028.271311988544,9145.898159310427,5970.749558054185]
MJ      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1315.206321750198,1.599230058650526,1.006274380327883,-2.7208483981554,1.702262719567507,-0.3336344655640055,0.5851633683692923,6123.681144041253,4208.879528858515,7625.280231352584,5091.190116446857]
PI      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1040.359603039049,2.015870643904685,1.297584348509677,-3.422661750068991,2.051984203691556,-0.1752179554187868,0.625382499042994,7446.846626605789,4973.286352001192,9200.911151239434,6040.469516939555]
MJ      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [2056.827104147074,0.6969653180001977,0.5026500071613408,-1.539526411095017,1.333168361525386,-1.205142789226661,0.6457357287148752,4362.936467349854,3118.514061447938,5739.541487386377,4094.4444510553]
KI      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [2595.720157415741,0.5163475309230526,0.7707831677360033,-1.609464385287863,0.6391376890497206,-1.091660522613616,0.2434028653397404,2245.471581325966,1932.755290423922,3219.551710692477,2600.234934440349]
FJ      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [2000.813854424802,-0.1645196557230545,0.0271698872028618,-1.136148599089293,1.199419424319289,-1.596267278271581,1.616290624329739,4340.908808342276,3155.426978423527,5643.263654816839,4006.305187235153]
GN      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [714.201770611258,0.3322650152566928,-0.128924730742915,-1.497052055771412,1.889908667964611,-1.18328154703613,2.040965402442796,6411.664479403819,4214.549479233159,7917.864243044486,5153.2871400763]
PN      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [676.7845833423586,0.1119963611895549,-0.4614956061196153,-0.7783442013329294,1.680735950870798,-1.110059082233565,1.926793017792492,5379.745050208609,3591.380424598063,6620.153862582291,4307.434978894435]
GL      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [766.9657214036708,0.3283061830008722,-0.3885600107901345,-1.031650548898253,1.912288786544761,-1.036499883901753,2.01321049032323,6312.725946828255,4249.957068368147,7723.98867795246,5012.0279192467]
LN      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1272.697206108888,-0.3546159778199272,-0.7521309963906442,-0.1806331494361637,1.527697751794935,-1.486437217294949,2.136800392269752,5073.89079322631,3559.651506707118,6317.965379534476,4229.397904810504]
RM      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1869.479624807111,-0.0175694426730242,-0.7678796689175619,-0.2643173159395689,1.862033543014759,-1.44967470564508,2.028361828380722,5639.625182760593,4124.447639836587,7033.466549718048,4777.911629224665]
GN      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1936.02506453734,0.0845940044872068,-0.8282752540396139,-0.2824304083282199,1.982789807497455,-1.350085518779075,2.085883725566998,5911.195073473721,4372.189044548059,7316.534104301676,4945.624347822407]
CR      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1844.238763352675,-0.4606751585910102,-1.187448989349241,0.2320045292554417,1.900279565663612,-1.62110507361112,2.534343850099422,5907.730651516376,4364.59879103891,7282.962351393813,4893.24121551531]
ER      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1716.303347926322,-0.2450617860724134,-0.9482067759826802,-0.03979477150523128,1.79416546386642,-1.453641927846228,2.284520496569503,5710.722665215339,4183.828568899002,7048.670774203967,4734.907606214866…]
GP      0       13:35:07.283    dimension reduction test (EURUSD,H1)    Train acc = 0.8087284075835584
ER      0       13:35:07.283    dimension reduction test (EURUSD,H1)    Test acc = 0.7286157353628964

基于训练样本的准确率为 80%，而基于测试样本的准确率为 72%。

非负矩阵分解（NMF）

另一方面，NMF 无法产生任何有价值的东西，因为它产生的任何东西都是无效值，此时，它不再是竞争对手。

LK      0       13:43:09.997    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [1/100] Loss = nan frobenius norm nan
II      0       13:43:09.997    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [2/100] Loss = nan frobenius norm nan
FG      0       13:43:09.997    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [3/100] Loss = nan frobenius norm nan
KF      0       13:43:09.997    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [4/100] Loss = nan frobenius norm nan
PD      0       13:43:09.997    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [5/100] Loss = nan frobenius norm nan
PR      0       13:43:09.998    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [6/100] Loss = nan frobenius norm nan
KP      0       13:43:09.998    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [7/100] Loss = nan frobenius norm nan
NO      0       13:43:09.998    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [8/100] Loss = nan frobenius norm nan
QM      0       13:43:09.998    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [9/100] Loss = nan frobenius norm nan
MH      0       13:43:09.998    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [10/100] Loss = nan frobenius norm nan
....
....
LM      0       13:43:10.006    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [97/100] Loss = nan frobenius norm nan
OO      0       13:43:10.006    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [98/100] Loss = nan frobenius norm nan
NI      0       13:43:10.006    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [99/100] Loss = nan frobenius norm nan
CI      0       13:43:10.006    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [100/100] Loss = nan frobenius norm nan
MI      0       13:43:10.008    dimension reduction test (EURUSD,H1)    NMF Reduced matrix[100x56]
FN      0       13:43:10.008    dimension reduction test (EURUSD,H1)    [[nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan]
EF      0       13:43:10.008    dimension reduction test (EURUSD,H1)     [nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan]
GK      0       13:43:10.008    dimension reduction test (EURUSD,H1)     [nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan]
QO      0       13:43:10.008    dimension reduction test (EURUSD,H1)     [nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan]
CL      0       13:43:10.008    dimension reduction test (EURUSD,H1)     
...
....
EO      0       13:43:10.008    dimension reduction test (EURUSD,H1)     [nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan…]
EL      0       13:43:10.010    dimension reduction test (EURUSD,H1)    Train acc = nan
GJ      0       13:43:10.010    dimension reduction test (EURUSD,H1)    Test acc = nan

我们尝试构建一个没有截断型 SVD 的线性回归模型，我们将整个数据应用于它，并观察其性能如何。

GM      0       13:53:03.686    dimension reduction test (EURUSD,H1)    None Reduced matrix[100x56]
MG      0       13:53:03.686    dimension reduction test (EURUSD,H1)    [[1.099900334222465,28.09636760954466,23.62682944559725,20.05254468697356,24.9034642580335,25.12500390358301,19.04617822178984,1.098553499999958,1.102834674021181,1.094272325978734,1.100734208567449,1.100855469999989,1.098655958571417,1.100133799959087,1.09983,1.097395,1.0950725,1.094895,1.10265,1.100030000000004,1.09944087984,0.03659425270713104,1.100626095746222,1.098825209694279,0.001265714285714323,1.705459946510501e-05,0.0009170545994650059,1655.083284093067,24.54629344924639,0.4388379204892836,0.1040346153847089,0.001226921314023466,0.0012463900886654,100.1775875415509,-1.946877464193406e-05,63.53135141907871,0.1040413928121892,0.1171616554839711,43.66576819407196,56.26437671196908,0.000170982627085528,-39.78494623655773,-2966278.270646845,59.66122501825306,-426422,2459,-0.0002127529411762598,1.096805768175659,1.098423909197834,1.099767192241293,0.00330055882353042,1.797693134862316e+308,1.797693134862316e+308,0.001618141022174502,0,0.03660024400162265]
DH      0       13:53:03.687    dimension reduction test (EURUSD,H1)     [1.099895090784212,25.44125240854614,20.47658551951762,17.37887206204375,24.10764337690182,24.31185250851098,18.42976333679036,1.098807999999958,1.102730359493936,1.09488564050598,1.100648597660533,1.100904089999989,1.09870448142856,1.100085345856641,1.09983,1.097395,1.0949775,1.09511,1.10237,1.100145000000004,1.09954,0.03659633771631932,1.100539015261062,1.098860393123325,0.001167857142857174,0.000137475370969975,0.0006774753709699599,1151.094538712408,-2.654176423441059,0.4388379204892836,0.1582615384614039,0.001148578761165142,0.001262448000841409,100.0618688017469,-0.0001138692396762668,61.34588689321424,0.1137518684603838,0.1082289779011129,39.39899833055219,47.44710420521373,0.000170240277350424,-32.25806451612595,-2966207.715091289,53.52331983100873,-424517,1905,-0.0003920588235292355,1.097045324469839,1.098718420548105,1.099909753793035,0.003008823529412785,1.797693134862316e+308,1.797693134862316e+308,0.001673096078265379,0,0.0283464566929126]
LG      0       13:53:03.687    dimension reduction test (EURUSD,H1)     [1.099896454740888,23.0468607955726,17.74637411691527,20.61724467599245,23.13044479515374,23.58127757886977,19.12803587728702,1.099111999999958,1.102374285088665,1.095849714911251,1.100636052620929,1.100962719999989,1.098762994285703,1.100079584777576,1.09983,1.097395,1.0949025,1.09511,1.10224,1.100252000000004,1.10126,0.03659849012444888,1.10032475011848,1.098869304036258,0.001062857142857168,-6.787825345444531e-05,0.0004021217465455251,385.6853260090575,21.57900929644156,0.4735973597359621,0.1358284615387142,0.001095648513071756,0.001261794377734486,100.0745976729165,-0.00016614586466273,63.02688593246703,0.1054308010829696,0.1073759442661703,21.12676056338241,34.73050902933566,0.000167907541851923,-45.79710144927351,-2967636.417218948,63.24364017027852,-427004,2487,-0.0004969529411762387,1.097296453356775,1.098949867979591,1.099885803034428,0.002709058823530563,1.797693134862316e+308,1.797693134862316e+308,0.001653414622816651,1,0.0188982710092469]
OH      0       13:53:03.687    dimension reduction test (EURUSD,H1)     [1.09988711983821,22.27698129412946,15.38019090132657,21.80270494870316,22.00511532835773,22.64977536234809,19.53807060936342,1.099376999999958,1.101815803805105,1.096938196194811,1.100524122300143,1.101012769999989,1.098812944285703,1.100014455800224,1.099825,1.097395,1.09474,1.09511,1.10151,1.100228000000004,1.1012264,0.03660061924403133,1.100053014395182,1.098898955035223,0.0009950000000000245,-0.0002124670743897106,0.0003975329256102889,-665.9989270069636,-29.795012402167,0.4599358974358811,0.1292584615385153,0.001012177253020718,0.001241318811166551,100.0636954266684,-0.000229141558145832,59.22581938383797,0.05654610290371272,0.09982547246710144,18.13186813187058,26.21920900860187,0.0001634553208976355,-53.91304347826081,-2969847.417218948,53.21227207754287,-429215,2211,-0.000519241176470371,1.097569033867792,1.099141134482142,1.099908642427543,0.002445970588236479,1.797693134862316e+308,1.797693134862316e+308,0.001572100614350314,1,0.02758932609678876]
HJ      0       13:53:03.687    dimension reduction test (EURUSD,H1)     [1.099803229128606,19.89136498265082,20.62876885414336,18.89567762220941,21.68993269258447,25.44873831711815,17.83416777391867,1.099577499999958,1.101202281523733,1.097952718476183,…]
EK      0       13:53:03.689    dimension reduction test (EURUSD,H1)    Train acc = -nan
MR      0       13:53:03.689    dimension reduction test (EURUSD,H1)    Test acc = -nan

线性回归模型无法为基于这个庞大的数据集自行生成结果，可以采取一些措施来解决这些降维技术面临的问题，诸如常规化输入数据、修复数值不稳定性、以及我们将在下一篇文章中讨论的更多内容。您始终可以在该 GitHub 存储库上跟踪本文中讨论的这些函数库的更新，以及未来更新：

我们看看每种降维技术的优点和缺点：

截断型奇异值分解（SVD）的优势

方差保持：

SVD 旨在保留原始数据中尽可能多的方差。它提供了一种在低维空间中表示数据，同时保留最重要信息的方法。

分量的正交性：

经由 SVD 获得的分量（奇异向量）是正交的，这在某些应用中可能是有益的。正交性简化了对分量的解释。

数值稳定性：

SVD 以其数值稳定性而闻名。它能很好地处理稀疏和嘈杂的数据。分解基于协方差矩阵的特征值分解。

图像压缩和降噪中的应用：

SVD 通常用于图像压缩和去噪。奇异值提供了重要性的度量，截断它们允许压缩，同时最大程度地减少信息损失。

非负矩阵分解（NMF）的优势

基于部件的表示：

NMF 针对 basis 矩阵和 coefficient 矩阵两者都强制执行非负性约束。这导致了基于部件的表示，这在基于部件特征的状况下是有益的（例如，在主题建模、或图像分析中）。

可解释性：

非负性约束通常会导致更可解释的因素。例如，在从文本数据中提取的主题中，每个主题都表示为单词的非否定线性组合，从而令主题更易于解释。

文档分析和图像处理中的应用：

NMF 通常用于文档分析（主题建模）、和图像处理。它可以识别数据中的底层形态，且当数据天然拥有非负分量时，它特别有用。

稀疏表示：

NMF 倾向于产生稀疏表示，其中仅有一个分量子集用来表示每个数据点。这在处理高维数据时可能是有利的。

共同优势

降维：

SVD 和 NMF 都提供了降低数据维数的有效技术，这对于处理高维数据集，以及提取有意义的特征至关重要。

特征提取：

它们可用于特征提取，从而允许识别数据中的重要形态或特征。

降噪：

这两种技术都可以通过捕获基本信息和过滤掉噪声来帮助对数据去噪。

截断型奇异值分解（SVD）的缺点

对异常值敏感：

SVD 可能对数据中的异常值很敏感，因为它试图最小化平方误差之和。异常值可能会对分解产生重大影响。

计算复杂度：

完整 SVD 的计算成本可能很高，尤其是对于大型数据集。截断型 SVD 提供了一个近似值，但对于高维数据也许仍是苛求。

对稀疏数据的适用性有限：

在处理高度稀疏的数据时，SVD 也许不那么有效，因为存在许多零值会影响分解的准确性。

缺乏可解释性：

虽然从 SVD 获得的分量是正交的，但这些分量的可解释性也许具有挑战性，特别是与强制执行非负性约束的 NMF 相比。

非负矩阵分解（NMF）的缺点

解的非唯一性：

NMF 不是唯一解，这意味着初始化不同，也许会导致不同的因式分解。这种缺乏唯一性可能令比较不同运行结果变得具有挑战性。

零值项的难度：

当面对数据矩阵中的零值项时，NMF 也许会遇到困难。处理缺失数据、或零值需要特别考虑，例如删除无效值和无穷大值。
void CDimensionReductionHelpers::ReplaceNaN(matrix &mat)
 {
   for (ulong i = 0; i < mat.Rows(); i++) 
     for (ulong j = 0; j < mat.Cols(); j++) 
       if (!MathIsValidNumber(mat[i][j]))
          mat[i][j] = 0.0;
 }

等级选择（分量数量）：

判定 NMF 的相应等级（分量数量）可能具有挑战性。不当的选择也许会导致数据过度拟合或欠拟合。

对负值的有限适用性：

NMF 强制非负性，这也许不适用于负值有意义的数据集。该约束限制了可以有效建模的数据类型。

共同的注意事项

可解释性对比重构造准确性：

NMF 也许会提供更多可解释的分量，但与 SVD 相比，这通常是以牺牲重构造精度为代价的。可解释性和准确性之间的选择取决于分析的具体目标。

降维权衡

这两种技术都涉及维度降低和信息丢失之间的权衡。挑战在于找到一个最佳平衡点，既要保留基本特征，又能最大限度地减少信息损失。

算法超参数：

SVD 和 NMF 也许都需要调整超参数，例如分量数量、或监管强度，以获得最佳结果。应考虑这些超参数的敏感性。

降维常见问答

问题：降维技术是如何工作的？

答：它们将数据转换为一组新的不相关变量分量，这些分量捕获原始数据中的最大方差。它们识别数据变化最大的方向。

问题：何时应该使用降维？

答：在处理高维数据时，例如在机器学习、图像处理和生物信息学中，降维非常有用。当存在冗余或不相关的特征时，它是有益的，以及需要优先考虑计算效率、可解释性、或可视化。

问题：降维是否可以应用于任何类型的数据

答：降维可应用于各种类型的数据，包括数值、分类、和文本数据。不过，技术的选择和注意事项可能因数据的性质而异。

问题：有没有线性降维技术的备选方案？

答：是的，有一些非线性技术，如内核 PCA、t-SNE、和自动编码器，可以捕获数据中超越线性变换的复杂关系。

问题：降维在机器学习中总是有益的吗？

答：不一定。虽然降维可以在计算效率、可解释性和可视化方面带来好处，但它也许并不总能提高模型性能。这取决于数据集和机器学习任务的具体特征。

问题：降维会导致信息丢失吗？

答：是的，降维会导致信息丢失，特别是当减少的表示丢弃相关特征时。目标是在降维和保留重要信息之间取得平衡。

问题：降维技术有哪些挑战？

答：挑战包括过度拟合的可能性、对异常值的敏感性、解的非唯一性（尤其是在 NMF 中）、以及需要仔细调整超参数。

附件：

文件	说明/用法
helpers.mqh	包含有助于在 NMF.mqh 和 TruncatedSVD.mqh 中执行降维操作的代码
Linear Regression.mqh	包含线性回归模型的代码
matrix_utils.mqh	其他矩阵运算
metrics.mqh	包含用于测量机器学习模型性能的代码的库
NMF	包含非负矩阵分解类
plots.mqh	用于在当前图表上绘制绘图的库
preprocessing.mqh	一个类，其中包含用于预处理数据以使其适合机器学习的函数
TruncatedSVD.mqh	包含截断的 SVD 类
dimension reduction test.mq5	用于测试本文中讨论的所有代码的脚本

出行平安。

本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/13968

附加的文件 |

下载ZIP

CODE.zip (26.25 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论

开发多币种 EA 交易（第 3 部分）：架构修改

我们在开发多币种 EA 方面已经取得了一些进展，该 EA 有几个并行工作的策略。考虑到所积累的经验，让我们回顾一下我们解决方案的架构，并尝试在我们走得太远之前对其进行改进吧。

种群优化算法：微人工免疫系统（Micro-AIS）

本文研究一种基于人体免疫系统原理的优化方法 — 微人工免疫系统（Micro-AIS） - AIS 的修订版。Micro-AIS 使用更简单的免疫系统模型，和更简单的免疫信息处理操作。本文还讨论了 Micro-AIS 与传统 AIS 相比的优缺点。

MQL5 简介（第 4 部分）：掌握结构、类和时间函数

在我们的最新文章中揭开 MQL5 编程的秘密！深入了解结构、类和时间函数的基本要素，为您的编码之旅赋能。无论您是初学者还是经验丰富的开发人员，我们的指南都简化了复杂的概念，为掌握 MQL5 提供了宝贵的见解。提升你的编程技能，在算法交易领域保持领先！

同时交易多种工具时平衡风险

本文将帮助初学者从头开始编写一个脚本的实现，用于在同时交易多种工具时平衡风险。此外，它还可以为有经验的用户提供新的思路，使他们可以根据本文提出的方案来实现自己的解决方案。