데이터 과학 및 머신 러닝(파트 05): 의사 결정 트리
355
0
의사 결정 트리란 무엇일까요?
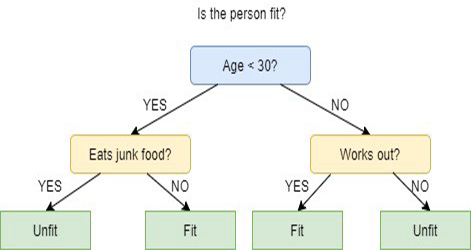
의사 결정 트리는 이전의 일련의 질문에 대해 답변을 한 방식을 기반으로 분류하거나 예측하거나 할때 사용되는 지도 학습 기술의 한 유형입니다. 모델은 지도 학습의 한 형태입니다. 즉 모델이 원하는 분류가 포함된 데이터 세트안에서 훈련되고 테스트된다는 의미입니다.
의사 결정 트리는 항상 명확한 답변이나 결정을 제공하지 못할 수 있습니다. 대신 데이터 과학자가 정보에 입각해 결정을 내릴 수 있도록 옵션을 제시할 수 있습니다. 의사 결정 트리는 인간이 생각하는 방식을 모방하므로 일반적으로 데이터 과학자가 결과를 이해하고 해석하기 쉽습니다.
용어에 대해!
이 시리즈의 첫 번째 기사에서 지도 학습과 비지도 학습이란 용어를 설명하는 것을 잊었으므로 여기서 설명합니다.
지도 학습
지도 학습은 인공지능(AI)을 개발하기 위한 접근법 중 하나로 입력 데이터에 대해 특정한 출력을 하도록 레이블 된 컴퓨터 알고리즘을 훈련시키는 것을 말하며 입력 데이터와 출력 사이의 기본 패턴과 관계를 감지할 수 있을 때까지 모델을 교육하는 접근 방식입니다. 이렇게 하여 이전에 본 적이 없는 데이터가 제시되었을 때 정확한 결과를 산출하도록 하는 것입니다.
지도 학습과 달리 이 접근 방식에서는 알고리즘에 레이블이 지정되지 않은 데이터가 표시되고 자체적으로 패턴이나 유사성을 감지하도록 설계되었습니다.
지도 학습 프로그램에서 일반적으로 사용되는 알고리즘은 다음과 같습니다.
지도 학습과 비지도 학습의 주요 차이점은 알고리즘이 학습하는 방식입니다. 비지도 학습에서는 레이블이 지정되지 않은 데이터가 교육 세트로 알고리즘에 제공됩니다. 감독 학습과 달리 올바른 출력 값이 없습니다. 알고리즘은 데이터를 외부의 것들과 관련시키지 않고 데이터 내에서 패턴과 유사성을 결정합니다. 즉 알고리즘은 데이터에 대해 더 많이 알아가고 인간이 찾지 않았던 흥미롭거나 예상치 못한 것을 찾기 위해 자유롭게 기능할 수 있습니다.
우리는 현재 지도 학습에 대해 알아보고 있습니다. 이후에 나올 기사에서는 비지도학습에 대해 알아볼 것입니다.
의사 결정 트리는 어떻게 작동할까요?
의사 결정 트리는 노드를 두 개 이상의 하위 노드로 분할하는 것을 결정하기 위해 여러개의 알고리즘을 사용합니다. 하위 노드를 생성하면 결과 하위 노드의 동질성이 증가합니다. 즉 목표 변수에 대한 노드의 순도가 높아진다고 할 수 있습니다. 의사결정 트리 알고리즘은 사용 가능한 모든 변수에서 노드를 분할한 다음 가장 동질적인 하위 노드를 생성하는 분할을 선택합니다.
알고리즘 선택은 대상 변수의 유형을 기반으로 합니다.
다음은 의사 결정 트리에서 사용되는 알고리즘입니다:
- ID3 > D3 확장
- C4.5 > ID3의 후계자
- CART > 분류 및 회귀 트리
- CHAID > 카이제곱 자동 상호 작용 감지, 분류 트리를 계산할 때 다단계 분할 수행
- MARS > 다변량 적응형 회귀 스플라인
이 기사에서는 ID3 알고리즘을 기반으로 의사 결정 트리를 만들 예정이며 이 시리즈의 다음 기사에서는 다른 알고리즘에 대해서 살펴보고 사용할 것입니다.
의사 결정 트리의 목표
의사 결정 트리 알고리즘의 주요 목표는 불순물이 있는 데이터를 순수하거나 노드에 가까운 노드로 분리하는 것입니다. 예를 들어 사과와 오렌지가 섞여 있는 바구니가 있고 의사 결정 트리가 색과 크기에 따라 사과가 어떻게 보이는지에 대해 훈련 받고 오렌지와 사과를 각각의 바구니에 분리시키는 것이 그 예가 될 것입니다.
ID3 알고리즘
ID3는 Iterative Dichotomiser 3의 약자로 알고리즘이 각 단계에서 특징을 두 개 이상의 그룹으로 반복적으로(반복적으로) 이분화(나누기)하기 때문에 붙여진 이름입니다.
Ross Quinlan이 발명한 ID3는 하향식 탐욕적 접근 방식을 사용하여 의사결정 트리를 구축합니다. 간단히 말해서 하향식 탐욕적 접근 방식은 위에서부터 트리를 구축하기 시작한다는 의미이며 탐욕적 접근 방식은 노드를 생성하기 위해 각각의 반복에서 현재 순간에 가장 좋은 특징을 선택한다는 것을 의미합니다.
일반적으로 ID3는 명목 데이터(기본적으로 측정할 수 없는 데이터)에 대한 분류 문제에만 사용됩니다.
즉 의사 결정 트리에는 두 가지 유형이 있습니다.
- 분류 트리
- 회귀 트리
01: 분류 트리
분류 트리는 이 기사에서 알아보려는 트리와 같은 것으로 분류하려는 연속적인 숫자 또는 정렬된 값이 없는 특징이 있습니다.
분류 트리는 사물을 범주로 분류합니다.
02: 회귀 트리
이들은 정렬된 값과 연속된 값으로 구성됩니다.
의사 결정 트리는 숫자 값을 예측합니다.
ID3 알고리즘의 단계
01: 원본 데이터 세트를 루트 노드로 시작합니다.
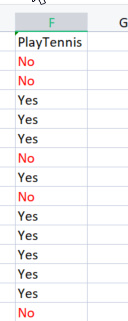
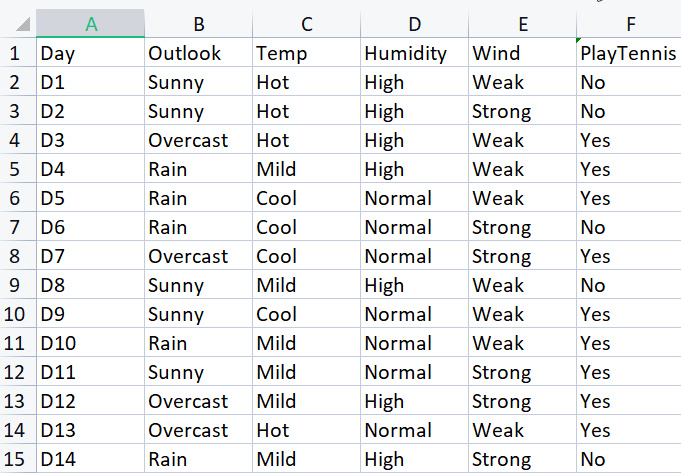
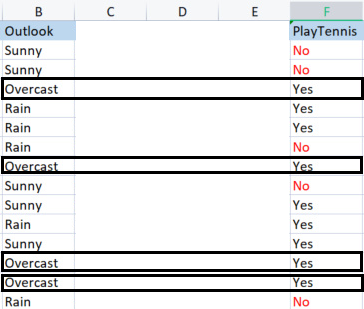
기본 라이브러리를 구축하기 위해 특정한 기상 조건에서 테니스를 치는 간단한 데이터 세트를 사용할 것입니다. 아래에 데이터 세트의 개요가 있습니다. 이것은 작은 데이터 세트(단지 14개 행)입니다.
이 알고리즘을 사용하여 의사 결정 트리를 그리려면 어떤 속성이 모든 Attributes 중에서 가장 많은 정보 이득을 제공하는지 이해해야 합니다. 이에 대해 설명해 보겠습니다.
이러한 속성(열) 중 하나는 루트 노드여야 하지만 루트 노드가 될 열을 어떻게 결정해야 할까요? 이부분이 우리가 정보 이득을 사용하는 부분입니다.
정보 획득
정보 이득은엔트로피의 감소를 계산하고 주어진 기능이 대상 클래스를 얼마나 잘 분리하거나 분류하는지를 측정합니다. 정보 획득이 가장 높은 기능이 최상의 기능으로 선택됩니다.
엔트로피
엔트로피는 무작위 변수의 불확실성의 측정이며 주어진 샘플의 불순물을 특성화합니다.
엔트로피의 공식은
우리가 해야 할 첫 번째 일은 전체 데이터 세트의 엔트로피를 찾는 것입니다. 이는 모든 열이 대상 열PlayTennis에 투영되기 때문에 대상 변수의 엔트로피를 찾는 것을 의미합니다.
코드를 작성해 보겠습니다.
우리는 타겟 변수들의 엔트로피를 찾기 전에 No로 표시된 음수 값의 총 수와Yes로 표시된 양수 값을 가지고 있어야 한다는 것을 잘 알고 있습니다. 이 값은 우리가 열 내부 요소의 확률을 얻는 데 도움을 줄 수 있습니다. 엔트로피 함수내에서 그러한 작업을 수행하는 코드를 작성해 보겠습니다.
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy; return(entropy_out); }
우리가 수식을 읽어 보았다면 함수를 한눈에 이해하기 쉽지만 배열SampleNumbers[]에 주의하세요. 샘플을 클래스라고 칭해도 됩니다. 이 대상 열에서 샘플은예및아니오입니다.
TargetArray 열에서 함수를 성공적으로 실행하면
12:37:48.394 TestScript There are 5 No 12:37:48.394 TestScript There are 9 Yes 12:37:48.394 TestScript There are 2 classes 12:37:48.394 TestScript "No" "Yes" 12:37:48.394 TestScript 5 9 12:37:48.394 TestScript Total contents = 14
이제 우리는 이 숫자를 얻었으므로 이 공식을 사용하여 엔트로피를 찾아봅시다.
의사결정 트리의 의 엔트로피 공식
공식을 주의 깊게 보면 여기에서 다루고 있는 로그가 밑이 2인 로그라는 것을 알 수 있습니다. 이는이진 로그입니다(자세한 내용은 읽어보세요).밑이 2인 로그를 찾기 위해 log2를 인수 값의 로그로 나눕니다.
double CDecisionTree::log2(double value) { return (log10(value)/log10(2)); }
베이스가 같으니 다 좋습니다.
또한 값 클래스의 확률을 얻는 데 도움이 되는Proba( )함수를 코딩했습니다.
double CDecisionTree::Proba(int number,double total) { return(number/total); }
방안의 코끼리. 열에 있는 요소의 확률을 찾기 위해 해당 열에 서 요속 얼마나 나타났는지 모든 요소의 총 수로 나눈 횟수를 찾습니다. 그러면아니오인 요소가 5개 있고예인요소가 9개라는 것을 찾을 수 있을 것입니다.
아니오의 확률 = 5/14(전체 요소 수) = 0.357142..
예의 확률 = 9/14(전체 요소 수) = 0.6428571...
마지막으로 Attribute/dataset 열의 엔트로피를 찾으려면
for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy;
Target 변수에서 이 함수를 실행하면 출력은 다음과 같습니다.
13:37:54.273 TestScript Proba1 0.35714285714285715 13:37:54.273 TestScript Proba1 0.6428571428571429 13:37:54.273 TestScript Entropy of the entire dataset = 0.9402859586706309
B A M
이제 우리는 기본적으로 y 값의 엔트로피인 전체 데이터 세트의 엔트로피를 알고 있으며 엔트로피를 찾기 위한 함수를 가지고 있습니다. 데이터 세트에서 각각의 모든 열의 엔트로피를 찾아봅시다.
우리는 이제 전체 데이터 세트의 엔트로피를 가지고 있습니다. 다음 단계는 각 독립 변수 열에 있는 멤버의 엔트로피를 찾는 것입니다. 독립 변수에서 이러한 종류의 엔트로피를 찾는 목적은 각 데이터 열에 대해정보 이득을 찾는 데 도움이 될 것입니다.
라이브러리를 사용해서 Outlook 열의 엔트로피를 찾기 전에 수동으로 계산해 보는 방식으로 수행 중인 작업을 명확하게 이해해 봅시다.
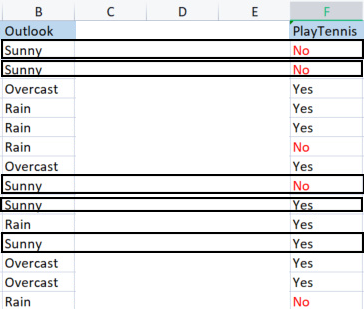
outlook 열을 대상 변수와 비교해 봅니다.
Outlook과 PlayTennis 칼럼
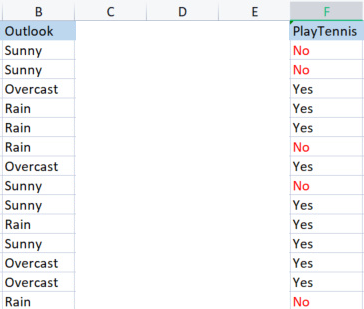
대상 변수의 엔트로피라고도 일컬어 지는 전체 데이터 세트의 엔트로피를 찾는 방법과 달리 독립 변수의 엔트로피를 찾으려면 우리는 대상 변수를 참조해야 합니다.
Outlook의 값
우리에게는 Sunny,Overcast및Rain 의 3 가지 값이 있습니다.대상 변수와 관련하여 각 값의 엔트로피를 찾아야 합니다.
Samples(Sunny)(Sunny의 양의 및 음의 샘플)= [양의 2개(예), 음의 3개(아니오)]
우리는 이제 양과 음의 수를가지고 있으므로 화창한 날에 테니스를칠확률은
확률1= 2(Yes가 나타난 횟수) / 5(총 화창한 날 수)
그러므로 2/5 = 0.4
반대로
화창한 날에 게임을 하지 않을 확률은0.6 입니다. 3/5 = 0.6
마지막으로 화창한 날의 엔트로피는 다음 공식을 참조하십시오.
엔트로피(맑음) = - (P1*log2P1+ P2*log2P2)
엔트로피(맑음) = -(0.4*log20.4 + 0.6*log20.6)
엔트로피(맑음) = 0.97095
이제 Overcast의 엔트로피를 구해봅시다.
흐린 날씨의 샘플.
양의 샘플4 (Target 열에Yes 가 있는 샘플), 음의 샘플0 (Target 열에No 가 있는 샘플). 이 상황은예외입니다.
ID3 알고리즘의 예외
0개의 음의 샘플이 있는 동안 양의 샘플이 있거나 그 반대인 경우는 음의 샘플이 있는 동안 0개의 양의 샘플이 있습니다. 이런 일이 발생할 때마다 엔트로피는 0에 바인딩됩니다.
우리는 그것을 순수 노드라고 칭합니다.동종 샘플이 있기 때문에 분할할 필요가 없습니다. 트리를 그릴 때 이것이 의미하는 바를 더 잘 이해할 것입니다.
또 다른 예외는 다음과 같습니다:
같은 수의 양의 샘플과 음의 샘플이 발생하면 수학적으로 엔트로피는1이 됩니다.
우리가 효과적으로 처리해야 하는 유일한 예외는 샘플에 0 값이 있는 경우입니다. 0이 0 분할로 이어질 수 있기 때문입니다. 여기 이와 같은 예외를 처리할 수 있는 새로운 함수가 있습니다.
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { if (SampleNumbers[i] == 0) { Entropy = 0; break; } //Exception double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } if (Entropy==0) entropy_out = 0; //handle the exception else entropy_out = -Entropy; return(entropy_out); }
이제 비의 엔트로피를 구해봅시다.
Rain Samples;
3개의 양의 샘플이 있습니다(대상 열에 yes가 있는 샘플).
음의 샘플이 2개 있습니다(대상 열에 아니오가 있는 샘플).
마지막으로 비오는 날 테니스를 치는 엔트로피.
엔트로피(비) = - (P1*log2P1 + P2*log2P2)
엔트로피(비) = -(0.6*log2 0.6 + 0.4*log2 0.4)
엔트로피(비) = 0.97095
다음은 Outlook 열에서 얻은 엔트로피 값입니다.
| Outlook 열에서 얻은 엔트로피 |
|---|
| 엔트로피(화창함) = 0.97095 |
| 엔트로피(흐림) = 0 |
| 엔트로피(비) = 0.97095 |
이것이 샘플의 엔트로피를 수동적으로 찾는 방법입니다. 프로그램을 사용하여 해당 엔트로피를 찾으면 다음과 같은 출력을 얻습니다:
PD 0 13:47:20.571 TestScript <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript << Sunny >> total > 5 MH 0 13:47:20.571 TestScript "No" "Yes" DM 0 13:47:20.571 TestScript 3 2 CQ 0 13:47:20.571 TestScript Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript << Overcast >> total > 4 OI 0 13:47:20.571 TestScript "No" "Yes" MJ 0 13:47:20.571 TestScript 0 4 CM 0 13:47:20.571 TestScript Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript << Rain >> total > 5 GN 0 13:47:20.571 TestScript "No" "Yes" JH 0 13:47:20.571 TestScript 2 3 HR 0 13:47:20.571 TestScript Entropy of Rain = 0.97095
이 값을 사용하여이전에논의한 공식을 사용하여 전체 데이터의 정보 이득을 찾을 것입니다.
이제 뒤에서 무슨 일이 일어나고 있는지 이해할 수 있도록 수동으로 엔트로피를 찾아보겠습니다.
Information Gain(IG) = EntropyofEntireDataset - 샘플의 확률과 해당 엔트로피의 곱 합계입니다.
IG = E(데이터 세트) -(Prob(화창) *E(화창)+Prob(흐림)*E(흐림)+Prob(비)*E(비))
IG = 0.9402 - ( 5/14 * (0.97095) + 4/14 * (0) + 5/14(0.97095) )
IG = 0.2467(outlook 칼럼의 정보 획득량)
수식을 코드로 변환하면 다음과 같습니다.
double CDecisionTree::InformationGain(double parent_entropy, double &EntropyArr[], int &ClassNumbers[], int rows_) { double IG = 0; for (int i=0; i<ArraySize(EntropyArr); i++) { double prob = ClassNumbers[i]/double(rows_); IG += prob * EntropyArr[i]; } return(parent_entropy - IG); }
함수 호출
if (m_debug) printf("<<<<<< Column Information Gain %.5f >>>>>> \n",IGArr[i]);
출력:
PF 0 13:47:20.571 TestScript <<<<<< Column Information Gain 0.24675 >>>>>>
이제 모든 열에 대해 프로세스를 반복하고 해당되는 정보 이득을 찾아야 합니다. 출력은 다음과 같을 것입니다:
RH 0 13:47:20.571 TestScript (EURUSD,H1) Default Parent Entropy 0.9402859586706309 PD 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript (EURUSD,H1) << Sunny >> total > 5 MH 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DM 0 13:47:20.571 TestScript (EURUSD,H1) 3 2 CQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript (EURUSD,H1) << Overcast >> total > 4 OI 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" MJ 0 13:47:20.571 TestScript (EURUSD,H1) 0 4 CM 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript (EURUSD,H1) << Rain >> total > 5 GN 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" JH 0 13:47:20.571 TestScript (EURUSD,H1) 2 3 HR 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Rain = 0.97095 PF 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24675 >>>>>> QP 0 13:47:20.571 TestScript (EURUSD,H1) KH 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> PR 0 13:47:20.571 TestScript (EURUSD,H1) << Hot >> total > 4 QF 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OS 0 13:47:20.571 TestScript (EURUSD,H1) 2 2 NK 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Hot = 1.00000 GO 0 13:47:20.571 TestScript (EURUSD,H1) << Mild >> total > 6 OD 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" KQ 0 13:47:20.571 TestScript (EURUSD,H1) 2 4 GJ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Mild = 0.91830 HQ 0 13:47:20.571 TestScript (EURUSD,H1) << Cool >> total > 4 OJ 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OO 0 13:47:20.571 TestScript (EURUSD,H1) 1 3 IH 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Cool = 0.81128 OR 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.02922 >>>>>> ID 0 13:47:20.571 TestScript (EURUSD,H1) HL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> FH 0 13:47:20.571 TestScript (EURUSD,H1) << High >> total > 7 KM 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" HF 0 13:47:20.571 TestScript (EURUSD,H1) 4 3 GQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of High = 0.98523 QK 0 13:47:20.571 TestScript (EURUSD,H1) << Normal >> total > 7 GR 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DD 0 13:47:20.571 TestScript (EURUSD,H1) 1 6 OF 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Normal = 0.59167 EJ 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15184 >>>>>> EL 0 13:47:20.571 TestScript (EURUSD,H1) GE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> IQ 0 13:47:20.571 TestScript (EURUSD,H1) << Weak >> total > 8 GE 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" EO 0 13:47:20.571 TestScript (EURUSD,H1) 2 6 LI 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Weak = 0.81128 FS 0 13:47:20.571 TestScript (EURUSD,H1) << Strong >> total > 6 CK 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" ML 0 13:47:20.571 TestScript (EURUSD,H1) 3 3 HO 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Strong = 1.00000 LE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04813 >>>>>> IE 0 13:47:20.571 TestScript (EURUSD,H1)
이제 우리는 모든 열에 대한 정보 이득을 가지고 있으므로 의사 결정 트리 그리기를 시작할 것입니다.어떻게 하는 걸까요?
이러한 초기 프로세스의 목적은 모든 컬럼에 대한 정보 이득을 찾아 어떤 컬럼이 루트 노드가 될지 결정하는 것이었습니다. 정보 이득이 많은 컬럼이 다른 어떤 것보다 루트 노드가 될 것입니다. Outlook이 가장 높은 정보 이득을 가지고 있으므로 Outlook이 의사 결정 트리의루트 노드가 될 경우 이제 트리를 그려 보겠습니다.
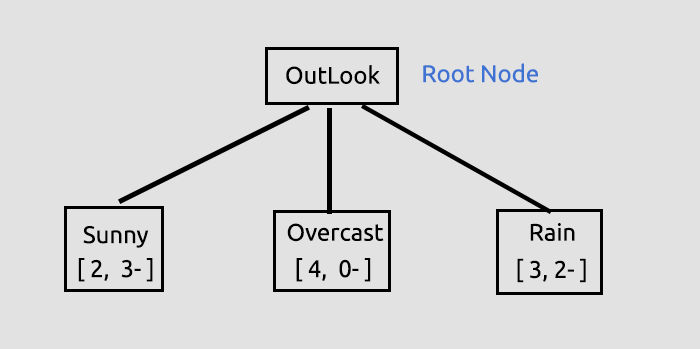
Outlook에 대한 정보는 라이브러리에서 제공하며 기사 끝에 링크된 Script Test Script를 실행하면 기본 라이브러리의 디버그 모드에서 많은 정보가 인쇄됩니다.
정보 이득은 함수로부터 얻습니다. 이후 모든 정보 이득을 저장하는 이중 값 배열에 저장하게 되고 이후 배열 내부의 최대 값이 우리의 목표 값이 될 것입니다.
//--- Finding the Information Gain ArrayResize(IGArr,i+1); //information gains matches the columns number IGArr[i] = InformationGain(P_EntropyArr[A],EntropyArr,ClassNumbers,rows); max_gain = ArrayMaximum(IGArr);출력을 하면 다음과 같을 것입니다.
QR 0 13:47:20.571 TestScript (EURUSD,H1) Parent Noce will be Outlook with IG = 0.24675 IK 0 13:47:20.574 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers NL 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Overcast" "Rain" NH 0 13:47:20.574 TestScript (EURUSD,H1) 0.9710 0.0000 0.9710 FR 0 13:47:20.574 TestScript (EURUSD,H1) 5 4 5
여기까지 우리가 그린 트리에 대한 설명입니다.
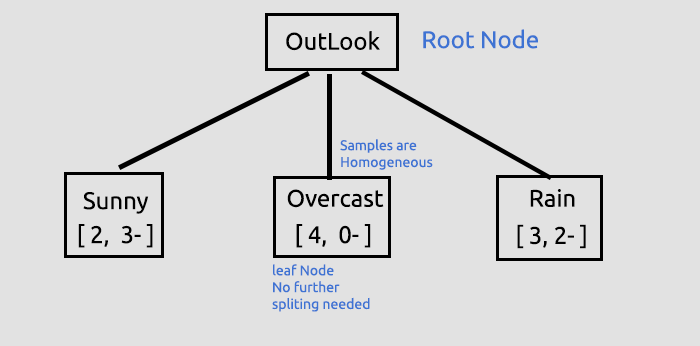
여기까지가 우리가 루트 노드를 찾고 해당 루트 노드를 가지와 잎으로 분할하는 첫 번째 중요한 단계였습니다. 우리는 분할할 것이 없을 때까지 데이터를 계속 분할할 것입니다. 그리고 다음과 같이 프로세스를 계속할 것입니다.맑음아이템으로 가지를 나누고비아이템으로 가지를 나눕니다.
흐림은 동질적인 항목(순수함)으로 구성됩니다. 그러므로 우리는 이것이 완전히 분류되었다고 할수 있습니다. 의사결정 트리에서는 이를 리프라고 합니다. 흐림은 가지를 생성하지 않습니다.
그러나 데이터를 더 분할하기 전에 우리에게는 현재 가지고 있는 데이터 세트로 수행해야 할 중요한 단계가 있습니다.
나머지 데이터 세트 매트릭스 분류
우리는 동일한 값을 가진 행을 오름차순으로 배치하기 위해 나머지 데이터 세트 행렬을 분류해야 합니다. 이것은 동종 콘텐츠(우리가 열망하는 것)로 가지와 잎을 만드는 데 도움이 될 것입니다.
void CDecisionTree::MatrixClassify(string &dataArr[],string &Classes[], int cols) { string ClassifiedArr[]; ArrayResize(ClassifiedArr,ArraySize(dataArr)); int fill_start = 0, fill_ends = 0; int index = 0; for (int i = 0; i<ArraySize(Classes); i++) { int start = 0; int curr_col = 0; for (int j = 0; j<ArraySize(dataArr); j++) { curr_col++; if (Classes[i] == dataArr[j]) { //printf("Classes[%d] = %s dataArr[%d] = %s ",i,Classes[i],j,dataArr[j]); if (curr_col == 1) fill_start = j; else { if (j>curr_col) fill_start = j - (curr_col-1); else fill_start = (curr_col-1) - j; fill_start = fill_start; //Print("j ",j," j-currcol ",j-(curr_col-1)," curr_col ",curr_col," columns ",cols," fill start ",fill_start ); } fill_ends = fill_start + cols; //printf("fillstart %d fillends %d j index = %d i = %d ",fill_start,fill_ends,j,i); //--- //if (ArraySize(ClassifiedArr) >= ArraySize(dataArr)) break; //Print("ArraySize Classified Arr ",ArraySize(ClassifiedArr)," dataArr size ",ArraySize(dataArr)," i ",i); for (int k=fill_start; k<fill_ends; k++) { index++; //printf(" k %d index %d",k,index); //printf("dataArr[%d] = %s index = %d",k,dataArr[k],index-1); ClassifiedArr[index-1] = dataArr[k]; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } if (curr_col == cols) curr_col = 0; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } ArrayCopy(dataArr,ClassifiedArr); ArrayFree(ClassifiedArr); }
주석 처리된 코드가 너무 많은 이유는 무엇일까요? 우리의 라이브러리는 여전히 개선이 필요하며 주석은 디버깅을 위한 것입니다.
이 함수를 호출하고 출력을 하면 다음을 얻을 수 있습니다.
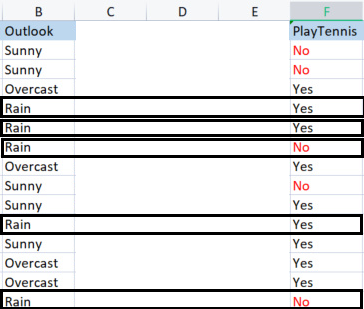
JG 0 13:47:20.574 TestScript (EURUSD,H1) Classified matrix dataset KL 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " GS 0 13:47:20.574 TestScript (EURUSD,H1) [ QF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" JF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" ND 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" PN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" EH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "High" "Weak" "Yes" MH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Cool" "Normal" "Strong" "Yes" MN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Mild" "High" "Strong" "Yes" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "Normal" "Weak" "Yes" MG 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" QO 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" LN 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" LE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" FE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" GS 0 13:47:20.574 TestScript (EURUSD,H1) ] DH 0 13:47:20.574 TestScript (EURUSD,H1) columns = 5 rows = 70
B A M, 함수가 마술처럼 작동합니다
좋습니다. 이제 다음으로 중요한 단계는
데이터 세트에서 잎 노드 제거
우리가 지금까지 수행한 모든 프로세스를 반복하기 전에 잎 노드들을 제거하는 것이 매우 중요합니다. 잎 노드들은 가지를 만들지 않을 것이기 때문입니다,맞지요?그건 그렇고 잎 노들들은 순수한 값의 노드입니다.
잎 노드 값이 있는 모든 행을 제거합니다. 이 경우에는흐림을 사용하여 모든 행을 제거합니다.
//--- Search if there is zero entropy in the Array int zero_entropy_index = 0; bool zero_entropy = false; for (int e=0; e<ArraySize(P_EntropyArr); e++) if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array if (m_debug) { printf("%s is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is ..",p_Classes[zero_entropy_index]); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total); } //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]);
이 코드 블록을 실행한 후의 출력은 다음과 같습니다.
NQ 0 13:47:20.574 TestScript (EURUSD,H1) Overcast is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. GP 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " KG 0 13:47:20.574 TestScript (EURUSD,H1) [ FS 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" EI 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" IP 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" KK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" JK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" FL 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" OI 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" IQ 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" LG 0 13:47:20.575 TestScript (EURUSD,H1) ] IL 0 13:47:20.575 TestScript (EURUSD,H1) columns = 5 rows = 50 HE 0 13:47:20.575 TestScript (EURUSD,H1) rows total 50 Rain 5
B A M
이 시점에서 마지막으로 중요한 프로세스는 다음과 같습니다:
데이터 세트에서 부모 또는 루트 노드 열 제거
우리는 이미 이를 루트 노드로 감지하고 우리의 트리에 그렸으므로 더 이상 우리의 데이터 세트에 필요하지 않습니다. 그러므로 데이터 세트는 분류되지 않은 값으로 유지되어야 합니다.
//--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assign the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- printf("Column %d removed from the Matrix, The remaining dataset is",max_gain+1); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total);
이 코드 블록을 실행한 결과는 다음과 같습니다.
OM 0 13:47:20.575 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is ON 0 13:47:20.575 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " HF 0 13:47:20.575 TestScript (EURUSD,H1) [ CR 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" JE 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" JR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" NG 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" JI 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" PR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JJ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" QQ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" OG 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" KD 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" DR 0 13:47:20.575 TestScript (EURUSD,H1) ]
B A M
이제 우리가 데이터세트의 일부를 자신 있게 남길 수 있었던 이유는 데이터세트가 들어가는 위치에 대한 단서를 남기는 트리를 라이브러리가 그리기 때문입니다. 여기 우리가 이 지점까지 그린 트리가 있습니다.
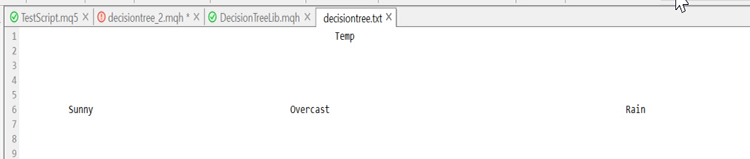
못생겼지만 데모용으로는 충분합니다. 다음 기사에서 HTML로 생성해 보겠습니다. 이를 위해 GitHub 저장소는 아래에 링크되어 있습니다. 이제 트리를 만드는 나머지 프로세스를 설명하면서 마무리하겠습니다. 분할할 것이 없을 때까지 이 프로세스를 반복한 후의 로그는 다음과 같습니다.
HI 0 13:47:20.575 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers RK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Rain" CL 0 13:47:20.575 TestScript (EURUSD,H1) 0.9710 0.9710 CE 0 13:47:20.575 TestScript (EURUSD,H1) 5 5 EH 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.97095 A = 1 >>>>>>>> OF 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> RP 0 13:47:20.575 TestScript (EURUSD,H1) << Hot >> total > 2 MD 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" MQ 0 13:47:20.575 TestScript (EURUSD,H1) 2 0 QE 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 FQ 0 13:47:20.575 TestScript (EURUSD,H1) << Mild >> total > 5 KJ 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" NO 0 13:47:20.575 TestScript (EURUSD,H1) 2 3 DH 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 IS 0 13:47:20.575 TestScript (EURUSD,H1) << Cool >> total > 3 KH 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" LM 0 13:47:20.575 TestScript (EURUSD,H1) 1 2 FN 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 KD 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.20999 >>>>>> EF 0 13:47:20.575 TestScript (EURUSD,H1) DJ 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> HJ 0 13:47:20.575 TestScript (EURUSD,H1) << High >> total > 5 OS 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" FD 0 13:47:20.575 TestScript (EURUSD,H1) 4 1 NG 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of High = 0.72193 KM 0 13:47:20.575 TestScript (EURUSD,H1) << Normal >> total > 5 CP 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" JR 0 13:47:20.575 TestScript (EURUSD,H1) 1 4 MD 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Normal = 0.72193 EL 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24902 >>>>>> IN 0 13:47:20.575 TestScript (EURUSD,H1) CS 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> OS 0 13:47:20.575 TestScript (EURUSD,H1) << Weak >> total > 6 CK 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" GM 0 13:47:20.575 TestScript (EURUSD,H1) 2 4 OO 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 HE 0 13:47:20.575 TestScript (EURUSD,H1) << Strong >> total > 4 GI 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" OJ 0 13:47:20.575 TestScript (EURUSD,H1) 3 1 EM 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 PG 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.09546 >>>>>> EG 0 13:47:20.575 TestScript (EURUSD,H1) HK 0 13:47:20.575 TestScript (EURUSD,H1) Parent Noce will be Humidity with IG = 0.24902 OI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers JO 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" QJ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 QO 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 PJ 0 13:47:20.578 TestScript (EURUSD,H1) Classified matrix dataset NM 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " EF 0 13:47:20.578 TestScript (EURUSD,H1) [ FM 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" OD 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" GR 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" QG 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JD 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" KS 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" OJ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" CL 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" LJ 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" NH 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" ER 0 13:47:20.578 TestScript (EURUSD,H1) ] LI 0 13:47:20.578 TestScript (EURUSD,H1) columns = 4 rows = 40 CQ 0 13:47:20.578 TestScript (EURUSD,H1) rows total 36 High 5 GH 0 13:47:20.578 TestScript (EURUSD,H1) Column 2 removed from the Matrix, The remaining dataset is MP 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " QG 0 13:47:20.578 TestScript (EURUSD,H1) [ LL 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Weak" "No" OE 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Strong" "No" QQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "No" QE 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" LQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "No" HE 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" RM 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" PF 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" MR 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Strong" "No" IF 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" EN 0 13:47:20.578 TestScript (EURUSD,H1) ] ME 0 13:47:20.578 TestScript (EURUSD,H1) columns = 3 rows = 22 ER 0 13:47:20.578 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers HK 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" CQ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 OK 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 NS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.91830 A = 2 >>>>>>>> JM 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> CG 0 13:47:20.578 TestScript (EURUSD,H1) << Hot >> total > 2 DM 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" LF 0 13:47:20.578 TestScript (EURUSD,H1) 2 0 HN 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 OJ 0 13:47:20.578 TestScript (EURUSD,H1) << Mild >> total > 5 JS 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" GD 0 13:47:20.578 TestScript (EURUSD,H1) 2 3 QG 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 LL 0 13:47:20.578 TestScript (EURUSD,H1) << Cool >> total > 3 JQ 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" IR 0 13:47:20.578 TestScript (EURUSD,H1) 1 2 OE 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 RO 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15733 >>>>>> PO 0 13:47:20.578 TestScript (EURUSD,H1) JS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> JR 0 13:47:20.578 TestScript (EURUSD,H1) << Weak >> total > 6 NH 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JM 0 13:47:20.578 TestScript (EURUSD,H1) 2 4 JL 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 QD 0 13:47:20.578 TestScript (EURUSD,H1) << Strong >> total > 4 JN 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JK 0 13:47:20.578 TestScript (EURUSD,H1) 3 1 DM 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 JF 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04281 >>>>>> DG 0 13:47:20.578 TestScript (EURUSD,H1) LI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Noce will be Temp with IG = 0.15733 LH 0 13:47:20.584 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers GR 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Mild" "Cool" CD 0 13:47:20.584 TestScript (EURUSD,H1) 0.0000 0.9710 0.9183 GN 0 13:47:20.584 TestScript (EURUSD,H1) 2 5 3 CK 0 13:47:20.584 TestScript (EURUSD,H1) Classified matrix dataset RL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " NK 0 13:47:20.584 TestScript (EURUSD,H1) [ CQ 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Weak" "No" LI 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Strong" "No" JM 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" NI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" CL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" KI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" LR 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" KJ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" IQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" DE 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" NR 0 13:47:20.584 TestScript (EURUSD,H1) ] OI 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 30 OO 0 13:47:20.584 TestScript (EURUSD,H1) Hot is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. HL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " DJ 0 13:47:20.584 TestScript (EURUSD,H1) [ DL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" LH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" QL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" MH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" RQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" MI 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" KQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" FD 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" HQ 0 13:47:20.584 TestScript (EURUSD,H1) ] NN 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 24 IF 0 13:47:20.584 TestScript (EURUSD,H1) rows total 24 Mild 5 CO 0 13:47:20.584 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is DM 0 13:47:20.584 TestScript (EURUSD,H1) "Wind" "PlayTennis " PD 0 13:47:20.584 TestScript (EURUSD,H1) [ LN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "No" JI 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EL 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" GO 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "Yes" JG 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JE 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EP 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" HK 0 13:47:20.584 TestScript (EURUSD,H1) ] PP 0 13:47:20.584 TestScript (EURUSD,H1) columns = 2 rows = 10 HG 0 13:47:20.584 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers FQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Cool" OF 0 13:47:20.584 TestScript (EURUSD,H1) 0.9710 0.9183 IO 0 13:47:20.584 TestScript (EURUSD,H1) 5 3
다음은 BUILD TREE 함수에 대한 개요입니다. 값을 수동으로 계산할 때는 프로세스가 쉬워 보이지만 이 코드 부분이 읽기 어렵고 혼란스러워서 여기에서 자세히 설명하기로 했습니다.
void CDecisionTree::BuildTree(void) { int ClassNumbers[]; int max_gain = 0; double IGArr[]; //double parent_entropy = Entropy(p_ClassNumbers,single_rowstotal); string p_Classes[]; //parent classes double P_EntropyArr[]; //Parent Entropy int p_ClassNumbers[]; //parent/ Target variable class numbers GetClasses(TargetArr,m_DatasetClasses,p_ClassNumbers); ArrayResize(P_EntropyArr,1); P_EntropyArr[0] = Entropy(p_ClassNumbers,single_rowstotal); //--- temporary disposable arrays for parent node information string TempP_Classes[]; double TempP_EntropyArr[]; int TempP_ClassNumbers[]; //--- if (m_debug) Print("Default Parent Entropy ",P_EntropyArr[0]); int cols = m_colschosen; for (int A =0; A<ArraySize(P_EntropyArr); A++) { printf("<<<<<<<< Parent Entropy %.5f A = %d >>>>>>>> ",P_EntropyArr[A],A); for (int i=0; i<cols-1; i++) //we substract with one to remove the independent variable coumn { int rows = ArraySize(m_dataset)/cols; string Arr[]; //ArrayFor the current column string ArrTarg[]; //Array for the current target ArrayResize(Arr,rows); ArrayResize(ArrTarg,rows); printf(" <<<<< C O L U M N %s >>>>> ",DataColumnNames[i]); int index_target=cols-1; for (int j=0; j<rows; j++) //get column data and its target column { int index = i+j * cols; //Print("index ",index); Arr[j] = m_dataset[index]; //printf("ArrTarg[%d] = %s m_dataset[%d] =%s ",j,ArrTarg[j],index_target,m_dataset[index_target]); ArrTarg[j] = m_dataset[index_target]; //printf("Arr[%d] = %s ArrTarg[%d] = %s ",j,Arr[j],j,ArrTarg[j]); index_target += cols; //the last index of all the columns } //--- Finding the Entropy //The function to find the Entropy of samples in a given column inside its loop //then restores all the entropy into one array //--- Finding the Information Gain //The Function to find the information gain from the entropy array above //--- if (i == max_gain) { //Get the maximum information gain of all the information gain in all columns then //store it to the parent information gain } //--- ZeroMemory(ClassNumbers); ZeroMemory(SamplesNumbers); } //---- Get the parent Entropy, class and class numbers // here we store the obtained parent class from the information gain metric then we store them into a parent array ArrayCopy(p_Classes,TempP_Classes); ArrayCopy(P_EntropyArr,TempP_EntropyArr); ArrayCopy(p_ClassNumbers,TempP_ClassNumbers); //--- string Node[1]; Node[0] = DataColumnNames[max_gain]; if (m_debug) printf("Parent Node will be %s with IG = %.5f",Node[0],IGArr[max_gain]); if (A == 0) DrawTree(Node,"parent",A); DrawTree(p_Classes,"child",A); //--- CLASSIFY THE MATRIX MatrixClassify(m_dataset,p_Classes,cols); //--- Search if there is zero entropy in Array if there is any remove its data from the dataset if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]); //--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assing the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- } }
결론
이제 여러분이 분류 트리와 관련된 기본 계산을 이해했기를 바랍니다. 사실 기사 하나로 다루기에는 어렵고 긴 주제입니다. 라이브러리에는 여러분들의 거래에서 사용할 수 있는 결정 트리 알고리즘을 구축하기 위해 필요한 거의 모든 것이 있습니다. 다음 기사에서 모든 설명을 완료할 수 있기를 바랍니다.
읽어 주셔서 감사합니다.https://github.com/MegaJoctan/DecisionTree-Classification-tree-MQL5링크는 저의 GitHub 저장소입니다.
MetaQuotes 소프트웨어 사를 통해 영어가 번역됨
원본 기고글: https://www.mql5.com/en/articles/11061
볼륨으로 거래 시스템을 설계하는 방법 알아보기
데이터 과학 및 머신 러닝(파트 04): 현재 주식 시장 붕괴 예측
Expert Advisor 개발 기초부터 (파트 13): Time and Trade (II)
MQL5에서 행렬 및 벡터
