神经网络变得轻松（第十八部分）：关联规则

MetaTrader 5 — 交易系统 | 20 九月 2022, 08:42

1 115

Dmitriy Gizlyk

内容

概述

分析数据量的成长导致对无监督学习方法的兴趣增长。在最近几篇文章中，我们已经看到了属于无监督学习方法的聚类和降维算法。在本文中，我们继续研究无监督学习方法。这一次，我们将研究可用这些方法定位的另一类问题：关联规则挖掘。这种问题类型起源于超市购物营销，用于分析市场篮子，目的是找到最热销的产品集。今日，解决这些问题的算法广泛应用于各个领域。我们将查看如何在交易中运用这些算法。

1. 关联规则

关联规则分析问题属于数据挖掘应用问题。甚或，它是最基本的方法之一，因为它能够识别大型数据库中数据之间的有趣关系。

这类问题最初是在零售购物过程中形成和定义的。市场营销人员面临的问题是，通过分析销售网点系统在册的交易数据的大型数据库，可以获取哪些商业利益。以前只会分析总销售量。对客户购物行为的分析开辟了新的领域，因为它能够分析客户购买的特定产品集。

第一个算法是由 IBM 的一组开发人员于 1993 年创建的。当主要原则形成时，之后就会形成一整套算法的基础。

首先，由算法检测到的规则必须是经常会遇到。这意味着它们不能是纯随机的，并且必须在分析的数据库中至少重复了一定次数。意即，它们必须能够得到确认。从统计学的角度来看，包含此类规则的业务样本应具有代表性。为了满足这一要求，所有用来判定关联规则的算法都有一个最少支持率参数 MinSup，该参数以 “1” 为底表示规则出现频率与分析样本中业务总数的比率。

根据组合的规则，如果我们有一组 3 项：a，B 和 C，在不考虑元素位置的情况下，我们可以得到 7 个不同的集合，这些项包含从 1 到 3。随着项数的增加，可能的组合数量也增加。考虑到给定数据库的容量，直接重新计算每个集合的频率变为一项相当消耗资源的任务。经常性地重新计算是不可能的。因此，作者使用了抗单调属性。

如果在数据库中，A 项只是所有可能项其中一组，其出现频率将等于 A 本身的频率。如果遇到的集合次数越多，则它们的频率只能越少，因为它们在所分析样本中出现的总数将等于 A 的出现次数。因此，如果任何项的出现频率小于 MinSup，则包含该项的集合的所有可能变体的频率就会小于 MinSup。如此，我们计算每项的出现频率就足够了，从而剔除对我们没有实际价值的随机集合的绝大部分。

正如您所看到的，关联规则搜索算法与之前研究过的所有算法区别很大。之前，我们尝试充分利用所有可用数据。与其鲜明对比，关联规则挖掘的算法可以立即消除随机（噪声）项。

所有关联规则算法中用到的第二个参数是最小置信度 MinConf。它也用以 1 为底的分数表示。为了解释这个参数，我们应该知道每个规则都由两部分组成：前因和后果。前因和后果都可由一项或整套项组成。在一般情况下，规则听起来如下：如果前因为真，那么通常会有一个后果。

注意，在前因发生之后，后果发生的概率并非 100%。而后果发生的最小概率由 MinConf 参数设定。满足此参数时，规则被视为有效，并保存到规则数组中。它定义为规则执行频率与前因频率的比率。

2. Apriori 算法

寻找关联规则最著名的算法之一可能就是 Apriori 算法，它由 Rakesh Agrawal 和 Ramakrishnan Srikant 于 1994 年提出。该算法基于搜索数据库中最频繁形态的迭代过程。之后，从所选形态中提取规则。

为了更好地理解它，我们看一下算法在 10 笔业务和 5 项的小示例上的操作。

业务 ID	内容
T1	BCDE
T2	BCD
T3	B
T4	BCD
T5	D
T6	ACD
T7	BCDE
T8	BCE
T9	CDE
T10	AD

我们在问题中引入最小支持率 0.3 和最小置信度 0.7 的常数（分别为 30% 和 70%）。

请注意，所有关联规则算法都使用二元数组。因此，从一开始，我们就把上述数据表示为二元表格。

业务 ID	A	B	C	D	E
T1	0	1	1	1	1
T2	0	1	1	1	0
T3	0	1	0	0	0
T4	0	1	1	1	0
T5	0	0	0	1	0
T6	1	0	1	1	0
T7	0	1	1	1	1
T8	0	1	1	1	0
T9	0	0	1	1	1
T10	1	0	0	1	0

根据该表格，很容易计算出项 A 仅出现两次，其支持率等于 0.2 或 20%。类似地，我们计算对其它项的支持率：B — 0.6, C — 0.7, D — 0.8, E — 0.4。如您所见，只有 A 不满足最低支持率要求。如此，我们根据抗单调性，将其排除在进一步处理之外。

从剩余的元素中，我们为频繁出现的形态创建候选者。我们在上一步中已判定了频繁发生项。根据该算法，我们判定候选者为两个项的集合：BC、BD、BE、CD、CE、DE。

现在，我们需要处理整个数据库，并判定每个选定候选者的支持率。

业务 ID	BC	BD	BE	CD	CE	DE
T1	1	1	1	1	1	1
T2	1	1	0	1	0	0
T3	0	0	0	0	0	0
T4	1	1	0	1	0	0
T5	0	0	0	0	0	0
T6	0	0	0	1	0	0
T7	1	1	1	1	1	1
T8	1	0	1	0	1	0
T9	0	0	0	1	1	1
T10	0	0	0	0	0	0

这一次，我们所有候选者的支持率都满足最低支持率条件： BC — 0.5, BD — 0.4, BE — 0.3, CD — 0.6, CE — 0.4, DE — 0.3。但这并非始终发生。在解决实际问题时，一些候选者更有可能被淘汰。

接下来，我们继续迭代过程。这次，我们创建三个项的候选者集合。为此，我们从上一次迭代中提取选出的频繁形态，并组合配对，其中仅有一个元素不同。我们可以判定 4 个候选者：BCD、BCE、BDE 和 CDE。

根据 Apriori 算法，我们必须再次遍历整个数据库，从而判定所有新候选者的支持率。

业务 ID	BCD	BCE	BDE	CDE
T1	1	1	1	1
T2	1	0	0	0
T3	0	0	0	0
T4	1	0	0	0
T5	0	0	0	0
T6	0	0	0	0
T7	1	1	1	1
T8	0	1	0	0
T9	0	0	0	1
T10	0	0	0	0

结果就是，我们得到以下我们的候选者的支持率： BCD — 0.4, BCE — 0.3, BDE — 0.2, CDE — 0.3。在本次迭代中，对 BDE 项的支持率不满足最低支持率要求，因此我们将其剔除在外。其它候选者都被认定为频繁形态。

在下一次迭代中，我们编译 4 项的候选者集合。基于来自上一次迭代中选择的形态，我们只能生成一个候选者 BCDE。但在计算这个候选者支持率之前，我们先要关注其组成部分 BDE。该候选项在上一次迭代后被删除，因为它的支持率仅为 0.2，而最低支持率要求为 0.3。因此，根据抗单调性规则，BCDE 候选者的支持率不能大于 0.2。但这低于最低支持率。

鉴于我们没有任何其它候选者，我们停止搜索频繁形态的过程，并继续下一个子过程 — 基于选定的频繁形态判定规则。为此，我们把所选择的形态切分为前因和后果。之后，我们可以判定每个规则的置信等级，并将其与所需的最小置信等级进行比较。

我们将为集合中的每项依次构建规则。由于在开始第一阶段，我们通过 A 剔除了所有形态（它的支持率低于 MinSup），因此我们开始依据 B 判定规则。

从所选的形态中，我们判定包含分析项的所有形态。从形态中提取项 B 作为后果备用，而其余部分将作为前因项。我们还将判定每个所创建规则的置信度。

规则置信度表示当形成前因时，后果出现的概率。为了判定它，我们不需要重新迭代整个数据库。我们只需要把全部形态的支持率切分为前因的支持率，其数值在频繁形态选择阶段已计算得出。

形态	前因	支持率	规则
BC (0.5)	C (0.7)	0.71	C -> B
BD (0.4)	D (0.8)	0.50	D -> B
BE (0.3)	E (0.4)	0.75	E -> B
BCD (0.4)	CD (0.6)	0.67	CD -> B
BCE (0.3)	CE (0.4)	0.75	CE -> B

规则 D -> B 和 CD -> B 不满足 0.7 的最低支持率要求，因此我们将其排除在外。

按照类似的方式判定其它规则。

形态	前因	支持率	规则
BC (0.5)	B (0.6)	0.83	B -> C
CD (0.6)	D (0.8)	0.75	D -> C
CE (0.4)	E (0.4)	1.00	E -> C
BCD (0.4)	BD (0.4)	1.00	BD -> C
BCE (0.3)	BE (0.3)	1.00	BE -> C
CDE (0.3)	DE (0.3)	1.00	DE -> C
CD (0.6)	C (0.7)	0.86	C -> D
DE (0.3)	E (0.4)	0.75	E -> D
BCD (0.4)	BC (0.5)	0.80	BC -> D
CDE (0.3)	CE (0.4)	0.75	CE -> D

我们已经见识过关联规则挖掘最著名的算法之一 Apriori。然而，尽管它即简单且受欢迎，但在实践中却很少使用。这是因为所研究方法的瓶颈在于，为评估候选者针对频繁形态的支持率，所需的遍历数据库的迭代次数。随着需分析的数据库数量的增长，这一问题变得越来越严重。该问题在下一算法中得到有效解决。它只需要对任何容量和任何数量的分析项的数据库进行迭代。

3. FP-成长算法

我们用一个寻找关联规则的最快算法的示例来研究上述问题的解决方案：FP-成长（频繁形态增长）。由于算法构造的特殊性，在其执行过程中，训练样本所有元素的彻底迭代仅执行 2 遍。除了这两遍次之外，该算法不调用训练样本。

与之前研究的关联规则挖掘算法类似，FP-成长可以有条件地化分为两个子问题：

寻找频繁出现的形态。在本示例中，此阶段称为 FP 树的构建。
判定规则。

该算法从消除随机项开始。为了做到这一点，与前面的算法一样，我们对整个训练集合执行第一遍，并计算每项的支持率。之后，删除频率小于 MinSup 的所有项。

其余项按其支持率的降序排列。上述示例产生以下序列：

D (0.8) -> C (0.7) -> B (0.6) -> E(0.4)

接下来，我们将拔高 FP 树。为此，针对训练样本执行第二次验算。在每笔业务中，我们只获取按支持率降序排列的频繁项，并在树中构建路径。因此，支持率最高的节点将位于树根处，而支持率最低的节点将为叶片。我们还为每个节点创建一个计数器。在第一遍迭代中，我们将计数器值设置为 1（或 1/N，其中 N 是训练样本的尺寸）。

FP 树的第一条路径

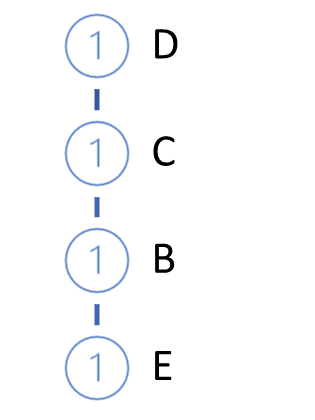
然后我们从数据库中获取下一笔业务。以同样的方式为其构建路径。加到我们的树中。为此，从树根开始，我们检查已有分支的路径。当从根重复路径时，我们只需增加现有节点的计数器。对于新部分，创建一个分支。

FP-树的第二条路径

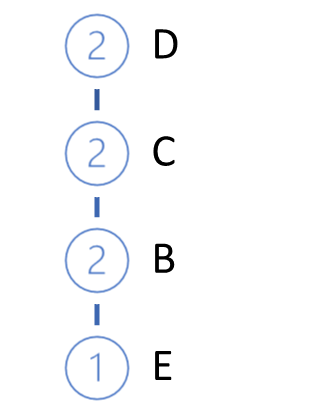
重复迭代循环，直到整个训练集的完全迭代。对于上述示例，我们将得到以下 FP-树。

FP-树

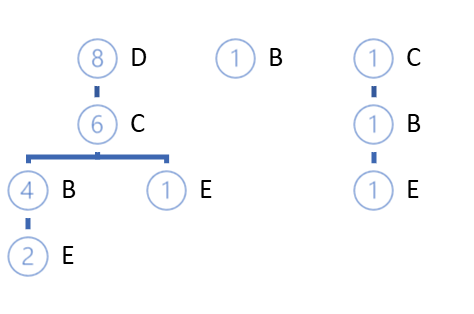
依据高概率，我们可以找到与根本身不同的路径。有两种可能的选择：

构造一片森林
创建一个特定根节点，来统一整个选择。

显然，在 FP-树成长过程开始时，大多数部分下将创建新节点。但在沿着训练样本移动的过程中，我们在不创建新分支的情况下增加现有节点的计数器。该算法的具体特点是，在构建树的过程中，我们可以将训练样本压缩到这样的尺寸，即我们可以在计算机的 RAM 中轻松操作，而无需访问数据库。

与规则定义相关的深入工作仅依据 FP-树执行，无需用到原始数据库。

所有项的规则均已考虑到，并按支持率升序排列。

在第一阶段，我们已经消除了频率低于指定频率的所有项，现在我们的树只包含频繁出现的项。此外，在构建树时，我们针对所有项按降序排序。这意味着支持率最低的项是树叶。

因此，为了判定从最低支持率项开始的规则，我们从叶行进到根。在此，我们可以追溯尚未明确的因果关系。该算法假设拥有较低支持率的项作为拥有更多支持率的特征组合的结果。

但是，我们返回到我们的规则定义算法。获取最低支持项，并判定 FP-树中指向该项的所有路径。在选择路径时，我们首先注意所需项的出现频率，它来自路径项形态成型时。路径选择准则是每项支持率与前一节点支持率的比值。比率不得小于规则的最小置信度。

在上面的示例中，最低支持率由 E 表示。在 FP-树中有三条路径通往它：DCBE（0.2），DCE（0.1），CBE（0.1）。所有路径均不满足最低支持率要求。其中两个不符合最低置信度要求。因此，我们无法依据 E 创建规则。注意，通过 Apriori 算法获得的结果证实了这一点。

从树中删除 E 叶片，并得到以下 FP-树视图。

删除 E 叶片后的 FP-树

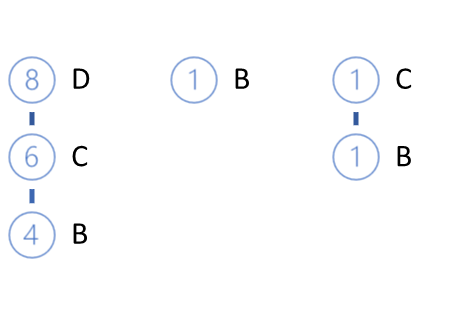
下一个要分析的元素是 B。它在这些叶片中的支持率最低。它有三条路径：DCB (0.4), B (0.1), CB (0.1)。

在选定的支持路径中，已分析项之前的每一项，都赋值为给定路径中已分析项的支持率。

基于选择的路径，我们形成一个参与项的列表，并确定每项的支持率。请注意，支持率被判定为所选路径中该项出现次数与原始训练数据集中记录总数的比率。因此，每项的新支持率不能超过初始项的支持率，或已分析项的支持率（正在判定规则的那个）。

同样，我们也删除了低于最小支持率的项。按支持率降序排列其余项。

在本示例中，我们有 C（0.5），D（0.4）。

请注意，由于我们仅用所选路径计算每项的支持率，因此结果可能与初始路径有很大不同。作为这个因素的结果，一些项可以被删除，它们在新的层次结构中的顺序也会改变。

进而，根据新的层次结构，我们采用选定的路径构建一个新的私有树。该树构造算法与 FP-树的构造没有区别。

构造的私有树的分支将是规则的前因，其后果将是我们所分析的项。

特征 B 的私有 FP-树

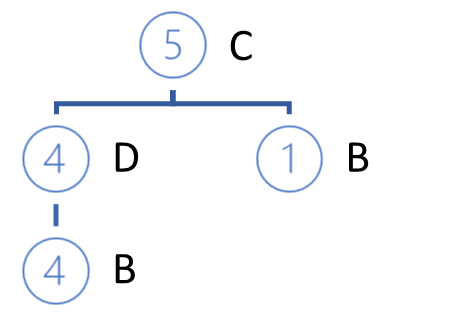
在构造私有树之后，我们从原始 FP-树中移除所分析项的节点。诀窍在于，我们所分析项的支持率最小。这意味着包含这些项的所有节点都是 FP-树的叶片。因此，移除它们不会影响其它项的路径（我们提到的因果关系稍微高一点）。

此外，通过逐渐删除已分析特征，我们逐渐缩减了FP 树。因此，我们减少了在其它项分析中进一步搜索的数据量。这会影响算法的整体性能。

类似地，我们为 FP 树的原始层次结构中的每一项构建规则。

注意，我们只能为 FP 树中至少有一个根节点的项构建规则。我们无法为根节点项创建规则，因为我们没有任何可参考的前因项。当然，除了潜在顾客去超市参观之外。如果顾客来到超市，他们会买些东西。这很可能是最畅销的商品之一。但这超出了所研究算法的范畴。

结束语

在本文中，我们研究了非监督学习方法解决的另一类问题：关联规则挖掘。我们讨论了两种关联规则挖掘算法：Apriori 和 FP-成长。但还有许多其它算法。不幸的是，我无法在一篇文章中涵盖整个主题。甚至，它只提供了理论方面的内容。在下一篇文章中，我们将研究利用 MQL5 实际构造关联规则挖掘算法。我们还将评估其应用于实际交易任务的绩效效率。