
データサイエンスと機械学習(第05回):決定木
決定木について
決定木は、教師付き機械学習の一種で、過去の質問に対する回答に基づいて分類や予測をおこなうために使用されます。モデルとは、教師あり学習の一種であり、目的の分類を含むデータセットに対してモデルの訓練とテストをおこなうことを意味します。
決定木は、必ずしも明確な答えや決定を与えるとは限りません。しかし、データサイエンティストが十分な情報を得た上で自ら決定できるように、選択肢を提示することはできます。決定木は人間の思考方法を模倣しているので、一般的にデータサイエンティストがその結果を理解し解釈するのは簡単です。

専門用語について
連載第1回で教師あり学習と教師なし学習の用語を説明するのを忘れたので、ここで説明します。
教師あり学習
教師あり学習は、人工知能(AI)を作るためのアプローチで、特定の出力に対してラベル付けされた入力データでコンピュータアルゴリズムを訓練します。モデルは、入力データと出力ラベルの間の基本的なパターンと関係を検出できるまで訓練され、初めて見るデータが提示されたときに正確な結果を出すことができるようになります。
教師あり学習とは異なり、このアプローチでは、アルゴリズムにはラベルのないデータが提示され、パターンや類似点を独自に検出するように設計されています。
教師あり学習プログラムでよく使われるアルゴリズムには、以下のようなものがあります。
教師あり学習と教師なし学習の主な違いは、アルゴリズムの学習方法です。教師なし学習では、アルゴリズムにラベルのないデータを学習セットとして与えます。教師あり学習とは異なり、正しい出力値があるわけではありません。アルゴリズムは、データを外部の測定値に関連付けるのではなく、データ内のパターンと類似性を判断します。つまり、アルゴリズムは自由に機能して、データについてさらに学習し、人間が探していなかった興味深いものや予期しないものを見つけることができます。
現在は教師あり学習について学んでいますが、今後数回に分けて教師なし学習について学びます。
決定木の仕組み
決定木は、複数のアルゴリズムを使用して、ノードを2つ以上のサブセットノードに分割することを決定します。サブノードを作成することで、結果的にサブノードの均質性を高めることができます。つまり、目的変数に関するノードの純度が上がっていると言えます。決定木アルゴリズムは、利用可能なすべての変数でノードを分割し、最も均質なサブノードになる分割を選択します。
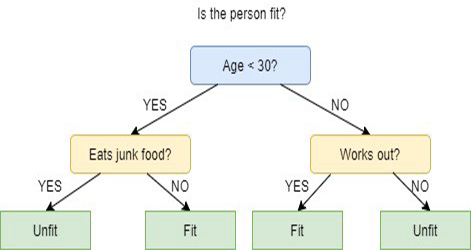
アルゴリズムの選択は、目的変数の種類に基づきます。
次は、決定木で使用されるアルゴリズムです。
- ID3 > D3の拡張
- C4.5 > ID3の後継
- CART > 分類と回帰木
- CHAID > カイ二乗自動相互作用検出、分類木を計算する際に多段階の分割を実行
- MARS > 多変量適応回帰スプライン
今回は、ID3アルゴリズムに基づいて決定木を作成します。他のアルゴリズムについては、本連載の次回の記事で説明し、使用する予定です。
決定木の目的
決定木アルゴリズムの主な目的は、不純なデータを純粋なノードまたは純粋に近いノードに分離することです。 例えば、りんごとみかんが混ざったかごがあるとします。りんごが色とサイズの観点からどのように見えるかについて訓練された決定木はみかんを独自のかごに分け、りんごも独自のバスケットに分けます。
ID3アルゴリズム
ID3はIterative Dichotomiser 3の略で、ステップごとに繰り返し特徴を2つ以上のグループに分けることから、このように呼ばれています。
Ross Quinlanによって考案されたID3は、トップダウンの貪欲なアプローチによって決定木を構築します。簡単に言うと、トップダウンの貪欲なアプローチは、上から順に木を構築していくことを意味し、貪欲なアプローチは、各反復において、現時点で最適な特徴を選択してノードを作成することを意味します。
一般にID3は、公称データ(基本的に測定できないデータ)の分類問題にのみ使用されます。
それはそれで、決定木には2つのタイプがあります。
- 分類木
- 回帰木
01:分類木
分類木は、この記事で学習する木と同じように、分類したい連続した数値または順序付けされた値を持たない特徴があります。
分類木は、物事をカテゴリに分類します。
02:回帰木
これらは、順序付けられた値と連続値で構築されています。
決定木は数値を予測します。
ID3アルゴリズムのステップ
01:元のデータセットを根ノードとして開始します。
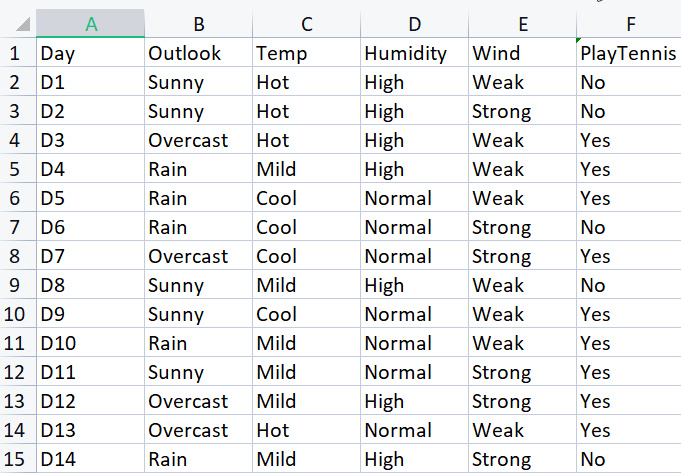
基本的なライブラリを構築するために、特定の気象条件でテニスをする単純なデータセットを使用します。これがデータセットの概要です。これは小さなデータセット (14 行のみ) です。
このアルゴリズムを使って決定木を描くには、すべての属性の中でどの属性の情報利得が最大であるかを理解する必要があります。説明します。.
そもそも、これらの属性(列)のうち1つは根ノードでなければならないのですが、どの列を根ノードにするかはどのように決めるのでしょうか。ここが情報利得の出番です。
情報利得
情報利得はエントロピーの減少を計算し、与えられた特徴がどの程度対象クラスを分離または分類しているかを測定します。情報利得が最大の特徴が最適なものとして選択されます。
![]()
エントロピー
エントロピーは確率変数の不確実性の尺度であり、与えられた試料中の不純物を特徴づけます。
エントロピーの計算式は
![]()
です。最初にやらなければならないことは、データセット全体のエントロピーを見つけることです。これらの列はすべて目的列PlayTennisに投影されるため、目的変数のエントロピーを見つけることを意味します。
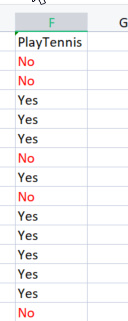
コードを書いてみましょう。
目的変数のエントロピーを見つける前に、Noとマークされた負の値とYesとマークされた正の値の総数が必要であることは確かです。これらの値は、列内の要素がそのような値を得る確率を取得するのに役立ちます。 Entropy関数内でそのようなことをおこなうコードを書きましょう。
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy; return(entropy_out); }
この関数は、特に数式を読んでいれば一目瞭然ですが、SampleNumbers[]配列に注目してください。標本は列の中身ですが、例えばこのTarget列の標本はYesとNOというように、標本をクラスと呼ぶこともできます。
TargetArray列に対してこの関数を実行すると、次のような結果が得られます。
12:37:48.394 TestScript There are 5 No 12:37:48.394 TestScript There are 9 Yes 12:37:48.394 TestScript There are 2 classes 12:37:48.394 TestScript "No" "Yes" 12:37:48.394 TestScript 5 9 12:37:48.394 TestScript Total contents = 14
これらの数値が得られたので、この式を使ってエントロピーを求めましょう。
![]()
この式に注目すると、ここで扱っている対数は底2の対数であることがわかります。これは、二進対数(詳しくはこちら)です。 底2の対数を求めるには、引数値の対数をlog2で徐算します。
double CDecisionTree::log2(double value) { return (log10(value)/log10(2)); }
定数が同じなので、問題ありません。
また、値のあるクラスの確率を求めるのに役立つ関数Proba()をコード化したので、紹介します。
double CDecisionTree::Proba(int number,double total) { return(number/total); }
誰でもわかると思います。列の要素の確率を見つけるには、その要素が何回出現したかを、その列のすべての要素の総数で割ります。5つの要素がNoであり、9つの要素がYesであることにお気付lきかと思います。
Noの確率 = 5/14(全要素数)=0.357142...
Yesの確率 = 9/14(全要素数)=0.6428571...
最後に、属性/データセット列のエントロピーを求めるには
for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy;
この関数を目的変数に対して実行すると、次のような出力が得られます。
13:37:54.273 TestScript Proba1 0.35714285714285715 13:37:54.273 TestScript Proba1 0.6428571428571429 13:37:54.273 TestScript Entropy of the entire dataset = 0.9402859586706309
BAM
これで、データセット全体のエントロピー、つまり基本的にはyの値のエントロピーがわかり、エントロピーを求める関数も手元に揃いました。データセットの各列のエントロピーを求めましょう。
データセット全体のエントロピーがわかったので、次のステップは、各独立変数列の中のメンバーのエントロピーを求めることです。独立変数のこのようなエントロピーを求める目的は、各データ列の情報利得を見つけるのに役立てるためです。
ライブラリを使ってOutlook列のエントロピーを求める前に、何がおこなわれているのかを明確に理解できるように、手計算で計算してみましょう。
その目的変数との比較でOutlook列をとります。
Outlook列 vs PlayTennis列
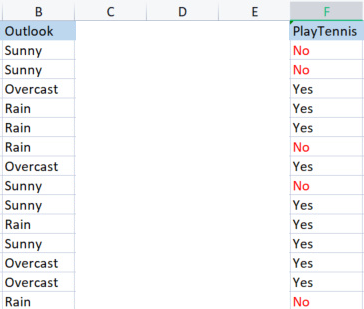
目的変数のエントロピーと呼ばれる全体のデータセットのエントロピーの求め方とは異なり、独立変数のエントロピーを求めるには、目的変数を参照する必要があります。それが私たちの目的だからです。
Outlookの値
Sunny、Overcast、Rainの3つの値があり、それぞれの値の目的変数に対するエントロピーを求めなければなりません。
Samples(Sunny)(Sunnyの正と負の標本)=[2:正(Yes)、3:負(No)]
正と負の数がわかったので、晴れた日にテニスをする確率は次のようになります。
確率1 = 2(Yesの出現回数)/5(晴天日数の総数)
(2/5 = 0.4)。
対照的に
晴れの日にテニスをしない確率は0.6となります(3/5 = 0.6)。
最後に、晴れた日にテニスをすることのエントロピーは、次の式で表されます。
Entropy(Sunny) = - (P1*log2P1 + P2*log2P2)
Entropy(Sunny) = -(0.4*log2 0.4 + 0.6*log2 0.6)
Entropy(Sunny) = 0.97095
次に、Overcastのエントロピーを求めます。
Overcastの標本
4:正(Target列がYes)、0:負(Target列がNo)。この状況は例外です。
ID3アルゴリズムにおける例外
正の標本があるが負の標本がゼロであったり、逆に負の標本があるが正の標本がゼロであったりする場合、エントロピーはゼロに束縛されることになります。
これは純粋なノードと言い、均質な標本を持っているので、分割する必要はありません。
次はもう1つの例外です。
正の標本と負の標本が同数である場合、数学的にはエントロピーは1になります。
このような例外を効果的に処理する必要があるのは、標本にゼロの値があるときだけです。ゼロはゼロ除算につながる可能性があるからです。
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { if (SampleNumbers[i] == 0) { Entropy = 0; break; } //Exception double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } if (Entropy==0) entropy_out = 0; //handle the exception else entropy_out = -Entropy; return(entropy_out); }
最後に、Rainのエントロピーを求めます。
Rainの標本
正の標本(Target列がYes)は3つあります。
負の標本(Target列がNo)は2つあります。
最後は、雨の日にテニスをするエントロピーです。
Entropy(Rain) = - (P1*log2P1 + P2*log2P2)
Entropy(Rain) = -(0.6*log2 0.6 + 0.4*log2 0.4)
Entropy(Rain) = 0.97095
Outlook列から取得したエントロピーの値は以下の通りです。
| Outlook列から取得したエントロピー |
|---|
| Entropy(Sunny) = 0.97095 |
| Entropy(Overcast) = 0 |
| Entropy(Rain) = 0.97095 |
このように、手動で標本のエントロピーを求めることができます。
PD 0 13:47:20.571 TestScript <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript << Sunny >> total > 5 MH 0 13:47:20.571 TestScript "No" "Yes" DM 0 13:47:20.571 TestScript 3 2 CQ 0 13:47:20.571 TestScript Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript << Overcast >> total > 4 OI 0 13:47:20.571 TestScript "No" "Yes" MJ 0 13:47:20.571 TestScript 0 4 CM 0 13:47:20.571 TestScript Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript << Rain >> total > 5 GN 0 13:47:20.571 TestScript "No" "Yes" JH 0 13:47:20.571 TestScript 2 3 HR 0 13:47:20.571 TestScript Entropy of Rain = 0.97095
これらの値を使って、前回説明した計算式でデータ全体のInformationgainを求めることにします。
![]()
では、密室で何が起こっているのかを理解していただくために、手動でエントロピーを求めます。
情報利得(IG) = データセット全体のエントロピー - 標本の確率とそのエントロピーの積の総和
IG = E(dataset) - ( Prob(sunny) * E(sunny) + Prob(Overcast)*E(Overcast) + Prob(Rain)*E(Rain) )
IG = 0.9402 - ( 5/14 * (0.97095) + 4/14 * (0) + 5/14(0.97095) )
IG = 0.2467(Outlook列の情報利得)
この数式をコードに変換すると、次のようになります。
double CDecisionTree::InformationGain(double parent_entropy, double &EntropyArr[], int &ClassNumbers[], int rows_) { double IG = 0; for (int i=0; i<ArraySize(EntropyArr); i++) { double prob = ClassNumbers[i]/double(rows_); IG += prob * EntropyArr[i]; } return(parent_entropy - IG); }
関数の呼び出し
if (m_debug) printf("<<<<<< Column Information Gain %.5f >>>>>> \n",IGArr[i]);
出力
PF 0 13:47:20.571 TestScript <<<<<< Column Information Gain 0.24675 >>>>>>
ここで、すべての列についてこの作業を繰り返し、その情報利得を求める必要があります。出力は次のようになります。
RH 0 13:47:20.571 TestScript (EURUSD,H1) Default Parent Entropy 0.9402859586706309 PD 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript (EURUSD,H1) << Sunny >> total > 5 MH 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DM 0 13:47:20.571 TestScript (EURUSD,H1) 3 2 CQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript (EURUSD,H1) << Overcast >> total > 4 OI 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" MJ 0 13:47:20.571 TestScript (EURUSD,H1) 0 4 CM 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript (EURUSD,H1) << Rain >> total > 5 GN 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" JH 0 13:47:20.571 TestScript (EURUSD,H1) 2 3 HR 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Rain = 0.97095 PF 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24675 >>>>>> QP 0 13:47:20.571 TestScript (EURUSD,H1) KH 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> PR 0 13:47:20.571 TestScript (EURUSD,H1) << Hot >> total > 4 QF 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OS 0 13:47:20.571 TestScript (EURUSD,H1) 2 2 NK 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Hot = 1.00000 GO 0 13:47:20.571 TestScript (EURUSD,H1) << Mild >> total > 6 OD 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" KQ 0 13:47:20.571 TestScript (EURUSD,H1) 2 4 GJ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Mild = 0.91830 HQ 0 13:47:20.571 TestScript (EURUSD,H1) << Cool >> total > 4 OJ 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OO 0 13:47:20.571 TestScript (EURUSD,H1) 1 3 IH 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Cool = 0.81128 OR 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.02922 >>>>>> ID 0 13:47:20.571 TestScript (EURUSD,H1) HL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> FH 0 13:47:20.571 TestScript (EURUSD,H1) << High >> total > 7 KM 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" HF 0 13:47:20.571 TestScript (EURUSD,H1) 4 3 GQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of High = 0.98523 QK 0 13:47:20.571 TestScript (EURUSD,H1) << Normal >> total > 7 GR 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DD 0 13:47:20.571 TestScript (EURUSD,H1) 1 6 OF 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Normal = 0.59167 EJ 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15184 >>>>>> EL 0 13:47:20.571 TestScript (EURUSD,H1) GE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> IQ 0 13:47:20.571 TestScript (EURUSD,H1) << Weak >> total > 8 GE 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" EO 0 13:47:20.571 TestScript (EURUSD,H1) 2 6 LI 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Weak = 0.81128 FS 0 13:47:20.571 TestScript (EURUSD,H1) << Strong >> total > 6 CK 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" ML 0 13:47:20.571 TestScript (EURUSD,H1) 3 3 HO 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Strong = 1.00000 LE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04813 >>>>>> IE 0 13:47:20.571 TestScript (EURUSD,H1)
すべての列の情報利得がわかったところで、決定木を描き始めることにします。
この最初のプロセスの目的は、すべての列の情報利得を見つけることで、どの列を根ノードにするかを決定することです。この場合、Outlookは最も高い情報利得を持っているので、決定木の根ノードになります。
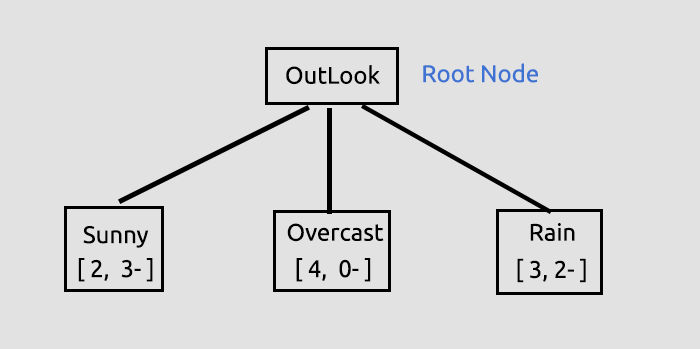
このOutlookに関する情報は、記事の最後にリンクされているテストスクリプトを実行すると、ライブラリのデフォルトであるデバッグモードで、多くの情報が出力されるライブラリによって提供されます。
情報利得は、その関数から取得し、すべての情報利得を格納する2値の配列に格納し、最終的に配列内の最大値を目標値とします。
//--- Finding the Information Gain ArrayResize(IGArr,i+1); //information gains matches the columns number IGArr[i] = InformationGain(P_EntropyArr[A],EntropyArr,ClassNumbers,rows); max_gain = ArrayMaximum(IGArr);出力は次のようになります。
QR 0 13:47:20.571 TestScript (EURUSD,H1) Parent Noce will be Outlook with IG = 0.24675 IK 0 13:47:20.574 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers NL 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Overcast" "Rain" NH 0 13:47:20.574 TestScript (EURUSD,H1) 0.9710 0.0000 0.9710 FR 0 13:47:20.574 TestScript (EURUSD,H1) 5 4 5
ここまで描いた「木」について、さらに詳しく解説します。
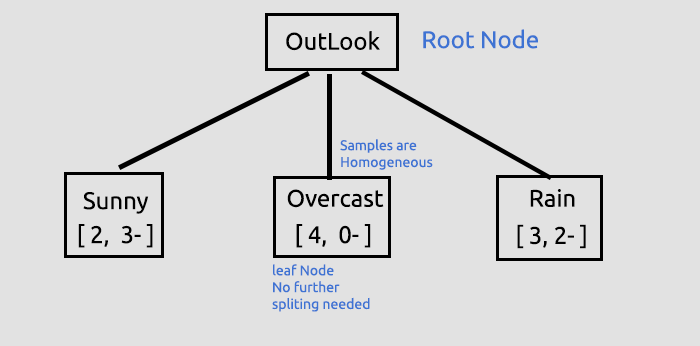
これは、根ノードを見つけ、その根ノードを枝と葉に分割する最初の、しかし重要なステップでした。分割するものがなくなるまで、データを分割し続けます。ここでは、Sunnyを持つ枝とRainを持つ枝を分割してプロセスを継続するつもりです。
Overcastは均質(純粋)なものから構成されているので、完全に分類されたと言い、決定木では「葉」と呼ぶことになります。枝は発生しません。
しかし、データをさらに分割する前に、現在のデータセットでおこなうべき重要な手順があります。
残りのデータセット行列の分類
残りのデータセット行列を分類して、同じ値を持つ行を昇順に並べる必要があります。これは、(私たちがぜひ実現したい)均質な内容を持つ枝や葉を作成するのに役立ちます。
void CDecisionTree::MatrixClassify(string &dataArr[],string &Classes[], int cols) { string ClassifiedArr[]; ArrayResize(ClassifiedArr,ArraySize(dataArr)); int fill_start = 0, fill_ends = 0; int index = 0; for (int i = 0; i<ArraySize(Classes); i++) { int start = 0; int curr_col = 0; for (int j = 0; j<ArraySize(dataArr); j++) { curr_col++; if (Classes[i] == dataArr[j]) { //printf("Classes[%d] = %s dataArr[%d] = %s ",i,Classes[i],j,dataArr[j]); if (curr_col == 1) fill_start = j; else { if (j>curr_col) fill_start = j - (curr_col-1); else fill_start = (curr_col-1) - j; fill_start = fill_start; //Print("j ",j," j-currcol ",j-(curr_col-1)," curr_col ",curr_col," columns ",cols," fill start ",fill_start ); } fill_ends = fill_start + cols; //printf("fillstart %d fillends %d j index = %d i = %d ",fill_start,fill_ends,j,i); //--- //if (ArraySize(ClassifiedArr) >= ArraySize(dataArr)) break; //Print("ArraySize Classified Arr ",ArraySize(ClassifiedArr)," dataArr size ",ArraySize(dataArr)," i ",i); for (int k=fill_start; k<fill_ends; k++) { index++; //printf(" k %d index %d",k,index); //printf("dataArr[%d] = %s index = %d",k,dataArr[k],index-1); ClassifiedArr[index-1] = dataArr[k]; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } if (curr_col == cols) curr_col = 0; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } ArrayCopy(dataArr,ClassifiedArr); ArrayFree(ClassifiedArr); }
なぜ多くのコードがコメントアウトされているのでしょうか。 ライブラリはまだ改良が必要で、コメントはデバッグのためのものです、使ってみていだけると幸いです。
この関数を呼び出して出力を表示すると、次のようになります。
JG 0 13:47:20.574 TestScript (EURUSD,H1) Classified matrix dataset KL 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " GS 0 13:47:20.574 TestScript (EURUSD,H1) [ QF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" JF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" ND 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" PN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" EH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "High" "Weak" "Yes" MH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Cool" "Normal" "Strong" "Yes" MN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Mild" "High" "Strong" "Yes" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "Normal" "Weak" "Yes" MG 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" QO 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" LN 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" LE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" FE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" GS 0 13:47:20.574 TestScript (EURUSD,H1) ] DH 0 13:47:20.574 TestScript (EURUSD,H1) columns = 5 rows = 70
その関数はまるで魔法のようです。
次の重要なステップです。
葉ノードをデータセットから削除する
この時点までにおこなったすべての処理の次の反復の前に、葉ノードを削除することが非常に重要です。なぜなら、葉ノードはいかなる分岐もおこなわないからです。
葉ノードの値を持つ行をすべて削除します。この場合、Overcastの行をすべて削除します。
//--- Search if there is zero entropy in the Array int zero_entropy_index = 0; bool zero_entropy = false; for (int e=0; e<ArraySize(P_EntropyArr); e++) if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array if (m_debug) { printf("%s is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is ..",p_Classes[zero_entropy_index]); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total); } //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]);
このブロックのコードを実行すると、出力は次のようになります。
NQ 0 13:47:20.574 TestScript (EURUSD,H1) Overcast is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. GP 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " KG 0 13:47:20.574 TestScript (EURUSD,H1) [ FS 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" EI 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" IP 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" KK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" JK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" FL 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" OI 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" IQ 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" LG 0 13:47:20.575 TestScript (EURUSD,H1) ] IL 0 13:47:20.575 TestScript (EURUSD,H1) columns = 5 rows = 50 HE 0 13:47:20.575 TestScript (EURUSD,H1) rows total 50 Rain 5
できました。
最後になりますが、この時点で次の重要なプロセスがあります。
データセットからの親または根ノード列の削除
すでに根ノードとして検出され、木に描画されているので、データセットにはもはや必要ありません。データセットは未分類の値のままでなければなりません。
//--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assign the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- printf("Column %d removed from the Matrix, The remaining dataset is",max_gain+1); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total);
このブロックのコードの出力は次のようになります。
OM 0 13:47:20.575 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is ON 0 13:47:20.575 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " HF 0 13:47:20.575 TestScript (EURUSD,H1) [ CR 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" JE 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" JR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" NG 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" JI 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" PR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JJ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" QQ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" OG 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" KD 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" DR 0 13:47:20.575 TestScript (EURUSD,H1) ]
できました。
今、私たちが自信を持ってデータセットの一部を残すことができた理由は、ライブラリがデータセットがどこに入るかの手がかりを残す木を描いているからです。
見栄えは悪いですが、実証の目的には十分です。連載の次の記事でHTMLを使用して作成してみます。これを実現するために、この GitHubリポジトリを以下にリンクします。ここでは木を作る残りのプロセスの説明を終わらせてください。 分割するものがなくなるまでこのプロセスを繰り返した後のログは次のとおりです。
HI 0 13:47:20.575 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers RK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Rain" CL 0 13:47:20.575 TestScript (EURUSD,H1) 0.9710 0.9710 CE 0 13:47:20.575 TestScript (EURUSD,H1) 5 5 EH 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.97095 A = 1 >>>>>>>> OF 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> RP 0 13:47:20.575 TestScript (EURUSD,H1) << Hot >> total > 2 MD 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" MQ 0 13:47:20.575 TestScript (EURUSD,H1) 2 0 QE 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 FQ 0 13:47:20.575 TestScript (EURUSD,H1) << Mild >> total > 5 KJ 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" NO 0 13:47:20.575 TestScript (EURUSD,H1) 2 3 DH 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 IS 0 13:47:20.575 TestScript (EURUSD,H1) << Cool >> total > 3 KH 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" LM 0 13:47:20.575 TestScript (EURUSD,H1) 1 2 FN 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 KD 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.20999 >>>>>> EF 0 13:47:20.575 TestScript (EURUSD,H1) DJ 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> HJ 0 13:47:20.575 TestScript (EURUSD,H1) << High >> total > 5 OS 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" FD 0 13:47:20.575 TestScript (EURUSD,H1) 4 1 NG 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of High = 0.72193 KM 0 13:47:20.575 TestScript (EURUSD,H1) << Normal >> total > 5 CP 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" JR 0 13:47:20.575 TestScript (EURUSD,H1) 1 4 MD 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Normal = 0.72193 EL 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24902 >>>>>> IN 0 13:47:20.575 TestScript (EURUSD,H1) CS 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> OS 0 13:47:20.575 TestScript (EURUSD,H1) << Weak >> total > 6 CK 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" GM 0 13:47:20.575 TestScript (EURUSD,H1) 2 4 OO 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 HE 0 13:47:20.575 TestScript (EURUSD,H1) << Strong >> total > 4 GI 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" OJ 0 13:47:20.575 TestScript (EURUSD,H1) 3 1 EM 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 PG 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.09546 >>>>>> EG 0 13:47:20.575 TestScript (EURUSD,H1) HK 0 13:47:20.575 TestScript (EURUSD,H1) Parent Noce will be Humidity with IG = 0.24902 OI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers JO 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" QJ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 QO 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 PJ 0 13:47:20.578 TestScript (EURUSD,H1) Classified matrix dataset NM 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " EF 0 13:47:20.578 TestScript (EURUSD,H1) [ FM 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" OD 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" GR 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" QG 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JD 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" KS 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" OJ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" CL 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" LJ 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" NH 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" ER 0 13:47:20.578 TestScript (EURUSD,H1) ] LI 0 13:47:20.578 TestScript (EURUSD,H1) columns = 4 rows = 40 CQ 0 13:47:20.578 TestScript (EURUSD,H1) rows total 36 High 5 GH 0 13:47:20.578 TestScript (EURUSD,H1) Column 2 removed from the Matrix, The remaining dataset is MP 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " QG 0 13:47:20.578 TestScript (EURUSD,H1) [ LL 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Weak" "No" OE 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Strong" "No" QQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "No" QE 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" LQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "No" HE 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" RM 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" PF 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" MR 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Strong" "No" IF 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" EN 0 13:47:20.578 TestScript (EURUSD,H1) ] ME 0 13:47:20.578 TestScript (EURUSD,H1) columns = 3 rows = 22 ER 0 13:47:20.578 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers HK 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" CQ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 OK 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 NS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.91830 A = 2 >>>>>>>> JM 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> CG 0 13:47:20.578 TestScript (EURUSD,H1) << Hot >> total > 2 DM 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" LF 0 13:47:20.578 TestScript (EURUSD,H1) 2 0 HN 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 OJ 0 13:47:20.578 TestScript (EURUSD,H1) << Mild >> total > 5 JS 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" GD 0 13:47:20.578 TestScript (EURUSD,H1) 2 3 QG 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 LL 0 13:47:20.578 TestScript (EURUSD,H1) << Cool >> total > 3 JQ 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" IR 0 13:47:20.578 TestScript (EURUSD,H1) 1 2 OE 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 RO 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15733 >>>>>> PO 0 13:47:20.578 TestScript (EURUSD,H1) JS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> JR 0 13:47:20.578 TestScript (EURUSD,H1) << Weak >> total > 6 NH 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JM 0 13:47:20.578 TestScript (EURUSD,H1) 2 4 JL 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 QD 0 13:47:20.578 TestScript (EURUSD,H1) << Strong >> total > 4 JN 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JK 0 13:47:20.578 TestScript (EURUSD,H1) 3 1 DM 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 JF 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04281 >>>>>> DG 0 13:47:20.578 TestScript (EURUSD,H1) LI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Noce will be Temp with IG = 0.15733 LH 0 13:47:20.584 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers GR 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Mild" "Cool" CD 0 13:47:20.584 TestScript (EURUSD,H1) 0.0000 0.9710 0.9183 GN 0 13:47:20.584 TestScript (EURUSD,H1) 2 5 3 CK 0 13:47:20.584 TestScript (EURUSD,H1) Classified matrix dataset RL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " NK 0 13:47:20.584 TestScript (EURUSD,H1) [ CQ 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Weak" "No" LI 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Strong" "No" JM 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" NI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" CL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" KI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" LR 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" KJ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" IQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" DE 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" NR 0 13:47:20.584 TestScript (EURUSD,H1) ] OI 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 30 OO 0 13:47:20.584 TestScript (EURUSD,H1) Hot is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. HL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " DJ 0 13:47:20.584 TestScript (EURUSD,H1) [ DL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" LH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" QL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" MH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" RQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" MI 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" KQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" FD 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" HQ 0 13:47:20.584 TestScript (EURUSD,H1) ] NN 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 24 IF 0 13:47:20.584 TestScript (EURUSD,H1) rows total 24 Mild 5 CO 0 13:47:20.584 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is DM 0 13:47:20.584 TestScript (EURUSD,H1) "Wind" "PlayTennis " PD 0 13:47:20.584 TestScript (EURUSD,H1) [ LN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "No" JI 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EL 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" GO 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "Yes" JG 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JE 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EP 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" HK 0 13:47:20.584 TestScript (EURUSD,H1) ] PP 0 13:47:20.584 TestScript (EURUSD,H1) columns = 2 rows = 10 HG 0 13:47:20.584 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers FQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Cool" OF 0 13:47:20.584 TestScript (EURUSD,H1) 0.9710 0.9183 IO 0 13:47:20.584 TestScript (EURUSD,H1) 5 3
次はBuildTree関数の概要です。このコードは、手動で値を計算するときは簡単に見えるにもかかわらず、読むのが難しく、わかりにくいので、このセクションで詳細に説明することにしました。
void CDecisionTree::BuildTree(void) { int ClassNumbers[]; int max_gain = 0; double IGArr[]; //double parent_entropy = Entropy(p_ClassNumbers,single_rowstotal); string p_Classes[]; //parent classes double P_EntropyArr[]; //Parent Entropy int p_ClassNumbers[]; //parent/ Target variable class numbers GetClasses(TargetArr,m_DatasetClasses,p_ClassNumbers); ArrayResize(P_EntropyArr,1); P_EntropyArr[0] = Entropy(p_ClassNumbers,single_rowstotal); //--- temporary disposable arrays for parent node information string TempP_Classes[]; double TempP_EntropyArr[]; int TempP_ClassNumbers[]; //--- if (m_debug) Print("Default Parent Entropy ",P_EntropyArr[0]); int cols = m_colschosen; for (int A =0; A<ArraySize(P_EntropyArr); A++) { printf("<<<<<<<< Parent Entropy %.5f A = %d >>>>>>>> ",P_EntropyArr[A],A); for (int i=0; i<cols-1; i++) //we substract with one to remove the independent variable coumn { int rows = ArraySize(m_dataset)/cols; string Arr[]; //ArrayFor the current column string ArrTarg[]; //Array for the current target ArrayResize(Arr,rows); ArrayResize(ArrTarg,rows); printf(" <<<<< C O L U M N %s >>>>> ",DataColumnNames[i]); int index_target=cols-1; for (int j=0; j<rows; j++) //get column data and its target column { int index = i+j * cols; //Print("index ",index); Arr[j] = m_dataset[index]; //printf("ArrTarg[%d] = %s m_dataset[%d] =%s ",j,ArrTarg[j],index_target,m_dataset[index_target]); ArrTarg[j] = m_dataset[index_target]; //printf("Arr[%d] = %s ArrTarg[%d] = %s ",j,Arr[j],j,ArrTarg[j]); index_target += cols; //the last index of all the columns } //--- Finding the Entropy //The function to find the Entropy of samples in a given column inside its loop //then restores all the entropy into one array //--- Finding the Information Gain //The Function to find the information gain from the entropy array above //--- if (i == max_gain) { //Get the maximum information gain of all the information gain in all columns then //store it to the parent information gain } //--- ZeroMemory(ClassNumbers); ZeroMemory(SamplesNumbers); } //---- Get the parent Entropy, class and class numbers // here we store the obtained parent class from the information gain metric then we store them into a parent array ArrayCopy(p_Classes,TempP_Classes); ArrayCopy(P_EntropyArr,TempP_EntropyArr); ArrayCopy(p_ClassNumbers,TempP_ClassNumbers); //--- string Node[1]; Node[0] = DataColumnNames[max_gain]; if (m_debug) printf("Parent Node will be %s with IG = %.5f",Node[0],IGArr[max_gain]); if (A == 0) DrawTree(Node,"parent",A); DrawTree(p_Classes,"child",A); //--- CLASSIFY THE MATRIX MatrixClassify(m_dataset,p_Classes,cols); //--- Search if there is zero entropy in Array if there is any remove its data from the dataset if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]); //--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assing the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- } }
結論
これで分類木に関わる基本的な計算を理解していただけたと思いますが、これは1回の記事でカバーするのが難しく長いトピックです。次の1、2回の記事で完了することを願っていますが、ライブラリには、関心のある取引の問題を解決するのに役立つ決定木アルゴリズムの構築を開始するために必要なものがほとんどすべて揃っています。 .
読んでいただいてありがとうございました。私のGitHubリポジトリはこちらにリンクされていますhttps://github.com/MegaJoctan/DecisionTree-Classification-tree-MQL5。
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/11061
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 ニューラルネットワークが簡単に(第18部):アソシエーションルール
ニューラルネットワークが簡単に(第18部):アソシエーションルール
 知っておくべきMQL5ウィザードのテクニック(第01回):回帰分析
知っておくべきMQL5ウィザードのテクニック(第01回):回帰分析
 一目均衡表による取引システムの設計方法を学ぶ
一目均衡表による取引システムの設計方法を学ぶ
 一からの取引エキスパートアドバイザーの開発(第21部):新規受注システム(IV)
一からの取引エキスパートアドバイザーの開発(第21部):新規受注システム(IV)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
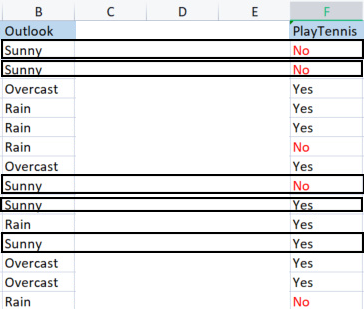
こんにちは、オメガさん、
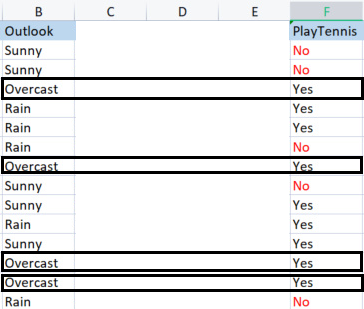
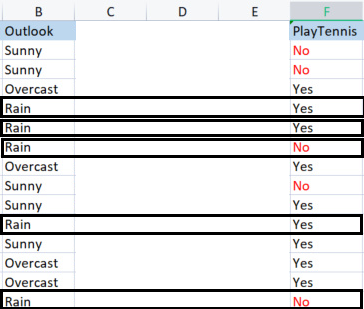
ID3ソリューション、ありがとうございます。しかし、私はこの点に関して、あなたの説明のために明確であると思うエクセルシートを提供し、添付しました。
ありがとうございました、
F.Mahmoudian
オメガさん、こんにちは、
ID3ソリューション、ありがとうございます。しかし、私はこの点に関して、あなたの説明のために明確であると思うエクセルシートを提供し、添付しました。
ありがとうございました、
F.Mahmoudian
スクリプトにツリーそのものを描画させる方法をまだ考えているところです。
many thanks to it, I'm still trying to figure out how to let the script draw the tree itself
本当にありがとう
ところで、そうだ、なぜみんなMOやAIやDeepLearningに夢中なのだろう?トピ主が思い出させてくれた、忘れ去られた古いものがある。エキスパートシステムとか、いろいろな重み付け評価がある。もちろん、その手法は30~50年前のもので、流行のものではないが、物理モデルと因果関係にこだわっており、その結果は解釈可能だ。私はそこを掘り下げなければならない。
すでに計算された信号のフィルターになる可能性があるのは、この方法だけだ。この方向の他の方法はダメだ。
ところで、そうだ、なぜみんなMOやAIやDeepLearningに夢中なのだろう?トピ主が思い出させてくれた、忘れ去られた古いものがある。エキスパートシステムとか、いろいろな重み付け評価がある。もちろん、その手法は30~50年前のもので、流行のものではないが、物理モデルと因果関係にこだわっており、その結果は解釈可能だ。もっと詳しく調べてみる必要がありそうだ。
すでに計算された信号のフィルターになる可能性があるのは、この方法だけだ。この方向の他の方法はめちゃくちゃだ。