
Veri Bilimi ve Makine Öğrenimi (Bölüm 05): Karar Ağaçları
Karar Ağacı Nedir?
Karar ağacı, önceki soruların nasıl yanıtlandığına bağlı olarak kategorizasyon yapmak veya öngörülerde bulunmak için kullanılan bir denetimli makine öğrenimi tekniğidir. Model, denetimli öğrenmenin bir biçimidir, yani, istenen sınıflandırmayı içeren veri kümesi üzerinde eğitilir ve test edilir.
Karar ağacı her zaman net yanıtlar veya kararlar sağlamayabilir. Bunun yerine seçenekler sunabilir ve veri bilimci bu seçeneklere dayanarak kendi bilinçli kararlarını verebilir. Karar ağaçları biz insanların düşünme şeklini taklit eder, bu sayede veri bilimcilerin sonuçları anlaması ve yorumlaması genellikle çok daha kolay olur.

Terminoloji uyarısı!
Bu serinin ilk makalesinde denetimli ve denetimsiz öğrenme terminolojilerini açıklamayı atlamışım. Şimdi onları burada açıklayalım.
Denetimli Öğrenme
Denetimli öğrenme, bilgisayar algoritmasının etiketlenmiş veriler üzerinde eğitildiği yapay zeka (Artificial Intelligence, AI) oluşturmaya yönelik bir yaklaşımdır. Model, girdi verileri ile etiketlenmiş veriler arasındaki kalıpları ve benzerlikleri algılayabilene kadar eğitilir. Böylece ona daha önce hiç görmediği veriler sunulduğunda doğru sonuçlar vermesi mümkün hale gelir.
Denetimli öğrenme programlarında yaygın olarak kullanılan algoritmalar şunlardır:
- Lineer regresyon
- Lojistik regresyon
- Karar ağaçları
- Destek vektör makineleri
- Rastgele ormanlar
Denetimli ve denetimsiz öğrenme arasındaki ana fark, algoritmanın nasıl öğrendiğidir. Denetimsiz öğrenmede, algoritmaya eğitim veri kümesi olarak etiketlenmemiş veriler sunulur ve kalıpları ve benzerlikleri kendi başına algılaması beklenir. Denetimli öğrenmeden farklı olarak, doğru çıktı değerleri yoktur. Algoritma, girdi verilerini harici etiketlerle ilişkilendirmek yerine, tüm kalıpları ve benzerlikleri arar. Başka bir deyişle, algoritmalar, veriler hakkında daha fazla bilgi edinmek ve bizim aramadığımız ilginç veya beklenmedik şeyleri bulmak için özgürce çalışabilir.
Bu makalede denetimli öğrenmeye odaklanacağız, denetimsiz öğrenmeyi ise sonraki makalelerde ele alacağız.
Karar Ağaçları Nasıl Çalışır?
Karar ağaçları, bir düğümü iki veya daha fazla alt düğüme bölmeye karar vermek amacıyla birden fazla algoritma kullanır. Alt düğümlerin oluşturulması, ortaya çıkan alt düğümlerin homojenliğini artırır. Yani düğümün homojenliğinin (saflığının) hedef değişkenle ilişkili olarak arttığını söyleyebiliriz. Karar ağacı algoritması, düğümleri tüm mevcut değişkenlere böler ve ardından en homojen alt düğümlerle sonuçlanan bölümü seçer.
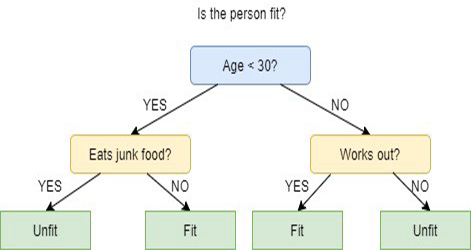
Algoritma seçimi, hedef değişkenlerin türüne bağlıdır.
Karar ağacında kullanılan algoritmalar şunlardır:
- ID3: Yinelemeli bölücü 3 (Iterative Dichotomiser 3, ID3), D3'ün devamıdır
- C4.5: ID3'ün devamıdır
- CART: Sınıflandırma ve regresyon ağacı (Classification And Regression Tree, CART)
- CHAID: Ki-kare otomatik etkileşim tespiti (CHi-square Automatic Interaction Detection, CHAID), karar ağacını hesaplarken çok seviyeli bölmeler gerçekleştirir
- MARS: Çok değişkenli uyarlanabilir regresyon splineları (Multivariate Adaptive Regression Splines, MARS)
Bu makalede ID3 algoritmasına dayalı bir karar ağacı oluşturacağız, diğer algoritmaları bu serinin sonraki makalelerinde tartışıp kullanacağız.
Karar Ağacının Amacı
Karar ağacı algoritmasının temel amacı, heterojen verilerden homojen veya homojene yakın verileri ayırmaktır. Örneğin elma ile portakalın karıştırıldığı bir sepet olsun. Karar ağacı, elmaların renk ve büyüklük bakımından nasıl göründükleri konusunda eğitildiğinde, elmaları kendi sepetine, portakalları da kendi sepetine ayıracaktır.
ID3 Algoritması
ID3 (Yinelemeli bölücü 3, Iterative Dichotomiser 3), özellikleri her adımda yinelemeli olarak iki veya daha fazla gruba bölen bir algoritmadır.
Ross Quinlan tarafından keşfedilen ID3, bir karar ağacı oluşturmak için yukarıdan aşağıya açgözlü (greedy) yaklaşımını kullanır. Yukarıdan aşağıya ifadesi ağacı yukarıdan oluşturmaya başladığı, açgözlü ifadesi de düğüm oluşturmak için her yinelemede o anki en iyi özelliği seçtiği anlamına gelir.
Genel olarak ID3, yalnızca nominal veriler (ölçülemeyen veriler) içeren sınıflandırma problemlerinde kullanılır.
İki tür karar ağacı vardır.
- Sınıflandırma ağaçları
- Regresyon ağaçları
1: Sınıflandırma ağaçları
Sınıflandırma ağaçları, bu makalede inceleyeceğimiz ağaca benzer şekilde, sınıflandırmak istediğimiz sürekli sayısal veya sıralı değerleri olmayan özelliklere sahiptir.
Sınıflandırma ağaçları kategorizasyon yapar.
2: Regresyon ağaçları
Bu ağaçlar sürekli ve sıralı değerlerle oluşturulur.
Burada karar ağacı sayısal değerleri öngörür.
ID3 Algoritmasında Adımlar
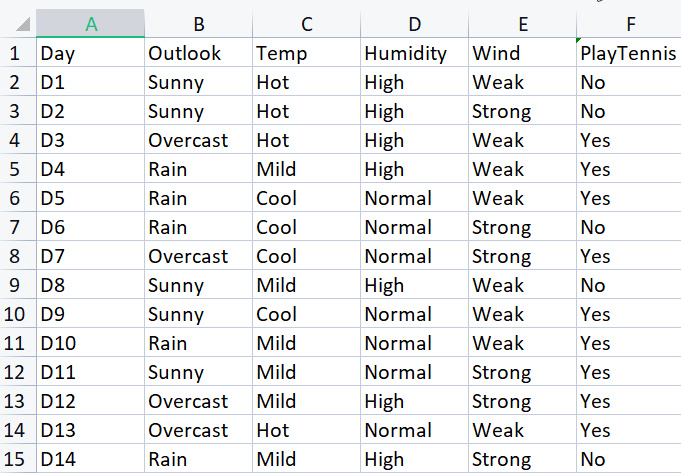
Temel kütüphaneyi oluşturmak adına, belirli hava koşullarında tenis oynamaya ilişkin basit bir veri kümesi kullanacağız. İşte küçük veri kümemiz (yalnızca 14 satır):
Bu algoritmayı kullanarak bir karar ağacı çizmek için, hangi özelliklerin tüm özellikler arasında en fazla bilgi kazancını sağladığını bilmemiz gerekir.
Başlamak için bu özelliklerden (sütunlar) biri kök düğüm olmalıdır. Ancak, hangi sütunun kök düğüm olacağına nasıl karar vereceğiz? İşte bilgi kazancını kullandığımız yer burasıdır.
Bilgi Kazancı
Bilgi kazancı, entropideki azalmayı hesaplar ve belirli bir özelliğin hedef sınıfları ne kadar iyi ayırdığını/sınıflandırdığını belirler. Bilgi kazancı en yüksek olan özellik en iyi olarak seçilir.
![]()
Entropi
Entropi, rastgele bir değişkenin belirsizliğinin ölçüsüdür, yani örneklemdeki heterojenliği karakterize eder.
Entropi formülü:
![]()
Yapmamız gereken ilk şey, tüm veri kümesinin entropisini bulmaktır, bu, tüm sütunlar PlayTennis hedef sütununa yansıdığı için hedef değişkenlerin entropisini bulmak anlamına gelir.
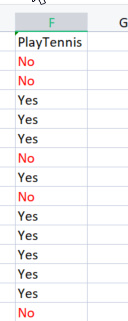
Şimdi biraz kod yazalım.
Hedef değişkenlerimizin entropisini bulmadan önce, No olarak işaretlenmiş olumsuz değerlerin ve Yes olarak işaretlenmiş olumlu değerlerin sayısını belirlemeliyiz. Bu değerler sütunumuzdaki öğelerin olasılıklarını elde etmemizi sağlayacaktır. Bu değerleri almak için entropi fonksiyonunda kod yazalım:
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy; return(entropy_out); }
Formülü incelediyseniz, fonksiyonu bir bakışta anlamak kolaydır. Ancak, SampleNumbers[] dizisine dikkat edin. Bu dizideki öğe sayısı sütununun içindeki ilgili öğe sayısıdır. Öğelerin çeşitliliği için de sınıf ifadesini kullanabiliriz. Örneğin, hedef sütunumuzdaki sınıf sayımız 2’dir: Yes ve No.
Fonksiyonu hedef değişken sütunumuzda çalıştırırsak aşağıdaki sonucu elde ederiz:
12:37:48.394 TestScript There are 5 No 12:37:48.394 TestScript There are 9 Yes 12:37:48.394 TestScript There are 2 classes 12:37:48.394 TestScript "No" "Yes" 12:37:48.394 TestScript 5 9 12:37:48.394 TestScript Total contents = 14
Artık bu sayılara sahip olduğumuza göre, formülümüzü kullanarak entropiyi bulmaya devam edebiliriz.
![]()
Formüle yakından bakarsanız, ele aldığımız logaritmanın 2 tabanlı logaritma olduğunu fark edeceksiniz. 2 tabanlı logaritmayı 10 tabanlı ifadeyle bulmak için: logaritmasını almak istediğimiz sayının 10 tabanlı logaritmasını 2’nin 10 tabanlı logaritmasına böleriz.
double CDecisionTree::log2(double value) { return (log10(value)/log10(2)); }
Değer sınıflarının olasılıklarını elde etmemizi sağlayacak Proba() fonksiyonunu da kodladım, işte burada:
double CDecisionTree::Proba(int number,double total) { return(number/total); }
Şu detay önemlidir. Sütunundaki bir öğenin olasılığını bulmak için, o öğenin sütunda kaç kez göründüğünü belirler ve sütundaki tüm öğelerin toplam sayısına böleriz. No değerine sahip 5 öğe ve Yes değerine sahip 9 öğe olduğunu fark etmişsinizdir, böylece:
No olasılığı = 5/14 = 0.357142...
Yes olasılığı = 9/14 = 0,642857...
Son olarak, özellik / veri kümesi sütununun entropisini bulmak için:
for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy;
Fonksiyonu hedef değişken sütunumuzda çalıştırırsak şu çıktıyı elde ederiz:
13:37:54.273 TestScript Proba1 0.35714285714285715 13:37:54.273 TestScript Proba1 0.6428571428571429 13:37:54.273 TestScript Entropy of the entire dataset = 0.9402859586706309
Ta-da!
Artık, esas olarak y değerlerinin entropisi olan tüm veri kümesinin entropisini biliyoruz ve entropiyi bulma fonksiyonuna da sahibiz. Şimdi veri kümesindeki her bir sütunun entropisini bulalım.
Artık tüm veri kümesinin entropisine sahibiz. Bir sonraki adım, her bir bağımsız değişken sütunundaki öğelerin entropisini bulmaktır. Bağımsız değişkenlerde entropiyi bulmanın amacı, her bir veri sütunu için bilgi kazancını hesaplamaktır.
Outlook sütununun entropisini bulmak için kütüphanemizi kullanmadan önce, nelerin yapıldığının net bir şekilde anlaşılabilmesi adına onu manuel olarak hesaplayalım.
Outlook sütunundaki her bir öğeyi ilgili hedef değişkeniyle karşılaştırıyoruz.
Outlook ile PlayTennis sütununu karşılaştırma
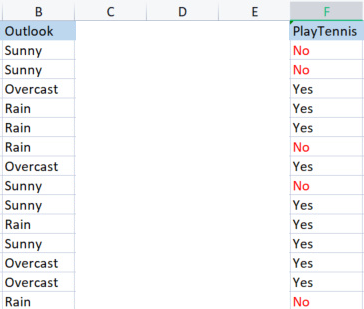
Hedef değişkenin entropisi olarak da adlandırılan tüm veri kümesinin entropisini nasıl bulduğumuzdan farklı olarak, bağımsız değişkenin entropisini bulmak için onu hedef değişkenle ilişkilendirmeliyiz, çünkü hedefimiz orasıdır.
Outlook sütunundaki değerler
Sunny(güneşli), Overcast(bulutlu) ve Rain(yağmurlu) olmak üzere 3 farklı değerimiz vardır. Bu değerlerin her birinin hedef değişkenine dayalı olarak entropisini bulmamız gerekiyor.
Sunny: 2 Yes, 3 No.
Sunny için olumlu ve olumsuz değerlerin sayısına sahip olduğumuza göre, güneşli bir günde tenis oynama için Yes olasılığı şu şekilde olacaktır:
p 1 = 2 (Sunny için Yes sayısı) / 5 (toplam Sunny sayısı)
Böylece, 2/5=0.4
Olumsuz durumda,
3/5=0.6. Yani, güneşli bir günde tenis oynamama olasılığı 0.6 olacaktır.
Son olarak, güneşli bir günde tenis oynamanın entropisini bulalım (formüle göz atın):
Sunny’nin entropisi = -(p1*log2p1 + p2*log2p2)
Sunny’nin entropisi = -(0.4*log20.4 + 0.6*log20.6)
Sunny’nin entropisi = 0.97095
Şimdi Overcast’in entropisini bulalım.
Overcast: 4 Yes, 0 No. Böyle bir durum istisnadır.
ID3 Algoritmasındaki İstisnalar
Olumlu değerler varken 0 olumsuz değer olduğunda veya tam tersi şekilde, olumsuz değerler varken 0 olumlu değer olduğunda, entropi 0 olur.
Bu düğüm saf bir düğümdür. Halihazırda homojen değerlere sahip olduğu için onu daha fazla bölmeye gerek yoktur. Bununla ne demek istediğimi karar ağacını çizerken daha iyi anlayacaksınız.
Diğer bir istisna ise:
Eşit sayıda olumlu ve olumsuz değer olduğunda, matematiksel olarak entropi 1 olur.
Etkin bir şekilde ilgilenmemiz gereken tek istisna, 0 değer olduğu zamandır çünkü bu, sıfıra bölme hatasına yol açabilir. İşte bu tür istisnaları işleme yeteneğine sahip yeni fonksiyon:
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { if (SampleNumbers[i] == 0) { Entropy = 0; break; } //Exception double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } if (Entropy==0) entropy_out = 0; //handle the exception else entropy_out = -Entropy; return(entropy_out); }
Ve son olarak, Rain’in entropisini bulalım.
Rain:
3 Yes,
2 No.
Yağmurlu bir günde tenis oynamanın entropisi:
Rain’in entropisi = -(p1*log2p1 + p2*log2p2)
Rain’in entropisi = -(0,6*log20,6 + 0,4*log20.4)
Rain’in entropisi = 0.97095
İşte Outlook sütunundan elde ettiğimiz entropi değerleri:
| Outlook sütunundan entropi değerleri |
|---|
| Sunny’nin entropisi = 0.97095 |
| Overcast’in entropisi = 0 |
| Rain’in entropisi = 0.97095 |
Böylece Outlook sütunundaki 3 sınıfın entropilerini manuel olarak hesapladık. Programımızı bu entropileri bulmak için çalıştırırsak, sonuç şu şekilde olacaktır:
PD 0 13:47:20.571 TestScript <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript << Sunny >> total > 5 MH 0 13:47:20.571 TestScript "No" "Yes" DM 0 13:47:20.571 TestScript 3 2 CQ 0 13:47:20.571 TestScript Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript << Overcast >> total > 4 OI 0 13:47:20.571 TestScript "No" "Yes" MJ 0 13:47:20.571 TestScript 0 4 CM 0 13:47:20.571 TestScript Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript << Rain >> total > 5 GN 0 13:47:20.571 TestScript "No" "Yes" JH 0 13:47:20.571 TestScript 2 3 HR 0 13:47:20.571 TestScript Entropy of Rain = 0.97095
Daha önce bahsettiğimiz formülü kullanarak tüm verilerin bilgi kazancını bulmak için bu değerleri kullanacağız.
![]()
Şimdi, kapalı kapılar ardında neler olup bittiğinin daha iyi anlaşılması adına bilgi kazancını manuel olarak bulalım.
Bilgi kazancı (Information Gain, IG) = Tüm veri kümesinin entropisi - Sınıfların olasılığıyla entropisinin çarpımlarının toplamı.
IG = E(dataset) - (Prob(Sunny)*E(Sunny) + Prob(Overcast)*E(Overcast) + Prob(Rain)*E(Rain))
IG = 0.9402 - (5/14*0.97095 + 4/14*0 + 5/14*0.97095)
IG = 0.2467 (Bu, Outlook sütununun bilgi kazancıdır)
Formülü koda dönüştürdüğümüzde:
double CDecisionTree::InformationGain(double parent_entropy, double &EntropyArr[], int &ClassNumbers[], int rows_) { double IG = 0; for (int i=0; i<ArraySize(EntropyArr); i++) { double prob = ClassNumbers[i]/double(rows_); IG += prob * EntropyArr[i]; } return(parent_entropy - IG); }
Fonksiyonu çağıralım:
if (m_debug) printf("<<<<<< Column Information Gain %.5f >>>>>> \n",IGArr[i]);
Çıktı:
PF 0 13:47:20.571 TestScript <<<<<< Column Information Gain 0.24675 >>>>>>
Şimdi yaptığımız işlemleri tüm sütunlar için tekrarlamamız ve bilgi kazançlarını bulmamız gerekiyor. Çıktı şu şekilde olacaktır:
RH 0 13:47:20.571 TestScript (EURUSD,H1) Default Parent Entropy 0.9402859586706309 PD 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript (EURUSD,H1) << Sunny >> total > 5 MH 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DM 0 13:47:20.571 TestScript (EURUSD,H1) 3 2 CQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript (EURUSD,H1) << Overcast >> total > 4 OI 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" MJ 0 13:47:20.571 TestScript (EURUSD,H1) 0 4 CM 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript (EURUSD,H1) << Rain >> total > 5 GN 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" JH 0 13:47:20.571 TestScript (EURUSD,H1) 2 3 HR 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Rain = 0.97095 PF 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24675 >>>>>> QP 0 13:47:20.571 TestScript (EURUSD,H1) KH 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> PR 0 13:47:20.571 TestScript (EURUSD,H1) << Hot >> total > 4 QF 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OS 0 13:47:20.571 TestScript (EURUSD,H1) 2 2 NK 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Hot = 1.00000 GO 0 13:47:20.571 TestScript (EURUSD,H1) << Mild >> total > 6 OD 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" KQ 0 13:47:20.571 TestScript (EURUSD,H1) 2 4 GJ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Mild = 0.91830 HQ 0 13:47:20.571 TestScript (EURUSD,H1) << Cool >> total > 4 OJ 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OO 0 13:47:20.571 TestScript (EURUSD,H1) 1 3 IH 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Cool = 0.81128 OR 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.02922 >>>>>> ID 0 13:47:20.571 TestScript (EURUSD,H1) HL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> FH 0 13:47:20.571 TestScript (EURUSD,H1) << High >> total > 7 KM 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" HF 0 13:47:20.571 TestScript (EURUSD,H1) 4 3 GQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of High = 0.98523 QK 0 13:47:20.571 TestScript (EURUSD,H1) << Normal >> total > 7 GR 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DD 0 13:47:20.571 TestScript (EURUSD,H1) 1 6 OF 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Normal = 0.59167 EJ 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15184 >>>>>> EL 0 13:47:20.571 TestScript (EURUSD,H1) GE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> IQ 0 13:47:20.571 TestScript (EURUSD,H1) << Weak >> total > 8 GE 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" EO 0 13:47:20.571 TestScript (EURUSD,H1) 2 6 LI 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Weak = 0.81128 FS 0 13:47:20.571 TestScript (EURUSD,H1) << Strong >> total > 6 CK 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" ML 0 13:47:20.571 TestScript (EURUSD,H1) 3 3 HO 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Strong = 1.00000 LE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04813 >>>>>> IE 0 13:47:20.571 TestScript (EURUSD,H1)
Tüm sütunlar için bilgi kazançlarına sahip olduğumuza göre, artık karar ağacımızı çizmeye başlayabiliriz. Ama nasıl?
Az önce gerçekleştirdiğimiz bilgi kazançlarını bulma sürecinin amacı, hangi sütunun kök düğüm olacağına karar vermekti. Diğerlerinden daha fazla bilgi kazancına sahip olan sütun, kök düğüm olacaktır. Bizim durumumuzda, Outlook en yüksek bilgi kazancına sahiptir, dolayısıyla karar ağacımızın kök düğümü o olacaktır. Şimdi ağacımızı çizelim.
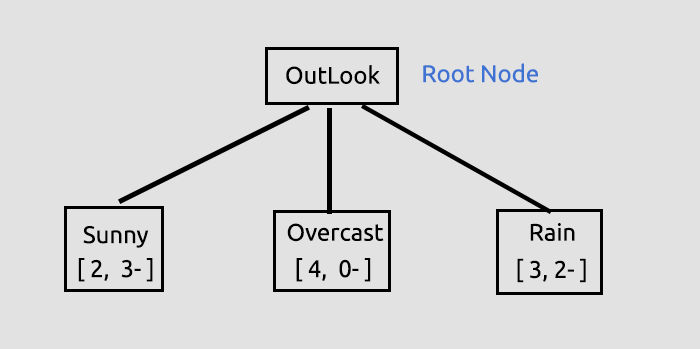
Outlook ile ilgili bu bilgiler, test komut dosyası çalıştırıldığında kütüphane tarafından sağlanır. Test komut dosyası makalenin sonuna eklenmiştir. Kütüphanenin varsayılan olan hata ayıklama modunda birçok bilgi yazdırılır.
Bilgi kazançlarını elde ettik. Ardından, tüm bilgi kazançlarını double türünde dizide depoladık. Sonrasında da dizideki maksimum değeri kök düğümümüz olarak kabul ettik.
//--- Finding the Information Gain ArrayResize(IGArr,i+1); //information gains matches the columns number IGArr[i] = InformationGain(P_EntropyArr[A],EntropyArr,ClassNumbers,rows); max_gain = ArrayMaximum(IGArr);Çıktı şu şekildedir:
QR 0 13:47:20.571 TestScript (EURUSD,H1) Parent Noce will be Outlook with IG = 0.24675 IK 0 13:47:20.574 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers NL 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Overcast" "Rain" NH 0 13:47:20.574 TestScript (EURUSD,H1) 0.9710 0.0000 0.9710 FR 0 13:47:20.574 TestScript (EURUSD,H1) 5 4 5
Çizdiğimiz ağaca ilişkin ayrıntı:
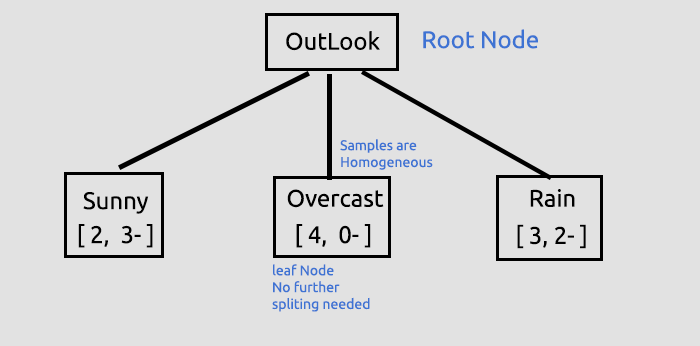
Bu, kök düğümü bulduğumuz ve onu dallara ve yapraklara böldüğümüz ilk ama çok önemli adımdı. Bölünecek hiç bir şey kalmayıncaya kadar verileri bölmeye devam edeceğiz. Karar ağacımızda Sunny ve Rain dallarını bölerek ilerleyeceğiz.
Overcast, homojendir (saftır), bu nedenle ona tamamen sınıflandırılmış diyoruz. Karar ağacında ise böyle bir düğüm için yaprak ifadesini kullanıyoruz. Çünkü bu düğüm artık dallara bölünemez.
Ancak verileri bölmeye devam etmeden önce, elimizdeki mevcut veri kümesiyle yapmamız gereken birkaç önemli adım var.
Kalan veri kümesi matrisini sınıflandırma
Aynı öğelere sahip satırları artan sırada düzenlemek amacıyla kalan veri kümesi matrisini sınıflandırmalıyız. Bu, homojen içerikli dallar ve yapraklar oluşturmakta bize yardımcı olacaktır (ki elde etmeye çalıştığımız şey de budur).
void CDecisionTree::MatrixClassify(string &dataArr[],string &Classes[], int cols) { string ClassifiedArr[]; ArrayResize(ClassifiedArr,ArraySize(dataArr)); int fill_start = 0, fill_ends = 0; int index = 0; for (int i = 0; i<ArraySize(Classes); i++) { int start = 0; int curr_col = 0; for (int j = 0; j<ArraySize(dataArr); j++) { curr_col++; if (Classes[i] == dataArr[j]) { //printf("Classes[%d] = %s dataArr[%d] = %s ",i,Classes[i],j,dataArr[j]); if (curr_col == 1) fill_start = j; else { if (j>curr_col) fill_start = j - (curr_col-1); else fill_start = (curr_col-1) - j; fill_start = fill_start; //Print("j ",j," j-currcol ",j-(curr_col-1)," curr_col ",curr_col," columns ",cols," fill start ",fill_start ); } fill_ends = fill_start + cols; //printf("fillstart %d fillends %d j index = %d i = %d ",fill_start,fill_ends,j,i); //--- //if (ArraySize(ClassifiedArr) >= ArraySize(dataArr)) break; //Print("ArraySize Classified Arr ",ArraySize(ClassifiedArr)," dataArr size ",ArraySize(dataArr)," i ",i); for (int k=fill_start; k<fill_ends; k++) { index++; //printf(" k %d index %d",k,index); //printf("dataArr[%d] = %s index = %d",k,dataArr[k],index-1); ClassifiedArr[index-1] = dataArr[k]; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } if (curr_col == cols) curr_col = 0; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } ArrayCopy(dataArr,ClassifiedArr); ArrayFree(ClassifiedArr); }
Neden çok sayıda kod yorum olarak bırakıldı? Kütüphanemizin hala iyileştirmelere ihtiyacı vardır ve bu yorumlar hata ayıklamak için elzemdir. Umarım onlar üzerinde çalışarak kütüphanede ileri iyileştirmeler yaparsınız.
Fonksiyonu çağırdığımızda şu çıktıyı elde ediyoruz:
JG 0 13:47:20.574 TestScript (EURUSD,H1) Classified matrix dataset KL 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " GS 0 13:47:20.574 TestScript (EURUSD,H1) [ QF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" JF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" ND 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" PN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" EH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "High" "Weak" "Yes" MH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Cool" "Normal" "Strong" "Yes" MN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Mild" "High" "Strong" "Yes" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "Normal" "Weak" "Yes" MG 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" QO 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" LN 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" LE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" FE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" GS 0 13:47:20.574 TestScript (EURUSD,H1) ] DH 0 13:47:20.574 TestScript (EURUSD,H1) columns = 5 rows = 70
Ta-da! Fonksiyon sihir gibi çalışıyor.
Şimdi bir sonraki önemli adıma geçelim.
Veri kümesinden yaprak düğümleri kaldırma
Bu noktaya kadar yaptığımız tüm işlemlerin bir sonraki yinelemesinden önce, herhangi bir dal oluşturmayacakları için yaprak düğümleri kaldıracağız. Mantıklı, değil mi?
Yaprak düğümündeki tüm satırları kaldırıyoruz. Bizim durumumuzda, Overcast’in tüm satırlarını kaldırıyoruz.
//--- Search if there is zero entropy in the Array int zero_entropy_index = 0; bool zero_entropy = false; for (int e=0; e<ArraySize(P_EntropyArr); e++) if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array if (m_debug) { printf("%s is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is ..",p_Classes[zero_entropy_index]); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total); } //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]);
Bu kod bloğunun çıktısı şu şekilde olacaktır:
NQ 0 13:47:20.574 TestScript (EURUSD,H1) Overcast is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. GP 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " KG 0 13:47:20.574 TestScript (EURUSD,H1) [ FS 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" EI 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" IP 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" KK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" JK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" FL 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" OI 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" IQ 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" LG 0 13:47:20.575 TestScript (EURUSD,H1) ] IL 0 13:47:20.575 TestScript (EURUSD,H1) columns = 5 rows = 50 HE 0 13:47:20.575 TestScript (EURUSD,H1) rows total 50 Rain 5
Ta-da!
Son önemli adım:
Kök düğüm sütununu veri kümesinden kaldırma
Onu halihazırda kök düğüm olarak tanımlayıp ağacımıza çizdiğimiz için, artık ona veri kümemizde ihtiyacımız yoktur. Veri kümemizde sadece sınıflandırılmamış öğeler kalmalıdır.
//--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assign the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- printf("Column %d removed from the Matrix, The remaining dataset is",max_gain+1); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total);
Bu kod bloğunun çıktısı da aşağıdadır:
OM 0 13:47:20.575 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is ON 0 13:47:20.575 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " HF 0 13:47:20.575 TestScript (EURUSD,H1) [ CR 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" JE 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" JR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" NG 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" JI 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" PR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JJ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" QQ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" OG 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" KD 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" DR 0 13:47:20.575 TestScript (EURUSD,H1) ]
Ta-da!
Veri kümesinin belirli kısımlarını bu kadar güvenle çıkartabilmemizin nedeni, kütüphanenin veri kümesinde neler olduğuna dair bize ipuçları bırakan bir ağaç çizmesidir:
Çirkin görünüyor, ancak anlaşılması açısından yeterli. Sonraki makalelerde onu HTML ile oluşturmayı deneyeceğiz. Bu konuda bana yardımcı olun - GitHub depomun linkini aşağıya ekledim. Şimdi başladığımız işi bitirelim ve karar ağacı oluşturma sürecinin kalan kısmına bakalım. Bölünecek hiç bir şey kalmayıncaya kadar işlemi yinelediğimizde günlüğe kaydedilecek olan çıktı şudur:
HI 0 13:47:20.575 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers RK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Rain" CL 0 13:47:20.575 TestScript (EURUSD,H1) 0.9710 0.9710 CE 0 13:47:20.575 TestScript (EURUSD,H1) 5 5 EH 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.97095 A = 1 >>>>>>>> OF 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> RP 0 13:47:20.575 TestScript (EURUSD,H1) << Hot >> total > 2 MD 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" MQ 0 13:47:20.575 TestScript (EURUSD,H1) 2 0 QE 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 FQ 0 13:47:20.575 TestScript (EURUSD,H1) << Mild >> total > 5 KJ 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" NO 0 13:47:20.575 TestScript (EURUSD,H1) 2 3 DH 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 IS 0 13:47:20.575 TestScript (EURUSD,H1) << Cool >> total > 3 KH 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" LM 0 13:47:20.575 TestScript (EURUSD,H1) 1 2 FN 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 KD 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.20999 >>>>>> EF 0 13:47:20.575 TestScript (EURUSD,H1) DJ 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> HJ 0 13:47:20.575 TestScript (EURUSD,H1) << High >> total > 5 OS 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" FD 0 13:47:20.575 TestScript (EURUSD,H1) 4 1 NG 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of High = 0.72193 KM 0 13:47:20.575 TestScript (EURUSD,H1) << Normal >> total > 5 CP 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" JR 0 13:47:20.575 TestScript (EURUSD,H1) 1 4 MD 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Normal = 0.72193 EL 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24902 >>>>>> IN 0 13:47:20.575 TestScript (EURUSD,H1) CS 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> OS 0 13:47:20.575 TestScript (EURUSD,H1) << Weak >> total > 6 CK 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" GM 0 13:47:20.575 TestScript (EURUSD,H1) 2 4 OO 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 HE 0 13:47:20.575 TestScript (EURUSD,H1) << Strong >> total > 4 GI 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" OJ 0 13:47:20.575 TestScript (EURUSD,H1) 3 1 EM 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 PG 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.09546 >>>>>> EG 0 13:47:20.575 TestScript (EURUSD,H1) HK 0 13:47:20.575 TestScript (EURUSD,H1) Parent Noce will be Humidity with IG = 0.24902 OI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers JO 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" QJ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 QO 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 PJ 0 13:47:20.578 TestScript (EURUSD,H1) Classified matrix dataset NM 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " EF 0 13:47:20.578 TestScript (EURUSD,H1) [ FM 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" OD 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" GR 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" QG 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JD 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" KS 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" OJ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" CL 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" LJ 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" NH 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" ER 0 13:47:20.578 TestScript (EURUSD,H1) ] LI 0 13:47:20.578 TestScript (EURUSD,H1) columns = 4 rows = 40 CQ 0 13:47:20.578 TestScript (EURUSD,H1) rows total 36 High 5 GH 0 13:47:20.578 TestScript (EURUSD,H1) Column 2 removed from the Matrix, The remaining dataset is MP 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " QG 0 13:47:20.578 TestScript (EURUSD,H1) [ LL 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Weak" "No" OE 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Strong" "No" QQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "No" QE 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" LQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "No" HE 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" RM 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" PF 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" MR 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Strong" "No" IF 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" EN 0 13:47:20.578 TestScript (EURUSD,H1) ] ME 0 13:47:20.578 TestScript (EURUSD,H1) columns = 3 rows = 22 ER 0 13:47:20.578 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers HK 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" CQ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 OK 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 NS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.91830 A = 2 >>>>>>>> JM 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> CG 0 13:47:20.578 TestScript (EURUSD,H1) << Hot >> total > 2 DM 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" LF 0 13:47:20.578 TestScript (EURUSD,H1) 2 0 HN 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 OJ 0 13:47:20.578 TestScript (EURUSD,H1) << Mild >> total > 5 JS 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" GD 0 13:47:20.578 TestScript (EURUSD,H1) 2 3 QG 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 LL 0 13:47:20.578 TestScript (EURUSD,H1) << Cool >> total > 3 JQ 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" IR 0 13:47:20.578 TestScript (EURUSD,H1) 1 2 OE 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 RO 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15733 >>>>>> PO 0 13:47:20.578 TestScript (EURUSD,H1) JS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> JR 0 13:47:20.578 TestScript (EURUSD,H1) << Weak >> total > 6 NH 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JM 0 13:47:20.578 TestScript (EURUSD,H1) 2 4 JL 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 QD 0 13:47:20.578 TestScript (EURUSD,H1) << Strong >> total > 4 JN 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JK 0 13:47:20.578 TestScript (EURUSD,H1) 3 1 DM 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 JF 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04281 >>>>>> DG 0 13:47:20.578 TestScript (EURUSD,H1) LI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Noce will be Temp with IG = 0.15733 LH 0 13:47:20.584 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers GR 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Mild" "Cool" CD 0 13:47:20.584 TestScript (EURUSD,H1) 0.0000 0.9710 0.9183 GN 0 13:47:20.584 TestScript (EURUSD,H1) 2 5 3 CK 0 13:47:20.584 TestScript (EURUSD,H1) Classified matrix dataset RL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " NK 0 13:47:20.584 TestScript (EURUSD,H1) [ CQ 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Weak" "No" LI 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Strong" "No" JM 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" NI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" CL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" KI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" LR 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" KJ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" IQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" DE 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" NR 0 13:47:20.584 TestScript (EURUSD,H1) ] OI 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 30 OO 0 13:47:20.584 TestScript (EURUSD,H1) Hot is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. HL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " DJ 0 13:47:20.584 TestScript (EURUSD,H1) [ DL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" LH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" QL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" MH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" RQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" MI 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" KQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" FD 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" HQ 0 13:47:20.584 TestScript (EURUSD,H1) ] NN 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 24 IF 0 13:47:20.584 TestScript (EURUSD,H1) rows total 24 Mild 5 CO 0 13:47:20.584 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is DM 0 13:47:20.584 TestScript (EURUSD,H1) "Wind" "PlayTennis " PD 0 13:47:20.584 TestScript (EURUSD,H1) [ LN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "No" JI 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EL 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" GO 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "Yes" JG 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JE 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EP 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" HK 0 13:47:20.584 TestScript (EURUSD,H1) ] PP 0 13:47:20.584 TestScript (EURUSD,H1) columns = 2 rows = 10 HG 0 13:47:20.584 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers FQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Cool" OF 0 13:47:20.584 TestScript (EURUSD,H1) 0.9710 0.9183 IO 0 13:47:20.584 TestScript (EURUSD,H1) 5 3
Manuel olarak hesaplamalar yaparken süreç oldukça basit görünmesine rağmen, kodlamalar bana oldukça kafa karıştırıcı geldi. Bu yüzden, bir karar ağacı oluşturma sürecini burada genel hatlarıyla açıklamaya karar verdim. İşte genel olarak bir karar ağacı oluşturma fonksiyonu:
void CDecisionTree::BuildTree(void) { int ClassNumbers[]; int max_gain = 0; double IGArr[]; //double parent_entropy = Entropy(p_ClassNumbers,single_rowstotal); string p_Classes[]; //parent classes double P_EntropyArr[]; //Parent Entropy int p_ClassNumbers[]; //parent/ Target variable class numbers GetClasses(TargetArr,m_DatasetClasses,p_ClassNumbers); ArrayResize(P_EntropyArr,1); P_EntropyArr[0] = Entropy(p_ClassNumbers,single_rowstotal); //--- temporary disposable arrays for parent node information string TempP_Classes[]; double TempP_EntropyArr[]; int TempP_ClassNumbers[]; //--- if (m_debug) Print("Default Parent Entropy ",P_EntropyArr[0]); int cols = m_colschosen; for (int A =0; A<ArraySize(P_EntropyArr); A++) { printf("<<<<<<<< Parent Entropy %.5f A = %d >>>>>>>> ",P_EntropyArr[A],A); for (int i=0; i<cols-1; i++) //we substract with one to remove the independent variable coumn { int rows = ArraySize(m_dataset)/cols; string Arr[]; //ArrayFor the current column string ArrTarg[]; //Array for the current target ArrayResize(Arr,rows); ArrayResize(ArrTarg,rows); printf(" <<<<< C O L U M N %s >>>>> ",DataColumnNames[i]); int index_target=cols-1; for (int j=0; j<rows; j++) //get column data and its target column { int index = i+j * cols; //Print("index ",index); Arr[j] = m_dataset[index]; //printf("ArrTarg[%d] = %s m_dataset[%d] =%s ",j,ArrTarg[j],index_target,m_dataset[index_target]); ArrTarg[j] = m_dataset[index_target]; //printf("Arr[%d] = %s ArrTarg[%d] = %s ",j,Arr[j],j,ArrTarg[j]); index_target += cols; //the last index of all the columns } //--- Finding the Entropy //The function to find the Entropy of samples in a given column inside its loop //then restores all the entropy into one array //--- Finding the Information Gain //The Function to find the information gain from the entropy array above //--- if (i == max_gain) { //Get the maximum information gain of all the information gain in all columns then //store it to the parent information gain } //--- ZeroMemory(ClassNumbers); ZeroMemory(SamplesNumbers); } //---- Get the parent Entropy, class and class numbers // here we store the obtained parent class from the information gain metric then we store them into a parent array ArrayCopy(p_Classes,TempP_Classes); ArrayCopy(P_EntropyArr,TempP_EntropyArr); ArrayCopy(p_ClassNumbers,TempP_ClassNumbers); //--- string Node[1]; Node[0] = DataColumnNames[max_gain]; if (m_debug) printf("Parent Node will be %s with IG = %.5f",Node[0],IGArr[max_gain]); if (A == 0) DrawTree(Node,"parent",A); DrawTree(p_Classes,"child",A); //--- CLASSIFY THE MATRIX MatrixClassify(m_dataset,p_Classes,cols); //--- Search if there is zero entropy in Array if there is any remove its data from the dataset if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]); //--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assing the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- } }
Sonuç
Bu makalede sınıflandırma ağaçlarında yer alan temel hesaplamaları ele aldık. Bu, bir makalede ele alınamayacak kadar karmaşık ve uzun bir konudur. Umarım bu konuyu sonraki bir veya iki makaleyle tamamlayacağız. Şu anda da kütüphane, ticaret sorunlarını çözmenize yardımcı olacak karar ağacı algoritmaları oluşturmaya başlamanız için ihtiyacınız olan hemen hemen her şeye sahiptir.
Okuduğunuz için teşekkürler! GitHub depomun linki: https://github.com/MegaJoctan/DecisionTree-Classification-tree-MQL5. Bir sonraki makalede görüşmek dileğiyle.
MetaQuotes Ltd tarafından İngilizceden çevrilmiştir.
Orijinal makale: https://www.mql5.com/en/articles/11061
Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.
Bu makale sitenin bir kullanıcısı tarafından yazılmıştır ve kendi kişisel görüşlerini yansıtmaktadır. MetaQuotes Ltd, sunulan bilgilerin doğruluğundan veya açıklanan çözümlerin, stratejilerin veya tavsiyelerin kullanımından kaynaklanan herhangi bir sonuçtan sorumlu değildir.
 Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 14): Hacim profili ekleme (II)
Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 14): Hacim profili ekleme (II)
 Veri Bilimi ve Makine Öğrenimi (Bölüm 04): Borsa Çöküşünü Öngörme
Veri Bilimi ve Makine Öğrenimi (Bölüm 04): Borsa Çöküşünü Öngörme
 Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 15): İnternetteki verilere erişme (I)
Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 15): İnternetteki verilere erişme (I)
 MQL5'te matrisler ve vektörler
MQL5'te matrisler ve vektörler
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Merhaba Bay Omega,
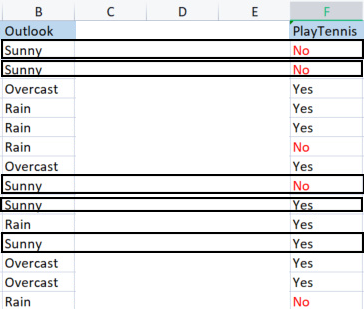
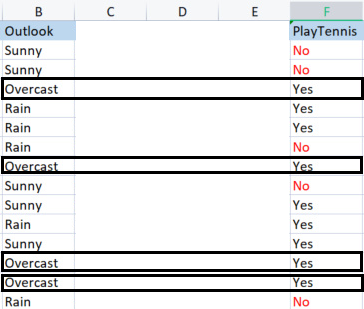
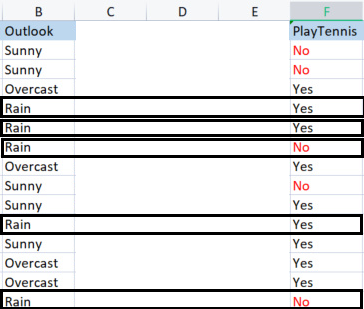
ID3 çözümü için çok teşekkür ederim. benim için çok faydalı oldu. Bununla birlikte, bu konuda bir excel sayfası sağladım ve ekledim, açıklamalarınız için net olduğunu düşünüyorum.
Tekrar çok teşekkürler,
F.Mahmoudian
Merhaba Bay Omega,
ID3 çözümü için çok teşekkür ederim. benim için çok faydalı oldu. Bununla birlikte, bu konuda bir excel sayfası sağladım ve ekledim, açıklamalarınız için net olduğunu düşünüyorum.
Tekrar çok teşekkürler,
F.Mahmoudian
çok teşekkürler, hala betiğin ağacı kendisinin çizmesine nasıl izin vereceğimi bulmaya çalışıyorum
many thanks to it, I'm still trying to figure out how to let the script draw the tree itself
Çok teşekkür ederim.
Ve bu arada, evet, neden herkes MO, AI ve DeepLearning'e bu kadar takmış durumda? Konuyu başlatan kişinin hatırlattığı, unutulmuş eski bir şey var. Uzman sistemler ve her türlü ağırlıklı değerlendirmeler var. Elbette yöntemler 30-50 yıllık, moda değil ama fiziksel modele ve neden-sonuç ilişkilerine sadık kalıyorlar ve sonuçları yorumlanabilir. ORAYA GIRMEM LAZIM.
Zaten hesaplanmış sinyaller için potansiyel olarak bir filtre olabilecek tek şey bu. Bu yöndeki diğer yöntemler berbat.
Ve bu arada, evet, neden herkes MO, AI ve DeepLearning'e bu kadar takmış durumda? Konuyu başlatan kişinin bize hatırlattığı, unutulmuş eski bir şey var. Uzman sistemler ve her türlü ağırlıklı değerlendirmeler var. Elbette yöntemler 30-50 yıllık, moda değil ama fiziksel modele ve neden-sonuç ilişkilerine sadık kalıyorlar ve sonuçları yorumlanabilir. ORAYA BAKMAM GEREKECEK.
Zaten hesaplanmış sinyaller için potansiyel olarak filtre olabilecek tek şey bu. Bu yöndeki diğer yöntemler berbattır.