
Die Verwendung der Fuzzy-Logik im Trading mit Hilfe von MQL4
Einführung
Im heutigen Handeln werden immer mehr automatisierte Handelssysteme verwendet, in der Regel nennt man sie Expert Advisors oder Roboter. Die meisten, wenn nicht alle von ihnen verfügen eine klare hartcodierte Trading-Strategie und ein Money-Management-System. Ihr Hauptvorteil ist ein starrer Algorithmus, um den menschlichen Faktor auszuschließen. Allerdings ist dieser Vorteil auch ihr Hauptnachteil, da einem Trading-Roboter Flexibilität fehlt. Unabhängig von den Marktbedingungen verwendet ein Expert Advisor immer die gleiche Handelsstrategie mit den gleichen streng kategorisierten Parametern. Mit den anderen Worten wirkt das System immer grob: Bei einem mittelfristigen Trend tritt er den Markt mit einem Lot ein, bei einem starken Trend mit zwei Lots. Keine Abweichungen!
Im Gegensatz zu einem automatisierten System, denken menschlicher Händler in Fuzzy-Kategorien und können unterschiedliche Meinungen zu ähnlichen Markteinstiegssignalen haben? Man ist oft zweifelhaft und stellt die Fragen, ob der Trend mittelfristig oder stark ist. Und selbst wenn der Trend so oder so scheint, ist es stark genug, um nach der Strategie mit zwei Lots einzutreten? Solche Fuzzy-Kategorien können durch die Fuzzy-Logik beschrieben werden. Die Fuzzy-Logik setzt keine starren Grenzen zwischen den Kategorien. Stattdessen verwischt sie ihnen und gestaltet ein Handelssystem flexibler, sodass die Disziplin eines Trading-Roboters mit der Flexibilität des menschlichen Geistes kombiniert werden. Der Artikel enthält Beispiele für die Fuzzy-Logik-Systeme im Trading mit Hilfe von MQL4.
Zugehörigkeitsfunktionen
Lesen Sie den Artikel Theoretische Einführung in die Fuzzy-Logik, um die allgemeinen Konzepte der Fuzzy-Logik zu verstehen. Außerdem erfahren Sie die Grundlagen der Bibliothek FuzzyNet für MQL4, da es für die Realisierung der Beispiele verwendet wird.
Lassen Sie uns die Zugehörigkeitsfunktionen beschreiben, die im Artikel erwähnt werden.
Die dreieckige Zugehörigkeitsfunktion
Wie der Name schon andeutet, ist dies eine dreieckförmige Zugehörigkeitsfunktion. Dies ist eine einfache und am häufigsten verwendete Funktion, die durch die folgenden analytischen Formel definiert wird:
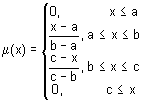
In der Regel, um Unsicherheiten einzugeben, werden die folgenden Arten verwendet: "ungefähr gleich", "Mittelwert", "innerhalb des Bereichs", "ähnlich dem Objekt", "sieht wie das Objekt aus" usw. Die Parameter der Dreiecksfunktion werden in der Regel folgendermaßen interpretiert:
- [a, c] — Der Bereich der Variable;
- b — wahrscheinlichste Variablenwert.
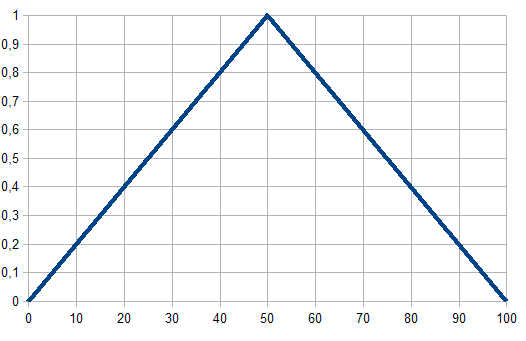
in Abb. 1. Die dreieckige Zugehörigkeitsfunktion
Trapez - Zugehörigkeitsfunktion
Die trapezförmige Zugehörigkeitsfunktion. Sie wird durch die folgende Formel definiert:
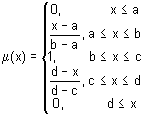
Die trapezförmigen Zugehörigkeitsfunktionsparameter werden wie folgt interpretiert:
- [a, d] — Fuzzy-Set Träger, pessimistische Einschätzung der Variablenwerte;
- [b, c] — Der Kern eines Fuzzy-Sets, optimistische Einschätzung der Variablenwerte;
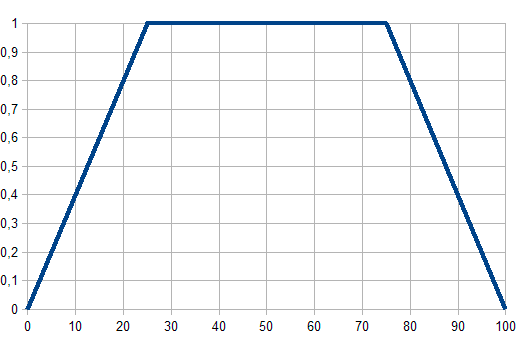
in Abb. 2. Trapez - Zugehörigkeitsfunktion
Glockenförmige Zugehörigkeitsfunktion
Die Zugehörigkeitsfunktion in Form von symmetrischer glockenförmiger Kurve. Diese Funktion wird durch die folgende Formel definiert:
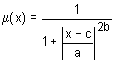
Die Parameterwerte werden wie folgt interpretiert:
- a — Das Konzentrationsverhältnis der Zugehörigkeitsfunktion;
- b — Das Steigung-Verhältnis der Zugehörigkeitsfunktion;
- c — Die Koordinaten vom Maximum der Zugehörigkeitsfunktion.
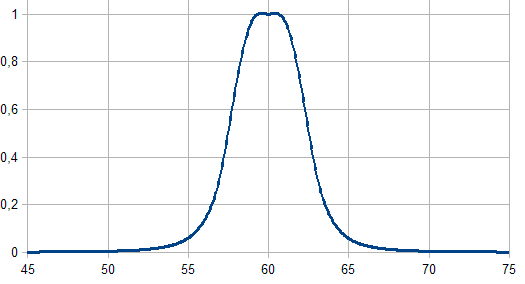
in Abb. 3. Glockenförmige Zugehörigkeitsfunktion
Sigmoid Zugehörigkeitsfunktion
Die Funktion wird nach der folgenden Formel berechnet und sie wird angewendet, wenn monotonen Zugehörigkeitsfunktionen eingegeben werden müssen:
![]()
Ihre Parameter sollten wie folgt interpretiert werden:
- a — Das Steigung-Verhältnis der Zugehörigkeitsfunktion;
- с — Die Koordinaten von der Wende der Zugehörigkeitsfunktion.
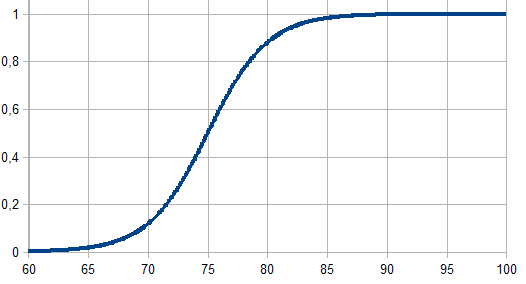
in Abb. 4. Sigmoid Zugehörigkeitsfunktion
Beispielimplementierung eines Indikators durch die FuzzyNet Bibliothek für MQL4
Wir werden das Average Directional Movement Index (ADX) als Beispiel verwenden. Dies ist ein Trend-Indikator, der die Leistung des aktuellen Trends (dicke grüne Linie) zeigt. Lassen Sie uns zunächst die genauen Leistungskriterien des Trends definieren (in Abb. 5):- Weak Trend — die grüne Haupt-Linie liegt im Bereich von 30 bis 50. Die Werte in diesem starr gegebenen Bereich werden als ein schwacher Trend definieren.
- Average Trend — die grüne Haupt-Linie liegt im Bereich von 50 bis 70. Die Werte in diesem Bereich werden als ein mittelfristiger Trend definieren.
- Strong Trend — Die grüne Haupt-Linie liegt oberhalb von 70 bis zu 100 (starker Trend). Das ist das Zeichen eines starken Trends.
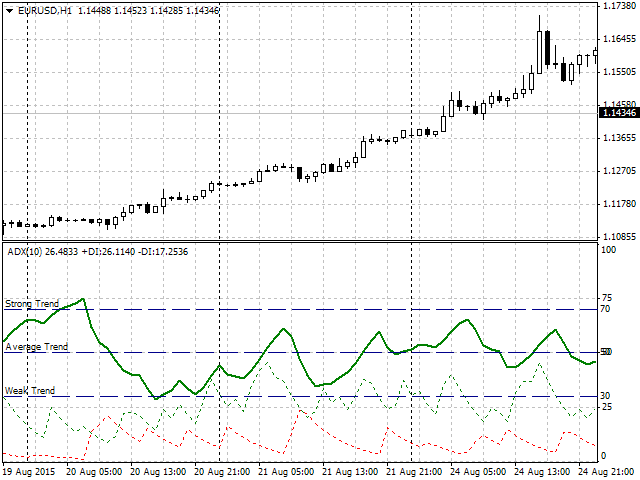
in Abb. 5. Das Beispiel der Funktionalität und der ausgewählten Größenordnung nach der Trendkraft
Diese drei starr definierten Kategorien haben einige Nachteile, die sich durch ihre klare und strenge Klassifizierungslogik bezeichnen:
- Der erste Nachteil ist die subjektive Natur der Klassifikation. Und dabei ist die Frage zu Recht, warum es 30, 50 und 70 als Grenze Werte sind? Warum wir wählen nicht 25, 50 und 75, oder einige anderen? Und teilweise hat man Recht mit dieser Frage. Genauso wie mit anderen. Aber diese verschiedenen Meinungen können stark die ADX-Arbeit beeinflussen und sogar zu diametral entgegengesetzten Handelsergebnissen führen.
- Das zweite Problem ist die Grenzbereiche der ausgewählten Kategorien. Zum Beispiel 50 ist die Grenze zwischen einem schwachen und einem Durchschnittstrend. Wenn wir eine strenge Logik anwenden, müssen wir zugeben, dass 48 und 49 zu den schwachen Trends gehören, und 50, 51 zu den Durchschnittstrends. Aber wie soll man den Übergang von 49 zu 50 definieren? In beiden Fällen (48-49 und 49-50) ist die Differenz zwischen den Werten nur Eins.
Also, was bietet die Fuzzy-Logik an, um diese Probleme zu lösen?
Es wird folgendes passieren: die angegebenen Grenzen werden verschwommen, von daher undeutlich. Das heißt, in Grenzbereichen der streng eingegebenen Kategorien entsteht Duplizität, die Trendkraft gehört dann zu zwei Begriffen, aber mit unterschiedlichem Grad der Zugehörigkeit. Der aktuelle Trend kann als schwach bezeichnet, wenn seine Trendkraft (30%) ist, aber wenn es (70%) ist, dann ist es eher ein Durchschnittstrend. Ein menschlicher Händler würde dies wie folgt beschreiben: Der Trend ist eher Durchschnittlich als schwach. Ich glaube, dies ist der Hauptvorteil der Fuzzy-Logik. Ein streng eingegebener Parameter wird flexibel und variabel bewertet. Ich habe die folgenden Zugehörigkeitsfunktionen für unser Beispiel mit dem ADX-Indikator ausgewählt:
- Die Trapez-Zugehörigkeitsfunktion für die Konzeptbeschreibung eines schwachen Trends.
- Die glockenförmige Zugehörigkeitsfunktion für die Konzeptbeschreibung eines durchschnittlichen Trends.
- Die Sigmoid-Funktion für die Konzeptbeschreibung eines starken Trends.
Die komplexeren Systeme, die zahlreiche Kategorien enthalten, können mit anderen Funktionen beschrieben werden, die in der Bibliothek FuzzyNet verfügbar sind. Derzeit enthält die Bibliothek über ein Dutzend Funktionen. Die graphische Darstellung unseres Beispiels wird unten dargestellt:
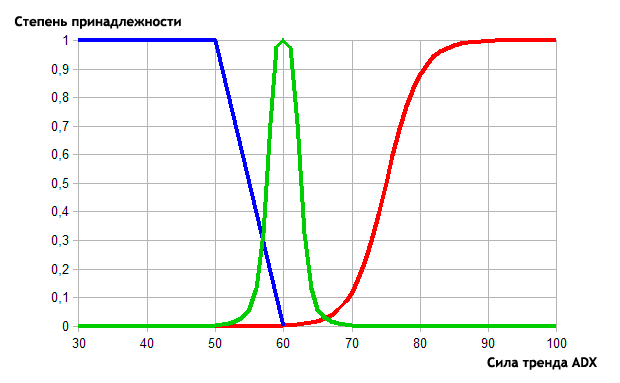
in Abb. 6. Die Beschreibung einen Trend mit der Fuzzy-Logik
Wie wir sehen können, hat das Chart nun die Bereiche mit zwei Trendkategorien gleichzeitig. Der Trend im Bereich von 50 bis 60 ist schwach und durchschnittlich, während in 60-70 ist es durchschnittlich und stark. So haben wir für die drei Kategorien einen Begriff zusammen mit den anderen vorbestimmten Zugehörigkeitsfunktionen definiert. Nun, da wir den ADX-Eingangswert durch die Zugehörigkeitsfunktionen beschrieben haben, sollten wir definieren, was für einen Ausgangswert, ein Defuzzifizierungsergebnis sein wird, sowie wählen Wir einen Fuzzy-logischen Ausgangs-Algorithmus.
Für unser Beispiel habe ich als Ausgangswert den Prozentsatz des Deposites ausgewählt, im Bezug auf die Fuzzy-Variable der Trendkraft, die am Eingang eingegeben wurde. Mit anderen Worten, der Trend ist je stärker, umso das Risiko und Prozentsatz des Deposites im Handel höher ist. Ich habe Mamdani als logischer Ausgangs-Algorithmus gewählt.
Wie bei der Trendkraft lassen Sie uns nach dem Risiko-Grad drei Kategorien eingeben:
- Geringes Risiko (Low) - 2-4% vom Deposit.
- Normales Risiko (Normal) — 4-5%.
- Hohes Risiko (High) — von 5 bis zum Maximalwert von 10% vom Deposit.
Jetzt wollen wir Risikokategorien durch die Zugehörigkeitsfunktionen definieren:
- Trapez ist für ein geringes Risiko.
- Die dreieckige Zugehörigkeitsfunktion ist für normales Risiko.
- Sigmoid ist für ein hohes Risiko.
Als Ergebnis erhält man die folgende grafische Beschreibung mittels Fuzzy-Logik:
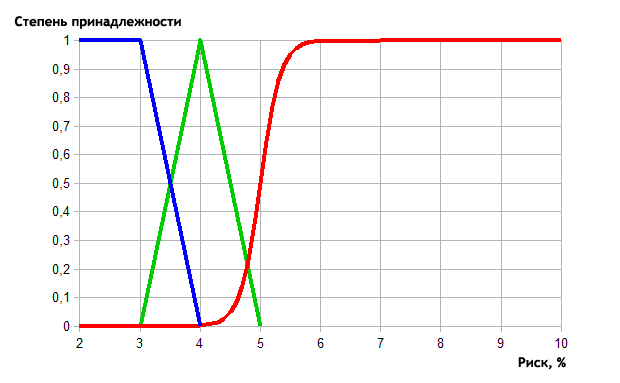
in Abb. 7. Beschreiben wir ein gewisses Risiko mit Hilfe der Fuzzy-Logik
Lassen Sie uns die beschriebenen Daten durch die Bibliothek FuzzyNet für MQL4 realisieren:
//+------------------------------------------------------------------+ //| ADX_Fuzzy.mq4 | //| Alexander Fedosov | //| https://www.mql5.com/ru/users/alex2356 | //+------------------------------------------------------------------+ #property copyright "Alexander Fedosov" #property link "https://www.mql5.com/ru/users/alex2356" #property version "1.00" #property strict #property indicator_separate_window #property indicator_buffers 2 #property indicator_color1 Green #property indicator_color2 Red #property indicator_minimum 0 #property indicator_maximum 10 //+------------------------------------------------------------------+ //| Connecting libraries | //+------------------------------------------------------------------+ #include <Math\FuzzyNet\MamdaniFuzzySystem.mqh> //--- input parameters input string p1="==== Parameters ===="; input int visual=100; // Visual Period input int adx_period=10; // ADX Period //--- double Buffer1[],Buffer2[],adx,adx_di_minus,adx_di_plus; int limit; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexStyle(0,DRAW_HISTOGRAM,0,2); SetIndexBuffer(0,Buffer1); SetIndexEmptyValue(0,0.0); //--- SetIndexStyle(1,DRAW_HISTOGRAM,0,2); SetIndexBuffer(1,Buffer2); SetIndexEmptyValue(1,0.0); //--- ArrayResize(Buffer1,visual); ArrayResize(Buffer2,visual); ArrayInitialize(Buffer1,0.0); ArrayInitialize(Buffer2,0.0); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int count_bars=IndicatorCounted(); //--- if(count_bars<0) return(-1); //--- if(Bars-1<adx_period) return(0); //--- for(int i=0; i<visual;i++) { adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits); adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits); adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits); //--- double r=(adx_di_plus-adx_di_minus); if(MathAbs(r)>10 && adx>=30.0) if(r>0) Buffer1[i]=mamdani(adx); else if(r<0) Buffer2[i]=mamdani(adx); } return(rates_total); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double mamdani(double v) { double res=0; //--- Mamdani Fuzzy System MamdaniFuzzySystem *fsRisk=new MamdaniFuzzySystem(); //--- Create input variables for the system FuzzyVariable *fsTrend=new FuzzyVariable("trend",30.0,100.0); //--- fsTrend.Terms().Add(new FuzzyTerm("weak", new TrapezoidMembershipFunction(20.0, 30.0, 50.0, 60.0))); fsTrend.Terms().Add(new FuzzyTerm("average", new GeneralizedBellShapedMembershipFunction(2.5,2.0,60.0))); fsTrend.Terms().Add(new FuzzyTerm("strong",new SigmoidalMembershipFunction(0.4,75.0))); fsRisk.Input().Add(fsTrend); //--- Create Output FuzzyVariable *fvRisk=new FuzzyVariable("risk",2.0,10.0); fvRisk.Terms().Add(new FuzzyTerm("low", new TrapezoidMembershipFunction(1.0, 2.0, 3.0, 4.0))); fvRisk.Terms().Add(new FuzzyTerm("normal", new TriangularMembershipFunction(3.0, 4.0, 5.0))); fvRisk.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,5.0))); fsRisk.Output().Add(fvRisk); //--- Create three Mamdani fuzzy rules MamdaniFuzzyRule *rule1 = fsRisk.ParseRule("if (trend is weak) then risk is low"); MamdaniFuzzyRule *rule2 = fsRisk.ParseRule("if (trend is average) then risk is normal"); MamdaniFuzzyRule *rule3 = fsRisk.ParseRule("if (trend is strong) then risk is high"); //--- Add three Mamdani fuzzy rules in the system fsRisk.Rules().Add(rule1); fsRisk.Rules().Add(rule2); fsRisk.Rules().Add(rule3); //--- Set input value CList *in=new CList; Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double; p_od_in.SetAll(fsTrend,v); in.Add(p_od_in); //--- Get result CList *result; Dictionary_Obj_Double *p_od_out; result=fsRisk.Calculate(in); p_od_out=result.GetNodeAtIndex(0); res=NormalizeDouble(p_od_out.Value(),_Digits); //--- delete in; delete result; delete fsRisk; return res; } //+------------------------------------------------------------------+
Die Visualisierung des Risikograd / Trendkraft-Verhältnis ( Aufwärtstrend rot und grün Abwärtstrend) habe ich als einen einfachen Histogrammindikator dargestellt. Die Höhe der Histogrammbalken zeigen einen numerischen Wert eines Risikograds bei verschiedenen Trendkräfte innerhalb der oben beschriebenen Grenzen. Lassen Sie uns den Code gründlicher betrachten.
Lassen Sie uns zunächst die beiden Puffers für angewendeten Histogramme definieren sowie ihre Farbe und den Bereich, an dem die vertikale Achse von Null auf das höchste spezifizierte Risiko von 10% ist.
#property indicator_separate_window #property indicator_buffers 2 #property indicator_color1 Green #property indicator_color2 Red #property indicator_minimum 0 #property indicator_maximum 10
Als nächstes verbinden wir die Bibliotheken, um das System nach Mamdanisalgorithmus zu erstellen, und fügen wir Variablen für die Visualisierung der Anzahl der Bars von dem nullwertigen Bar ein und für den bereinigten ADX Zeitraum.
//+------------------------------------------------------------------+ //| Connecting libraries FuzzyNet | //+------------------------------------------------------------------+ #include <Math\FuzzyNet\MamdaniFuzzySystem.mqh> //--- input parameters input string p1="==== Parameters ===="; input int visual=100; // Visual Period input int adx_period=10; // ADX Period
Bei der Initialisierung sollen wir das Kennzeichen in Form eines Histogramms einstellen.
//+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexStyle(0,DRAW_HISTOGRAM,0,2); SetIndexBuffer(0,Buffer1); SetIndexEmptyValue(0,0.0); //--- SetIndexStyle(1,DRAW_HISTOGRAM,0,2); SetIndexBuffer(1,Buffer2); SetIndexEmptyValue(1,0.0); //--- ArrayResize(Buffer1,visual); ArrayResize(Buffer2,visual); ArrayInitialize(Buffer1,0.0); ArrayInitialize(Buffer2,0.0); //--- return(INIT_SUCCEEDED); }
Im Haupt-Code definieren wir die grundlegenden Messwerte von ADX-Indikator, auch finden wir in der Variable r die Differenz zwischen den beiden Trendrichtungsindikatoren + DI und -DI. Weiterhin fügen wir den Trend-Filter als Differenz zwischen dem absoluten + DI und über 10 -D Werte, und der Haupttrendkraft über 30 (die untere Grenze eines schwachen Trends). Als nächstes bestimmen wir die Trend-Richtung aus der Variable r und platzieren den Wert der Funktion mamdani() im vorbestimmten Array.
int count_bars=IndicatorCounted(); //--- if(count_bars<0) return(-1); //--- if(Bars-1<adx_period) return(0); //--- for(int i=0; i<visual;i++) { adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits); adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits); adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits); //--- double r=(adx_di_plus-adx_di_minus); if(MathAbs(r)>10 && adx>=30.0) if(r>0) Buffer1[i]=mamdani(adx); else if(r<0) Buffer2[i]=mamdani(adx); }
Die Beschreibung der Funktion mamdani:
1. Erstellen wir ein neues System der Fuzzy-Logik der Typ von *fsRisk.
2. Fügen Sie die Variable *fsTrend mit einem vorgegebenen Namen trend, mit den Minimal- und Maximalwerten von 30 und 100.
//--- Mamdani Fuzzy System MamdaniFuzzySystem *fsRisk=new MamdaniFuzzySystem(); //--- Create input variables for the system FuzzyVariable *fsTrend=new FuzzyVariable("trend",30.0,100.0);
3. Als nächstes sollen wir die Fuzzy-Begriffe, die oben beschrieben sind (Abb. 6) mit den ausgewählten Zugehörigkeitsfunktionen für jede Kategorie hinzufügen.
fsTrend.Terms().Add(new FuzzyTerm("weak", new TrapezoidMembershipFunction(30.0, 40.0, 50.0, 60.0))); fsTrend.Terms().Add(new FuzzyTerm("average", new GeneralizedBellShapedMembershipFunction(2.5,2.0,60.0))); fsTrend.Terms().Add(new FuzzyTerm("strong",new SigmoidalMembershipFunction(0.4,75.0))); fsRisk.Input().Add(fsTrend);
4. Führen Sie die Schritte 2-3 für den Ausgangswert: erstellen wir die Variable *fvRisk mit dem Namen risk und den minimalen und maximalen Risikowerten von 2% und 10%.
//--- Create Output FuzzyVariable *fvRisk=new FuzzyVariable("risk",2.0,10.0); fvRisk.Terms().Add(new FuzzyTerm("low", new TriangularMembershipFunction(2.0, 3.0, 4.0))); fvRisk.Terms().Add(new FuzzyTerm("normal", new TriangularMembershipFunction(3.0, 4.0, 5.0))); fvRisk.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,5.0))); fsRisk.Output().Add(fvRisk);
5. Lassen Sie uns nun einen Satz von drei Fuzzy-Regeln erstellen, die unser System darstellen:
- Wenn ein Trend zu schwach ist, dann ist das Risiko gering.
- Wenn ein Trend durchschnittlich ist, dann ist das Risiko normal.
- Wenn ein Trend stark ist, dann ist das Risiko hoch.
//--- Create three Mamdani fuzzy rules MamdaniFuzzyRule *rule1 = fsRisk.ParseRule("if (trend is weak) then risk is low"); MamdaniFuzzyRule *rule2 = fsRisk.ParseRule("if (trend is average) then risk is normal"); MamdaniFuzzyRule *rule3 = fsRisk.ParseRule("if (trend is strong) then risk is high");
6. Fügen wir unsere Regeln zu System hinzu:
//--- Add three Mamdani fuzzy rules in the system
fsRisk.Rules().Add(rule1);
fsRisk.Rules().Add(rule2);
fsRisk.Rules().Add(rule3);
7. Erstellen Sie die Listen für die Ein- und Ausgangsvariablen und fügen Sie den Eingabeparameter v, der als Funktionsargument zu mamdani sein wird. Das heißt, es wird für das gesamte System mamdani das Fuzzy-Logik-System mit spezifizierten Eingang und Ausgang Fuzzy-Variablen erstellt, und zum Eingang wird der Indikatorwert ADX geführt.
//--- Set input value CList *in=new CList; Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double; p_od_in.SetAll(fsTrend,v); in.Add(p_od_in); //--- Get result CList *result=new CList; Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double; result=fsRisk.Calculate(in); p_od_out=result.GetNodeAtIndex(0); res=NormalizeDouble(p_od_out.Value(),_Digits);
8. Der Funktionswert und das Ergebnis wird die Variable res, auf deren Basis das Histogramm gebaut wird.
adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits); adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits); adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits); //--- double r=(adx_di_plus-adx_di_minus); if(MathAbs(r)>10 && adx>=30.0) if(r>0) Buffer1[i]=mamdani(adx); else if(r<0) Buffer2[i]=mamdani(adx);
Schließlich können wir visuelle Operationsergebnisse vom Indikator beobachten:
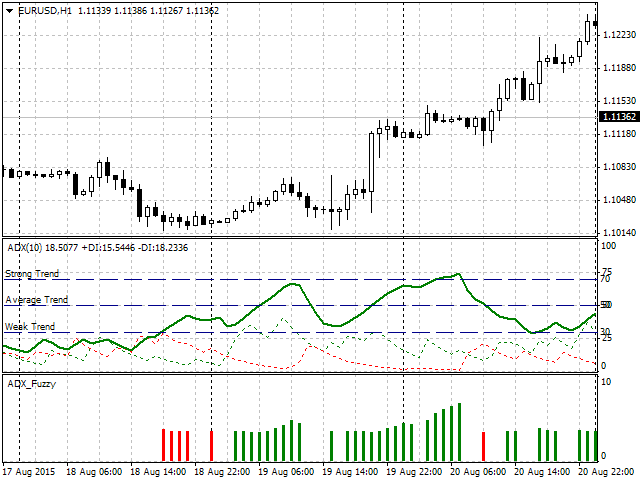
in Abb. 8. Die Arbeit des Indikators
Wie wir aus seiner Arbeit sehen können, zeigt der Indikator das Vorhandensein eines Trends in Form von einem Histogramm einer bestimmten Farbe, und die Balkenhöhe zeigt einen empfohlenen Prozentsatz des Risikos vom Deposit. Die offensichtliche Frage wird zu Recht gestellt - was der Unterschied wäre, wenn der Indikator mit klaren Intervallen realisiert wurde? Dafür betrachten wir es gründlicher im folgenden Intervall(Abb. 9). Der grüne Pfeil zeigt die Spalte vom Histogramm, und links davon sind seine Zahlenwerte und Trendkraft von ADX. Wie es zuvor definiert wurde, der Wert ADX über 70 bedeutet einen starken Trend, und bei ihm sollte der Risikowert nicht mehr als 5% sein. In Abb.9 sehen wir aber, dass ADX = 69.7923 ist, das heißt, wenn wir also strenge Regeln halten, dann ist dies immer noch ein durchschnittlicher Trend und das Risiko sollte nicht mehr als 5% überschreiten. Es ist jedoch gleich 5,6406, d.h. es ist höher.
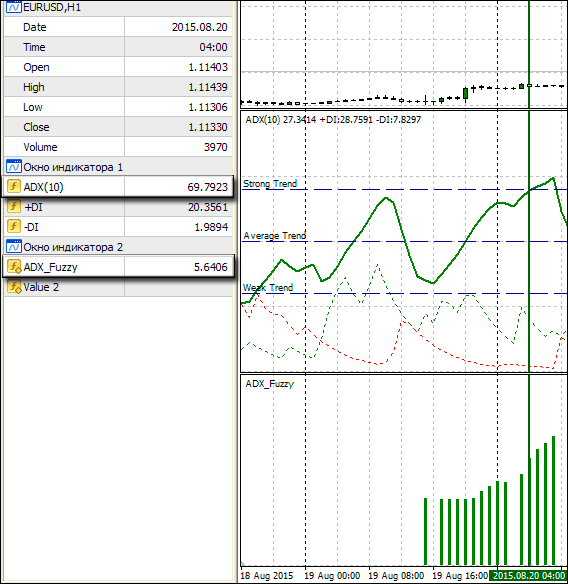
in Abb. 9. Es werden die Unterschiede zwischen Fuzzy-und Standard-Logik dargestellt
Hier können wir die Fuzzy-Logik in Aktion sehen. Sie hat festgestellt, dass, obwohl der Wert kleiner als 70 ist, geht der Trend in dem Bereich eher stärker als durchschnittlich. Wir können das durch die Abb.6 sehen , wenn die X-Achse den Wert 69,7923 zeigt, hat die Zugehörigkeitssfunktion eines starken Trends den höheren Wert als die Funktion eines durchschnittlichen Trends. Aus diesem Grund hat unser System das Risiko von mehr als 5% angeboten, und näherte sich dem Grenzbereich zwischen starken und durchschnittlichen Trends als dies das System mit der strengen Logik gemacht hätte.
Beispielimplementierung eines Expertes durch die FuzzyNet Bibliothek für MQL4
Hier möchte ich den Unterschied in der Expert Advisors Arbeit zeigen, falls es bei klar definierten Bedingungen und bei Fuzzy-Logik-Elemente verwendet wird. Um das möglichst vollständig zu vergleichen, habe ich als Beispiel Experten aus meinem anderen Artikel Handelsideen basierend auf der Kursrichtung und der Bewegungsgeschwindigkeit genommen. In dem wurde gründlich die Funktionalität eines Handels-Roboters beschrieben, und nicht dasselbe zu wiederholen, nehmen wir den Roboter als Grundlage, aber mit einigen Unterschieden:
- Also. Die Logik des EAs basiert auf der Persistenz-Idee der Kursbewegung. Die Bewegungsparameter werden durch die folgenden Indikatoren beschrieben: RSI (Geschwindigkeitsindikator) und AC (Beschleunigungsindikator). Die Einschätzung der Geschwindigkeit und Beschleunigung wird durch die Indizierung der Wertebereiche dieser Indikatoren durchgeführt. Nun wollen wir die Fuzzy-Set-Theorie zu den RSI-Index Werten und seiner Berechnung verwenden. Schließlich werden RSI-Werte beim Eingang verwendet, und beim Ausgang wird ein Fuzzy-Geschwindigkeitsindex verwendet, das nicht nur ganzzahlige Werte wie 1-4 haben wird, sondern auch 1,3 oder 3,85.
- Wiederum wird der Fuzzy-Indexwert als eine Eingabe für ein anderes System verwendet, in dem der Ausgang ein Gewinnwert ist. So wird der Wert, der im Anfangsexpert gleich bleibt, die Take-Profit sein.
Die Idee hinter der Verbindung ist einfach. Wenn RSI und AC Bewegungsparameter sind, dann je höher die Geschwindigkeit ist, desto höher die Persistenz dieser Bewegung ist, und von daher ist es sinnvoll, eine größere Take-Profit zu platzieren. Wenn die Bewegungsgeschwindigkeit niedrig ist, sollte ein Ziel für Gewinn umso weniger eingestellt werden, um Roll-Back oder eine Trendumkehr im Laufe zu bekommen. in Abb. 10 zeigt ein Blockdiagramm für ein klareres Verständnis der Fuzzy-Logik-Anwendung im EA.
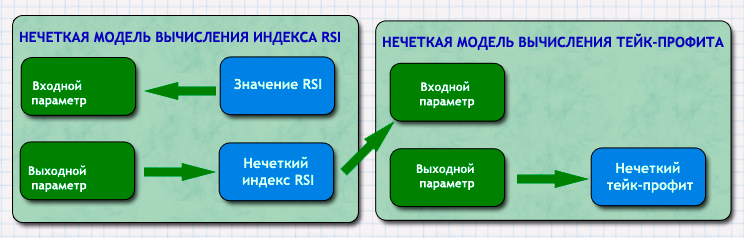
in Abb. 10. Die Verwendung eines Blockdiagramms in der Fuzzy-Logik-Anwendung im EA
Genauso wie mit dem Indikator ist, lassen Sie uns für beide Fuzzy-Modelle die Zugehörigkeitsfunktionen beschreiben. Der erste ist ein Fuzzy-Modell der Berechnung RSI Index, wo zum Eingang der Indikatorwert gegeben wird. Lassen Sie uns die erforderlichen Werte in drei Kategorien unterteilen:
- Weak. Die erste Kategorie. Ein schwacher Trend. Der Wert RSI: 60-70.
- Average. Die zweite Kategorie. Ein durchschnittlicher Trend. Im Bereich RSI: 70-80.
- Strong. Die dritte Kategorie, ist ein starker Trend. Der Bereich 80-85.
Suchen wir die Zugehörigkeitsfunktion aus, um die gegebenen Kategorien zu beschreiben:
- Weak. Die Sigmoid-Funktion mit der Steigung-Verhältnis von -0,75 und Wendepunkt 67.5.
- Average. Die Gaußsche-Funktion mit den Koordinaten des Maximums von 72,5 und dem Konzentrationsverhältnis von 2,2.
- Strong. Die Gaußsche-Funktion mit den Koordinaten des Maximums von 80 und dem Konzentrationsverhältnis von 1,4.
Die visuelle Darstellung ist wie folgt:
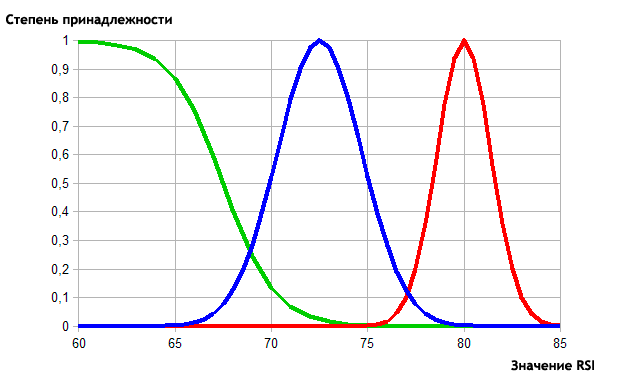
in Abb. 11. Die Beschreibung der Kategorien der RSI-Werte von den Zugehörigkeitsfunktionen
Der Ausgang-Parameter dieses Fuzzy-Modells ist RSI-Index. Für die Beschreibung werden die folgenden Kategorien und Zugehörigkeitsfunktionen verwendet:
- Low. Low-Index, im Bereich 1-2. Die Zugehörigkeitsfunktion ist die Sigmoid mit der Neigung von -11 und Wendepunkt von 1,5.
- Normal. Normal-Index, im Bereich 2-3. Die Zugehörigkeitsfunktion ist die Gaußsche mit dem maximalen Punkt 2 und dem Konzentrationsverhältnis von 0,3.
- High. Hohe-Index, im Bereich 3-4. Die Zugehörigkeitsfunktion ist die Sigmoid mit der Steigung von 6 und Wendepunkt 3.
Als Ergebnis erhält man die folgenden Visualisierung:
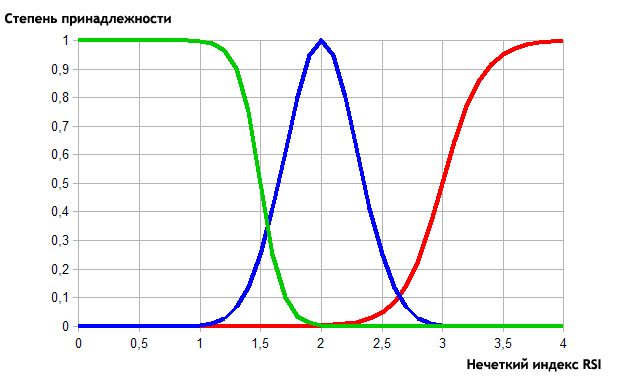
in Abb. 12. Die Beschreibung der Kategorien der RSI-Werte von den Zugehörigkeitsfunktionen
Als nächstes wollen wir das zweite Fuzzy-Modell aus Abb beschreiben. 10 — Fuzzy-Take-Profit-Berechnungsmodell. Die Eingang-Parameter haben das Modell bereits als die Ausgang-Parameter des ersten Modells (RSI Fuzzy-Index) beschrieben. Ein Take-Profit-Wert wird als ausgehender Wert hier verwendet. Lassen Sie uns für sie kurze Kategorien definieren:
- Minimal. Die minimale Take-Profit-Kategorie im Bereich 30-40.
- Average. Die durchschnittliche Take-Profit-Kategorie im Bereich 40-60.
- Maximal. Die höhe Kategorie im Bereich 60-70.
Nun lassen Sie uns die Zugehörigkeitsfunktionen beschreiben:
- Minimal. Die Zugehörigkeitsfunktion ist die Sigmoid mit der Neigung von -0,8 und Wendepunkt von 37,5.
- Average. Die Gaußsche-Funktion mit den Koordinaten des Maximums von 50 und dem Konzentrationsverhältnis von 3.
- Maximal. Die Zugehörigkeitsfunktion ist die Sigmoid mit der Neigung von -0,8 und Wendepunkt von 62,5.
Die grafische Realisierung sieht wie folgt aus:
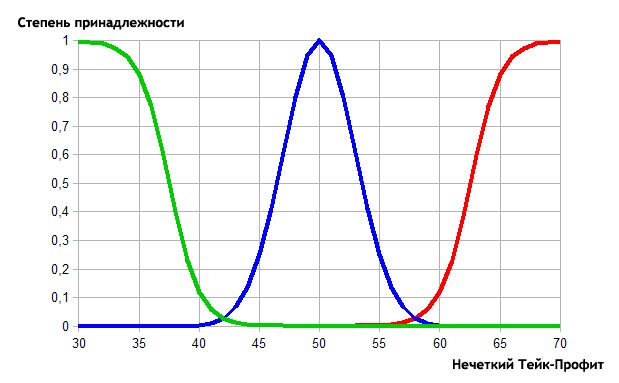
in Abb. 13. Die Beschreibung der Kategorien der Take-Profit von den Zugehörigkeitsfunktionen
Nun, da alle Parameter definiert sind, ist es die Zeit, die Idee im Trading-Roboter zu realisieren. Wir werden zwei Fuzzy-Modelle für aufeinanderfolgender Berechnung von Stop-Loss hinzufügen und nehmen Gewinne durch RSI.
//+------------------------------------------------------------------+ //| tester.mq4 | //| Alexander Fedosov | //| | //+------------------------------------------------------------------+ #property copyright "Alexander Fedosov" #property strict #include "trading.mqh" // Die Hilfsbibliothek für Handelsoperationen //+------------------------------------------------------------------+ //| Connecting libraries | //+------------------------------------------------------------------+ #include <Math\FuzzyNet\MamdaniFuzzySystem.mqh> //+------------------------------------------------------------------+ //| EA-Parameter | //+------------------------------------------------------------------+ input bool Lot_perm=false; // Die Lot von der Balance? input double Risk = 2; // Das Risiko des Deposites, % input double lt=0.01; // Lot input int magic=2356; // Magik input int period=14; // Die RSI-Indikator Periode input ENUM_TIMEFRAMES tf=PERIOD_CURRENT; // Die aktuelle Timeframe //--- int index_rsi,index_ac; double tkp,stl; double rs,mdm; CTrading tr; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { tr.Trading(magic,5,lt,Lot_perm,Risk); tr.exp_name="Tester Fuzzy Logic"; return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Die Hauptfunktion der Berechnung | //+------------------------------------------------------------------+ void OnTick() { //--- Die Überprüfung auf das Vorhandensein der offenen Orders if(!tr.isOpened(magic)) { depth_trend(); speed_ac(); rs=tr.ND(iRSI(_Symbol,tf,period,PRICE_CLOSE,0),2); //--- Die Überprüfung der Bedingungen auf den Verkauf if(Buy() && rs<=85.0) { mdm = mamdani_rsi(rs); tkp = MathCeil(mamdani_tp(mdm)); stl = MathCeil(tkp*0.43); if(tr.OpnOrd(OP_BUY,lt,(int)tkp,(int)stl)) Print("RSI равно ",rs," TP gleich ",tkp," SL gleich ",stl); } //--- Die Überprüfung der Bedingungen auf den Kauf if(Sell() && rs>=15.0) { mdm = mamdani_rsi(100-rs); tkp = MathCeil(mamdani_tp(mdm)); stl = MathCeil(tkp*0.43); if(tr.OpnOrd(OP_SELL,lt,(int)tkp,(int)stl)) Print("RSI равно ",rs," TP gleich ",tkp," SL gleich ",stl); } } //--- Gibt es geöffnete Orders? if(tr.isOpened(magic)) { //--- Wir überprüfen und schließen die Orders auf Kauf, welche die Abschlussbedingungen erfüllen if(Sell_close()) tr.ClosePosAll(OP_SELL); //--- Wir überprüfen und schließen die Orders auf Verkauf, welche die Abschlussbedingungen erfüllen if(Buy_close()) tr.ClosePosAll(OP_BUY); } } //+------------------------------------------------------------------+ //| Die Funktion, die die Tiefe des Trends bestimmt | //+------------------------------------------------------------------+ void depth_trend() { //--- Die Definition des Index für den Markteintritt double rsi=iRSI(_Symbol,tf,period,PRICE_CLOSE,0); //--- index_rsi=0; if(rsi>90.0) index_rsi=4; else if(rsi>80.0) index_rsi=3; else if(rsi>70.0) index_rsi=2; else if(rsi>60.0) index_rsi=1; else if(rsi<10.0) index_rsi=-4; else if(rsi<20.0) index_rsi=-3; else if(rsi<30.0) index_rsi=-2; else if(rsi<40.0) index_rsi=-1; } //+------------------------------------------------------------------+ //| Die Funktion, die die Geschwindigkeit des Trends bestimmt | //+------------------------------------------------------------------+ void speed_ac() { double ac[]; ArrayResize(ac,5); ArrayInitialize(ac,0.0); for(int i=0; i<5; i++) ac[i]=iAC(_Symbol,tf,i); //--- index_ac=0; //--- Die Indexs für Kauf if(ac[0]>ac[1]) index_ac=1; else if(ac[0]>ac[1] && ac[1]>ac[2]) index_ac=2; else if(ac[0]>ac[1] && ac[1]>ac[2] && ac[2]>ac[3]) index_ac=3; else if(ac[0]>ac[1] && ac[1]>ac[2] && ac[2]>ac[3] && ac[3]>ac[4]) index_ac=4; //--- Die Indexs für Verkauf else if(ac[0]<ac[1]) index_ac=-1; else if(ac[0]<ac[1] && ac[1]<ac[2]) index_ac=-2; else if(ac[0]<ac[1] && ac[1]<ac[2] && ac[2]<ac[3]) index_ac=-3; else if(ac[0]<ac[1] && ac[1]<ac[2] && ac[2]<ac[3] && ac[3]<ac[4]) index_ac=-4; } //+------------------------------------------------------------------+ //| Die Überprüfungsfunktion der Bedingungen auf den Kauf | //+------------------------------------------------------------------+ bool Buy() { return (((index_rsi==2 && index_ac>=1) || (index_rsi==3 && index_ac==1))?true:false); } //+------------------------------------------------------------------+ //| Die Überprüfungsfunktion der Bedingungen auf den Verkauf | //+------------------------------------------------------------------+ bool Sell() { return (((index_rsi==-2 && index_ac<=-1) || (index_rsi==-3 && index_ac==-1))?true:false); } //+------------------------------------------------------------------+ //| Die Überprüfungsfunktion der Abschlussbedingungen einer Position auf den Kauf | //+------------------------------------------------------------------+ bool Buy_close() { return ((index_rsi>2 && index_ac<0)?true:false); } //+------------------------------------------------------------------+ //| Die Überprüfungsfunktion der Abschlussbedingungen einer Position auf den Verkauf | //+------------------------------------------------------------------+ bool Sell_close() { return ((index_rsi<-2 && index_ac>0)?true:false); } //+------------------------------------------------------------------+ //| Die Funktion des Fuzzy-Berechnungsmodells für das RSI-Index | //+------------------------------------------------------------------+ double mamdani_rsi(double rsi) { double res=0; //--- Mamdani Fuzzy System MamdaniFuzzySystem *fsRSI=new MamdaniFuzzySystem(); //--- Die Erstellung der Eingabeparameter für das System und die Bestimmung der Begriffe FuzzyVariable *fsTrend=new FuzzyVariable("rsi",60.0,85.0); //--- fsTrend.Terms().Add(new FuzzyTerm("weak", new SigmoidalMembershipFunction(-0.75,67.5))); fsTrend.Terms().Add(new FuzzyTerm("average", new NormalMembershipFunction(72.5,2.2))); fsTrend.Terms().Add(new FuzzyTerm("strong", new NormalMembershipFunction(80.0,1.4))); fsRSI.Input().Add(fsTrend); //--- Die Erstellung der Ausgangsparameter für das System und die Bestimmung der Begriffe FuzzyVariable *fsIndex=new FuzzyVariable("index",1.0,4.0); fsIndex.Terms().Add(new FuzzyTerm("low", new SigmoidalMembershipFunction(-11.0,1.5))); fsIndex.Terms().Add(new FuzzyTerm("normal", new NormalMembershipFunction(2.0,0.3))); fsIndex.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,3.0))); fsRSI.Output().Add(fsIndex); //--- Die Erstellung der Fuzzy-Regeln und deren Hinzufügen zum System MamdaniFuzzyRule *rule1 = fsRSI.ParseRule("if (rsi is weak) then (index is low)"); MamdaniFuzzyRule *rule2 = fsRSI.ParseRule("if (rsi is average) then (index is normal)"); MamdaniFuzzyRule *rule3 = fsRSI.ParseRule("if (rsi is strong) then (index is high)"); fsRSI.Rules().Add(rule1); fsRSI.Rules().Add(rule2); fsRSI.Rules().Add(rule3); //--- Die Einstellung der Eingabewerte CList *in=new CList; Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double; p_od_in.SetAll(fsTrend,rsi); in.Add(p_od_in); //--- Die Anzeige des Ergebnis CList *result=new CList; Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double; result=fsRSI.Calculate(in); p_od_out=result.GetNodeAtIndex(0); res=NormalizeDouble(p_od_out.Value(),_Digits); //--- delete in; delete result; delete fsRSI; return res; } //+------------------------------------------------------------------+ //| Die Funktion des Fuzzy-Berechnungsmodells für das Take-Profit-Index | //+------------------------------------------------------------------+ double mamdani_tp(double ind_rsi) { double res=0; //--- Mamdani Fuzzy System MamdaniFuzzySystem *fsTP=new MamdaniFuzzySystem(); //--- Die Erstellung der Eingabeparameter für das System und die Bestimmung der Begriffe FuzzyVariable *fsIndex=new FuzzyVariable("index",1.0,4.0); fsIndex.Terms().Add(new FuzzyTerm("low", new SigmoidalMembershipFunction(-11.0,1.5))); fsIndex.Terms().Add(new FuzzyTerm("normal", new NormalMembershipFunction(2.0,0.3))); fsIndex.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,3.0))); fsTP.Input().Add(fsIndex); //--- Die Erstellung der Ausgangsparameter für das System und die Bestimmung der Begriffe FuzzyVariable *fsProfit=new FuzzyVariable("TP",30.0,70.0); fsProfit.Terms().Add(new FuzzyTerm("minimal", new SigmoidalMembershipFunction(-0.8,37.5))); fsProfit.Terms().Add(new FuzzyTerm("average", new NormalMembershipFunction(50.0,3.0))); fsProfit.Terms().Add(new FuzzyTerm("maximal", new SigmoidalMembershipFunction(0.8,62.5))); fsTP.Output().Add(fsProfit); //--- Die Erstellung der Fuzzy-Regeln und deren Hinzufügen zum System MamdaniFuzzyRule *rule1 = fsTP.ParseRule("if (index is low) then (TP is minimal)"); MamdaniFuzzyRule *rule2 = fsTP.ParseRule("if (index is normal) then (TP is average)"); MamdaniFuzzyRule *rule3 = fsTP.ParseRule("if (index is high) then (TP is maximal)"); fsTP.Rules().Add(rule1); fsTP.Rules().Add(rule2); fsTP.Rules().Add(rule3); //--- Die Einstellung der Eingabewerte CList *in=new CList; Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double; p_od_in.SetAll(fsIndex,ind_rsi); in.Add(p_od_in); //--- Die Anzeige des Ergebnis CList *result=new CList; Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double; result=fsTP.Calculate(in); p_od_out=result.GetNodeAtIndex(0); res=NormalizeDouble(p_od_out.Value(),_Digits); //--- delete in; delete result; delete fsTP; return res; } //+------------------------------------------------------------------+
Nun wollen wir die großen Veränderungen untersuchen, die im EA eingefügt wurden:
- Die wichtigste Änderung ist die Realisierung der beiden Fuzzy-Modelle in Form von Funktionen mamdani_rsi und mamdani_tp.
- Stop-Loss und Take-Profit-Parameter wurden entfernt. Sie werden nun mit Hilfe der Fuzzy-Logik berechnet.
- Hier betrachten wir, wie diese Berechnung durchgeführt wird:
if(OrdersTotal()<1) { depth_trend(); speed_ac(); rs=tr.ND(iRSI(_Symbol,tf,period,PRICE_CLOSE,0),2); //--- Die Überprüfung der Bedingungen auf den Verkauf if(Buy() && rs<=85.0) { mdm = mamdani_rsi(rs); tkp = MathCeil(mamdani_tp(mdm)); stl = MathCeil(tkp*0.43); if(tr.OpnOrd(OP_BUY,lt,tkp,stl)) Print("RSI равно ",rs," TP gleich ",tkp," SL gleich ",stl); } //--- Die Überprüfung der Bedingungen auf den Kauf if(Sell() && rs>=15.0) { mdm = mamdani_rsi(100-rs); tkp = MathCeil(mamdani_tp(mdm)); stl = MathCeil(tkp*0.43); if(tr.OpnOrd(OP_SELL,lt,tkp,stl)) Print("RSI равно ",rs," TP gleich ",tkp," SL gleich ",stl); } }
Wenn es keine offenen Orders mit dem EA-Magik gibt, verwendet das System die Funktionen depth_trend() und speed_ac() und verfolgt die Bewegungsparameter auf dem Markt, und wenn Buy() oder Sell() der Bedingungen entspricht, dann tritt den Markt ein. Als nächstes, wenn die Bedingungen erfüllt werden, wird der Wert des Fuzzy-Modell-Operationsergebnis zum Parameter mdm zugewiesen, der den aktuellen Wert RSI am Eingang hat und einem Fuzzy-Index am Ausgang. Wiederum wird die Fuzzy-Indexwert zum Eingang unseres anderen Systems verwendet, in dem der Ausgang die Take-Profit in Punkten ist. Die Werte der Take-Profit wird der tkp-Variablen zugewiesen.
Das Verhältnis von 0,43 wird auf dem maximalen Wert von 70 Punkten basierend genommen und die entsprechende Stop-Loss wird 30. Falls eine Order erfolgreich eröffnet wird, zeigt unser EA auch den RSI-Wert, bei dem der eröffnet wurde, sowie die Stop-Loss und Take-Profit-Parameter, die von seinen Werten berechnet wurden. Das macht den Test bequem.
Außerdem ist es notwendig, die folgenden Momente zu erklären:
- Falls es verkauft wird, dann wird mamdani_rsi(100-rs) dem mdm zugeordnet. Dies geschieht, weil ihre Bereiche und Grenzen relativ der Extremwerte RSI (0 und 100) gespiegelt sind.
- Der zweite Moment ist die zwei Bedingungen: beim Kauf rs<=85 und in ähnlicher Weise beim Verkauf rs>=15. Dies geschieht, weil, wenn bei der Erstellung der Eingangsvariable des Berechnung-RSI-Indexs vom Fuzzy-Modell die Grenzen zu 60-85 eingestellt sind, wird der Wert von 15 für den Kauf.
Das Arbeitsbeispiel des Eas ist in Abb. 14. , wie wir sehen können, Stop-Loss und TAke-Profit werden bei unterschiedlichen RSI-Werte neu berechnet.
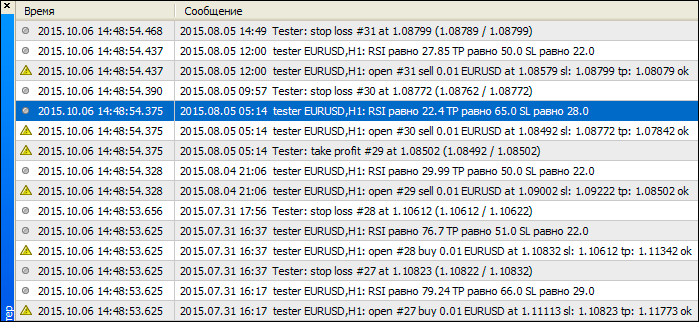
in Abb. 14. Arbeitsergebnisse des EAs
Fazit
In diesem Artikel haben wir die Realisierungsbeispiele der Fuzzy-Set-Theorie mit der FuzzyNet-Bibliothek durch MQL4 betrachtet. Wir haben gezeigt, dass die Systeme auf der Basis der Fuzzy-Logik flexibler sind, wenn sie mit den strengen Kategorien wie Trend-Klassifikation oder Risikodifferenzierung zu tun haben. Im Expert Advisor wurde gezeigt, wie ein auf der Fuzzy-Logik basierte System die Kraft eines Handelssignals analysiert, abgesehen von seiner eigenen Handelsstrategie und definiert selbst die entsprechenden Stop-Loss und Take-Profit-Werte. Ich glaube, dass die Handelssysteme auf Basis der Fuzzy-Logik sind, sind eine Symbiose von den besten Eigenschaften, die für einen erfolgreichen Handel nötig sind - darunter Disziplin eines Trading-Roboters und die Flexibilität eines menschlichen Geistes.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/2032
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Wie ein Marktindikator für alle nicht standarten Charts geschrieben werden soll
Wie ein Marktindikator für alle nicht standarten Charts geschrieben werden soll
 Grafische Interfaces I: Vorbereitung der Bibliotheksstruktur (Kapitel 1)
Grafische Interfaces I: Vorbereitung der Bibliotheksstruktur (Kapitel 1)
 Selbst-organisierende Feature Maps (Kohonen Maps) - Wiederaufgreifen des Themas
Selbst-organisierende Feature Maps (Kohonen Maps) - Wiederaufgreifen des Themas
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.