MetaTrader 4 / 示例
English Русский Español Deutsch 日本語 Português
在交易中以 MQL4 手段运用模糊逻辑

在交易中以 MQL4 手段运用模糊逻辑

MetaTrader 4 — 示例 |
9 176 0
Alexander Fedosov
Alexander Fedosov

介绍

在现代每日交易里, 难以想象没有通常称为智能交易系统或机器人的自动交易系统。大多数情况下, 但并非它们全部, 拥有一个清晰的, 固化编码的交易策略和资金管理系统。它们的主要优点是排除了人性因素的刚性算法。然而, 这种优势也是它们的主要缺点, 因为交易机器人缺乏灵活性。无视市场状况, EA 总是应用参数严格类同的同一交易策略。换言之, 系统总是严格执行: 平缓趋势 >以一手入场, 强趋势则以两手入场。没有偏差！

与自动系统不同, 人类交易员按照模糊分类思考, 并在类似的入场信号可能有不同的见解。 market entry signals. 他们通常多疑, 并持续自问, 是否趋势是中度或是强烈。而且即使趋势显著, 但以两手入场是否足够强健？这种模糊分类可以通过模糊逻辑来处理。模糊逻辑不会在类别之间设置刚性边界。相反, 它将其 "虚化", 令交易系统更加灵活, 并结合了交易机器人的刚性与人类思维的灵活性。本文举例说明在交易中以 MQL4 手段运用模糊逻辑系统。


隶属函数

参阅文章 "模糊逻辑介绍" 来掌握模糊逻辑理论的一般概念。还有, 了解基本的 用于 MQL4 的模糊函数库, 因为本例将会用它们来实现。

让我们来说明文章中使用的隶属函数。


三角型隶属函数

顾名思义, 这是一个三角形隶属函数。它是简单但使用频繁的函数, 由以下解析公式定义:

三角型函数定义

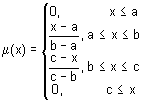
它通常用于指定以下不确定类型: "大致相等", "平均值", "位于的范围内", "类似的物体", "看着像物体", 等等。三角隶属函数参数通常解释如下:

  • [a, c] — 变量范围;
  • b — 最可能的变量值。

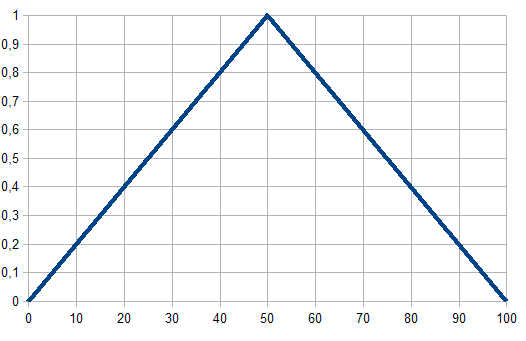
图例. 1. 三角型隶属函数


梯形隶属函数

梯形隶属函数由下式所定义:

梯形隶属函数

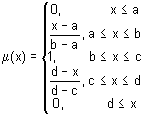
梯形隶属函数的参数解释如下:

  • [a, d] – 模糊集载体, 悲观评估变量;
  • [b, c] – 模糊集核心, 乐观评估变量;

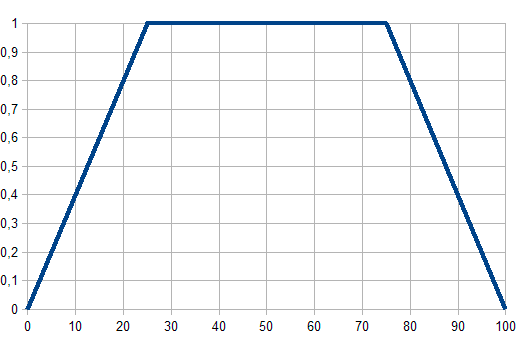
图例. 2. 梯形隶属函数


钟形隶属函数

由对称钟形曲线形成的隶属函数按照如下公式定义:

钟形隶属函数

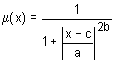
参数值的含义如下:

  • a – 隶属函数浓缩率;
  • b – 隶属函数斜率;
  • c – 隶属函数最高点坐标。

图例. 3. 钟形隶属函数


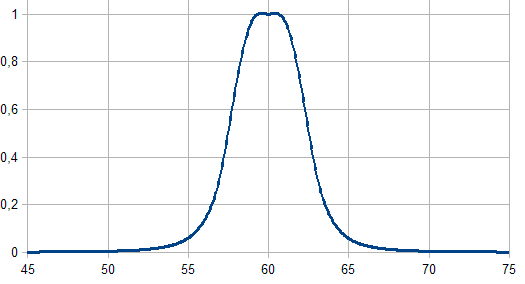
S 型隶属函数

公式使用以下公式计算, 并在设定单调隶属函数时应用此函数:

S 型隶属函数

其参数含义如下:

  • a – 隶属函数斜率;
  • с – 隶属函数拐点坐标。

图例. 4. S 型隶属函数


利用 MQL4 版本的 FuzzyNet 函数库实现的一款指标样本

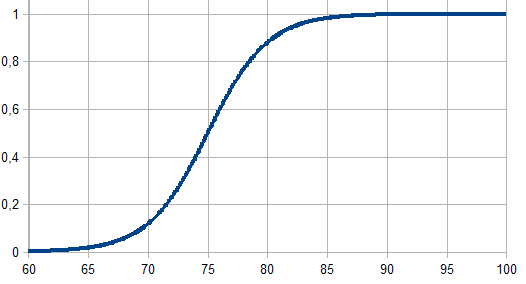
我们将使用 平均方向走势指数 (ADX) 作为例子。这是一款趋势指标, 判断当前趋势的的强度 (绿色粗线)。首先, 让我们定义趋势强度精度的准则 (图例. 5):
  • 弱趋势 – 绿色主线处于范围 30-50 之间。数值在这个严格定义的范围内被认为是弱趋势。
  • 平缓趋势 – 绿色主线处于范围 50-70 之间 (平缓趋势)。
  • 强趋势 – 绿色主线处于范围 70-100 之间 (强趋势)。

图例. 5. ADX 的操作和实施按照趋势强度划分

由于明确和严格的分类逻辑, 导致三个严格定义的类别有一些瑕疵:

  • 第一个缺点是主观分类性质。事实上, 为什么选择 30, 50, 70 作为边界值？为什么我们不选 25, 50, 和 75, 或是其它一些？这些不同的见解可能会极大地影响 ADX 操作, 甚至导致截然相反的交易结果。
  • 第二个问题是所选类别的边界区域。例如, 50 是弱趋势和平缓趋势的边界。如果我们按照严格逻辑, 我们不得不承认 48 和 49 依然属于弱趋势范围, 而 50 和 51 则已经是在平缓趋势区域。但是从 49 到 50 如何过渡？在这两种情况下 (48-49 和 49-50), 数值间的差值均为一。然而, 出于一些原因, 后者的情况可认为是从一个类别过渡到另一个。

所以, 模糊逻辑如何能解决这些问题？

如前所述, 模糊逻辑 "虚化" (模糊化) 指定边界。硬性规定的类别边界值一次分配到两个类别, 但成分有所不同。在这种情况下可能的样本描述如下所示: 当前趋势可描述为弱趋势 (30%), 但很大可能它会被描述为平缓趋势 (70%)。一位人类交易者将会如下描述: 走势平缓, 而非弱势。我相信, 这就是模糊逻辑的优势。处理硬性规定的参数时, 它很灵活多变。我选择了以下隶属函数和 ADX 指标用于我们的例子:

  • 梯形隶属函数用来描述弱趋势概念。
  • 钟形隶属函数用来描述平缓趋势概念。
  • S 形隶属函数用来描述强趋势概念。

更复杂系统包含的多种数量分类, 可以使用在 FuzzyNet 函数库里提供的其它函数来描述。当前, 函数库包含了超过十二种函数。我们例程的图解如下所示:


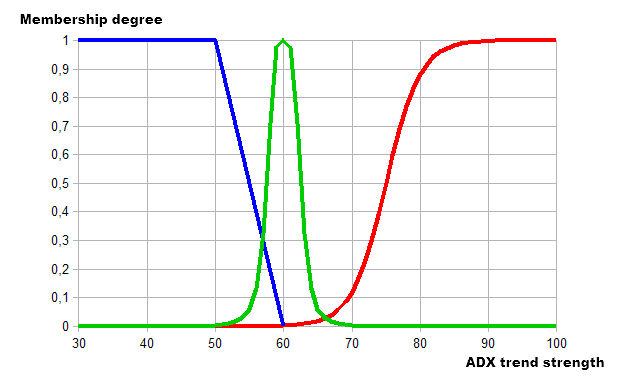
图例. 6. 使用模糊逻辑描绘趋势

我们可以看到, 图中现在存在同时具有两个趋势类别的区域。趋势在 50-60 区域为弱趋势和平缓趋势, 而在 60-70 则为平缓趋势和强趋势。因此, 我们已经利用预定隶属函数定义为三个类别定义条件集合。现在, 我们已有了经由隶属函数描述的 ADX 输入, 我们应该定义我们所考虑的一个输出值和模糊化的结果, 以及选择一个模糊逻辑的输出算法。

对于我们的例子, 我选择了相对于初值的资金风险比例定为模糊趋势强度的变量。换言之, 强趋势, 则应用较高的风险和资金百分比。我已选择 Mamdani 作为逻辑输出算法。

与趋势强度相似, 让我们根据风险程度介绍三种不同的类别:

  • 低风险 – 资金的 2-4%。
  • 正常风险 (正常) – 4-5%。
  • 高风险 (高) – 资金从 5% 到最大 10%。

现在, 让我们来使用隶属函数定义风险类别:

  • 梯形 – 用于低风险。
  • 三角形 – 用于正常风险。
  • S 型 – 用于高风险。

其结果是, 我们通过模糊逻辑的手段获得了以下图形描述:


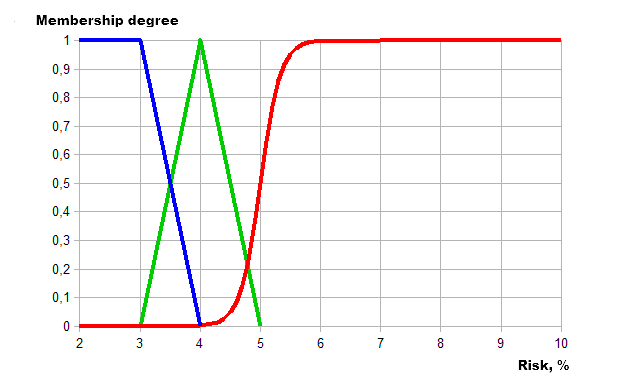
图例. 7. 使用模糊逻辑手段描绘风险程度


让我们使用 MQL4 版本的 FuzzyNet 函数库来实现描述的数据:

//+------------------------------------------------------------------+
//|                                                    ADX_Fuzzy.mq4 |
//|                                                Alexander Fedosov |
//|                           https://www.mql5.com/zh/users/alex2356 |
//+------------------------------------------------------------------+
#property copyright "Alexander Fedosov"
#property link      "https://www.mql5.com/zh/users/alex2356"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 2
#property indicator_color1 Green
#property indicator_color2 Red
#property indicator_minimum 0
#property indicator_maximum 10
//+------------------------------------------------------------------+
//| 连接函数库                                                        |
//+------------------------------------------------------------------+
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>
//--- 输入参数
input string  p1="==== 参数 ====";
input int    visual=100;             // 可视周期
input int    adx_period=10;          // ADX 周期
//---
double Buffer1[],Buffer2[],adx,adx_di_minus,adx_di_plus;
int limit;
//+------------------------------------------------------------------+
//| 自定义初始化函数                                                  |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- 指标缓存映射
   SetIndexStyle(0,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(0,Buffer1);
   SetIndexEmptyValue(0,0.0);
//---
   SetIndexStyle(1,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(1,Buffer2);
   SetIndexEmptyValue(1,0.0);
//---
   ArrayResize(Buffer1,visual);
   ArrayResize(Buffer2,visual);
   ArrayInitialize(Buffer1,0.0);
   ArrayInitialize(Buffer2,0.0);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| 自定义迭代函数                                                    |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
   int count_bars=IndicatorCounted();
//---
   if(count_bars<0)
      return(-1);
//---
   if(Bars-1<adx_period)
      return(0);
//---
   for(int i=0; i<visual;i++)
     {
      adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits);
      adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits);
      adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits);
      //---
      double r=(adx_di_plus-adx_di_minus);
      if(MathAbs(r)>10 && adx>=30.0)
         if(r>0)
            Buffer1[i]=mamdani(adx);
      else if(r<0)
         Buffer2[i]=mamdani(adx);
     }
   return(rates_total);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double mamdani(double v)
  {
   double res=0;
//--- Mamdani 模糊系统  
   MamdaniFuzzySystem *fsRisk=new MamdaniFuzzySystem();
//--- 创建系统使用的输入变量
   FuzzyVariable *fsTrend=new FuzzyVariable("趋势",30.0,100.0);
//---
   fsTrend.Terms().Add(new FuzzyTerm("弱", new TrapezoidMembershipFunction(20.0, 30.0, 50.0, 60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("平缓", new GeneralizedBellShapedMembershipFunction(2.5,2.0,60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("强",new SigmoidalMembershipFunction(0.4,75.0)));
   fsRisk.Input().Add(fsTrend);
//--- 创建输出
   FuzzyVariable *fvRisk=new FuzzyVariable("风险",2.0,10.0);
   fvRisk.Terms().Add(new FuzzyTerm("低", new TrapezoidMembershipFunction(1.0, 2.0, 3.0, 4.0)));
   fvRisk.Terms().Add(new FuzzyTerm("正常", new TriangularMembershipFunction(3.0, 4.0, 5.0)));
   fvRisk.Terms().Add(new FuzzyTerm("高", new SigmoidalMembershipFunction(6.0,5.0)));
   fsRisk.Output().Add(fvRisk);
//--- 创建 Mamdani 模糊规则
   MamdaniFuzzyRule *rule1 = fsRisk.ParseRule("如果 (趋势弱) 则风险低");
   MamdaniFuzzyRule *rule2 = fsRisk.ParseRule("如果 (趋势平缓) 则风险正常");
   MamdaniFuzzyRule *rule3 = fsRisk.ParseRule("如果 (趋势强) 则风险高");
//--- 在系统里添加三条 Mamdani 模糊规则
   fsRisk.Rules().Add(rule1);
   fsRisk.Rules().Add(rule2);
   fsRisk.Rules().Add(rule3);
//--- 设置输入值
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsTrend,v);
   in.Add(p_od_in);
//--- 获取结果
   CList *result;
   Dictionary_Obj_Double *p_od_out;
   result=fsRisk.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);
//---
   delete in;
   delete result;
   delete fsRisk;
   return res;
  }
//+------------------------------------------------------------------+

我已经开发出一款简单的可视化风险程度/趋势强度比率直方图指标 (绿色 - 多头趋势, 红色 - 空头趋势)。直方图柱线'高度显示上述范围内的各种趋势强度的风险程度数值。让我们来审查详细的代码。

首先, 让我们为使用直方图定义两个缓冲器, 它们的颜色, 以及从零到规定的最高风险 10％ 对应垂直轴上的范围。

#property indicator_separate_window
#property indicator_buffers 2
#property indicator_color1 Green
#property indicator_color2 Red
#property indicator_minimum 0
#property indicator_maximum 10

接着, 根据 Mamdani 算法连接函数库创建系统, 并添加变量, 用于可视化柱线的数量, 范围从零到调整的 ADX 周期。

//+------------------------------------------------------------------+
//| 连接 FuzzyNet 函数库                                              |
//+------------------------------------------------------------------+
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>
//--- 输入参数
input string  p1="==== 参数 ====";
input int    visual=100;             // 可视周期
input int    adx_period=10;          // ADX 周期

当初始化时, 我们应设置指标形成直方图。

//+------------------------------------------------------------------+
//| 自定义初始化函数                                                  |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- 指标缓存映射
   SetIndexStyle(0,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(0,Buffer1);
   SetIndexEmptyValue(0,0.0);
//---
   SetIndexStyle(1,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(1,Buffer2);
   SetIndexEmptyValue(1,0.0);
//---
   ArrayResize(Buffer1,visual);
   ArrayResize(Buffer2,visual);
   ArrayInitialize(Buffer1,0.0);
   ArrayInitialize(Buffer2,0.0);
//---
   return(INIT_SUCCEEDED);
  }

在主代码中, 我们定义了 ADX 指标的基本读取。r 变量用于查找两个趋势方向指标 +DI 和 -DI 之间的差值。进而, 我们介绍的趋势存在滤波器与 +DI 和 -DI 的绝对值间有高于 10 的差异, 主要趋势强度高于 30 (弱趋势限制更低)。接下来, 让我们基于 r 变量符号定义一个趋势方向, 并将 mamdani() 函数置于一个预定值。

int count_bars=IndicatorCounted();
//---
   if(count_bars<0)
      return(-1);
//---
   if(Bars-1<adx_period)
      return(0);
//---
   for(int i=0; i<visual;i++)
     {
      adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits);
      adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits);
      adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits);
      //---
      double r=(adx_di_plus-adx_di_minus);
      if(MathAbs(r)>10 && adx>=30.0)
         if(r>0)
            Buffer1[i]=mamdani(adx);
      else if(r<0)
         Buffer2[i]=mamdani(adx);
     }

Mamdani 函数说明:

1. 让我们来创建 Mamdani-类型模糊逻辑系统的新系统 *fsRisk。

2. 添加 *fsTrend 变量于其内, 指定 trend 名称和 30 和 100 的最小/最大值。

//--- Mamdani 模糊系统  
   MamdaniFuzzySystem *fsRisk=new MamdaniFuzzySystem();
//--- 创建系统使用的输入变量
   FuzzyVariable *fsTrend=new FuzzyVariable("趋势",30.0,100.0);

3. 下一步, 我们应为每个类别选择隶属函数并添加上述的模糊条件 (图例. 6)。

fsTrend.Terms().Add(new FuzzyTerm("weak", new TrapezoidMembershipFunction(30.0, 40.0, 50.0, 60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("平缓", new GeneralizedBellShapedMembershipFunction(2.5,2.0,60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("强",new SigmoidalMembershipFunction(0.4,75.0)));
   fsRisk.Input().Add(fsTrend);

4. 对于输出值掠过步骤 2-3: 创建 *fvRisk 变量, 名为 风险 且最小和最大风险值为 2% 和 10%。

//--- 创建输出
   FuzzyVariable *fvRisk=new FuzzyVariable("风险",2.0,10.0);
   fvRisk.Terms().Add(new FuzzyTerm("低", new TriangularMembershipFunction(2.0, 3.0, 4.0)));
   fvRisk.Terms().Add(new FuzzyTerm("正常", new TriangularMembershipFunction(3.0, 4.0, 5.0)));
   fvRisk.Terms().Add(new FuzzyTerm("高", new SigmoidalMembershipFunction(6.0,5.0)));
   fsRisk.Output().Add(fvRisk);

5. 现在, 让我们创建一个三条模糊规则的集合代表我们的系统:

  • 如果弱趋势, 低风险。
  • 如果平缓趋势, 正常风险。
  • 如果强趋势, 高风险。
//--- 创建 Mamdani 模糊规则
   MamdaniFuzzyRule *rule1 = fsRisk.ParseRule("如果 (趋势弱) 则风险低");
   MamdaniFuzzyRule *rule2 = fsRisk.ParseRule("如果 (趋势平缓) 则风险正常");
   MamdaniFuzzyRule *rule3 = fsRisk.ParseRule("如果 (趋势强) 则风险高");

6. 让我们将规则加进系统:

//--- 在系统里添加三条 Mamdani 模糊规则
   fsRisk.Rules().Add(rule1);
   fsRisk.Rules().Add(rule2);
   fsRisk.Rules().Add(rule3);

7. 创建输入和输出变量列表并添加 v 输入作为 mamdani 函数参量。因此, 具有指定输入和输出模糊变量的完整模糊逻辑系统已为整个 mamdani 函数设置完毕, 而 ADX 指标数值作为输入。

//--- 设置输入值
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsTrend,v);
   in.Add(p_od_in);
//--- 获取结果
   CList *result=new CList;
   Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double;
   result=fsRisk.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);

8. 结果函数值是基于直方图的变量 res。

adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits);
      adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits);
      adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits);
      //---
      double r=(adx_di_plus-adx_di_minus);
      if(MathAbs(r)>10 && adx>=30.0)
         if(r>0)
            Buffer1[i]=mamdani(adx);
      else if(r<0)
         Buffer2[i]=mamdani(adx);

可视指标运算结果如下:

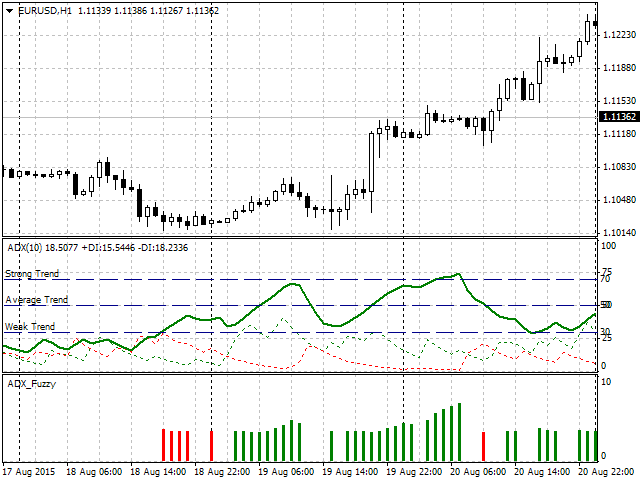
图例. 8. 指标操作

我们可以看到, 指标使用直方图颜色揭示趋势存在, 而柱线高度显示建议的资金风险百分比。一个显而易见的问题出现了 - 如果指标按照明确的时间间隔实现将会有什么区别？要回答这个问题, 让我们考虑下一部分的更多细节 (图9)。绿色箭头表示直方图柱线, 而它的数字值和 ADX 趋势强度显示在左侧。如早前定义, ADX 超过 70 是强趋势, 意味着风险值应超过 5％。正如我们在图例.9 中清楚地看到, ADX = 69.7923。因此, 如果我们运用严格的规则, 这仍是一个平缓趋势且风险不应超过 5％。不过, 它等于 5.6406, 即, 它是较高的。


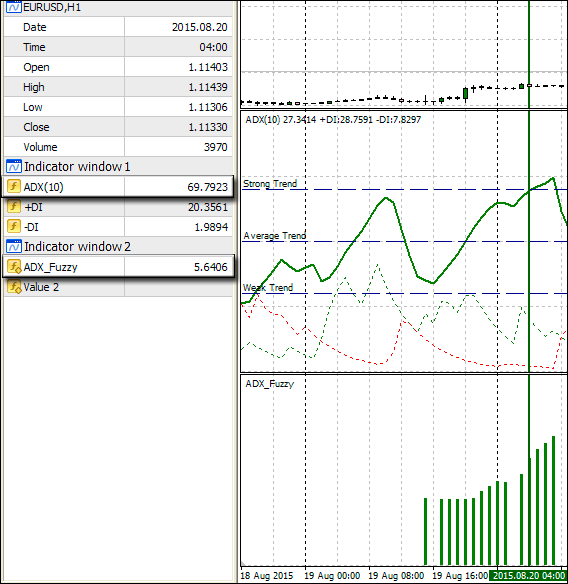
图例. 9. 揭示模糊和标准逻辑之间的差异

在这里, 我们可以在动作里看到模糊逻辑。它已定义为即使数值小于 70, 在该区域的趋势依然强于平缓趋势。我们可以通过检查图例.6 看到自己。当 X 轴值显示 69.7923, 强趋势的隶属函数比平缓趋势更高。所以, 我们的系统在接近强趋势和平缓趋势之间的边界区域所提供的风险值超过 5%, 与严格逻辑体系相比方式更加灵活。


运用 MQL4 的 FuzzyNet 函数库实现的一款智能交易系统的样本。

在此, 我要揭示明确界定条件和模糊逻辑元素情况下, 智能交易系统操作的差异。为了令比较尽可能地接地气, 我决定使用来自我的其它文章 "基于价格方向和运动速度的交易思想" 中的 EA, 在那篇文章里详细讲述了交易机器人的思路。为了避免过度重复, 我将使用的这个 EA 基本上带有以下变化:

  • EA 的逻辑基于价格运动的持久性的思路。运动参数由以下指标描述: RSI (速度指标) 和 AC (加速度指标)。速度和加速度按照这些指标的数值范围指数评估。现在, 让我们运用模糊集理论处理 RSI 指数值。其结果是, RSI 值作为输入, 而输出是模糊速度指数, 不仅有整数值, 如 1-4, 还有 1.3 或 3.85。
  • 反之, 模糊指数值被用作另一系统的输入, 其输出是利润值。因此, 止盈在最初的 EA 里原封不动。

连接背后的想法是简单的。如果 RSI 和 AC 是运动参数, 则速度越高, 运动的持久性更高, 所以放置更大止盈是合理的。如果运动速度降低, 目标利润应该设置得更贴近, 以避免回滚或趋势反转。图例. 10 显示框图以便更清楚地了解 EA 中的模糊逻辑应用。


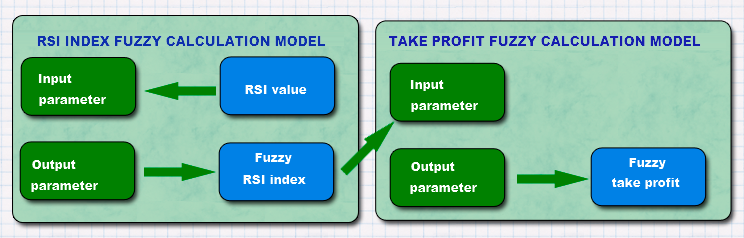
图例. 10. 在 EA 里运用模糊逻辑

在配合指标的情况下, 我们来为模糊模型描述隶属函数。第一个是计算 RSI 指数的模糊模型, 此处输入是指标的值。让我们将必要的值划分为三类:

  • 弱。第一类定义弱趋势。RSI: 60-70。
  • 平缓。第二类定义平缓趋势。RSI: 70-80。
  • 强。第三类定义强趋势。RSI: 80-85。

让我们来选择描述指定类别的隶属函数:

  • 弱。斜率 -0.75 且拐点 67.5 的 S 型函数。
  • 平缓。最大坐标 72.5 且 浓度 2.2 的高斯函数。
  • 强。最大坐标 80 且 浓度 1.4 的高斯函数。

直观表现如下:


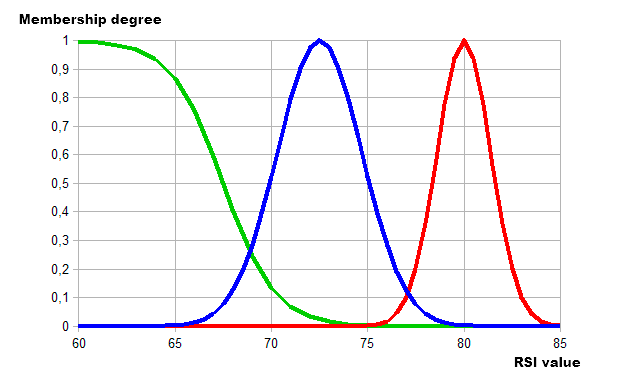
图例. 11. 使用隶属函数来描述 RSI 值的类别

这种模糊模型的输出是 RSI 指数。以下类别和隶属函数用来描述它:

  • 低。低指数, 范围 1-2。斜率 -11 且拐点 1.5 的 S 型隶属函数。
  • 正常. 平缓指数, 范围 2-3。隶属函数是最大坐标 2 且 浓度 0.3 的高斯函数。
  • 高。高指数, 范围 3-4。斜率 6 且拐点 3 的 S 型隶属函数。

作为结果, 我们得到以下的视图:


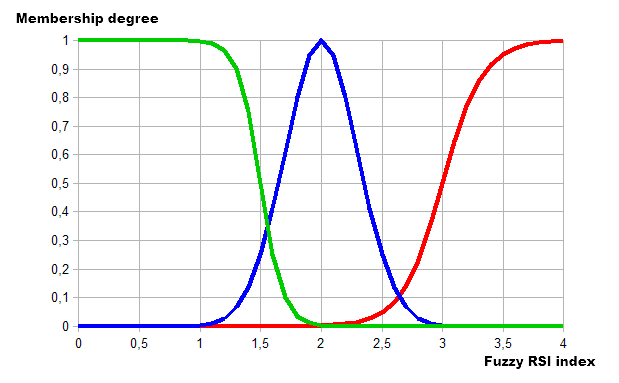
图例. 12. 使用隶属函数来描述 RSI 指数值的类别

接下来, 让我们来描述来自图例. 10 的第二个模糊模型 - 模糊止盈计算模型。模型的输入已经作为第一个模型 (RSI 模糊指数) 的输出描述过。止盈值在此作为输出。让我们来为它定义一个简明的类别:

  • 最小。 最小止盈类别, 范围在 30-40 之内。
  • 平缓。 平缓止盈类别范围在 40-60 之内。
  • 最大。 高止盈类别在范围 60-70 之内。

现在, 让我们来使用隶属函数进行说明:

  • 最小。 斜率 -0.8 且拐点 37.5 的 S 型隶属函数。
  • 平缓。 隶属函数是最大坐标 50 且浓度 3 的高斯函数。
  • 最大. 斜率 0.8 且拐点 62.5 的 S 型隶属函数。

图形执行如下所示:


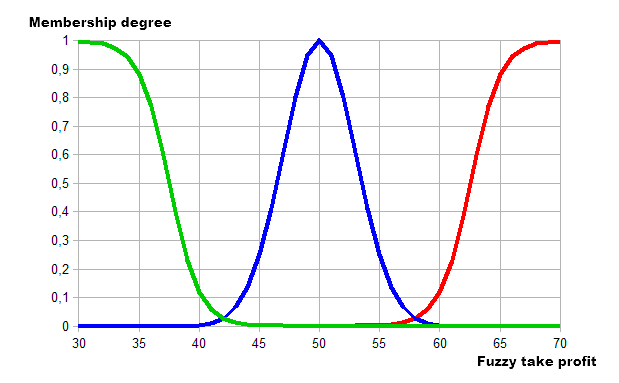
图例. 13. 使用隶属函数来描述止盈值的类别

现在, 所有的参数都已定义, 是时候在交易机器人里实现这个想法。我们将根据 RSI 读数增加两个模糊模型计算连续止损和止盈。

//+------------------------------------------------------------------+
//|                                                       tester.mq4 |
//|                                                Alexander Fedosov |
//|                                                                  |
//+------------------------------------------------------------------+
#property copyright "Alexander Fedosov"
#property strict
#include "trading.mqh" //支持交易操作的函数库
//+------------------------------------------------------------------+
//| 连接函数库                                                        |
//+------------------------------------------------------------------+
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>
//+------------------------------------------------------------------+
//| Parameters                                                       |
//+------------------------------------------------------------------+
input bool           Lot_perm=false;               // 余额手数？
input double         Risk = 2;                     // 资金风险, %
input double         lt=0.01;                      // 手数
input int            magic=2356;                   // 魔幻数字
input int            period=14;                    // RSI 指标周期
input ENUM_TIMEFRAMES tf=PERIOD_CURRENT;           // 工作时间帧
//---
int index_rsi,index_ac;
double tkp,stl;
double rs,mdm;
CTrading tr;
//+------------------------------------------------------------------+
//| EA 初始化函数                                                     |
//+------------------------------------------------------------------+
int OnInit()
  {
   tr.Trading(magic,5,lt,Lot_perm,Risk);
   tr.exp_name="模糊逻辑测试器";
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| 主要计算函数                                                      |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- 检查存在的已开订单
   if(!tr.isOpened(magic))
     {
      depth_trend();
      speed_ac();
      rs=tr.ND(iRSI(_Symbol,tf,period,PRICE_CLOSE,0),2);
      //--- 检查买入条件
      if(Buy() && rs<=85.0)
        {
         mdm = mamdani_rsi(rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_BUY,lt,(int)tkp,(int)stl))
            Print("RSI 等于 ",rs," 止盈等于 ",tkp," 止损等于 ",stl);
        }
      //--- 检查卖出条件
      if(Sell() && rs>=15.0)
        {
         mdm = mamdani_rsi(100-rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_SELL,lt,(int)tkp,(int)stl))
            Print("RSI 等于 ",rs," 止盈等于 ",tkp," 止损等于 ",stl);
        }
     }
//--- 此处开单么？
   if(tr.isOpened(magic))
     {
      //--- 检查并将满足条件的空头单平仓
      if(Sell_close())
         tr.ClosePosAll(OP_SELL);
      //--- 检查并将满足条件的多头单平仓
      if(Buy_close())
         tr.ClosePosAll(OP_BUY);
     }
  }
//+---------------------------------------------------------------+
//| 判断趋势深度的函数                                             |
//+---------------------------------------------------------------+
void depth_trend()
  {
//--- 定义入场指数
   double rsi=iRSI(_Symbol,tf,period,PRICE_CLOSE,0);
//---
   index_rsi=0;
   if(rsi>90.0)
      index_rsi=4;
   else if(rsi>80.0)
      index_rsi=3;
   else if(rsi>70.0)
      index_rsi=2;
   else if(rsi>60.0)
      index_rsi=1;
   else if(rsi<10.0)
      index_rsi=-4;
   else if(rsi<20.0)
      index_rsi=-3;
   else if(rsi<30.0)
      index_rsi=-2;
   else if(rsi<40.0)
      index_rsi=-1;
  }
//+----------------------------------------------------------------+
//| 判断趋势速度的函数                                              |
//+----------------------------------------------------------------+
void speed_ac()
  {
   double ac[];
   ArrayResize(ac,5);
   ArrayInitialize(ac,0.0);
   for(int i=0; i<5; i++)
      ac[i]=iAC(_Symbol,tf,i);
//---
   index_ac=0;
//--- 买入指数
   if(ac[0]>ac[1])
      index_ac=1;
   else if(ac[0]>ac[1] && ac[1]>ac[2])
      index_ac=2;
   else if(ac[0]>ac[1] && ac[1]>ac[2] && ac[2]>ac[3])
      index_ac=3;
   else if(ac[0]>ac[1] && ac[1]>ac[2] && ac[2]>ac[3] && ac[3]>ac[4])
      index_ac=4;
//--- 卖出指数
   else if(ac[0]<ac[1])
      index_ac=-1;
   else if(ac[0]<ac[1] && ac[1]<ac[2])
      index_ac=-2;
   else if(ac[0]<ac[1] && ac[1]<ac[2] && ac[2]<ac[3])
      index_ac=-3;
   else if(ac[0]<ac[1] && ac[1]<ac[2] && ac[2]<ac[3] && ac[3]<ac[4])
      index_ac=-4;
  }
//+----------------------------------------------------------------+
//| 检查买入条件的函数                                              |
//+----------------------------------------------------------------+
bool Buy()
  {
   return (((index_rsi==2 && index_ac>=1) || (index_rsi==3 && index_ac==1))?true:false);
  }
//+----------------------------------------------------------------+
//| 检查卖出条件的函数                                              |
//+----------------------------------------------------------------+
bool Sell()
  {
   return (((index_rsi==-2 && index_ac<=-1) || (index_rsi==-3 && index_ac==-1))?true:false);
  }
//+----------------------------------------------------------------+
//| 检查多头单平仓条件的函数                                         |
//+----------------------------------------------------------------+
bool Buy_close()
  {
   return ((index_rsi>2 && index_ac<0)?true:false);
  }
//+----------------------------------------------------------------+
//| 检查空头单平仓条件的函数                                         |
//+----------------------------------------------------------------+
bool Sell_close()
  {
   return ((index_rsi<-2 && index_ac>0)?true:false);
  }
//+----------------------------------------------------------------+
//| RSI 指数模糊计算模型                                            |
//+----------------------------------------------------------------+
double mamdani_rsi(double rsi)
  {
   double res=0;
//--- Mamdani 模糊系统  
   MamdaniFuzzySystem *fsRSI=new MamdaniFuzzySystem();
//--- 创建系统输入并定义条件
   FuzzyVariable *fsTrend=new FuzzyVariable("rsi",60.0,85.0);
//---
   fsTrend.Terms().Add(new FuzzyTerm("弱", new SigmoidalMembershipFunction(-0.75,67.5)));
   fsTrend.Terms().Add(new FuzzyTerm("平缓", new NormalMembershipFunction(72.5,2.2)));
   fsTrend.Terms().Add(new FuzzyTerm("强", new NormalMembershipFunction(80.0,1.4)));
   fsRSI.Input().Add(fsTrend);
//--- 创建系统输出并定义条件
   FuzzyVariable *fsIndex=new FuzzyVariable("指数",1.0,4.0);
   fsIndex.Terms().Add(new FuzzyTerm("低", new SigmoidalMembershipFunction(-11.0,1.5)));
   fsIndex.Terms().Add(new FuzzyTerm("正常", new NormalMembershipFunction(2.0,0.3)));
   fsIndex.Terms().Add(new FuzzyTerm("高", new SigmoidalMembershipFunction(6.0,3.0)));
   fsRSI.Output().Add(fsIndex);
//--- 创建模糊规则并将它们添加系统
   MamdaniFuzzyRule *rule1 = fsRSI.ParseRule("如果 (rsi 弱) 则 (指数低)");
   MamdaniFuzzyRule *rule2 = fsRSI.ParseRule("如果 (rsi 平缓) 则 (指数正常)");
   MamdaniFuzzyRule *rule3 = fsRSI.ParseRule("如果 (rsi 强) 则 (指数高)");
   fsRSI.Rules().Add(rule1);
   fsRSI.Rules().Add(rule2);
   fsRSI.Rules().Add(rule3);
//--- 设置输入值
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsTrend,rsi);
   in.Add(p_od_in);
//--- 结果输出
   CList *result=new CList;
   Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double;
   result=fsRSI.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);
//---
   delete in;
   delete result;
   delete fsRSI;
   return res;
  }
//+----------------------------------------------------------------+
//| 止盈指数计算的模糊模型                                           |
//+----------------------------------------------------------------+
double mamdani_tp(double ind_rsi)
  {
   double res=0;
//--- Mamdani 模糊系统  
   MamdaniFuzzySystem *fsTP=new MamdaniFuzzySystem();
//--- 创建系统输入并定义条件
   FuzzyVariable *fsIndex=new FuzzyVariable("指数",1.0,4.0);
   fsIndex.Terms().Add(new FuzzyTerm("低", new SigmoidalMembershipFunction(-11.0,1.5)));
   fsIndex.Terms().Add(new FuzzyTerm("正常", new NormalMembershipFunction(2.0,0.3)));
   fsIndex.Terms().Add(new FuzzyTerm("高", new SigmoidalMembershipFunction(6.0,3.0)));
   fsTP.Input().Add(fsIndex);
//--- 创建系统输入并定义条件
   FuzzyVariable *fsProfit=new FuzzyVariable("止盈",30.0,70.0);
   fsProfit.Terms().Add(new FuzzyTerm("最小", new SigmoidalMembershipFunction(-0.8,37.5)));
   fsProfit.Terms().Add(new FuzzyTerm("平缓", new NormalMembershipFunction(50.0,3.0)));
   fsProfit.Terms().Add(new FuzzyTerm("最大", new SigmoidalMembershipFunction(0.8,62.5)));
   fsTP.Output().Add(fsProfit);
//--- 创建模糊规则并将它们添加系统
   MamdaniFuzzyRule *rule1 = fsTP.ParseRule("如果 (指数低) 则 (止盈最小)");
   MamdaniFuzzyRule *rule2 = fsTP.ParseRule("如果 (指数正常) 则 (止盈平缓)");
   MamdaniFuzzyRule *rule3 = fsTP.ParseRule("如果 (指数高) 则 (指数最大)");
   fsTP.Rules().Add(rule1);
   fsTP.Rules().Add(rule2);
   fsTP.Rules().Add(rule3);
//--- 设置输入值
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsIndex,ind_rsi);
   in.Add(p_od_in);
//--- 结果输出
   CList *result=new CList;
   Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double;
   result=fsTP.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);
//---
   delete in;
   delete result;
   delete fsTP;
   return res;
  }
//+------------------------------------------------------------------+

现在, 让我们来看看 EA 已经作出的重大变化:

  • 最重要的变化是实现两个模糊模型, mamdani_rsi 和 mamdani_tp 函数。
  • 止损和止盈参数就这样被删除。它们现在使用模糊逻辑计算。
  • 此处是这个计算是如何实现的:
if(OrdersTotal()<1)
     {
      depth_trend();
      speed_ac();
      rs=tr.ND(iRSI(_Symbol,tf,period,PRICE_CLOSE,0),2);
      //--- 检查买入条件
      if(Buy() && rs<=85.0)
        {
         mdm = mamdani_rsi(rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_BUY,lt,tkp,stl))
            Print("RSI 等于 ",rs," 止盈等于 ",tkp," 止损等于 ",stl);
        }
      //--- 检查卖出条件
      if(Sell() && rs>=15.0)
        {
         mdm = mamdani_rsi(100-rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_SELL,lt,tkp,stl))
            Print("RSI 等于 ",rs," 止盈等于 ",tkp," 止损等于 ",stl);
        }
     }

如果没有与 EA 的魔幻数字相符的已开订单, 系统使用 depth_trend() 和 speed_ac() 函数来跟踪行情走势参数。如果匹配 Buy() 或 Sell() 则执行入场。接着, 如果条件满足, 则模糊模型运算结果被分配给 mdm 参数, 其使用当前的 RSI 值作为输入以及一个模糊指数作为输出。反之, 模糊指数值作为其它系统的输入, 其输出的止盈值按照点数。止盈值分配到 tkp 变量。

比率 0.43 是基于最大盈利值 70 点得来的, 而相应的止损是 30。在成功开单的情况下, 我们的 EA 还显示开单处的 RSI 值, 并根据它计算止损和止盈参数。为了测试方便, 这就干脆地完成了。

此外, 以下有必要澄清:

  1. 在卖出条件情况下, mamdani_rsi(100-rs) 被分配给 mdm。这样做是因为它们的范围和边界相对于 RSI 极值 (0 和 100) 是镜像。
  2. 两个附加条件: 当买入 rs<=85 以及类似地当卖出 rs>=15。这样做是因为在创建 RSI 指数计算模糊模型输入时, 边界设为 60-85。因此， 值 15 就变成卖出的极值。

EA 的操作示例显示在图例. 14。正如我们所看到的, 止损和止盈在 RSI 数值不同的情况下, 重新进行了计算。


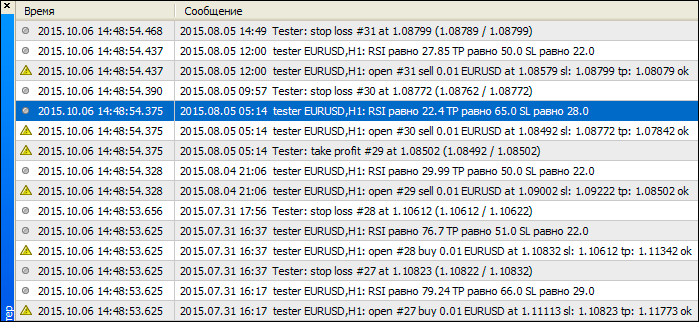
图例. 14. EA 操作结果


结论

在本文中, 我们已经研究了通过 MQL4 手段运用 FuzzyNet 函数库实现模糊集理论的示例。我们已经揭示, 当处理严格分类的问题时, 譬如趋势分类或风险分化, 基于模糊逻辑的系统更加灵活。EA 展示了当应用其自身的交易策略, 并定义适当的止损和止赢值时, 基于模糊逻辑的系统是如何分析一个交易信号强度的。我相信, 基于模糊逻辑的交易系统能够结合成功交易所必要的最佳品质 - 交易机器人的纪律和人类思维的灵活性。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/2032

附加的文件 |
下载ZIP
trading.mqh (42.67 KB)
tester.mq4 (20.49 KB)
adx_fuzzy.mq4 (10.62 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

该作者的其他文章

前往讨论
信号计算器 信号计算器
直接从MetaTrader 5终端中进行信号运行的计算是非常有利的，因为终端提供了信号的预先选择和排序。通过这种方式，用户可以在终端中看到与他们的交易账户兼容得最好的信号。
MQL5酷客宝典 - 滑动通道编程 MQL5酷客宝典 - 滑动通道编程
本文提出了一种用于等距通道系统的编程方法，在此将会探讨构建这种通道的细节，并且提供了通道的分类，提出了一个统一的滑动通道方法。在代码的实现中使用了面向对象的编程(OOP)。
通过分析组件评估交易系统的效益 通过分析组件评估交易系统的效益
本文探讨了通过分析单独组件的效能来评估复杂交易系统的效益。任何分析，不论是基于指标的图形化分析还是其他，都是在金融市场上成功交易的关键组成部分，在一定程度上，本文也是一项在联合应用程序中对其中几个简单独立的交易系统进行的研究，分析了它们的有效性和可用性。
图形界面 IV: 多窗口模式与优先级系统 (第二章) 图形界面 IV: 多窗口模式与优先级系统 (第二章)
在本章中，我们将扩展库的实现，为MQL应用程序创建多窗口界面。我们还将开发一个优先级系统，用于管理鼠标左键对图形对象的点击，它是用于避免元件对用户操作没有回应的问题的。