MetaTrader 4 / Exemplos
English Русский 中文 Español Deutsch 日本語
Lógica difusa na negociação via MQL4

Lógica difusa na negociação via MQL4

MetaTrader 4 — Exemplos | 1 agosto 2016, 10:51
1 170 0
Alexander Fedosov
Alexander Fedosov

Introdução

Na negociação atual, cada vez mais estão sendo utilizados sistemas de negociação automática, isto é, Expert Advisors ou robôs de negociação. A maioria deles possuem um claro e estrito código para estratégias de negociação e sistemas de gerenciamento financeiro. Além disso, os recursos desses sistemas de negociação automática eliminam o fator humano, pois agem estritamente de acordo com um algoritmo específico. No entanto, o defeito da negociação automática está na ausência de flexibilidade da estratégia de negociação que está sendo aplicada, pois sempre trabalha seguindo parâmetros estabelecidos rigorosamente. Independentemente das condições do mercado, o Expert Advisor sempre aplica a mesma estratégia de negociação usando uns parâmetros estritamente categorizados.

Durante a negociação, o humano, ao contrário da máquina -caraterizada pela imprecisão inerente de categorias-, pode possuir diversas opiniões acerca de sinais semelhantes para entrar no mercado. Na maioria dos casos, eles tentam avaliar a tendência, fazendo perguntas do tipo: "Quão moderada é a tendência? Será que está perto da tendência forte? Ou será que a tendência é forte, mas não o suficiente para entrar no mercado com dois lotes segundo a estratégia?" Afortunadamente, a lógica difusa está em condições de descrever todo isto. Em vez de hesitar, ela faz o sistema de negociação mais flexível e combina a rigidez do robô de negociação com a flexibilidade da mente humana. Este artigo apresenta exemplos que tratam da aplicação do sistema de lógica difusa usando os recursos MQL4.


Descrição das funções de associação

Para se familiarizar com os conceitos gerais da teoria de lógica difusa, recomendamos ler o artigo Uma introdução à lógica fuzzi e estudar os princípios de trabalho da biblioteca FuzzyNet para MQL4, já que ela será utilizada para implementação de exemplos.

Consideremos as funções de associação que serão utilizadas no artigo.


Função de associação triangular

Função de associação na forma de um triângulo. Esta função simples e freqüente é definida pela seguinte fórmula analítica:

Fórmula da função triangular

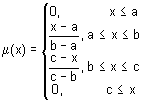
Normalmente, usa-se para definir associações do tipo: «aproximadamente», «valor médio», «localizado no intervalo», «semelhante ao objeto», «parecido com o objeto», etc. Os parâmetros da função triangular de associação são geralmente interpretados da seguinte forma:

  • [a, c] — intervalo de alteração da variável;
  • b — maior valor possível da variável.

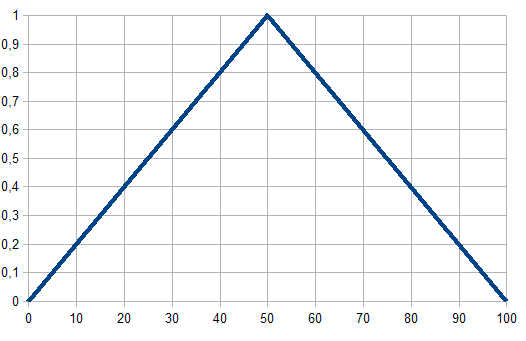
Fig. 1. Função de associação triangular


Função de associação trapezoidal

Função de associação na forma de um trapézio. Ela é especificada pela seguinte fórmula:

Função de associação trapezoidal

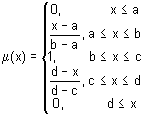
Os parâmetros da função trapezoidal de associação são geralmente interpretados da seguinte forma:

  • [a, d] — transportador do conjunto difuso, avaliação pessimista do valor da variável;
  • [b, c] — núcleo do conjunto difuso, avaliação otimista do valor da variável.

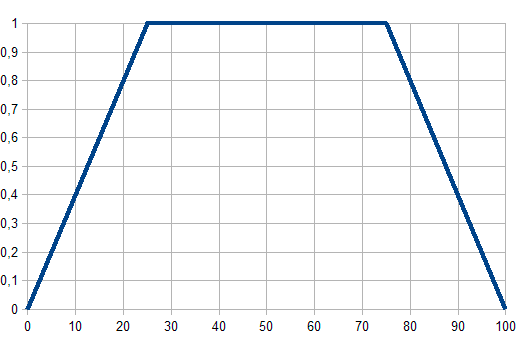
Fig. 2. Função de associação trapezoidal


Função de associação em forma de sino

Função de associação como curva simétrica em forma de sino. Essa função é dada pela fórmula:

Função de associação em forma de sino

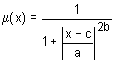
Os valores dos parâmetros são interpretados da seguinte forma:

  • a — coeficiente de concentração da função de associação;
  • b — coeficiente de inclinação da função de associação;
  • c — coordenada da função de associação.

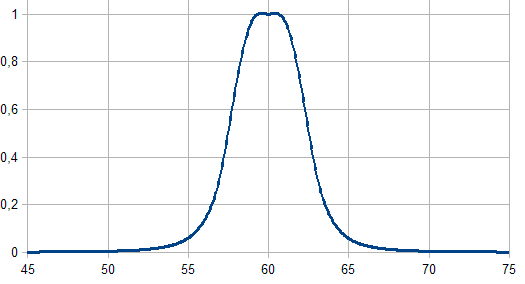
Fig. 3. Função de associação em forma de sino


Função de associação sigmóide

Define-se pela seguinte fórmula e usa-se para estabelecer funções de associação monótonas:

Função de associação sigmóide

É necessário interpretar seus parâmetros da seguinte forma:

  • a — coeficiente de inclinação da função de associação;
  • c — coordenada de inflexão da função de associação.

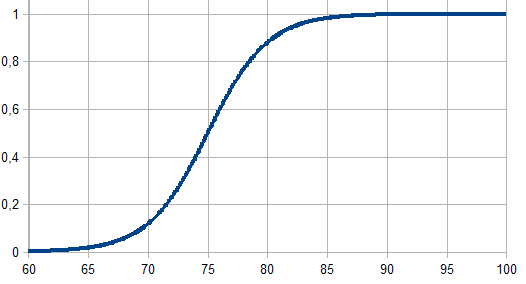
Fig. 4. Função de associação sigmóide


Exemplo de implementação do indicador usando os recursos da biblioteca FuzzyNert para MQL4.

Decidi usar, como exemplo, o Índice de Movimento Direcional Médio (Average Directional Movement Index) ou ADX. Ele é um indicador de tendência que mostra a força da tendência atual (linha grossa verde). Para começar, introduziremos as categorias precisas de força da tendência (Fig. 5), a saber:
  • Weak Trend — o valor da linha verde principal se encontra no intervalo de 30 a 50. Classificaremos os valores dentro desse intervalo, estritamente definido, como uma tendência fraca.
  • Average Trend — o valor da linha verde principal se encontra no intervalo de 50 a 70. Classificaremos os valores dentro desse intervalo, estritamente definido, como uma tendência média o moderada.
  • Strong Trend — o valor da linha verde principal se encontra no intervalo de 70 a 100. Este será um sinal de uma tendência forte.

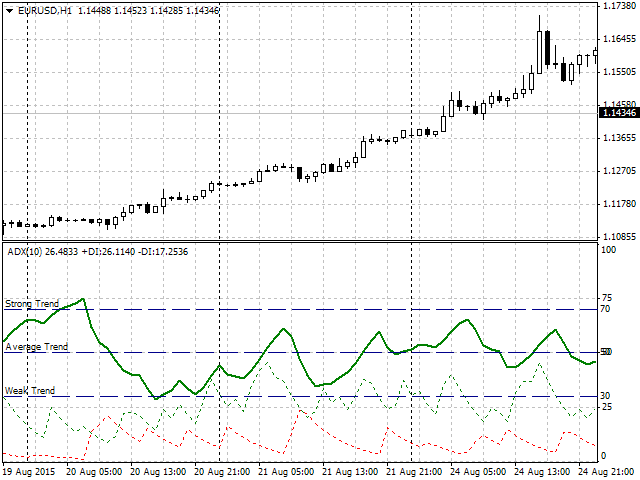
Fig. 5. Exemplo de trabalho e divisão selecionada pela força da tendência

Estas três categorias estritamente definidas têm alguns inconvenientes causados pela sua clara e estrita lógica de classificação:

  • O primeiro inconveniente é a natureza subjectiva da classificação. Na verdade, por que nós escolhemos 30, 50 e 70 como valores limite? Por que não escolhemos 25, 50, 75 ou algum outro valor? Estas opiniões dissonantes podem afectar grandemente o trabalho do ADX e até levar a resultados diametralmente opostos.
  • O segundo inconveniente reside nas zonas limite das categorias selecionadas. Por exemplo, 50 é o limite entre a tendência fraca e a moderada. Se aplicarmos a lógica estrita, temos que admitir que 48 e 49 ainda pertencem à área de tendência fraca, enquanto 50 e 51 à área da tendência moderada. Aqui existe um problema com a definição da transição de 49 a 50. Em ambos os casos (48-49 e 49-50), a diferença entre os valores é igual a um. No entanto, por alguma razão, o último caso é considerado como uma transição de uma categoria para outra.

Então, o que oferece a lógica difusa para corrigir estas deficiências?

Ocorre o seguinte: os limites especificados são "diluídos" para se tornar difusos. Ou seja, nas zonas limite das categorias estritamente definidas, aparece a dualidade, isto é, a tendência pode se relacionar diretamente às duas noções, mas com diferentes graus de associação. Isto pode ser descrito como segue: a força da tendência atual pode, em menor grau, ser descrita como fraca (30%), mas, em maior grau, pode ser descrita como moderada (70%). O humano poderia caraterizar isto como: a tendência talvez seja mais moderada do que fraca. Na minha opinião, esta é a principal vantagem da lógica difusa, ou seja, a flexibilidade e a variabilidade ao avaliar qualquer parâmetro originalmente estritamente definido. Para nosso exemplo com o ADX, eu escolhi as seguintes funções descritas acima:

  • A função trapezoidal para descrever o conceito de tendência fraca.
  • A função em forma de sino para descrever o conceito de tendência média ou moderada.
  • A função sigmóide para a tendência forte.

É possível descrever sistemas mais complexos com um grande número de categorias usando outras funções disponíveis na biblioteca FuzzyNet. Atualmente, há mais de uma dúzia deles. Então, eis o que aconteceu no final:


Fig. 6. Descrição de força da tendência através de lógica difusa

Como você pode ver no gráfico, agora vemos áreas em que, ao mesmo tempo, existem 2 categorias de tendência. A zona 50-60 abarca tanto a tendência fraca coma a média, enquanto а zona 60-70 compreende a moderada e a forte. Assim, para as três categorias de termos, estabelecemos o conjunto com as funções de associação definidas. Agora, tendo os valores de entrada do ADX, descritos pelas funções de associação, precisamos determinar qual será o valor de saída, o resultado de exclusão da difusão e selecionar o algoritmo de saída de lógica difusa.

Para nosso exemplo, selecionei, como valor de saída, o percentual de risco de depósito em relação à -inicialmente especificada- variável difusa de força de tendência. Isto é, quanto mais forte for a tendência, maior o risco e o percentual do depósito usado na negociação. Escolhi Mamdani como o algoritmo de saída lógica.

Como com a força da tendência, vamos apresentar três categorias distintas de acordo com o grau de risco:

  • Baixo risco (Low) — intervalo de 2 a 4% do depósito.
  • Risco normal (Normal) — 4-5%.
  • Alto risco (High) — de 5 ao valor máximo de 10% do depósito.

Agora, vamos definir categorias de risco usando as funções de associação:

  • Trapezoidal para baixo risco.
  • Triangular para um risco normal.
  • Sigmóide para alto risco.

Como resultado, obtemos a seguinte descrição gráfica através da lógica difusa:


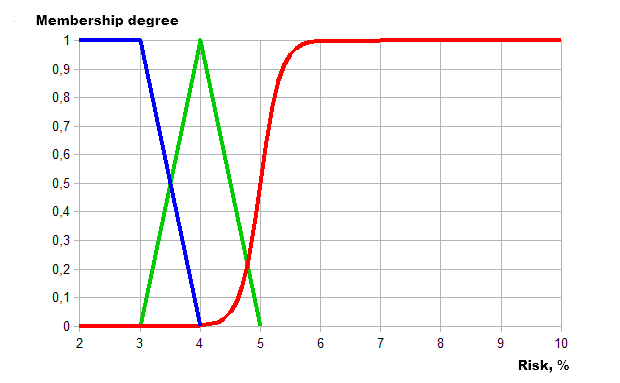
Fig. 7. Descrição do grau de risco através da lógica difusa


Implementamos os dados descritos usando a biblioteca FuzzyNet para MQL4:

//+------------------------------------------------------------------+
//|                                                    ADX_Fuzzy.mq4 |
//|                                                Alexander Fedosov |
//|                           https://www.mql5.com/pt/users/alex2356 |
//+------------------------------------------------------------------+
#property copyright "Alexander Fedosov"
#property link      "https://www.mql5.com/pt/users/alex2356"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 2
#property indicator_color1 Green
#property indicator_color2 Red
#property indicator_minimum 0
#property indicator_maximum 10
//+------------------------------------------------------------------+
//| Connecting libraries                                             |
//+------------------------------------------------------------------+
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>
//--- input parameters
input string  p1="==== Parameters ====";
input int    visual=100;             // Visual Period
input int    adx_period=10;          // ADX Period
//---
double Buffer1[],Buffer2[],adx,adx_di_minus,adx_di_plus;
int limit;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexStyle(0,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(0,Buffer1);
   SetIndexEmptyValue(0,0.0);
//---
   SetIndexStyle(1,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(1,Buffer2);
   SetIndexEmptyValue(1,0.0);
//---
   ArrayResize(Buffer1,visual);
   ArrayResize(Buffer2,visual);
   ArrayInitialize(Buffer1,0.0);
   ArrayInitialize(Buffer2,0.0);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
   int count_bars=IndicatorCounted();
//---
   if(count_bars<0)
      return(-1);
//---
   if(Bars-1<adx_period)
      return(0);
//---
   for(int i=0; i<visual;i++)
     {
      adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits);
      adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits);
      adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits);
      //---
      double r=(adx_di_plus-adx_di_minus);
      if(MathAbs(r)>10 && adx>=30.0)
         if(r>0)
            Buffer1[i]=mamdani(adx);
      else if(r<0)
         Buffer2[i]=mamdani(adx);
     }
   return(rates_total);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double mamdani(double v)
  {
   double res=0;
//--- Mamdani Fuzzy System  
   MamdaniFuzzySystem *fsRisk=new MamdaniFuzzySystem();
//--- Create input variables for the system
   FuzzyVariable *fsTrend=new FuzzyVariable("trend",30.0,100.0);
//---
   fsTrend.Terms().Add(new FuzzyTerm("weak", new TrapezoidMembershipFunction(20.0, 30.0, 50.0, 60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("average", new GeneralizedBellShapedMembershipFunction(2.5,2.0,60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("strong",new SigmoidalMembershipFunction(0.4,75.0)));
   fsRisk.Input().Add(fsTrend);
//--- Create Output
   FuzzyVariable *fvRisk=new FuzzyVariable("risk",2.0,10.0);
   fvRisk.Terms().Add(new FuzzyTerm("low", new TrapezoidMembershipFunction(1.0, 2.0, 3.0, 4.0)));
   fvRisk.Terms().Add(new FuzzyTerm("normal", new TriangularMembershipFunction(3.0, 4.0, 5.0)));
   fvRisk.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,5.0)));
   fsRisk.Output().Add(fvRisk);
//--- Create three Mamdani fuzzy rules
   MamdaniFuzzyRule *rule1 = fsRisk.ParseRule("if (trend is weak) then risk is low");
   MamdaniFuzzyRule *rule2 = fsRisk.ParseRule("if (trend is average) then risk is normal");
   MamdaniFuzzyRule *rule3 = fsRisk.ParseRule("if (trend is strong) then risk is high");
//--- Add three Mamdani fuzzy rules in the system
   fsRisk.Rules().Add(rule1);
   fsRisk.Rules().Add(rule2);
   fsRisk.Rules().Add(rule3);
//--- Set input value
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsTrend,v);
   in.Add(p_od_in);
//--- Get result
   CList *result;
   Dictionary_Obj_Double *p_od_out;
   result=fsRisk.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);
//---
   delete in;
   delete result;
   delete fsRisk;
   return res;
  }
//+------------------------------------------------------------------+

Desenvolvi um indicador simples como histograma que serve para visualizar a relação entre o grau de risco e a força da tendência, (verde para a tendência ascendente e vermelho para a tendência decrescente), a altura desse indicador mostra o valor numérico do grau de risco durante a força da tendência, nos limites descritos acima. Consideremos o código em mais detalhe.

Primeiro, definimos 2 buffers para os histogramas aplicados, sua cor e a escala no eixo vertical de zero a um valor máximo de risco pré-determinado igual a 10%.

#property indicator_separate_window
#property indicator_buffers 2
#property indicator_color1 Green
#property indicator_color2 Red
#property indicator_minimum 0
#property indicator_maximum 10

Em seguida, conectamos a biblioteca para criar o sistema de acordo com o algoritmo de Mamdani, adicionamos tanto as variáveis para visualização do número de barras, começando com zero, como o valor de período personalizado do indicador ADX.

//+------------------------------------------------------------------+
//| Connecting libraries FuzzyNet                                    |
//+------------------------------------------------------------------+
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>
//--- input parameters
input string  p1="==== Parameters ====";
input int    visual=100;             // Visual Period
input int    adx_period=10;          // ADX Period

Durante a inicialização, estabelecemos qual será o nosso indicador na forma de histograma.

//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexStyle(0,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(0,Buffer1);
   SetIndexEmptyValue(0,0.0);
//---
   SetIndexStyle(1,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(1,Buffer2);
   SetIndexEmptyValue(1,0.0);
//---
   ArrayResize(Buffer1,visual);
   ArrayResize(Buffer2,visual);
   ArrayInitialize(Buffer1,0.0);
   ArrayInitialize(Buffer2,0.0);
//---
   return(INIT_SUCCEEDED);
  }

No código principal, definimos as indicações básicas do indicador ADX, encontramos, na variável r, a diferença entre os dois indicadores de direção da tendência +DI e -DI. Inserimos o filtro de presença de tendência como a diferença entre os valores absolutos +DI e -DI superiores a 10 e o valor principal de força de tendência superior a 30 (limite inferior da tendência fraca). Em seguida, definimos a direção da tendência com base no sinal da variável r e colocamos o valor da função mamdani() na matriz previamente especificada.

int count_bars=IndicatorCounted();
//---
   if(count_bars<0)
      return(-1);
//---
   if(Bars-1<adx_period)
      return(0);
//---
   for(int i=0; i<visual;i++)
     {
      adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits);
      adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits);
      adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits);
      //---
      double r=(adx_di_plus-adx_di_minus);
      if(MathAbs(r)>10 && adx>=30.0)
         if(r>0)
            Buffer1[i]=mamdani(adx);
      else if(r<0)
         Buffer2[i]=mamdani(adx);
     }

Descrição da função mamdani:

1. Criamos um novo sistema de lógica difusa do tipo Mamdani *fsRisk.

2. Adicionamos a variável de entrada *fsTrend, definimos o nome trend e acrescentamos os valores máximos e mínimos 30 e 100.

//--- Mamdani Fuzzy System  
   MamdaniFuzzySystem *fsRisk=new MamdaniFuzzySystem();
//--- Create input variables for the system
   FuzzyVariable *fsTrend=new FuzzyVariable("trend",30.0,100.0);

3. Em seguida, adicionamos os termos difusos descritos acima (Fig. 6), com funções de associação selecionadas para cada categoria.

fsTrend.Terms().Add(new FuzzyTerm("weak", new TrapezoidMembershipFunction(30.0, 40.0, 50.0, 60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("average", new GeneralizedBellShapedMembershipFunction(2.5,2.0,60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("strong",new SigmoidalMembershipFunction(0.4,75.0)));
   fsRisk.Input().Add(fsTrend);

4. Fazemos os pontos 2-3 para o valor de saída: criamos a variável *fvRisk com nome risk e os valores de risco mínimo e máximo, 2% e 10% respetivamente.

//--- Create Output
   FuzzyVariable *fvRisk=new FuzzyVariable("risk",2.0,10.0);
   fvRisk.Terms().Add(new FuzzyTerm("low", new TriangularMembershipFunction(2.0, 3.0, 4.0)));
   fvRisk.Terms().Add(new FuzzyTerm("normal", new TriangularMembershipFunction(3.0, 4.0, 5.0)));
   fvRisk.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,5.0)));
   fsRisk.Output().Add(fvRisk);

5. Agora, criamos um conjunto de regras difusas, elas representarão nosso sistema:

  • Se a tendência é fraca, o risco é baixo.
  • Se a tendência é média, o risco é normal.
  • Se a tendência é forte, o risco é elevado.
//--- Create three Mamdani fuzzy rules
   MamdaniFuzzyRule *rule1 = fsRisk.ParseRule("if (trend is weak) then risk is low");
   MamdaniFuzzyRule *rule2 = fsRisk.ParseRule("if (trend is average) then risk is normal");
   MamdaniFuzzyRule *rule3 = fsRisk.ParseRule("if (trend is strong) then risk is high");

6. Adicionamos nossas regras ao sistema:

//--- Add three Mamdani fuzzy rules in the system
   fsRisk.Rules().Add(rule1);
   fsRisk.Rules().Add(rule2);
   fsRisk.Rules().Add(rule3);

7. Criamos listas para as variáveis de entrada e saída, e adicionamos o parâmetro de entrada v, ele servirá como argumento da função mamdani. Ou seja, para todas as funções mamdani, cria-se um sistema de lógica difusa com variáveis difusas de entrada e saída definidas, enquanto o valor do indicador ADX é utilizado na entrada.

//--- Set input value
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsTrend,v);
   in.Add(p_od_in);
//--- Get result
   CList *result=new CList;
   Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double;
   result=fsRisk.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);

8. A variável res é o valor da função e o resultado em cuja base é construído o histograma.

adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits);
      adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits);
      adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits);
      //---
      double r=(adx_di_plus-adx_di_minus);
      if(MathAbs(r)>10 && adx>=30.0)
         if(r>0)
            Buffer1[i]=mamdani(adx);
      else if(r<0)
         Buffer2[i]=mamdani(adx);

Como resultado, podemos observar o seguinte resultado visual do trabalho do indicador:

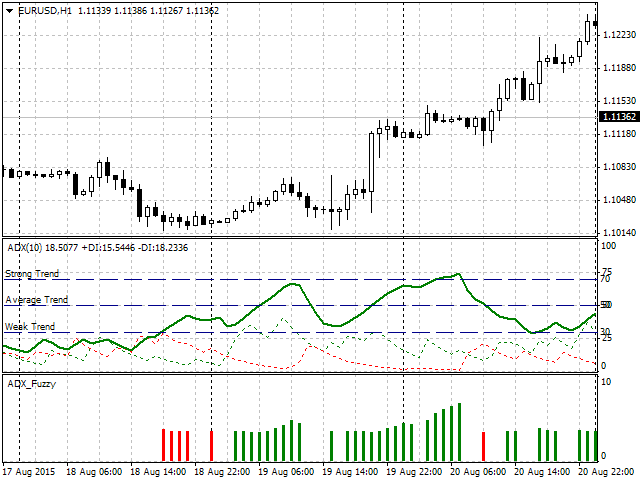
Fig. 8. Trabalho do indicador

Como podemos ver, o indicador mostra a presença de uma tendência usando certa cor de histograma, enquanto uma barra de altura exibe a porcentagem de risco a partir do depósito. A pergunta óbvia será: Qual seria a diferença se o mesmo indicador for implementado como de costume, isto é, com intervalos claros? Para fazer isso, consideraremos a seguinte seção com mais detalhe (Fig. 9). A seta verde mostra a barra de histograma, enquanto seus valores numérico e de força de tendência do ADX são exibidos à esquerda. Como foi definido anteriormente, um ADX superior a 70 é uma tendência forte, enquanto, durante uma tendência forte, o valor do risco deveria estar acima de 5%. Mas na Fig. 9 vemos claramente que o ADX = 69.7923, ou seja, se aplicarmos regras rígidas, isto ainda seria uma tendência média e o risco não deveria exceder o 5%. No entanto, neste caso, é igual a 5.6406, ou seja, é mais elevado.


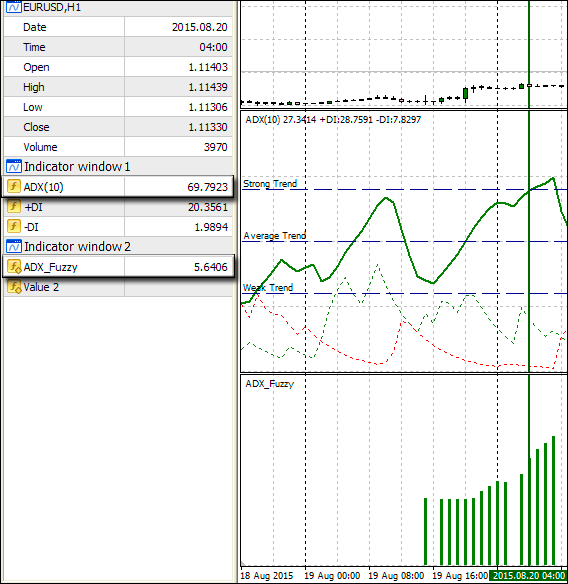
Fig. 9. Diferenças entre a lógica difusa e a padrão

Aqui podemos ver a lógica difusa em ação. Ela definiu que o valor era inferior a 70, no entanto a tendência na área era mais forte do que média. Isto pode ser visto olhando para a Fig. 6, onde o valor do eixo X exibe 69.7923, a função de associação de tendência forte é superior à função de tendência média. Portanto, nosso sistema tem oferecido um valor de risco superior a 5%, aproximando-se da avaliação no limite das categorias das tendências média e forte de forma mais flexível em comparação com o sistema de lógica clara.


Exemplo de implementação de um Expert Advisor usando a biblioteca FuzzyNet para MQL4

Aqui, quero mostrar a diferença em caso de condições claramente definidas e uso de elementos de lógica difusa. Para fazer a comparação tão bem fundamentada quanto possível, eu decidi usar o Expert Advisor do meu outro artigo "Ideias de negociação baseadas na velocidade de movimento e direção de preços", ele descreve em detalhe a ideia do robô de negociação.

  • A fim de evitar repetições excessivas, vou usar este EA como uma base com as seguintes alterações: A lógica deste EA é baseada na ideia da persistência do movimento de preço. Os parâmetros de movimento são descritos pelos seguintes indicadores: RSI (indicador de velocidade) e AC (indicador de aceleração). A velocidade e aceleração são estimados indexando os intervalos dos valores destes indicadores. Agora, vamos aplicar a teoria dos conjuntos difusos para os valores do índice RSI. Como resultado, os valores RSI vão ser usados como entradas, enquanto, como saída, o índice de velocidade difusa que pode ter não apenas valores inteiros, como 1-4, mas também 1.3 ou 3,85.
  • Por sua vez, o valor de índice difuso será usado como entrada para outro sistema, em que a saída será um valor de lucro. Assim, o lucro permanecerá intacto no EA inicial.

A ideia por trás da conexão é simples. Se o RSI e o AC são parâmetros de movimento, então, quanto maior a velocidade, maior a inércia do movimento e, portanto, é razoável colocar um Take-Profit maior. Se a velocidade de movimento é baixa, o Take-Profit objetivo deve ser definido mais modesto para não encontrar uma reversão ou uma inversão de tendência e obter uma perda. Fig. 10 mostra um diagrama de blocos para uma compreensão mais clara da aplicação de lógica digusa em esse EA.


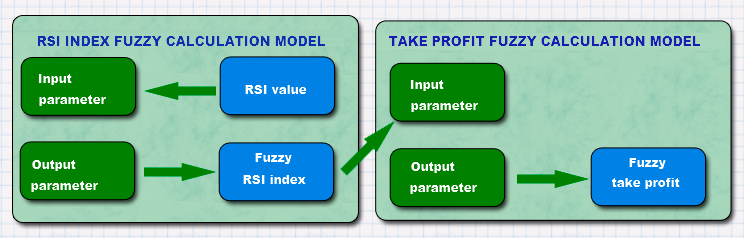
Fig. 10. Diagrama de blocos da aplicação da lógica difusa no EA

Assim como no exemplo com o indicador, descrevemos a função de associação para ambos os modelos difusos. A primeira será o modelo de cálculo do índice RSI, onde a entrada é o valor do próprio indicador, por isso, dividimos os valores de nosso interesse em três categorias:

  • Weak. Primeira categoria. Ela carateriza a tendência fraca. Valor do RSI: 60-70.
  • Average. Segunda categoria. Ela carateriza a tendência média. Intervalo do RSI: 70-80.
  • Strong. Terceira categoria, ela relaciona-se com a tendência forte. Intervalo 80-85.

Escolhemos as funções de associação, para descrever as categorias definidas:

  • Weak. Função sigmóide com coeficiente de inclinação -0,75 e ponto de inflexão 67,5.
  • Average. Função gaussiana com coordenada máxima no ponto 72,5 e coeficiente de concentração igual a 2,2.
  • Strong. Função gaussiana com coordenada máxima no ponto 80 e coeficiente de concentração igual a 1,4.

A apresentação visual é a seguinte:


Fig. 11. Descrição pelas funções de associação das categorias dos valores do RSI

Neste caso, os parâmetros desse modelo difuso são o índice RSI. Usamos as seguintes categorias e funções de associação para a sua descrição:

  • Low. Baixo índice, localiza-se no intervalo 1-2. Função de associação sigmóide com inclinação -11 e inflexão no ponto 1,5.
  • Normal. Índice médio com intervalo 2-3. Função de associação gaussiana com máximo no ponto 2 e coeficiente de concentração 0,3.
  • High. Alto valor de índice com intervalo 3-4. Função de associação sigmóide com inclinação -6 e inflexão no ponto 3.

Como resultado, obtemos a seguinte descrição gráfica:


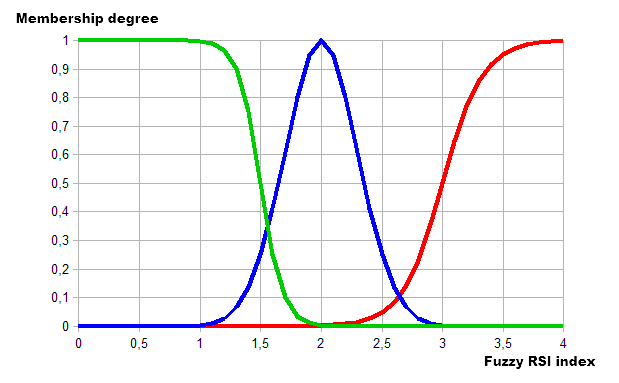
Fig. 12. Descrição pelas funções de associação das categorias dos valores do RSI

A seguir, descrevemos um segundo modelo difuso a partir da Fig. 10, isto é, o modelo difuso de cálculo de Take-Profit. Os parâmetros de entrada deste modelo já fora descritos como os parâmetros de saída do primeiro modelo, nomeadamente, do índice difuso RSI. O valor do Take-Profit será o valor de saída. Definimos categorias claras para ele:

  • Minimal. Categoria do Take-Profit mínimo no intervalo 30-40.
  • Average. Categoria do valor médio de Take-Profit no intervalo 40-60.
  • Maximal. Categoria de alto valor no intervalo 60-70.

Agora descrevemos usando as funções de associação:

  • Minimal. Função de associação sigmóide com inclinação -0,8 e inflexão no ponto 37,5.
  • Average. Função de associação gaussiana com coordenada máxima no ponto 50 e coeficiente de concentração igual a 3.
  • Maximal. Função de associação sigmóide com inclinação 0,8 e inflexão no ponto 62,5.

Por conseguinte, a implementação gráfica será a seguinte:


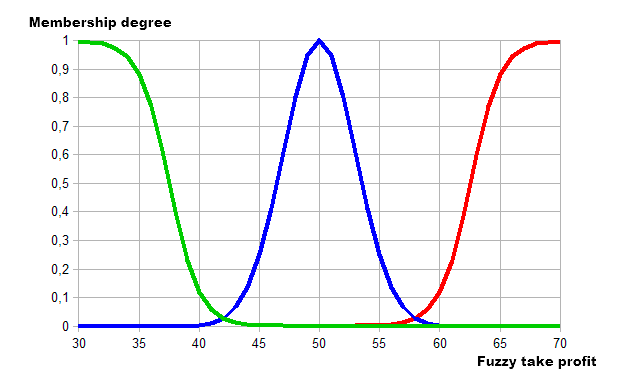
Fig. 13. Descrição pelas funções de associação das categorias dos valores do Take-Profit

Agora que todos os parâmetros já foram definidos, é hora de implementar a ideia para o robô de negociação. Vamos adicionar dois modelos difusos para cálculos sucessivos de valores Take-Profit e Stop-Loss com base nas leituras do indicador RSI.

//+------------------------------------------------------------------+
//|                                                       tester.mq4 |
//|                                                Alexander Fedosov |
//|                                                                  |
//+------------------------------------------------------------------+
#property copyright "Alexander Fedosov"
#property strict
#include "trading.mqh" //Biblioteca auxiliar para operações de negociação
//+------------------------------------------------------------------+
//| Connecting libraries                                             |
//+------------------------------------------------------------------+
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>
//+------------------------------------------------------------------+
//| Parâmetros do Expert Advisor                                              |
//+------------------------------------------------------------------+
input bool           Lot_perm=false;               // Lote do saldo?
input double         Risk = 2;                     // Risco do depósito, %
input double         lt=0.01;                      // Lote
input int            magic=2356;                   // Número mágico
input int            period=14;                    // Período do indicador RSI
input ENUM_TIMEFRAMES tf=PERIOD_CURRENT;           // Timeframe em execução
//---
int index_rsi,index_ac;
double tkp,stl;
double rs,mdm;
CTrading tr;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   tr.Trading(magic,5,lt,Lot_perm,Risk);
   tr.exp_name="Tester Fuzzy Logic";
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Função principal de cálculo                                          |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- verificar se não há mais posições abertas
   if(!tr.isOpened(magic))
     {
      depth_trend();
      speed_ac();
      rs=tr.ND(iRSI(_Symbol,tf,period,PRICE_CLOSE,0),2);
      //--- verificação de condições para compra
      if(Buy() && rs<=85.0)
        {
         mdm = mamdani_rsi(rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_BUY,lt,(int)tkp,(int)stl))
            Print("RSI равно ",rs," TP igual a ",tkp," SL igual a ",stl);
        }
      //--- verificação de condições para venda
      if(Sell() && rs>=15.0)
        {
         mdm = mamdani_rsi(100-rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_SELL,lt,(int)tkp,(int)stl))
            Print("RSI равно ",rs," TP igual a ",tkp," SL igual a ",stl);
        }
     }
//--- há ordens abertas?
   if(tr.isOpened(magic))
     {
      //--- verificamos e fechas essas ordens de venda que satisfaçam as condições de fechamento
      if(Sell_close())
         tr.ClosePosAll(OP_SELL);
      //--- verificamos e fechas essas ordens de compra que satisfaçam as condições de fechamento
      if(Buy_close())
         tr.ClosePosAll(OP_BUY);
     }
  }
//+------------------------------------------------------------------+
//| Função de definição de profundidade da tendência                               |
//+------------------------------------------------------------------+
void depth_trend()
  {
//--- definição do índice para entrar no mercado
   double rsi=iRSI(_Symbol,tf,period,PRICE_CLOSE,0);
//---
   index_rsi=0;
   if(rsi>90.0)
      index_rsi=4;
   else if(rsi>80.0)
      index_rsi=3;
   else if(rsi>70.0)
      index_rsi=2;
   else if(rsi>60.0)
      index_rsi=1;
   else if(rsi<10.0)
      index_rsi=-4;
   else if(rsi<20.0)
      index_rsi=-3;
   else if(rsi<30.0)
      index_rsi=-2;
   else if(rsi<40.0)
      index_rsi=-1;
  }
//+------------------------------------------------------------------+
//| Função de definição de velocidade da tendência                              |
//+------------------------------------------------------------------+
void speed_ac()
  {
   double ac[];
   ArrayResize(ac,5);
   ArrayInitialize(ac,0.0);
   for(int i=0; i<5; i++)
      ac[i]=iAC(_Symbol,tf,i);
//---
   index_ac=0;
//--- Índices para compra
   if(ac[0]>ac[1])
      index_ac=1;
   else if(ac[0]>ac[1] && ac[1]>ac[2])
      index_ac=2;
   else if(ac[0]>ac[1] && ac[1]>ac[2] && ac[2]>ac[3])
      index_ac=3;
   else if(ac[0]>ac[1] && ac[1]>ac[2] && ac[2]>ac[3] && ac[3]>ac[4])
      index_ac=4;
//--- Índices para venda
   else if(ac[0]<ac[1])
      index_ac=-1;
   else if(ac[0]<ac[1] && ac[1]<ac[2])
      index_ac=-2;
   else if(ac[0]<ac[1] && ac[1]<ac[2] && ac[2]<ac[3])
      index_ac=-3;
   else if(ac[0]<ac[1] && ac[1]<ac[2] && ac[2]<ac[3] && ac[3]<ac[4])
      index_ac=-4;
  }
//+------------------------------------------------------------------+
//| Função de verificação de condições para compra                              |
//+------------------------------------------------------------------+
bool Buy()
  {
   return (((index_rsi==2 && index_ac>=1) || (index_rsi==3 && index_ac==1))?true:false);
  }
//+------------------------------------------------------------------+
//| Função de verificação de condições para venda                              |
//+------------------------------------------------------------------+
bool Sell()
  {
   return (((index_rsi==-2 && index_ac<=-1) || (index_rsi==-3 && index_ac==-1))?true:false);
  }
//+------------------------------------------------------------------+
//| Função de verificação da condição de fechamento da posição para compra             |
//+------------------------------------------------------------------+
bool Buy_close()
  {
   return ((index_rsi>2 && index_ac<0)?true:false);
  }
//+------------------------------------------------------------------+
//| Função de verificação da condição de fechamento da posição para venda             |
//+------------------------------------------------------------------+
bool Sell_close()
  {
   return ((index_rsi<-2 && index_ac>0)?true:false);
  }
//+------------------------------------------------------------------+
//| Função do modelo difuso de cálculo do índice RSI                   |
//+------------------------------------------------------------------+
double mamdani_rsi(double rsi)
  {
   double res=0;
//--- Mamdani Fuzzy System  
   MamdaniFuzzySystem *fsRSI=new MamdaniFuzzySystem();
//--- criação de variáveis de entrada para o sistema e definição de termos
   FuzzyVariable *fsTrend=new FuzzyVariable("rsi",60.0,85.0);
//---
   fsTrend.Terms().Add(new FuzzyTerm("weak", new SigmoidalMembershipFunction(-0.75,67.5)));
   fsTrend.Terms().Add(new FuzzyTerm("average", new NormalMembershipFunction(72.5,2.2)));
   fsTrend.Terms().Add(new FuzzyTerm("strong", new NormalMembershipFunction(80.0,1.4)));
   fsRSI.Input().Add(fsTrend);
//--- criação de variáveis de saída para o sistema e definição de termos
   FuzzyVariable *fsIndex=new FuzzyVariable("index",1.0,4.0);
   fsIndex.Terms().Add(new FuzzyTerm("low", new SigmoidalMembershipFunction(-11.0,1.5)));
   fsIndex.Terms().Add(new FuzzyTerm("normal", new NormalMembershipFunction(2.0,0.3)));
   fsIndex.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,3.0)));
   fsRSI.Output().Add(fsIndex);
//--- criação de regras e adicionamento deles ao sistema
   MamdaniFuzzyRule *rule1 = fsRSI.ParseRule("if (rsi is weak) then (index is low)");
   MamdaniFuzzyRule *rule2 = fsRSI.ParseRule("if (rsi is average) then (index is normal)");
   MamdaniFuzzyRule *rule3 = fsRSI.ParseRule("if (rsi is strong) then (index is high)");
   fsRSI.Rules().Add(rule1);
   fsRSI.Rules().Add(rule2);
   fsRSI.Rules().Add(rule3);
//--- configuração de parâmetros de entrada
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsTrend,rsi);
   in.Add(p_od_in);
//--- saída de resultados
   CList *result=new CList;
   Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double;
   result=fsRSI.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);
//---
   delete in;
   delete result;
   delete fsRSI;
   return res;
  }
//+------------------------------------------------------------------+
//| Função do modelo difuso de cálculo do índice de Take-Profit                   |
//+------------------------------------------------------------------+
double mamdani_tp(double ind_rsi)
  {
   double res=0;
//--- Mamdani Fuzzy System  
   MamdaniFuzzySystem *fsTP=new MamdaniFuzzySystem();
//--- criação de variáveis de entrada para o sistema e definição de termos
   FuzzyVariable *fsIndex=new FuzzyVariable("index",1.0,4.0);
   fsIndex.Terms().Add(new FuzzyTerm("low", new SigmoidalMembershipFunction(-11.0,1.5)));
   fsIndex.Terms().Add(new FuzzyTerm("normal", new NormalMembershipFunction(2.0,0.3)));
   fsIndex.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,3.0)));
   fsTP.Input().Add(fsIndex);
//--- criação de variáveis de saída para o sistema e definição de termos
   FuzzyVariable *fsProfit=new FuzzyVariable("TP",30.0,70.0);
   fsProfit.Terms().Add(new FuzzyTerm("minimal", new SigmoidalMembershipFunction(-0.8,37.5)));
   fsProfit.Terms().Add(new FuzzyTerm("average", new NormalMembershipFunction(50.0,3.0)));
   fsProfit.Terms().Add(new FuzzyTerm("maximal", new SigmoidalMembershipFunction(0.8,62.5)));
   fsTP.Output().Add(fsProfit);
//--- criação de regras e adicionamento deles ao sistema
   MamdaniFuzzyRule *rule1 = fsTP.ParseRule("if (index is low) then (TP is minimal)");
   MamdaniFuzzyRule *rule2 = fsTP.ParseRule("if (index is normal) then (TP is average)");
   MamdaniFuzzyRule *rule3 = fsTP.ParseRule("if (index is high) then (TP is maximal)");
   fsTP.Rules().Add(rule1);
   fsTP.Rules().Add(rule2);
   fsTP.Rules().Add(rule3);
//--- configuração de parâmetros de entrada
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsIndex,ind_rsi);
   in.Add(p_od_in);
//--- saída de resultados
   CList *result=new CList;
   Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double;
   result=fsTP.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);
//---
   delete in;
   delete result;
   delete fsTP;
   return res;
  }
//+------------------------------------------------------------------+

Agora, consideremos as alterações básicas que foram feitas no Expert Advisor:

  • A alteração mais importante consiste na implementação de dois modelos difusos na forma de funções mamdani_rsi e mamdani_tp.
  • Por conseguinte, esses parâmetros foram removidos do Expert Advisor, nomeadamente, o Take-Profit e Stop-Loss. Agora eles são calculados usando lógica difusa.
  • Examinemos, como é realizado esse cálculo:
if(OrdersTotal()<1)
     {
      depth_trend();
      speed_ac();
      rs=tr.ND(iRSI(_Symbol,tf,period,PRICE_CLOSE,0),2);
      //--- verificação de condições para compra
      if(Buy() && rs<=85.0)
        {
         mdm = mamdani_rsi(rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_BUY,lt,tkp,stl))
            Print("RSI равно ",rs," TP igual a ",tkp," SL igual a ",stl);
        }
      //--- verificação de condições para venda
      if(Sell() && rs>=15.0)
        {
         mdm = mamdani_rsi(100-rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_SELL,lt,tkp,stl))
            Print("RSI равно ",rs," TP igual a ",tkp," SL igual a ",stl);
        }
     }

Se não houver nenhuma ordem aberta com número mágico de Expert Advisor, o sistema, usando as funções depth_trend() e speed_ac(), monitorizará os parâmetros de movimento no mercado e entrará no mercado segundo o Buy() ou Sell(). A seguir, se aparecerem as condições satisfatórias para a variável mdm, será definido o valor do resultado de trabalho do modelo difuso, em cuja entrada estiver o valor atual do indicador RSI, e saída, o índice difuso. Por sua vez, o valor da índice difuso será usado para a entrada do nosso segundo sistema, cuja saída é o Take-Profit em pontos. O valor do Take-Profit é definido pela variável tkp.

O coeficiente 0,43 foi tomado com base no valor máximo do Take-Profit em 70 pontos, enquanto tomei o Stop-Loss para ele em 30. Após uma abertura bem-sucedida da ordem, nosso Expert Advisor exibe o valor do RSI, no qual ele foi aberto, bem como os valores calculados a partir dele para o Stop-Loss e Take-Profit. Isso é feito somente para a facilitar o teste.

É necessário esclarecer os seguintes pontos:

  1. Supondo a condição para venda da variável mdm , é atribuído mamdani_rsi(100-rs). Isto é feito porque seus intervalos e limites, dependendo dos valores - mínimo e máximo - do RSI (0 e 100), são espelhados.
  2. O segundo ponto consiste em dois condições adicionais: ao comprar rs<=85 e, da mesma forma, ao vender rs>=15. Isto é feito porque ao criar as variáveis de entrada de modelo difuso de cálculo do índice RSI, os limites são definidos no intervalo 60-85, o valor limite espelhado para venda é 15.

O exemplo de trabalho do Expert Advisor é apresentado na Fig. 14, onde é possível verificar que, ao ter diferentes valores de indicador RSI, acontece o recálculo dos valores de Stop e Take.


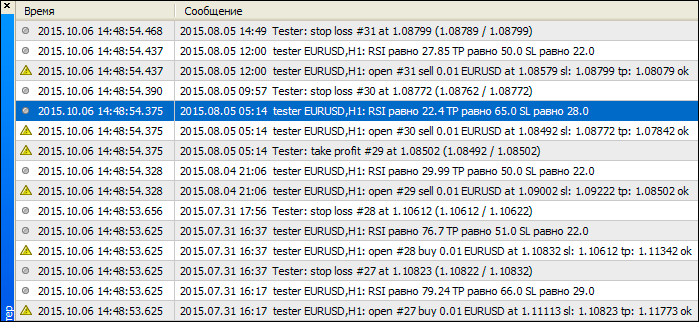
Fig. 14. Resultados do Expert Advisor


Conclusão

Neste artigo foram examinados exemplos que tratam de implementação da teoria de conjuntos difusos na negociação usando a biblioteca FuzzyNet através da MQL4. Foi demostrado que os sistemas baseados na lógica difusa são mais apropriados para se ocupar do problema das categorias claras, em particular, a classificação da tendência ou delimitação do risco. No Expert Advisor, foi demostrado como o sistema, na lógica difusa, analisa a força do sinal de negociação a partir da sua estratégias de negociação e define os valores limite de perdas e valores do lucro-alvo. Acho que os sistemas de negociação baseados na lógica difusa são uma simbiose das melhores caraterísticas necessárias em uma negociação bem-sucedida, isto é, a disciplina do robô de negociação e a flexibilidade do pensamento humano.

Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/2032

Arquivos anexados |
Baixar como ZIP
trading.mqh (42.67 KB)
tester.mq4 (20.49 KB)
adx_fuzzy.mq4 (10.62 KB)
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Como criar bots para Telegram em MQL5 Como criar bots para Telegram em MQL5
Este artigo contém instruções passo-a-passo para a criação de bots para o Telegram em MQL5. Esta informação pode ser útil aos usuários que desejam sincronizar o seu robô de negociação a um dispositivo móvel. Existem exemplos de bots no artigo que fornecem sinais de negociação, busca de informações em sites, enviam informações sobre o balanço da conta, cotações e imagens de gráficos ao seu telefone celular.
Expert Advisor Universal: Um Trailing Stop Customizado (Parte 6) Expert Advisor Universal: Um Trailing Stop Customizado (Parte 6)
A sexta parte do artigo sobre o Expert Advisor universal descreve o uso do recurso "Trailing Stop". O artigo irá guiá-lo através de como criar um módulo "Trailing Stop" personalizado com regras unificadas, bem como adicioná-lo ao motor de negociação para gerir automaticamente as posições.
Interfaces Gráficas II: O Elemento de Menu (Capítulo 1) Interfaces Gráficas II: O Elemento de Menu (Capítulo 1)
Na segunda parte da série, nós vamos mostrar em detalhes o desenvolvimento de tais elementos de interface como o menu principal e o menu de contexto. Nós também vamos mencionar os elementos de desenho e criar uma classe especial para ele. Nós vamos discutir detalhadamente tais questões como a gestão de eventos do programa, incluindo aquelas que são personalizadas.
Interfaces gráficas I: Biblioteca de Testes em Programas de Diferentes Tipos e no Terminal MetaTrader 4 (Capítulo 5) Interfaces gráficas I: Biblioteca de Testes em Programas de Diferentes Tipos e no Terminal MetaTrader 4 (Capítulo 5)
No capítulo anterior da primeira parte da série sobre interfaces gráficas, a classe de formulário foi enriquecida por métodos que permitiram gerir o formulário através dos cliques em seus controles. Neste artigo, nós vamos testar nosso trabalho em diferentes tipos de programa MQL, como indicadores e scripts. Já que a biblioteca foi concebida para ser multi-plataforma para que ela pudesse ser utilizada em todas as plataformas MetaTrader, nós também vamos testá-la no MetaTrader 4.