Introduction to MQL5 (Part 21): Automating Harmonic Pattern Detection

Introduction

Welcome back to Part 21 of the Introduction to MQL5 series! In Part 20, I introduced you to harmonic patterns and explained the mathematical concepts behind Fibonacci retracements and extensions, as well as how to implement them in MQL5. In this article, we’ll take things a step further by focusing on automating the detection of the Gartley harmonic pattern.

You'll learn how to recognize possible Gartley patterns programmatically on your charts by utilizing Fibonacci levels, price swings, and chart objects. The logic and methods we discuss here can be applied to other harmonic patterns, such as the Bat, Butterfly, Crab, and Deep Crab, even though we'll be focusing on the Gartley pattern for simplicity's sake.

This article's distinctiveness is found in its approachable style for beginners and the way we simplify difficult ideas into manageable stages. Instead of overloading you with theory, we'll be working on a project-based strategy in which we create an Expert Advisor (EA) that recognizes the Gartley pattern automatically.

Setting up the Project

The goal of this project is to create an Expert Advisor (EA) that can recognize Gartley Harmonic Patterns on a chart automatically. Based on predetermined criteria, the EA will evaluate swings in prices, calculate important Fibonacci retracement and extension levels, and spot possible Gartley formations.

Four major legs (XA, AB, BC, and CD) and particular Fibonacci relationships define the Gartley pattern: point B has to retrace roughly 78.6 percent of the XA leg, point C needs to retrace between 38.2 and 88.6 percent of the AB leg, and point D needs to retrace roughly 78.6 percent of the XA leg. The EA is adaptable and easy for beginners to use because it allows traders to modify the Fibonacci retracement and extension ranges to suit their own trading style.

Logic for Buy

To detect a bullish Gartley pattern, the EA will follow these steps:

• Identify X as a swing low point.
• Detect A as a significant swing high after X.
• Locate B, which must retrace within the specified range of the XA leg.
• Confirm C, which retraces within the specified range of the AB leg.
• Calculate the potential D point, which should fall within a specified range of retracement of the XA leg.
• Ensure all legs follow the required Fibonacci alignment for a valid Gartley structure.
• Once point D is confirmed, the EA will generate a buy signal, expecting the price to reverse upward from this level.
• Additionally, the EA will allow users to adjust all Fibonacci retracement and extension percentages through the input settings, giving flexibility based on different market conditions.

Once the EA confirms a valid bullish Gartley pattern:

• Entry: A buy trade is opened at point D, right after the pattern is completed.
• Stop Loss (SL): Placed at the swing low that formed point D.
• Take Profit (TP): Set using a 1:3 risk-to-reward ratio, meaning the TP distance will be three times the size of the SL.

Logic for Sell

To detect a bearish Gartley pattern, the EA will follow these steps:

• Identify X as a swing high point.
• Detect A as a significant swing low after X.
• Locate B, which must retrace within the specified range of the XA leg.
• Confirm C, which retraces between specified range AB leg.
• Calculate the potential D point, which should fall within a range of the XA leg.
• Ensure all legs follow the required Fibonacci alignment for a valid Gartley structure.
• Once point D is confirmed, the EA will generate a sell signal, expecting the price to reverse downward from this level.
• Additionally, the EA will allow users to adjust all Fibonacci retracement and extension percentages through the input settings, giving flexibility based on different market conditions.

Once the EA confirms a valid bearish Gartley pattern:

• Entry: A sell trade is opened at point D, right after the pattern is completed.
• Stop Loss (SL): Placed at the swing high that formed point D.
• Take Profit (TP): Set using a 1:3 risk-to-reward ratio, meaning the TP distance will be three times the size of the SL.

Identifying Bearish Gartley Pattern

In the last article, I explained in detail the difference between bullish and bearish harmonic patterns. Like I always say, when you are working with chart patterns, you will need candle data, and you must be able to identify swing highs and swing lows. The beginning point X for the bearish Gartley pattern needs to be a swing high. The structure then follows the necessary Fibonacci retracement and extension levels as it moves into the XA, AB, BC, and CD legs. The EA can map out the XABCD structure and determine whether it fits the parameters of a bearish Gartley by accurately identifying these swings.

Example:

input ENUM_TIMEFRAMES timeframe = PERIOD_CURRENT; // TIMEFRAME


double open[];
double close[];
double low[];
double high[];
datetime time[];

datetime time_bar;
int bars_check = 500;
int total_symbol_bars;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {

   total_symbol_bars = Bars(_Symbol, timeframe);
   time_bar = iTime(_Symbol, timeframe, 0);

   CopyOpen(_Symbol, timeframe, time_bar, bars_check, open);
   CopyClose(_Symbol, timeframe, time_bar, bars_check, close);
   CopyLow(_Symbol, timeframe, time_bar, bars_check, low);
   CopyHigh(_Symbol, timeframe, time_bar, bars_check, high);
   CopyTime(_Symbol, timeframe, time_bar, bars_check, time);

  }

//+------------------------------------------------------------------+
//| FUNCTION FOR SWING LOW                                           |
//+------------------------------------------------------------------+
bool IsSwingLow(const double &low_price[], int index, int lookback)
  {
   for(int i = 1; i <= lookback; i++)
     {
      if(low_price[index] > low_price[index - i] || low_price[index] > low_price[index + i])
         return false;
     }
   return true;
  }

//+------------------------------------------------------------------+
//| FUNCTION FOR SWING HIGH                                          |
//+------------------------------------------------------------------+
bool IsSwingHigh(const double &high_price[], int index, int lookback)
  {
   for(int i = 1; i <= lookback; i++)
     {
      if(high_price[index] < high_price[index - i] || high_price[index] < high_price[index + i])
         return false; // If the current high is not the highest, return false.
     }
   return true;
  }

Explanation:

Setting the Expert Advisor's timeframe to correspond with the chart it is operating on is the first step in the procedure. To record historical candle data, including open, close, high, low, and time, arrays are ready. The timestamp of the most recent bar, the total number of bars available, and the number of bars to analyze are tracked by other variables. Later on, market data will be stored in these arrays to allow for a detailed analysis of price fluctuations.

The program collects the time of the most recent bar and determines how many bars are available for each market update. To guarantee that the analysis is always predicated on the state of the market, it then collects the most recent collection of price and time data. This offers a solid basis for additional computations as well as for spotting technical trends in the price data.

By comparing each bar to its neighbors, custom functions identify significant highs and lows. One function verifies a clear low, while another verifies a clear high. Bullish and bearish Gartley setups are examples of harmonic patterns that the computer consistently detects by only monitoring these points when a new bar forms.

Identifying X

Finding point X is the first step in identifying a bearish Gartley pattern. Point X needs to be a swing high on the chart for the setup to be bearish. This implies that it ought to be evident as a peak where the price increases before declining.

Example:

double X;
datetime X_time;
string X_letter;
int z = 4;
long chart_id = ChartID();

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {

   total_symbol_bars = Bars(_Symbol, timeframe);
   time_bar = iTime(_Symbol, timeframe, 0);

   CopyOpen(_Symbol, timeframe, time_bar, bars_check, open);
   CopyClose(_Symbol, timeframe, time_bar, bars_check, close);
   CopyLow(_Symbol, timeframe, time_bar, bars_check, low);
   CopyHigh(_Symbol, timeframe, time_bar, bars_check, high);
   CopyTime(_Symbol, timeframe, time_bar, bars_check, time);

   if(total_symbol_bars >= bars_check)
     {

      for(int i = z ; i < bars_check - z; i++)
        {

         if(IsSwingHigh(high, i, z))
           {

            X = high[i];
            X_time = time[i];
            X_letter = StringFormat("X  %d",i);

            ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X);
            ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

           }
        }
     }
  }

Explanation:

To ensure that there are enough candles accessible for investigation, the program starts with a safety check. It makes sure that at least 500 bars are present on the chart before continuing because it requires this amount. Errors are prevented, and the Expert Advisor is certain to use only comprehensive market data by exercising this caution. After this check, the software uses a loop and a lookback period (z) to go over the candles and compare each one to its neighbors. To avoid out-of-range mistakes and accurately determine swing points, for example, z is set to 4 so that each candle is compared to the four candles that preceded and followed it.

The algorithm establishes point X, the bearish Gartley pattern's first anchor, within this loop by looking for a swing high. The price, time, and index are kept when a legitimate swing high is identified, and the chart is immediately marked with a text label that reads "X." In addition to emphasizing the crucial swing point, this visual marker offers a clear reference for the subsequent phases in determining the remaining Gartley pattern.

Identifying A

The next stage is to look for point A after X has been correctly marked as a legitimate swing high. A is typically a swing low that develops following X in a bearish harmonic pattern. The EA moves forward from the bar where X was detected to locate this. Similar to how we used IsSwingHigh for X, it uses the IsSwingLow function to search for a swing low by checking each bar in the range.

Example:

double A;
datetime A_time;
string A_letter;
string xa_line;

if(total_symbol_bars >= bars_check)
     {

      for(int i = z ; i < bars_check - z; i++)
        {

         if(IsSwingHigh(high, i, z))
           {

            X = high[i];
            X_time = time[i];
            X_letter = StringFormat("X  %d",i);

            ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X);
            ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

            for(int j = i; j < bars_check - z; j++)
              {

               if(IsSwingLow(low, j, z) && low[j] < X)
                 {

                  A = low[j];
                  A_time = time[j];
                  A_letter = StringFormat("A %d",j);

                  ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A);
                  ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");
                  
                  xa_line = StringFormat("XA Line  %d",i);
                  ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A);
                  
                  break;

                 }
              }
           }
        }
     }

Output:

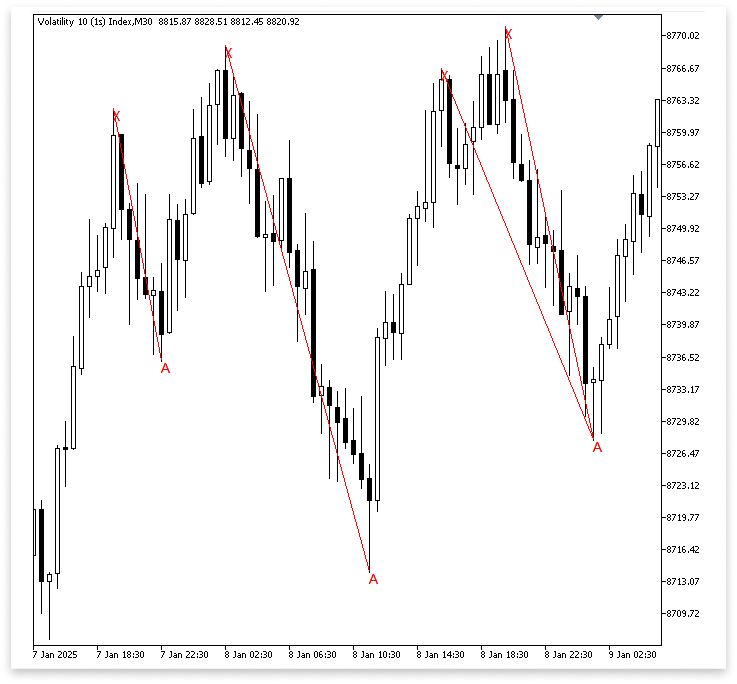
Explanation:

The Expert Advisor quickly starts looking for point A, the pattern's next crucial point, after determining that point X is a legitimate swing high. It starts at the position of X and looks at each bar that comes after it to determine a low that is appropriate for being a swing low. To make sure the structure fits a bearish harmonic pattern, the program verifies during this search if the new low is, in fact, lower than the previously indicated high. When a bar satisfies these requirements, the software marks this crucial level on the chart with a label and logs the price and time as point A.

The EA plots a text label "A" at the selected point using ObjectCreate to make the identification on the chart clear. Next, it uses the OBJ_TREND object to create a trend line from X to A. This line connects the first swing high to the subsequent swing low and graphically represents the XA leg of the harmonic pattern. To ensure that the computer latches onto the closest and most pertinent A point after X rather than searching for more, the search is ended using the break; instruction when the first valid swing low is located.

The outer loop (for(int i = z; i < bars_check - z; i++)) is made to traverse through every bar in the range when the EA is searching for X (the swing high). To identify possible beginning points for a harmonic pattern, the EA must examine each of the data's possible swing highs. The EA would overlook other legitimate X points that might develop patterns later in the chart if a break were introduced here because the loop would stop after identifying the first swing high.

On the other hand, the EA will instantly search for the comparable A (a swing low that follows X) after locating an X. In this instance, since it defines the XA leg, the program just requires the first valid swing low following X. This break makes sure the EA doesn't keep looking for lows after the first legitimate A, which could cause confusion or overlap with XA legs. Finding the X that is closest to A while making sure that every A is paired with the closest legitimate X is the answer. By doing this, the XA leg stays constant and steers clear of overlapping detections.

Example:

if(total_symbol_bars >= bars_check)
  {

   for(int i = z ; i < bars_check - z; i++)
     {

      if(IsSwingHigh(high, i, z))
        {

         for(int j = i; j < bars_check - z; j++)
           {

            if(IsSwingLow(low, j, z) && low[j] < high[i])
              {

               A = low[j];
               A_time = time[j];
               A_letter = StringFormat("A %d",j);

               for(int a = j; a >= i; a--)
                 {

                  if(IsSwingHigh(high, a, z) && high[a] > A)
                    {

                     X = high[a];
                     X_time = time[a];
                     X_letter = StringFormat("X  %d",a);

                     ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X);
                     ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

                     ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A);
                     ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

                     xa_line = StringFormat("XA Line  %d",i);
                     ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A);

                     break;

                    }
                 }

               break;

              }
           }
        }
     }
  }
  }
  }

  }

Output: 

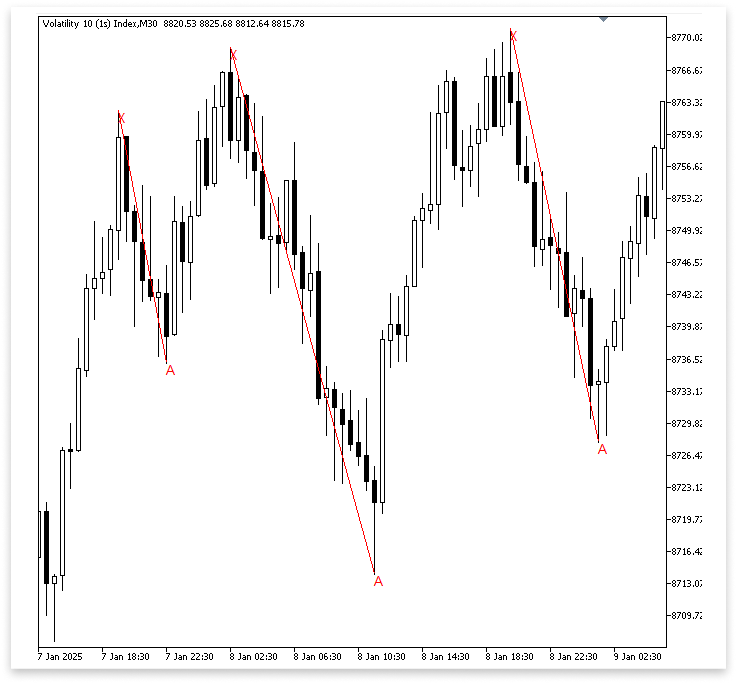
Explanation:

We are only utilizing high[i] as a temporary reference when we first use the condition low[j] < high[i] to check for a swing low. Which swing high should be formally selected as X is still up in the air. The structure is still appropriate for beginning a XA leg because using high[i] merely guarantees that A (the swing low) is lower than at least one swing high before to it. Stated differently, high[i] serves as a placeholder check that eliminates lows that are inconsistent with A.

Since that swing high might not be the strongest or closest contender before A, we cannot just choose high[i] as X once a legitimate A has been determined. The reverse loop for(int a = j; a >= i; a--) is introduced to improve this. This loop moves backward toward the initial high from the position of A. It is the most sensible option for X since it seeks to identify the swing high that is closest to A and higher than A. This guarantees that, rather than being predicated on an arbitrary prior high, our XA leg is securely and appropriately generated.

Since we only want to draw these elements after verifying that X is valid, we finally transfer the object creation process (marking X, marking A, and drawing the XA line) within this backward loop. Plotting X and A too soon, possibly with the incorrect swing high, would result from keeping object creation outside. We ensure that the chart will only display the XA leg once the valid, nearest swing high has been verified by doing so inside the loop.

Identifying BC

Finding the BC leg comes next after finishing the XA leg. Two points, B and C, make up this section of the structure in a bearish Gartley pattern. Point C must form as a swing low that follows Point B, and Point B must appear as a swing high that follows Point A. We start outlining the second part of the harmonic pattern by establishing these two locations.

Currently, no Fibonacci retracement or extension conditions are being introduced. The focus instead is on determining the natural swing points of the price movement.

Example:

double B;
datetime B_time;
string B_letter;

double C;
datetime C_time;
string C_letter;
string ab_line;
string bc_line;

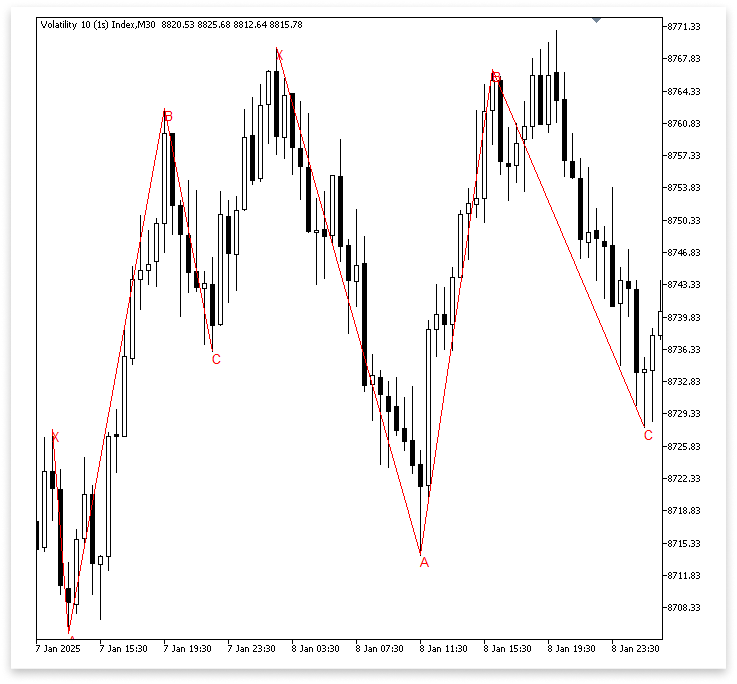
for(int k = j; k < bars_check - z; k++)
  {

   if(IsSwingHigh(high, k, z) && high[k] > A)
     {

      B = high[k];
      B_time = time[k];
      B_letter =  StringFormat("B %d",k);


      for(int l = k; l < bars_check - z; l++)
        {

         if(IsSwingLow(low, l, z) && low[l] < B)
           {

            C = low[l];
            C_time = time[l];
            C_letter = StringFormat("C  %d",l);

            ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,B_time,B);
            ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B");

            ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,C_time,C);
            ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C");

            ab_line = StringFormat("AB Line  %d",i);
            ObjectCreate(chart_id,ab_line,OBJ_TREND,0,A_time,A,B_time,B);

            bc_line = StringFormat("BC Line  %d", i);
            ObjectCreate(chart_id,bc_line,OBJ_TREND,0,B_time,B,C_time,C);

            ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X);
            ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

            ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A);
            ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

            xa_line = StringFormat("XA Line  %d",i);
            ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A);

            i = l+1;

            break;
           }
        }

      break;
     }
  }

Output:

Explanation:

Starting from the point of A, the first loop, for(int k = j; k < bars_check - z; k++), begins looking for B. The software uses IsSwingHigh to search for a swing high inside this loop. It also verifies that high[k] > A, which indicates that the swing high is above point A, to make sure B makes sense as a component of the structure. The software logs the value, time, and label for B after this condition is met.

To determine C, which must be a swing low that arises after B, a second loop, for(int l = k; l < bars_check - z; l++), is then employed. The bearish Gartley's proper downward structure is maintained by the criterion low[l] < B, which guarantees that C is in fact lower than the swing high B. Details (price, time, and label) are saved when a valid C is discovered. The program redraws X and A to maintain the pattern's clarity after identifying points B and C and labeling them on the chart. 

The algorithm skips ahead and avoids continually detecting the same places by using the expression i = l+1; to advance the outer loop. The algorithm may miss a lot of legitimate Gartley signals if i = l+1 is used after identifying C. It misses possible swing points because it leaps too far forward. This strategy should be avoided in favor of letting the loops function normally or refining signals using filtering techniques to preserve opportunities.

Identifying D

Finding point D is the next stage in finishing the Gartley pattern once X, A, B, and C have been successfully identified. Since Point D is the possible entry zone, it is the last leg of the construction and is crucial. We search for a swing high that develops following point C to identify D. To complete the CD leg, this swing should preferably travel in the opposite direction as BC.

Example:

double D;
datetime D_time;
string D_letter;
string cd_line;

for(int m = l; m < bars_check - z; m++)
  {

   if(IsSwingHigh(high, m, z) && high[m] > B)
     {

      D = high[m];
      D_time = time[m];
      D_letter = StringFormat("D  %d",m);

      ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D);
      ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D");

      cd_line = StringFormat("CD Line  %d",i);
      ObjectCreate(chart_id,cd_line,OBJ_TREND,0,C_time,C,D_time,D);

      ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,B_time,B);
      ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B");

      ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,C_time,C);
      ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C");

      ab_line = StringFormat("AB Line  %d",i);
      ObjectCreate(chart_id,ab_line,OBJ_TREND,0,A_time,A,B_time,B);

      bc_line = StringFormat("BC Line  %d", i);
      ObjectCreate(chart_id,bc_line,OBJ_TREND,0,B_time,B,C_time,C);

      ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X);
      ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

      ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A);
      ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

      xa_line = StringFormat("XA Line  %d",i);
      ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A);

      i = m+1;
      break;
     }
  }

Output:

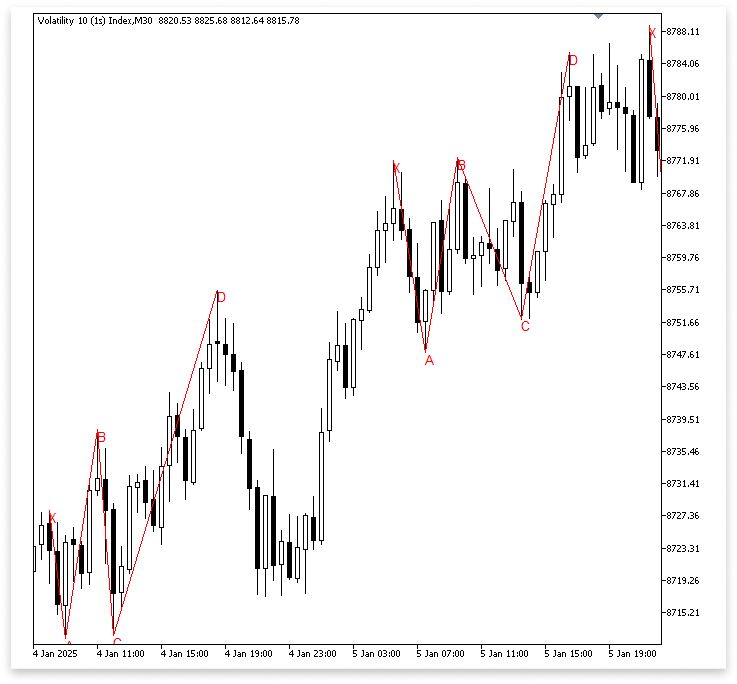
Explanation:

The loop begins scanning the chart from the index of point C (l) forward, searching for possible swing highs that might be point D. The condition IsSwingHigh(high, m, z) && high[m] > B guarantees that the selected D is higher than point B and not simply any swing high. Because point D needs to surpass level B in a bearish Gartley to preserve the proper structure, this rule is crucial.

After identifying such a swing high, the code creates the CD line to connect it with point C, labels it as "D" on the chart, and enters its price and time data into the D variables. The code simultaneously redraws the lines that correspond to the other significant points.

The next step is to confirm that each point correctly depicts the dominant swing inside each leg after the swings have been effectively identified. Marking highs and lows is insufficient because even little adjustments could cause the framework to become confusing. Strict guidelines for verifying the legitimacy of every swing point must be implemented to prevent false signals.

First, between C and D, point C must be the lowest low. By doing this, the CD leg is guaranteed to begin from a genuine swing low as opposed to a brief dip. To ensure that the BC leg retraces from a legitimate dominant peak, point B must also be the highest high between B and C.

Similarly, it should be verified that point A is the lowest low between points A and B. This condition confirms that, rather than starting at a random fluctuation, the AB leg starts at the proper low. Lastly, between X and A, point X must be the highest high. The XA leg will begin at the strongest swing high in that area thanks to this check.

Example:

int x_a_bars;
int x_highest_index;
double x_a_hh;
datetime x_a_hh_t;

int a_b_bars;
int a_lowest_index;
double a_b_ll;
datetime a_b_ll_t;

int b_c_bars;
int b_highest_index;
double b_c_hh;
datetime b_c_hh_t;

int c_d_bars;
int c_lowest_index;
double c_d_ll;
datetime c_d_ll_t;

for(int m = l; m < bars_check - z; m++)
  {

   if(IsSwingHigh(high, m, z) && high[m] > B)
     {

      D = high[m];
      D_time = time[m];
      D_letter = StringFormat("D  %d",m);

      c_d_bars = Bars(_Symbol,PERIOD_CURRENT,C_time,D_time);
      c_lowest_index = ArrayMinimum(low,l,c_d_bars);
      c_d_ll = low[c_lowest_index];
      c_d_ll_t = time[c_lowest_index];

      b_c_bars = Bars(_Symbol, PERIOD_CURRENT, B_time, c_d_ll_t);
      b_highest_index = ArrayMaximum(high, k, b_c_bars);
      b_c_hh = high[b_highest_index];
      b_c_hh_t = time[b_highest_index];

      a_b_bars = Bars(_Symbol,PERIOD_CURRENT,A_time,b_c_hh_t);
      a_lowest_index = ArrayMinimum(low,j,a_b_bars);
      a_b_ll = low[a_lowest_index];
      a_b_ll_t = time[a_lowest_index];

      x_a_bars = Bars(_Symbol, PERIOD_CURRENT, X_time, a_b_ll_t);
      x_highest_index = ArrayMaximum(high, a, x_a_bars);
      x_a_hh = high[x_highest_index];
      x_a_hh_t = time[x_highest_index];

      ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D);
      ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D");

      cd_line = StringFormat("CD Line  %d",i);
      ObjectCreate(chart_id,cd_line,OBJ_TREND,0,c_d_ll_t,c_d_ll,D_time,D);

      ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,b_c_hh_t,b_c_hh);
      ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B");

      ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,c_d_ll_t,c_d_ll);
      ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C");

      ab_line = StringFormat("AB Line  %d",i);
      ObjectCreate(chart_id,ab_line,OBJ_TREND,0,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh);

      bc_line = StringFormat("BC Line  %d", i);
      ObjectCreate(chart_id,bc_line,OBJ_TREND,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll);

      ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,x_a_hh_t,x_a_hh);
      ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

      ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,a_b_ll_t,a_b_ll);
      ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

      xa_line = StringFormat("XA Line  %d",i);
      ObjectCreate(chart_id,xa_line,OBJ_TREND,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll);

      i = m+1;
      break;
     }
  }

Explanation:

Verifying the accuracy of the swing points that have been found and making sure that the Gartley structure is derived from the most notable highs and lows in each leg are the main goals of this section of the code. When a new swing high that is higher than point B is discovered after point C, the process begins. Although point D is assigned to this swing high, the code first verifies all earlier points before concluding the pattern.

The C–D range is where the validation starts. The code in this part looks for the lowest low to ensure that point C is the actual bottom between those two points and not merely a transient drop. To determine the highest high, the range between B and C is then examined. This guarantees that, instead of a minor bump that can distort the pattern, point B is the strongest peak in that section.

To verify that point A is, in fact, the most prominent trough in that leg, the range between A and B is then examined for the lowest low. To confirm that X is the strongest peak before the decline to A, the range between X and A is finally examined for the highest high. The code ensures that all the points X, A, B, and C are the proper structural swings for creating the harmonic pattern by carrying out these checks.

Fibonacci Retracement

Finding out if the structure truly meets the criteria for being a Gartley pattern comes next, following the identification and validation of the swing points. Since not every collection of swings creates a legitimate harmonic pattern, simply having points X, A, B, C, and D indicated on the chart is insufficient. We must use Fibonacci retracement and extension criteria on the various structural legs to distinguish between them.

The "filters" that verify whether price movements match the ratios necessary for a Gartley pattern are these Fibonacci measurements. For instance, certain Fibonacci ranges must be met by the expansion of point D in relation to the other swings, the retracement of point B from XA, and the retracement of point C from AB. The structure can be categorized as a legitimate Gartley pattern if these requirements are satisfied.

Example:

input double b_xa_max = 78.6; // MAX B RETRACEMENT LEVEL FOR XA
input double b_xa_min = 61.8; // MIN B RETRACEMENT LEVEL FOR XA

input double c_ab_max = 88.6; // MAX C RETRACEMENT LEVEL FOR AB
input double c_ab_min = 38.2; // MIN C RETRACEMENT LEVEL FOR AB

input double d_xa_max = 76.0; // MAX D RETRACEMENT LEVEL FOR XA
input double d_xa_min = 80.0; // MIN D RETRACEMENT LEVEL FOR XA

double lvl_max_b;
double lvl_min_b;

double lvl_max_c;
double lvl_min_c;

double lvl_max_d;
double lvl_min_d;

if(IsSwingHigh(high, m, z) && high[m] > B)
  {

   D = high[m];
   D_time = time[m];
   D_letter = StringFormat("D  %d",m);

   c_d_bars = Bars(_Symbol,PERIOD_CURRENT,C_time,D_time);
   c_lowest_index = ArrayMinimum(low,l,c_d_bars);
   c_d_ll = low[c_lowest_index];
   c_d_ll_t = time[c_lowest_index];

   b_c_bars = Bars(_Symbol, PERIOD_CURRENT, B_time, c_d_ll_t);
   b_highest_index = ArrayMaximum(high, k, b_c_bars);
   b_c_hh = high[b_highest_index];
   b_c_hh_t = time[b_highest_index];

   a_b_bars = Bars(_Symbol,PERIOD_CURRENT,A_time,b_c_hh_t);
   a_lowest_index = ArrayMinimum(low,j,a_b_bars);
   a_b_ll = low[a_lowest_index];
   a_b_ll_t = time[a_lowest_index];

   x_a_bars = Bars(_Symbol, PERIOD_CURRENT, X_time, a_b_ll_t);
   x_highest_index = ArrayMaximum(high, a, x_a_bars);
   x_a_hh = high[x_highest_index];
   x_a_hh_t = time[x_highest_index];

   lvl_min_b = a_b_ll + ((b_xa_min / 100) * (x_a_hh - a_b_ll));
   lvl_max_b = a_b_ll + ((b_xa_max / 100) * (x_a_hh - a_b_ll));

   lvl_min_c = b_c_hh - ((c_ab_min / 100) * (b_c_hh - a_b_ll));
   lvl_max_c = b_c_hh - ((c_ab_max / 100) * (b_c_hh - a_b_ll));

   lvl_min_d = a_b_ll + ((d_xa_min / 100) * (x_a_hh - a_b_ll));
   lvl_max_d = a_b_ll + ((d_xa_max / 100) * (x_a_hh - a_b_ll));

   if(b_c_hh >= lvl_min_b && b_c_hh <= lvl_max_b && c_d_ll <= lvl_min_c && c_d_ll >= lvl_max_c
      && D >= lvl_min_d && D <= lvl_max_d)
     {

      ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D);
      ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D");

      cd_line = StringFormat("CD Line  %d",i);
      ObjectCreate(chart_id,cd_line,OBJ_TREND,0,c_d_ll_t,c_d_ll,D_time,D);

      ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,b_c_hh_t,b_c_hh);
      ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B");

      ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,c_d_ll_t,c_d_ll);
      ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C");

      ab_line = StringFormat("AB Line  %d",i);
      ObjectCreate(chart_id,ab_line,OBJ_TREND,0,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh);

      bc_line = StringFormat("BC Line  %d", i);
      ObjectCreate(chart_id,bc_line,OBJ_TREND,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll);

      ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,x_a_hh_t,x_a_hh);
      ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

      ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,a_b_ll_t,a_b_ll);
      ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

      xa_line = StringFormat("XA Line  %d",i);
      ObjectCreate(chart_id,xa_line,OBJ_TREND,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll);

     }

// i = m+1;
   break;
  }

  }

Explanation:

We begin with the input parameters. To determine whether the structure of X, A, B, C, and D is a valid Gartley pattern, the Expert Advisor will employ these user-defined Fibonacci retracement levels. For instance, depending on the inputs, point B should be between the stated retracement of the XA leg, position C on the given retracement of the AB leg, and point D on the provided Fibonacci retracement of the XA leg.

The actual price levels at which each swing point should form are represented by the computed variables. Based on the Fibonacci principles established in the inputs, they are calculated from the high and low prices of the XA and AB legs. For instance, the retracement of the XA leg establishes the legal range for point B, and the same method is used to calculate the ranges for points C and D in relation to AB and XA.

Every pattern point is verified to be inside the necessary Fibonacci range by the last condition check. It confirms that the retracement conditions for points B, C, and D are met. When all of these requirements are met, the program generates chart objects to visually represent the recognized Gartley pattern by identifying points X, A, B, C, and D and drawing the connecting lines.

Trade Execution

Trade execution follows the successful identification of a legitimate Gartley pattern. To make sure the structure complies with Gartley formation guidelines, the Expert Advisor has so far concentrated on examining price data, identifying swing highs and lows, and verifying Fibonacci linkages. However, merely identifying the pattern gives the trader a possible trading opportunity; it does not provide profits on its own. When the EA makes trades in the market using this knowledge, the real action starts.

In actuality, this means that the EA now has to choose where to enter, where to put the take profit, and where to set the stop loss. For instance, the EA would normally initiate a sell order at point D in a bearish Gartley pattern. To guard against pattern invalidation, the stop loss would be placed slightly above the swing high at D. The take profit might be determined using Fibonacci extension goals or a risk-to-reward ratio like 1:3. The EA guarantees consistent performance without hesitation or emotional bias by automating this process.

Example:

#include <Trade/Trade.mqh>
CTrade trade;
input int MagicNumber = 61626;
input double lot_size = 0.1;

double ask_price;
datetime time_price[];
double take_p;

string XAB;
string BCD;
datetime lastTradeBarTime = 0;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   trade.SetExpertMagicNumber(MagicNumber);
   ArraySetAsSeries(time_price,true);

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

   ObjectsDeleteAll(chart_id);

  }

CopyTime(_Symbol, timeframe, 0, 2, time_price);
ask_price = SymbolInfoDouble(_Symbol,SYMBOL_ASK);
datetime currentBarTime = iTime(_Symbol,timeframe,0);

if(b_c_hh >= lvl_min_b && b_c_hh <= lvl_max_b && c_d_ll <= lvl_min_c && c_d_ll >= lvl_max_c
   && D >= lvl_min_d && D <= lvl_max_d)
  {

   ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D);
   ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D");

   cd_line = StringFormat("CD Line  %d",i);
   ObjectCreate(chart_id,cd_line,OBJ_TREND,0,c_d_ll_t,c_d_ll,D_time,D);

   ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,b_c_hh_t,b_c_hh);
   ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B");

   ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,c_d_ll_t,c_d_ll);
   ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C");

   ab_line = StringFormat("AB Line  %d",i);
   ObjectCreate(chart_id,ab_line,OBJ_TREND,0,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh);

   bc_line = StringFormat("BC Line  %d", i);
   ObjectCreate(chart_id,bc_line,OBJ_TREND,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll);

   ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,x_a_hh_t,x_a_hh);
   ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

   ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,a_b_ll_t,a_b_ll);
   ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

   xa_line = StringFormat("XA Line  %d",i);
   ObjectCreate(chart_id,xa_line,OBJ_TREND,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll);

   XAB = StringFormat("XAB TRIANGLE %d", i);
   BCD = StringFormat("BCD TRIANGLE %d", i);

   ObjectCreate(chart_id,XAB,OBJ_TRIANGLE,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh);
   ObjectSetInteger(chart_id,XAB,OBJPROP_FILL,true);
   ObjectSetInteger(chart_id,XAB,OBJPROP_COLOR,clrPink);
   ObjectSetInteger(chart_id,XAB,OBJPROP_BACK,true);

   ObjectCreate(chart_id,BCD,OBJ_TRIANGLE,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll,D_time,D);
   ObjectSetInteger(chart_id,BCD,OBJPROP_FILL,true);
   ObjectSetInteger(chart_id,BCD,OBJPROP_COLOR,clrPink);
   ObjectSetInteger(chart_id,BCD,OBJPROP_BACK,true);

   if(time[m+z] == time_price[1] && currentBarTime != lastTradeBarTime)
     {

      take_p = ask_price - (MathAbs(D - ask_price) * 3);
      trade.Sell(lot_size,_Symbol,ask_price,D,take_p);

      lastTradeBarTime = currentBarTime;

     }

  }

Output:

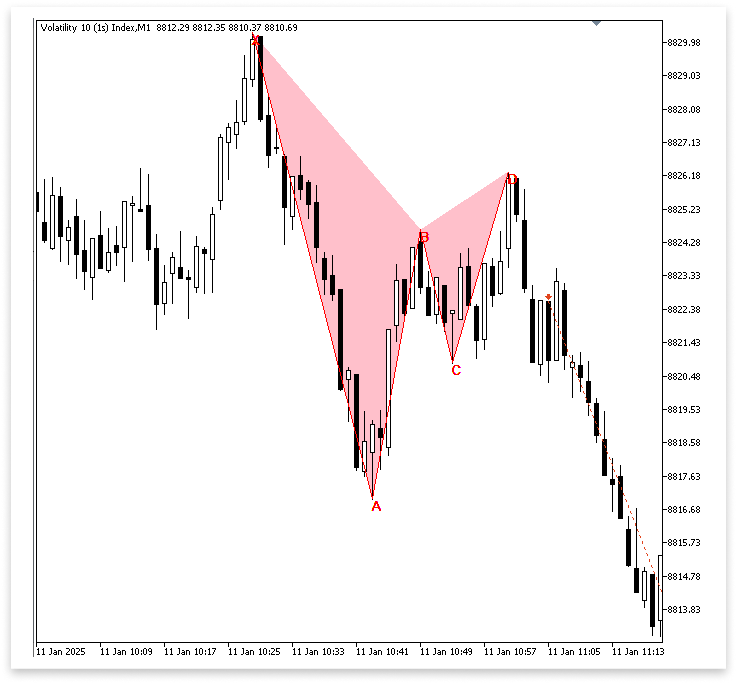
Explanation:

This section of the program manages the visual representation of the Gartley pattern on the chart as well as the trading logic. The standard MQL5 trade library is first included using #include <Trade/Trade.mqh>. A CTrade object called trade is constructed from this library to manage all trade-related tasks, including opening and closing positions. An input parameter called MagicNumber is declared and used with transactions to differentiate the trades made by this Expert Advisor from others.MagicNumber; SetExpertMagicNumber;.

The amount of volume that will be exchanged is determined by other crucial factors like lot_size. To store the market price, time data, and computed take-profit levels, supporting variables like ask_price, time_price[], and take_p are declared. As a precaution, the variable lastTradeBarTime is utilized to ensure that a new transaction is not opened on the same bar more than once.

The most recent element is kept at index zero by applying ArraySetAsSeries(time_price, true); to guarantee that the price data is treated appropriately. The opening timings of the final two bars are then copied into the time_price array by the method CopyTime(_Symbol, timeframe, 0, 2, time_price). Ask_price = SymbolInfoDouble(_Symbol, SYMBOL_ASK); yields the current ask price, and currentBarTime = iTime(_Symbol, timeframe, 0); stores the timestamp of the most recent bar.

The computer can use these specifics to pinpoint the precise instant that trade requirements are satisfied. By comparing bar times, the conditional check makes sure the program only reacts once every bar. If valid, a sell order is executed with trade, and a take-profit level is determined using take_p = ask_price - (MathAbs(D - ask_price) * 3);. Sell(lot_size, D, take_p, ask_price, _Symbol);. To prevent the same bar from triggering another transaction, lastTradeBarTime is then changed.

The program not only executes trades but also shows the Gartley pattern right on the chart. For example, XAB = StringFormat("XAB TRIANGLE %d", i); and BCD = StringFormat("BCD TRIANGLE %d", i); are strings that are constructed using StringFormat to uniquely name the graphical objects. ObjectCreate is then used to draw two triangular shapes using these identifiers. The XAB portion of the pattern is represented by the first triangle, and the BCD portion by the second. According to the corresponding swing points found earlier in the software, their coordinates are established.

The triangles' properties are set using ObjectSetInteger, where they are filled, tinted pink, and transmitted to the background to make these patterns stand out. The program not only reacts to recognized Gartley patterns, but also makes them accessible to the trader for verification thanks to the combination of automatic trade execution and understandable graphical visualization.

Conclusion

In this article, we explored how to build and trade the Gartley Pattern in MQL5. We started by identifying the swing points (X, A, B, C, and D), applied Fibonacci retracement and extension levels to confirm the structure, and then automated trade execution once the pattern was valid. Finally, we added chart objects for clear visualization, making it easier to see the pattern as it forms. This project shows how complex harmonic patterns can be coded and traded automatically. With this foundation, you can refine the rules, add confirmations, or extend the logic to other harmonic patterns.