特征向量和特征值：MetaTrader 5 中的探索性数据分析

MetaTrader 5 — 示例 | 3 二月 2025, 15:11

248

Francis Dube

概述

主成分分析（PCA，Principal Component Analysis）因其在数据探索过程中的降维作用而广为人知。然而，它的潜力远远超出了减少大型数据集的范围。PCA的核心是特征值和特征向量，它们在揭示数据中的隐藏关系方面起着至关重要的作用。在本文中，我们将探索利用特征结构来揭示这些隐藏关系的技术。

我们将从因子分析开始，演示特征结构如何帮助识别潜在变量，从而更全面地了解数据的底层结构。通过识别潜在变量，我们可以揭示看似独立的变量之间的冗余，展示多个变量如何简单地反映相同的潜在因素。此外，我们将研究如何使用特征向量和特征值来评估变量随时间变化的关系。通过分析在不同时间间隔收集的数据的特征结构，我们可以对变量之间的动态关系获得有价值的见解。使我们能够识别随时间同步变化或表现出相反行为的变量。

数据中的潜在变量：主因子分析

因子分析是一种旨在揭示隐藏因子的方法，这些隐藏因子可以解释数据中观察到的变量之间的相互关系。它将测量变量表示为潜在因子的组合，而潜在因子表示已知有影响但难以测量或量化的构造。例如，考虑交易者用来评估市场行为的指标。因子分析可揭示这些指标受投资者情绪或风险偏好等潜在因子的影响。计算技术指标可能很简单，但量化市场情绪或风险偏好则更具挑战性。这就像观察浑浊水体表面的涟漪。涟漪代表了我们所看到的，而根本原因仍然隐藏着。因子分析旨在揭示这些隐藏的原因。

因子分析经常被误认为是主成分分析（PCA）的替代品。这两种技术都能降低数据的维度，但在降维后的变量与原始数据集的关系中有所不同。PCA 将一大组变量还原成较小的一组不相关或正交的变量，称为主成分。这些成分捕捉了原始数据的最大方差。想象一下，一个包含数百个变量的密集数据集，进行 PCA 可能会发现，只有三个变量代表了 99% 以上的数据信息。这三个主要成分对应于观测数据中固有的不同属性，通过组合原始数据的比特来解释。每个主成分都受到密集变量集的影响。相比之下，因子分析理论认为潜在变量会影响观察到的变量。在本文中，我们专注于计算这些隐藏的维度以及它们对观察到的变量提供的独特视角，而不是降维。

特征值和特征向量是理解本文至关重要的基本数学概念。如果矩阵 A 是一个 p 乘 p 的矩阵，x 是一个长度为 p 的列向量，E 是一个标量，那么如果 Ax=Ex，x 是 A 的一个特征向量，其特征值为 E。特征向量的方向是重要的，而不是它的长度，它通常被归一化为单位长度。从几何上讲，将向量乘以矩阵通常会使其旋转，但特征向量在乘以矩阵时保持方向不变。这一方向是它们相关性的关键所在。在标准化多元正态分布中，协方差矩阵是相关矩阵 R，设 V 为 p 乘 m 矩阵，新的随机向量 y=V'x 具有协方差矩阵 C=V'RV。

矩阵 V 具有转换为 y 的理想性质。对于 m=1，V 是单列，C 是 y 的方差。归一化 V，使其分量之和为 1，得到与最大特征值对应的 R 的特征向量。将其扩展到 m=2，与第一列正交的 V 的第二列是与第二大特征值对应的 R 的特征向量。这个过程对所有 p 列都继续进行，使 R 的特征向量成为将 x 变量映射到捕获最大方差的独立 y 变量的变换矩阵。

散点图

为了说明前两段的意思，考虑一个散点图，其中 x 轴表示体重，y 轴表示人群样本的身高。如果在最匹配测量值分布的点上画一条线，这条线将描绘出主要模式：身材较高的人往往更重。现在，把特征向量想象成一个指向这个主要方向的箭头，显示最大的趋势或主导模式。相应的特征值会告诉你这种现象有多强烈。如果另一个箭头垂直于第一个箭头，它会显示一个次要的模式，比如有些人的身高可能比平时重或轻。

这些箭头（特征向量）和数字（特征值）帮助我们理解任何一组数字中最重要的模式。这就好比找到了解释数据的隐藏规则。通过使用这些工具，我们可以快速了解我们正在查看的数字中最重要的是什么。因此，在我们的探索中，我们首先通过相关性的特征结构分析来检查数据集的主成分。最初，主成分代表模型中的因子。对原始数据集进行标准化，以消除不同尺度的影响，并计算标准化变量的相关矩阵。特征结构是指特定矩阵的数学特性。在此背景下，我们分析了标准化观测变量的相关矩阵。观测变量是对所研究事物的测量。比如身高和体重值或交易者会跟踪的指标值。

目标是确定每个观察到的变量与相关矩阵的特征值之间的关系。这涉及计算特征值和观测变量之间的相关性。这些相关性形成了一个特殊的矩阵，称为因子载荷矩阵，通过将每个特征向量乘以其相应特征值的平方根得出。通过研究变量与某些特征值的相关性，我们可以假设对观测变量的影响。这种分析有助于我们了解哪些变量与因子最相关，并提供了影响观察到的变量的适当数量的因子的线索。

示例：金融指标的主因子分析

在本节中，我们将对一个金融指标数据集进行主因子分析（PFA）演示。我们将使用 MQL5 来执行计算因子载荷矩阵所涉及的所有步骤。我们首先要收集感兴趣的数据。在这种情况下，它将由在指定窗口长度范围内采样的几个指标组成。出于演示目的，我们将使用两个常见指标，即提供趋势信息的移动平均线（MA）指标和提供波动性基本衡量的平均真实范围（ATR）指标。这些指标的几个窗口长度将在一段时间内收集。

MA 和 ATR 指标

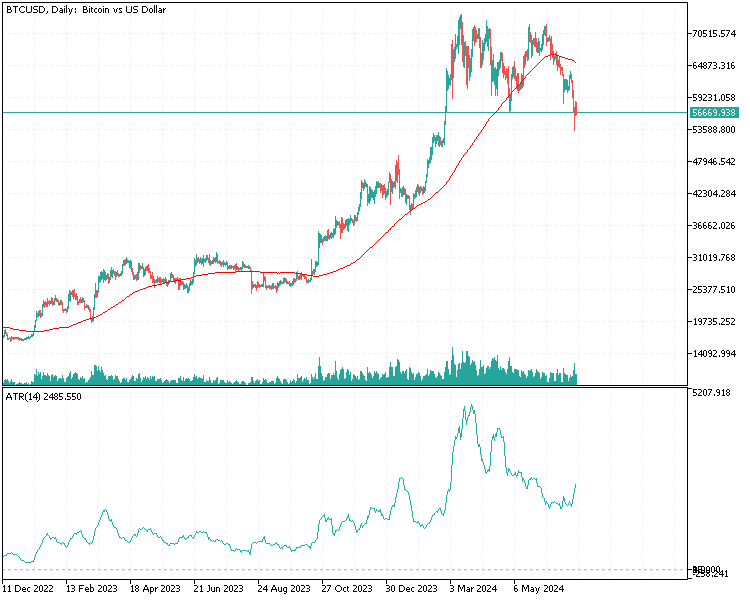
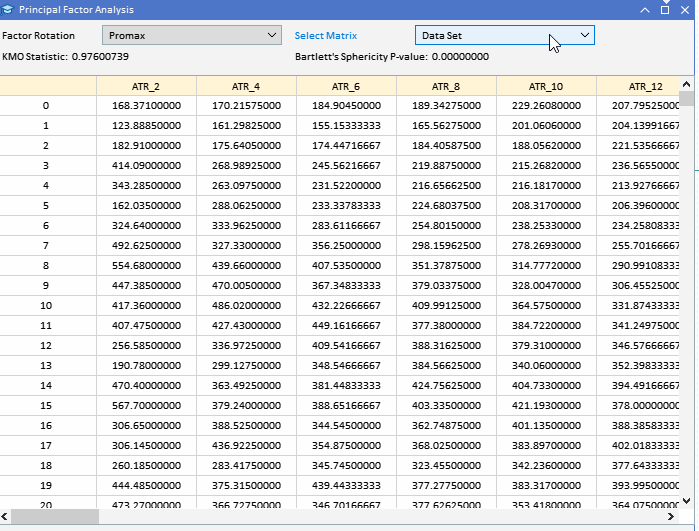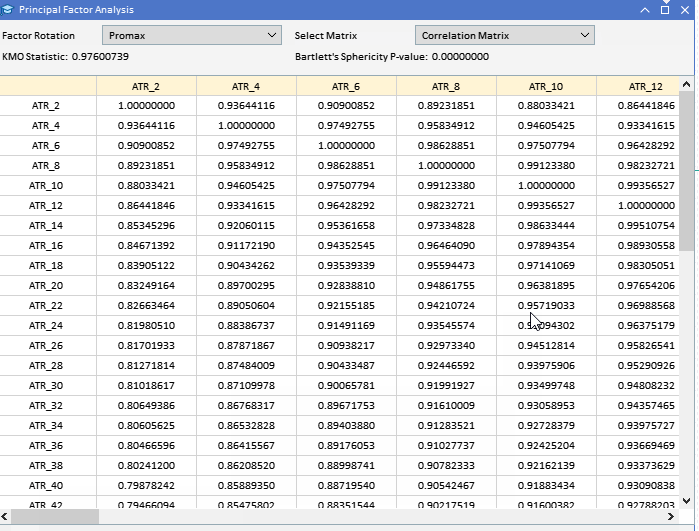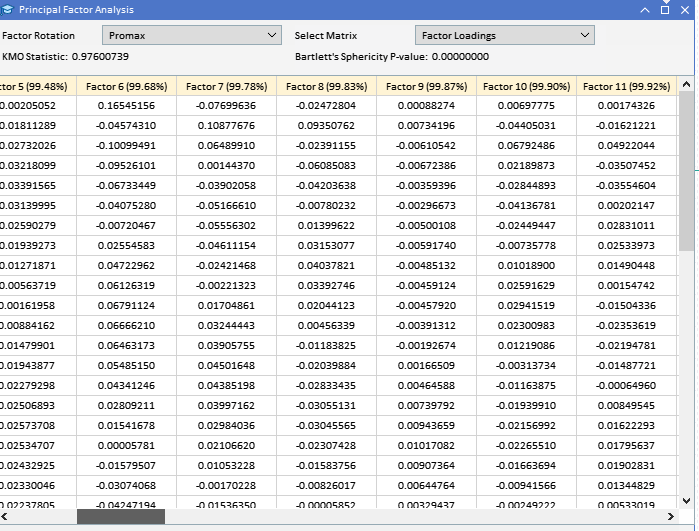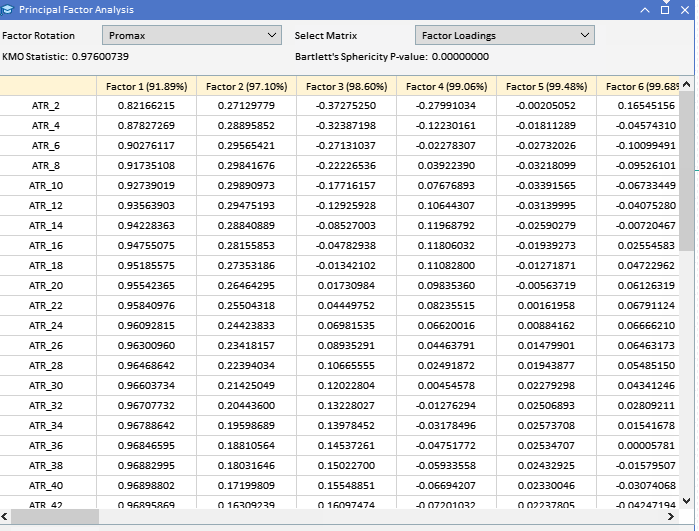
由于大多数分析都涉及对潜在大型矩阵的检查，因此由于它们的大小，简单地将它们打印到终端的专家选项卡上是不够的。鉴于要在 MetaTrader 5 中执行所有分析，而无需切换到 Python 或 R 等其他平台，因此在实现 PFA 的应用程序中加入了图形用户界面。下图显示了我们将在本例中使用的数据集。每一列都包含一个指标在特定窗口长度下的数值，具体数值由列标题给出。"ATR_2" 指窗口长度为 2 的 ATR 指标。根据比特币 (BTCUSD) 的每日价格，零索引指向 2019.12.31 至 2022.12.31 期间的最旧值。

应用演示

在尝试提取主因子之前，谨慎的做法是评估数据集是否适合进行因子分析。可以对数据集进行两个统计检验，以确定变量是否可能由潜在因子解释。第一种是 Kaiser-Meyer-Olkin (KMO) 检验。KMO 标准是一种统计方法，用于衡量因子分析样本数据的充分性。它量化变量之间的相关程度，并评估可能是共同方差的变量之间的方差比例，这些方差可归因于潜在因子。KMO 度量将观测到的相关系数的幅度与偏相关系数的大小进行比较。它的范围是 0 到 1，其中：

数值接近 1 表示数据非常适合进行因子分析。
低于 0.6 的值一般表示数据不适合进行因子分析。

KMO 统计量的数学定义是：

KMO 公式

其中：
- r(ij)是变量 i 和 j 之间的相关系数。
- p(ij) 是变量 i 和 j 之间的偏相关系数。

下面是 KMO 检验的 MQL5 实现。函数 "kmo()" 需要三个输入参数。"in" 矩阵应与所研究的变量数据集一起提供。测试结果将分别输出到第二个和第三个输入参数。"kwo_per_item" 向量将包含每个变量的 KMO 值（对应于 "in" 矩阵的每一列），而 "kwo_total" 则是合并变量的总体 KMO 统计量。

//+---------------------------------------------------------------------------+
//| Calculate the Kaiser-Meyer-Olkin criterion                                |
//|   In general, a KMO < 0.6 is considered inadequate.                       |
//+---------------------------------------------------------------------------+
void kmo(matrix &in, vector &kmo_per_item, double &kmo_total)
  {
   matrix partial_corr = partial_correlations(in);
   matrix x_corr = (stdmat(in)).CorrCoef(false);

   np::fillDiagonal(x_corr,0.0);
   np::fillDiagonal(partial_corr,0.0);

   partial_corr = pow(partial_corr,2.0);
   x_corr = pow(x_corr,2.0);

   vector partial_corr_sum = partial_corr.Sum(0);
   vector corr_sum  =  x_corr.Sum(0);
   kmo_per_item = corr_sum/(corr_sum+partial_corr_sum);

   double corr_sum_total = x_corr.Sum();
   double partial_corr_sum_total = partial_corr.Sum();
   kmo_total = corr_sum_total/(corr_sum_total + partial_corr_sum_total);
   return;
  }

评估数据集的另一种测试或附加测试是巴特利特均匀性测试 (BTS)。这是一种统计检验方法，用于检验相关矩阵是否为同一矩阵，如果是，则表明变量不相关，不适合采用因子分析等结构检测方法。本质上，它测试观察到的相关矩阵是否与恒等式矩阵显著偏离，其中所有对角元素都是 1，表示变量与自身完全相关，非对角元素是 0，表示不同变量之间没有相关性。该测试基于卡方检验，其检验统计量使用以下公式计算：

BTS 公式

其中：
- n 是观测数据的数量。
- p 是变量的数量。
- |R| 是相关矩阵 R 的行列式。

检验统计量遵循卡方分布，具有 (p(p-1))/2 个自由度。如果巴特利特检验统计量较大，相关的 p 值较小，通常 p 值小于 0.05，我们就拒绝零假设。这表明相关矩阵与恒等式矩阵存在显著差异，表明变量是相关的，适合进行因子分析。否则，如果 p 值较大，我们无法拒绝零假设，这表明相关矩阵接近恒等矩阵，变量之间没有显著相关性。

下面的代码定义了实现 BTS 的 "bartlet_sphericity()" 函数。函数将结果输出到最后的两个输入参数。"statistic" 是卡方统计量，"p_value" 是计算出的概率值。

//+------------------------------------------------------------------+
//| Compute the Bartlett sphericity test.                            |
//+------------------------------------------------------------------+
void bartlet_sphericity(matrix &in, double &statistic, double &p_value)
  {
   long n,p;
   n = long(in.Rows());
   p = long(in.Cols());

   matrix x_corr = (stdmat(in)).CorrCoef(false);

   double corr_det = x_corr.Det();
   double neg = -log(corr_det);
   statistic = (corr_det>0.0)?neg*(double(n)-1.0-(2.0*double(p)+5.0)/6.0):DBL_MAX;
   double degrees_of_freedom = double(p)*(double(p)-1.0)/2.0;
   int error;
   p_value = 1.0 - MathCumulativeDistributionChiSquare(statistic,degrees_of_freedom,error);
   if(error)
      Print(__FUNCTION__, " MathCumulativeDistributionChiSquare() error ", error);

   return;
  }

如果其中一项或两项测试提供了令人鼓舞的结果，我们可以继续进行主因子提取。使用指标的数据集，我们可以看到这两个测试都表明变量适合因子提取。

下一步涉及一点预处理，对数据集进行标准化。数据的标准化确保了每个指标对分析的贡献是平等的，无论其规模如何。

//+------------------------------------------------------------------+
//| standardize a matrix                                             |
//+------------------------------------------------------------------+
matrix            stdmat(matrix &in)
  {
   vector mean = in.Mean(0);
   vector std = in.Std(0);
   std+=1e-10;
   matrix out = in;

   for(ulong row =0; row<out.Rows(); row++)
      if(!out.Row((in.Row(row)-mean)/std,row))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return matrix::Zeros(in.Rows(), in.Cols());
        }

   return out;
  }

根据标准化数据计算相关矩阵。

m_data = stdmat(in);
m_corrmat = m_data.CorrCoef(false);

然后我们计算相关矩阵的特征值和特征向量。由于在使用本地矩阵的 "Eig()" 方法时遇到问题，我们选择使用 Aglib 库提供的特征向量去分解实现。

  CMatrixDouble cdata(m_corrmat);
      CMatrixDouble vects;
      CRowDouble vals;


      if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

这个问题最好通过一个例子来说明，下面的代码定义了一个脚本，用于分解对称矩阵的特征向量和值。

//+------------------------------------------------------------------+
//|                                        TestEigenDecompostion.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<Math\Alglib\linalg.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix dataset =
     {
        {1,0.5,-0.2},
        {0.5,1,-0.8},
        {-0.2,-0.8,1}
     };

   matrix evectors;
   vector evalues;

   dataset.Eig(evectors,evalues);

   Print("Eigen decomposition of \n", dataset);

   Print(" EVD using built in Eig() \n", evectors);
   Print(evalues);

   CMatrixDouble data(dataset);
   CMatrixDouble vects;
   CRowDouble vals;
   CEigenVDetect::SMatrixEVD(data,data.Rows(),1,true,vals,vects);

   Print(" EVD using Alglib implementation \n", vects.ToMatrix());
   Print(vals.ToVector());
  }
//+------------------------------------------------------------------+

脚本的输出结果如下。

EVD 测试输出

它显示了特征向量和特征值呈现方式的不同。Alglib 实现按升序对向量和值进行排序，这更方便。MQL5 原生方法 "Eig()" 不提供任何排序，但这不是贬低它的主要原因。查看最后一个特征向量（列），我们注意到各个值的符号与 Alglib 代码输出的相应值的符号完全相反。目前尚不清楚为什么会出现这种情况。为了确认这是否是异常，使用 Python 的 Numpy 进行了相同的分解，并复制了 Alglib 的结果。很明显，因子载荷对特征向量成员值的符号很敏感。鉴于载荷被定义为相关性，该值的符号具有重要意义。

因子载荷矩阵是通过将每个特征向量乘以其相应特征值的平方根而得出的。为了防止得到无效数字的可能性，我们首先将任何小于 0 的特征值替换为 0。这有效地丢弃了因子载荷矩阵中的相关维度（特征向量）。

 m_structmat = m_eigvectors;
      vector copyevals = m_eigvalues;

      if(!copyevals.Clip(0.0,DBL_MAX))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

      for(ulong i = 0; i<m_structmat.Cols(); i++)
         if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i))
           {
            Print(__FUNCTION__, "error ", GetLastError());
            return m_fitted;
           }

      if(!m_structmat.Clip(-1.0,1.0))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

到目前为止，我们看到的代码片段是从 Cpfa 类中提取的，用于在 MetaTrader 5 中进行主因子分析（PFA）。下面显示了完整的类，后面是一个记录其公有方法的表格。

//+------------------------------------------------------------------+
//| Principal factor extraction                                      |
//+------------------------------------------------------------------+
class Cpfa
  {
private:
   bool              m_fitted;   //flag showing if principal factors were extracted
   matrix m_corrmat,             //correlation matrix
          m_data,                //standardized data is here
          m_eigvectors,          //matrix of eigen vectors of correlation matrix
          m_structmat;           //factor loading matrix
   vector m_eigvalues,           //vector of eigen values
          m_cumeigvalues;        //eigen values sorted in descending order
   long              m_indices[];//original order of column indices in input data matrix
public:
   //+------------------------------------------------------------------+
   //|  constructor                                                     |
   //+------------------------------------------------------------------+

                     Cpfa(void)
     {

     }
   //+------------------------------------------------------------------+
   //|  destructor                                                      |
   //+------------------------------------------------------------------+

                    ~Cpfa(void)
     {

     }
   //+------------------------------------------------------------------+
   //| fit() called with input matrix and extracts principal factors    |
   //+------------------------------------------------------------------+

   bool              fit(matrix &in)
     {
      m_fitted = false;
      m_data = stdmat(in);
      m_corrmat = m_data.CorrCoef(false);

      CMatrixDouble cdata(m_corrmat);
      CMatrixDouble vects;
      CRowDouble vals;


      if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

      m_eigvectors = vects.ToMatrix();
      m_eigvalues = vals.ToVector();
      double sum = 0.0;
      double total = m_eigvalues.Sum();

      if(!np::reverseVector(m_eigvalues) ||  !np::reverseMatrixCols(m_eigvectors))
         return m_fitted;

      m_cumeigvalues = m_eigvalues;
      for(ulong i=0 ; i<m_cumeigvalues.Size() ; i++)
        {
         sum += m_eigvalues[i] ;
         m_cumeigvalues[i] = 100.0 * sum/total;
        }

      m_structmat = m_eigvectors;
      vector copyevals = m_eigvalues;

      if(!copyevals.Clip(0.0,DBL_MAX))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

      for(ulong i = 0; i<m_structmat.Cols(); i++)
         if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i))
           {
            Print(__FUNCTION__, "error ", GetLastError());
            return m_fitted;
           }

      if(!m_structmat.Clip(-1.0,1.0))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

      m_fitted = true;

      return m_fitted;

     }
   //+------------------------------------------------------------------+
   //| returns factor loading matrix                                    |
   //+------------------------------------------------------------------+

   matrix            get_factor_loadings(void)
     {
      if(!m_fitted)
        {
         Print(__FUNCTION__, " invalid function call ");
         return matrix::Zeros(1,1);
        }

      return m_structmat;
     }
   //+------------------------------------------------------------------+
   //| get the eigenvector and values of correlation matrix             |
   //+------------------------------------------------------------------+

   bool              get_eigen_structure(matrix &out_eigvectors, vector &out_eigvalues)
     {
      if(!m_fitted)
        {
         Print(__FUNCTION__, " invalid function call ");
         return false;
        }

      out_eigvalues = m_eigvalues;
      out_eigvectors = m_eigvectors;

      return true;
     }
   //+------------------------------------------------------------------+
   //| returns variance contributions for each factor as a percent      |
   //+------------------------------------------------------------------+

   vector            get_cum_var_contributions(void)
     {
      if(!m_fitted)
        {
         Print(__FUNCTION__, " invalid function call ");
         return vector::Zeros(1);
        }
      return m_cumeigvalues;
     }
   //+------------------------------------------------------------------+
   //|  get the correlation matrix of the dataset                       |
   //+------------------------------------------------------------------+

   matrix            get_correlation_matrix(void)
     {
      if(!m_fitted)
        {
         Print(__FUNCTION__, " invalid function call ");
         return matrix::Zeros(1,1);
        }

      return m_corrmat;
     }

   //+------------------------------------------------------------------+
   //|  returns the rotated factor loadings                             |
   //+------------------------------------------------------------------+

   matrix            rotate_factorloadings(ENUM_FACTOR_ROTATION factor_rotation_type)
     {
      if(!m_fitted)
        {
         Print(__FUNCTION__, " invalid function call ");
         return matrix::Zeros(1,1);
        }

      CRotator rotator;

      if(!rotator.fit(m_structmat,factor_rotation_type,4,true))
         return matrix::Zeros(1,1);
      else
         return rotator.get_transformed_loadings();
     }
  };

方法	描述	返回值类型
fit	从输入矩阵 `in` 中提取主因子。该函数对输入数据进行标准化处理，计算相关矩阵，并执行特征分解。它还能计算因子载荷矩阵和累积特征值。这是对象实例化后应首先调用的方法。	bool
get_factor_loadings	如果已提取主因子，则返回因子载荷矩阵；否则，返回零矩阵。载荷将按照相对于最大特征值的降序进行排序。在 "fit()" 成功完成后，可以调用此方法和其他方法来获取分析结果的属性。	matrix
get_eigen_structure	返回相关矩阵的特征向量和特征值，可选择对它们进行排序。	matrix vector
get_cum_var_contributions	如果已提取主因子，则以百分比形式返回各因子的累积方差贡献率；否则，返回一个零向量。	vector
get_correlation_matrix	如果已提取主因子，则返回数据集的相关矩阵；否则，返回零矩阵。	matrix
rotate_factorloadings	如果已提取主因子，则使用指定的旋转类型返回旋转因子载荷矩阵；否则返回零矩阵。	matrix

我们现在知道如何获得因子载荷，在下一节中，我们将看到这些相关性传达了什么。

解释因子载荷

因子负荷表示观测变量与潜在因子之间的相关性，它们表明变量与因子的关联程度。为了便于解释，特征向量根据其相应特征值的大小按降序排列。这确保了第一个特征向量对应于最大的特征值，该特征值引用了对观测变量影响最大的潜在因子。因子加载矩阵的行遵循与原始数据集的列相同的顺序，这意味着每一行对应一个变量。而列描述了按解释方差降序排列的因子。相关性高于 0.4 或低于 -0.4 均被视为显著。任何载荷在 -0.4 至 0.4 范围内的变量都表明相应的因素对该变量的影响很小。

变量	因子 1	因子 2	因子 3
X1	0.8	0.3	0.1
X2	-0.3	-0.93	0.00002
X3	0.0	0.342	-1
X4	0.5	0.1	-0.38
X5	0.5	-0.33	0.44

具有简单因子结构的数据集的变量在一个因子上的载荷较高，而在其他因子上的载荷较低。上表表示假设数据集的因子载荷。变量 X1 至 X4 表明，它们显著地加载到不同的因子上，而变量 X5 由于同时对两个因子进行轻微加载而产生混合信号。测量变量的特征及其因子载荷可以提供有关潜在因子性质的线索。例如，如果几个经济指标对一个因子的影响很大，那么这个因子可能代表一个潜在的经济趋势或市场情绪。相反，如果一个变量在多个因子上载荷适中，则可能表明该变量受到几个潜在因子的影响，每个因子都对变量行为的不同方面做出了贡献。

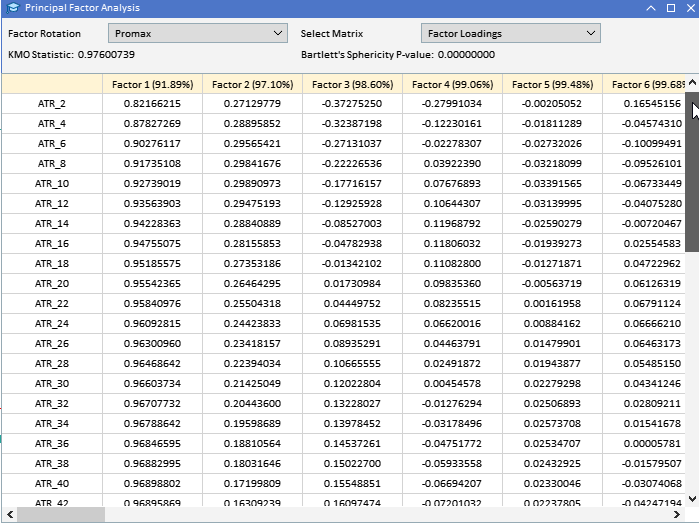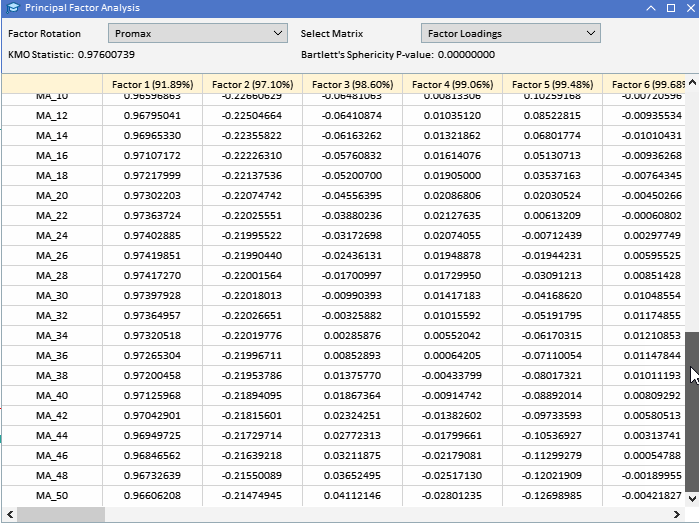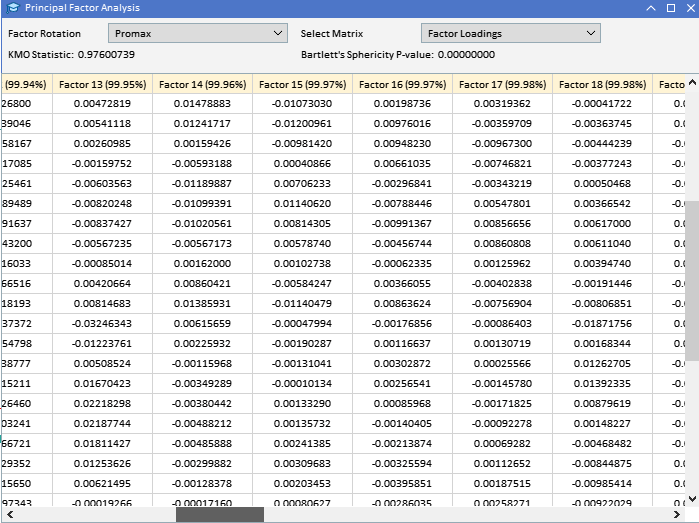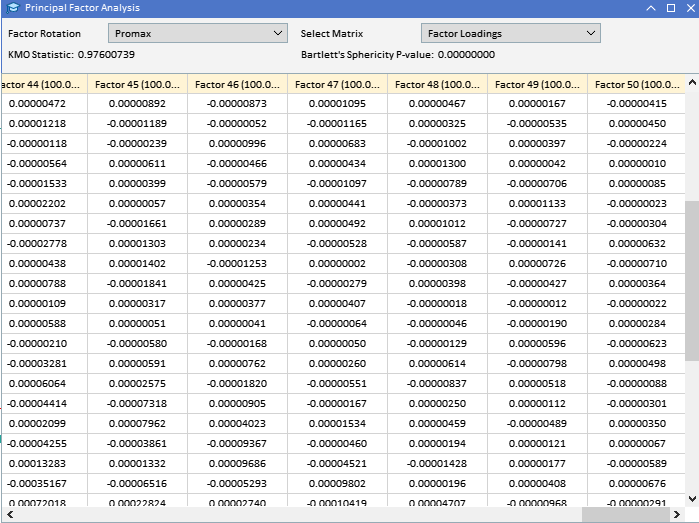
查看之前收集的 ATR 变量的因子载荷，我们可以看到大多数变量对因子 1 的载荷很高，这表明这些变量主要受到该因子的影响。因子 1 解释了这些变量中很大一部分的方差，括号中的数字表示了方差的百分比（91.89%）。虽然因子 1 似乎占主导地位，但一些变量在其他因子上也有显著的载荷。ATR_4、ATR_6、ATR_10、ATR_14 和其他因子在因子 2 上的载荷量适中，表明其具有次要影响。ATR_2、ATR_4、ATR_6 和 ATR_8 在因子 3 上的载荷较小，但很显著。因子 4 及以上在各种变量中的载荷较小，表明与前三个因子相比，它们在数据集中所占的方差较小。

如果由于复杂的因子结构，因子载荷太难解释，可以通过转换载荷来简化载荷，以提高可解释性。这种转换称为因子旋转。有两种类型的旋转可以应用于因子载荷矩阵，正交旋转保持了因子的独立性，例如 varimax 和 equamax 旋转。如果认为因子是独立的，则应进行正交旋转。斜交旋转允许因子之间存在一些依赖性，例如 Promax 旋转和 oblimin 旋转。如果怀疑各因子之间相互关联，则适合采用斜向旋转。通过旋转转换相关性将因子结构矩阵的原始相关性驱动到极值（-1,0,1），从而使相关性的解释更容易，放大了对观测变量的影响。

为了便于旋转，我们引入了 CRotator 类，该类实现了 promax 和 varimax 旋转。

//+------------------------------------------------------------------+
//| class implementing factor rotations                              |
//| implements varimax and promax rotations                          |
//+------------------------------------------------------------------+
class CRotator
  {
private:
   bool              m_normalize,        //normalization flag
                     m_done;             //rotation flag
   int m_power,                          //exponent to which to raise the promax loadings
       m_maxIter;                        //maximum number of iterations. Used for 'varimax'
   double            m_tol;                         //convergence threshold. Used for 'varimax'
   matrix m_loadings,                    //the rotated factor loadings
          m_rotation_mtx,                //the rotation matrix
          m_phi;                         //factor correlations matrix.
   ENUM_FACTOR_ROTATION m_rotation_type; //rotation method employed
   //+------------------------------------------------------------------+
   //| implements varimax rotation                                      |
   //+------------------------------------------------------------------+

   bool              varimax(matrix &in)
     {
      ulong rows,cols;
      rows = in.Rows();
      cols = in.Cols();
      matrix X = in;
      vector norm_mat(X.Rows());
      if(m_normalize)
        {
         for(ulong i = 0; i<X.Rows(); i++)
            norm_mat[i]=sqrt((pow(X.Row(i),2.0)).Sum());

         X = X.Transpose()/np::repeat_vector_as_rows_cols(norm_mat,X.Rows());
         X = X.Transpose();
        }

      m_rotation_mtx = matrix::Eye(cols,cols);

      double d = 0,old_d;
      matrix diag,U,V,transformed,basis;
      vector S,ones;

      for(int i =0; i< m_maxIter; i++)
        {
         old_d = d;
         basis = X.MatMul(m_rotation_mtx);
         ones = vector::Ones(rows);
         diag.Diag(ones.MatMul(pow(basis,2.0)));
         transformed = X.Transpose().MatMul(pow(basis,3.0) - basis.MatMul(diag)/double(rows));
         if(!transformed.SVD(U,V,S))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }
         m_rotation_mtx = U.Inner(V);
         d = S.Sum();
         if(d<old_d*(1.0+m_tol))
            break;
        }
      X = X.MatMul(m_rotation_mtx);
      if(m_normalize)
        {
         matrix xx = X.Transpose();
         X = xx * np::repeat_vector_as_rows_cols(norm_mat,xx.Rows());
        }
      else
         X = X.Transpose();
      m_loadings = X.Transpose();
      return true;
     }
   //+------------------------------------------------------------------+
   //| implements promax rotation                                       |
   //+------------------------------------------------------------------+

   bool              promax(matrix &in)
     {
      ulong rows,cols;
      rows = in.Rows();
      cols = in.Cols();
      matrix X = in;
      matrix weights,h2;
      h2.Init(1,1);
      if(m_normalize)
        {
         matrix array = X;
         matrix m = array.MatMul(array.Transpose());
         vector dg = m.Diag();
         h2.Resize(dg.Size(),1);
         h2.Col(dg,0);
         weights = array/np::repeat_vector_as_rows_cols(sqrt(dg),array.Cols(),false);
        }
      else
         weights = X;

      if(!varimax(weights))
         return false;

      X = m_loadings;
      ResetLastError();
      matrix Y = X * pow(MathAbs(X),double(m_power-1));
      matrix coef = (((X.Transpose()).MatMul(X)).Inv()).MatMul(X.Transpose().MatMul(Y));
      vector diag_inv = ((coef.Transpose()).MatMul(coef)).Inv().Diag();
      if(GetLastError())
        {
         diag_inv = ((coef.Transpose()).MatMul(coef)).PInv().Diag();
         ResetLastError();
        }
      matrix D;
      D.Diag(sqrt(diag_inv));
      coef = coef.MatMul(D);
      matrix z = X.MatMul(coef);
      if(m_normalize)
         z = z * np::repeat_vector_as_rows_cols(sqrt(h2).Col(0),z.Cols(),false);
      m_rotation_mtx = m_rotation_mtx.MatMul(coef);
      matrix coef_inv = coef.Inv();
      m_phi = coef_inv.MatMul(coef_inv.Transpose());
      m_loadings = z;

      return true;
     }
public:
   //+------------------------------------------------------------------+
   //| constructor                                                      |
   //+------------------------------------------------------------------+

                     CRotator(void)
     {

     }
   //+------------------------------------------------------------------+
   //|   destructor                                                     |
   //+------------------------------------------------------------------+

                    ~CRotator(void)
     {

     }
   //+------------------------------------------------------------------+
   //| performs rotation on supplied factor loadings passed to /in/     |
   //+------------------------------------------------------------------+

   bool              fit(matrix &in, ENUM_FACTOR_ROTATION rot_type=MODE_VARIMX, int power = 4, bool normalize = true, int maxiter = 500, double tol = 1e-05)
     {

      m_rotation_type = rot_type;
      m_power =  power;
      m_maxIter = maxiter;
      m_tol = tol;
      m_done=false;

      if(in.Cols()<2)
        {
         m_loadings = in;
         m_rotation_mtx = matrix::Zeros(in.Rows(), in.Cols());
         m_phi = matrix::Zeros(in.Rows(),in.Cols());
         m_done = true;
         return true;
        }

      switch(m_rotation_type)
        {
         case MODE_VARIMX:
            m_done = varimax(in);
            break;
         case MODE_PROMAX:
            m_done = promax(in);
            break;
         default:
            return m_done;
        }

      return m_done;
     }
   //+------------------------------------------------------------------+
   //|  get the rotated loadings                                        |
   //+------------------------------------------------------------------+

   matrix            get_transformed_loadings(void)
     {
      if(m_done)
         return m_loadings;
      else
         return matrix::Zeros(1,1);
     }
   //+------------------------------------------------------------------+
   //| get the rotation matrix                                          |
   //+------------------------------------------------------------------+

   matrix            get_rotation_matrix(void)
     {
      if(m_done)
         return m_rotation_mtx;
      else
         return matrix::Zeros(1,1);
     }
   //+------------------------------------------------------------------+
   //| get the factor correlation matrix                                |
   //+------------------------------------------------------------------+

   matrix            get_phi(void)
     {
      if(m_done && m_rotation_type==MODE_PROMAX)
         return m_phi;
      else
         return matrix::Zeros(1,1);
     }
  };

下面是其公有方法的概述：

方法	描述	参数	返回值类型
fit	对提供的因子载荷矩阵执行指定的旋转（varimax 或 promax）。	in:待旋转的因子载荷矩阵 rot_type：旋转方法（MODE_VARIMX 表示 varimax，MODE_PROMAX 表示 promax）。 power:promax 旋转的功率参数（默认为 4）。 normalize:表示是否对载荷进行归一化处理的标志（默认为 true）。 maxiter：方差旋转的最大迭代次数（默认为 500）。 tol:方差旋转的收敛阈值（默认为 1e-05）。	bool
get_transformed_loadings	返回旋转后的因子载荷矩阵	无	matrix
get_rotation_matrix	返回变换中使用的旋转矩阵。	无	matrix
get_phi	返回因子相关矩阵（仅适用于 promax 旋转）。	无	matrix

对因子载荷矩阵进行旋转。

CRotator rotator;

if(!rotator.fit(m_structmat,MODE_PROMAX,4,false))
   return;

Print(" Rotated Loadings Matrix ", rotator.get_transformed_loadings());

Promax旋转因子载荷

经过旋转的因子载荷（promax rotated factor loadings）清楚地表明了因子 1 和因子 2 对两类变量的影响。因子 1 是 MA 变量的主要影响因素。

MA 旋转因子载荷

因子 2 反映了对 ATR 变量的其他影响。通过捕捉数据中不太重要的模式，其他因素的最小影响被大大放大。这种旋转解决方案提供了对数据集底层结构的更清晰理解，有助于更好地解释。虽然因子旋转可以大大提高因子载荷的可解释性，但有几个缺点和局限性需要考虑：

旋转可能会迫使变量在单个因子上高度加载，从而过度简化底层结构，可能掩盖更复杂的相互关系。
正交旋转和斜交旋转之间的选择取决于关于因子独立性的理论假设，这些假设可能并不总是清晰或合理的。
在某些情况下，旋转可能会导致解释方差的轻微损失，因为旋转的目标是可解释性，而不是最大化解释方差。
由于存在大量变量和因素，旋转载荷的解释仍然具有挑战性，特别是在没有明确简单结构的情况下。
对于大型数据集来说，旋转，尤其是迭代旋转（如 varimax）的计算成本会很高，可能会影响实时应用的性能。

我们关于主因子提取的讨论到此结束，接下来，我们将探索基于潜在因子的变量冗余，研究潜在因子如何揭示隐藏的关系。

基于潜在因子的变量冗余

在处理大量变量时，找出明显冗余的变量集是非常有用的。这意味着一些变量提供了类似的信息，我们可能不需要考虑所有变量。通常，重要信息来自冗余本身，因为它可以指示影响多个变量的共同效应。通过识别高度冗余的变量组，我们可以通过关注几个代表性变量或与组相关的单个因子来简化我们的分析。

发现冗余变量的一种流行方法是在主轴或旋转正交轴上使用散点图。在图上聚集在一起的变量可能是多余的。然而，这种方法有其局限性。首先，这是主观的，通常一次只处理两个维度来进行有效的分析是可行的。检测冗余的直观方法涉及考虑不可观察的潜在因子。例如，如果我们有三个因子（V1、V2、V3）产生观测变量（X1、X2、X3），并且我们发现一个因子（V3）只是噪声，那么当忽略 V3 时，X1 和 X2 可能是冗余的。换句话说，如果 X2 只是 X1 的缩放版本，那么就重要因子（V1 和 V2）而言，它们是冗余的。

为了严格衡量冗余度，我们将观测变量视为由基本因子定义的空间中的向量。当我们观察到变量时，我们可以将它们表示为多维空间中的向量，其中每个维度对应一个基础因子。这些向量显示了每个变量与因子之间的关系。这些向量之间的角度表示变量在携带有关潜在因子的信息方面有多相似。较小的角度意味着矢量指向几乎相同的方向，表明冗余度很高。换句话说，这些变量提供了类似的信息。

为了量化这种冗余，我们可以使用归一化向量（长度为 1 的向量）的点积。这个点积的范围是 -1 到 1，点积为 1 表示向量完全相同，表示完全冗余。点积为 -1 意味着两个矢量的方向相反，这也可以说是多余的，因为知道一个矢量就可以得到另一个矢量的负值。点积为 0 表示向量是正交的（独立的），表示没有冗余。

利用主成分可以找到从基本因子计算观测变量的系数。主成分（具有较大特征值）通常包含大部分有用信息，而具有较小特征值的成分通常是噪声。因子载荷矩阵显示了因子与变量的相关性，可用于从主成分计算标准化的观测变量。出于实际目的，我们通常采用点积的绝对值来衡量冗余，认识到相反的向量也表示冗余。对向量进行归一化可以确保它们的长度为 1，从而使点积可以直接测量它们之间的角度余弦。

为了计算两个变量在隐藏因子方面的相关程度，我们通常首先必须确定我们认为重要的主成分的数量。聚类计算将集中在因子载荷矩阵的第一列中的数据上。这些列中的每一行都将被重新缩放，因此它们加起来都是 1。这两个变量之间的相似度成为变换后的因子加载矩阵的两个对应行的点积的绝对值。

下一步是将这些数据分组为多个集合，这些集合根据它们与潜在因子的关系构成非常相似的变量。分层聚类是一种更好的聚类算法，以擅长产生良好的结果而闻名。在分层聚类（也称为层次聚类（AHC））中，分组的第一步是将每个变量分配到一个有一个成员的组中。对每一对可能的组进行测试，以找到最接近的两个组。这些组被合并为一个组。这个过程会重复，直到剩下一个组或相似程度变得太小。

Alglib 库的 MQL5 移植提供了 AHC 的实现。它特别适合我们的目的，因为它支持实现自定义距离度量的能力。此功能通过三个 Alglib 类提供。要使用 Alglib 的分层聚集聚类实现，我们需要一个 CAHCReport 结构的实例来存储操作结果。

CAHCReport        m_rep;

CClusterizerState 类封装了聚类引擎，没有它，就无法进行聚类。

CClusterizerState m_cs;

首先，通过调用 CClustering 类的静态方法 "ClusterizerCreate()" 来初始化聚类引擎。

CClustering::ClusterizerCreate(m_cs);

初始化后，我们可以使用 CClustering 的其他静态方法设置聚类过程的参数。所有这些都需要一个初始化的集群引擎。

CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN);

CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true);

CClustering::ClusterizerSetAHCAlgo(m_cs,linkage);

最后，"ClusterizerRunAHC()" 会触发实际操作。

CClustering::ClusterizerRunAHC(m_cs,m_rep);

可以通过 CAHCReport 实例属性访问结果。

如前所述，我们将为该操作实现自定义距离度量。这是通过为每个变量（因子载荷中的行）提供一个具有初始距离的矩阵来实现的。下面的代码片段显示了如何根据提供的载荷计算初始距离。

for(int i=0 ; i<nvars ; i++)
           {
            length = 0.0 ;
            for(int j=0 ; j<ndim ; j++)
               length += structure[i][j] * structure[i][j] ;
            length = 1.0 / sqrt(length) ;
            for(int j=0 ; j<ndim ; j++)
               out[0][i][j] = length * structure[i][j] ;
           }

我们首先根据所考虑的数字维度对载荷进行归一化。

for(int irow1=0 ; irow1<nvars-1 ; irow1++)
           {
            for(int irow2=irow1+1 ; irow2<nvars ; irow2++)
              {
               dotprod = 0.0 ;
               for(int i=0 ; i<ndim ; i++)
                  dotprod += out[0][irow1][i] * out[0][irow2][i] ;
               out[1][irow1][irow2] = fabs(dotprod) ;
              }
           }

这些用于计算距离。此外，归一化载荷是传递给聚类器的载荷，而不是原始因子载荷。实现聚类的所有代码都在 CCluster 类中给出。

//+------------------------------------------------------------------+
//|  cluster a set of points                                         |
//+------------------------------------------------------------------+
class CCluster
  {
private:
   CClusterizerState m_cs;
   CAHCReport        m_rep;
   matrix            m_pd[];
    //+------------------------------------------------------------------+
    //| Preprocesses input matrix before clusterization                  |
    //+------------------------------------------------------------------+
    
   bool              customDist(matrix &structure, ulong num_factors, matrix& out[], bool calculate_custom_distances = true)
     {
      int nvars;
      double  dotprod, length;

      nvars = int(structure.Rows());
      int ndim = (num_factors && num_factors<=structure.Cols())?int(num_factors):int(structure.Cols());

      if(out.Size()<2)
         if(out.Size()<2 && (ArrayResize(out,2)!=2 || !out[0].Resize(nvars,ndim) || !out[1].Resize(nvars,nvars)))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }

      if(calculate_custom_distances)
        {
         for(int i=0 ; i<nvars ; i++)
           {
            length = 0.0 ;
            for(int j=0 ; j<ndim ; j++)
               length += structure[i][j] * structure[i][j] ;
            length = 1.0 / sqrt(length) ;
            for(int j=0 ; j<ndim ; j++)
               out[0][i][j] = length * structure[i][j] ;
           }

         out[1].Fill(0.0);

         for(int irow1=0 ; irow1<nvars-1 ; irow1++)
           {
            for(int irow2=irow1+1 ; irow2<nvars ; irow2++)
              {
               dotprod = 0.0 ;
               for(int i=0 ; i<ndim ; i++)
                  dotprod += out[0][irow1][i] * out[0][irow2][i] ;
               out[1][irow1][irow2] = fabs(dotprod) ;
              }
           }
        }
      else
        {
         out[0] = np::sliceMatrixCols(structure,0,ndim);
        }


      return true;
     }

public:
   //+------------------------------------------------------------------+
   //|  constructor                                                     |
   //+------------------------------------------------------------------+

                     CCluster(void)
     {
      CClustering::ClusterizerCreate(m_cs);
     }
   //+------------------------------------------------------------------+
   //|  destructor                                                      |
   //+------------------------------------------------------------------+

                    ~CCluster(void)
     {

     }
   //+------------------------------------------------------------------+
   //| cluster a set                                                     |
   //+------------------------------------------------------------------+

   bool              cluster(matrix &in_points, ulong factors=0, ENUM_LINK_METHOD linkage=MODE_COMPLETE, ENUM_DIST_CRIT dist = DIST_CUSTOM)
     {
      if(!customDist(in_points,factors,m_pd,dist==DIST_CUSTOM))
         return false;

      CMatrixDouble pp(m_pd[0]);
      CMatrixDouble pd(m_pd[1]);

      CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN);

      if(dist==DIST_CUSTOM)
         CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true);

      CClustering::ClusterizerSetAHCAlgo(m_cs,linkage);

      CClustering::ClusterizerRunAHC(m_cs,m_rep);

      return m_rep.m_terminationtype==1;
     }
   //+------------------------------------------------------------------+
   //|     output clusters to vector array                              |
   //+------------------------------------------------------------------+

   bool              get_clusters(vector &out[])
     {
      if(m_rep.m_terminationtype!=1)
        {
         Print(__FUNCTION__, " no cluster information available");
         return false;
        }

      if(ArrayResize(out,m_rep.m_pz.Rows())!=m_rep.m_pz.Rows())
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }

      for(int i = 0; i<m_rep.m_pm.Rows(); i++)
        {
         int zz = 0;
         for(int j = 0; j<m_rep.m_pm.Cols()-2; j+=2)
           {
            int from = m_rep.m_pm.Get(i,j);
            int to = m_rep.m_pm.Get(i,j+1);
            if(!out[i].Resize((to-from)+zz+1))
              {
               Print(__FUNCTION__, " error ", GetLastError());
               return false;
              }
            for(int k = from; k<=to; k++,zz++)
               out[i][zz] = m_rep.m_p[k];
           }
        }

      return true;
     }

  };

"cluster()" 函数对一组给定的输入点进行分层聚类。它需要四个参数：输入点矩阵参考、要考虑的因子数量、要使用的链接方法以及距离标准。首先，如果指定的距离标准是自定义的，它会计算一个自定义距离矩阵。如果距离计算失败，函数将返回 false。接下来，它会根据计算出的距离数据初始化两个矩阵 pp 和 pd。然后，该函数使用距离标准设置聚类点，如果标准未设置为自定义选项，则默认为欧几里德。如果距离标准是自定义的，则会相应地设置聚类的距离。在设置距离和点之后，该函数使用指定的链接方法配置分层聚类算法。它运行聚类分层聚类算法，并检查聚类过程的终止类型。如果终止类型为 1，函数返回 true，表示聚类成功，否则返回 false。

'get_clusters()' 函数从分层聚类过程的结果中提取并输出聚类。它只需一个参数：一个向量数组 out[] ，该数组中将填入聚类。函数首先检查聚类过程的终止类型是否为 1，表示聚类成功。如果没有，则打印错误信息并返回 false。然后，函数遍历矩阵 m_rep.m_pm 的每一行，其中包含聚类信息。对于每一行，它初始化一个变量 zz 来跟踪输出向量中的索引。然后，它迭代当前行的列，处理成对的列（表示聚类的开始和结束索引）。对于每一对，它计算索引的范围，并调整当前输出向量的大小以适应聚类元素。如果调整大小失败，则会打印错误信息并返回 false。最后，该函数用聚类的元素填充当前输出向量，从开始到结束迭代，并为每个元素递增 zz。如果过程成功完成，函数将返回 true，表明已成功提取并将聚类存储到 out 数组中。

下面的代码片段展示了如何使用 CCluster 类。

vector clusters[];
   CCluster fc;
   if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion))
      return;
   if(!fc.get_clusters(clusters))
      return;
   
   for(uint i =0; i<clusters.Size(); i++)
     {
      Print("cluster at ", i, "\n variable indices ", clusters[i]);
     }

MetaTrader 5 缺乏直接可视化聚集层次聚类（AHC，Agglomerative Hierarchical Clustering）结果的工具。虽然终端的控制台可以显示一些输出，但对于查看 AHC 等复杂结果来说，它并不友好。AHC 结果最好通过树状图进行可视化，树状图显示了数据分组的层次结构。树状图说明了如何通过逐步合并数据点或聚类来形成聚类。下面是一个手动绘制的树状图，显示了我们指标数据集中的分组。

聚类 MA 和 ATR 变量的树状图

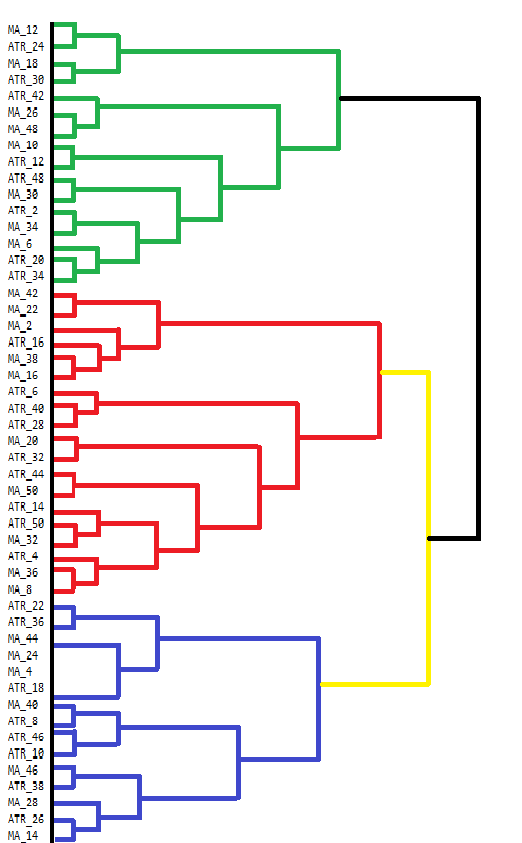
树状图显示了变量之间较为相似的聚类。在较低级别（更靠近树状图底部）合并的变量比在较高级别合并的变量更相似。例如，与 ATR_18 相比，MA_12 和 MA_24 更为相似。树状图用不同的颜色表示不同的聚类。绿色、红色、蓝色和黄色的聚类突出显示了密切相关的变量组。每种颜色代表一组表现出高度相似性或冗余性的变量。

两个聚类合并的高度表明了它们之间的差异。高度越低，聚类越相似。在更高层次上合并的聚类，如顶部的黑色合并，表明这些聚类之间的差异更大。这种分层聚类可以为变量选择的决策提供信息。通过分析聚类，人们可能会决定将重点放在每个聚类内的某些代表性变量上进行进一步分析，从而在不丢失重要信息的情况下简化数据集。

用于收集和分析指标数据集的 MQL5 代码包含在脚本 EDA.mq5 中。它使用了本文中描述的所有代码工具，这些工具在 pfa.mqh 中定义。

//+------------------------------------------------------------------+
//|                                                          EDA.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\Slope.ex5"
#resource "\\Indicators\\CMMA.ex5"
#include<pfa.mqh>
#include<ErrorDescription.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
//|indicator type                                                    |
//+------------------------------------------------------------------+
enum SELECT_INDICATOR
  {
   CMMA=0,//CMMA
   SLOPE//SLOPE
  };
//--- input parameters
input uint     period_inc=2;//lookback increment
input uint     max_lookback=50;
input ENUM_MA_METHOD         AppliedMA = MODE_SMA;
input datetime SampleStartDate=D'2019.12.31';
input datetime SampleStopDate=D'2022.12.31';
input string   SetSymbol="BTCUSD";
input ENUM_TIMEFRAMES SetTF = PERIOD_D1;
input ENUM_FACTOR_ROTATION AppliedFactorRotation = MODE_PROMAX;
input ENUM_DIST_CRIT AppliedDistanceCriterion = DIST_CUSTOM;
input ENUM_LINK_METHOD AppliedClusterAlgorithm = MODE_COMPLETE;
input ulong Num_Dimensions = 10;
//----
string csv_header="";                 //csv file header
int size_sample,                      //training set size
    size_observations,                //size of of both training and testing sets combined
    maxperiod,                        //maximum lookback
    indicator_handle=INVALID_HANDLE;  //long moving average indicator handle
//---
vector indicator[];                   //indicator indicator values;
//---
matrix feature_matrix;          //full matrix of features;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---get relative shift of sample set
   int samplestart,samplestop,num_features;
   samplestart=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStartDate);
   samplestop=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStopDate);
   num_features = int((max_lookback/period_inc)*2);
//---check for errors from ibarshift calls
   if(samplestart<0 || samplestop<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//---set the size of the sample sets
   size_observations=(samplestart - samplestop) + 1 ;
   maxperiod=int(max_lookback);
//---check for input errors
   if(size_observations<=0 || maxperiod<=0)
     {
      Print("Invalid inputs ");
      return;
     }
//---allocate memory
   if(ArrayResize(indicator,num_features)<num_features)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//----get the full collection of indicator values
   int period_len;
   int k=0;
//---
   for(SELECT_INDICATOR select_indicator = 0; select_indicator<2; select_indicator++)
     {
      for(int iperiod=0; iperiod<int(indicator.Size()/2); iperiod++)
        {
         period_len=int((iperiod+1) * period_inc);
         int try=10;
         while(try)
           {
            switch(select_indicator)
              {
               case CMMA:
                  indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\CMMA.ex5",AppliedMA,period_len);
                  break;
               case SLOPE:
                  indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\Slope.ex5",period_len);
                  break;
              }

            if(indicator_handle==INVALID_HANDLE)
               try--;
            else
               break;
           }

         if(indicator_handle==INVALID_HANDLE)
           {
            Print("Invalid indicator handle ",EnumToString(select_indicator)," ", GetLastError());
            return;
           }

         Comment("copying data to buffer for indicator ",period_len);
         try = 0;
         while(!indicator[k].CopyIndicatorBuffer(indicator_handle,0,samplestop,size_observations) && try<10)
              {
               try++;
               Sleep(5000);
              }

         if(try<10)
            ++k;
         else
           {
            Print("error copying to indicator buffers ",GetLastError());
            Comment("");
            return;
           }

         if(indicator_handle!=INVALID_HANDLE && IndicatorRelease(indicator_handle))
            indicator_handle=INVALID_HANDLE;
        }
     }
     
//---resize matrix
   if(!feature_matrix.Resize(size_observations,indicator.Size()))
     {
      Print(ErrorDescription(GetLastError()));
      Comment("");
      return;
     }
//---copy collected data to matrix
   for(ulong i = 0; i<feature_matrix.Cols(); i++)
      if(!feature_matrix.Col(indicator[i],i))
        {
         Print(ErrorDescription(GetLastError()));
         Comment("");
         return;
        }
//---
   Comment("");
//---test dataset for principal factor analysis suitability
//---kmo test
   vector kmo_vect;
   double kmo_stat;
   kmo(feature_matrix,kmo_vect,kmo_stat);
   Print("KMO test statistic ", kmo_stat);
//---Bartlett sphericity test
   double bs_stat,bs_pvalue;
   bartlet_sphericity(feature_matrix,bs_stat,bs_pvalue);
   Print("Bartlett sphericity test p_value ", bs_pvalue);
//---Extract the principal factors
   Cpfa fa;
//---
   if(!fa.fit(feature_matrix))
      return;
//---
   matrix fld = fa.get_factor_loadings();
//---
   matrix rotated_fld = fa.rotate_factorloadings(AppliedFactorRotation);
//---
   Print(" factor loading matrix ", fld);
//---
   Print("\n rotated factor loading matrix ", rotated_fld);
//---
   matrix egvcts;
   vector egvals;
   fa.get_eigen_structure(egvcts,egvals,false);
   Print("\n vects ", egvcts);
   Print("\n evals ", egvals);
//---
   vector clusters[];
   CCluster fc;
   if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion))
      return;
   if(!fc.get_clusters(clusters))
      return;
   
   for(uint i =0; i<clusters.Size(); i++)
     {
      Print("cluster at ", i, "\n variable indices ", clusters[i]);
     }
  }
//+------------------------------------------------------------------+

时间序列的一致性

随着时间的推移，分析变量时，它们之间的关系可能会发生意外变化。通常相关的变量可能会突然出现分歧，预示着潜在的问题。例如，温度变化会影响电力需求，进而影响天然气价格。如果它们通常的模式发生了变化，这可能表明正在发生一些不寻常的事情。同样，通常独立表现的变量可能会突然一起移动，例如当股市的不同板块因积极的经济消息而同时上涨时。

衡量一致性涉及量化一组时间序列变量在移动时间窗口内的关联程度。一种基本方法是检查最大特征值捕获了多少方差。不过，这种方法可能会有局限性，因为它只考虑了一个维度。一种更全面的方法涉及对最大特征值求和，特别是在变量之间存在多个关系的情况下。这种方法可以更准确地反映具有复杂相互关系的系统中的整体一致性，但需要事先知道哪些是最相关的因素。这也许是不可能的，或者太主观了。

对于关系数量未知或随时间波动的情况，特别是涉及大量变量的情况，需要一种更通用的方法。在维数未知的情况下，我们可以将排序后的特征值从最大到最小可视化，就像管弦乐队的成员。制作优美音乐的关键是以统一的方式相应地调节不同的乐器。如果管弦乐队的每个成员都不能在正确的水平上跟上，那么演奏出来的音乐就会很糟糕，凝聚力会很差。想象一下，每个乐团成员的声音输出都是一个加权值，对观众所听到的音乐做出了贡献。这些值的不平衡代表了一致性，我们计算的是加权总和，权重表示一种乐器可以产生的音量。

平衡与失衡

如果每个乐器（变量）都独立演奏自己的曲调，那么整体声音就会杂乱无章，代表零一致性。然而，当乐器完美同步、和谐演奏时，它们就会演奏出具有凝聚力的美妙乐曲，代表着完全的一致性。在这个比喻中，一致性就像管弦乐队的和声，表示乐器（变量）的配合程度。如果和声突然发生变化，说明乐器或乐曲出现了异常。

让我们考虑两个极端情况，如果变量完全独立，这些变量的相关矩阵将是一个同一矩阵，所有特征值都相等（1.0）。加权和（由于权重对称）将为零，反映出一致性为零。或者，如果变量之间完全相关，则只存在一个非零特征值，等于变量的数量。加权和变为变量数，经过归一化处理（除以变量数）后，一致性为 1.0，反映了完全相关性。这种方法根据特征值分布的不平衡提供了 0 到 1 的一致性度量，而无需对维度做任何假设。

为说明一致性，我们将制作一个指标，用于衡量一个时间窗口内不同交易品种收盘价的一致性。该指标名为 Coherence.mq5。用户可以通过以逗号分隔的工具名称列表来添加众多交易品种，从而测量它们之间的内聚力。该指标采用不同的方法计算多个变量之间的相关性。这一次，我们使用斯皮尔曼非参数相关系数。

covar[0][0] = 1.0 ;

      for(int i=1 ; i<npred ; i++)
        {
         for(int j=0 ; j<i ; j++)
           {
            for(int k=0 ; k<lookback ; k++)
              {
               nonpar1[k] = iClose(stringbuffer[i],PERIOD_CURRENT,ibar+k);
               nonpar2[k] = iClose(stringbuffer[j],PERIOD_CURRENT,ibar+k);
              }
            if(!MathCorrelationSpearman(nonpar1,nonpar2,covar[i][j]))
               Print(" MathCorrelationSpearman failed ", GetLastError(), " :", ibar);
           }
         covar[i][i] = 1.0 ;
        }

由于我们使用 Aglib 的 EVD 实现，我们不需要定义完整的校正矩阵，我们只需要构造上三角形或下三角形。我们不需要特征向量，只需要特征值。

 CMatrixDouble cdata(covar);
      if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Rows(),0,false,evals,evects))
        {
         Print(" EVD failed ", GetLastError(), " :", ibar);
         coherenceBuffer[ibar]=0.0;
         continue;
        }

为了得到特征值在正确方向上的分布，我们必须反转向量。

vector eval = evals.ToVector();

      if(!np::reverseVector(eval))
         Print(" failed vecter reversal operation : ", ibar);

使用特征值计算内聚力。

  double center = 0.5 * (npred - 1) ;
      double sum = 0.0;
      for(ulong i=0 ; i<eval.Size() ; i++)
        {
         sum += (center - i) * eval[i] / center ;
        }

      coherenceBuffer[ibar] =  sum / eval.Sum();

完整代码附在文章末尾。通过衡量加密货币 BTCUSD、DOGUSD 和 XRPUSD 之间的一致性，让我们看看指标在不同窗口长度下的表现。

3 个加密交易品种的 60 个周期一致性

通过观察 60 天的 "一致性" 曲线图，我们发现这些交易品种的移动具有显著的一致性，从而消除了个人的成见。令人惊讶的是，它的波动幅度如此之大，值在所有可能值的范围内都有所不同。

3 个加密交易品种的 252 个周期一致性

随着窗口长度的增加，我们开始看到相干性的稳定期，但这种相干性的性质同样出乎意料。在相当长的一段时间里，相干性几乎为零。

结论

在这些先进技术中使用特征值和特征向量突显了它们在数据科学中的通用性和根本重要性。它们为降维、模式识别和复杂数据集中潜在结构的发现提供了一个强大的框架。通过超越 PCA，我们解锁了一套更丰富的工具，提供了细致入微的见解。本文证明了特征向量和特征值远不止是数学抽象；它们是现代交易者可以利用的复杂分析技术的基石，以获得优势。本文中演示的所有代码都附在压缩的归档文件中。下表列出了可供下载的文件。

文件	描述
Mql5\Include\np.mqh	包含各种矩阵和矢量函数实用程序的包含文件
Mql5\Include\pfa.mqh	pfa.mqh 提供了 Cpfa 类、CCluster 类和 CRotator 类的定义，以及 KMO 和 BTS 测试实现的函数定义
Mql5\Scripts\EDA.mq5	该脚本通过收集用于主因子分析的自定义指标数据集，演示了文章中介绍的所有代码工具的使用方法
Mql5\Scripts\TestEigenDecomposition.mq5	该脚本重现了上述问题，涉及内置的 "Eig()" 矩阵方法
Mql5\Indicators\Coherence.mq5	这是应用于 3 个交易品种的相干性指标
Mql5\Experts\PrincipalFactors.mq5	是用于查看大型矩阵的应用程序的源代码。代码依赖于 MQL5 代码库中古老的 Easy and Fast GUI 库
Mql5\Experts\PrincipalFactors.ex5	这是上述列表的已编译版本