MetaTrader 5 / Торговые системы
English Español Deutsch 日本語 Português
preview
Нейросети — это просто (Часть 56): Использование ядерной нормы для стимулирования исследования

Нейросети — это просто (Часть 56): Использование ядерной нормы для стимулирования исследования

MetaTrader 5 — Торговые системы | 29 августа 2023, 15:43
870 0
Dmitriy Gizlyk
Dmitriy Gizlyk

Введение

Обучение с подкреплением построено на парадигме самостоятельного исследования окружающей среды Агентом. Своими действиями Агент воздействует на окружающую среду, что приводит к её изменению. Взамен Агент получает некое вознаграждение.

И здесь выделяются 2 основные проблемы обучения с подкреплением: исследование окружающей среды и функция вознаграждения. Правильно выстроенная функция вознаграждения побуждает Агента к исследованию окружающей среды и поиску наиболее оптимальных стратегий поведения.

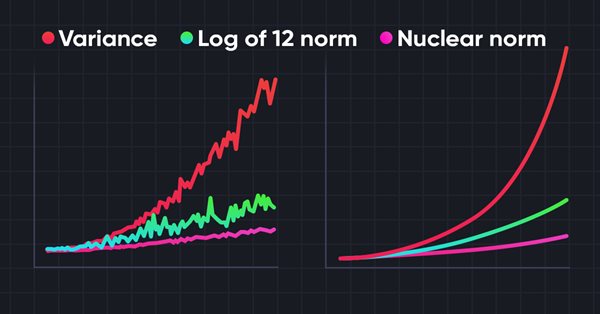
Однако, при решении большинства практических задач мы сталкиваемся с разреженными внешними вознаграждениями. Для преодоление данного барьера было предложено использование так называемых внутренних вознаграждений. Они позволяют Агенту осваивать новые навыки, которые могут пригодиться для получения внешних вознаграждений в будущем. Тем не менее, внутренние вознаграждения могут быть зашумленными вследствие стохастичности окружающей среды. Непосредственное применение зашумленных прогнозных значений для наблюдений может негативно влиять на эффективность обучения политики Агента. Более того, многие методы используют L2 норму или дисперсию для измерения новизны исследования, что усиливает шум из-за операции возведения в квадрат.

Для решения указанной проблемы в статье "Nuclear Norm Maximization Based Curiosity-Driven Learning" было предложено использование нового алгоритма стимулирования любопытства Агента на основе максимизации ядерной нормы (Nuclear Norm Maximization - NNM). Такое внутреннее вознаграждение может более точно оценить новизну исследования окружающей среды. В то же время оно позволяет обеспечить высокую устойчивость к шуму и выбросам.


1. Ядерная норма и её применение

Матричные нормы, включая ядерную норму, широко используются в анализе и вычислительных методах линейной алгебры. Ядерная норма играет важную роль в изучении свойств матриц, оптимизационных задач, оценке обусловленности и многих других областях математики и прикладных наук.

Ядерная норма матрицы — это числовая характеристика, которая определяет "размер" матрицы. Она является частным случаем нормы Шаттена и равна сумме сингулярных значений матрицы.

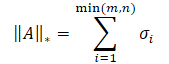
где σi — элементы вектора сингулярных значений матрицы A.

По своей сути, ядерная норма представляет собой выпуклую оболочку функции ранга для множества матриц с одинаковой спектральной нормой. Это позволяет использовать её при решении различных задач оптимизации.

Основная идея метода Nuclear Norm Maximization (NNM) заключается в точной оценке новизны с использованием ядерной нормы матрицы при посещении состояния, со смягчением влияния шума и различных выбросов. Матрица размером n*m состоит из n закодированных состояний окружающей среды. Каждое состояние имеет размерность m. Матрица объединяет текущее состояние s и его (n - 1) ближайших соседних состояний. Здесь s представляет абстрактное состояние, отображая исходное многомерное наблюдение в низкоразмерное абстрактное пространство. Поскольку каждая строка матрицы S представляет собой закодированное состояние, rank(S) можно использовать для представления разнообразия внутри матрицы. Более высокий ранг матрицы S означает большее линейное расстояние между закодированными состояниями. Авторы метода творчески подходят к решению задачи и применяют максимизацию ранга матрицы для увеличения разнообразия исследования. Это побуждает Агента нашей модели посещать более разные состояния с высоким разнообразием.

Существуют два подхода к использованию максимума ранга матрицы: в качестве функции потерь или в качестве вознаграждения. Максимизация ранга матрицы напрямую является довольно трудной задачей с не выпуклой функцией. Поэтому мы не будем его использовать в качестве функции потерь. Однако, значение ранга матрицы является дискретным и не может точно отражать новизну состояний. Следовательно, использование сырого значения ранга матрицы в качестве награды для руководства обучением модели также не эффективно.

Математически, вычисление ранга матрицы обычно заменяется на её ядерную норму. Следовательно, новизна может быть поддержана путем приближенной максимизации ядерной нормы. В сравнении с рангом, ядерная норма обладает несколькими хорошими свойствами. Во-первых, выпуклость ядерной нормы позволяет разрабатывать быстрые и сходящиеся алгоритмы оптимизации. Во-вторых, ядерная норма является непрерывной функцией, что важно для многих задач обучения.

Авторы метода NNM предлагают внутреннее вознаграждение определить по формуле

где:
      λ    — вес для настройки диапазона значений ядерной нормы;
      ‖S‖⋆ — ядерная норма матрицы состояний;
      ‖S‖F — норма Фробениуса матрицы состояний.

С ядерной нормой матрицы мы уже познакомились, а норма Фробениуса вычисляется как квадратный корень из суммы квадратов всех элементов матрицы.

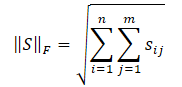
Неравенство Коши-Буняковского позволяет нам сделать следующие преобразования.

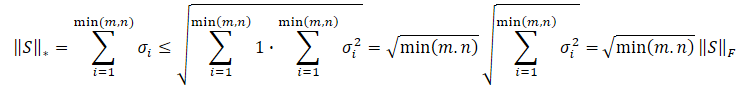
Очевидно, что квадратный корень из суммы квадратов значений всегда будет меньше или равен сумме самих значений. Следовательно, ядерная норма матрицы всегда будет больше или равна нормы Фробениуса той же матрицы. И мы можем вывести следующие неравенства.

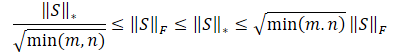
Это неравенство показывает, что ядерная норма и норма Фробениуса ограничивают друг друга. Если ядерная норма увеличивается, то и норма Фробениуса имеет тенденцию к росту.

Кроме того, норма Фробениуса имеет ещё одно свойство, полезное для нас — она строго противоположна энтропии в монотонности. Её увеличение равносильно уменьшению энтропии. В результате, влияния ядерной нормы можно разделить на две части:

  1. Высокое разнообразие.
  2. Низкая энтропия.

Нам необходимо стимулировать Агента посещать более новые состояния, и наша цель — разнообразие. Однако снижение энтропии означает рост агрегации состояний. То есть большую схожесть состояний. Поэтому мы стремимся поощрять первый эффект и уменьшить влияние второго. Для этого мы делим ядерную норму матрицы на её норму Фробениуса.

Разделив представленные выше неравенства на норму Фробениуса мы получаем.

Очевидно, что непосредственное использование подобной шкалы вознаграждений может нанести вред производительности обучения модели. Кроме того, корень из минимального измерения матрицы состояний может меняться в разных средах или с разной архитектурой обучаемых моделей. Поэтому желательно перенормировать нашу шкалу вознаграждений. И поскольку min(m, n) ≤ max(m, n), мы получаем:

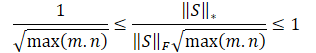
Приведенные выше математические выкладки позволяют нам автоматически определить коэффициент настройки диапазона значений ядерной нормы матрицы λ, как

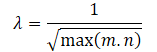
Таким образом, формула внутреннего вознаграждения примет вид:

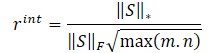
Ниже представлена авторская визуализация метода Nuclear Norm Maximization.


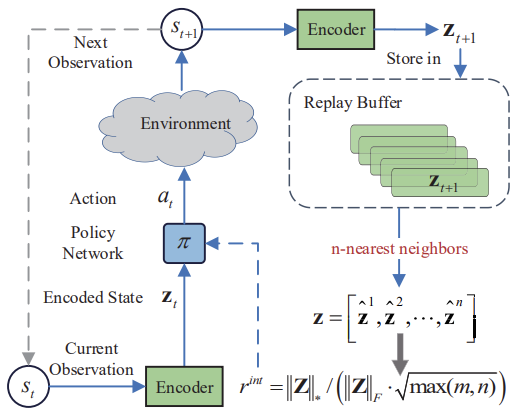
Приведенные в авторской статье результаты тестов демонстрируют превосходство предложенного метода над другими алгоритмами исследования окружающей среды. В том числе и над ранее рассмотренными нами Intrinsic Curiosity Module и Self-Supervised Exploration via Disagreement. Кроме того, обращает внимание тот факт, что метод демонстрирует лучшие результаты при добавлении шума к исходным данным. Предлагаю перейти к практической части нашей статьи и оценить возможности метода в решении наших задач.


2. Реализация средствами MQL5

Перед началом реализации метода Nuclear Norm Maximization (NNM) давайте выделим его основное нововведение — новая формула внутреннего вознаграждения. Следовательно, данный подход может быть реализован в качестве дополнения практически к любому ранее рассмотренному алгоритму обучения с подкреплением.

Тут же следует обратить внимание, что в алгоритме используется кодировщик для перевода состояний окружающей среды в некое сжатое представление. А также применяется алгоритм k-ближайших соседей для формирования матрицы сжатых представлений состояния окружающей среды.

На мой субъективный взгляд, наиболее простым видится решение внедрение предложенного внутреннего вознаграждения в алгоритм RE3. В нем так же используется кодировщик для перевода состояний окружающей среды в сжатое представление. Для этих целей в RE3 мы используем случайный сверточный Энкодер. Что позволяет сократить затраты на обучение кодировщика.

Кроме того, в RE3 так же используются k-ближайших состояний окружающей среды для формирования внутреннего вознаграждения. Только это вознаграждение формируется иначе.

Направление наших действий ясно и мы приступаем к работе. Вначале мы скопируем все файлы из каталога "...\Experts\RE3\" в  "...\Experts\NNM\". Напомню, что там находится 4 файла:

  • Trajectory.mqh — библиотека общих констант, структур и методов.
  • Research.mq5 — советник взаимодействия с окружающей средой и сбора обучающей выборки.
  • Study.mq5 — советник непосредственного обучения моделей.
  • Test.mq5 — советник тестирования обученных моделей.

Мы также будем использовать декомпозированное вознаграждение. Структура вектора вознаграждений будет иметь следующий вид.

//+------------------------------------------------------------------+
//| Rewards structure                                                |
//|   0     -  Delta Balance                                         |
//|   1     -  Delta Equity ( "-" Drawdown / "+" Profit)             |
//|   2     -  Penalty for no open positions                         |
//|   3     -  NNM                                                   |
//+------------------------------------------------------------------+

В файле "...\NNM\Trajectory.mqh" мы увеличим размеры сжатого представления состояния окружающей среды и внутреннего полносвязного слоя наших моделей.

#define                    EmbeddingSize   16            
#define                    LatentCount    512

В этом же файле находится метод описания архитектуры используемых моделей CreateDescriptions. Сегодня мы будем использовать 3 модели нейронных сетей: Актер, Критик и Кодировщик. В качестве последнего мы будем использовать случайный сверточный Энкодер.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic, CArrayObj *convolution)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }
   if(!convolution)
     {
      convolution = new CArrayObj();
      if(!convolution)
         return false;
     }

В теле метода мы создаем локальную переменную хранения указателя на объект описания одного нейронного слоя CLayerDescription и, при необходимости, инициализируем динамические массивы описания архитектурных решений используемых моделей.

Первым мы создадим описание архитектуры Актера, который состоит из 2 блоков: предварительной обработки исходных данных и принятия решения.

На вход блока предварительной обработки исходных данных мы подаем исторические данные о движении цены анализируемого инструмента и показатели индикаторов. Как можно заметить, разные индикаторы имеют различную область значений своих показателей. Что оказывает отрицательное воздействие на эффективность обучения моделей. Поэтому, полученные данные мы нормализуем с использованием слоя пакетной нормализации CNeuronBatchNormOCL.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Нормализованные данные мы пропускаем через 2 сверточных слоя, для поиска отдельных паттернов индикаторов.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.step = HistoryBars;
   int prev_wout=descr.window_out = HistoryBars/2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count;
   descr.window = prev_wout;
   descr.step = prev_wout;
   descr.window_out = 8;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Полученные данные обрабатываются полносвязными нейронными слоями.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

На этом этапе работы блока предварительной обработки исходных данных мы ожидаем получить некое латентное представление исторических данных по анализируемому инструменту. Этого может быть достаточно для определения направления открытия или удержания позиции, но не достаточно для реализации функций мани-менеджмента. Дополним данные информацией о состоянии счета.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = AccountDescr;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Далее следует блок принятия решений из полносвязных слоев, который завершается стохастическим слоем латентного представления вариационного автоэнкодера. Как и ранее, мы используем данный тип слоя на выходе модели для реализации стохастической политики Актера.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Мы полностью описали архитектуру Актера. При этом мы построили модель для реализации стохастической политики, чтобы подчеркнуть возможность использования метода Nuclear Norm Maximization для подобных решений. Кроме того, наш Актер будет работать в непрерывном пространстве действий. Однако это не ограничивает область использования метода NNM.

Следующим этапом мы будем создавать описание архитектуры Критика. Здесь мы воспользуемся уже отработанным приемом и исключим блок предварительной обработки данных. А в качестве исходных данных возьмем латентное представление состояния исторических данных инструмента и состояния счета из внутренних нейронных слоев Актера. При этом мы объединяем внутренне представление состояния окружающей среды и сгенерированные Актером тензор действий.

//--- Critic
   critic.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = NActions;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

Полученные данные обрабатываются полносвязными слоями нашего Критика и генерируется вектор прогнозных значений в разрезе декомпозиции нашей функции вознаграждения.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = NRewards;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

Мы уже описали архитектуру 2 моделей. И нам остается создать архитектуру Кодировщика. Здесь мы возвращаемся к теоретической части и обращаем внимание, что методом NNM предусмотрено сопоставление состояний окружающей среды после перехода St+1. Очевидно, что метод был разработан для онлайн обучения. Но об этом мы поговорим немного позже. А на стадии формирования архитектуры моделей нам важно понимать, что кодировщик будет обрабатывать исторические данные анализируемого инструмента и показатели состояния счета. Создадим слой исходных данных достаточного размера.

//--- Convolution
   convolution.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (HistoryBars * BarDescr) + AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

Обратите внимание, что мы не используем ни слой нормализации данных, ни объединение двух тензоров данных. Это связано с тем, что мы не планируем обучать данную модель. Она используется лишь для перевода многомерного представления окружающей среды в некоторое случайное сжатое пространство. В котором мы и будем измерять расстояние между состояниями. Но мы воспользуемся полносвязным слоем, который позволит представить данные в некотором сопоставимом виде.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 1024;
   descr.window = prev_count;
   descr.step = NActions;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

Далее идет блок сверточных слоев для понижения размерности данных.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = 1024 / 16;
   descr.window = 16;
   descr.step = 16;
   prev_wout = descr.window_out = 4;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = (prev_count * prev_wout) / 8;
   descr.window = 8;
   descr.step = 8;
   prev_wout = descr.window_out = 4;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = (prev_count * prev_wout) / 4;
   descr.window = 4;
   descr.step = 4;
   prev_wout = descr.window_out = 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

И в завершении понижаем размерность данных для заданного размера с помощью полносвязного слоя.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = EmbeddingSize;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Использование полносвязных слоев на входе и выходе Кодировщика позволяют нам настроить архитектуру сверточных слоев без привязки к размерам исходных данных и эмбединга сжатого представления.

На этом мы завершаем работу с архитектурой моделей и вернемся к вопросу описания будущего состояния. В процессе онлайн обучения мы бы не испытывали затруднений в данном вопросе. Но онлайн обучение имеет свои недостатки. А вот при использовании буфера воспроизведения опыта у нас нет вопросов по историческим данных ценового движения анализируемого инструмента и индикаторов. Влияние на них действий Актера настолько незначительное, что этим можно пренебречь. Другое дело состояние счета. Оно напрямую зависит от направления и объема открытой позиции. И нам предстоит спрогнозировать состояние счета в зависимости от вектора действий, сгенерированного Актером по результатам анализа текущего состояния. И такой функционал мы реализуем в функции ForecastAccount.

В параметрах методу мы передадим:

  • prev_account — массив описания текущего состояния счета (до действий агента);
  • actions          — вектор действий Актера;
  • prof_1l          — прибыль на 1 лот длинной позиции;
  • time_label    — временная метка прогнозируемого бара.

Можно заметить "разношёрстность" типов параметров. Это связано с источником получения данных. Описание текущего состояния счета и временную метку прогнозного бара мы получаем из буфера воспроизведения опыта, где данные хранятся в динамических массивах типа float.

Действия Актера мы получаем по результатам прямого прохода модели в виде вектора. 

vector<float> ForecastAccount(float &prev_account[],
                              vector<float> &actions,
                              double prof_1l,
                              float time_label
                             )
  {
   vector<float> account;
   double min_lot = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
   double step_lot = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP);
   double stops = MathMax(SymbolInfoInteger(_Symbol,SYMBOL_TRADE_STOPS_LEVEL), 1) * Point();
   double margin_buy,margin_sell;
   if(!OrderCalcMargin(ORDER_TYPE_BUY,_Symbol,1.0,SymbolInfoDouble(_Symbol,SYMBOL_ASK),margin_buy) ||
      !OrderCalcMargin(ORDER_TYPE_SELL,_Symbol,1.0,SymbolInfoDouble(_Symbol,SYMBOL_BID),margin_sell))
      return vector<float>::Zeros(prev_account.Size());

В теле функции мы проводим небольшую подготовительную работу. Определяем минимальный лот инструмента и шаг изменения объема позиции. Запрашиваем текущие стоп-уровни. И размер маржи на одну сделку. Здесь надо обратить внимание, что мы не стали вводить дополнительный параметр для идентификации анализируемого инструмента. Мы используем инструмент графика, на котором запущена программа. Поэтому, при обучении моделей очень важно соблюдать инструмент сбора исходных данных обучающей выборки и графика, к которому прикрепляется программа обучения моделей.

Далее мы корректируем вектор действий Актера для выбора сделки только в одном направлении на разницу объемов. Аналогичные операции мы выполняем и в советниках взаимодействия с окружающей средой. Соблюдение единых правил во всех программах процесса обучения моделей очень важно для достижения желаемого результата.

Тут же мы проверяем достаточность средств на счете для открытия позиции.

   account.Assign(prev_account);
//---
   if(actions[0] >= actions[3])
     {
      actions[0] -= actions[3];
      actions[3] = 0;
      if(actions[0]*margin_buy >= MathMin(account[0],account[1]))
         actions[0] = 0;
     }
   else
     {
      actions[3] -= actions[0];
      actions[0] = 0;
      if(actions[3]*margin_sell >= MathMin(account[0],account[1]))
         actions[3] = 0;
     }

И уже на основании скорректированного вектора действий мы прогнозируем состояние счета. Вначале мы проверяем длинные позиции. При необходимости закрытия позиции мы переносим накопленную прибыль на баланс счета. После чего обнуляем объем открытой позиции и накопленную прибыль.

При удержании открытой позиции мы проверяем необходимость частичного закрытия или доливки позиции. При частичном закрытии позиции мы делим накопленную прибыль пропорционально закрываемой и оставшейся части. И долю закрываемой позиции переносим из накопленной прибыли на баланс счета.

При необходимости корректируем объем открытой позиции и изменяем размер накопленной прибыли/убытка на пропорционально удерживаемому объему позиции.

//--- buy control
   if(actions[0] < min_lot || (actions[1] * MaxTP * Point()) <= stops || 
      (actions[2] * MaxSL * Point()) <= stops)
     {
      account[0] += account[4];
      account[2] = 0;
      account[4] = 0;
     }
   else
     {
      double buy_lot = min_lot + MathRound((double)(actions[0] - min_lot) / step_lot) * step_lot;
      if(account[2] > buy_lot)
        {
         float koef = (float)buy_lot / account[2];
         account[0] += account[4] * (1 - koef);
         account[4] *= koef;
        }
      account[2] = (float)buy_lot;
      account[4] += float(buy_lot * prof_1l);
     }

Аналогичные операции повторяем для коротких позиций.

//--- sell control
   if(actions[3] < min_lot || (actions[4] * MaxTP * Point()) <= stops || 
      (actions[5] * MaxSL * Point()) <= stops)
     {
      account[0] += account[5];
      account[3] = 0;
      account[5] = 0;
     }
   else
     {
      double sell_lot = min_lot + MathRound((double)(actions[3] - min_lot) / step_lot) * step_lot;
      if(account[3] > sell_lot)
        {
         float koef = float(sell_lot / account[3]);
         account[0] += account[5] * (1 - koef);
         account[5] *= koef;
        }
      account[3] = float(sell_lot);
      account[5] -= float(sell_lot * prof_1l);
     }

Далее мы корректируем суммарный объем накопленной прибыли/убытка в обоих направлениях и Эквити счета.

   account[6] = account[4] + account[5];
   account[1] = account[0] + account[6];

На основании полученных прогнозных значений мы подготовим вектор описания состояния счета в формате предоставления данных в модель. И результат операций возвращаем вызывающей программе.

   vector<float> result = vector<float>::Zeros(AccountDescr);
   result[0] = (account[0] - prev_account[0]) / prev_account[0];
   result[1] = account[1] / prev_account[0];
   result[2] = (account[1] - prev_account[1]) / prev_account[1];
   result[3] = account[2];
   result[4] = account[3];
   result[5] = account[4] / prev_account[0];
   result[6] = account[5] / prev_account[0];
   result[7] = account[6] / prev_account[0];
   double x = (double)time_label / (double)(D'2024.01.01' - D'2023.01.01');
   result[8] = (float)MathSin(2.0 * M_PI * x);
   x = (double)time_label / (double)PeriodSeconds(PERIOD_MN1);
   result[9] = (float)MathCos(2.0 * M_PI * x);
   x = (double)time_label / (double)PeriodSeconds(PERIOD_W1);
   result[10] = (float)MathSin(2.0 * M_PI * x);
   x = (double)time_label / (double)PeriodSeconds(PERIOD_D1);
   result[11] = (float)MathSin(2.0 * M_PI * x);
//--- return result
   return result;
  }

На этом мы завершаем подготовительную работу и переходим к обновлению программ взаимодействия с окружающей средой и обучения моделей. Напомню, что метод NNM вносит изменения в функцию внутреннего вознаграждения. И данный функционал не затрагивает процесс взаимодействия с окружающей средой. Поэтому советники "...\NNM\Research.mq5" и "...\NNM\Test.mq5" остались без изменений. С их кодом можно ознакомиться во вложении. А описание алгоритмов дано в предыдущих статьях.

А вот на советнике обучения моделей "...\NNM\Study.mq5" мы остановимся подробнее. Прежде всего надо сказать, что метод NNM разработан в первую очередь для онлайн обучения. И на это указывает сопоставление последующих состояний. Конечно, мы можем генерировать прогнозные состояния довольно долго. Но их отсутствие в базе сравнений состояний может оказать негативное влияние на процесс обучения в целом. Ведь при их отсутствии модель будет воспринимать состояния как новые и стимулировать их повторное посещение, не зная об их предыдущих посещениях в процессе обучения.
Теоретически есть 2 варианта решения данного вопроса:

  1. Добавление прогнозных состояний в базу примеров.
  2. Сокращение итераций цикла обучения.

Оба подхода имеют свои недостатки. При добавлении прогнозных состояний в базу примеров мы наполняем её недостоверными и неполными данными. Да, мы осуществили математический расчет на основании наших априорных знаний и ряда допущений. И все же мы допускаем наличие некой доли ошибки в них. Кроме того, у нас нет актуальных значений вознаграждений для данных действий, чтобы обучать модель. Поэтому мы выбрали 2 метод, хотя он и предполагает увеличение ручного труда в части большего количества запусков сбора обучающих данных и обучения моделей.

Мы сокращаем количество итераций обучающего цикла.

//+------------------------------------------------------------------+
//| Input parameters                                                 |
//+------------------------------------------------------------------+
input int                  Iterations     = 10000;
input float                Tau            = 0.001f;

В процессе обучения мы будем использовать одного Актера, 2 Критика и их целевые модели. А также случайный сверточный Кодировщик. Все модели Критиков будут иметь одну архитектуру, но разные параметры. Которые формируются в процессе обучения.

CNet                 Actor;
CNet                 Critic1;
CNet                 Critic2;
CNet                 TargetCritic1;
CNet                 TargetCritic2;
CNet                 Convolution;

Мы будем обучать Актера и 2 Критиков. Целевые модели Критиков будем мягко обновлять от параметров соответствующего Критика с параметром Tau. Кодировщик мы не обучаем.

В методе инициализации советника OnInit мы загружаем предварительно собранные исходные данные. И, при невозможности загрузить предварительно обученные модели, инициализируем новые в соответствии с заданной архитектурой. Данный процесс остался без изменений и Вы можете самостоятельно ознакомиться с ним во вложении. А мы переходим непосредственно к методу обучения моделей Train.

В данном методе мы сначала определяем количество траекторий, сохраненных в буфере воспроизведения опыта, и подсчитываем общее количество состояний в них.

Подготавливаем матрицы для записи эмбединга состояний и соответствующих внешних вознаграждений.

//+------------------------------------------------------------------+
//| Train function                                                   |
//+------------------------------------------------------------------+
void Train(void)
  {
   int total_tr = ArraySize(Buffer);
   uint ticks = GetTickCount();
//---
   int total_states = Buffer[0].Total;
   for(int i = 1; i < total_tr; i++)
      total_states += Buffer[i].Total;
   vector<float> temp, next;
   Convolution.getResults(temp);
   matrix<float> state_embedding = matrix<float>::Zeros(total_states,temp.Size());
   matrix<float> rewards = matrix<float>::Zeros(total_states,NRewards);

Далее мы организовываем систему вложенных циклов, в теле которых мы организовываем кодировку всех состояний из буфера воспроизведения опыта. Полученными данными заполняем матрицы эмбединга состояний и соответствующих вознаграждений. Обратите внимание, что вознаграждения мы сохраняем за отдельный переход в новое состояние без учета накопленных значений до конца прохода. Тем самым мы хотим привести в сопоставимый вид близкие по "духу" состояния, но разорванные во времени.

   int state = 0;
   for(int tr = 0; tr < total_tr; tr++)
     {
      for(int st = 0; st < Buffer[tr].Total; st++)
        {
         State.AssignArray(Buffer[tr].States[st].state);
         float PrevBalance = Buffer[tr].States[MathMax(st,0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(st,0)].account[1];
         State.Add((Buffer[tr].States[st].account[0] - PrevBalance) / PrevBalance);
         State.Add(Buffer[tr].States[st].account[1] / PrevBalance);
         State.Add((Buffer[tr].States[st].account[1] - PrevEquity) / PrevEquity);
         State.Add(Buffer[tr].States[st].account[2]);
         State.Add(Buffer[tr].States[st].account[3]);
         State.Add(Buffer[tr].States[st].account[4] / PrevBalance);
         State.Add(Buffer[tr].States[st].account[5] / PrevBalance);
         State.Add(Buffer[tr].States[st].account[6] / PrevBalance);
         double x = (double)Buffer[tr].States[st].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_MN1);
         State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_W1);
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_D1);
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         if(!Convolution.feedForward(GetPointer(State),1,false,NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            ExpertRemove();
            return;
           }
         Convolution.getResults(temp);
         state_embedding.Row(temp,state);
         temp.Assign(Buffer[tr].States[st].rewards);
         next.Assign(Buffer[tr].States[st + 1].rewards);
         rewards.Row(temp - next * DiscFactor,state);
         state++;
         if(GetTickCount() - ticks > 500)
           {
            string str = StringFormat("%-15s %6.2f%%", "Embedding ", 
                                      state * 100.0 / (double)(total_states));
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }
   if(state != total_states)
     {
      rewards.Resize(state,NRewards);
      state_embedding.Reshape(state,state_embedding.Cols());
      total_states = state;
     }

После подготовки эмбединга состояний мы переходим непосредственно к организации цикла обучения моделей. Как обычно, количество итераций цикла задается внешним параметром и мы добавляем проверку события завершения программы пользователем.

В теле цикла мы случайным образом выбираем траекторию и отдельное состояние на ней из буфера воспроизведения опыта.

   vector<float> rewards1, rewards2;
   int bar = (HistoryBars - 1) * BarDescr;
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int tr = (int)((MathRand() / 32767.0) * (total_tr - 1));
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2));
      if(i < 0)
        {
         iter--;
         continue;
        }
      vector<float> reward, target_reward = vector<float>::Zeros(NRewards);
      reward.Assign(Buffer[tr].States[i].rewards);

Подготавливаем вектора для записи вознаграждений.

Далее мы подготавливаем описание следующего состояния. Обратите внимание, что мы подготавливаем его независимо от необходимости использования целевых моделей. Ведь оно нам в любом случае потребуется для формирования внутреннего вознаграждения по методу NNM.

      //--- Target
      TargetState.AssignArray(Buffer[tr].States[i + 1].state);

А вот вектор описания последующего состояния счета и прямой проход целевых моделей мы осуществляем только при необходимости.

      if(iter >= StartTargetIter)
        {
         float PrevBalance = Buffer[tr].States[i].account[0];
         float PrevEquity = Buffer[tr].States[i].account[1];
         Account.Clear();
         Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance);
         Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity);
         Account.Add(Buffer[tr].States[i + 1].account[2]);
         Account.Add(Buffer[tr].States[i + 1].account[3]);
         Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
         double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1);
         Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1);
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1);
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         //---
         if(Account.GetIndex() >= 0)
            Account.BufferWrite();
         if(!Actor.feedForward(GetPointer(TargetState), 1, false, GetPointer(Account)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         //---
         if(!TargetCritic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
            !TargetCritic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         TargetCritic1.getResults(rewards1);
         TargetCritic2.getResults(rewards2);
         if(rewards1.Sum() <= rewards2.Sum())
            target_reward = rewards1;
         else
            target_reward = rewards2;
         for(ulong r = 0; r < target_reward.Size(); r++)
            target_reward -= Buffer[tr].States[i + 1].rewards[r];
         target_reward *= DiscFactor;
        }

Затем осуществляется обучение Критиков. В этом блоке мы сначала подготавливаем данные текущего состояния окружающей среды.

      //--- Q-function study
      State.AssignArray(Buffer[tr].States[i].state);
      float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      Account.Clear();
      Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[1] / PrevBalance);
      Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      Account.Add(Buffer[tr].States[i].account[2]);
      Account.Add(Buffer[tr].States[i].account[3]);
      Account.Add(Buffer[tr].States[i].account[4] / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[5] / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
      double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1);
      Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      if(Account.GetIndex() >= 0)
         Account.BufferWrite();

И осуществляем прямой проход Актера.

      if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Здесь надо обратить внимание, что для обучения Критиков мы используем фактические действия Актера при взаимодействии с окружающей средой и фактически подученное вознаграждение. Но вы все же осуществили прямой проход Актера с целью использования его блока предварительной обработки исходных данных, который был исключен из архитектуры Критика.

Подготавливаем буфер действий Актера из буфера воспроизведения опыта и осуществляем прямой проход обоих Критиков.

      Actions.AssignArray(Buffer[tr].States[i].action);
      if(Actions.GetIndex() >= 0)
         Actions.BufferWrite();
      //---
      if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)) ||
         !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

После прямого прохода нам необходимо осуществить обратный проход и обновить параметры моделей. Но напомню, что мы используем декомпозированную функцию вознаграждения. И для оптимизации градиентов применяется метод CAGrad. Очевидно, что, несмотря на единую цель, градиенты ошибки для каждого Критика будут отличаться. И мы выполняем обновление моделей последовательно. Сначала корректируем градиенты ошибки и осуществляем обратный проход Критика 1.

      Critic1.getResults(rewards1);
      Result.AssignArray(CAGrad(reward + target_reward - rewards1) + rewards1);
      if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

После чего повторяем операции для Критика 2. И, конечно, контролируем процесс выполнения операций на каждом шаге.

      Critic2.getResults(rewards2);
      Result.AssignArray(CAGrad(reward + target_reward - rewards2) + rewards2);
      if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Модели Критиков обучаются корректно оценивать действия Актера в конкретном состоянии окружающей среды. В результате работы модели Критика мы ожидаем получить корректное прогнозное вознаграждение. Это так сказать вершина айсберга. Но есть и его подводная часть. В процессе обучения Критик аппроксимирует Q-функцию и выстраивает определенные зависимости между действиями Актера и вознаграждением.

Наша цель максимизации внешнего вознаграждения. Но оно напрямую не зависит от качества обучения Критика. Напротив, вознаграждение достигается действиями Актера. А вот для корректировки действий Актера мы воспользуемся аппроксимированной Q-функцией. Градиент ошибки между оценкой Критиком действий Актера и полученным вознаграждением укажет направление корректировки действий Актера. Вероятность переоцененных действий будет снижаться, а недооцененных — повышаться.

Для обучения Актера мы будем использовать Критика с минимальной средней скользящей ошибкой прогнозирования, что потенциально нам дает более точную оценку действий Актера.

      CNet *critic = NULL;
      if(Critic1.getRecentAverageError() <= Critic2.getRecentAverageError())
         critic = GetPointer(Critic1);
      else
         critic = GetPointer(Critic2);

Прямой проход Актера мы уже осуществили и, для оценки выбранных действий нам необходимо осуществить прямой проход выбранного Критика. Но прежде давайте подготовим вектор целевых значений вознаграждения. Задача не тривиальная. Нам нужно каким-то образом спрогнозировать внешнее вознаграждение от окружающей среды и дополнить его внутренним вознаграждением для стимулирования исследовательского потенциала Актера.

И как это не покажется странным, мы начнем с внутреннего вознаграждения, которое мы определим по методу NNM. Выше было описано, что для определения внутреннего вознаграждения нам не обходимо получить кодированное представление последующего состояния. Исторические данные последующего состояния уже добавлены в буфер TargetState. Прогнозное состояние счета мы получаем с помощью ранее описанной функции ForecastAccount.

      Actor.getResults(rewards1);
      double cl_op = Buffer[tr].States[i + 1].state[bar];
      double prof_1l = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE_PROFIT) * cl_op /
                       SymbolInfoDouble(_Symbol, SYMBOL_POINT);
      vector<float> forecast = ForecastAccount(Buffer[tr].States[i].account,rewards1,
                                               prof_1l,Buffer[tr].States[i + 1].account[7]);
      TargetState.AddArray(forecast);

Конкатенируем 2 тензора и осуществляем прямой проход 2 моделей. Критика для оценки действий Актера. И Кодировщика для получения сжатого представления прогнозного состояния.

      if(!critic.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
         !Convolution.feedForward(GetPointer(TargetState)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Далее мы переходим к формированию вектора вознаграждения. Напомню, что в векторе target_reward содержится отклонение оценки действий Актера целевым Критиком от фактического накопительного вознаграждения, полученного при взаимодействии с окружающей средой. По сути данный вектор представляет влияние изменения политики на общий результат.

В качестве целевого внешнего вознаграждения текущего действия Актера мы воспользуемся фактическими вознаграждениями k-ближайших соседей, скорректированных на расстояние между векторами. Здесь мы исходим из предположения, что вознаграждение за действие обратно пропорционально расстоянию до соответствующего соседа.

Непосредственно выбор k-ближайших соседей и формирование внутреннего вознаграждения осуществляется в функции KNNReward, на алгоритм которой мы посмотрим немного позже.

Но тут нужно обратить внимание еще на один момент. В матрицу вознаграждений кодированных состояний мы сохраняли внешнее вознаграждения только за последний переход, без накопительного итога. Поэтому, чтобы получить сопоставимые цели нам необходимо добавить к target_reward накопительные вознаграждения, полученные до завершения текущего прохода из буфера воспроизведения опыта.

      next.Assign(Buffer[tr].States[i + 1].rewards);
      target_reward+=next;
      Convolution.getResults(rewards1);
      target_reward=KNNReward(7,rewards1,state_embedding,rewards) + next * DiscFactor;
      if(forecast[3] == 0.0f && forecast[4] == 0.0f)
         target_reward[2] -= (Buffer[tr].States[i + 1].state[bar + 6] / PrevBalance) / DiscFactor;
      critic.getResults(reward);
      reward += CAGrad(target_reward - reward);

Отклонение целевых значений вознаграждений от оценки Критиком мы скорректируем по методу Conflict-Averse Gradient Descent и полученные значения мы прибавим к прогнозным значения Критика. Таким образом, мы получаем вектор целевых значений, скорректированный с учетом декомпозиции вознаграждения. И мы используем его для обратного прохода и обновления параметров Актера. Предварительно отключаем режим обучения Критика, чтобы не подстраивать его параметры под скорректированные цели.

      Result.AssignArray(reward);
      critic.TrainMode(false);
      if(!critic.backProp(Result, GetPointer(Actor)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         critic.TrainMode(true);
         break;
        }
      critic.TrainMode(true);

После успешного обновления параметров Актера мы возвращаем модель Критика в режим обучения и обновляем целевые модели обоих Критиков.

      //--- Update Target Nets
      TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau);
      TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);

На этом завершаются итерации цикла обучения моделей. Нам остается лишь проинформировать пользователя о процессе выполнения операций.

      if(GetTickCount() - ticks > 500)
        {
         string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", 
                                    iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError());
         str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", 
                                    iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

После успешного завершения всех итераций цикла обучения мы очищаем область комментариев графика. Выводим в журнал результаты обучения моделей и инициализируем процесс завершения работы советника.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, 
               "Critic1", Critic1.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, 
               "Critic2", Critic2.getRecentAverageError());
   ExpertRemove();
//---
  }

И теперь для полноты понимания работы алгоритма обучения моделей мы посмотрим на функцию формирования вознаграждения KNNReward. Надо сказать, что именно в этой функции и содержатся основные особенности рассматриваемого метода Nuclear Norm Maximization.

В параметрах функция получает количество анализируемых ближайших соседей, эмбединг анализируемого состояния, матрицы эмбединга состояний и соответствующих вознаграждений из буфера воспроизведения опыта.

vector<float> KNNReward(ulong k, 
                        vector<float> &embedding, 
                        matrix<float> &state_embedding, 
                        matrix<float> &rewards
	               )
  {
   if(embedding.Size() != state_embedding.Cols())
     {
      PrintFormat("%s -> %d Inconsistent embedding size", __FUNCTION__, __LINE__);
      return vector<float>::Zeros(0);
     }

В теле метода мы осуществляем проверку размерности эмбединга текущего состояния и состояний из буфера воспроизведения опыта. В текущей реализации данная проверка может показаться избыточной. Ведь все эмбединги мы получаем с помощью одного кодировщика в рамках данного советника. Но она может быть очень даже полезной, если вы решите генерировать эмбединг состояний в процессе взаимодействия с окружающей средой и сохранять его в буфере воспроизведения опыта, как это рекомендовалось в авторской статье метода RE3.

Далее мы проведем небольшую подготовительную работу, определив некоторые константы в локальные переменные. И тут же мы, при необходимости, уменьшим число ближайших соседей до количества состояний в буфере воспроизведения опыта. Вероятность такой необходимости довольно мала. Но такая деталь делает наш код более универсальным и защищенным от ошибок в процессе выполнения.

   ulong size = embedding.Size();
   ulong states = state_embedding.Rows();
   k = MathMin(k,states);
   ulong rew_size = rewards.Cols();
   matrix<float> temp = matrix<float>::Zeros(states,size);

Следующим шагом мы определяем расстояние между вектором анализируемого состояния и состояниями в буфере воспроизведения опыта. Полученные значения сохраняем в вектор distance.

   for(ulong i = 0; i < size; i++)
      temp.Col(MathPow(state_embedding.Col(i) - embedding[i],2.0f),i);
   vector<float> distance = MathSqrt(temp.Sum(1));

Теперь нам предстоит определить k-ближайших соседей. Их параметры мы сохраним в матрицы k_embeding и k_rewards. Обратите внимание, что в матрице k_embeding мы создаем на одну строку больше. В неё мы запишем эмбединг анализируемого состояния.

Данные в матрицы мы будем переносить в цикле по числу искомых векторов. В теле цикла мы с помощью векторной операции ArgMin определяем позицию минимального значения в векторе расстояний. Это и будет наш ближайший сосед. Мы переносим его данные в соответствующие строки наших матриц. А в векторе расстояний установим в данную позицию максимально возможную константу. Таким образом, после копирования данных мы изменили минимальную дистанцию на максимальное значение. И на следующей итерации цикла операция ArgMin нам выдаст позицию следующего соседа.

Обратите внимание, что при переносе вектора вознаграждений мы корректируем его значения на коэффициент, обратный расстоянию между векторами состояний.

   matrix<float> k_rewards = matrix<float>::Zeros(k,rew_size);
   matrix<float> k_embeding = matrix<float>::Zeros(k + 1,size);
   for(ulong i = 0; i < k; i++)
     {
      ulong pos = distance.ArgMin();
      k_rewards.Row(rewards.Row(pos) * (1 - MathLog(distance[pos] + 1)),i);
      k_embeding.Row(state_embedding.Row(pos),i);
      distance[pos] = FLT_MAX;
     }
   k_embeding.Row(embedding,k);

Такой алгоритм имеет целый ряд преимуществ:

  • количество итераций не зависит от размера буфера воспроизведения опыта, что удобно при использовании объемных баз данных;
  • не требуется сортировка данных, которая часто требует много ресурсов;
  • мы копируем данные каждого соседа только 1 раз, другие данные мы не копируем.

После переноса данных всех необходимых соседей последней строкой матрицы k_embeding мы добавляем текущее состояние.

Далее для определения ядерной нормы матрицы k_embeding и реализации метода NNM нам необходимо найти сингулярные значения матрицы. Для этого мы воспользуемся матричной операцией SVD.

   matrix<float> U,V;
   vector<float> S;
   k_embeding.SVD(U,V,S);

Теперь сингулярные значения матрицы хранятся в векторе S и для определения ядерной нормы нам достаточно суммировать его значения. Но прежде мы сгенерируем вектор внешних вознаграждений, как вектор средних значений по столбцам матрицы отобранных вознаграждений k_rewards.

Внутренне вознаграждение мы определяем по методу NNM, как отношение ядерной нормы матрицы эмбеденга состояний к её норме Фробениуса и скорректируем на коэффициент масштабирования ядерной нормы. Полученное значение записываем в соответствующий элемент вектора вознаграждений и возвращаем вектор вознаграждений вызывающей программе.

   vector<float> result = k_rewards.Mean(0);
   result[rew_size - 1] = S.Sum() / (MathSqrt(MathPow(k_embeding,2.0f).Sum() * MathMax(k + 1,size)));
//---
   return (result);
  }

На этом мы завершаем работу по реализации метода Nuclear Norm Maximization средствами MQL5. С полным кодом всех используемых в статье программ можно ознакомиться во вложении.


3. Тестирование

Мы проделали довольно объемную работу по реализации интеграции метода Nuclear Norm Maximization в алгоритм RE3. И пришло время перейти на этап тестирования проделанной работы. Как всегда, обучение и тестирование моделей осуществляется на исторических данных EURUSD тайм-фрейм H1 за 1-5 месяцы 2023 года. Параметры всех индикаторов используются по умолчанию.

При создании советника обучения "...\NNM\Study.mq5" мы уже говорили об особенностях данного метода и проблеме отсутствия генерируемых состояний в буфере воспроизведения опыта. Тогда мы решили уменьшить количество итераций одного цикла обучения. Разумеется, это накладывает свой отпечаток и на весь процесс обучения.

Мы не стали уменьшать буфер воспроизведения опыта в целом. Но в то же время, согласитесь, для выполнения 10К итераций обновления параметров модели нет необходимости в базе из 1.3М состояний. Да, большая база данных позволяет лучше настроить модель. Но когда на 1 итерацию обновления приходится более 100 состояний мы не в состоянии их все проработать. Поэтому буфер воспроизведения опыта мы будем заполнять постепенно. На первой итерации мы запускаем советник сбора обучающих данных всего на 50 проходов. На указанном историческом промежутке это уже дает нам порядка 120К состояний для обучения моделей.


И после первой итерации обучения моделей мы дополняем базу примеров еще на 50 проходов. Таким образом, мы постепенно заполняем буфер воспроизведения опыта новыми состояниями, которые соответствуют действиям Актера в рамках обучаемой политики.

Да, такой подход значительно увеличивает ручной труд по запуску советников. Но это позволяет нам поддерживать базу примеров в относительно актуальном состоянии. И генерируемое нами внутреннее вознаграждение будет направлять Актера к изучению новых состояний окружающей среды.

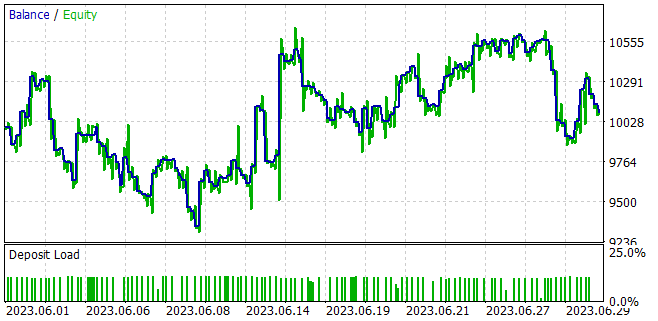
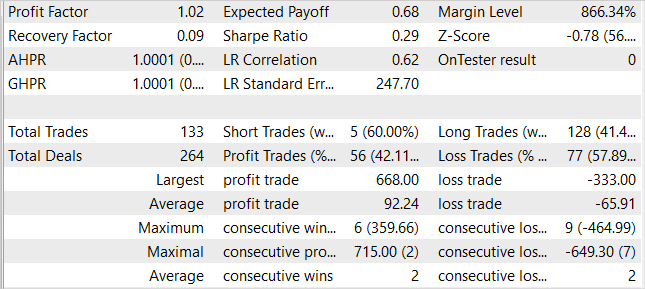
В процессе обучения моделей нам удалось получить модель, способную генерировать прибыль на обучающей выборе и обобщать полученные знания на последующие состояния окружающей среды. Так, в тестере стратегий обученная нами модель за 1 месяц, следующий за обучающей выборкой, смогла сгенерировать прибыль в размере 1%. За период тестирования модель совершила 133 торговых операции 42% из которых были закрыты с прибылью. Максимальная прибыль на одну сделку почти в 2 раза превышает максимальную убыточную сделку. А средняя прибыль на одну сделку на 40% процентов превышает средний убыток. Все это в совокупности позволило получить профит фактор на уровне 1.02.

График тестирования Результаты тестирования


Заключение

В данной статье мы познакомились с новым подходом к стимулированию исследования в обучении с подкреплением на основе максимизации ядерной нормы. Данный метод позволяет эффективно оценить новизну исследования окружающей среды, учитывая историческую информацию и обеспечивая высокую устойчивость к шуму и выбросам. 

В практической части статьи мы интегрировали метод Nuclear Norm Maximization в алгоритм RE3. Обучили модель и провели её тестирование в тестере стратегий MetaTrader 5. По результатам тестирования можно сказать, что предложенный метод значительно разнообразил поведение Актера, по сравнению с результатами обучения модели чистым методом RE3. Однако мы получили более хаотичную торговлю. Что может свидетельствовать о необходимости проработки баланса между исследованием и эксплуатацией, путем введения дополнительных коэффициентов влияния в функции вознаграждения.

Ссылки


Программы, используемые в статье

# Имя Тип Описание
1 Research.mq5 Советник Советник сбора примеров
2 Study.mq5  Советник Советник обучения агента
3 Test.mq5 Советник Советник для тестирования модели
4 Trajectory.mqh Библиотека класса Структура описания состояния системы
5 NeuroNet.mqh Библиотека класса Библиотека классов для создания нейронной сети
6 NeuroNet.cl Библиотека Библиотека кода программы OpenCL

Прикрепленные файлы |
Загрузить ZIP
MQL5.zip (468.82 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
Разработка системы репликации - Моделирование рынка (Часть 08): Блокировка индикатора Разработка системы репликации - Моделирование рынка (Часть 08): Блокировка индикатора
В этой статье мы рассмотрим, как заблокировать индикатор при простом использовании языка MQL5, и сделаем это очень интересным и удивительным способом.
Разработка системы репликации - Моделирование рынка (Часть 07): Первые улучшения (II) Разработка системы репликации - Моделирование рынка (Часть 07): Первые улучшения (II)
В предыдущей статье мы внесли исправления в некоторые моменты и добавили тесты в нашу систему репликации для обеспечения максимально возможной стабильности. Мы также начали создавать и использовать конфигурационный файл для данной системы.
Делаем информационную панель для отображения данных в индикаторах и советниках Делаем информационную панель для отображения данных в индикаторах и советниках
В статье рассмотрим создание класса информационной панели для использования её в индикаторах и советниках. Это вводная статья в небольшой серии статей с шаблонами подключения и использования стандартных индикаторов в советниках. Начнем мы с создания панели — аналога окна данных MetaTrader 5.
Брутфорс-подход к поиску закономерностей (Часть VI): Циклическая оптимизация Брутфорс-подход к поиску закономерностей (Часть VI): Циклическая оптимизация
В этой статье я покажу первую часть доработок, которые позволили мне не только замкнуть всю цепочку автоматизации для торговли в MetaTrader 4 и 5, но и сделать что-то гораздо интереснее. Отныне данное решение позволяет мне полностью автоматизировать как процесс создания советников, так и процесс оптимизации, а также минимизировать трудозатраты на поиск эффективных торговых конфигураций.