Нейросети в трейдинге: Декомпозиция вместо масштабирования (SSCNN)
156
0
Введение
Прогнозирование временных рядов по-прежнему остаётся одним из фундаментальных направлений в анализе данных, машинном обучении и статистике. Его значение трудно переоценить: от финансов и метеорологии до городской инфраструктуры и телекоммуникаций — везде, где важны динамика и предсказуемость, временные ряды играют ключевую роль. Однако классические одномерные модели, такие как ARIMA или методы экспоненциального сглаживания, всё чаще оказываются бессильны перед сложностью открытых и динамично меняющихся систем.
Ситуация начала кардинально меняться с появлением методов глубокого обучения. Особенно заметный прорыв произошёл после внедрения архитектуры Transformer, способной не только выявлять сложные попарные зависимости в последовательностях, но и извлекать их многоуровневые представления. Именно эти свойства сделали Transformer одной из ключевых технологий в современном прогнозировании, установив новую планку точности моделей.
На фоне стремительного развития больших языковых моделей (LLM), увеличение масштаба нейросетей стало, по сути, доминирующим направлением. Сегодня подавляющее большинство передовых моделей насчитывает миллионы параметров, а в случае предварительно обученных LLM — и вовсе миллиарды. Казалось бы, такая экспансия должна была бы обеспечить качественный скачок в результатах. Однако, вопреки ожиданиям, улучшения оказались скорее умеренными: прирост точности (в терминах MSE и MAE) не превышает 30%, при этом число параметров возрастает в сотни и тысячи раз по сравнению с простыми линейными моделями. Более того, начиная с модели PatchTST, прогресс стал стремительно замедляться — последующие модели показывают лишь постепенные, несущественные улучшения.
Эти наблюдения ставят под сомнение само направление, в котором движется область. Очевидно, что масштаб модели сам по себе не является гарантией высокого качества. На этом фоне всё более актуальным становится противоположный вектор — снижение числа параметров без потери прогностической мощности.
Однако, прежде чем предложить альтернативное решение, важно разобраться, почему действующие методы плохо работают при снижении параметров. В большинстве современных архитектур используется так называемый патчинг — разбиение данных на фрагменты по временным или пространственным измерениям. В сочетании с механизмом внимания такой подход действительно позволяет захватывать сложные зависимости. Но у него есть и обратная сторона. При патчинге нарушаются временные (или пространственные) идентификаторы, теряются связи между наблюдениями, а значит — исчезает та самая структура, которую модель должна уловить.
Чтобы частично компенсировать эти потери, исследователи вводят дополнительное кодирование идентичностей и временных позиций, расширяя скрытое пространство признаков. Но чем больше таких идентичностей нужно сохранить, тем выше размерность пространства, а вместе с ней — и число параметров. В результате, масштаб модели раздувается экспоненциально. Это, в свою очередь, повышает риск переобучения — особенно в тех случаях, когда доступно ограниченное количество обучающих данных, что типично для задач временных рядов.
Если цель — получить не просто эффективную, но и экономную модель, необходимо переосмыслить саму парадигму: вместо того, чтобы воссоздавать структуру в скрытом пространстве, лучше сохранить и использовать регулярности данных изначально. Последние исследования показывают, что разложение признаков (feature decomposition) способно значительно повысить точность без необходимости в гигантских моделях. Однако и у этого подхода есть свои ограничения. Прежде всего, он слабо применим к задачам долгосрочного прогнозирования, особенно когда данные демонстрируют сложные пространственно-временные взаимосвязи. Кроме того, есть аналитическая сторона вопроса — почему и как работает разложение, чем оно лучше патчинга?
В ответ на эти проблемы авторы работы "Parsimony or Capability? Decomposition Delivers Both in Long-term Time Series Forecasting" предлагают новый подход — нейросетевую архитектуру SSCNN (Selective Structured Components-based Neural Network). Эта модель сочетает в себе точность, экономичность и аналитическую обоснованность. В отличие от предыдущих решений, SSCNN впервые предлагает формальный анализ преимуществ разложения признаков по сравнению с патчингом, обосновывая его с точки зрения и эффективности, и компактности. Более того, базовое разложение здесь усилено механизмом селекции: модель способна выделять важные зависимости на уровне отдельных временных шагов, что существенно повышает точность восстановления структурных компонентов, а следовательно — и общий уровень прогноза.
Результаты тестирования SSCNN на эталонных задачах, проведенного авторами фреймворка, показывают, что модель стабильно превосходит существующие методы по качеству прогнозирования, при этом требует в 99% случаев меньше параметров, чем модели PatchTST или iTransformer. Ещё более поразительно: при решении задач долгосрочного прогнозирования SSCNN использует на 87% меньше параметров, чем даже сверхкомпактная модель DLinear.
SSCNN представляет собой шаг вперёд — не за счёт наращивания вычислительной мощи, а благодаря вдумчивому использованию структуры данных и точной инженерии. Это решение говорит о том, что путь к качественному прогнозу лежит не через количество, а через понимание.
Алгоритм SSCNN
В задаче многомерного прогнозирования временных рядов, имея исторические наблюдения X = {x1, …, xN} ∈ RN*Tin, где N — число переменных, а Tin — длина анализируемой последовательности, необходимо спрогнозировать значения на будущем интервале длиной Tout, обозначаемом как X̂ ∈ RN*Tout. Исходные данные проходят предварительную обработку с целью прогнозирования будущих, ещё неизвестных значений. В ходе прогнозирования формируется последовательность промежуточных представлений, отражающих внутреннюю динамику данных.
Архитектура SSCNN организована в виде двух функционально различных ветвей. Верхняя ветвь отвечает за процесс инференции: она извлекает структурные компоненты временного ряда вместе с соответствующими остатками. Нижняя ветвь, в свою очередь, фокусируется на экстраполяции — то есть на прогнозировании возможной эволюции этих компонентов во времени.
Полученные компоненты и остатки объединяются в один широкий вектор, который затем поступает на вход полиномиального регрессионного слоя. Этот слой позволяет выявить сложные взаимосвязи между элементами, сохранив при этом структурную разметку данных.
Авторы фреймворка SSCNN вводят новый механизм нормализации — T-AttnNorm, основанный на временном внимании. Он позволяет пошагово выделять основные составляющие временного ряда: долгосрочную, сезонную и краткосрочную компоненты. Каждый из этих элементов извлекается индивидуально для каждой переменной вдоль временной оси. При этом формируется карта внимания (selection map), отражающая динамику интересующей компоненты.
После извлечения компонент, модель отделяет его от общего представления ряда, получая остаточный сигнал, в котором аккумулируется информация, не попавшая в структуру выделенного элемента. Таким образом, из начального представления временного ряда H ∈ RN*Tin*d формируются два потока: структурный компонент µ ∈ RN*Tin*d и остаток R ∈ RN*Tin*d. Карта выбора I ∈ RN*Tin*Tin управляет формированием каждой компоненты.
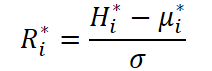
Чтобы сохранить корректность нормализации, строки матрицы I* нормированы так, что их сумма была равна 1. Различие между долгосрочной, сезонной и краткосрочной компонентой заключается именно в способе построения этой матрицы.
Важно отметить, что остаток, полученный на одном этапе, подаётся на вход следующего блока. Например, для выделения сезонной компоненты в качестве входа используется остаток, оставшийся после извлечения долгосрочной.
После декомпозиции каждого структурного компонента и остаточного сигнала, оба потока подвергаются экстраполяции на будущий временной горизонт с помощью линейного отображения, задаваемого матрицей E* ∈ RN*Tin*Tout. Подобно карте внимания I*, матрица E* также нормирована по строкам.
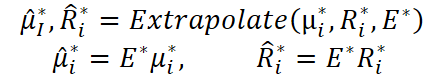
В результате получаем прогнозируемые компоненты ̂µ* и R̂* ∈ RN*Tout*d.
Долгосрочная компонента модели служит для выявления и описания устойчивых трендов во временных рядах. Чтобы получить максимально объективную оценку этой составляющей, авторы фреймворка усредняют значения, собранные за несколько сезонов. Такой подход позволяет минимизировать влияние сезонных и краткосрочных колебаний, которые оказывают лишь локальное воздействие и могут искажать общее направление динамики.
Реализация механизмов выделения и экстраполяции долгосрочной компоненты выражается через простые матрицы со всеми равными значениями: каждая ячейка таких матриц принимает значение 1/Tin. Это означает, что каждая временная точка в прошлом вносит равный вклад в формирование долгосрочной картины. Таким образом, ни один участок ряда не получает приоритета — напротив, модель опирается на глобальное, усреднённое поведение.
Авторы фреймворка сознательно исключили механизм внимания (attention) из обработки долгосрочной компоненты. Практика показала, что в рассматриваемых наборах данных это не приводит к росту точности прогнозов. Внимание действительно может быть полезным, когда распределение компоненты заметно меняется во времени — тогда оно помогает снизить смещение оценки. Однако, в случае долгосрочной компоненты такое распределение остаётся стабильным на всём протяжении входного интервала. Поэтому применение attention в данном контексте не оправдано и становится лишь лишней сложностью без практической пользы.
Сезонная компонента модели предназначена для описания регулярных колебаний, повторяющихся с заданной цикличностью. Её извлечение опирается на предположение о стабильной длине цикла, что упрощает выявление сезонных закономерностей. Здесь вводится обозначение c — длина одного цикла. Тогда τin указывает число полных циклов, содержащихся в анализируемой последовательности (τin • c ≤ Tin), а τout — минимальное количество циклов, необходимое для покрытия выходной последовательности (τout • c ≥ Tout). Для удобства дальнейших вычислений предполагается, что длина входа Tin кратна c.
Чтобы получить точную и несмещённую оценку сезонной компоненты, авторы фреймворка SSCNN вводят обучаемую матрицу параметров Wse ∈ Rτin*τin, каждая ячейка которой отражает взаимосвязь между парой циклов. Эта матрица нормализуется построчно с помощью SoftMax. Таким образом, при вычислении весов для текущего цикла учитывается вклад всех предыдущих циклов, что позволяет захватывать локальные и глобальные закономерности.
Модель строит специальную карту выбора, своего рода фильтр, который позволяет извлекать только значения, соответствующие одинаковым фазам разных циклов. То есть сравниваются, скажем, только первые дни каждого месяца, или только понедельники всех недель — в зависимости от масштаба цикла. Это достигается путем учитывания лишь элементов с разницей между индексами кратной c, а принадлежность к конкретному циклу фиксируется с помощью целочисленного деления.
При переходе к экстраполяции, то есть при прогнозировании сезонной компоненты на будущие временные точки, используется аналогичная логика. Вводится матрица Ŵse ∈ Rτout*τin, отражающую связи между циклами в выходной и входной последовательностях. Она также нормализуется и формирует карту выбора для экстраполяции, обеспечивая логичное и согласованное продолжение уже выявленных сезонных закономерностей в будущее.
Такая организация позволяет модели точно учитывать повторяющиеся структуры данных и использовать их как якорь для предсказаний, обеспечивая высокую устойчивость и точность сезонных прогнозов.
Краткосрочная компонента предназначена для выявления локальных аномалий и кратковременных эффектов, которые не попадают в рамки сезонных и долгосрочных закономерностей. В отличие от тренда, она формируется на основе ограниченного окна наблюдений δ, который определяет глубину временного взгляда назад. Такие данные сохраняют актуальность лишь в ближайшей временной перспективе и демонстрируют различную степень взаимосвязи в зависимости от лагов, то есть от расстояния между точками наблюдений.
Именно поэтому извлечение краткосрочной компоненты основывается на параметрическом векторе wst ∈ Rδ, который позволяет по-разному взвешивать значения в пределах заданного окна. Эти веса проходят через SoftMax-нормализацию, что позволяет подчеркнуть наиболее значимые наблюдения, сохраняя при этом числовую стабильность модели. Таким образом, внимание сосредоточено только на последних значениях временного ряда, что обеспечивает фокус на ближайших к прогнозу изменениях.
Когда речь заходит о прогнозировании краткосрочной компоненты, подход зависит от того, насколько далеко простирается временной горизонт. Если предсказание охватывает ближайшие шаги, то сохраняются корреляции с недавними значениями, и используется регрессионная модель на основе параметрической матрицы wst ∈ Rδ*δ. Однако, по мере удаления на более дальние горизонты, накапливаются неопределённости, которые снижают надёжность прогнозов. В таких случаях модель применяет метод обнуления (zero-padding), сознательно отказываясь от избыточных параметров, которые могли бы привести к переобучению.
Таким образом, краткосрочная компонента остаётся компактной и гибкой, точно захватывая локальные колебания без нагромождения модели лишними вычислениями и весами. Эта адаптивность особенно важна в условиях нестабильных или шумных данных, где именно краткосрочная динамика играет ключевую роль в принятии решений.
Пространственная компонента охватывает те аспекты временных рядов, которые не поддаются описанию с помощью ранее выделенных временных структур — долгосрочной, сезонной и краткосрочной. Иными словами, она отражает временно нерегулярные, но пространственно согласованные особенности, которые проявляются схожим образом в нескольких рядах одновременно.
Извлечение этой компоненты происходит через специальный механизм нормализации, основанный на пространственном внимании — S-AttnNorm. В отличие от временной нормализации, которая применяется вдоль оси времени, здесь обработка происходит покадрово, вдоль пространственного измерения. То есть на каждом временном шаге модель анализирует поведение всех рядов одновременно, выявляя их общие черты.
Вычисления организованы аналогично временной нормализации: для каждого кадра вычисляется среднее значение (центроид), стандартное отклонение и остаточный компонент. Однако, векторизация здесь идёт поперёк временного измерения — каждый временной шаг рассматривается как срез в пространстве.
Чтобы выявить взаимосвязи между рядами, в особенности те, что сохраняются после устранения основных временных структур (тренда, сезонности и краткосрочной динамики), применяется корреляционный анализ. Каждый временной ряд представлен в виде матрицы Tin * d, которая затем векторизуется. Это позволяет построить матрицу сходства Isi ∈ RN*N, отражающую условную корреляцию между парами рядов. Таким образом, модель получает возможность выделить группы рядов, которые реагируют на внешние факторы схожим образом, несмотря на временную нестабильность этих реакций.
Завершая декомпозицию временных и пространственных компонент, модель переходит к этапу агрегации и интерпретации, где извлечённые компоненты объединяются в единое представление для окончательного прогноза. Этот этап реализуется через полиномиальный регрессионный слой — важный элемент архитектуры, позволяющий учитывать линейные и нелинейные взаимодействия между компонентами.
В своей реализации авторы фреймворка SSCNN существенно расширили функционал модуля: к аддитивным (суммирующим) отношениям добавлены мультипликативные зависимости, что позволяет моделировать более сложные формы взаимосвязей между компонентами, в том числе эффекты второго порядка.
Вектор Si представляет собой конкатенацию всех ранее полученных компонент и соответствующих остатков.
Подобная структура позволяет слою не просто суммировать полученные признаки, а выявлять их взаимозависимости и комбинированные эффекты, что особенно важно в контексте высокоразмерных, взаимосвязанных временных рядов.
Результат обработки Hi — обобщённое представление, в котором уже учтены все ключевые паттерны. Это представление передаётся в последующий уровень модели, начиная с новой итерации долгосрочного блока Hlt i , тем самым замыкая архитектурный цикл и обеспечивая целостную прогнозную динамику. Такой подход повышает выразительность модели и её способность к тонкой настройке под реальные рыночные данные, в которых простое сложение компонент часто оказывается недостаточным.
Авторская визуализация фреймворка SSCNN представлена ниже.
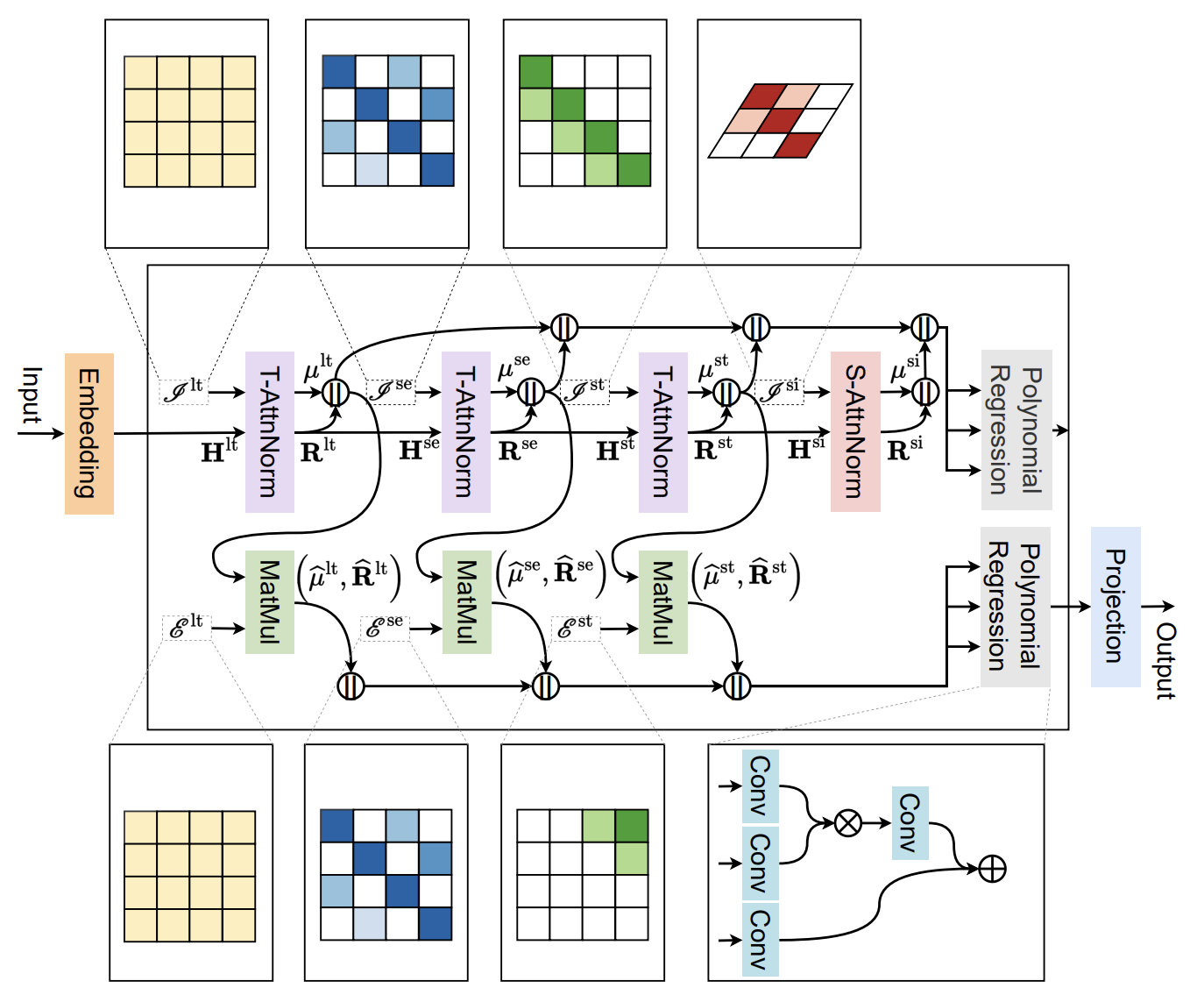
Реализация средствами MQL5
После глубокого погружения в теоретические основы фреймворка SSCNN, мы переходим к практической части статьи. Здесь мы подробно рассмотрим одну из реализаций предложенных методов с использованием возможностей среды MQL5. Это позволит нам закрепить концептуальные идеи и продемонстрировать их эффективное применение в реальных условиях финансового рынка.
В ходе изучения теоретической части, думаю, вы уже обратили внимание на заметное концептуальное сходство представленного фреймворка SSCNN с ранее рассмотренным подходом SCNN. Это сходство отражается даже в названиях фреймворков, что не случайно. Оба метода опираются на идею декомпозиции временного ряда на отдельные компоненты, позволяя более тонко и структурировано анализировать данные.
Однако, ключевое отличие заключается в самом подходе к выделению этих компонент и их дальнейшей экстраполяции. Если SCNN использует более традиционные методы разложения и прогнозирования, то SSCNN внедряет инновационные адаптивные механизмы, такие как селективная структурированная декомпозиция и специализированные карты внимания, что значительно повышает точность и эффективность прогноза.
Впрочем, выделение долгосрочной компоненты с помощью матрицы, заполненной одинаковыми фиксированными значениями, по сути сводится к классической нормализации — усреднению по всему временному интервалу. Это упрощает задачу и позволяет использовать уже проверенные и готовые решения без необходимости изобретать что-то новое.
Однако ситуация меняется, когда речь заходит о выделении более сложных компонент — сезонной и краткосрочной. Здесь потребуется значительно больше усилий и тонкой настройки. Для их корректного извлечения нужны адаптивные механизмы, способные улавливать цикличность, изменчивость и локальные особенности временного ряда. Это включает построение специализированных карт внимания, параметризацию взаимосвязей между периодами и учет локальных корреляций.
Переходим к ключевому элементу реализации — написанию и разбору кернела прямого прохода на языке OpenCL. Именно здесь, на низком уровне вычислительной архитектуры, начинается непосредственная обработка данных, обеспечивающая основополагающие операции нормализации и внимания, без которых невозможна высокая точность и стабильность модели.
Такой переход логичен и необходим. Мы уже знаем, как важно аккуратно и последовательно выделять долгосрочные, сезонные и краткосрочные компоненты временного ряда. Однако для того, чтобы реализовать эти концепции эффективно и масштабируемо, нужно иметь в арсенале мощный инструмент для параллельной обработки больших массивов данных. OpenCL — именно такой инструмент, дающий гибкий и производительный доступ к ресурсам современных GPU и CPU.
Начинаем с создания кернела AttentNorm, основного рабочего модуля, отвечающего за применение механизмов внимания и нормализации исходных данных. Его задача — взять сырые временные данные, взвесить их с помощью заранее рассчитанной матрицы внимания, вычислить локальные средние значения и стандартные отклонения, а затем выполнить стандартизацию, приводя данные к нормированному виду.
В параметрах кернела передаются указатели на анализируемые данные, веса внимания, массивы для средних значений и стандартных отклонений, а также буфер для записи нормализованных результатов. Помимо этого, передаются константы — общее количество элементов в унитарной последовательности и размер сегмента, который будет обрабатываться.
__kernel void AttentNorm(__global const float* inputs, __global const float* attention, __global float* means, __global float* stdevs, __global float* outputs, const int total_inputs, const int segment_size ) { const size_t s = get_global_id(0); const size_t i = get_local_id(1); const size_t v = get_global_id(2); const size_t total_segments = get_global_size(0); const size_t total_local = get_local_size(1); const size_t variables = get_global_size(2);
Далее внутри кернела мы получаем индексы текущих вычислительных потоков в трёх измерениях. Переменная s указывает на глобальный индекс сегмента, i — локальный индекс внутри блока, а v — глобальный индекс переменной или канала. Эти значения позволяют каждому потоку знать, за какой именно участок данных он отвечает. Также определяется общее количество сегментов, размер локального блока и количество переменных, чтобы обеспечить правильное распределение работы.
Для временного хранения промежуточных результатов объявляется локальный массив Temp в быстрой памяти устройства. Затем вычисляется смещение — индекс в массиве исходных данных, который соответствует текущему потоку, переменной и сегменту.
__local float Temp[LOCAL_ARRAY_SIZE]; const int shift = v * total_inputs + s * segment_size + i;
В начале вычислений инициализируются переменные для хранения среднего значения, стандартного отклонения и временного значения, которые будут постепенно накапливаться. Далее запускается цикл, в котором каждый локальный поток по очереди обрабатывает элементы сегмента с определённым шагом, обеспечивая параллельность и равномерное распределение вычислений. При этом осуществляется проверка на выход за границы, чтобы избежать ошибок доступа к памяти.
float mean = 0, stdev = 0; float val = 0; for(uint l = 0; l < segment_size; l += total_local) { if((l + i) >= segment_size || (s * segment_size + l + i) >= total_inputs) break; float val_l = IsNaNOrInf(inputs[shift + l], 0); if(l == 0) val = val_l; float att = IsNaNOrInf(attention[v * segment_size + l + i], 0); mean += val_l * att; stdev += val_l * val_l * att; }
На каждой итерации цикла из исходного массива извлекается значение с учётом смещения, при этом применяется функция, которая защищает от некорректных данных — заменяет нечисловые или бесконечные значения на ноль. Для первой итерации текущее значение сохраняется в отдельную переменную для дальнейшего использования. Аналогично из массива весов внимания извлекается соответствующий вес, который также проверяется на корректность.
Затем происходит накопление суммы взвешенных значений для вычисления среднего, а также суммы взвешенных квадратов значений для последующего расчёта дисперсии. После завершения цикла, с помощью функции локального суммирования происходит редукция по всем локальным потокам внутри блока: все частичные суммы объединяются в единую, обеспечивая точное вычисление статистик. Для корректной синхронизации потоков используется барьер, гарантирующий, что все потоки завершили свои вычисления перед тем, как продолжить дальше.
mean = LocalSum(mean, 1, Temp); BarrierLoc; stdev = LocalSum(stdev, 1, Temp); //--- stdev -= mean * mean; stdev = IsNaNOrInf(sqrt(stdev), 1); if(stdev <= 0) stdev = 1;
Следующим шагом вычисляется дисперсия путем вычитания квадрата среднего из суммы квадратов, после чего берётся квадратный корень для получения стандартного отклонения. Важно, что если значение стандартного отклонения оказывается нулевым, отрицательным или некорректным, оно заменяется на единицу, чтобы избежать ошибок при последующей нормализации.
После этого, один из локальных потоков записывает рассчитанные среднее и стандартное отклонение в соответствующие выходные массивы, обеспечивая сохранение результатов для каждого сегмента и переменной.
if(i == 0) { int shift_ms = v * total_segments + s; means[shift_ms] = mean; stdevs[shift_ms] = stdev; }
Затем запускается ещё один цикл, в котором происходит сама нормализация данных: от каждого входного значения отнимается среднее и делится на стандартное отклонение, с обязательной проверкой на корректность результата. Нормализованные значения сохраняются в выходной буфер, готовые для дальнейшей обработки.
for(uint l = 0; l < segment_size; l += total_local) { if((l + i) >= segment_size || (s * segment_size + l + i) >= total_inputs) break; if(l > 0) val = inputs[shift + l]; outputs[shift + l] = IsNaNOrInf((val - mean) / stdev, 0); } }
Данный кернел эффективно распределяет работу между потоками, обеспечивает аккуратное вычисление статистик с учетом весов внимания и корректно нормализует данные, что особенно важно при работе с временными рядами в задачах прогноза и анализа. Благодаря использованию локальной памяти и синхронизации, достигается высокая производительность и стабильность вычислений.
Кроме того, важно отметить одно из ключевых допущений, заложенных в основу алгоритма работы данного кернела. А именно — предполагается, что размер локальной рабочей группы равен размеру анализируемого сегмента. Это не просто формальное равенство, а существенное условие, которое позволяет упростить вычислительную логику и повысить эффективность выполнения кода на GPU.
При выполнении этого условия, циклы, предназначенные для итеративного обхода сегмента с шагом, равным размеру локальной группы, фактически сводятся к одной итерации. Это значит, что каждый поток обрабатывает ровно один элемент своего сегмента, не заходя в повторные проходы. Такой подход резко снижает сложность внутренних циклов, упрощает логику, и, что особенно важно, минимизирует количество обращений к глобальной памяти.
Вместо многократного считывания данных из глобального буфера, каждое значение сегмента сохраняется в локальной переменной при первой возможности и далее используется из регистра. А это уже совсем другой уровень производительности: обращение к регистру или локальной памяти на порядок быстрее, чем к глобальной, особенно в условиях, когда требуется обработать сотни или тысячи параллельных сегментов в реальном времени.
Таким образом, правильно подобранное соотношение размеров рабочей группы и сегмента становится не просто элементом конфигурации, а активным фактором оптимизации. Оно позволяет в полной мере раскрыть потенциал аппаратного ускорения, снижая накладные расходы и повышая эффективность всей системы обработки временных рядов.
Тем не менее, несмотря на всю элегантность и эффективность описанного подхода, в реальных условиях нельзя полагаться исключительно на идеальные сценарии. Технические возможности оборудования, увы, не всегда подчиняются нашим желаниям. GPU-платформы различаются по архитектуре, объёму доступной памяти, ограничениям по размеру локальной группы и даже особенностям драйверов. Всё это делает строгое равенство между размером рабочей группы и длиной сегмента скорее желаемым, чем гарантированным.
Именно поэтому в коде мы всё же сохраняем цикл — как элемент адаптивности и универсальности. Пусть он и выполняется лишь один раз в оптимальном случае, он остаётся необходимым для тех ситуаций, когда оборудование не позволяет задать локальную группу нужного размера. Это своего рода страховка: если сегмент окажется длиннее доступной локальной группы, цикл аккуратно пройдёт по частям, обеспечивая корректность вычислений при любом раскладе.
Такой компромисс между эффективностью и гибкостью позволяет сохранить производительность там, где это возможно, и при этом гарантировать корректную работу даже на менее мощных устройствах. В мире вычислительных задач как в жизни — всегда стоит держать под рукой план «Б», особенно когда работаешь с железом, которое не склонно к компромиссам.
После завершения описания прямого прохода, где каждый элемент нормализуется на основе среднего и стандартного отклонения своего сегмента, мы переходим к более тонкой и в то же время критически важной части — алгоритму обратного прохода. Здесь простого распространения ошибок недостаточно. Нужно учитывать, что каждый элемент выходного градиента влияет на все элементы исходного сегмента, так как и среднее значение, и дисперсия вычисляются на всём наборе данных одновременно. Это накладывает определённые особенности на реализацию.
Чтобы было понятнее, давайте на минуту обратимся к выражению, описывающему производную нормализованного значения по входу.
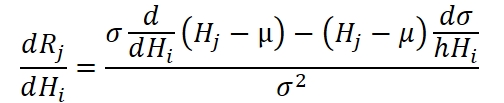
Оно содержит два слагаемых: одно зависит от производной по входному значению напрямую, другое — от производной по стандартному отклонению, в свою очередь зависящей от всех значений в сегменте. Это значит, что вычисление градиента для одного элемента невозможно без учёта вклада всех других.
Формально это выражается в том, что каждый выходной градиент должен быть проецирован обратно на весь сегмент, а не только на свою «ячейку» входа. Таким образом, чтобы корректно вычислить градиент по конкретному входному элементу, необходимо пройтись по всем выходным элементам сегмента и собрать их вклад с учётом того, как изменилось бы среднее и стандартное отклонение при варьировании данного входа.
Особую роль играет случай, когда индекс текущего выходного элемента совпадает с индексом элемента входа, для которого мы собираем градиент. Тогда влияние распространяется не только через изменение статистик, но и напрямую — через производную нормализации самого значения. Если же индексы различаются, остаётся лишь косвенное влияние, и оно полностью определяется изменением средних и дисперсии.
В реализации это означает, что для каждого входного элемента мы должны пройтись по всем выходным градиентам сегмента, суммируя влияние каждого. Такой подход усложняет структуру кернела, но позволяет добиться точного соответствия математике. Это особенно важно, если мы хотим, чтобы обучение нейросетевой модели происходило корректно и эффективно.
Переходя к рассмотрению алгоритма кернела AttentNormGrad, мы оказываемся в самом сердце алгоритма обратного распространения ошибки. Именно здесь рассчитываются градиенты по исходным данным и коэффициентам внимания с учётом зависимости нормализованного выхода от всей совокупности значений сегмента.
__kernel void AttentNormGrad(__global const float* inputs, __global float* inputs_gr, __global const float* attention, __global float* attention_gr, __global const float* means, __global const float* stdevs, __global const float* means_gr, __global const float* outputs_gr, const int total_inputs, const int segment_size ) { const size_t i = get_global_id(0); // main const size_t loc = get_local_id(1); // local to sum const size_t v = get_global_id(2); // variable const size_t total_main = get_global_size(0); // total const size_t total_loc = get_local_size(1); // local dimension const size_t variables = get_global_size(2); // total variables
В начале кернела определяются индексы:
- i — глобальный идентификатор текущего элемента,
- loc — локальный индекс внутри группы потоков,
- v — номер переменной, с которой мы работаем.
__local float Temp[LOCAL_ARRAY_SIZE]; //--- Inputs gradient { const int s = i / segment_size; const int shift_in = v * total_inputs + i; const int shift_ms = v * segment_size + s; float grad = 0; if(loc == 0 && i < total_inputs) { Temp[0] = IsNaNOrInf(inputs[shift_in], 0); Temp[1] = IsNaNOrInf(means[shift_ms], 0); Temp[2] = IsNaNOrInf(stdevs[shift_ms], 1); Temp[3] = IsNaNOrInf(means_gr[shift_ms], 0); Temp[4] = IsNaNOrInf(attention[(v - s) * segment_size + i], 0); } BarrierLoc;
Далее начинается первая часть кернела — расчёт градиентов для исходных данных inputs. Здесь мы определяем, к какому сегменту принадлежит элемент i, вычисляем нужные смещения в памяти и, если мы находимся на первом потоке внутри локальной группы (loc == 0), загружаем необходимые значения в локальный буфер: само значение входа, среднее, стандартное отклонение, градиент среднего и соответствующий коэффициент внимания. После этого — барьер синхронизации, чтобы все потоки дождались загрузки данных и могли безопасно с ними работать.
Теперь начинается самая важная работа. Мы проходим по всему сегменту и анализируем вклад каждого нормализованного выхода в градиент интересующего нас входного значения. При этом особое внимание уделяется тому, совпадают ли позиции — то есть, тот ли это элемент, по которому берём градиент (same). Если да, то его вклад считается напрямую, если нет — то лишь опосредованно через изменение статистик сегмента. Для этого в расчёте участвуют как отклонение значения от среднего, так и его влияние на стандартное отклонение. Всё это аккуратно собирается в переменную grad. Мы так же учитываем градиента по среднему, накопленному по другим информационным потокам.
if(i < total_inputs) { float x = Temp[0]; float mean = Temp[1]; float stdev = Temp[2]; float mean_gr = Temp[3]; float att = Temp[4]; for(int l = 0; l < segment_size; l += total_loc) { if((l + loc) >= segment_size || (i * segment_size + loc + l) >= total_inputs) break; float out_gr = IsNaNOrInf(outputs_gr[v * total_inputs + s * segment_size + loc + l], 0); bool same = (i - s * segment_size) == (loc + l); float xl = x; if(!same) xl = IsNaNOrInf(inputs[v * total_inputs + s * segment_size + loc + l], 0); float dy = ((int)same - att) * (1 / stdev - (xl - mean) * att * x / pow(stdev, 3.0f)); float dmean = (same ? IsNaNOrInf(mean_gr * att, 0) : 0); grad += IsNaNOrInf(dy * out_gr + dmean, 0); } } grad = LocalSum(grad, 1, Temp); if(loc == 0 && i < total_inputs) inputs_gr[shift_in] = grad; BarrierLoc; }
Полученные результаты локально суммируются и записываются в буфер inputs_gr.
Когда с градиентами по исходным данным покончено, мы переходим ко второй части — расчёту градиентов по коэффициентам внимания. Здесь всё зеркально: аналогичная логика, но акцент смещается. Теперь мы для каждого i (элемента сегмента) пробегаемся по всем исходным данным и смотрим, как меняется выход при изменении коэффициента внимания. Структура остаётся той же: расчёт локального градиента, проверка условий совпадения, учёт вклада через изменение стандартного отклонения и среднего. И снова — аккуратная локальная сумма и сохранение результата в attention_gr.
//--- Attention gradient { float grad = 0; int shift_att = v * segment_size + i; if(i < segment_size) { float att = IsNaNOrInf(attention[shift_att], 0); for(int l = 0; l < total_inputs; l += total_loc) { if((l + loc) >= total_inputs) break; int shift_out = (l + loc) + v * total_inputs; int s = (l + loc) / segment_size; int shift_in = v * total_inputs + s * segment_size + i; float x = IsNaNOrInf(inputs[shift_in], 0); float out_gr = IsNaNOrInf(outputs_gr[shift_out], 0); float mean = means[v * segment_size + s]; float stdev = stdevs[v * segment_size + s]; float mean_gr = means_gr[v * segment_size + s]; bool same = (i - s * segment_size) == (loc + l); float xl = x; if(!same) xl = IsNaNOrInf(inputs[shift_out], 0); float dy = -x / stdev - (xl - mean) * x * x * (1 - 2 * att) / (2 * pow(stdev, 3.0f)); float dmean = IsNaNOrInf(mean_gr * x, 0); grad += IsNaNOrInf(dy * out_gr + dmean, 0); } } grad = LocalSum(grad, 1, Temp); if(loc == 0 && i < segment_size) attention_gr[shift_att] = grad; } }
Наш кернел реализует градиентное выражение в соответствии с выведенной ранее формулой. Весь код — это не просто набор команд, а тонко организованная система. Каждый поток аккуратно оценивает, как изменение каждого отдельного входа или коэффициента внимания влияет на выходы всей группы. Здесь есть и оптимизация через локальные буферы, и точная синхронизация, и забота о граничных условиях. Именно так выглядит настоящее инженерное решение — строгое, выверенное, но при этом адаптивное к возможностям аппаратуры и особенностям численного дифференцирования.
Мы детально разобрали реализацию ключевого компонента фреймворка SSCNN — модуля нормализации с вниманием на стороне OpenCL-программы. На наших глазах теория трансформировалась в работающий алгоритм, способный учитывать вес каждого элемента и распределять влияние по всей структуре данных с точностью, достойной высокой инженерии. Мы увидели, насколько важна тонкая настройка взаимодействия между локальной и глобальной памятью, как критично учитывать особенности архитектуры оборудования и почему даже формально несложная операция нормализации превращается в полноценную вычислительную задачу в условиях параллельной среды.
Однако наш путь ещё не завершён. Нормализация — это лишь одна грань многокомпонентного механизма, на который опирается весь фреймворк SSCNN. В следующей статье мы продолжим работу. Самое интересное только начинается.
Заключение
В данной статье мы познакомились с теоретическими аспектами фреймворка SSCNN, в котором особое внимание уделено идее структурного разложения временного ряда и выделению компонент с использованием нормализации на основе механизма внимания. Авторы фреймворка предложили обоснованную архитектуру, способную работать с высокоразмерными временными рядами при минимальных вычислительных издержках.
В практической части статьи мы подробно рассмотрели реализацию одного из ключевых компонентов фреймворка — слоя T-AttnNorm. Особое внимание было уделено особенностям прямого и обратного прохода, взаимодействию с глобальной и локальной памятью. Были выявлены тонкости поведения алгоритма в частных случаях и даны практические комментарии по его адаптации под архитектуру OpenCL.
Мы заложили основу для реализации полного стека SSCNN и обеспечили базу для его обучаемости, подтвердив важность точного сбора градиентов и расчёта производных. В следующей статье мы продолжим наш путь.
Ссылки
- Parsimony or Capability? Decomposition Delivers Both in Long-term Time Series Forecasting
- Другие статьи серии
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Study.mq5 | Советник | Советник офлайн обучения моделей |
| 2 | StudyOnline.mq5 | Советник | Советник онлайн обучения моделей |
| 3 | Test.mq5 | Советник | Советник для тестирования модели |
| 4 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 5 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 6 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |
Гауссовcкие процессы в машинном обучении (Часть 2): Реализация и тестирование модели классификации в MQL5
Интеграция MQL5 с пакетами обработки данных (Часть 4): Обработка больших данных
Автоматизация торговых стратегий с помощью MQL5 (Часть 2): Система прорыва Кумо с Ichimoku и Awesome Oscillator
Создание самооптимизирующихся советников на MQL5 (Часть 2): Стратегия скальпинга на USDJPY
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования