Алгоритм докупки: симуляция мультивалютной торговли

Содержание

• Введение
• Обоснование необходимости симуляции торговли
• Математическая модель симуляции цен с использованием логики дискретизации
• Тестирование модели
• Тестовый советник
• Заключение

Введение

В предыдущей статье я вам показал множество полезных фич, которые вы, наверняка, не знали, но мысль не закончена, и впереди остается самое интересное — исследование или симуляция торговли. Что же это такое и зачем такие сложности? Иногда недостаточно тестера стратегий, хоть это и очень удобный инструмент для знакомства с рынком, но это лишь первый шаг. Если вы внимательно читали предыдущую статью, то вы, скорее всего, не будете задавать вопросов в духе "зачем" и "почему". Остальным же я рекомендую ознакомиться с предыдущим материалом, чтобы понимать, зачем это все. Несмотря на все это, я стараюсь делать статью читаемой, независимо от того, кто заинтересовался и зашел ее почитать, и данная статья будет иметь максимальный вес для читателя даже без изучения предыдущей.

Обоснование необходимости симуляции торговли

Ответ на вопрос, зачем же симулировать торговлю, лежит напрямую в том факте, что количество исторических данных любых торговых инструментов ограничено. Я здесь очень сильно смягчил проблему, на самом деле. Проблему эту можно увидеть, только поняв тот материал, который я показал в предыдущей статье, или иным альтернативным путем. Все же такие люди найдутся, я уверен. 

Суть проблемы в том, что не всегда достаточно просто истории котировок, потому что данная история формируется на стыке многих случайных и неслучайных мировых событий, и существует бесчисленное множество сценариев развития того или иного события. Сейчас я стараюсь рассказывать ближе к пониманию среднестатистического обывателя, но если перейти к языку теории вероятностей и одновременно использовать наработки предыдущей статьи, мы понимаем, что история котировок всех известных нам инструментов могла развиваться иначе.

Данный факт очевиден, хотя бы потому, что многие смотрели фильм "Назад в будущее". Да, там много ляпов и смешных нестыковок с точки зрения ученого человека, но, тем не менее, данный фильм передает основную мысль того послания, что я вам даю. Суть послания в том, что нам мало одной ветки развития событий, а мы должны рассмотреть максимальное их число. А история предоставляет нам лишь одну, и не всегда ее размера хватает для объективной оценки. Например, не так давно у многих брокеров появились некоторые из самых популярных криптоинструментов. Это очень хорошо с точки зрения возможности тестирования и торговли на данных инструментах. Но минус в том, что для советников, которые работают по барам, если честно, недостаточно исторических данных для разработки устойчивых торговых систем.

Симуляция позволит создавать искусственные инструменты и генерировать их котировки каждый раз абсолютно разным способом. Это будет обеспечивать нам максимально широкие рамки для исследования математической модели докупки и остальных важных математических принципов, о которых я рассказывал в предыдущей статье. Еще одним немаловажным преимуществом будет являться то, что мы сможем симулировать неограниченное количество независимых инструментов для параллельной торговли. В конечном итоге у нас отпадает ограничение на длительность тестирования и количество независимо торгуемых инструментов. Конечно, это будут не реальные котировки, но они ничем не будут отличаться от реальных с точки зрения законов ценообразования.

Математическая модель симуляции цен с использованием логики дискретизации

В контексте нашей задачи использование именно подхода "произвольная дискретизация" более чем достаточно, потому что сильная дискретизация будет лишь способствовать увеличению эффективности нашего алгоритма, хотя бы потому, что такие системы автоматически более эффективно сопротивляются спредам. Тем не менее, я построил алгоритм, допускающий и имитацию тиков. Тик - это, ведь, практически самый маленький таймфрейм. Просто время между приходами тиков сильно разное, но если вычислить среднее время между тиками, то можно в первом приближении имитировать тики.

Под баром в данном случае мы понимаем фиксированный отрезок времени, который нам удобно воспринимать с визуальной точки зрения. Но это удобно только потому, что вам сказали, что это удобно, и вы никуда не можете деться от этого, ведь все торговые терминалы заточены именно под данную парадигму. Тем не менее, это далеко не лучший способ дискретизации ценообразования. Наверняка многие знакомы с "ренко". Данный подход к дискретизации ценовых данных предназначен лишь для одного - уйти от времени. Ценность данного подхода может быть совершенно разной для разных подходов и трейдеров. Все это индивидуально. Тем не менее, этот пример я использую лишь для того, чтобы показать один из альтернативных способов дискретизации ценовых рядов. Данный пример в моем понимании должен вам сказать о том, что в контексте нашей задачи мы будем использовать совершенно иную и не знакомую вам логику дискретизации, но именно она позволит нам очень просто и эффективно смоделировать ценообразование без излишних вычислительных затрат.

Для правильного построения эффективной и экономной к вычислительным мощностям парадигмы можно прийти взглянуть на данную картинку:

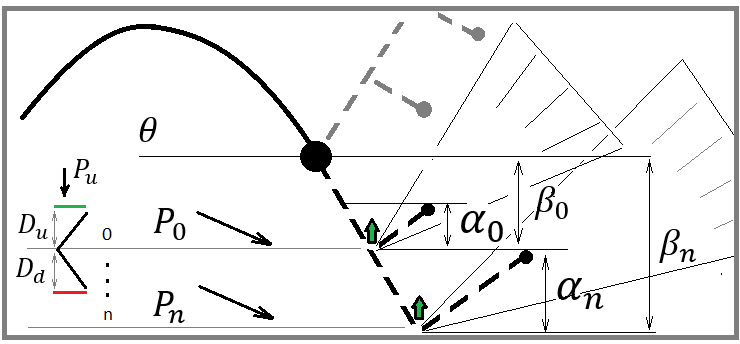
На данной картинке изображена пара возможных сценариев откатного движения цены. Эти два отката у меня обозначают произвольные две точки, которые можно выбрать абсолютно любым способом, и способ выбора не играет роли. Важно то, что мы можем произвольным образом выбрать любую точку, которая может быть рассмотрена как вероятная точка разворота.

Слово "вероятная" должно немедленно сказать каждому математику, что в данной точке существует некая вероятность какого-то желаемого события. В нашем случае мы можем сказать, что данное событие может быть произвольным. Событие отката характеризуется верхней и нижней границей приращения цены. Вероятность данного события можно посчитать вот так:

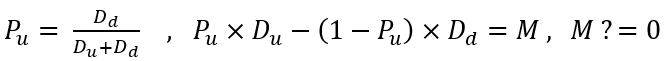
Здесь вероятность достижения верхней границы, и уравнение, из которого получена данная формула. Уравнение характеризует математическое ожидание приращения цены в случае, если нет предсказательного момента. Отсутствие предсказательного момента выражается в нулевом математическом ожидании, но в нашей симуляции я хочу, чтобы можно было регулировать параметры предсказательного момента, для того чтобы можно было удобно усиливать или ослаблять флетовые характеристики нашего моделируемого ценообразования. В конечном итоге, вы увидите, как это сказывается на алгоритм докупки, и вы получите от меня рабочую математическую модель диверсифицированной торговли с помощью алгоритма докупки. Но я хочу дать вам полную математику и разжевать, что здесь и зачем.

Продолжая двигаться дальше, можно понять, что все эти формулы очень красивы и, вроде как, даже полезны, но пока не просматривается в них удобного алгоритма для регулировки флетовости (откатности) инструмента. Чтобы прийти к нему, нужно ввести следующие величины:

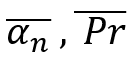
Первая величина – фактически усредненная величина "альфа". Можно еще назвать ее математическим ожиданием величины отката цены после произвольного движения вниз – что в свою очередь представляет собой одно и то же. Вторая величина – это математическое ожидание процента отката, выраженное в относительной величине к предшествующему его движению. Суть этих величин одна и та же, за единственным исключением:

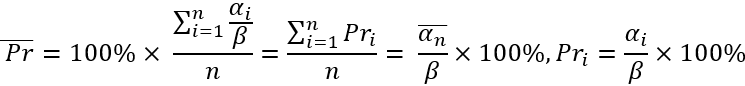
Тут я просто показываю вам, как связаны данные величины и как они вычисляются. Так вот, в нашей с вами модели, мы будем регулировать средний откат, задавая именно средний его процент, и будем идти от обратного, определяя с помощью него средний откат цены. Согласитесь, средний процент отката очень удобен как регулирующее значение для показателя флетовости рынка. Если данный процент поставить равным нулю, то мы фактически требуем случайного ценообразования (это просто для примера). Единственное, хочу отметить, что все просадки цены считаются относительно точки "тета", и я надеюсь, вы простите мне вольность в моих обозначениях, ведь данный материал полностью мой, и здесь нет ни капли чужого. Данные формулы нужны для понимания того, что я буду делать дальше.

Ещё одной немаловажной характеристикой любого ценообразования является волатильность (скорость изменения цен). Данный параметр сопряжён со временем, и мы должны придумать некий крайне удобный способ задания данной величины. Это должно позволить нам просто и эффективно контролировать скорость ценообразования, а также правильно вычислять временные характеристики торговых циклов. Я понимаю, что сейчас мало что понятно, но будет гораздо понятнее, когда я перейду к практике и начну вам показывать, как это работает. Давайте сначала разберёмся с волатильностью.

В классическом истолковании волатильность это немного другое, скорее степень возможного относительного движения цены от минимума к максимуму и наоборот, от максимума к минимуму. Это совсем неудобный способ задания скорости движения цен. Есть гораздо более удобный способ, заключается он в измерении среднего движения цены за фиксированный отрезок времени. Такие отрезки у нас есть, они называются барами. Фактически, мы имеем закон распределения случайной величины модуля изменения цены за один бар. Чем больше данная величина, тем больше в итоге будет волатильность цены, или что то же самое, скорость её изменения. Получается, мы вводим следующие настройки:

Касаемо того, следует ли симулировать случайное распределение величины "S", я могу сказать, что это совсем не обязательно. Единственное, что нужно знать, это то, что реальное ценообразование будет отличаться от того способа, которым мы будем пользоваться в математической модели. Предлагаю зафиксировать величину "S" на уровне ее среднего значения. А так как время каждого шага уже фиксировано, то мы получаем как величину шага, так и его длительность во времени. Это позволит нам в последующем оценивать годовую прибыльность торговой системы, а также замерить среднее время торгового цикла. Теперь давайте разберемся со следующей картинкой, чтобы продвинуться дальше:

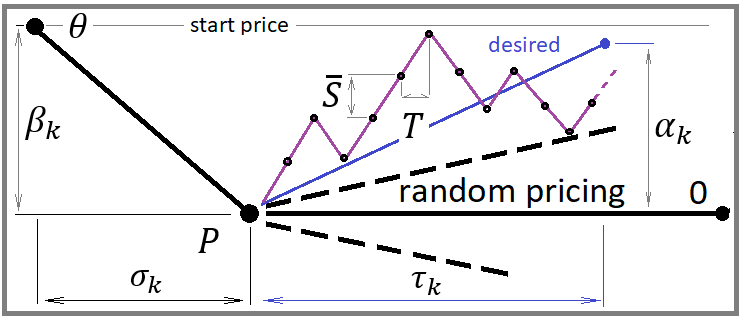
Так как придется симулировать ценообразование для каждого шага, очевидно, что шаг может быть как вниз, так и вверх. Если задавать равновероятный шаг в обоих направлениях, то мы получаем случайное ценообразование. Значит, чтобы регулировать флетовость, мы должны изменять эти вероятности шага. Это и будет обеспечением некоей "гравитации" к стартовой точке цены, от которой началось движение цены вверх или вниз. В нашем случае нужно будет осознать следующее:  

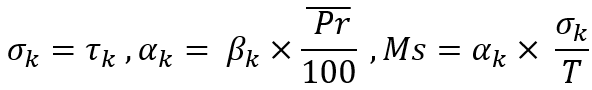
В данном случае, для упрощения модели, я положил, что для выбранного среднего возвратного движения цены требуется ровно то же время, что было затрачено на предшествующий рост или падение цены. Цель данных вычислений - определить мгновенное математическое ожидание для единичного шага, чтобы потом по нему вычислить вероятность того, что шаг произойдет вверх. С помощью данной вероятности регулируется симуляция нового шага. Данная величина пересчитывается после каждого шага для каждого отдельного торгового инструмента.

Теперь очень важный момент: если мы описываем каждый инструмент отдельно, то нам придется составлять некий массив с данными о среднем изменении цены для каждого из них. Но в рамках моей задачи все инструменты равноправны, и потому можно ввести общую и более удобную характеристику для описания шага в виде среднего процента изменения цены:

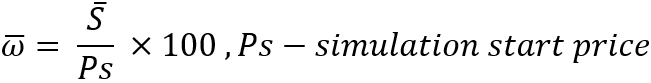
Плюс данной характеристики в том, что она инвариантна относительно любой текущей цены. И, более того, после её рассмотрения можно понять, что если мы рассматриваем идеальные инструменты, то не важно, с какой цены стартует симуляция, потому что это никак не повлияет на прибыль или убыток при тестировании. Ну и, само собой, после того, как мы это понимаем, то мы можем спокойно стартовать параллельный трейдинг для нашего алгоритма докупки с цены, скажем, равной 1. После определения данной величины уже можно считать саму величину шага:

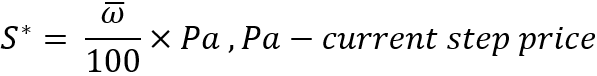
Теперь, зная шаг, мы можем констатировать, что мы собрали все необходимые данные для вычисления вероятности того, что шаг произойдет вверх. Для этого используем нашу первоначальную формулу для математического ожидания шага с некоторыми подстановками:

После данной подстановки мы сможем разрешить это уравнение относительно вероятности шага вверх и, окончательно, получить недостающую вероятность:

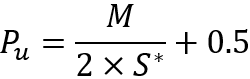
Единственное, стоит отметить, что данные формулы справедливы для случая, когда цена симуляции опускается ниже стартовой точки. Но что делать, когда цена ушла вверх? Все очень просто, нужно всего лишь рассмотреть зеркальный график. Так можно сделать, потому что мы рассматриваем идеальные инструменты. Если представить, что график цены можно описать неким выражением "P = P(t)", то переворот инструмента будет выглядеть следующим образом:

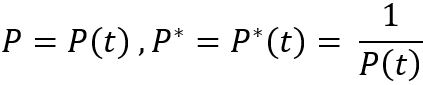
Данный переворот позволит сохранить формулы работающими и для ситуации, когда цена ушла выше стартовой точки. Единственное, мы должны понимать, что все величины в наших выражениях, которые вычисляются с использованием цен (например, дельты), должны использовать уже преобразованную цену, возведенную в минус первую степень.

Давайте теперь построим модель торговли. Я сделал ее односторонней, поскольку она первоначально предназначалась для спотовой торговли криптовалютой. Тем не менее, данная торговая модель годится и для валютных пар на форекс. Все дело в том, что если модель работает, например, только в случае докупки, то одинаково хорошо она будет работать и для допродаж. Единственное, что при тестировании мы будем пропускать верхние полуволны, а работать только по нижним. Для управления торговой моделью я ввел следующие характеристики:

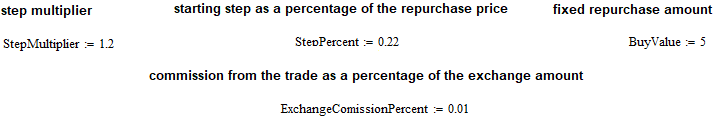
Стартовая докупка начинается с цены "1-Step Percent/100", а шаг докупки при этом будет равен "Step Percent/100". На самом деле, там еще должно быть умножение на стартовую цену, но так как данную цену мы принимаем равной единице, то вычисление шага сильно упрощается. Кроме того, введена возможность рекуррентного увеличения шага. Например, можно либо увеличивать в "N" раз каждый следующий шаг докупки относительно предыдущего, либо точно также уменьшать. Все это зависит от величины соответствующего коэффициента. Шаг докупки измеряется в нижней валюте инструмента (не базовой). Данное правило работает и для криптовалют.

Единственное, для упрощения модели, предполагается, что торговые инструменты в данном случае используются примерно такие: "EURUSD, GBPUSD, NZDUSD" и так далее, то есть нижняя валюта торгуемого инструмента у всех торгуемых инструментов должна быть одна и та же. Это упрощает и без того очень сложную модель, но ее вполне достаточно как для проверки математических принципов из прошлой статьи, так и для оптимизации докупочных алгоритмов. Спред в нашем случае учитывается в виде комиссии, что одно и то же. В целом параметров достаточно для прототипа математической модели. Давайте посмотрим на процесс докупки:

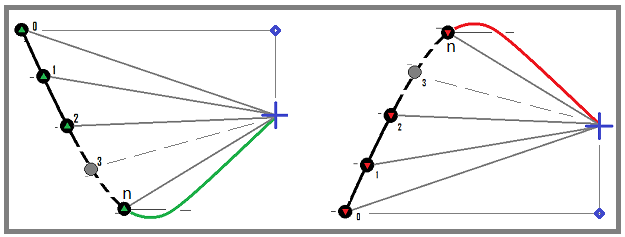
Мы будем использовать первый вариант, который с зеленым возвратным движением. Это фактически покупка базовой валюты, а потом продажа в синей точке. При таком подходе любой завершенный торговый цикл будет прибыльным. То же самое касается продажного цикла с красным возвратным движением, но их мы будем пропускать, как я уже сказал, для того чтобы модель была максимально мультифункциональной и подходила как к торговле на рынке форекс, так и к спотовой торговле на криптовалютных биржах.

Модель сделана так, что торговое плечо не играет роли. Думаю, данной теоретической информации я вам дал достаточно, чтобы вы смогли лучше понять практическую часть, а кому-то может быть и поможет построить свою собственную модель, используя мои наработки.

Тестирование модели

Начнем наше тестирование с различных вариаций генерации котировок. Чтобы наглядно показать вам разницу в генерации котировок, давайте сначала выставим модель в следующее положение:

Данной настройкой мы добьемся случайного ценообразования. Давайте посмотрим на парочку сгенерированных котировок таким способом:

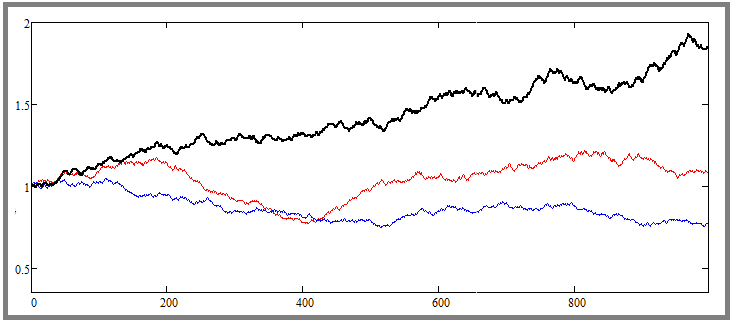
Это график из математической модели, на котором изображены две случайно вынутые из колоды котировки и еще одна дополнительная кривая, которая имеет наибольшее отклонение от стартовой цены. В математической модели есть возможность задавать требуемое количество параллельно симулируемых инструментов, и естественно, что их там очень много, и всегда найдется та, которая наименее симметрична. Она и является самой волатильной. Но я надеюсь, что вы понимаете, что это лишь результат вероятностных процессов. Теперь давайте поставим параметр в другое положение:

Как многие уже поняли, данный шаг позволит создать возвратную гравитацию цены к стартовой точке. Результат получился таким:

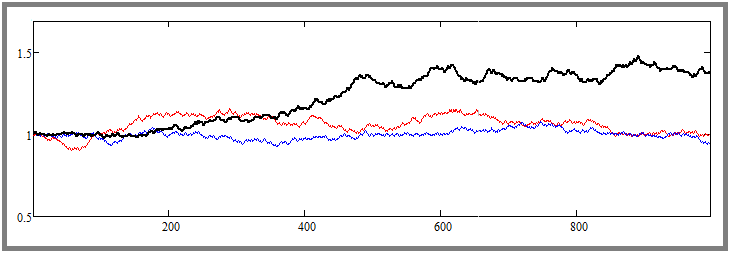
Заметьте разницу между предыдущей и данной картинкой. Здесь мы уже довольно-таки неплохо прижали флетовую регулировку в желаемую нами сторону. Видно, что кривые сильно прижались к стартовой цене, - то же самое произошло с максимально волатильной котировкой, окрашенной в черное. В обеих примерах симулируется ровно тысяча шагов для каждого инструмента. Позже я увеличу данные числа, и мы поиграемся с ними, чтобы понять, как все это работает и какие параметры на что влияют.

Теперь необходимо определить, с какими параметрами и как тестировать искусственную торговлю. Давайте быстренько вспомним, как звучали интересующие нас вопросы, на которые я отвечал в предыдущей статье. Если проще и понятнее, то звучало это примерно так:

1. Условие прибыльности торговых систем с докупкой.
2. Стремится ли линия прибыли к идеальной прямой при бесконечной торговле для идеальных торговых инструментов?
3. Стремится ли линия прибыли к идеальной прямой при увеличении количества инструментов до бесконечности при фиксированном временном отрезке торговли?

Давайте выясним условие прибыльности. Для этого сначала проведем параллельный трейдинг с использованием случайного ценообразования и посмотрим на результат. Он будет выглядеть плюс-минус вот так:

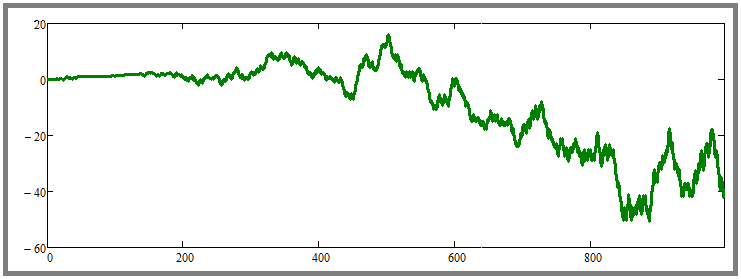
В разных генерациях получались то прибыльные, то убыточные кривые. Пока непонятно, но подтверждением бесполезности докупки при случайном ценообразовании может быть экстремальное увеличение количества параллельно торгуемых инструментов. Давайте посмотрим, что будет, если увеличить их число, скажем, до сотни, и одновременно увеличим количество шагов симуляции для каждого инструмента до 10000:

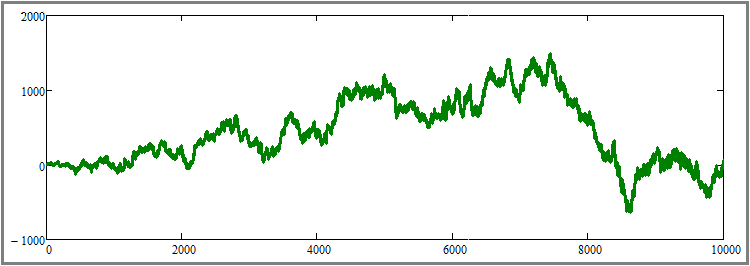
Как видно, ни увеличение количества параллельно торгуемых инструментов, ни увеличение длительности тестирования не дало видимого эффекта. Скорее, это все красноречиво подтверждает доказанный математический факт из предыдущей статьи о том, что при полностью случайном ценообразовании, без наличия предсказательного момента, любая торговая система, в том числе алгоритм докупки, является сливным. На этом считаю пункт "1" теоретически и практически доказанным. Давайте теперь перейдем ко второму пункту и выставим следующую настройку:

Данная возвратная гравитация, по моим тестам, оказалась вполне достаточной для возможности визуальной оценки эффекта для любого читателя. Конечно, можно выставить и более низкий процент, но при нем эффект будет не настолько ярко выражен. Я убрал количество шагов симуляции на первоначальное значение в тысячу шагов. Теперь давайте посмотрим на результат:

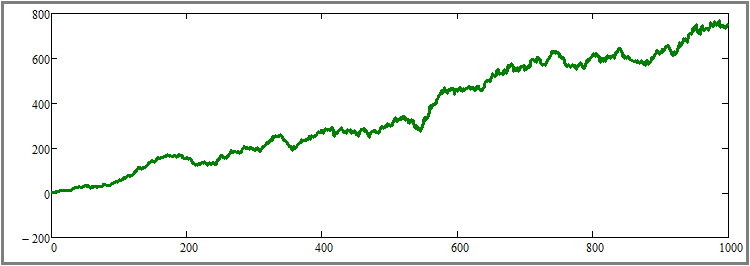
Думаю, не составит труда понять, что данный график, в том числе, является дополнением к доказательству предыдущего пункта, но, в то же время, и отправной точкой к доказательству следующего подпункта. На очереди увеличение длительности всех участков тестирования, без изменения любых других параметров. Для большей наглядности, я увеличил количество шагов симуляции для каждого инструмента с "1000" до "50000", то есть ровно в пятьдесят раз. Это достаточно большое увеличение, но только так можно визуально ощутить данный эффект без множественного тестирования и усреднения результатов. Давайте посмотрим на результат:

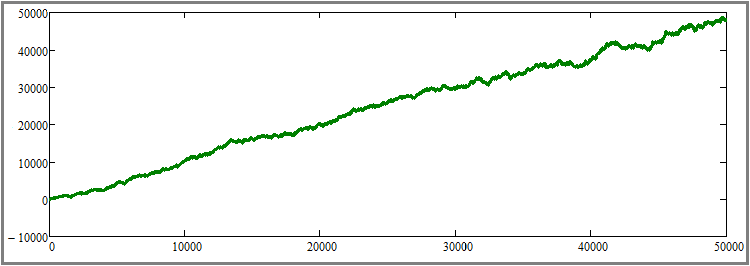
Как видно, кривая стала намного гладче и приближается к прямой линии, а это значит, что и второй принцип увеличения фактора линейности (красоты графика) при увеличении длительности теста работает абсолютно так же, как и предсказывалось. Конечно, это только с тем допущением, что известно о том, что выбранная стратегия прибыльна. На этом второй подпункт считаю теоретически и практически доказанным.

Теперь давайте вернём количество шагов симуляции на первоначальный уровень в тысячу шагов, а количество параллельно торгуемых инструментов наоборот увеличим в десять раз, до величины в "1000". По легенде мы должны получить видимое увеличение красоты графика. Ну, что же, давайте посмотрим, так ли это:

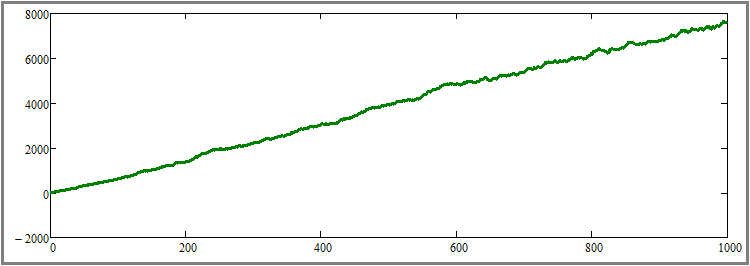
Как видно, данная гипотеза подтвердилась, причем, эффект крайне ярко выражен. На этом считаю, что все три гипотезы теоретически и практически доказаны. Результаты таковы:

1. Условием прибыльности любой торговой системы является наличие предсказательного момента.
2. При увеличении длительности торговли или бектеста любая кривая прибыльной торговой системы становится красивее и прямее (без авто лота) + [при соблюдении пункта 1].
3. При увеличении количества торгуемых валютных пар для одной мультивалютной торговой системы либо увеличении количества одновременно торгуемых систем, кривая прибыльности торговой системы становится красивее и прямее + [при соблюдении пункта 1 для каждой из этих систем].

Тестовый советник

Мы разобрались с тем, как правильно использовать торговые системы, в том числе алгоритм докупки, чтобы максимально эффективно и безопасно зарабатывать как при автоматической торговле, так и при ручной. Расчет мани-менеджмента и прочие различные ситуации для правильного комбинирования торговых систем заслуживают отдельной статьи, которую я напишу чуть позже.

А данный раздел я добавил для того, чтобы можно было наглядно увидеть тот факт, что алгоритм докупки является рабочей стратегией. Для этого я создал тестовый советник, который повторяет нашу математическую модель, с тем лишь отличием, что в нем также обрабатываются и верхние полуволны, то есть торговые циклы на продажу. Я нашел кое-какие настройки, которые доказывают возможность создания подобной торговой системы для MetaTrader 5. Вот демонстрация одной из них:

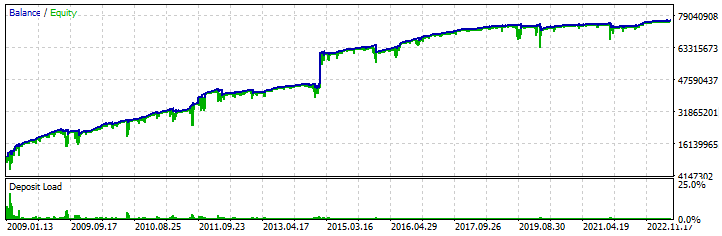
Тестирование проводилось в промежутке с 2009 года по 2023 год с применением параллельного тестирования всех "28" валютных пар, аналогично нашей математической модели. Благодаря тому, что у меня есть шаблон мультибота, который я описывал в одной из предыдущих статей, на нем был построен данный тестовый алгоритм. Конечно, кривая прибыли далека от идеала, да и стартовый депозит для подобной торговли должен быть огромным, но, тем не менее, моя задача в данной статье - не дать вам готового робота, а продемонстрировать близость к математической модели. Самое главное, что вы должны уяснить - при определенных доработках данный алгоритм будет гораздо безопаснее, эффективнее и жизнеспособнее. О сути доработок я предлагаю вам подумать самостоятельно, я считаю, что это будет честно, учитывая, что я показываю то, что лучше не показывать.

Советник вместе с сетом, а также сама математическая модель, будут приложены к статье файлом, и вы сможете, при желании, изучить их структуру более подробно, возможно, что-то подчерпнуть для себя или развить идею гораздо дальше. На самом деле в моей математической модели гораздо больше полезностей, чем я описал здесь. Она вычисляет многие важные торговые характеристики благодаря своему собственному набору выводимых параметров после бектеста. Конечно, ее функциональность сильно ограничена, но достаточна для доказательства и приблизительных прикидок.

Заключение

В данной статье я завершил практическую часть доказательства того, что принцип диверсификации работает, и им следует пользоваться. Самое важное, что в совокупности с предыдущей статьей были доказаны как теоретически, так и практически, важнейшие вещи, благодаря которым вы увеличите, как минимум, эффективность своей торговли. Кроме того, с помощью созданного советника была доказана живучесть алгоритма докупки на протяжении более чем десятка лет.

А раз доказана живучесть алгоритма докупки, то, фактически, мы получаем подтверждение волновой теории ценообразования, или флетовости рынка, как хотите. Кроме того, в качестве дополнительного подтверждения данного факта я советую обратить внимание на следующую статью. В данной статье автор уделяет максимальное внимание именно такому же алгоритму, как я описывал в своей статье. Вы сможете почерпнуть оттуда дополнительные знания о том, как использовать данные эффекты для улучшения моего тестового советника или разработки своего.