自适应指标

概述

大概，每位交易者的梦想就是有一款指标，能够适应当前市场状况、定义横盘和趋势区段，并考虑到相关价格变化。 传统的技术指标在处理输入信号时均采用恒定比率。 这些比率无法以任何方式依据输入信号的特性及其变化，随时间推移进行调整。

自适应指标的区别在于输入值和输出信号之间存在反馈。 这种反馈令指标能够独自调整到处理金融时序数据的最优状态。 更简单地说，自适应指标是一种规则的线性指标，其比率能够根据当前的市场状况随时间推移而变化。

适应算法十分丰富。 选择特定算法取决于指标的用途。 但大多数情况下，这些算法基于各种最小二乘法。 我们来看几个开发自适应指标的示例。

首次尝试

我们尝试创建一个自适应指标。 调整指标的最显见方式是参考其在一种或多种情况下的最新误差。 我们看看如何做到这一点。

设 Indicator[i] 是第 i 根柱线上的指标值。 那么误差是 Error[i] = price[i] - Indicator[i]。

此误差可在下一次计数期间校正指标值。 甚至，我们能以不同的方式处理误差。 例如，我们可以取最后少量误差的平均值，或对它们进行指数平滑。

我们看看这种方法在图表上的样子。 我将采用来自有关技术指标的文章中例举的模板作为基础。 不过，我要对其进行一些修改。 首先，设置误差数量

      double sum=0;
      for(int j=0; j<size; j++)
         sum=sum+coeff[j]*price[i+j];//Calculate the indicator value

      if(i>0)
        {
        double cur_error=price[i]-sum;//Current error
         if(NumErrors==0)
            cur_error=(error+cur_error)/2;
         if(NumErrors==1)
            error=cur_error/2;
         if(NumErrors>1)
           {
            for(int j=NumErrors-1; j>0; j--)
               errors[j]=errors[j-1];
            errors[0]=cur_error;

            cur_error=0;
            for(int j=0; j<NumErrors; j++)
               cur_error=cur_error+errors[j];
            error=cur_error/NumErrors;
           }
        }

      buffer[i]=sum+error;//Indicator value considering the error

这就是我们的新指标与简单移动平均线（红线）相比的样子。

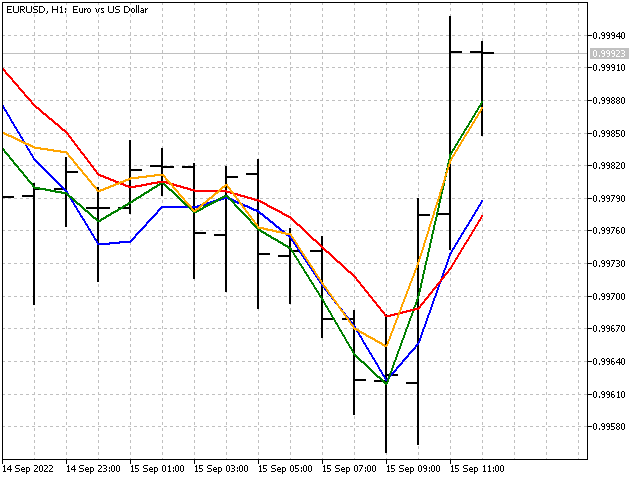
图片看起来挺漂亮，但我们的指标是自适应的吗？ 很不幸，它并不是。 事实上，我们得到的只是一个普通的线性指标，尽管它的权重系数是隐性设置的。

我们取一条简单移动平均线，周期为 3，以最后三个误差的平均值为特征。 我们先计算误差：

Error[1] = price[1] - (price[1] + price[2] + price[3])/3

Error[2] = price[2] - (price[2] + price[3] + price[4])/3

Error[3] = price[3] - (price[3] + price[4] + price[5])/3

然后指标方程将如下所示：

Indicator[0] = (price[0] + price[1] + price[2])/3+(Error[1] + Error[2] + Error[3])/3 =>

Indicator[0] = (3*price[0] + 5*price[1] + 4*price[2] + 0*price[3] - 2*price[4] - 1*price[5])/9

结果就是，我们得到了一个规则的线性指标。 这牵扯出一个简单的结论 – 仅靠误差处理并不能令指标自适应。

日出

皮埃尔-西蒙·拉普拉斯（Pierre-Simon Laplace）曾经提出过这个问题，后来被称为“日出问题”。 这个问题的本质可以这样描述 — 如果我们连续 1000 天看到日出，那么我们对太阳会在第 1001 天升起的信心是什么？ 这个问题很有趣。 我们从交易的角度来看待它。 假设您完成了九笔交易，其中六笔翻示盈利。 基于这些信息，尝试回答这个问题：盈利交易的概率是多少？

作为规则，概率定义为盈利交易与其总数的比率：

在我们的示例中，概率为 6/9。 然而，我们若更进一步 — 未来交易获胜的概率是多少？ 对于任何产出，分数的分母将加一。 但对于分子，有两种可能的选择 — 未来的交易可能会盈利，也可能一无所获。 换言之，我们有两种可能的选项：

我们取这些值的平均值。 在这种情况下，我们对获胜概率的估算如下：

这略小于 6/9 的原始值。 此方法称为拉普拉斯（Laplace）平滑。 它可用于数据分类，其中变量可以取多个定义的值（在我们的示例中为“成功或失败”）。

我们尝试在指标中应用这种平滑。 为此，我们做一个小假设。 我们假设价格流中还有另一个隐含价格（我们称之为虚数），其会影响指标读数。

我们看看在这种情况下指标方程是如何变化的。 简单移动平均方程如下所示：

这就是对应假想价格的相同平均值的样子：

乍一看，一切看起来都很棒。 但这里有一些不愉快的事情。 首先，假想价格本身会不稳定：

其次，如果我们将虚数价格移动到时间序列中的下一个点，那么我们的指标将被简化：

这种简化并未帮助我们稳定指标（price[1] 比率等于 1）。 不过，这种失败可作为另一个指标的基础。

首先，设置 iPeriod 指标周期。 然后找到所有 N 的 SL 值，数值从 1 到 iPeriod。 下一步是计算所有 SL 值之和的平均值。 结果就是，我们将得到一个显示稳定价格值的指标。 该指标可以描述如下：天真的预测（过去=未来）加上略微弱化的线性趋势。

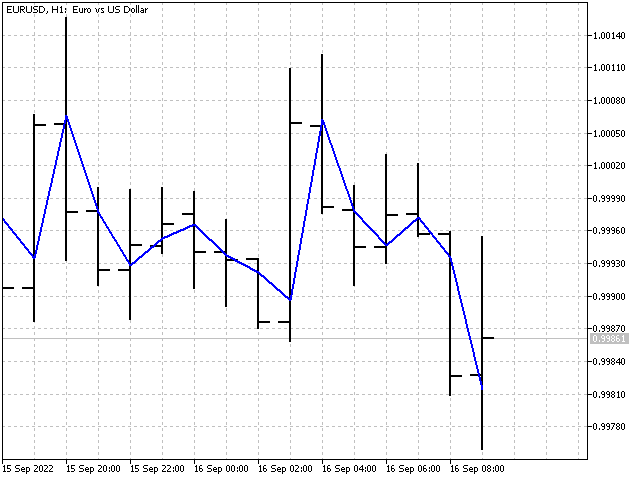
现在我们就得到一个指标。 然而，自适应尚未达成。 再一次尝试，再一次惨败。 我们短暂休息一下，然后尝试重新创建一个自适应指标。 否则，我将不得不更改文章的标题。

月落

一位俄罗斯科幻作家科兹马·普鲁特科夫（Kozma Prutkov）曾十分明智地说过：“如果有人问：太阳或月亮哪个更有用？请回应：月亮。 因为太阳只在白天曝晒，不过那时本就明亮，而月亮则在夜间照耀”。 我们看看这个说法如何转化到交易世界。

在拉普拉斯平滑中，我们取用具有相同权重比率的价格值。 但如果我们给价格某种权重会发生什么？ 在窗口函数中，权重比率取决于给定读数与指标权重中心的距离。 现在我们将以不同的方式进行。 首先，我们将选择某个价格值作为中心值。 它将承载最大的权重。 其余价格的权重比率将取决于价格与该值的距离 — 越远，其权重就越小。 换言之，我们将创建一个窗口函数，不是在时域当中，而是在价格域当中。 我们来看看这种算法在实践中表现如何。

      double value=price[i+center],//Price value at the center
             max=_Point;           //Maximum deviation
      for(int j=0; j<period; j++)//Calculate price deviations from the central one and the max deviation
        {
         weight[j]=MathAbs(value-price[i+j]);
         max=MathMax(max,weight[j]);
        }

      double width=(period+1)*max/period,//correct the maximum deviation from the center so that there are no zeros at the ends
             sum=0,
             denom=0;
      for(int j=0; j<period; j++)//calculate weight ratios for each price
        {
         if(Smoothing==Linear)//linear smoothing
            weight[j]=1-weight[j]/width;
         if(Smoothing==Quadratic)//quadratic smoothing
            weight[j]=1-MathPow(weight[j]/width,2);
         if(Smoothing==Exponential)//exponential smoothing
            weight[j]=MathExp(-weight[j]/width);

         sum=sum+weight[j]*price[i+j];
         denom=denom+weight[j];
        }

      buffer[i]=sum/denom;//indicator value

这就是我们的指标在图表上的外观。

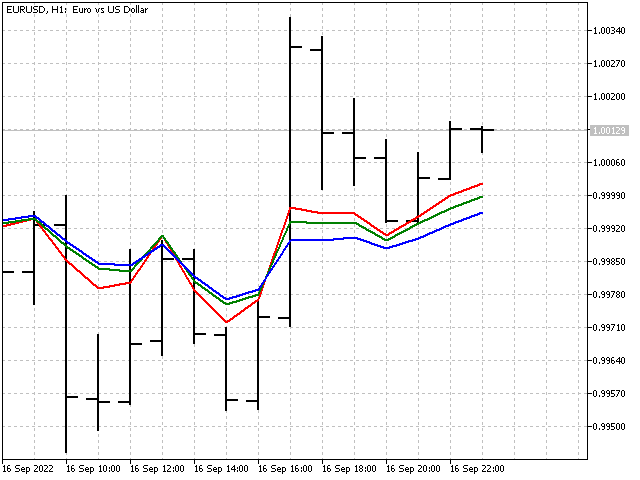
指标权重比率变化。 但我们仍然不能称之为自适应。 更正确的说法是，该指标会根据当前的市场情况进行调整。 自适应指标没有奏效，但至少我们迈出了第一步。

第二次尝试

我们以矩形窗口函数作为基础。 但我们对它进行一些小的修改 — 假设窗口开始和结束时的比率可以更改。 然后指标公式将如下所示：

其中 N 是一个指标周期，而 C1 和 C2 是自适应比率。

假设我们已经有了这些比率值。 新的价格值出现。 伴随而来的是，指标误差也会变化。

为了降低误差，我们需要按一定的 R 校正因子来校正每个比率：

不言而喻，我将努力确保比率的变化能将指标的误差降至为零。 但这不会是唯一的条件。 我们附加的要求 R 校正越小越好。 如果同时满足这两个条件，我们希望自适应比率值能围绕某个最优值（如果有的话）波动。

故此，我们需要找到以下问题的解决方案：

我们采用最小二乘方法来查找 R 校正。 在这种情况下，可以采取若干步骤进行计算。 首先，计算收敛因子：

然后，校正值将等于 R = 价格*误差*M。

相应地，更新比率的公式如下：

这就是我们的指标与简单移动平均线（红线）相比的样子。

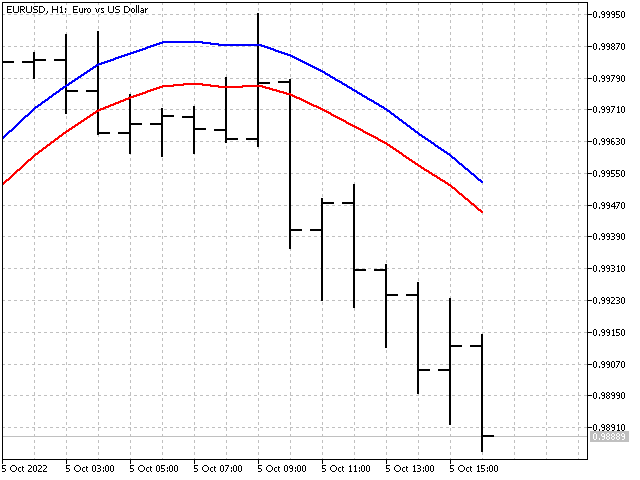
自适应

我们已设法得到了两个比率。 是否有可能创建一个指标，其所有比率都是自适应的？ 是的，可以。 这种指标比率的计算与前一种研究的情况相似。 唯一的区别是收敛因子的计算：

P 参数允许调整每一步的比率变化。 其值应为 1 或更高。 在 P 较小的情况下，指标比率会很快达到最优值。 然而，指标比率的变化可能会变得过度。 在 P 较大的情况下，指标比率变化缓慢。 P 值越高，指标越平滑。 例如，这是 P = 1 和 P = 1000 时的指标外观。

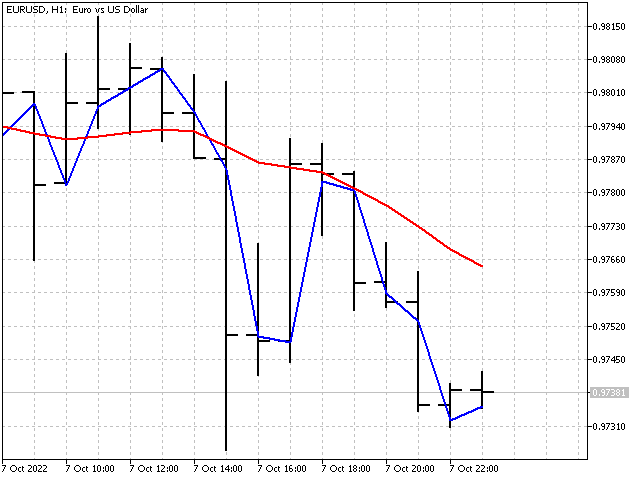
一般建议：首先将参数值设置为等于指标周期，然后沿一个或另外方向进行变更，直到获得所需的结果。

自适应指标的一个重要特征是其潜在的不稳定性。 此类指标的比率之和不等于 1，并且可能因输入数据而异。 我们以指数平均值为例。 常规方程如下所示：

自适应 EMA 方程则如下所示：.

C1 和 C2 彼此不相互依赖。 比率的更新方式与上一个指标相同。 不同之处在于，除了价格之外，还要取指标本身的先期值。

然后，更新的比率将等于：

具有不同 P 值的自适应 EMA 本身如下所示。

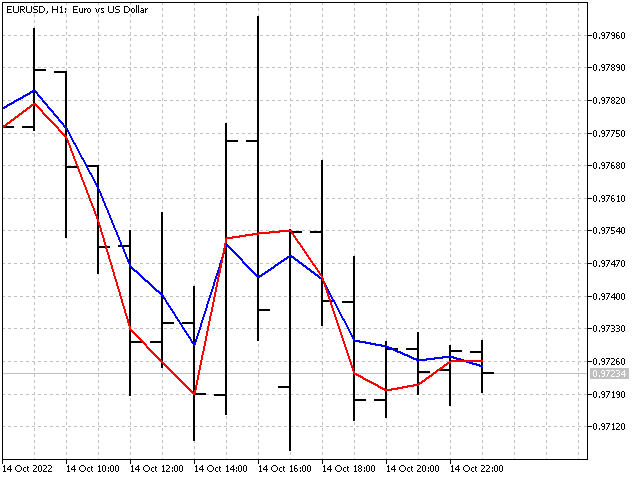
自适应算法也可应用于窗口函数。 然而，结果不是那么令人印象深刻，因为自适应的产生是由于归一化比率的变化。

我们以周期为 5 的 LWMA 指标为基础。 它的方程可以这样写：.

此处 C 是常规化比率。 在通常情况下，这个比率的值是恒定的，可以提前计算。 现在我们允许它向一个或另外方向改变的可能性。

首先，我们需要计算权重累计：

在这种情况下，可采用以下公式找到归一化比率的调整值：

这种方式对于周期较短的指标很有用。 而对于长周期，自适应和 P 参数的影响几乎难以察觉。

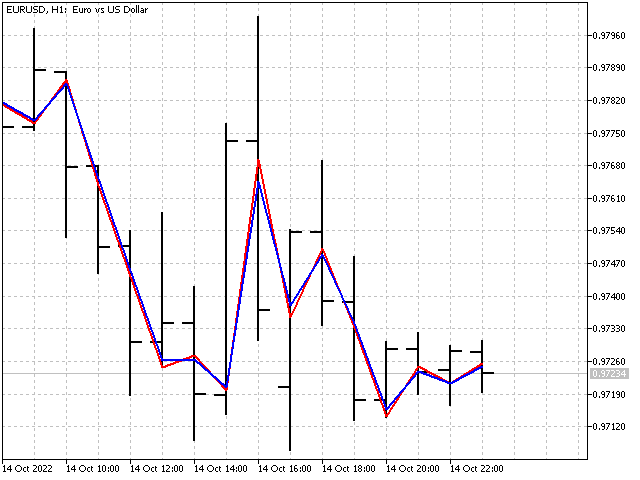
基于自适应指标，我们可以创建各种振荡器。 例如，这就是 CCI 自适应指标的外观。

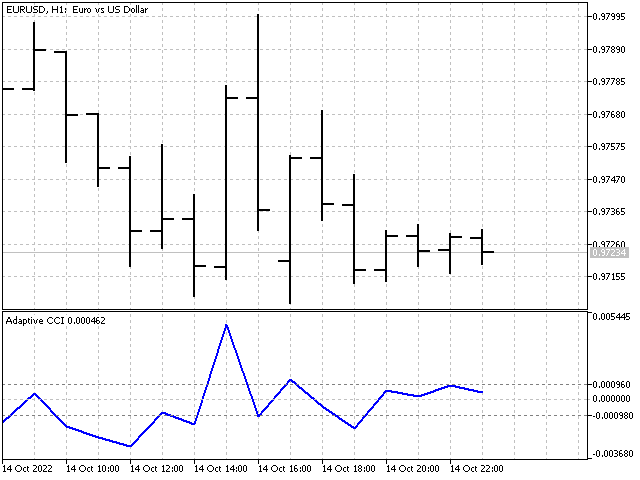
线性预测

构建自适应指标在许多方面类似于解决线性预测问题。 事实上，如果我们利用指标值和未来（相对于指标本身）价格之间的差值作为误差，那么自适应指标就会变成预测指标。

例如，我们取 开盘 价。 那么指标方程和误差值将如下所示：

所有其它计算都是根据我们已经熟悉的方程执行。 我们唯一要添加到该指标的是平均预测误差的计算。 结果就是，我们得到索引为 -1 的柱线开盘价的预测值。

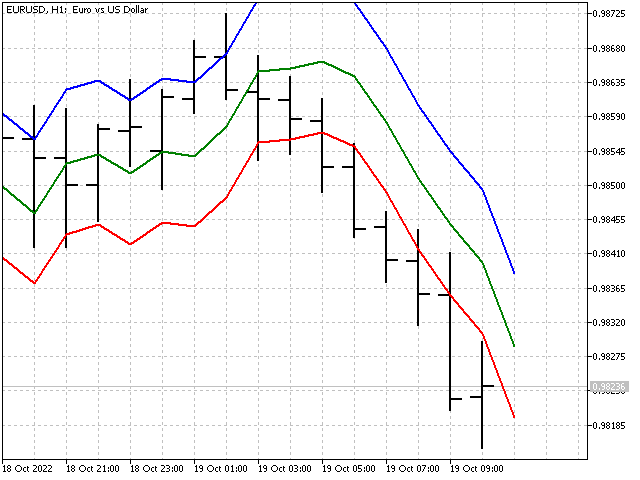
线性概率预测

线性预测的任务也可以用价格变化方程来表示。 在物理世界中，一切看起来都很简单：如果一个点的当前位置、速度和加速度是已知的，那么预测它在下一刻的位置就不难了。 在价格变动的情况下，一切都更加复杂。

我们知道价格的数值。 在数学语言中，速度和加速度是一阶和二阶导数。 我们将用离散模拟替换它们 — 相应阶数的差商。 差商的比率可以从帕斯卡三角形的相应行中获取。 我们只需交替更改每个比率前面的符号。 以这种方式，我们将得到：

1*open[0] -1*open[1] – 速度的离散模拟;

1*open[0] -2*open[1] +1*open[2] – 加速度的离散模拟。

那么价格变动方程可以表示如下：

open[0] + (open[0] – open[1]) + (open[0] – 2*open[1] + open[2]).

我们将自适应比率添加到等式中，结果我们得到：

open[-1] = open[0] + c1*(open[0] – open[1]) + c2*(open[0] – 2*open[1] + open[2]).

我们打开括号，并排列比率。 之后等式将如下所示：

open[-1] = (1 + с1 + с2)*open[0] + (-c1 – 2*с2)*open[1] + c2*open[2].

您可能还记得，稳定指标的比率应该在 -1 到 +1 范围之内。 那么，我们需要解决求解一组不等式：

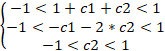
结果就是，我们得到了三种可能的选项：

现在我们就能选择比率值，并用在指标当中。

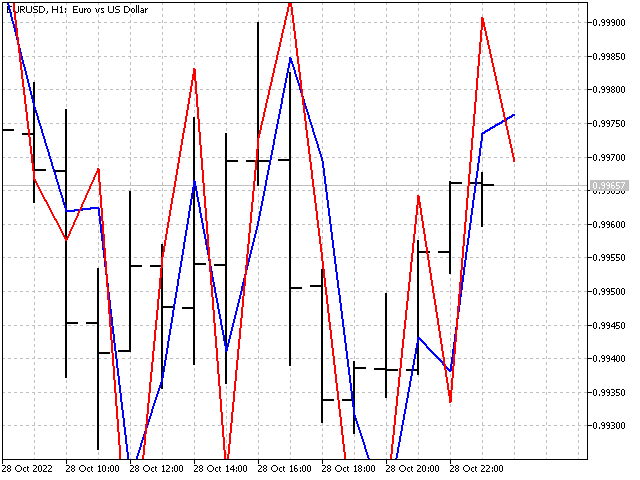
当然，使用更高阶的差商将提供更多可能的选择，并对指标的外观产生有利地影响。

结束语

自适应算法的运用，令我们获得非比寻常的指标成为可能。 它们的主要优势是能够自我调整，从而适应当前的市场形势。 缺点包括控制参数数量的增加，其选择可能需要一些时间。 另一方面，自适应指标可以在非常广泛的范围内变化，从而推动产生新的技术分析方法。