多层感知机与反向传播算法

介绍

• 这两种方法的普及性日益增加，因此在 Matlab、R、Python、C++ 等领域开发了大量的库，它们接收到一个训练集作为输入，并自动为问题创建合适的网络。

• 然而，当使用现成的库时，很难理解到底发生了什么以及我们如何得到一个优化的网络。对解决方案基础知识的理解对于这些方法的进一步发展至关重要。在本文中，我们将创建一个非常简单的神经网络结构。

• 让我们试着理解基本的神经网络类型是如何工作的（包括单神经元感知机和多层感知机）。我们将考虑一个令人兴奋的算法，它负责网络训练（梯度下降和反向传播）。现有的复杂模型往往基于这样简单的网络模型。

历史概述

• 第一个神经网络是由沃伦·麦卡洛赫（Warren McCulloch）和沃尔特·皮特（Walter Pitts）于1943年提出的。他们写了一篇关于神经元应该如何工作的文章，他们还根据自己的想法建立了一个模型：他们用电路创建了一个简单的神经网络。

• 人工智能研究进展迅速，1980年，福岛邦彦（Kunihiko Fukushima）开发了第一个真正的多层神经网络。

• 神经网络的最初目的是创造一个计算机系统，能够以类似人脑的方式解决问题。然而，随着时间的推移，研究人员改变了研究重点，开始使用神经网络来解决各种特定任务。现在，神经网络执行各种各样的任务，包括计算机视觉、语音识别、机器翻译、社交媒体过滤、棋盘游戏或视频游戏、医疗诊断、天气预报、时间序列预测、图像/文本/语音识别等。

神经元的计算机模型：感知机（perceptron）

感知机

感知机的灵感来自于处理单个神经元信息的想法。神经元通过树突接收信号作为输入，树突将电信号传递给细胞体。类似地，感知机接收来自训练数据集的输入信号，这些数据集已经被预先加权并组合成一个称为激活的线性方程。

• z = sum(weight_i * x_i) + bias

这里“weight”是网络权重，“x”是输入，“i”是权重或输入的索引，“bias”是没有乘数输入的特殊权重（因此我们可以假设输入总是1.0）。

然后使用传递函数（激活函数）将激活转换为输出（预测）值。

• 如果 z >= 0.0, y = 1.0 否则就是 0.0

因此，感知机是一种两类问题分类算法（二元分类器），其中可以使用线性方程来分离这两类问题。

这与线性回归和逻辑回归密切相关，它们以类似的方式生成预测（例如，作为输入的加权和）。

感知机算法是最简单的人工神经网络类型。它是一个单神经元模型，可用于两元分类问题。它还为进一步发展更大的网络提供了基础。

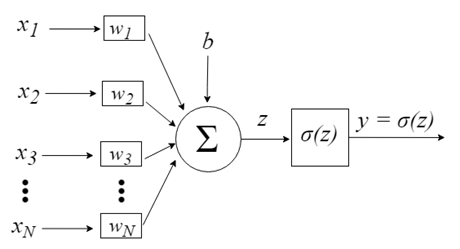
神经元输入由向量x=[x1，x2，x3，…，xN]表示，该向量可以对应于例如资产价格序列、技术指标值或图像像素。当它们到达神经元时，它们被乘以适当的突触权重——向量w的元素=[w1，w2，w3，…，wN]。这将通过以下公式生成z值（通常称为“激活电位（Activation Potential)”）：

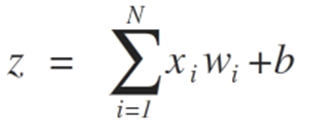
b提供了更高的自由度，因此它不依赖于输入。通常这对应着 "偏离（bias）". 然后z值通过σ激活函数，该函数负责将该值限制在某个间隔内（例如，0-1），从而产生最终输出和神经元值。一些使用的激活函数包括阶跃(step)、S形(sigmoid)、双曲正切、softmax 和 ReLU（“校正线性单元”）。

让我们用两种情况来观察达到类可分离性极限的过程，这两种情况证明了它们收敛到稳定状态，只考虑两个输入{x1和x2}

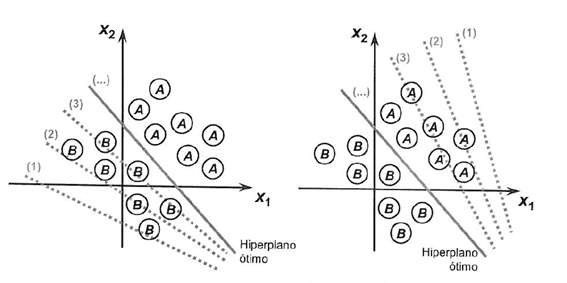
感知机算法的权值估计需要基于训练数据，采用随机梯度下降法（stochastic gradient descent）。

随机梯度

梯度下降是在成本函数的梯度方向上最小化函数的过程。

这意味着要知道成本形式，以及导数，这样我们就可以知道从某个点开始的梯度，并且可以朝这个方向移动，例如向下，朝着最小值移动。

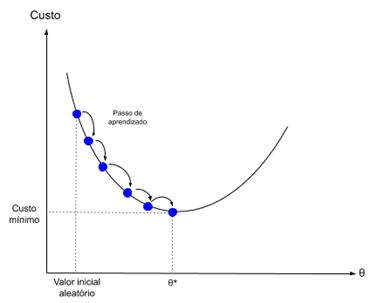
在机器学习中，我们可以使用一种技术来评估和更新每次迭代的权重，称为随机梯度下降。它的目的是最小化训练数据中的模型误差。

该算法的思想是每次向模型显示一个训练实例，该模型为训练实例创建预测，然后计算误差并更新模型，以减少下一次预测中的误差。

这个过程可以用来寻找一组产生最小误差的模型权重。

对于感知机算法，使用以下等式在每次迭代时更新权重w：

• w = w + learning_rate * (expected - predicted) * x

其中，w是一个可优化的值，learning_rate是一个您应该设置的学习率（例如，0.1），（expected - predicted）是一个关于训练模型的预测误差，x是一个输入。

随机梯度下降需要两个参数：

• 学习率（Learning rate）：用于限制每次更新时每个权重的修正量。
• 历元（Epochs）-更新权重时，需要运行多少次训练数据。

这些以及训练数据将成为函数的参数。

我们需要在函数中执行3个循环：

1. 为每个 epoch 循环.

2. 在 epoch 中为训练数据的每一行循环.

3. 循环每个权重，一次更新一行。

权重根据模型产生的误差进行更新。将误差计算为实际值与使用权重进行的预测之间的差值。

每个输入属性都有自己的权重。权重会不断更新，例如：

• w(t+1)= w(t) + learning_rate * (expected(t) - predicted(t)) * x(t)

偏差以类似的方式更新，除了输入，因为偏差没有特定的输入：

• bias(t+1) = bias(t) + learning_rate * (expected(t) - predicted(t)).

应用神经元模型

现在，让我们进入实际应用。

本节分为两部分：

1. 做预测

2. 优化网络权重

这些步骤为感知器算法在其它分类问题中的实现和应用提供了基础。

我们需要定义集合X中的列数。为此，我们需要定义一个常量。

#define nINPUT 3

---

在MQL5中，多维数组可以是静态的，也可以仅适用于第一个维度的动态数组。因此，由于所有其他维度都是静态的，因此必须在数组声明期间指定大小。

 

1. 进行预测

第一步是开发一个可以进行预测的函数。

无论是在随机梯度下降过程中评估候选权重时，还是在模型完成后，这都是必要的。应根据试验数据和新数据进行预测。

下面是 predict 函数，它根据一组特定的权重来预测输出值。

第一个权重总是一个偏差，因为它是自主管理的，所以它不适用于特定的输入值。

// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }

神经元传输：

一旦一个神经元被激活，我们就需要传输激活来查看神经元的实际输出。

//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }

我们将输入集X、权重数组（W）和预测输入集X的行输入到预测函数中。

让我们用一个小数据集来检查预测函数。

我们也可以使用预先准备好的权重来预测这个数据集。

double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};

把它们放在一起之后，我们可以测试预测函数。

#define nINPUT 3
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   random.seed(42);
   double dataset[][nINPUT] = {     //X1     //X2   //Y  
                               {2.7810836,2.550537003,0},
                               {1.465489372,2.362125076,0},
                               {3.396561688,4.400293529,0},
                               {1.38807019,1.850220317,0},
                               {3.06407232,3.005305973,0},
                               {7.627531214,2.759262235,1},
                               {5.332441248,2.088626775,1},
                               {6.922596716,1.77106367,1},
                               {8.675418651,-0.242068655,1},
                               {7.673756466,3.508563011,1}
                              };
   double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};
   for(int row=0; row<ArrayRange(dataset, 0); row++)
     {
      double predict = predict(dataset, weights, row);
      printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict);
     }
  }
//+------------------------------------------------------------------+
// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }
//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }

有两个输入值（X1和X2）和三个权重（bias、w1和w2）。此问题的激活公式如下所示：

activation = (w1 * X1) + (w2 * X2) + b

或者对于特定的权重，手动设置为：

activation = (0.206 * X1) + (-0.234 * X2) + -0.1

在函数执行之后，我们得到与预期输出值y

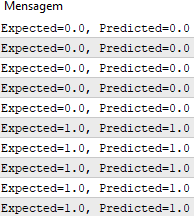
我们现在可以实现随机梯度下降来优化权重值。

2. 优化网络权重

如前所述，可以使用随机梯度下降来评估训练数据的权重。

下面是 train_weights（）函数，它使用随机梯度下降法计算训练数据集的权重。

在MQL5中，无法从该训练数据集数组返回结果，因为与变量不同，数组只能通过引用传递给函数。这意味着函数不会创建自己的数组实例，相反，它直接与传递给它的数组一起工作。因此，在函数中对该数组所做的所有更改都会影响原始数组。

 //+------------------------------------------------------------------+
//|  Estimate Perceptron weights using stochastic gradient descent   |
//+------------------------------------------------------------------+
template <typename Array>
void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5)
  {
   ArrayResize(weights, ArrayRange(X, 1));
   for(int i=0; i<ArrayRange(X, 1); i++)
     {
      weights[i]=random.random();
     }
     
   for(int epoch=0; epoch<n_epoch; epoch++)
     {
      double sum_error = 0.0;
      for(int row=0; row<ArrayRange(X, 0); row++)
        {
         double y = predict(X, weights, row);
         double error = X[row][nINPUT-1] - y;
         sum_error += pow(error, 2);
         weights[0] = weights[0] + l_rate * error;

         for(int i=0; i<ArrayRange(X, 1)-1; i++)
           {
            weights[i+1] = weights[i+1] + l_rate * error * X[row][i];
           }
        }
      printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error);
     }
  }

在每个 epoch 中，我们跟踪误差平方和（正值）以监测误差的减少。因此，我们可以看到算法如何从一个 epoch 到另一个 epoch 朝着误差最小化的方向发展。

我们可以用上述相同的数据集来测试我们的函数。

#define nINPUT 3
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   random.seed(42);
   double dataset[][nINPUT] = {     //X1     //X2   //Y  
                               {2.7810836,2.550537003,0},
                               {1.465489372,2.362125076,0},
                               {3.396561688,4.400293529,0},
                               {1.38807019,1.850220317,0},
                               {3.06407232,3.005305973,0},
                               {7.627531214,2.759262235,1},
                               {5.332441248,2.088626775,1},
                               {6.922596716,1.77106367,1},
                               {8.675418651,-0.242068655,1},
                               {7.673756466,3.508563011,1}
                              };
   double weights[];
   train_weights(weights, dataset);
   ArrayPrint(weights, 20);
   for(int row=0; row<ArrayRange(dataset, 0); row++)
     {
      double predict = predict(dataset, weights, row);
      printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict);
     }
  }
//+------------------------------------------------------------------+
// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }
//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }
//+------------------------------------------------------------------+
//|  Estimate Perceptron weights using stochastic gradient descent   |
//+------------------------------------------------------------------+
template <typename Array>
void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5)
  {
   ArrayResize(weights, ArrayRange(X, 1));
   ArrayInitialize(weights, 0);
     
   for(int epoch=0; epoch<n_epoch; epoch++)
     {
      double sum_error = 0.0;
      for(int row=0; row<ArrayRange(X, 0); row++)
        {
         double y = predict(X, weights, row);
         double error = X[row][nINPUT-1] - y;
         sum_error += pow(error, 2);
         weights[0] = weights[0] + l_rate * error;

         for(int i=0; i<ArrayRange(X, 1)-1; i++)
           {
            weights[i+1] = weights[i+1] + l_rate * error * X[row][i];
           }
        }
      printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error);
     }
  }

学习率为0.1，整个数据集的模型仅为5个epoch。

在执行期间，为每个 epoch 以及最终数据集打印具有平方误差和的消息。

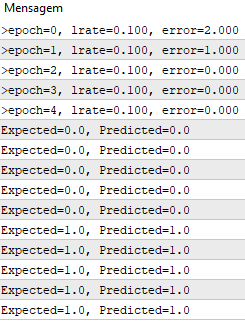
我们看到算法学习问题的速度有多快。

此测试在下面附件的 PerceptronScript.mq5 文件中。

多层感知机

• 将神经元组合成层

   一个神经元能做的事情不多。但是神经元可以组合成一个多层结构，每一层有不同数量的神经元，并形成一个称为多层感知器（Multi-Layer Perceptron, MLP）的神经网络。输入向量 X 通过初始层传入，该层的输出值被输入到下一层，以此类推，直到最后一层输出最终结果。这个网络可以被组织成几个层次，使得它很深，能够学习越来越复杂的关系。

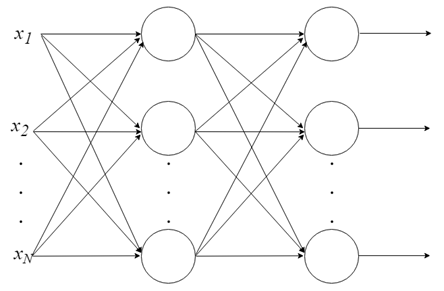
MLP 训练

   在网络开始工作之前，需要对该网络进行训练。就像教孩子读书一样，在机器学习的背景下，监督训练被用来训练MLP，但是它是如何工作的呢？

监督学习:

• 我们有一组带标签的数据，我们已经知道哪个是正确的输出。学习是建立在输入和输出之间有联系的思想基础上的。
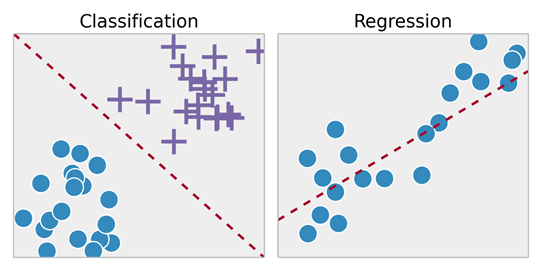
• 监督学习问题又分为“回归”问题和“分类”问题。在回归问题中，我们试图预测连续输出的结果，这意味着我们试图将输入变量映射到某个连续函数。在分类问题中，我们试图以离散输出预测结果。换句话说，我们尝试将输入变量映射到不同的类别中。

示例 1:

• 根据房地产市场的房屋大小数据，尝试预测其价格。价格取决于大小是一个连续的结果，所以这是一个回归问题。
• 这个问题可以转化为一个分类问题——预测“房子的售价是否能超过规定的价格”。这里的房子将按价格分为两类。

反向传播

无疑，反向传播是神经网络发展史上最重要的算法。如果没有有效的反向传播，就不可能像今天这样培养深度学习网络。反向传播可以被认为是现代神经网络和深度学习的基石。

我们不是从错误中吸取教训吗？

反向传播算法的思想如下：根据神经网络输出层的计算误差，重新计算最后一层神经元的W向量权重。然后从后向前移动到上一层。因此，该算法意味着通过反向传播网络接收到的错误，更新从最后一层到网络输入层的所有层的权重W。换句话说，它计算出网络预测值和实际值之间的误差（实际值为1，预测值为0；我们有一个误差！），因此重新计算所有权重的值，从最后一层开始到第一层，始终注意如何减少此误差。

反向传播算法包括两个步骤：

1. 前向传递：输入通过网络并接收输出预测（此步骤也称为传播步骤）。

2. 反向传递：在网络的最后一层（预测层）计算损失函数梯度。然后使用它递归应用链式规则来更新网络中的权重（也称为权重更新或反向传播）

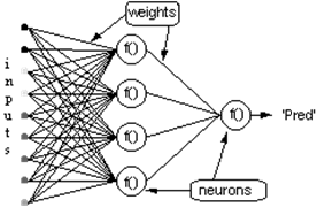
考虑具有一层隐藏神经元和一个输出神经元的网络。当输入向量在网络上传播时，当前权重集有一个输出Pred（y），监督训练的目的是调整权重，以减少Pred（y）和所需输出要求（y）之间的差异。这需要减少绝对误差的算法，类似于减少平方误差，其中：

(1)

网络误差 = Pred - Req

      = E

 

算法应调整权重，以最小化E²。反向传播是一种通过梯度下降最小化E²的算法。为了使E²最小化，有必要计算其对每个重量的灵敏度。换句话说，我们需要知道每种权重的变化对E²的影响。如果我们知道这种影响，我们将能够调整权重，以减少绝对误差。下图显示了反向传播规则的工作原理。

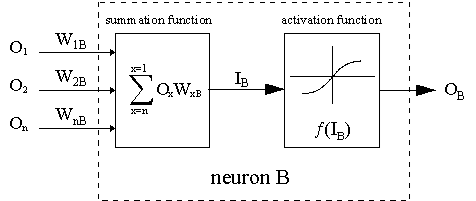
虚线表示神经元B，它可以是隐藏的或输出的神经元。神经元的输出（O1）... O n) 前一层作为神经元B的输入数据。如果神经元B在隐层，它只是一个输入向量。输出乘以适当的权重（W1B）... WnB), 其中WnB是连接神经元n和神经元B的权重。求和函数将所有这些乘积相加，得到输入IB，由神经元B的触发函数f（.）处理。f（IB）是神经元B的输出OB。为了说明这一点，让我们把神经元1称为A，考虑连接两个神经元的权重WAB。更新权重的方法基于 delta 法则：

(2)

where - 是学习率参数，并且

是误差E²对权重WAB的灵敏度；它决定了新WAB权重在权重空间中的搜索方向，如下图所示。

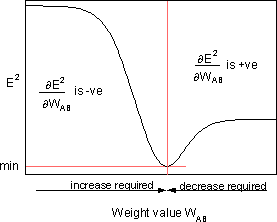
为了最小化E²，delta 法则提供了所需的权重变化方向。

上述方程的关键概念是计算表达式∂E²/∂WAB，，其中包括计算E²误差函数的偏导数，与向量W的每个权重有关。

链式法则:

(3)

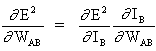
以及

(4)

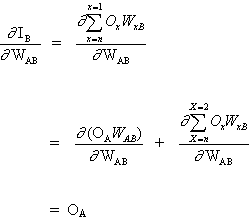
因为其他神经元的输入不依赖于权重WAB。因此，基于公式（3）和（4），公式（2）变为

(5)

而WAB权重变化取决于输入IB处平方误差E²的灵敏度，单位为B和输入信号OА。

可能有两种情况：

1. B 是一个输出神经元;

2. B 是一个隐藏神经元.

考虑第一种情况:

由于B是输出神经元，因此由于WAB的调整而引起的平方误差的变化仅仅是输出信号B的平方误差的变化。

(6)

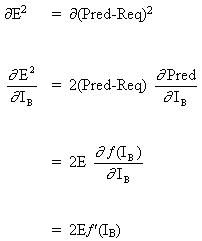
将公式（5）和（6）组合起来，得到

(7)

当神经元B是输出神经元时，如果输出激活函数f（.）是逻辑函数，则改变权重的规则：

(8)

关于参数x的微分方程（8）：

(9)

但是

(10)

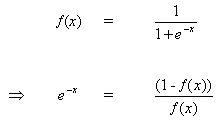
当把（10）插入到（9）时，我们得到：

(11)

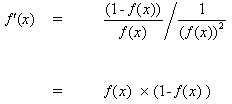
同样对于函数tanh

或线性函数（identity）

这样，我们就得到:

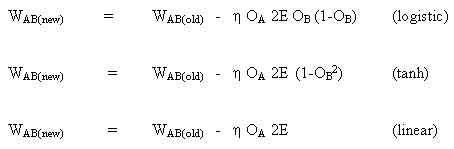
考虑第二种情况

B 是一个隐藏神经元

(12)

其中 O 是输出神经元

(13)

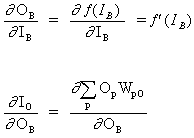
其中p是一个涵盖所有神经元的指数，包括向输出神经元提供输入信号的神经元B。展开 公式（13）的右边部分，

(14)

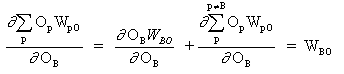
因为其它神经元的权重 WpO (p!= B) 不依赖于 OB.

当把 (13) 插入到 (12):

(15)

因此，现在表示为的函数，如等式（6）中所述进行计算。

更新向神经元B发送信号的神经元A之间的权重WAB的完整规则如下：

(16)

其中

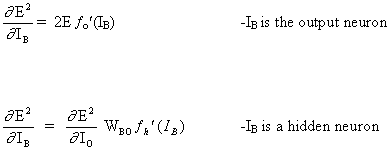
其中fo（.）和fh（.）分别是隐藏的激活和输出函数。

示例

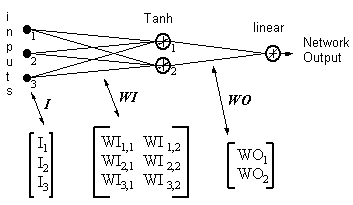
网络输出 = [tanh(I ^T .WI)] . WO

HID = [Tanh(I ^T.WI)] ^T- 隐藏神经元的输出

ERROR = (网络输出 - 所需输出)

LR = 学习率

权重更新变成,

 

线性输出神经元:

(17)

WO = WO - ( LR x ERROR x HID )

隐藏神经元:

(18)

WI = WI - { LR x [ERROR x WO x (1- HID ²)] . I ^T } ^T

 

等式 17 和 18 表明权重更新是输入乘以局部梯度。这提供了方向，其大小也取决于误差的大小。如果我们选择一个没有幅度的方向，所有的变化都是相同的大小，这取决于学习率。由于只有一个输出神经元，上述算法是一个简化的版本。原来的算法可以有多个输出，而梯度的减少使所有输出的总平方误差最小化。为了提高学习速度，还有许多其他的算法是从原来的算法演变而来的。总结如下：

 

“反向传播家庭相册”-技术报告C/TR96-05，澳大利亚新南威尔士州麦格理大学计算系.

 

反向传播是一种优雅而巧妙的算法，现代的深度学习模型，如卷积神经网络，在与图像分类相关的任务中表现出了更优越的性能，或递归神经网络，用于自然语言处理任务，也使用了反向传播算法。最不可思议的是，这样的模型能够找到人类无法观察和理解的模式。它真的很吸引人，它让我们可以期待深度学习算法的进一步发展，这将帮助我们解决人类面临的许多基本问题。

MLP模型的应用

本教程分为5个部分:

1.       网络的初始化.

2.       前馈.

3.       反向传播.

4.       网络的训练.

5.       预测.

 

让我们用纯MQL创建一个实现。我们已经讨论了其他语言的库，这些语言要复杂得多。因此，出于实用和性能原因，强烈建议使用这些库。然而，为了更好地控制整个过程，理解这些库的内部结构是很重要的。在下面的测试中没有使用OOP，因为它只是一个演示前面讨论的方程的算法，所以OOP在这里并不是真正必要的。但是，请注意，在实际案例中，使用OOP要实际得多，因为它提供了项目的可伸缩性。

1. 网络初始化

每个神经元都有一组需要保存的权值，每个输入连接的权值和偏差的附加权值。

建议为小的随机数初始化网络权重。在这个例子中，将使用从0到1的随机数。为此，我们创建了一个生成随机数的函数。

double random(void)
  {
   return ((double)rand())/(double)SHORT_MAX;
  }

下面是为我们的神经网络创建权重的函数 initialize_network（）。

// Forward propagate input to a network output
void forward_propagate(void)
  {
//calculate the outputs of the hidden neurons
//the hidden neurons are tanh
   int i = 0;
   for(i = 0; i<numHidden; i++)
     {
      hiddenVal[i] = 0.0;
      for(int j = 0; j<numInputs; j++)
        {
         hiddenVal[i] += (X[patNum][j] * weightsIH[j][i]);
        }
      hiddenVal[i] = tanh(hiddenVal[i]);
     }
//calculate the output of the network
//the output neuron is linear
   outPred = 0.0;
   for(i = 0; i<numHidden; i++)
     {
      outPred += hiddenVal[i] * weightsHO[i];
     }
//calculate the error
   errThisPat = outPred - y[patNum];
  }

3. 反向传播

根据权值的训练方式来命名反向传播算法

计算期望输出和前馈网络输出之间的误差。然后，这些错误通过网络传播回来，从输出层传播到隐藏层，转移错误的责任，并在输入时更新权重。

上面已经解释了反向传播错误机制背后的数学。

//+------------------------------------------------------------------+
//|        Backpropagate error and change network weights            |
//+------------------------------------------------------------------+
void backward_propagate_error(void)
  {
//adjust the weights hidden-output
   for(int k = 0; k<numHidden; k++)
     {
      double weightChange = LR_HO * errThisPat * hiddenVal[k];
      weightsHO[k] -= weightChange;
      //regularisation on the output weights
      regularisationWeights(weightsHO[k]);
     }
// adjust the weights input-hidden
   for(int i = 0; i<numHidden; i++)
     {
      for(int k = 0; k<numInputs; k++)
        {
         double x = 1 - pow(hiddenVal[i],2);
         x = x * weightsHO[i] * errThisPat * LR_IH;
         x = x * X[patNum][k];
         double weightChange = x;
         weightsIH[k][i] -= weightChange;
        }
     }
  }

regularizationWeights 方法仅用于正则化介于-5和5之间的权重。

//regularisation on the output weights
void regularisationWeights(double &weight)
  {
   weight<-5?weight=-5:weight>5?weight=5:weight=weight;
  }

4. 网络的训练

网络采用随机梯度下降法训练，

这包括几次迭代，在迭代过程中，数据被送入网络，每个数据行的输入被前馈，偏差被传回，权值被更新。

//# Train a network for a fixed number of epochs
void train(void)
  {
   for(int j = 0; j <= numEpochs; j++)
     {
      for(int i = 0; i<numPatterns; i++)
        {
         //select a pattern at random
         patNum = rand()%numPatterns;
         //calculate the current network output
         //and error for this pattern
         forward_propagate();
         backward_propagate_error();
        }
      //display the overall network error
      //after each epoch
      calcOverallError();
      printf("epoch = %d RMS Error = %f",j,RMSerror);
     }
  }

5. 预测

使用经过训练的神经网络进行预测非常简单。

我们已经看到了如何传播输入模式以接收输出，为了做出预测，我们只需要做这些。我们可以直接使用输出值，作为模式属于每个输出类的概率。

// # Make a prediction with a network
void predict(void)
  {
   for(int i = 0; i<numPatterns; i++)
     {
      patNum = i;
      forward_propagate();
      printf("real = %d predict = %f",y[patNum],outPred);
     }
  }

下面的附件中提供了一个完整的示例 MLP_Script.mq5。

结论

我们探讨了在感知器神经元发展过程中进行的计算，以及一个称为“多层感知机（MLP）”,我们还看到了如何使用反向传播和梯度下降算法来训练这种类型的神经网络。