
Многослойный перцептрон и алгоритм обратного распространения ошибки
Введение
- В последнее время, с ростом популярности этих двух методов появилось много библиотек на Matlab, R, Python, C ++ и т.д., которые получают на вход обучающий набор и автоматически создают соответствующую нейронную сеть для вашей задачи.
- Однако при использовании готовых библиотек бывает сложно понять, что именно происходит и как мы получаем оптимизированную сеть. А ведь знание основ решения важно для дальнейшего развития этих методов. Итак, в данной статье мы создадим очень простую структуру для алгоритма нейронной сети.
- Мы постараемся понять, как работает базовый тип нейронной сети — перцептрон с одним нейроном и многослойный перцептрон — замечательный алгоритм, который отвечает за обучение сети (градиентный спуск и обратное распространение). Эти сетевые модели будут основой для более сложных моделей, существующих на сегодняшний день.
Краткий обзор истории
- Первая нейронная сеть была задумана Уорренном Маккалоком и Уолтером Питтсом в 1943 году. Они написали великолепную статью о том, как должны работать нейроны, а затем построили модель на основе своих идей — создали простую нейронную сеть с электрическими цепями.
- Исследования в области искусственного интеллекта быстро развивались, и в 1980 году Кунихико Фукусима разработал первую настоящую многослойную нейронную сеть.
- Первоначальной целью нейронной сети было создание компьютерной системы, способной решать проблемы подобно тому, как это делает человеческий мозг. Однако, со временем исследователи сменили фокус и начали использовать нейронные сети для решения особенных задач. С тех пор нейронные сети выполняют самые разнообразные задачи, включая компьютерное зрение, распознавание голоса, машинный перевод, фильтрацию социальных сетей, настольные игры или видеоигры, медицинскую диагностику, прогноз погоды, прогнозирование временных рядов, распознавание (изображения, текста, голоса) и др.
Компьютерная модель нейрона: перцептрон
Перцептрон
Перцептрон вдохновлен идеей обработки информации единственной нервной клетки, называемой нейроном. Нейрон принимает на вход сигналы через свои дендриты, которые передают электрический сигнал телу клетки. Точно так же перцептрон получает входные сигналы из примеров обучающих данных, которые предварительно взвесили и объединили в линейное уравнение, называемое активацией.
- z = sum(weight_i * x_i) + bias
Где weight — это вес сети, X — это входное значение, i — индекс веса или входные данные, а смещение — это специальный вес, который не имеет множитель в виде входного значения (можем считать, что входные данные всегда равны 1.0).
Затем активация преобразуется в выходное (прогнозируемое) значение с помощью передаточной функции (функция активации).
- y = 1.0 если z >= 0.0, иначе 0.0
Таким образом, перцептрон представляет собой алгоритм классификации проблем с двумя классами (двоичный классификатор), где для разделения двух классов может использоваться линейное уравнение.
Это тесно связано с линейной регрессией и логистической регрессией, которые осуществляют прогнозы аналогичным образом (например, взвешенная сумма входов).
Алгоритм перцептрона — простейший вид искусственной нейронной сети. Это модель одного нейрона, которая может использоваться в задачах классификации двух классов и обеспечивает основу для дальнейшего развития гораздо более крупных сетей.
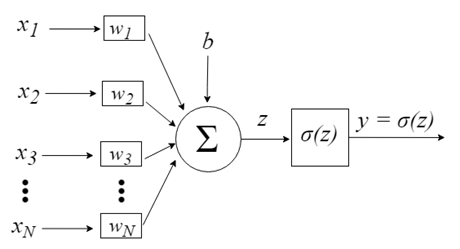
Входы нейронов представлены вектором x = [x1, x2, x3,…, xN], который может соответствовать, к примеру, ряду торговых цен актива, значениям технических индикаторов, числовой последовательности в пикселях изображения. Когда они попадают к нейрону, они умножаются на соответствующие синаптические веса, которые являются элементами вектора w = [w1, w2, w3, ..., wN], и таким образом генерируют значение z, обычно называемое потенциалом активации, согласно выражению:
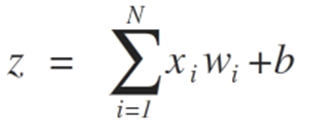
b обеспечивает более высокую степень свободы и не зависит от входа в это выражение, что обычно соответствует нейрону смещения (склонности). Затем z-значение проходит через функцию активации σ, которая отвечает за ограничение этого значения определенным интервалом (например, 0 - 1), что дает окончательное выходное значение и значение нейрона. Некоторые используемые триггерные функции: шаг, сигмоид, гиперболический тангенс, softmax и ReLU («rectified linear unit»).
Чтобы проиллюстрировать процесс, направленный на достижение предела разделимости классов, ниже мы показываем две ситуации, которые демонстрируют их сближение к стабилизации с учетом только двух входов {x1 и x2}
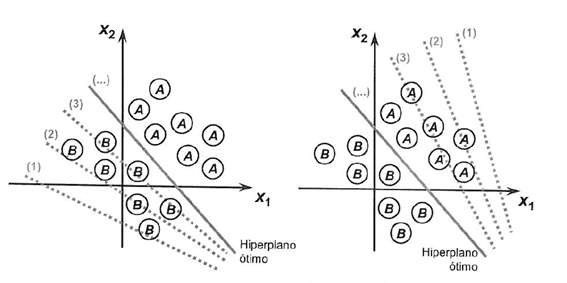
Веса алгоритма перцептрона следует оценивать на основе данных обучения с использованием стохастического градиентного спуска.
Стохастический градиент
Градиентный спуск — это процесс минимизации функции в направлении градиента функции стоимости.
Это подразумевает знание формулы стоимости, а также производной, чтобы с определенной точки мы могли узнать наклон и могли двигаться в этом направлении, например, вниз по направлению к минимальному значению.
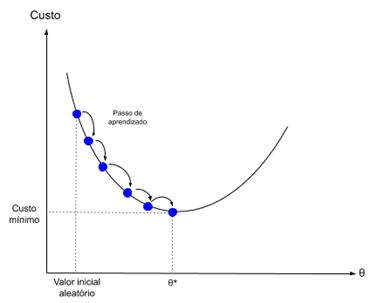
В машинном обучении мы можем использовать метод, который оценивает и обновляет веса для каждой итерации, называемый стохастическим градиентным спуском, чтобы минимизировать ошибку модели в наших обучающих данных.
Принцип работы этого алгоритма оптимизации заключается в том, что каждый обучающий экземпляр показывается модели по одному. Модель делает прогноз для обучающего экземпляра, вычисляет ошибку и обновляет модель, чтобы уменьшить ошибку для следующего прогноза.
Эту процедуру можно использовать для поиска набора весов в модели, который дает наименьшую ошибку для модели в обучающих данных.
Для алгоритма перцептрона на каждой итерации веса w обновляются с использованием уравнения:
- w = w + learning_rate * (expected - predicted) * x
Где w оптимизируется, learning_rate - это скорость обучения, которую мы должны установить (например, 0.1), (expected - predicted) - ошибка прогнозирования для модели в обучающих данных, относящихся к весу, а x - входное значение.
Для стохастического градиентного спуска требуются два параметра:
- Коэффициент обучения: используется для ограничения размера корректировки веса при каждом его обновлении.
- Эпохи - сколько раз обучающие данные должны выполняться при обновлении веса.
Они вместе с обучающими данными будут аргументами для функции.
Нам нужно выполнить 3 цикла в функции:
1. Цикл для каждой эпохи.
2. Цикл для каждой строки в обучающих данных для эпохи.
3. Цикл для каждого веса, который обновляется для одной строке в одной эпохи.
Веса обновляются в зависимости от ошибки, допущенной моделью. Ошибка рассчитывается как разница между фактическим значением и прогнозом, сделанным с помощью весов.
Для каждого входного атрибута есть свой вес, и они постоянно обновляются, например:
- w(t+1)= w(t) + learning_rate * (expected(t) - predicted(t)) * x(t)
Смещение обновляется аналогичным образом, только без входа, поскольку оно не связано с конкретным входным значением:
- bias(t+1) = bias(t) + learning_rate * (expected(t) - predicted(t)).
Теперь перейдем к практическому применению.
Этот урок разделен на 2 части:
1. Делаем прогнозы
2. Оптимизация веса сети
Эти шаги обеспечат основу для реализации и применения алгоритма перцептрона к другим задачам классификации.
Нам нужно определить количество столбцов в нашем наборе X, для этого мы определяем константу
#define nINPUT 3
В MQL5 многомерный массив может быть статическим или динамическим только для первого измерения, а поскольку все остальные измерения будут статическими, при объявлении массива необходимо указать размер.
1. Делаем прогнозы
Первый шаг - разработать функцию, которая может делать прогнозы.
Это будет необходимо как при оценке значений весов кандидатов при стохастическом градиентном спуске, так и после завершения модели. Прогнозы надо делать и на тестовых данных, и на новых.
Ниже приведена функция predict, которая прогнозирует выходное значение для строки исходя от определенного набора весов.
Первый вес всегда является смещением, поскольку он автономен и не работает с конкретным входным значением.
// Make a prediction with weights template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); }
Перенос нейронов:
Как только нейрон активирован, нам нужно передать активацию, чтобы увидеть, каковы на самом деле выходные данные нейрона.
//+------------------------------------------------------------------+ //| Transfer neuron activation | //+------------------------------------------------------------------+ double activation(const double activation) //# { return activation>=0.0?1.0:0.0; }
Мы получаем в качестве аргумента в функции прогнозирования входной набор X, массив с весами (W) и строку, для которой прогнозируется входной набор X.
Мы можем придумать небольшой набор данных, чтобы проверить нашу функцию прогнозирования.
Мы также можем использовать заранее подготовленные веса, чтобы делать прогнозы для этого набора данных.
double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};
После того, как мы собрали все это вместе, мы можем протестировать нашу функцию прогнозирования ниже.
#define nINPUT 3 //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- random.seed(42); double dataset[][nINPUT] = { //X1 //X2 //Y {2.7810836,2.550537003,0}, {1.465489372,2.362125076,0}, {3.396561688,4.400293529,0}, {1.38807019,1.850220317,0}, {3.06407232,3.005305973,0}, {7.627531214,2.759262235,1}, {5.332441248,2.088626775,1}, {6.922596716,1.77106367,1}, {8.675418651,-0.242068655,1}, {7.673756466,3.508563011,1} }; double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003}; for(int row=0; row<ArrayRange(dataset, 0); row++) { double predict = predict(dataset, weights, row); printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict); } } //+------------------------------------------------------------------+ // Make a prediction with weights template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); } //+------------------------------------------------------------------+ //| Transfer neuron activation | //+------------------------------------------------------------------+ double activation(const double activation) //# { return activation>=0.0?1.0:0.0; }
Есть два входных значения (X1 и X2) и три коэффициента веса (bias, w1 и w2). Уравнение активации, которое мы моделируем для данной проблемы, выглядит так:
activation = (w1 * X1) + (w2 * X2) + b
Или с конкретными значениями веса, мы вручную выбираем как:
activation = (0.206 * X1) + (-0.234 * X2) + -0.1
После завершения работы функции мы получаем прогнозы, которые соответствуют ожидаемым выходным значениям y.
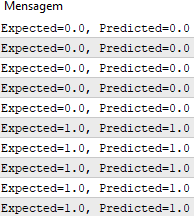
Теперь можем реализовать стохастический градиентный спуск для оптимизации значений веса.
2. Оптимизируем веса сети
Веса для наших обучающих данных можно оценить, используя стохастический градиентный спуск, как было сказано ранее.
Ниже приведена функция train_weights(), которая вычисляет значения веса для набора обучающих данных с использованием стохастического градиентного спуска.
В MQL5 мы не можем получить возврат из этого массива с данными обученных весов, потому что, в отличие от переменных, массивы могут быть переданы в функцию только по ссылке. Это означает, что функция не создает собственный экземпляр массива, а вместо этого работает напрямую с переданным ей массивом. Таким образом, все изменения, осуществляемые в этом массиве внутри функции влияют на исходный массив.
//+------------------------------------------------------------------+ //| Estimate Perceptron weights using stochastic gradient descent | //+------------------------------------------------------------------+ template <typename Array> void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5) { ArrayResize(weights, ArrayRange(X, 1)); for(int i=0; i<ArrayRange(X, 1); i++) { weights[i]=random.random(); } for(int epoch=0; epoch<n_epoch; epoch++) { double sum_error = 0.0; for(int row=0; row<ArrayRange(X, 0); row++) { double y = predict(X, weights, row); double error = X[row][nINPUT-1] - y; sum_error += pow(error, 2); weights[0] = weights[0] + l_rate * error; for(int i=0; i<ArrayRange(X, 1)-1; i++) { weights[i+1] = weights[i+1] + l_rate * error * X[row][i]; } } printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error); } }
На каждой эпохе мы отслеживаем сумму квадратичной ошибки (положительное значение), чтобы отслеживать уменьшение ошибки. Это позволяет наблюдать как алгоритм минимизирует ошибку на каждой эпохе.
Давайте протестируем нашу функцию с одним и тем же набором данных, представленным выше.
#define nINPUT 3 //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- random.seed(42); double dataset[][nINPUT] = { //X1 //X2 //Y {2.7810836,2.550537003,0}, {1.465489372,2.362125076,0}, {3.396561688,4.400293529,0}, {1.38807019,1.850220317,0}, {3.06407232,3.005305973,0}, {7.627531214,2.759262235,1}, {5.332441248,2.088626775,1}, {6.922596716,1.77106367,1}, {8.675418651,-0.242068655,1}, {7.673756466,3.508563011,1} }; double weights[]; train_weights(weights, dataset); ArrayPrint(weights, 20); for(int row=0; row<ArrayRange(dataset, 0); row++) { double predict = predict(dataset, weights, row); printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict); } } //+------------------------------------------------------------------+ // Make a prediction with weights template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); } //+------------------------------------------------------------------+ //| Transfer neuron activation | //+------------------------------------------------------------------+ double activation(const double activation) //# { return activation>=0.0?1.0:0.0; } //+------------------------------------------------------------------+ //| Estimate Perceptron weights using stochastic gradient descent | //+------------------------------------------------------------------+ template <typename Array> void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5) { ArrayResize(weights, ArrayRange(X, 1)); ArrayInitialize(weights, 0); for(int epoch=0; epoch<n_epoch; epoch++) { double sum_error = 0.0; for(int row=0; row<ArrayRange(X, 0); row++) { double y = predict(X, weights, row); double error = X[row][nINPUT-1] - y; sum_error += pow(error, 2); weights[0] = weights[0] + l_rate * error; for(int i=0; i<ArrayRange(X, 1)-1; i++) { weights[i+1] = weights[i+1] + l_rate * error * X[row][i]; } } printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error); } }
Мы используем скорость обучения 0,1 и обучаем модель только для 5 эпох или 5 показов весов для всего набора обучающих данных.
При выполнении примера для каждой эпохи печатается сообщение с суммой квадратичной ошибки для этой эпохи и окончательным набором весов.
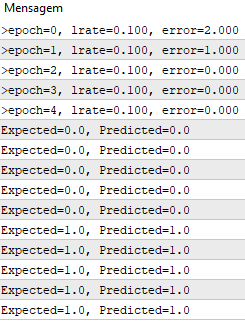
Мы видим, как быстро алгоритм выучивает проблему.
Этот тест можно найти в файле PerceptronScript.mq5.
Многослойный перцептрон
- Объединеняем нейроны в слои
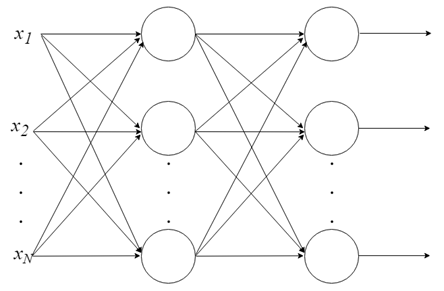
С одним нейроном мало что можно сделать, но мы можем объединить их в многоуровневую структуру, каждый с разным количеством нейронов, и сформировать нейронную сеть, называемую многослойным перцептроном («multi layer perceptron, MLP»). Вектор входных значений X проходит через начальный слой, выходные значения которого связаны со входами следующего уровня, и так далее, пока сеть не предоставит выходные значения последнего слоя в качестве результата. Сеть может быть организована в несколько слоев, что делает ее глубокой и способной выучить все более сложные отношения.
Обучение MLP
Для того, чтобы такая сеть работала, ее нужно обучать. Это как учить ребенка читать. Обучение MLP происходит в контексте машинного обучения с учителем, но как это работает?
Обучение с учителем:
- Нам дается набор отмеченных данных, для которых мы уже знаем какой именно является нашим правильным выходом, и он должен быть аналогичен набору, имея представление о том, что существует связь между входом и выходом.
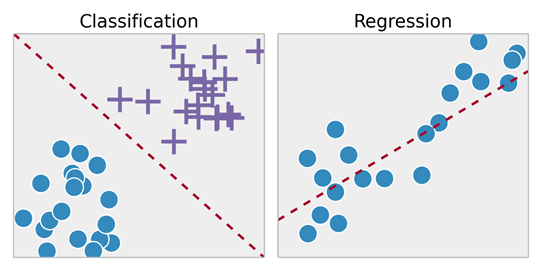
- Задачи обучения с учителем подразделяются на задачи «регрессии» и «классификации». В задачах регрессии мы пытаемся предсказать результаты на непрерывном выходе, что означает, что мы пытаемся сопоставить входные переменные с некоторой непрерывной функцией. В задачах классификации мы стараемся предсказать результаты на дискретном выходе. Другими словами, мы пытаемся сопоставить входные переменные по разным категориям.
Пример 1:
- Учитывая набор данных о размерах домов на рынке недвижимости, попробуйте спрогнозировать их цену. Цена в зависимости от размера - это непрерывный результат, так что это проблема регрессии.
- Мы могли бы также превратить этот пример в задачу классификации, чтобы прогнозировать о том, «продастся ли дом дороже или дешевле, чем запрашиваемая цена». Здесь мы рассортируем дома по цене на две разные категории.
Обратное распространение
Обратное распространение, без сомнений, является самым важным алгоритмом в истории нейронных сетей - без (эффективного) обратного распространения, было бы невозможно обучить сети глубокого обучения так, как мы это делаем сегодня. Обратное распространение можно считать краеугольным камнем современных нейронных сетей и глубокого обучения.
Разве мы не учимся на ошибках?
Идея алгоритма обратного распространения ошибки состоит в том, чтобы на основе расчетной ошибки, полученной на выходном слое нейронной сети, пересчитать значение весов вектора W последнего слоя нейронов. Затем мы переходим к предыдущему слою и так далее, от конца к началу, то есть, он состоит из обновления всех весов W слоев, от последнего до достижения входного слоя сети путем обратного распространения ошибки, полученной сетью. Другими словами, ошибка вычисляется между тем, что предсказала сеть, и тем, что она была на самом деле (фактический 1, предсказанный 0; у нас есть ошибка!), поэтому мы пересчитываем значения всех весов, начиная с последнего слоя и переходя к первому, всегда обращая внимание на уменьшение этой ошибки.
Алгоритм обратного распространения ошибки состоит из двух этапов:
1. Прямой проход («forward pass»), при котором наши входы проходят через сеть и получают прогнозы выхода (этот шаг также известен как фаза распространения).
2. Обратный проход («backward pass»), при котором мы вычисляем градиент функции потерь на последнем слое (то есть слое прогнозирования) сети и используем этот градиент для рекурсивного применения цепного правила («chain rule») для обновления весов в нашей сети (также известного как стадия обновления веса или обратное распространение)
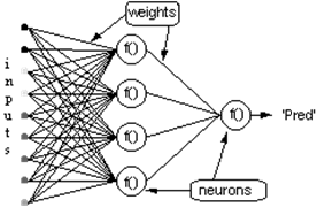
Рассмотрим сеть выше со слоем скрытых нейронов и выходным нейроном. Когда входной вектор распространяется по сети, для текущего набора весов существует выходной Pred(y). Цель обучения с учителем - настроить веса так, чтобы уменьшить разницу между Pred(y) сети и требуемым выходным Req(y). Для этого требуется алгоритм, который уменьшает абсолютную ошибку, что аналогично уменьшению квадратичной ошибки, где:
(1)
Сетевая ошибка = Pred - Req
= E
Алгоритм должен регулировать веса, чтобы минимизировать E². Обратное распространение - это алгоритм, который выполняет минимизацию градиентного спуска E². Чтобы минимизировать E², необходимо рассчитать его чувствительность к каждому весу. Другими словами, нам нужно знать, какое влияние будет иметь изменение каждого веса на E². Если нам будет известно, веса можно будет отрегулировать в направлении, уменьшающем абсолютную ошибку. Последующее описание правила обратного распространения основано на такой диаграмме:
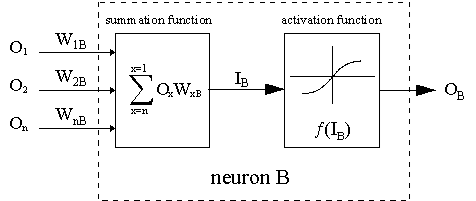
Пунктирная линия представляет нейрон B, который может быть скрытым или выходным нейроном. Выходы n нейронов (O 1 ... O n) на предыдущем слое являются взодами для нейрона B. Если нейрон B находится в скрытом слое, он просто является входным вектором. Эти выходы умножаются на соответствующие веса (W1B ... WnB), где WnB - вес, соединяющий нейрон n и нейрону B. Функция суммы складывает все эти произведения для получения входных данных, IB, который обрабатывается функцией триггера f(.) нейрона B. f (IB) это выход OB нейрона B. Рассмотрим пример. Назовем нейрон 1 нейроном A и рассмотрим вес WAB между двумя нейронами. Подход, используемый для изменения веса, определяется правилом дельты:
(2)
![]()
где ![]() - параметр скорости обучения, который определяет скорость обучения, а
- параметр скорости обучения, который определяет скорость обучения, а
![]()
является чувствительностью ошибки E² к весу WAB и определяет направление поиска в пространстве весов для нового веса WAB (новый), как изображено на рисунке ниже.
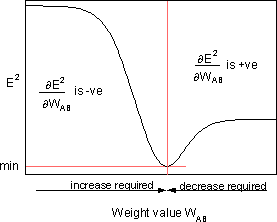
Чтобы минимизировать E², правило дельты обеспечивает необходимое направление изменения веса.
Ключевой концепцией приведенного выше уравнения является вычисление выражения ∂E² /∂WAB, которое состоит в вычислении частных производных функции ошибок E² по отношению к каждому весу вектора W.
Дифференцирование сложной функции:
(3)
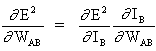
и
(4)
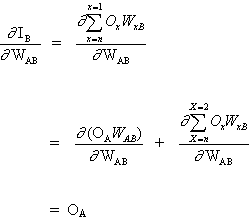
поскольку остальные входы нейрона B не зависят от веса WAB. Таким образом, исходя из уравнений (3) и (4), уравнение (2) становится
(5)
![]()
и изменение веса WAB зависит от чувствительности квадрата ошибки E² на входе IB, единицы B и входного сигнала OА.
Возможны две ситуации:
1. B - выходной нейрон;
2. B - скрытый нейрон.
Рассмотриваем первый случай:
Поскольку B является выходным нейроном, изменение квадрата ошибки из-за настроки WAB просто является изменением квадрата ошибки выходного сигнала B.
(6)
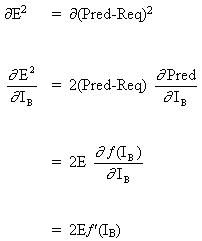
объединяя уравнение (5) и уравнение (6), получаем
(7)
![]()
Правило изменения весов, когда нейрон B является выходным нейроном, если выходная функция активации, f (.), является логистической функцией:
(8)
![]()
Дифференцируем уравнение (8) по аргументу x:
(9)
![]()
Но,
(10)
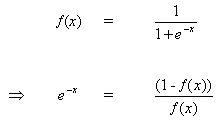
при вставке (10) в (9) получаем:
(11)
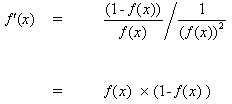
таким же образом для функции tanh
![]()
или для линейной функции (identity)
![]()
Так мы получаем:
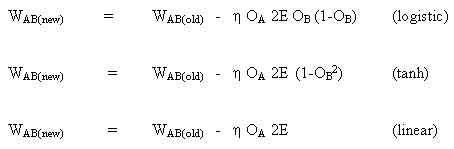
Рассматривая второй случай:
B это скрытый нейрон
(12)
![]()
где O представляет выходной нейрон
(13)
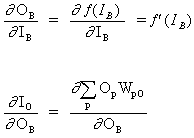
где p это индекс, который охватывает все нейроны, включая нейрон B, который обеспечивает входные сигналы для выходного нейрона. Расширяем правую часть уравнения (13),
(14)
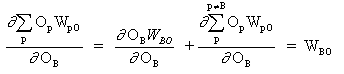
поскольку веса других нейронов WpO (p! = B) не имеют зависимости от OB.
При вставке (13) и (13) в (12):
(15)
![]()
Следовательно, ![]() теперь это выражается как функция от
теперь это выражается как функция от ![]() , вычисляемая, как описано в уравнении (6).
, вычисляемая, как описано в уравнении (6).
Полное правило изменения веса WAB между нейроном A, который посылает сигнал нейрону B, является таким:
(16)
![]()
где
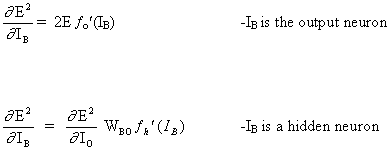
где fo (.) и fh (.) это скрытые функции активации и выхода соответственно.
Пример
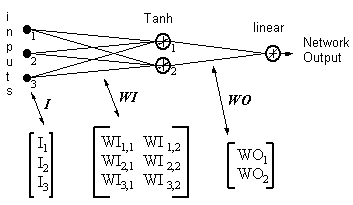
Выход из сети = [tanh(I T .WI)] . WO
HID = [Tanh(I T.WI)] T- выходы скрытых нейронов
ERROR = (выход из сети - нужный выход)
LR = коеффициент обучения
Обновления веса становятся
нейроном с линейным выходом
(17)
WO = WO - ( LR x ERROR x HID )
скрытым нейроном
(18)
WI = WI - { LR x [ERROR x WO x (1- HID 2)] . I T } T
Уравнения 17 и 18 показывают, что изменение веса - это входной сигнал, умноженный на локальный градиент. Это обеспечивает направление, величина которого также зависит от величины ошибки. Если берем направление без величины, все изменения будут одинакового размера, и это будет зависеть от темпа обучения. Вышеуказанный алгоритм является упрощенной версией, так как имеется только один выходной нейрон. В исходном алгоритме допускается более одного выхода, а уменьшение градиента минимизирует общую квадратную ошибку всех выходов. Есть много алгоритмов, которые произошли от исходного алгоритма для увеличения скорости обучения. Они кратко изложены в:
« Back Propagation family album" - Technical report C/TR96-05, Department of Computing, Macquarie University, NSW, Australia».
Обратное распространение - это элегантный и умелый алгоритм. Современные модели глубокого обучения, такие как сверточные нейронные сети, хотя и более совершенные, чем MLP, показали себя намного лучше в таких задачах, как классификация изображений и используют обратное распространение в качестве метода обучения, а также так называемые рекуррентные нейронные сети в условиях естественной языковой обработки, которые также используют этот алгоритм. Самое невероятное, что таким моделям удается находить ненаблюдаемые и непонятные закономерности для нас, людей, что удивляет и позволяет нам считать, что скоро мы получим помощь глубокого обучения для решения многих основных проблем, с которыми сталкивается человечество.
Применение модели MLP
Этот урок разделен на 5 частей:
1. Инициализация сети.
2. Прямое распространение (FeedForward).
3. Обратное распространение.
4. Обучение сети.
5. Прогноз.
Для нашей разработки мы реализуем применение на чистом MQL. Нам уже известно, что существуют библиотеки на других языках, которые уже являются гораздо более сложными, и настоятельно рекомендуется использовать их из практических соображений и соображений производительности, но, как уже было сказано в начале, важно понимать внутреннее устройство таких библиотек, чтобы иметь больший контроль над всем процессом. Мы также не использовали ООП в нашем тесте, поскольку это всего лишь алгоритм для иллюстрации предыдущих уравнений, в нем нет необходимости. Однако в реальных случаях гораздо практичнее использовать ООП, поскольку оно обеспечивает масштабируемость проекта.
1. Инициализация сети
У каждого нейрона есть набор весов, которые необходимо поддерживать. Вес для каждого входного соединения и дополнительный вес для смещения.
Рекомендуем инициализировать веса сети для небольших случайных чисел. В этом случае мы будем использовать случайные числа в диапазоне от 0 до 1. Для этого мы создали функцию для генерации случайных чисел.
double random(void) { return ((double)rand())/(double)SHORT_MAX; }
Ниже представлена функция под названием initialize_network(), которая создает веса нашей нейронной сети.
// Forward propagate input to a network output void forward_propagate(void) { //calculate the outputs of the hidden neurons //the hidden neurons are tanh int i = 0; for(i = 0; i<numHidden; i++) { hiddenVal[i] = 0.0; for(int j = 0; j<numInputs; j++) { hiddenVal[i] += (X[patNum][j] * weightsIH[j][i]); } hiddenVal[i] = tanh(hiddenVal[i]); } //calculate the output of the network //the output neuron is linear outPred = 0.0; for(i = 0; i<numHidden; i++) { outPred += hiddenVal[i] * weightsHO[i]; } //calculate the error errThisPat = outPred - y[patNum]; }
3. Обратное распространение
Алгоритм обратного распространения назван в честь способа обучения весов
Ошибка вычисляется между ожидаемыми выходами и выходными сигналами сети прямого распространения. Затем эти ошибки передаются обратно по сети от выходного слоя к скрытому слою, перекладывая ответственность за ошибку и обновляя веса по мере их поступления.
Математика ошибки обратного распространения была объяснена выше.
//+------------------------------------------------------------------+ //| Backpropagate error and change network weights | //+------------------------------------------------------------------+ void backward_propagate_error(void) { //adjust the weights hidden-output for(int k = 0; k<numHidden; k++) { double weightChange = LR_HO * errThisPat * hiddenVal[k]; weightsHO[k] -= weightChange; //regularisation on the output weights regularisationWeights(weightsHO[k]); } // adjust the weights input-hidden for(int i = 0; i<numHidden; i++) { for(int k = 0; k<numInputs; k++) { double x = 1 - pow(hiddenVal[i],2); x = x * weightsHO[i] * errThisPat * LR_IH; x = x * X[patNum][k]; double weightChange = x; weightsIH[k][i] -= weightChange; } } }
метод regularizationWeights был создан только для регуляризации весов в диапазоне от -5 до 5.
//regularisation on the output weights void regularisationWeights(double &weight) { weight<-5?weight=-5:weight>5?weight=5:weight=weight; }
4. Обучение сети
Сеть обучается методом стохастического градиентного спуска.
Это включает в себя несколько итераций, раскрывающих набор обучающих данных в сети, и для каждой строки данных прямое распространение входных данных, обратное распространение ошибки и обновление весов сети.
//# Train a network for a fixed number of epochs void train(void) { for(int j = 0; j <= numEpochs; j++) { for(int i = 0; i<numPatterns; i++) { //select a pattern at random patNum = rand()%numPatterns; //calculate the current network output //and error for this pattern forward_propagate(); backward_propagate_error(); } //display the overall network error //after each epoch calcOverallError(); printf("epoch = %d RMS Error = %f",j,RMSerror); } }
5. Прогноз
Делать прогнозы с помощью обученной нейронной сети довольно просто.
Мы уже видели, как распространить паттерн входа для получения выходных данных. Это все, что нам нужно сделать, чтобы осуществить прогноз. Мы можем использовать выходные значения напрямую как вероятность принадлежности паттерна к каждому выходному классу.
// # Make a prediction with a network void predict(void) { for(int i = 0; i<numPatterns; i++) { patNum = i; forward_propagate(); printf("real = %d predict = %f",y[patNum],outPred); } }
Полный пример можно найти в файле MLP_Script.mq5.
Заключение
Мы занимались вычислениями, задействованными в процессе развития нейрона перцептрона, а также сети нейронов перцептрона, называемой «multi layer perceptron, MLP». В данном процессе мы поняли, как осуществляется обучение этого типа сетей с использованием обратного распространения ошибки и градиентного спуска.
Перевод с португальского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/pt/articles/8908
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети — это просто (Часть 12): Dropout
Нейросети — это просто (Часть 12): Dropout
 Брутфорс-подход к поиску закономерностей (Часть IV): Минимальная функциональность
Брутфорс-подход к поиску закономерностей (Часть IV): Минимальная функциональность
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Опубликована новая статья Многослойная перцептронная машина с алгоритмом обратного распространения:
Джонатан Перейра
Привет, Джонатан,
Я с удовольствием прочитал вашу статью. Она очень помогла мне продвинуться в реализации нейронной сети на MQL5.
Прежде всего... Большое спасибо! Отличная статья.
Мне кажется, нам не хватает файла: Util.mqh.
В нем, вероятно, есть функция Random.
Не могли бы вы приложить его? Или описать случайную функцию в нем.
Еще раз спасибо. Я очень внимательно изучаю вашу статью.
"Ниже представлена функция под названием initialize_network(), которая создает веса нашей нейронной сети."
И тут же ниже...