MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
多層パーセプトロンとバックプロパゲーションアルゴリズム

多層パーセプトロンとバックプロパゲーションアルゴリズム

MetaTrader 5 — 例 | 20 5月 2021, 10:00
1 049 0
Jonathan Pereira
Jonathan Pereira

はじめに

  • これら2つの手法の人気が高まり、Matlab、R、Python、C ++などで多くのライブラリが開発されています。これらのライブラリは、入力として訓練セットを受け取り、問題に適切なネットワークを自動的に作成します。
  • ただし、既製のライブラリを使用する場合、何が起こっていてどのように最適化されたネットワークが取得されるのかを正確に理解するのは難しい場合があります。これらのメソッドをさらに開発するには、ソリューションの基本を理解することが不可欠です。本稿では、非常に単純なニューラルネットワークアーキテクチャの構造を作成します。
  • 基本的なニューラルネットワークタイプ(単一ニューロンパーセプトロンと多層パーセプトロンを含む)がどのように機能するかを理解してみましょう。ネットワーク訓練のためのエキサイティングな最急降下法およびバックプロパゲーションアルゴリズムを検討します。既存の複雑なモデルは、多くの場合、このような単純なネットワークモデルに基づいています。


歴史の簡単な概要

  • 最初のニューラルネットワークは、1943年にウォーレン・マカロックとウォルター・ピッツによって提案されました。彼らはニューロンがどのように機能するかについての素晴らしい記事を書き、自分たちのアイデアに基づいてモデルを構築しました。電気回路で単純なニューラルネットワークを作成したのです。
  • ニューラルネットワークの本来の目的は、人間の脳と同様の方法で問題を解決できるコンピューターシステムを作成することでしたが、時間が経つにつれて、研究者はその焦点を変えて、ニューラルネットワークを使用してさまざまな特定のタスクを解決し始めました。現在、ニューラルネットワークは、コンピュータービジョン、音声認識、機械翻訳、ソーシャルメディアフィルタリング、ボードゲームとビデオゲーム、医療診断、天気予報、時系列予測、画像/テキスト/音声認識などのさまざまなタスクを実行しています。


ニューロンのコンピューターモデル: パーセプトロン


パーセプトロン

パーセプトロンは、ニューロンと呼ばれる単一の神経細胞からの情報を処理するというアイデアに触発されました。ニューロンは、細胞体に電気信号を送信する樹状突起を介して入力として信号を受信します。同様に、パーセプトロンは、事前に重み付けされて活性化関数と呼ばれる線形方程式に結合された訓練データセットから入力信号を受信します。

  • z = sum(weight_i * x_i) + bias

ここで、「weight(重み)」はネットワークの重み、「X」は入力、「i」は重みまたは入力のインデックス、bias(バイアス)は乗数入力のない特別な重みです(したがって、入力は常に1.0であると想定できます)。

次に、伝達関数(活性化関数)を使用して、活性化が出力値(予測値)に変換されます。

  • y = 1.0(z >= 0.0)、y = 0.0(z < 0.0)

したがって、パーセプトロンは2クラスの問題分類アルゴリズム(二項分類器)であり、線形方程式を使用して2つのクラスを分離できます。

これは、線形回帰およびロジスティック回帰と密接に関連しており、同様の方法で予測を生成します(たとえば、入力の加重和として)。

パーセプトロンアルゴリズムは、最も単純なタイプの人工ニューラルネットワークです。これは、2クラスの分類問題に使用できる単一ニューロンモデルであるとともに、かなり大規模なネットワークをさらに開発するための基礎を備えています。


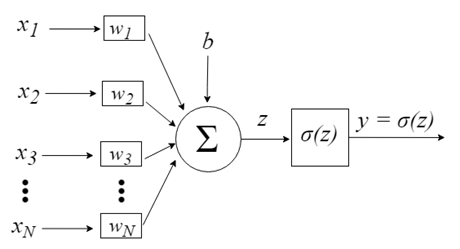
ニューロン入力は、ベクトルx = [x1、x2、x3、…、xN]で表されます。これは、たとえば、資産価格系列、テクニカル指標値、画像ピクセルなどに対応します。それらがニューロンに到達すると、適切なシナプスの重み(ベクトルw = [w1、w2、w3、...、wN]の要素)が乗算されます。これにより、次の式でz値(一般に「活動電位」と呼ばれます)が生成されます。

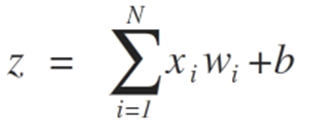
bはより高い自由度を提供し、これは入力に依存しないためです。通常、これは「バイアス」に対応します。次に、z値はσ活性化関数を通過します。この関数は、この値を特定の間隔(たとえば、0～1)に制限し、最終的な出力とニューロンの値を生成します。 使用される活性化関数には、ステップ関数、シグモイド関数、双曲線正接関数、ソフトマックス関数、ReLU(「正規化線形単位」)関数などがあります。

2つの入力{x1とx2}のみを考慮して、安定化への収束を示す2つの状況を使用して、クラスの分離可能性の制限に到達することを目的としたプロセスを見てみましょう。


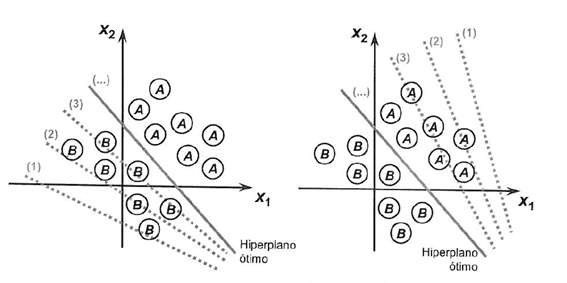
パーセプトロンアルゴリズムの重みは、確率的勾配降下法を使用した訓練データに基づいて推定する必要があります。


確率的勾配

最急降下法は、コスト関数の勾配の方向に関数を最小化するプロセスです。

これには、コスト形式と導関数がわかっていることが示唆されます。これにより、特定の点からの勾配を知ることができ、この方向、たとえば下向きに最小値に向かって移動できます。


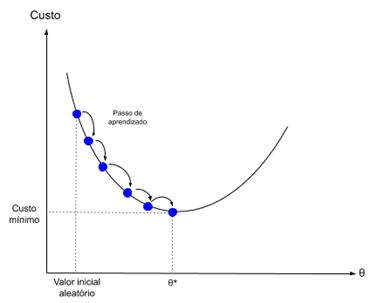
機械学習では、確率的勾配降下法と呼ばれる、反復ごとに重みを評価および更新する手法を使用できます。その目的は、訓練データのモデルエラーを最小限に抑えることです。

このアルゴリズムの概念は、各訓練インスタンスが一度に1つずつモデルに表示されるということです。モデルは、訓練インスタンスの予測を作成します。次に、エラーが計算され、モデルが更新されて、次の予測でエラーが減少します。

この手順を使用して、エラーが最小になるモデルの重みのセットを見つけることができます。

パーセプトロンアルゴリズムの場合、重みwは、次の式を使用して、反復ごとに更新されます。

  • w = w + learning_rate * (expected - predicted) * x

wが最適化可能な値である場合、Learning_rateは設定する必要のある学習率です(例: 0.1)。 (expected-predicted)は、重みに関するモデルの予測誤差であり、xは入力です。

確率的勾配降下法には、次の2つのパラメータが必要です。

  • 学習率: 各更新中に各重みが修正される量の上限
  • エポック: 重みを更新するときに訓練データを実行する回数

これらは、訓練データとともに、関数の引数になります。


関数では3つのループを実行する必要があります。

1. エポックごとのループ

2. エポックの訓練データの行ごとのループ

3. 重みごとのループ(一度に1行を更新)

重みは、モデルによって発生したエラーに基づいて更新されます。誤差は、実際の値と重みを使用して作成された予測との差として計算されます。

各入力属性には独自の重みがあって、重みは常に更新されます。次に例を示します。

  • w(t+1)= w(t) + learning_rate * (expected(t) - predicted(t)) * x(t)


バイアスは同様の方法で更新されますが、バイアスには特定の入力がないため入力は例外です。

  • bias(t+1) = bias(t) + learning_rate * (expected(t) - predicted(t)).


ニューロンモデルの適用

それでは、実用化に移りましょう。

このセクションは2つの部分に分かれています。

1. 予測を行う

2. ネットワークの重みを最適化する

これらの手順は、パーセプトロンアルゴリズムを実装し、他の分類問題に適用するための基礎を提供します。

セットXの列数を定義する必要があります。このために、定数を定義する必要があります。

#define nINPUT 3

MQL5では、多次元配列で静的か動的にできるのは最初の次元だけです。他のすべての次元は静的であるため、配列宣言時にサイズを指定する必要があります。

 

1. 予測を行う

最初の手順は、予測を行うことができる関数を開発することです。

これは、確率的勾配降下中の候補者の重みを評価するときと、モデルの完成後の両方で必要になります。予測は、テストデータと新しいデータに基づいて行います。

以下はpredict関数です。この関数は、特定の重みのセットに基づいて出力値を予測します。

最初の重みは自律的であるため常にバイアスであり、特定の入力値では機能しません。

// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }

ニューロンの転送:

ニューロンが活性化されたら、ニューロンの実際の出力を表示するために活性化を転送する必要があります。

//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }

予測関数に、入力セットX、重みの配列(W)、および入力セットXが予測される線を入力します。

小さなデータセットを使用して、予測関数を確認しましょう。


このデータセットの予測を行うために、事前に準備された重みを使用することもできます。

double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};

すべてをまとめたら、予測関数をテストできます。

#define nINPUT 3
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   random.seed(42);
   double dataset[][nINPUT] = {     //X1     //X2   //Y  
                               {2.7810836,2.550537003,0},
                               {1.465489372,2.362125076,0},
                               {3.396561688,4.400293529,0},
                               {1.38807019,1.850220317,0},
                               {3.06407232,3.005305973,0},
                               {7.627531214,2.759262235,1},
                               {5.332441248,2.088626775,1},
                               {6.922596716,1.77106367,1},
                               {8.675418651,-0.242068655,1},
                               {7.673756466,3.508563011,1}
                              };
   double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};
   for(int row=0; row<ArrayRange(dataset, 0); row++)
     {
      double predict = predict(dataset, weights, row);
      printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict);
     }
  }
//+------------------------------------------------------------------+
// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }
//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }


2つの入力値(X1とX2)と3つの重み(バイアス、 w1、w2)があります。この問題の活性化関数は次のようになります。

activation = (w1 * X1) + (w2 * X2) + b

または、特定の重みを使用して、手動で次のように設定します。

activation = (0.206 * X1) + (-0.234 * X2) + -0.1

関数の実行後、期待される出力値yに対応する予測を取得します。

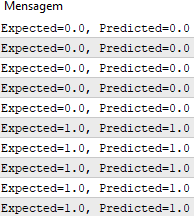
確率的勾配降下法を実装して、重み値を最適化できるようになりました。

2. ネットワークの重みの最適化

前述のように、訓練データの重みは、確率的勾配降下法を使用して評価できます。

以下は、確率的勾配降下法を使用して訓練データセットの重みを計算するtrain_weights()関数です。

MQL5では、配列は変数とは異なって参照によってのみ関数に渡すことができるため、この訓練データセット配列から結果を返す方法はありません。つまり、関数は配列の独自のインスタンスを作成せず、代わりに、渡された配列と直接連携します。したがって、関数内でその配列に加えられたすべての変更は、元の配列に影響します。

 //+------------------------------------------------------------------+
//|  Estimate Perceptron weights using stochastic gradient descent   |
//+------------------------------------------------------------------+
template <typename Array>
void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5)
  {
   ArrayResize(weights, ArrayRange(X, 1));
   for(int i=0; i<ArrayRange(X, 1); i++)
     {
      weights[i]=random.random();
     }
     
   for(int epoch=0; epoch<n_epoch; epoch++)
     {
      double sum_error = 0.0;
      for(int row=0; row<ArrayRange(X, 0); row++)
        {
         double y = predict(X, weights, row);
         double error = X[row][nINPUT-1] - y;
         sum_error += pow(error, 2);
         weights[0] = weights[0] + l_rate * error;

         for(int i=0; i<ArrayRange(X, 1)-1; i++)
           {
            weights[i+1] = weights[i+1] + l_rate * error * X[row][i];
           }
        }
      printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error);
     }
  }

各エポックで、誤差の二乗和(正の値)を追跡して誤差の減少を監視し、アルゴリズムがエポックからエポックへのエラー最小化に向けてどのように動くかを見ることができます。

上記と同じデータセットを使用して関数をテストできます。

#define nINPUT 3
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   random.seed(42);
   double dataset[][nINPUT] = {     //X1     //X2   //Y  
                               {2.7810836,2.550537003,0},
                               {1.465489372,2.362125076,0},
                               {3.396561688,4.400293529,0},
                               {1.38807019,1.850220317,0},
                               {3.06407232,3.005305973,0},
                               {7.627531214,2.759262235,1},
                               {5.332441248,2.088626775,1},
                               {6.922596716,1.77106367,1},
                               {8.675418651,-0.242068655,1},
                               {7.673756466,3.508563011,1}
                              };
   double weights[];
   train_weights(weights, dataset);
   ArrayPrint(weights, 20);
   for(int row=0; row<ArrayRange(dataset, 0); row++)
     {
      double predict = predict(dataset, weights, row);
      printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict);
     }
  }
//+------------------------------------------------------------------+
// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }
//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }
//+------------------------------------------------------------------+
//|  Estimate Perceptron weights using stochastic gradient descent   |
//+------------------------------------------------------------------+
template <typename Array>
void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5)
  {
   ArrayResize(weights, ArrayRange(X, 1));
   ArrayInitialize(weights, 0);
     
   for(int epoch=0; epoch<n_epoch; epoch++)
     {
      double sum_error = 0.0;
      for(int row=0; row<ArrayRange(X, 0); row++)
        {
         double y = predict(X, weights, row);
         double error = X[row][nINPUT-1] - y;
         sum_error += pow(error, 2);
         weights[0] = weights[0] + l_rate * error;

         for(int i=0; i<ArrayRange(X, 1)-1; i++)
           {
            weights[i+1] = weights[i+1] + l_rate * error * X[row][i];
           }
        }
      printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error);
     }
  }

学習率は0.1で、モデルはデータセット全体の5エポックでのみ取引されます。

実行中、各エポックでエラーの合計の2乗と最終的なデータセットを含むメッセージが出力されます。

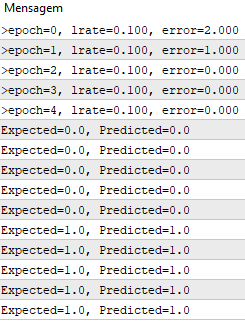
アルゴリズムが問題をどれだけ早く学習したかがわかります。

このテストは、以下に添付されているPerceptronScript.mq5ファイルで利用できます。


多層パーセプトロン

  • 層へのニューロンの結合

   単一のニューロンでできることはあまりありませんが、ニューロンは組み合わせて多層構造にすることができます。各層に異なる数のニューロンを持つ、多層パーセプトロン(MLP)と呼ばれるニューラルネットワークを形成します。入力ベクトル Xは最初の層を通過します。この層の出力値は、最後の層が最終結果を出力するまで、次の層に入力されます。ネットワークはいくつかの層に編成できるため、ネットワークは深くなり、ますます複雑になる関係を学習できます。

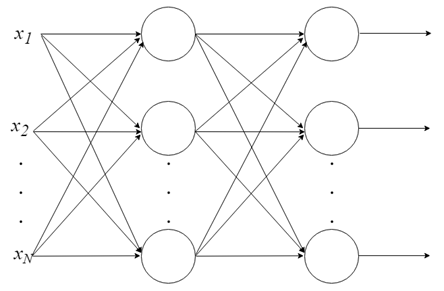
MLPの訓練

   ネットワークが機能し始める前に、このネットワークを訓練する必要があります。それは子供に読み方を教えるようなものです。教師あり学習は、機械学習のコンテキストでMLPを訓練するために使用されますが、どのように機能するのでしょうか。

教師あり学習:

  • ラベル付けされたデータのセットがあり、どちらが正しい出力であるかはすでにわかっています。学習は、入力と出力の間に関係があるという考えに基づいています。
  • 教師あり学習の問題は、「回帰」問題と「分類」問題に細分されます。回帰問題では、連続出力の結果を予測しようとします。つまり、入力変数をいくつかの連続関数にマッピングしようとします。分類問題では、離散出力で結果を予測しようとします。つまり、入力変数をさまざまなカテゴリにマッピングしようとします。

例1:

  • 不動産市場の住宅サイズのデータセットに基づいて、それらの価格を予測してみてください。サイズに応じた価格は連続的な結果であるため、これは回帰問題です。
  • この問題は、「家が指定された価格よりも多かれ少なかれ売れるかどうか」を予測するための分類問題に変わる可能性があります。ここでは、住宅は価格によって2つの異なるカテゴリにグループ化されます。


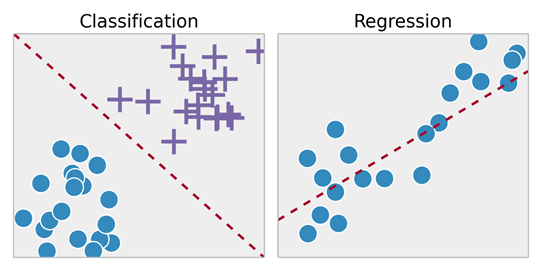
バックプロパゲーション

間違いなく、バックプロパゲーションはニューラルネットワークの歴史の中で最も重要なアルゴリズムです。効率的なバックプロパゲーションがなければ、今日のように深層学習ネットワークを訓練することは不可能です。バックプロパゲーションは、現代のニューラルネットワークと深層学習の基礎と見なすことができます。

私たちは間違いから学んでいないのでしょうか。

バックプロパゲーションアルゴリズムの背後にある考え方は次のとおりです。ニューラルネットワークの出力層で発生したエラーの計算に基づいて、ニューロンの最後の層のWベクトル重みの重みを再計算します。次に、前の層に後ろから前に移動します。つまり、このアルゴリズムは、ネットワークが受信したエラーを逆伝播することにより、ネットワークの最終層から入力層まで、すべての層のWの重みを更新します。言葉を変えれば、ネットワークの予測と実際のものとの違い(実際が1で予測が0ならエラーです)を計算するため、すべての重みの値を再計算します。最後の層から最初の層に進み、このエラーがどのように減少するかに常に注意を払います。

バックプロパゲーションアルゴリズムは、次の2つの手順で構成されます。

1. フォワードパス: 入力はネットワークを通過し、出力予測を受信します(この手順は伝播手順とも呼ばれます)。

2. バックワードパス: 損失関数の勾配は、ネットワークの最終層(予測層)で計算されます。次に、連鎖律を再帰的に適用して、ネットワーク内の重みを更新するために使用されます(重みの更新またはバックプロパゲーションとも呼ばれます)。

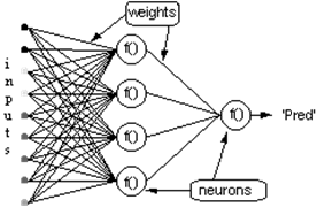
隠れニューロンと出力ニューロンの層を持つネットワークを考えてみましょう。入力ベクトルがネットワーク上を伝播するとき、現在の重みのセットの出力Pred(y)があります。教師あり学習の目的は、Pred(y)と必要な出力Req(y)の差を減らすために重みを調整することです。これは二乗誤差を減らすのと似ていて、絶対誤差を減らすアルゴリズムが必要です。ここで、

(1)

ネットワークエラー = Pred - Req

      = E

 

アルゴリズムは、E²を最小化することを目的として重みを調整する必要があります。バックプロパゲーションは、最急降下法によってE²を最小化するアルゴリズムです。E²を最小化するには、各重みに対する感度を計算する必要があります。つまり、各重みの変化がE²に与える影響を知る必要があります。この効果がわかれば、絶対誤差の減少に向けて重みを調整することができます。次の図は、バックプロパゲーションルールがどのように機能するかを示しています。

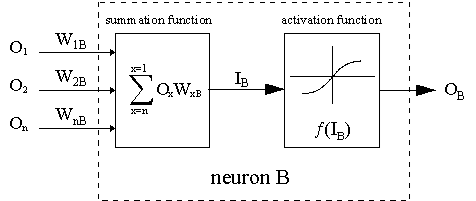
点線はニューロンBを示します。Bは隠れニューロンまたは出力ニューロンです。nニューロンの出力(O1... 前の層のO n)は、ニューロンBの入力データとして機能します。ニューロンBが隠れ層にある場合、それは単なる入力ベクトルです。出力は適切な重み(W1B ... WnB)で乗算されます。ここでWnBはニューロンnとニューロンBを接続する重みです。sum関数はこれらすべての積を加算して入力IBを取得します。IBはニューロンBのトリガー関数f(.)によって処理されます。 ニューロンBの出力OBは(IB)です。これを説明するために、ニューロン1をAと呼び、 2つのニューロンを接続する重みWABを検討します。重みを更新する方法はデルタルールに基づいています。

(2)

ここでは学習率パラメータであり、

は重みWABに対するエラーE²の感度です。次の図に示すように、新しいWAB重みの重みスペースでの検索方向を決定します。

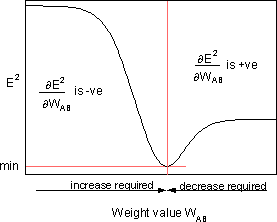
E²を最小化するために、デルタルールは必要な重みの変化方向を提供します。

上記の式の重要な概念は、ベクトルWの各重みについて式∂E² /∂WABを評価することです。これは、E²誤差関数の偏微分の計算で構成されます。

連鎖律:

(3)

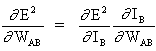
そして

(4)


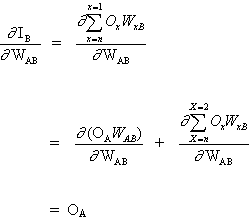
これは、他のニューロン入力は重みWABに依存しないためです。式(3)および(4)に基づいて、式(2)は次のようになります。

(5)

WABの重みの変化は、入力IBでの二乗誤差E²の感度、Bの単位および入力信号O Аに依存します。

2つの状況が考えられます。

1. Bは出力ニューロンです。

2. Bは隠れたニューロンです。

最初のケースを考えてみましょう。

Bは出力ニューロンであるため、WABの調整による二乗誤差の変化は、単に出力信号Bの二乗誤差の変化です。

(6)

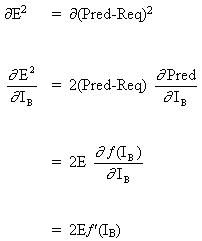
式(5)と(6)を組み合わせて、以下を取得します。

(7)

ニューロンBが出力ニューロンであり、出力活性化関数f(.)がロジスティック関数である場合の重みの変更規則:

(8)

引数xについて方程式(8)を微分します。

(9)

But

(10)

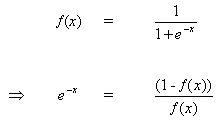
(10)を(9)に挿入すると、次のようになります。

(11)

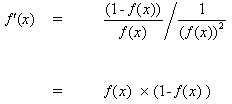
tanh関数の場合:

線形関数の場合(アイデンティティ):

以下のようになります。

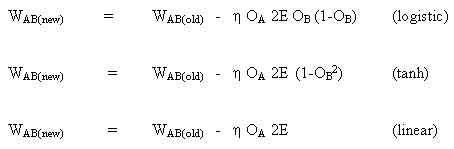
2番目のケースを考えてみましょう。

Bは隠れニューロンです。

(12)

ここでOは出力ニューロンです。

(13)

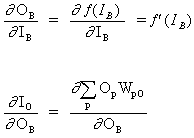
pは、出力ニューロンに入力信号を提供するニューロンBを含む、すべてのニューロンをカバーするインデックスです。式(13)の右の部分を展開します。

(14)


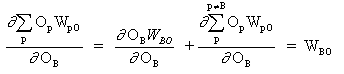
これは、他のニューロンの重みWpO(p! = B)はOBに依存しないためです。

(13)と(14)を(12)に挿入します。

(15)

したがって、は、式(6)で説明されているように計算されたの関数として表されます。

ニューロンBに信号を送信するニューロンA間の重みWABを更新するための完全なルールは次のとおりです。

(16)

ここで

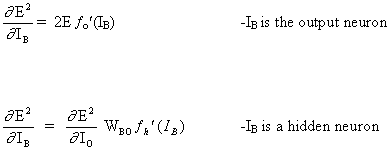
ここで、fo(.)とfh(.)は、それぞれ隠れた活性化関数と出力関数です。


例

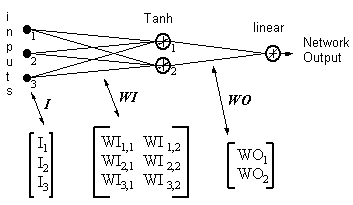
ネットワーク出力 = [tanh(I T .WI)] . WO

HID = [Tanh(I T.WI)] T- 隠れニューロンの出力

ERROR = (ネットワーク出力 - 必要な出力)

LR = 学習率

重みの更新は以下になります。

 

線形出力ニューロン:

(17)

WO = WO - ( LR x ERROR x HID )

隠れニューロン:

(18)

WI = WI - { LR x [ERROR x WO x (1- HID 2)] . I T } T

 

式17と18は、重みの更新が入力にローカル勾配を乗算したものであることを示しています。これは方向を提供し、その大きさはエラーの大きさにも依存します。大きさなしで方向をとると、すべての変化は同じサイズになり、これは学習率に依存します。上記のアルゴリズムは、出力ニューロンが1つしかない、簡略化されたバージョンです。元のアルゴリズムは複数の出力を持つことができますが、勾配を小さくすると、すべての出力の二乗誤差の合計が最小になります。学習率を上げるために元のアルゴリズムから進化した他の多くのアルゴリズムがあります。それらは次のように要約されます。

 

「バックプロパゲーションファミリーアルバム」- テクニカルレポートC /TR96-05、オーストラリア、ニューサウスウェールズ州マッコーリー大学コンピューティング学部。

 

バックプロパゲーションは、エレガントで独創的なアルゴリズムです。画像分類に関連するタスクではるかに優れたパフォーマンスを示した畳み込みニューラルネットワークや、自然言語処理タスクに使用される回帰型ニューラルネットワークなどの最新の深層学習モデルでも、バックプロパゲーションアルゴリズムが使用されています。最も驚くべきことは、そのようなモデルで、人間が観察および理解できないパターンを見つけることができるということです。これは本当に魅力的であり、深層学習アルゴリズムのさらなる開発を期待することができます。これは、人類が直面する基本的な問題の多くを解決するのに役立つでしょう。



MLPモデルの適用

このチュートリアルは5部に分かれています。

1.       ネットワークの初期化

2.       フィードフォワード

3.       バックプロパゲーション

4.       ネットワークの訓練

5.       予測

 

純粋なMQLで実装を作成しましょう。すでに、はるかに複雑な他の言語のライブラリについて説明しました。したがって、実用上およびパフォーマンス上の理由から、これらのライブラリを使用することを強くお勧めします。ただし、プロセス全体をより細かく制御するには、このようなライブラリの内部を理解することが重要です。以下のテストではOOPは使用されていません。これは、前述の方程式を示すアルゴリズムにすぎないため、ここではOOPは実際には必要ないためです。ただし、実際のケースでは、プロジェクトのスケーラビリティを提供するためにOOPを使用する方がはるかに実用的です。


1. ネットワークの初期化

各ニューロンには、維持する必要のある重みのセット、各入力接続の重み、およびバイアスの追加の重みがあります。

小さな乱数のネットワークの重みを初期化することをお勧めします。この場合、0から1の範囲の乱数が使用されます。この目的のために、乱数生成関数を作成しました。

double random(void)
  {
   return ((double)rand())/(double)SHORT_MAX;
  }

以下は、ニューラルネットワークの重みを作成するinitialize_network()関数です。

// Forward propagate input to a network output
void forward_propagate(void)
  {
//calculate the outputs of the hidden neurons
//the hidden neurons are tanh
   int i = 0;
   for(i = 0; i<numHidden; i++)
     {
      hiddenVal[i] = 0.0;
      for(int j = 0; j<numInputs; j++)
        {
         hiddenVal[i] += (X[patNum][j] * weightsIH[j][i]);
        }
      hiddenVal[i] = tanh(hiddenVal[i]);
     }
//calculate the output of the network
//the output neuron is linear
   outPred = 0.0;
   for(i = 0; i<numHidden; i++)
     {
      outPred += hiddenVal[i] * weightsHO[i];
     }
//calculate the error
   errThisPat = outPred - y[patNum];
  }

3. バックプロパゲーション

バックプロパゲーションアルゴリズムという名前は重みの訓練方法に応じて付けられています。

期待される出力とフィードフォワードネットワーク出力の間の誤差が計算されます。次に、これらのエラーはネットワークを介して出力層から隠れ層に伝播され、エラーの責任をシフトしながら重みを更新していきます。

バックプロパゲーションエラーメカニズムの背後にある数学は上で説明されています。

//+------------------------------------------------------------------+
//|        Backpropagate error and change network weights            |
//+------------------------------------------------------------------+
void backward_propagate_error(void)
  {
//adjust the weights hidden-output
   for(int k = 0; k<numHidden; k++)
     {
      double weightChange = LR_HO * errThisPat * hiddenVal[k];
      weightsHO[k] -= weightChange;
      //regularisation on the output weights
      regularisationWeights(weightsHO[k]);
     }
// adjust the weights input-hidden
   for(int i = 0; i<numHidden; i++)
     {
      for(int k = 0; k<numInputs; k++)
        {
         double x = 1 - pow(hiddenVal[i],2);
         x = x * weightsHO[i] * errThisPat * LR_IH;
         x = x * X[patNum][k];
         double weightChange = x;
         weightsIH[k][i] -= weightChange;
        }
     }
  }

regularizationWeightsメソッドは、-5から5の範囲の重みを正規化するためにのみ作成されています。

//regularisation on the output weights
void regularisationWeights(double &weight)
  {
   weight<-5?weight=-5:weight>5?weight=5:weight=weight;
  }

4. ネットワークの訓練

ネットワークは確率的勾配降下法を使用して訓練されます。

これには、データがネットワークにフィードされ、入力が各データラインにフィードフォワードされ、エラーが伝播され、重みが更新されるいくつかの反復が含まれます。

//# Train a network for a fixed number of epochs
void train(void)
  {
   for(int j = 0; j <= numEpochs; j++)
     {
      for(int i = 0; i<numPatterns; i++)
        {
         //select a pattern at random
         patNum = rand()%numPatterns;
         //calculate the current network output
         //and error for this pattern
         forward_propagate();
         backward_propagate_error();
        }
      //display the overall network error
      //after each epoch
      calcOverallError();
      printf("epoch = %d RMS Error = %f",j,RMSerror);
     }
  }

5. Prediction

訓練されたニューラルネットワークを使用して予測を行うのは非常に簡単です。

入力パターンを伝播して出力を受け取る方法については、すでに説明しました。予測を行うために必要なのはこれだけです。パターンが各出力クラスに属する確率として、出力値を直接使用できます。

// # Make a prediction with a network
void predict(void)
  {
   for(int i = 0; i<numPatterns; i++)
     {
      patNum = i;
      forward_propagate();
      printf("real = %d predict = %f",y[patNum],outPred);
     }
  }

完全な例は、以下に添付されているMLP_Script.mq5ファイルにあります。


終わりに

パーセプトロンニューロンの発達過程で実行される計算と、多層パーセプトロン(MLP)と呼ばれるパーセプトロンニューロンのネットワークを検討しました。また、このタイプのニューラルネットワークがバックプロパゲーションおよび勾配降下アルゴリズムを使用してどのように訓練されるかを見てきました。


MetaQuotes Ltdによりポルトガル語から翻訳されました。
元の記事: https://www.mql5.com/pt/articles/8908

添付されたファイル |
ZIPをダウンロード
PerceptronScript.mq5 (3.34 KB)
MLP_Script.mq5 (6.98 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
グリッドおよびマーチンゲール取引システムでの機械学習 - あなたはそれに賭けますか グリッドおよびマーチンゲール取引システムでの機械学習 - あなたはそれに賭けますか
本稿では、グリッドおよびマーチンゲール取引に適用される機械学習手法について説明します。驚いたことに、世界中のネットではこのアプローチはほとんどまたはまったくカバーされていません。記事を読んだ後は、自分自身の自動売買ボットを作成することができるでしょう。
自動取引のための便利でエキゾチックな技術 自動取引のための便利でエキゾチックな技術
本稿では、自動取引のためのいくつかの非常に興味深く有用な技術を紹介します。それらのいくつかには馴染みがあるかもしれません。最も興味深い手法を取り上げ、なぜ使用する価値があるのかを説明します。さらに、これらの技術の実際面での傾向を示します。エキスパートアドバイザーを作成し、説明されているすべての技術を相場履歴を使用してテストします。
パターン検索への総当たり攻撃アプローチ(第IV部): 最小限の機能 パターン検索への総当たり攻撃アプローチ(第IV部): 最小限の機能
本稿では、前の記事で設定した目標に基づいて改良された総当たり攻撃バージョンについてお話します。エキスパートアドバイザーをこの方法で取得した設定で使用して、このトピックをできるだけ広くカバーするようにします。新しいプログラムバージョンも添付されています。
取引におけるニューラルネットワークの実用化(第2部)コンピュータービジョン 取引におけるニューラルネットワークの実用化(第2部)コンピュータービジョン
コンピュータービジョンを使用すると、価格チャートと指標の視覚的表現に関してニューラルネットワークを訓練できるようになります。この方法では、ニューラルネットワークにデジタルでフィードする必要がないため、テクニカル指標全体でより幅広い操作が可能になります。