Mehrschicht-Perceptron und Backpropagation-Algorithmus

Einführung

• Die Popularität dieser beiden Methoden wächst, sodass viele Bibliotheken in Matlab, R, Python, C++ und anderen entwickelt wurden, die einen Trainingssatz als Eingabe erhalten und automatisch ein passendes Netzwerk für das Problem erstellen.

• Bei der Verwendung fertiger Bibliotheken kann es jedoch schwierig sein, zu verstehen, was genau passiert und wie wir ein optimiertes Netzwerk erhalten. Das Verständnis der Lösungsgrundlagen ist für die weitere Entwicklung dieser Methoden unerlässlich. In diesem Artikel werden wir eine sehr einfache Struktur einer neuronalen Netzarchitektur erstellen.

• Versuchen wir zu verstehen, wie der Grundtyp des neuronalen Netzes funktioniert (einschließlich Ein-Neuronen-Perzeptron und Mehrschicht-Perzeptron). Wir werden einen spannenden Algorithmus betrachten, der für das Training von Netzwerken zuständig ist (Gradientenabstieg und Backpropagation). Bestehende komplexe Modelle basieren oft auf solchen einfachen Netzwerkmodellen.

Ein kurzer Überblick über die Geschichte

• Das erste neuronale Netzwerk wurde von Warren McCulloch und Walter Pitts im Jahr 1943 vorgeschlagen. Sie schrieben einen großen Artikel darüber, wie Neuronen funktionieren sollten. Sie bauten auch ein Modell basierend auf ihren Ideen: Sie erstellten ein einfaches neuronales Netzwerk mit elektrischen Schaltkreisen.

• Die Forschung im Bereich der künstlichen Intelligenz schritt schnell voran, und 1980 entwickelte Kunihiko Fukushima das erste echte mehrschichtige neuronale Netz.

• Der ursprüngliche Zweck eines neuronalen Netzwerks war es, ein Computersystem zu schaffen, das in der Lage ist, Probleme ähnlich wie das menschliche Gehirn zu lösen. Im Laufe der Zeit änderten die Forscher jedoch ihren Fokus und begannen, neuronale Netzwerke zur Lösung verschiedener spezifischer Aufgaben einzusetzen. Heute führen neuronale Netzwerke eine Vielzahl von Aufgaben aus, z. B. Computer Vision, Spracherkennung, maschinelle Übersetzung, Filterung sozialer Medien, Brettspiele oder Videospiele, medizinische Diagnostik, Wettervorhersage, Zeitreihenvorhersage, Bild-/Text-/Stimmerkennung und vieles mehr.

Computermodell eines Neurons: Das Perceptron

Das Perceptron

Das Perceptron wurde von der Idee inspiriert, Informationen von einer einzelnen Nervenzelle, einem Neuron, zu verarbeiten. Ein Neuron empfängt Signale als Eingabe über seine Dendriten, die ein elektrisches Signal an den Zellkörper weiterleiten. In ähnlicher Weise empfängt das Perzeptron Eingangssignale aus Trainingsdatensätzen, die zuvor gewichtet und zu einer linearen Gleichung namens Aktivierung kombiniert wurden.

• z = sum(weight_i * x_i) + bias

Hier ist "weight" eine Gewichtung innerhalb des Netzwerks, "X" ist ein Eingang, "i" ist der Index eines Gewichts oder Eingangs und bias ist ein spezielles Gewicht, das keinen Multiplikator-Eingang hat (wir können also annehmen, dass der Eingang immer 1,0 ist).

Dann wird die Aktivierung mit Hilfe einer Übertragungsfunktion (Aktivierungsfunktion) in einen Ausgangswert (Prognose) umgewandelt.

• y = 1.0 wenn z >= 0.0, sonst 0.0

Das Perceptron ist also ein Algorithmus zur Klassifizierung eines Zwei-Klassen-Problems (binärer Klassifikator), bei dem eine lineare Gleichung zur Trennung der beiden Klassen verwendet werden kann.

Dies ist eng verwandt mit der linearen Regression und der logistischen Regression, die auf ähnliche Weise Vorhersagen generieren (z. B. als gewichtete Summe der Eingaben).

Der Perceptron-Algorithmus ist der einfachste Typ eines künstlichen neuronalen Netzes. Es ist ein Ein-Neuronen-Modell, das für Zwei-Klassen-Klassifikationsprobleme verwendet werden kann. Er bildet auch die Grundlage für die Weiterentwicklung von wesentlich größeren Netzen.

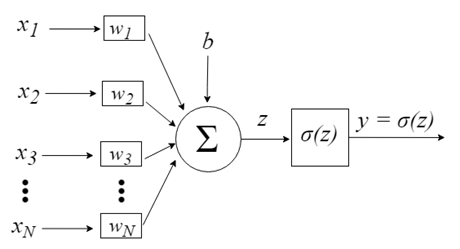
Die Eingaben der Neuronen werden durch den Vektor x = [x1, x2, x3,..., xN] repräsentiert, der z.B. einer Asset-Kursreihe, technischen Indikatorwerten oder Bildpunkten entsprechen kann. Wenn sie das Neuron erreichen, werden sie mit entsprechenden synaptischen Gewichten multipliziert - den Elementen des Vektors w = [w1, w2, w3, ..., wN]. Daraus ergibt sich der z-Wert (allgemein als "Aktivierungspotential" bezeichnet) nach der folgenden Formel:

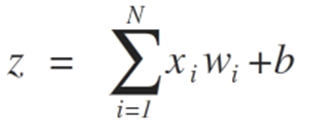
b bietet einen höheren Freiheitsgrad und ist nicht von der Eingabe abhängig. In der Regel entspricht dies einem "Bias". Der z-Wert durchläuft dann die σ-Aktivierungsfunktion, die dafür zuständig ist, diesen Wert in einem bestimmten Intervall (z. B. 0 - 1) zu begrenzen, was die endgültige Ausgabe und den Wert des Neurons ergibt. Einige der verwendeten Aktivierungsfunktionen sind Step, Sigmoid, Tangens Hyperbolicus, Softmax und ReLU ("rectified linear unit").

Betrachten wir den Prozess, der darauf abzielt, die Grenze der Klassentrennbarkeit zu erreichen, anhand von zwei Situationen, die ihre Konvergenz in Richtung Stabilisierung demonstrieren, unter Berücksichtigung von nur zwei Eingaben {x1 und x2}

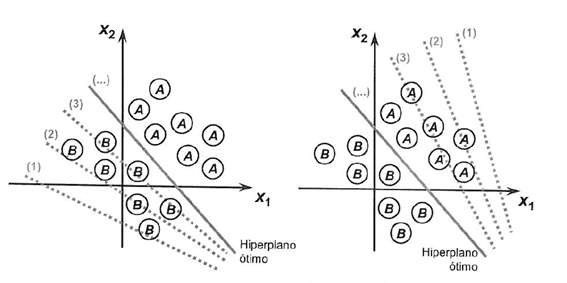
Die Gewichte des Perceptron-Algorithmus sollten auf der Grundlage von Trainingsdaten mittels stochastischem Gradientenabstieg geschätzt werden.

Stochastischer Gradient

Gradientenabstieg ist der Prozess der Minimierung einer Funktion in Richtung der Gradienten der Kostenfunktion.

Dies setzt die Kenntnis der Kostenform sowie der Ableitung voraus, so dass wir den Gradienten ab einem bestimmten Punkt kennen und uns in dieser Richtung, z. B. nach unten, in Richtung des Minimalwertes bewegen können.

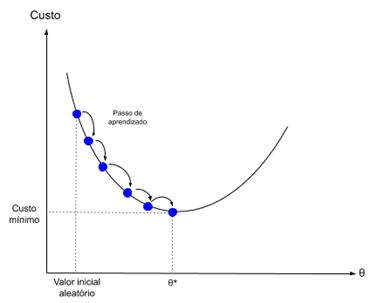
Beim maschinellen Lernen können wir eine Technik verwenden, die die Gewichte für jede Iteration auswertet und aktualisiert, genannt Stochastischer Gradientenabstieg. Sein Zweck ist es, einen Modellfehler in unseren Trainingsdaten zu minimieren.

Die Idee dieses Algorithmus ist, dass jede Trainingsinstanz dem Modell nacheinander gezeigt wird. Das Modell erstellt eine Prognose für die Trainingsinstanz. Dann wird ein Fehler berechnet und das Modell wird aktualisiert, um den Fehler in der nächsten Prognose zu reduzieren.

Dieses Verfahren kann verwendet werden, um einen Satz von Modellgewichten zu finden, der den geringsten Fehler erzeugt.

Für den Perceptron-Algorithmus werden die Gewichte w bei jeder Iteration unter Verwendung der folgenden Gleichung aktualisiert:

• w = w + learning_rate * (expected - predicted) * x

Dabei ist w ein optimierbarer Wert, learning_rate eine Lernrate, die Sie einstellen sollten (z. B. 0,1), (erwartet - vorhergesagt) ist der Vorhersagefehler für ein Modell bezüglich der Acht und x ist eine Eingabe.

Der Stochastische Gradientenabstieg benötigt zwei Parameter:

• Lernrate: wird verwendet, um zu begrenzen, um wie viel jedes Gewicht bei jeder Aktualisierung korrigiert wird.
• Epochs - wie oft die Trainingsdaten durchlaufen werden sollen, wenn die Gewichtung aktualisiert wird.

Diese, zusammen mit den Trainingsdaten, werden die Argumente für die Funktion sein.

Wir müssen 3 Schleifen in der Funktion ausführen:

1. Eine Schleife für jede Epoche.

2. Eine Schleife für jede Zeile in den Trainingsdaten für eine Epoche.

3. Eine Schleife für jede Gewichtung, in der jeweils eine Zeile aktualisiert wird.

Die Gewichte werden auf der Grundlage des vom Modell gemachten Fehlers aktualisiert. Ein Fehler wird als Differenz zwischen dem tatsächlichen Wert und der mithilfe der Gewichte erstellten Prognose berechnet.

Jedes Eingangsattribut hat sein eigenes Gewicht. Die Gewichtungen werden ständig aktualisiert, z. B:

• w(t+1)= w(t) + learning_rate * (expected(t) - predicted(t)) * x(t)

Der Bias wird auf ähnliche Weise aktualisiert, mit Ausnahme der Eingabe, da es keine spezifische Eingabe für einen Bias gibt:

• bias(t+1) = bias(t) + learning_rate * (expected(t) - predicted(t)).

Anwenden des Neuronenmodells

Kommen wir nun zur praktischen Anwendung.

Dieser Abschnitt ist in zwei Teile gegliedert:

1. Vorhersagen treffen

2. Optimierung des Netzgewichts

Diese Schritte bilden die Grundlage für die Implementierung und Anwendung des Perceptron-Algorithmus auf andere Klassifikationsprobleme.

Wir müssen die Anzahl der Spalten in der Menge X definieren. Dazu müssen wir eine Konstante definieren

#define nINPUT 3

---

In MQL5 kann ein mehrdimensionales Array nur für die erste Dimension statisch oder dynamisch sein. Da alle anderen Dimensionen statisch sein werden, muss die Größe bei der Array-Deklaration angegeben werden.

 

1. Vorhersagen treffen

Der erste Schritt besteht darin, eine Funktion zu entwickeln, die Vorhersagen machen kann.

Dies wird sowohl bei der Auswertung der Gewichte der Kandidaten während des stochastischen Gradientenabstiegs als auch nach der Fertigstellung des Modells notwendig sein. Die Vorhersage sollte auf der Grundlage von Testdaten und auf der Grundlage neuer Daten erfolgen.

Nachfolgend ist die Funktion predict dargestellt, die den Ausgabewert basierend auf einem bestimmten Satz von Gewichten vorhersagt.

Das erste Gewicht ist immer ein Bias, da es autonom ist, also nicht mit einem bestimmten Eingabewert arbeitet.

// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }

Neuronentransfer:

Sobald ein Neuron aktiviert ist, müssen wir die Aktivierung übertragen, um die tatsächlichen Ausgänge des Neurons zu sehen.

//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }

Wir übergeben der Vorhersagefunktion ein Array mit den Eingaben X, ein Array von Gewichten (W) und die Zeile, für die das Array mit den Eingaben X vorhergesagt wird.

Wir wollen einen kleinen Datensatz verwenden, um die Vorhersagefunktion zu überprüfen.

Wir können auch vorbereitete Gewichte verwenden, um Vorhersagen für diesen Datensatz zu treffen.

double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};

Nachdem wir alles zusammengefügt haben, können wir die Forecast-Funktion testen.

#define nINPUT 3
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   random.seed(42);
   double dataset[][nINPUT] = {     //X1     //X2   //Y  
                               {2.7810836,2.550537003,0},
                               {1.465489372,2.362125076,0},
                               {3.396561688,4.400293529,0},
                               {1.38807019,1.850220317,0},
                               {3.06407232,3.005305973,0},
                               {7.627531214,2.759262235,1},
                               {5.332441248,2.088626775,1},
                               {6.922596716,1.77106367,1},
                               {8.675418651,-0.242068655,1},
                               {7.673756466,3.508563011,1}
                              };
   double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};
   for(int row=0; row<ArrayRange(dataset, 0); row++)
     {
      double predict = predict(dataset, weights, row);
      printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict);
     }
  }
//+------------------------------------------------------------------+
// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }
//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }

Es gibt zwei Eingangswerte (X1 und X2)und drei Gewichte (bias, w1 und w2). Die Aktivierungsgleichung für dieses Problem sieht wie folgt aus:

activation = (w1 * X1) + (w2 * X2) + b

Oder mit bestimmten Gewichten, sie wird manuell eingestellt als:

activation = (0.206 * X1) + (-0.234 * X2) + -0.1

Nach Ausführung der Funktion erhalten wir Vorhersagen, die den erwarteten Ausgabewerten y. entsprechen

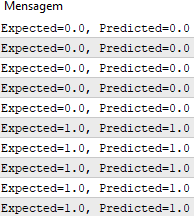
Wir können nun den stochastischen Gradientenabstieg implementieren, um die Gewichtswerte zu optimieren.

2. Optimierung der Netzgewichte

Wie bereits erwähnt, können die Gewichte für die Trainingsdaten mithilfe des stochastischen Gradientenabstiegs evaluiert werden.

Im Folgenden finden Sie die Funktion train_weights(), die die Gewichte für einen Trainingsdatensatz mithilfe des stochastischen Gradientenabstiegs berechnet.

Es gibt in MQL5 keine Möglichkeit, ein Ergebnis aus diesem Trainingsdatensatz-Array zurückzugeben, da Arrays im Gegensatz zu Variablen nur per Referenz an eine Funktion übergeben werden können. Das bedeutet, dass die Funktion nicht ihre eigene Instanz des Arrays erzeugt. Stattdessen arbeitet sie direkt mit dem ihr übergebenen Array. Somit wirken sich alle Änderungen, die innerhalb der Funktion an diesem Array vorgenommen werden, auf das ursprüngliche Array aus.

 //+------------------------------------------------------------------+
//|  Estimate Perceptron weights using stochastic gradient descent   |
//+------------------------------------------------------------------+
template <typename Array>
void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5)
  {
   ArrayResize(weights, ArrayRange(X, 1));
   for(int i=0; i<ArrayRange(X, 1); i++)
     {
      weights[i]=random.random();
     }
     
   for(int epoch=0; epoch<n_epoch; epoch++)
     {
      double sum_error = 0.0;
      for(int row=0; row<ArrayRange(X, 0); row++)
        {
         double y = predict(X, weights, row);
         double error = X[row][nINPUT-1] - y;
         sum_error += pow(error, 2);
         weights[0] = weights[0] + l_rate * error;

         for(int i=0; i<ArrayRange(X, 1)-1; i++)
           {
            weights[i+1] = weights[i+1] + l_rate * error * X[row][i];
           }
        }
      printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error);
     }
  }

In jeder Epoche verfolgen wir die Summe der quadrierten Fehler (positiver Wert), um die Abnahme des Fehlers zu überwachen. So können wir sehen, wie sich der Algorithmus von Epoche zu Epoche in Richtung Fehlerminimierung bewegt.

Wir können unsere Funktion mit demselben Datensatz testen, der oben vorgestellt wurde.

#define nINPUT 3
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   random.seed(42);
   double dataset[][nINPUT] = {     //X1     //X2   //Y  
                               {2.7810836,2.550537003,0},
                               {1.465489372,2.362125076,0},
                               {3.396561688,4.400293529,0},
                               {1.38807019,1.850220317,0},
                               {3.06407232,3.005305973,0},
                               {7.627531214,2.759262235,1},
                               {5.332441248,2.088626775,1},
                               {6.922596716,1.77106367,1},
                               {8.675418651,-0.242068655,1},
                               {7.673756466,3.508563011,1}
                              };
   double weights[];
   train_weights(weights, dataset);
   ArrayPrint(weights, 20);
   for(int row=0; row<ArrayRange(dataset, 0); row++)
     {
      double predict = predict(dataset, weights, row);
      printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict);
     }
  }
//+------------------------------------------------------------------+
// Make a prediction with weights
template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }
//+------------------------------------------------------------------+
//|                Transfer neuron activation                        |
//+------------------------------------------------------------------+
double activation(const double activation) //#
  {
   return activation>=0.0?1.0:0.0;
  }
//+------------------------------------------------------------------+
//|  Estimate Perceptron weights using stochastic gradient descent   |
//+------------------------------------------------------------------+
template <typename Array>
void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5)
  {
   ArrayResize(weights, ArrayRange(X, 1));
   ArrayInitialize(weights, 0);
     
   for(int epoch=0; epoch<n_epoch; epoch++)
     {
      double sum_error = 0.0;
      for(int row=0; row<ArrayRange(X, 0); row++)
        {
         double y = predict(X, weights, row);
         double error = X[row][nINPUT-1] - y;
         sum_error += pow(error, 2);
         weights[0] = weights[0] + l_rate * error;

         for(int i=0; i<ArrayRange(X, 1)-1; i++)
           {
            weights[i+1] = weights[i+1] + l_rate * error * X[row][i];
           }
        }
      printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error);
     }
  }

Wir verwenden eine Lernrate von 0,1 und trainieren das Modell für nur 5 Epochen oder 5 Gewichtsanzeigen für den gesamten Trainingsdatensatz.

Während der Ausführung wird für jede Epoche eine Meldung mit der Summe der quadrierten Fehler sowie der endgültige Datensatz ausgegeben.

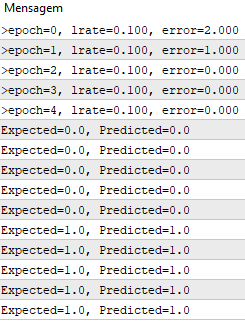
Wir sehen, wie schnell der Algorithmus das Problem gelernt hat.

Dieser Test ist in der unten angehängten Datei PerceptronScript.mq5 verfügbar.

Mehrschichtiges Perceptron

• Neuronen zu Schichten zusammenfassen

   Mit einem einzelnen Neuron lässt sich nicht viel anstellen. Aber Neuronen können zu einer mehrschichtigen Struktur kombiniert werden, wobei jede Schicht eine andere Anzahl von Neuronen hat, und ein neuronales Netz bilden, das Multi-Layer Perceptron, MLP genannt wird. Der Eingangsvektor X durchläuft die Anfangsschicht. Die Ausgangswerte dieser Schicht werden in die nächste eingegeben und so weiter, bis die letzte Schicht das Endergebnis ausgibt. Das Netzwerk kann in mehreren Schichten organisiert werden, wodurch es tief wird und in der Lage ist, immer komplexere Zusammenhänge zu lernen.

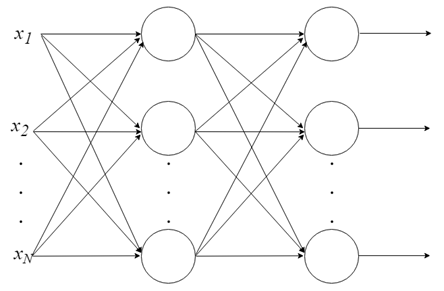
MLP-Training

   Bevor ein Netzwerk zu arbeiten beginnt, muss dieses Netzwerk trainiert werden. Das ist so, als würde man einem Kind das Lesen beibringen. Im Rahmen des maschinellen Lernens wird das MLP durch überwachtes Training trainiert, aber wie funktioniert das?

Überwachtes Lernen:

• Wir haben einen Satz beschrifteter Daten und wissen bereits, welches die richtige Ausgabe ist. Das Lernen basiert auf der Idee, dass es eine Verbindung zwischen der Eingabe und der Ausgabe gibt.
• Probleme des überwachten Lernens werden in "Regressions-" und "Klassifikationsprobleme" unterteilt. Bei Regressionsproblemen versuchen wir, die Ergebnisse für eine kontinuierliche Ausgabe vorherzusagen, d. h. wir versuchen, die Eingabevariablen auf eine kontinuierliche Funktion abzubilden. Bei Klassifizierungsproblemen versuchen wir, die Ergebnisse in einer diskreten Ausgabe vorherzusagen. Mit anderen Worten, wir versuchen, die Eingabevariablen auf verschiedene Kategorien abzubilden.

Beispiel 1:

• Basierend auf einem Datensatz von Hausgrößen auf dem Immobilienmarkt versuchen wir, deren Preis vorherzusagen. Der Preis in Abhängigkeit von der Größe ist ein kontinuierliches Ergebnis, es handelt sich also um ein Regressionsproblem.
• Dieses Problem könnte in ein Klassifikationsproblem umgewandelt werden - um vorherzusagen, ob "das Haus für mehr oder weniger als den angegebenen Preis verkauft werden kann". Hier werden die Häuser nach dem Preis in zwei verschiedene Kategorien eingeteilt.

Backpropagation

Zweifellos ist Backpropagation der wichtigste Algorithmus in der Geschichte der neuronalen Netzwerke. Ohne effiziente Backpropagation wäre es unmöglich, Deep Learning-Netzwerke so zu trainieren, wie wir es heute tun. Backpropagation kann als Grundstein für moderne neuronale Netzwerke und Deep Learning angesehen werden.

Lernen wir nicht aus Fehlern?

Die Idee hinter dem Backpropagation-Algorithmus ist folgende: Basierend auf dem berechneten Fehler, der in der Ausgabeschicht des neuronalen Netzwerks aufgetreten ist, berechnen wir die Vektorgewichte W der letzten Schicht von Neuronen neu. Dann gehen wir zu den vorherigen Schichten, von hinten nach vorne. Der Algorithmus impliziert also die Aktualisierung der Gewichte W aller Schichten, von der letzten bis zur Eingangsschicht des Netzes, durch Backpropagation des vom Netz empfangenen Fehlers. Mit anderen Worten, es wird ein Fehler berechnet zwischen dem, was das Netz vorhergesagt hat, und dem, was tatsächlich eintrat (tatsächlich 1, vorhergesagt 0; wir haben einen Fehler!), also werden die Werte aller Gewichte neu berechnet, beginnend mit der letzten Schicht und gehend zur ersten, wobei immer darauf geachtet wird, wie dieser Fehler reduziert wird.

Der Backpropagation-Algorithmus besteht aus zwei Schritten:

1. Vorwärtsdurchgang: Eingaben durchlaufen das Netzwerk und erhalten Ausgabevorhersagen (dieser Schritt wird auch als Propagationsschritt bezeichnet).

2. Rückwärtsdurchgang: Der Gradient der Verlustfunktion wird in der letzten Schicht des Netzwerks (Vorhersageschicht) berechnet. Er wird dann für die rekursive Anwendung der Kettenregel verwendet, um die Gewichte in unserem Netzwerk zu aktualisieren (auch bekannt als Gewichtsaktualisierung oder Backpropagation).

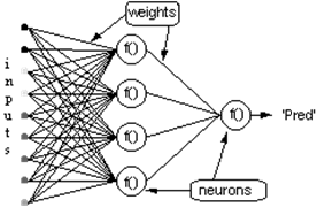
Betrachten wir das Netzwerk mit einer Schicht von versteckten Neuronen und einem Ausgangsneuron. Wenn sich der Eingabevektor über das Netzwerk ausbreitet, gibt es eine Ausgabe Pred(y) für den aktuellen Satz von Gewichten. Der Zweck des überwachten Trainings ist es, die Gewichte anzupassen, um die Differenz zwischen Pred(y) und der erforderlichen Ausgabe Req(y) zu verringern. Dies erfordert einen Algorithmus, der den absoluten Fehler reduziert, was einer Reduzierung des quadratischen Fehlers entspricht, wobei:

(1)

Netzwerkfehler = Pred - Req

      = E

 

Der Algorithmus sollte die Gewichte mit dem Ziel anpassen, E² zu minimieren. Backpropagation ist ein Algorithmus, der das E² durch Gradientenabstieg minimiert. Um E² zu minimieren, ist es notwendig, seine Empfindlichkeit gegenüber jedem Gewicht zu berechnen. Mit anderen Worten, wir müssen die Auswirkung einer Änderung der einzelnen Gewichte auf E² kennen. Wenn wir diesen Effekt kennen, können wir die Gewichtung in Richtung einer Verringerung des absoluten Fehlers anpassen. Das folgende Diagramm zeigt, wie die Backpropagation-Regel funktioniert.

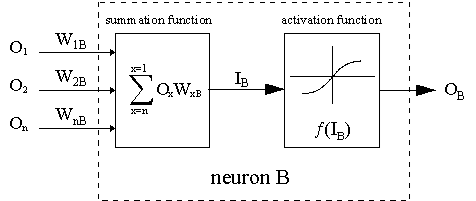
Die gestrichelte Linie zeigt das Neuron B, das ein verstecktes oder ein Ausgangsneuron sein kann. Die Ausgaben von n Neuronen (O 1 ... O n) der vorhergehenden Schicht dienen als Eingabedaten für das Neuron B. Befindet sich das Neuron B in der versteckten Schicht, ist es einfach ein Eingabevektor. Die Ausgänge werden mit den entsprechenden Gewichten multipliziert (W1B ... WnB), wobei WnB das Gewicht ist, das Neuron n und Neuron B verbindet. Die Summenfunktion addiert alle diese Produkte, um die Eingabe IB zu erhalten, die von der Triggerfunktion f(.) von Neuron B verarbeitet wird. f(IB) ist die Ausgabe OB von Neuron B. Zur Veranschaulichung sei Neuron 1 als A bezeichnet und das Gewicht WAB betrachtet, das die beiden Neuronen verbindet. Der Ansatz zur Aktualisierung des Gewichts basiert auf der Delta-Regel:

(2)

wobei - der Parameter der Lernrate ist, und

die Empfindlichkeit des Fehlers E² gegenüber dem Gewicht WAB; sie bestimmt die Suchrichtung im Gewichtsraum für das neue Gewicht WAB, wie in der Abbildung unten gezeigt.

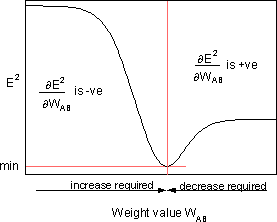
Um E² zu minimieren, liefert die Deltaregel die erforderliche Gewichtsänderungsrichtung.

Das Schlüsselkonzept der obigen Gleichung ist die Auswertung des Ausdrucks ∂E² /∂WAB, der darin besteht, partielle Ableitungen der Fehlerfunktion E² zu berechnen, in Bezug auf jedes Gewicht des Vektors W.

Kettenregel:

(3)

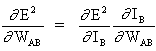
und

(4)

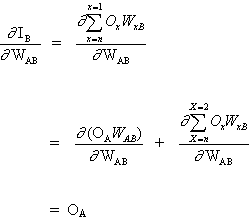
da andere Neuroneneingänge nicht von der Gewichtung WAB abhängen. Basierend auf den Gleichungen (3) und (4) wird die Gleichung (2) somit zu

(5)

und die Gewichtsänderung WAB hängt von der Empfindlichkeit des quadrierten Fehlers E² am Eingang IB, von der Einheit von B und dem Eingangssignal OА ab.

Es sind zwei Situationen möglich:

1. B ist ein Ausgangsneuron;

2. B ist ein verstecktes Neuron.

Betrachten wir den ersten Fall:

Da B ein Ausgangsneuron ist, ist eine Änderung des quadratischen Fehlers durch die Anpassung von WAB einfach eine Änderung des quadratischen Fehlers des Ausgangssignals B.

(6)

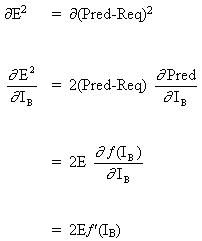
Kombinieren wir die Gleichungen (5) und (6), und wir erhalten

(7)

Die Regel für die Änderung der Gewichte, wenn Neuron B ein Ausgangsneuron ist, wenn die Ausgangsaktivierungsfunktion f (.) eine logistische Funktion ist:

(8)

Differenzieren wir Gleichung (8) nach dem Argument x:

(9)

Aber

(10)

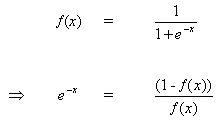
wenn wir (10) in (9) einfügen, erhalten wir:

(11)

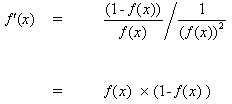
und, auf die gleiche Weise, für die Funktion tanh

oder für die lineare Funktion (Identische Abbildung)

Wir erhalten also:

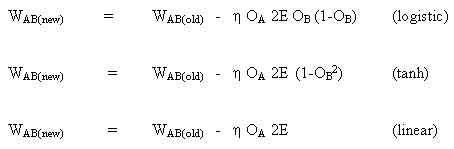
Betrachten wir den zweiten Fall

B ist ein verstecktes Neuron

(12)

wobei O das Ausgangsneuron ist

(13)

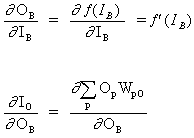
wobei p ein Index ist, der alle Neuronen umfasst, einschließlich Neuron B, das Eingangssignale für das Ausgangsneuron liefert. Erweitern wir den rechten Teil von Gleichung (13),

(14)

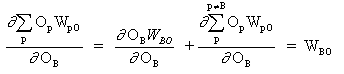
da die Gewichte der anderen Neuronen WpO (p! = B) keine Abhängigkeit von OB haben.

Beim Einsetzen von (13) und (13) in (12):

(15)

Folglich wird nun als eine Funktion von ausgedrückt, berechnet wie in Gleichung (6) beschrieben.

Die vollständige Regel für die Aktualisierung des Gewichts WAB zwischen Neuron A, das ein Signal an Neuron B sendet, lautet wie folgt:

(16)

mit

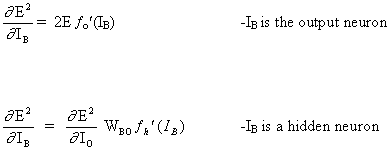
wobei fo(.) und fh(.) versteckte Aktivierungs- bzw. Ausgabefunktionen sind.

Beispiel

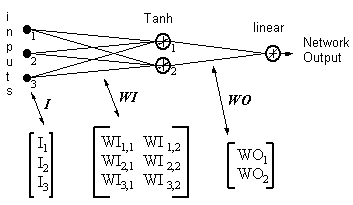
Netzwerkausgang = [tanh(I ^T .WI)] . WO

HID = [Tanh(I ^T.WI)] ^T- Ausgaben der versteckten Neuronen

ERROR = (Netzwerkausgang - gewünschter Ausgang)

LR = Lernrate

Gewichtsaktualisierungen werden zu

 

einem Neuron mit einem linearen Ausgang:

(17)

WO = WO - ( LR x ERROR x HID )

verstecktes Neuron:

(18)

WI = WI - { LR x [ERROR x WO x (1- HID ²)] . I ^T } ^T

 

Die Gleichungen 17 und 18 zeigen, dass das Gewichtsupdate eine Eingabe ist, die mit dem lokalen Gradienten multipliziert wird. Dies liefert die Richtung, deren Betrag auch von der Größe des Fehlers abhängt. Wenn wir eine Richtung ohne Größe nehmen, werden alle Änderungen gleich groß sein, und dies hängt von der Lernrate ab. Der obige Algorithmus ist eine vereinfachte Version, da es nur ein Ausgangsneuron gibt. Der ursprüngliche Algorithmus kann mehr als einen Ausgang haben, während eine Abnahme des Gradienten den gesamten quadratischen Fehler aller Ausgänge minimiert. Es gibt viele andere Algorithmen, die sich aus dem ursprünglichen Algorithmus entwickelt haben, um die Lernrate zu erhöhen. Sie sind zusammengefasst in:

 

"Back Propagation family album" - Technical report C/TR96-05, Department of Computing, Macquarie University, NSW, Australia.

 

Backpropagation ist ein eleganter und genialer Algorithmus. Moderne Deep-Learning-Modelle wie Convolutional Neural Networks, die eine viel bessere Leistung bei Aufgaben zur Bildklassifikation gezeigt haben, oder Recurrent Neural Networks, die für Aufgaben der natürlichen Sprachverarbeitung verwendet werden, nutzen ebenfalls den Backpropagation-Algorithmus. Das Unglaublichste daran ist, dass solche Modelle Muster finden können, die von Menschen nicht beobachtet und verstanden werden können. Das ist wirklich faszinierend und lässt uns eine weitere Entwicklung von Deep-Learning-Algorithmen erwarten, die uns bei der Lösung vieler grundlegender Probleme der Menschheit helfen werden.

Anwendung des MLP-Modells

Dieses Tutorial ist in 5 Teile gegliedert:

1. Netzwerk-Initialisierung.

2. FeedForward.

3. Backpropagation.

4. Netzwerk-Training.

5. Vorhersage.

 

Erstellen wir eine Implementierung in reinem MQL erstellen. Wir haben bereits über Bibliotheken in anderen Sprachen gesprochen, die viel komplexer sind. Es ist also aus praktischen und Performance-Gründen sehr empfehlenswert, diese Bibliotheken zu verwenden. Allerdings ist es wichtig, die Interna solcher Bibliotheken zu verstehen, um mehr Kontrolle über den gesamten Prozess zu haben. Im folgenden Test wird kein OOP verwendet, da es sich nur um einen Algorithmus handelt, der die zuvor besprochenen Gleichungen demonstriert, so dass OOP hier nicht wirklich notwendig ist. Bitte beachten Sie jedoch, dass es in realen Fällen viel praktischer ist, OOP zu verwenden, da es die Skalierbarkeit des Projekts gewährleistet.

1. Netzwerk-Initialisierung

Jedes Neuron hat einen Satz von Gewichten, die gepflegt werden müssen, ein Gewicht für jede Eingangsverbindung und ein zusätzliches Gewicht für den Bias.

Es wird empfohlen, die Netzwerkgewichte für kleine Zufallszahlen zu initialisieren. In diesem Fall werden Zufallszahlen im Bereich von 0 bis 1 verwendet. Zu diesem Zweck haben wir eine Funktion erstellt, die Zufallszahlen generiert.

double random(void)
  {
   return ((double)rand())/(double)SHORT_MAX;
  }

Nachfolgend finden Sie die Funktion initialize_network(), die Gewichte für unser neuronales Netzwerk erstellt.

// Forward propagate input to a network output
void forward_propagate(void)
  {
//calculate the outputs of the hidden neurons
//the hidden neurons are tanh
   int i = 0;
   for(i = 0; i<numHidden; i++)
     {
      hiddenVal[i] = 0.0;
      for(int j = 0; j<numInputs; j++)
        {
         hiddenVal[i] += (X[patNum][j] * weightsIH[j][i]);
        }
      hiddenVal[i] = tanh(hiddenVal[i]);
     }
//calculate the output of the network
//the output neuron is linear
   outPred = 0.0;
   for(i = 0; i<numHidden; i++)
     {
      outPred += hiddenVal[i] * weightsHO[i];
     }
//calculate the error
   errThisPat = outPred - y[patNum];
  }

3. Backpropagation

Der Backpropagation-Algorithmus wird nach der Art und Weise benannt, wie die Gewichte trainiert werden.

Es wird ein Fehler zwischen den erwarteten Ausgaben und den Ausgaben des Feedforward-Netzwerks berechnet. Diese Fehler werden dann durch das Netzwerk zurück propagiert, von der Ausgabeschicht zur versteckten Schicht, wobei die Verantwortung für den Fehler verschoben wird und die Gewichte aktualisiert werden, wenn sie eintreffen.

Die Mathematik hinter dem Backpropagation-Fehlermechanismus wurde oben erklärt.

//+------------------------------------------------------------------+
//|        Backpropagate error and change network weights            |
//+------------------------------------------------------------------+
void backward_propagate_error(void)
  {
//adjust the weights hidden-output
   for(int k = 0; k<numHidden; k++)
     {
      double weightChange = LR_HO * errThisPat * hiddenVal[k];
      weightsHO[k] -= weightChange;
      //regularisation on the output weights
      regularisationWeights(weightsHO[k]);
     }
// adjust the weights input-hidden
   for(int i = 0; i<numHidden; i++)
     {
      for(int k = 0; k<numInputs; k++)
        {
         double x = 1 - pow(hiddenVal[i],2);
         x = x * weightsHO[i] * errThisPat * LR_IH;
         x = x * X[patNum][k];
         double weightChange = x;
         weightsIH[k][i] -= weightChange;
        }
     }
  }

Die Methode regularizationWeights wurde nur für die Regularisierung von Gewichten im Bereich zwischen -5 und 5 erstellt.

//regularisation on the output weights
void regularisationWeights(double &weight)
  {
   weight<-5?weight=-5:weight>5?weight=5:weight=weight;
  }

4. Trainieren des Netzwerks

Das Netzwerk wird mithilfe des stochastischen Gradientenabstiegs trainiert.

Dies umfasst mehrere Iterationen, bei denen Daten in das Netz eingespeist werden, die Eingabe für jede Datenzeile vorwärts geleitet wird, Fehler zurück propagiert werden und die Gewichte aktualisiert werden.

//# Train a network for a fixed number of epochs
void train(void)
  {
   for(int j = 0; j <= numEpochs; j++)
     {
      for(int i = 0; i<numPatterns; i++)
        {
         //select a pattern at random
         patNum = rand()%numPatterns;
         //calculate the current network output
         //and error for this pattern
         forward_propagate();
         backward_propagate_error();
        }
      //display the overall network error
      //after each epoch
      calcOverallError();
      printf("epoch = %d RMS Error = %f",j,RMSerror);
     }
  }

5. Vorhersage

Das Erstellen von Vorhersagen mit einem trainierten neuronalen Netzwerk ist ziemlich einfach.

Wir haben bereits gesehen, wie das Eingabemuster propagiert wird, um die Ausgabe zu erhalten. Das ist alles, was wir tun müssen, um eine Vorhersage zu treffen. Wir können die Ausgabewerte direkt verwenden, und zwar als die Wahrscheinlichkeit, dass das Muster zu jeder Ausgabeklasse gehört.

// # Make a prediction with a network
void predict(void)
  {
   for(int i = 0; i<numPatterns; i++)
     {
      patNum = i;
      forward_propagate();
      printf("real = %d predict = %f",y[patNum],outPred);
     }
  }

Ein vollständiges Beispiel finden Sie in der unten angehängten Datei MLP_Script.mq5.

Schlussfolgerung

Wir haben die Berechnungen betrachtet, die bei der Entwicklung von Perceptron-Neuronen durchgeführt werden, sowie ein Netz von Perceptron-Neuronen, das "Multilayer perceptron, MLP" genannt wird. Wir haben auch gesehen, wie dieser Typ von neuronalen Netzen mit den Algorithmen Backpropagation und Gradientenabstieg trainiert wird.